Characterization of neuromagnetic brain rhythms over time scales of minutes using spatial independent component analysis

Abstract

Independent component analysis (ICA) of electroencephalographic (EEG) and magnetoencephalographic (MEG) data is usually performed over the temporal dimension: each channel is one row of the data matrix, and a linear transformation maximizing the independence of component time courses is sought. In functional magnetic resonance imaging (fMRI), by contrast, most studies use spatial ICA: each time point constitutes a row of the data matrix, and independence of the spatial patterns is maximized. Here, we show the utility of spatial ICA in characterizing oscillatory neuromagnetic signals. We project the sensor data into cortical space using a standard minimum‐norm estimate and apply a sparsifying transform to focus on oscillatory signals. The resulting method, spatial Fourier‐ICA, provides a concise summary of the spatiotemporal and spectral content of spontaneous neuromagnetic oscillations in cortical source space over time scales of minutes. Spatial Fourier‐ICA applied to resting‐state and naturalistic stimulation MEG data from nine healthy subjects revealed consistent components covering the early visual, somatosensory and motor cortices with spectral peaks at ∼10 and ∼20 Hz. The proposed method seems valuable for inferring functional connectivity, stimulus‐related modulation of rhythmic activity, and their commonalities across subjects from nonaveraged MEG data. Hum Brain Mapp, 2011. © 2011 Wiley‐Liss, Inc.

INTRODUCTION

The discovery of the brain's hemodynamic resting‐state networks, and their variability during health [Biswal et al.,1995; Gusnard and Raichle,2001], disease [Jafri et al.,2008; Sorg et al.,2007], naturalistic stimulation [Malinen et al.,2007] as well as naturalistic tasks [Bartels and Zeki,2005], have evoked growing interest in the reactivity and functional significance of spontaneous, nonaveraged electrophysiological brain rhythms. Just as data‐driven methods in the analysis of functional magnetic resonance imaging (fMRI) [Beckmann and Smith,2005; Calhoun et al.,2001; Malinen et al.,2007] have enabled detailed descriptions of and statistical inferences about the brain at rest, electrophysiological accounts of the brain's resting state [de Pasquale et al.,2010; Laufs,2008; Mantini et al.,2007] would benefit from a data‐driven characterization of the dynamics of brain rhythms over time scales of minutes.

Independent component analysis (ICA) is a data‐driven method. It can be applied to recordings of brain activity collected during rest or complex naturalistic stimulation even when the characteristic brain response is unknown and identical stimuli cannot be repeated. To any spatiotemporal dataset, ICA can be applied along the temporal or the spatial dimension to extract sources that are maximally independent temporally or spatially, respectively. The choice of applying temporal vs. spatial ICA depends on two key factors. First, the number of spatial and temporal data points available governs the accuracy of the ICA estimation. As a rule of thumb, the larger the number of observations compared with the number of variables, the more robust the estimation. Since fMRI datasets typically have significantly more spatial than temporal data points whereas the situation is the opposite in EEG/MEG datasets, spatial ICA is more robust for fMRI, and temporal ICA for EEG/MEG analysis. Second, the statistical properties of the data and the goal of the analysis matter, i.e., whether representative components of brain activity are more likely to be temporally or spatially independent. For instance, seed‐based correlation analysis of fMRI data suggests that spatially distinct brain networks can be temporally correlated. To capture spatially distinct, temporally correlated, brain regions as independent components, spatial ICA is more commonly applied in the analysis of fMRI data. By contrast, for EEG and MEG, ICA has been mainly applied to separate various artifacts from brain activity [Vigário et al.,1997]. Since the time courses of artifacts and brain activity are statistically independent in MEG and EEG, artifact rejection has so far been the typical application for temporal ICA.

We recently showed that (ordinary) temporal ICA is not optimally designed for finding physiologically interesting sources of rhythmic activity from the raw MEG time series owing to the high sparseness of artifactual signals in the time domain [Hyvärinen et al.,2010]. Therefore, applying a suitable sparsifying transform, such as the short‐time Fourier transform (STFT), before ICA, greatly improves the identification of oscillatory processes. STFTs of multichannel time series result in a 3‐way data structure with temporal (time points/windows), spatial (channels or source signals) and spectral (frequency bins) dimensions. The 3‐way data can be treated as a two‐dimensional matrix in several ways. Previously, we imposed sparseness on the time‐frequency dimension with no constraint on the spatial dimension [Hyvärinen et al.,2010].

In this work, we explored the feasibility of applying transformations that maximize spatial and spectral sparseness in cortical source space. First, we applied ICA along the spatial dimension to obtain independent and spatially sparse sources. In addition, we applied ICA to a suitable transformation of the 3‐way data in cortical source space. Many brain rhythms, although resulting from the interplay between thalamus and cortex, have rather focal cortical manifestations and narrow‐band spectral characteristics. However, they do not necessarily exhibit temporal sparseness. We therefore sought independent generative processes from the data by maximizing spatial and spectral sparseness of the components to be separated. Specifically, we performed linear, cortically‐constrained minimum‐norm estimation (MNE) to the neuromagnetic time series to obtain cortical current source time series. Then we computed STFTs of these time series and applied complex‐valued ICA along the spatiospectral dimension. We call this method spatial Fourier‐ICA (SFICA). In SFICA, each statistically independent component is characterized by its cortical distribution, its spectral profile, and its envelope dynamics over the entire duration of the recording. Using a realistically simulated MEG dataset, we compared SFICA applied on the 3‐way data in cortical source space with basic spatial ICA applied directly on the cortical projection of raw time series of MEG signals. Based on this comparison on simulated data, we consider SFICA more robust than basic spatial ICA for describing the dynamics of brain rhythms at the cortical level. We also applied SFICA to a real MEG dataset acquired while subjects were presented with naturalistic auditory, visual, and tactile stimuli and while they were resting with their eyes open.

MATERIALS AND METHODS

Subjects

Eleven healthy adults (6 females, 5 males; mean age 30 years, range 23–41 years) participated in the study after written informed consent. The recordings had prior approval by the Ethics Committee of the Helsinki and Uusimaa Hospital District (protocols No. 9‐49/2000 and No. 95/13/03/00/2008, granted to N. Forss and R. Hari). Data from nine of the eleven subjects were used in this analysis; data from two subjects had to be discarded due to improper delivery of auditory stimuli.

Experimental Setup

The stimuli used in the experiment were modified from those used in an earlier fMRI study [Malinen et al.,2007] and comprised auditory and visual stimuli in blocks of 6–33 s and tactile stimuli in blocks of 15 s. Auditory stimuli consisted of 0.1‐s tone beeps (at 250, 500, 1000, 2000, or 4000 Hz randomly varying in the same block; presentation rate 5 Hz) and of pre‐recorded speech (a male voice narrating the history of the local university, or the same male voice providing guitar fingering instructions). Visual blocks consisted of silent home‐made video clips of people with focus on faces or hands, and of buildings. Tactile stimuli were delivered at 4 Hz using pneumatic diaphragms attached to the index, middle, and ring fingers of both hands; the order was random but homologous left and right fingers were always stimulated simultaneously. The experiment consisted of three parts: (i) natstim: the subjects received an 8‐min sequence of auditory, visual and tactile blocks in a randomized order and concatenated without any rest periods in between, (ii) nat&rest: the subjects received a stimulus sequence similar to natstim but the stimulus blocks were interspersed with 15‐s rest blocks, so that the entire recording lasted for about 12 min, and (iii) restfix: the subjects were resting quietly for about 10 min with their eyes open, fixating on a crosshair on the screen.

Measurements

Measurements for each condition (natstim, restfix, and nat&rest) were repeated once, resulting in a total of 6 measurements per subject. In addition, after the experiment, a 2‐min recording was conducted without a subject in the scanner (emptyroom) to estimate noise statistics. MEG signals were acquired with a 306‐channel Elekta Neuromag® MEG system (Elekta Oy, Helsinki, Finland), filtered to 0–200 Hz and digitized at 600 Hz. Anatomical MRIs were obtained using a 3‐T General Electric Sigma MRI scanner (Milwaukee). During the MEG recording, four small head position indicator (HPI) coils, whose locations had been digitized with respect to anatomical landmarks, were continuously energized to track the subject's head position with respect to the MEG sensors. Vertical electro‐oculogram was monitored in all 11 subjects and electrocardiogram in 7.

Simulated Data

We simulated MEG data from a 306‐channel Elekta Neuromag® system, “sampled” at 150 Hz. Based on the anatomy of Subject #5, we placed three oscillating current dipoles perpendicular to the cortical surface in the left central sulcus (lCS; 19 Hz), the right central sulcus (rCS; 12 Hz) and the right parieto‐occipital sulcus (POS; 8 Hz). The duration of the simulated measurement was 2 min. Each oscillatory source was amplitude modulated by a different smoothed boxcar function (Fig. 2) with a SNR of 20 dB. Next, we applied a forward solution with a boundary‐element conductor model from Subject #5 (just as in the inverse modeling of the same subject's real MEG data; see Section Minimum‐Norm Inverse Solution) to simulate the 306‐channel MEG data. Finally, to make the simulations more realistic, we added real MEG data of the same duration measured from an empty room to yield an SNR of −10 dB. The simulated recording were filtered with signal space separation (SSS) exactly as the real data (see “Preprocessing” section).

Figure 2.

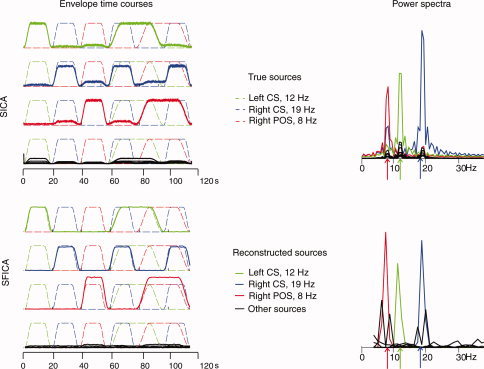
Comparison between SICA (top) and SFICA (bottom) applied to a simulated dataset. Left: Envelopes of the simulated (dashed lines) and estimated (solid lines) sources are given separately for SICA and SFICA. The colors green, blue and red refer to the 3 simulated sources viz. right parieto‐occipital sulcus, left central sulcus, and right central sulcus. Each panel has 4 time courses; the first three depict one correctly estimated sources (gauged by the correlation coefficients between the estimated and simulated sources; see text) overlaid on the true simulated sources. The last time course depicts all false sources. Correlation coefficients between each correctly estimated and the best matching true source are given. The largest correlation coefficient for all incorrectly estimated sources was less than 0.1. For SICA, the envelope of the time course is shown rather than the time course of the oscillatory source itself. Right: Power spectra of the estimated sources. The spectral peaks of the simulated sources (sinusoids) are represented by arrows.

Overview of Spatial Independent Component Analysis

In independent component analysis, one estimates a set of underlying sources represented by a matrix S, as well as their linear mixing matrix A, by observing only the linear mixture of the sources represented by matrix X. Thus, the model to be estimated is of the form

(1)

The ICA estimation algorithm maximizes the statistical independence of the sources (rows of S). Figure 1 describes the sequence of analysis steps we adopted for spatial ICA (“Spatial Independent Component Analysis” section) and spatial Fourier‐ICA (“Spatial Fourier‐ICA” section). For spatial ICA, X is the minimum‐norm current estimate of the observed MEG data, with each row representing a single time point and each column representing a location on the cortical surface (voxel). For spatial Fourier‐ICA, each row comprises the complex‐valued Fourier coefficients from each voxel at which the current estimate is computed, for each time window over which the short time Fourier transform is taken (see Fig. 1, right panel). First, we preprocessed the data to remove artifacts (see “Preprocessing” section); second, we computed the minimum‐norm inverse solution (see “Minimum‐norm inverse solution” section); third, for basic spatial ICA we projected the raw real‐valued MEG data into cortical source space and performed real‐valued ICA with real‐valued mixing coefficients; for spatial Fourier‐ICA we computed STFTs, projected the complex‐valued Fourier transforms into cortical source space, rearranged the 3‐way data and performed complex‐valued ICA with a complex‐valued mixing matrix.

Figure 1.

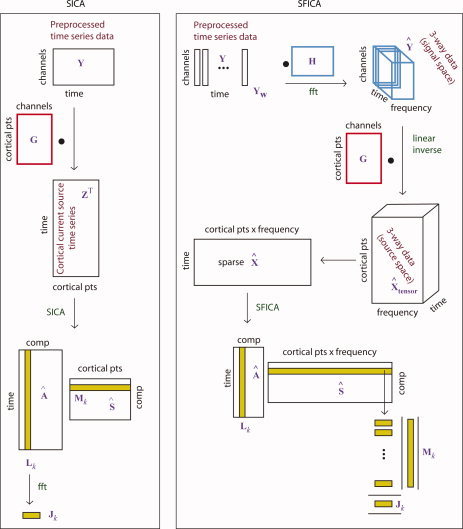
Illustration of the various steps in the spatial ICA (SICA) algorithm (left) contrasted with the spatial Fourier‐ICA (SFICA) algorithm (right). Left, SICA: the preprocessed time‐series data (Y) were projected into cortical space by a left multiplication with a linear inverse operator (G) to obtain the cortical current time series Z. Real‐valued ICA was done on Z ^T to obtain the spatial maps as the rows of S and the time courses as the columns of A. Right, SFICA: The preprocessed time‐series data (Y) was windowed (Y _w) and right‐multiplied by the FFT matrix to obtain channel‐wise short‐time Fourier transforms ( ). The STFTs were left‐multiplied by the precomputed linear inverse operator (G) to obtain 3‐way data in cortical space ( 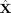). The complex valued 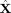was rearranged as time vs. cortical points x frequency (see text) and complex‐valued ICA was done on this matrix. The squared absolute values of the columns of A provide the envelopes of Fourier‐power and the rows of were decomposed into the spatial power map and power spectra (see text). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

We applied spatial ICA and spatial Fourier‐ICA to our data in the following way. First, to compare the two algorithms with known ground‐truth, we applied both algorithms to the simulated data and compared the extracted sources with the true underlying sources (those that were explicitly included in the simulation) in terms of their percentage variance explained. Second, as an additional comparison, we applied the two algorithms to a natstim recording from a single subject. Lastly, we applied spatial Fourier‐ICA to data from each subject separately, by first temporally concatenating the subject's 6 recordings. After estimating the ICs, we matched a few most salient components across subjects by visual inspection and averaged their time courses to obtain a group‐level representation; for details, see “Spatial Fourier‐ICA” section.

Preprocessing

Raw MEG data were manually examined for ‘bad channels’ that were omitted before Signal Space Separation (SSS) [Taulu and Kajola,2005] (“MaxFilter” version 2.0, Elekta Oy, Helsinki, Finland) was employed to suppress external interference and to correct for head movements. To additionally remove any DC‐jumps occasionally present in the data, we differentiated each time series, applied a median filter to reject large discontinuities and reintegrated the signals back. Finally, the data were downsampled by a factor of 4, i.e., to a sampling rate of 150 Hz.

Minimum‐Norm Inverse Solution

For each subject, the brain's cortical surface was reconstructed from an anatomical MRI using FreeSurfer (http://surfer.nmr.mgh.harvard.edu, Martinos Center for Biomedical Imaging, Massachusetts General Hospital). Dipolar current sources were estimated at cortically‐constrained discrete locations (source points) separated by 15 mm. Each source point contained one current dipole oriented along the normal to the cortical surface and two dipoles in the plane perpendicular to it. A single‐compartment boundary element model (BEM) was used to model the conductivity of the cranium. A forward solution was computed for each source point. Next, using the MNE Suite software package (http://www.nmr.mgh.harvard.edu/martinos/userInfo/data/sofMNE.php) an empirical noise covariance matrix was computed from the 2‐min emptyroom recordings, separately for each subject's data. To ensure that the noise statistics were adapted to the frequency range of interest (see “Spatial Independent Component Analysis” and “Spatial Fourier‐ICA” sections), we high‐pass filtered the emptyroom recordings at 4.7 Hz. A linear, depth‐weighted [Dale et al.,2000], minimum‐norm inverse operator G of dimensions N _s × N _c (where N _s is the number of source points and N _c is the number of channels; N _s >> N _c) was computed with a loose orientation constraint favoring source currents perpendicular to the local cortical surface by a factor of 2.5 with respect to the currents along the surface [Lin et al.,2006]. At each location, only sources normal to the cortical surface were retained for further analysis. Current estimates were subsequently noise‐normalized by the square‐root of the estimate of the noise variance at each source point [Dale et al.,2000].

Spatial Independent Component Analysis

We filtered the preprocessed MEG data Y to 4.7–75 Hz and projected them to cortical space with the linear inverse operator G, resulting in a source current matrix Z (N _s × N _t where N _t is the number of time points). The source current matrix was normalized by the square‐root of the estimated noise variance at each source point [Dale et al.,2000]. We applied principal component analysis (PCA) to reduce the dimensionality to 25, whitened the data, and then applied real‐valued FastICA with a real‐valued mixing matrix to Z ^T with symmetric estimation and tanh(·) nonlinearity.

Spatial Fourier‐ICA

Three‐way spectral estimation in cortical source space

For each preprocessed data matrix Y (N _c channels x N _t time points), we computed the Hamming‐windowed, complex‐valued short‐time Fourier transforms over N _w nonoverlapping windows, each one second in duration. The discrete Fourier transform of each time window Y _w may be interpreted as a matrix multiplication from the right. Let us denote this matrix by H. The Fourier transform is then obtained by

(2)

Here, Y _w is N _c channels x N _t/N _w time points and H is N _t/N _w time points x N _f frequency bins. The STFT across all time windows (N _c × N _w N _f) is then obtained by concatenating the matrices as

(3)

The STFT in cortical source space was then obtained by left‐multiplying the STFT by the linear inverse operator G, viz.

(4)

(N _s × N _w N _f) can be recognized as a 3‐way (N _s × N _w × N _f) tensor, written out as an ordinary (2‐way) matrix. As in the case of spatial ICA, we noise‐normalized the current estimates by the estimates of square‐root of the noise variance at each source point [Dale et al.,2000]. We then rearranged as a N _w × N _s N _f matrix 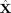, such that each row is a collection of Fourier coefficients of all source points concatenated together horizontally for its respective time window w. Our 15‐mm spacing between the source points resulted in N _s ∼3000, including both hemispheres. A 128‐point FFT used to compute the STFT resulted in 64 frequency bins for each 1‐s window. The 64 bins spanned a range of 0–75 Hz. Since the power is distributed very differently in the low and high frequency bands, whitening as a preprocessing step could potentially distort the current estimate. Hence, we separated the dataset into low (0–4.7 Hz) and high (4.7–75 Hz) frequencies and applied spatial Fourier‐ICA only on the high‐frequency data.

Application of complex‐valued ICA on concatenated data

For each subject's data, we temporally concatenated the rearranged STFT; 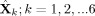runs (two runs each of natstim, restfix, and nat&rest) resulting in 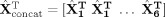. We considered temporal concatenation justified because the majority of brain networks are active during both task and rest [Smith et al., 2009]. Before concatenation, each run was normalized by the mean of the power across all time‐windows, Fourier bins and source points. We did not apply voxelwise normalizations applied in fMRI analysis because it would undo the effect of the noise‐normalization. From the restfix runs we discarded the first minute of the data to focus on a stable resting state. To , we applied complex‐valued ICA, treating each row as an observed signal assumed to be a linear mixture of unknown sources: we reduced the dimensionality of the data to 25 using complex‐valued eigenvalue decomposition, whitened the reduced data in the complex domain and then applied the complex‐valued FastICA algorithm [Bingham and Hyvärinen,2000]. Note that the whitening step here is a standard preprocessing step in ICA and should not be confused with the spatial whitening operator which is used to whiten the noise‐covariance matrix in the MNE inverse solution. The ICA estimation was symmetric, and the non‐Gaussianity measure was of the form 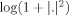. Thus, for each IC, we obtained one spatial map and power spectrum but six time‐courses (one corresponding to each run).

We arranged the simulated data similarly as the real MEG data, and analyzed the entire 2‐min time series as we did with for the real measurements. However, we reduced the temporal dimension to 10 (instead of 25, as we did for the real MEG data) with PCA and extracted 10 independent components. The reasoning for extracting 10 ICs only was as follows. First, the simulated 2‐min time‐series contained fewer observations than the 60‐min real data time‐series. Second, the simulated data contained only 3 sources and relatively unstructured noise from the emptyroom run.

Visualization of spatial Fourier‐ICs

Each complex‐valued IC resulted in a set of Fourier coefficients for each cortical source point. We visualized the spatial map M _k, of the IC with index k by taking the mean of the squared Fourier amplitude (squared magnitude of the complex Fourier coefficients) across all frequency bands. Since the distribution of mean‐squared Fourier amplitude over the whole brain is highly non‐Gaussian, we did not apply conventional z‐score‐based thresholding; instead, we applied a threshold to display for each component map only source points with the top 5% squared Fourier amplitude for the real MEG data and the top 1% for the simulated data. Since the source points represent only a sparse subset of the vertices in the triangular tessellation of the cortical surface, iterative smoothing was applied using the MNE suite with a smoothing factor of 15. Here the smoothing refers to the number of iteration steps during which each vertex of the image is assigned the average value of its nonzero neighbors. (http://www.nmr.mgh.harvard.edu/martinos/userInfo/data/sofMNE.php). To visualize the spectral profile J _k, we plotted the mean and standard deviation of the Fourier power spectrum over all source points exceeding the 95th percentile (real MEG data) or the 99th percentile (simulated data). The absolute values of the column of the estimated mixing matrix corresponding to the row of the estimated IC matrix give the time course of the Fourier amplitude envelope, L _k. We then plotted the time courses of each of the 6 runs.

Posthoc Characterization of Independent Components

We computed for each IC, from the envelope time course of the nat&rest conditions, a modulation score for each stimulus modality (auditory, visual, and tactile) as a percent signal change from a prestimulus baseline of ∼15 s in duration (i.e., the preceding rest block); a positive score indicates enhancement and a negative score suppression with respect to the baseline level. We visualized the modulation score averaged across the two nat&rest conditions.

Further, to classify the components as related to auditory, visual, or tactile stimuli, we formally tested the component time courses for stimulus‐related modulation treating each stimulus block as an independent observation. Specifically, for each component, we took the nat&rest time courses and computed the median signal for each stimulus block as well as the median signal for the rest block preceding the stimulus block. To bring the distributions closer to normal, we took the logarithms of these median values. We collected these values separately for each stimulus type viz. auditory, visual and tactile. We then compared the log(median(stimulus)) with the preceding log(median(rest)) using a two‐tailed t‐test with unequal variances at a confidence level of 0.95. Finally, we assigned to each component the label of “audition‐related,” “vision‐related,” or “touch‐related” depending on which stimulus type t‐test rejected the null hypothesis with the greatest confidence. If none of the comparisons were statistically significant, we labeled the component as “stimulus‐unrelated.”

Intersubject Consistency

Since we placed our source points very sparsely on the cortical surface (∼15‐mm separation between neighbors), we could not reliably apply any automatic spatial normalization method for matching the ICs (obtained from concatenated SFICA) across subjects.1 Instead, we manually selected one representative component from each of the eight subjects for the ∼10‐Hz occipital and the ∼20‐Hz rolandic rhythms, and averaged their time courses for the natstim and nat&rest runs.

RESULTS

Comparison of Spatial ICA and Spatial Fourier‐ICA

Simulation results

In the following, we consider the correctly estimated sources as those ICs whose time courses had sufficiently large (r > 0.8) correlation coefficient with those of the true simulated sources, and the rest of the ICs as false sources. Both SICA and SFICA were able to correctly estimate the three simulated sources as measured by the correlation coefficient between all pairs of estimated and true sources.

Figure 2 (above: SICA, below: SFICA) shows the envelope time courses and the power spectra for all three correctly reconstructed sources overlaid on the corresponding signals of the true sources. Dashed lines represent true simulated sources, whereas solid lines represent correctly estimated sources. The three different simulated sources—located in the left central sulcus, the right central sulcus, and the right parieto‐occipital sulcus—are represented in green, blue, and red. The time resolution of the envelope is 6.7 ms (150 Hz) for SICA and 1 s (1 Hz) for SFICA. The 7 false sources (in black) are also overlaid on the true underlying sources. The correlation coefficients between the false sources and the simulated sources were very low (r < 0.1). Note that the scaling of the reconstructed sources with respect to the true underlying sources is arbitrary, due to the scale ambiguity of ICA. However, the energies of the estimated time courses are not arbitrary with respect to each other.

Figure 2 illustrates several key differences between the methods. First, from the time courses, it is possible to see that with SFICA, the envelopes of the correctly estimated sources were much larger than those of the false sources; the same effect was observed to a lesser extent with spatial ICA. Second, the time courses of the SFICs are slightly lagged with respect to the true sources whereas the timecourses of the spatial ICs are not. This phenomenon is presumably related to the phase differences in the different sampling windows due to their arbitrary alignment with respect to the phase of the oscillatory signal. Third, for SFICA alone, some of the false sources have spatial patterns very similar—as estimated by the spatial correlation coefficient (spatial r > 0.9)—to one of the correctly estimated sources. As shown in Figure 2 (bottom right), the power spectra of these “shadow sources” exhibit peaks which are split around the peak of the true simulated source. Fortunately, such shadow sources have much smaller energies (i.e., norms of the columns of the mixing matrix), which enables us to reject them as artifactual sources. Spatial patterns of the true simulated and the estimated sources are not shown.

Figure 3 depicts the cumulative percentage of explained variance in reduced space by the components, arranged in descending order of percentage variance explained. The top 3 of the 10 ICs from SICA (which happen to be the correctly estimated sources) explained ∼96% of the variance, whereas the top 3 SFICA ICs explained 99% of the variance.

Figure 3.

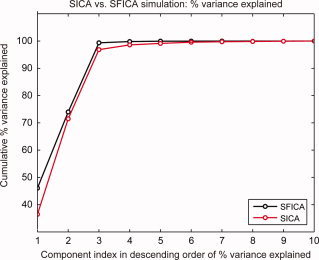
Comparison of percentage variance explained by components estimated from the simulated data. The figure shows the cumulative densities of percentage variance explained by the components ranked in descending order of percentage variance explained in reduced space for SICA (red) and SFICA (black). The first three components (correctly estimated sources) captured greater data variance in the case of SFICA than in the case of SICA.

Results from real MEG data

Since we do not know the ground truth for real MEG data, it is difficult to quantitatively compare the results from the two different algorithms. Both SICA and SFICA were able to detect the ∼10 Hz parieto‐occipital alpha rhythm. Figure 4 shows a representative 10‐Hz occipital component for both methods (SICA above, SFICA below). The spatial power map, the normalized Fourier power, and the envelope time course overlaid on the stimulus sequence, are shown for both components. SICA was unable to detect the ∼10/∼20 Hz rolandic mu rhythm components, while SFICA detected them. Further, SFICA detected components with a 1/f spectrum consistently, while they were not visible in the SICA results.

Figure 4.

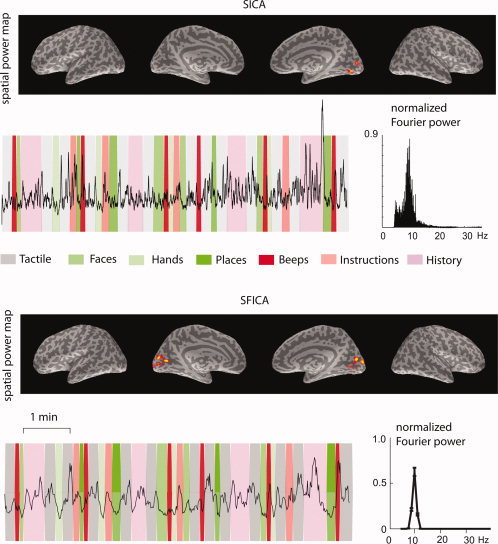
Comparison of SICA and SFICA in the analysis of real MEG data. A representative occipital ∼10‐Hz component for a single subject from each algorithm applied to a natstim sequence is shown. The spatial power maps, thresholded to show the surface points with top 5% strength, are overlaid on the inflated brain surfaces of that subject (from left to right: left hemisphere lateral, left hemisphere medial, right hemisphere medial, and right hemisphere lateral views). The time courses of the component are overlaid on the stimulus sequence, and the corresponding normalized power spectra are shown. The green bands represent visual stimuli, the red bands represent auditory stimuli, and the gray bands represent tactile stimuli.

Concatenated spatial Fourier‐ICA

SFICA was able to identify the parieto‐occipital alpha and the rolandic mu rhythms quite consistently in all subjects (based on visual inspection; see Figs. 6 and 7 below). In addition, the temporal‐lobe ∼8‐10 Hz rhythm was also detected in some subjects (see Fig. 8). Among the 25 components extracted from each individual subject's data, 2 ± 2 (median ± SD across 9 subjects) components were modulated by sounds, 9 ± 7 by videos, 3 ± 2 by tactile stimuli, and 11 ± 6 were stimulus‐unrelated. Table I shows the corresponding numbers of components for each subject.

Figure 6.

A recovered source from real MEG data of a single subject using SFICA (out of 25 recovered sources). This component was found across subjects and is representative of the ∼20‐Hz rolandic mu rhythm. The spatial power maps, thresholded to show the surface points with top 5% strength, are overlaid on the inflated brain surfaces of that subject (from left to right: left hemisphere lateral, left hemisphere medial, right hemisphere medial, and right hemisphere lateral views). The time courses show the z‐scores of the envelopes overlaid for the two runs each of natstim, restfix, and nat&rest. The dark line represents the mean across the two runs, and the lighter lines represent mean ± SEM. The background represents the stimulus sequence: green bands represent visual stimuli, red bands represent auditory stimuli, and gray bands represent tactile stimuli. The natstim and nat&rest conditions show a clear suppression to tactile stimuli. The component has relatively high scores of spatial sparseness, spectral sparseness and percent variance explained.

Figure 7.

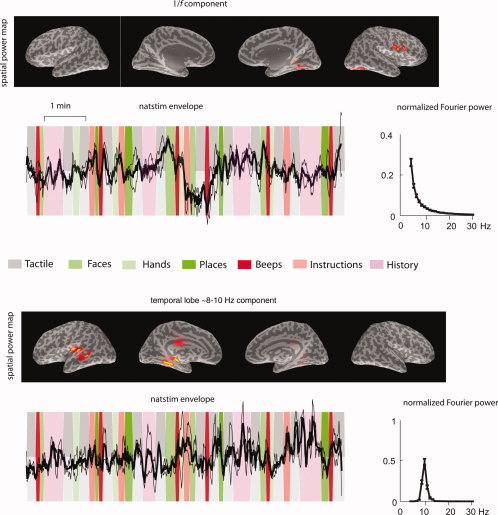
Above: A recovered source from real MEG data of a single subject using SFICA (out of 25 recovered sources). This component is representative of sources with a 1/f power spectrum. It has spatial maxima in the right Sylvian fissure and deep in the right mesial parieto‐occipital sulcus. The time courses show the z‐scores of the envelopes overlaid for the two runs each of natstim. Below: A recovered source from real MEG data of a single subject using SFICA (out of 25 recovered sources). This component is representative of sources with a ∼8‐Hz temporal‐lobe rhythm. It has spatial maxima in the right auditory cortex and the right superior temporal sulcus. The time courses show the z‐scores of the envelopes overlaid for the two runs each of natstim. For both components, the spatial power maps, thresholded to show the surface points with top 5% strength, are overlaid on the inflated brain surfaces of that subject (from left to right: left hemisphere lateral, left hemisphere medial, right hemisphere medial, and right hemisphere lateral views). The dark line represents the mean across the two runs, and the lighter lines represent mean ± SEM. The background represents the stimulus sequence: green bands represent visual stimuli, red bands represent auditory stimuli, and gray bands represent tactile stimuli.

Figure 8.

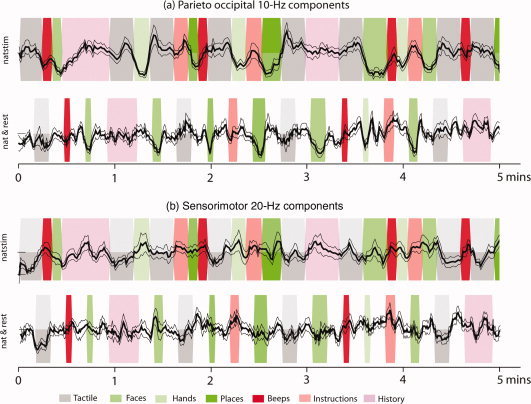
Above: Envelopes of ∼10‐Hz occipital components averaged across eight subjects; the components (one per subject) were selected manually by visual inspection for each subject. Clear suppression is observed during visual stimulation. Below: Envelopes of selected ∼20‐Hz rolandic components averaged across 8 subjects. Clear suppression is observed during tactile stimulation. The dark line represents the mean across the two runs, and the lighter lines represent mean ± SEM. The background represents the stimulus sequence: green bands represent visual stimuli, red bands represent auditory stimuli, and gray bands represent tactile stimuli.

Table I.

Number of SFICs whose time courses were strongly modulated by the stimuli (auditory, visual, or tactile) or were not significantly modulated (stimulus‐unrelated)

	Auditory	Visual	Tactile	Stimulus‐ unrelated
Subject01	2	4	2	17
Subject02	1	20	0	4
Subject03	0	15	1	9
Subject04	0	12	5	8
Subject05	3	4	4	14
Subject06	4	16	2	3
Subject07	0	2	4	19
Subject08	2	4	3	16
Subject09	1	10	0	14
Median ± SD	1 ± 1	10 ± 6	2 ± 2	14 ± 6

Numbers are given for each subject; the last row gives the median ± SD across all nine subjects. The stimulus‐related modulation was judged by a two‐sided t‐test with unequal variances comparing the block‐wise logarithm of the median signal with the corresponding logarithm of the median signal of its preceding rest block.

The component power spectra were narrowband in general, with the exception of those with a 1/f shape. Overall, 7 ± 2 components had no spectral peaks above 5 Hz (presumably 1/f components), 2 ± 1 components had peaks in the 5–8 Hz range, 13 ± 4 in the 8–15 Hz range, 3 ± 3 in the 15–30 Hz range, and none above 30 Hz. Table II gives the corresponding numbers for each subject.

Table II.

The number of SFICs across different frequency bands (as determined by peak power of the component power spectrum) for each subject

	∼1/f	5–8 Hz	8–15 Hz	15–30 Hz	> 30 Hz
Subject01	6	2	12	5	0
Subject02	6	3	14	2	0
Subject03	7	1	17	0	0
Subject04	5	0	16	4	0
Subject05	6	3	5	11	0
Subject06	6	4	14	1	0
Subject07	13	1	9	2	0
Subject08	8	4	12	1	0
Subject09	5	0	20	0	0
Mean ± SD	7 ± 2	2 ± 2	13 ± 4	3 ± 3	0

Figures 5 and 6 show representative components, capturing the ∼10‐Hz occipital alpha and the ∼20‐Hz rolandic mu rhythm, respectively. The spectra in the range 5–30 Hz, the z‐score of the time courses averaged across the two runs (mean ± SEM), and the bar graph representing the modulation score (mean ± SEM) are also shown. The alpha rhythm is clearly suppressed during visual stimulation. The mu rhythm appears to be suppressed to tactile stimuli, but in addition, enhanced during visual stimulation.

Figure 5.

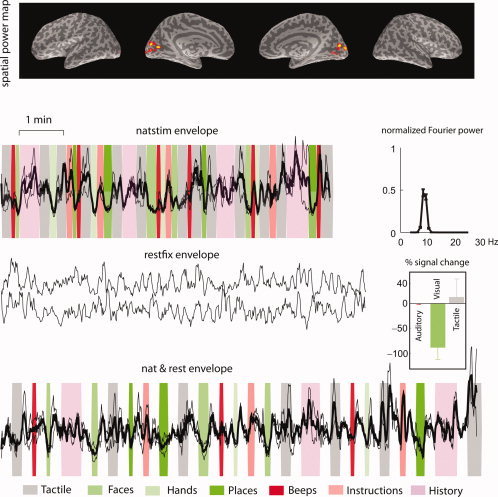
A recovered source from real MEG data of a single subject using concatenated SFICA (out of 25 recovered sources). This component was found across subjects and is representative of the ∼10‐Hz parieto‐occipital alpha rhythm. The spatial power maps, thresholded to show the surface points with top 5% strength, are overlaid on the inflated brain surfaces of that subject (from left to right: left hemisphere lateral, left hemisphere medial, right hemisphere medial, and right hemisphere lateral views). The time courses show the z‐scores of the envelopes overlaid for the two runs each of natstim, restfix, and nat&rest. The dark line represents the mean across the two runs, and the lighter lines represent mean ± SEM. The background represents the stimulus sequence: green bands represent visual stimuli, red bands represent auditory stimuli, and gray bands represent tactile stimuli. The natstim and nat&rest conditions show a clear suppression to all three categories of visual stimuli (faces, hands and places). The component has relatively high scores of spatial sparseness, spectral sparseness and percent variance explained.

Figure 7 shows two representative components from a single subject: a 1/f power spectrum component (top), and an auditory temporal‐lobe rhythm component (bottom). Only time courses for the natstim sequence are shown. The spatial maps of the 1/f components do not conform to any consistent spatial pattern; some of the maps highlight early sensory cortices (such as in this component), but some others also cluster in the premotor cortices or prefrontal cortices. The temporal‐lobe component has a clear spectral peak at ∼8‐10 Hz, but the time course does not show any consistent modulation to auditory stimulation.

Figure 8 shows the mean ± SEM time courses of representative alpha and mu components for the natstim and nat&rest conditions, for a selected duration of time (∼5 minutes), averaged across eight subjects.

DISCUSSION

Spatial ICA Vs. Spatial Fourier‐ICA

We showed that both SICA and SFICA were able to identify the true underlying sources from simulated MEG data. However, SFICA was able to separate the true and false sources more effectively, as measured by the percentage of data variance captured by the estimated true sources. When compared with SFICA, SICA generally allows a higher temporal resolution for the estimated sources (as high as the time resolution of the raw data) and it is more parsimonious (in terms of number of parameters estimated per observation) owing to its real‐valued mixing model. However, SFICA explicitly utilizes frequency information during source separation and is thus biased to detect oscillatory sources. This difference is probably the main reason for SFICA's superior performance when compared with SICA. Furthermore, given the vastly smaller number of variables (by a factor of almost 25), the cost of computing the principal components is also much lower for SFICA than for SICA. Given this computational advantage, the theoretical disposition of SFICA towards sparse oscillatory sources, as well as the results of the comparison on simulated data (Section Simulation results), SFICA seemed to be a more robust and physiologically valid method than SICA, for characterization of oscillatory dynamics over time scales of minutes.

SFICA Results From Real MEG Data

The method was consistently able to identify stimulus‐related oscillatory MEG components in several subjects; a majority of these likely represented classical alpha and mu rhythms [Hari and Salmelin,1997]. In some but not all subjects, the method identified temporal‐lobe ∼8‐10 Hz rhythms that according to their site of origin would represent the rarely reported auditory‐cortex tau rhythm [Lehtelä et al.,1997; Tiihonen et al.,1991]. However, we did not detect statistically significant reactivity of these components to sounds, and their morphology varied widely across subjects.

In more than half of the subjects, the majority of the components were not modulated by any of the stimulus categories. It is difficult to say which of these components were artifactual and which of them were of real neural origin. Many of the stimulus‐unrelated components displayed a 1/f spectrum and could have arisen from artifacts outside the head; however we did not observe any 1/f components in the simulated dataset that included noise from a real measurement done in the absence of a subject.

Recently, de Pasquale et al. [2010] used stationary and nonstationary seed‐based correlation metrics to characterize resting‐state networks in MEG data. In the stationary case, most networks were unilateral whereas bilateral networks were also found in the nonstationary case. Similarly, most of our components were lateralized to one hemisphere, with the exception of some occipital 10‐Hz components and some components with spatial maxima in the medial surfaces. This dominance of unilateral networks seems to contrast with many fMRI results where a single component often reveals bilateral networks, such as the sensorimotor or default‐mode networks. A possible explanation is that the high temporal resolution of MEG allows us to observe the fine differences in the dynamics of regions [functionally] coupled across the hemispheres whereas the sluggishness of the BOLD response may render these differences invisible to fMRI.

When compared with the spectral profile of components obtained using temporal Fourier‐ICA [Hyvärinen et al.,2010], the SFICA components seem to be more narrowband (i.e., spectrally sparse). This improved spectral resolution could be attributed to the selection of the top 5% active voxels for visualization.

Finally, it must be noted that the naturalistic stimuli employed in acquiring this dataset comprised unimodal stimulus blocks with rest‐blocks in‐between, which may have enhanced the separability of stimulus‐related modulations of rhythmic activity in our analysis.

Open Questions

Some questions regarding the ingredients of the algorithm and its applicability remain. Firstly, the ICA signal model (noisy vs. noiseless mixing) has implications on the correct thresholding method of the component spatial maps before visualization. Beckmann and Smith (2004) used a noisy mixture for their signal model and derived a Gaussian‐Gamma mixture model to represent the distribution of the spatial IC. The Gaussian distribution captures the noise while the Gamma distribution captures the signal. This has been standardized in their MELODIC software package. Calhoun et al. (2001) used the more standard noiseless ICA signal model and applied a z‐score‐based thresholding to visualize the spatial IC. In the case of MEG data, neither method was readily applicable. First, the inverse problem has its own assumptions about the statistical distribution of source currents (i.e., the priors implicit in the minimum‐norm source covariance by default), calling into question the validity of the Gaussian‐Gamma mixture model. Secondly, the distributions of the spatial ICs are far from Gaussian, making a z‐score‐based threshold invalid. Hence, for this analysis, we applied a percentile‐based threshold. More work is required to correctly characterize the statistical distribution of the component spatial maps and to enable more principled thresholding.

Second, the commonly applied normalization before whitening (voxelwise temporal variance normalization, voxelwise intensity normalization, global mean removal etc.) has important but (as yet) unclear implications on ICA. Since the dSPM inversion [Dale et al.,2000] already does a voxelwise normalization by noise variance, we did not employ any further normalization except for a global scaling of each recording by the mean current estimate.

Third, it is not completely clear whether we should do spatial ICA in the sensor space or the cortical space. Three considerations point towards an advantage of performing ICA in the cortical space. First, maximization of spatial sparseness is physiologically more meaningful in the cortical space; it is less meaningful in the sensor space because many sensors see signals from the same sources. Second, the anatomically informed cortical projection greatly increases the number of observations in the ICA model and thus improves its estimation accuracy. Third, it is more straightforward to combine the information from the magnetometer and gradiometer time‐series in cortical space. By contrast, in our earlier work on temporal ICA in sensor space [Hyvärinen et al.,2010], we discarded the magnetometer channels. Hence, for this article, we chose to analyze the data in the cortical space. Fourth, given the sequence of the processing stages, a comment on the inter‐relatedness of the dimensionality reduction offered by SSS, MNE, and PCA is clearly warranted. SSS reduces the number of degrees of freedom in the data in a data‐independent way to the number of spherical harmonic functions required to model the magnetic fields generated from within the skull. The dimensionality reduction offered by MNE is not as explicit, and depends on the regularization coefficient in the inverse projection. The last PCA step is not entirely redundant either because it uses spectral information in addition to MNE and SSS, which use only spatial information. Further, the last PCA is very useful for ICA because it explicitly reduces the number of data variables, completely removing dimensions of very small variance.

Finally, there is no consensus for inference from independent components at the group level. Various methods have been studied in the fMRI literature. The most widely applied are the temporally concatenated GIFT [Calhoun et al.,2001] and tensor PICA [Beckmann et al.,2005]. Broadly speaking, these methods estimate the independent components from group‐level data, followed by reconstruction of the individual‐level components (GIFT, tensor PICA). On the other hand, there is a school of thought which recommends estimation of individual‐level components followed by post‐hoc matching [Esposito et al.,2005; Langers,2010]. In the case of MEG data, the poorer spatial resolution and the errors in the individual co‐registrations between MEG sensors and anatomical MR images could result in non‐negligible errors when concatenating data across subjects. For this reason alone, it may be more reasonable to employ a post‐hoc matching method.

To conclude, the main value of spatial Fourier‐ICA is to enable inference about oscillatory activity under different conditions, such as resting state and natural stimulation, and across different subject groups, such as patients and healthy volunteers. By interrogating the component time courses (Fourier power) one can study e.g., functional connectivity between different components of the same subject, modulation of oscillatory activity by natural stimuli, and repeatability of activity time courses spanning several minutes, within and across subjects. In future work, we intend to pursue some of the open questions outlined earlier.