Abstract
Objectives: The purpose of this study was to test the hypothesis that the highest temporal correlations between 3‐dimensional EEG current source density corresponds to anatomical Modules of high synaptic connectivity. Methods: Eyes closed and eyes open EEG was recorded from 19 scalp locations with a linked ears reference from 71 subjects age 13–42 years. LORETA was computed from 1 to 30 Hz in 2,394 cortical gray matter voxels that were grouped into six anatomical Modules corresponding to the ROIs in the Hagmann et al.'s [2008] diffusion spectral imaging (DSI) study. All possible cross‐correlations between voxels within a DSI Module were compared with the correlations between Modules. Results: The Hagmann et al. [ 2008] Module correlation structure was replicated in the correlation structure of EEG three‐dimensional current source density. Conclusions: EEG Temporal correlation between brain regions is related to synaptic density as measured by diffusion spectral imaging. Hum Brain Mapp, 2011. © 2011 Wiley‐Liss, Inc.
Keywords: EEG, LORETA, DSI modules, synaptic connections
INTRODUCTION
Convergent evidence from different imaging modalities has demonstrated that the human brain is a network organized by “Nodes” with linkages and clustering of connections defined as “Modules” based on the density of synaptic connections and constituting “Functional Modules” [Achard et al., 2006; Scannell et al., 1999; Sporns et al., 2004]. Graph theory is commonly used to quantify the structural topology of the human brain using different imaging methods and achieving similar results from Diffusion Spectral Imaging (DSI), functional MRI (fMRI) and quantitative EEG/MEG [Achard and Bullmore, 2006; Achard et al., 2006; Bullmore and Sporns, 2009; Hagmann et al., 2008; Lee et al., 2008; Stam et al., 2007, 2009; Teipel et al., 2008). Recently, Hagmann et al. [ 2008] used DSI and tractography to trace the cortical white matter connections of the human cerebral cortex between 66 cortical regions with clear anatomical landmarks, using the same gyri and sulci as described by von Brodmann in 1909 [Brodmann, 1909]. From the 66 cortical regions, 998 subregions of interest (ROIs) were calculated using a connection matrix of inter‐regional cortical connectivity [see Table VI and S5 in the methods section of Hagmann et al., 2008]. Network spectral analyses of nodes and edges of the 998 ROIs were grouped into six anatomical Modules with maximum centrality defined as high within density connectivity [Hagmann et al., 2008]. However, little is known about the Electrical Neuroimaging correlates of the connection modules of the brain as measured by Diffusion Spectral Imaging. In the present paper we explore these correlations by using ‘Low Resolution Electromagnetic Tomography’ (LORETA) and limiting our analyses to the six major anatomical Modules as shown in Figure 6A in Hagmann et al. [ 2008]. The six main DSI anatomical Modules included but are not exclusive of the posterior cingulate, the bilateral precuneus, the bilateral paracentral lobule, the unilateral cuneus, the bilateral isthmus of the cingulate gyrus, and the bilateral superior temporal sulcus [see Fig. 1 of Hagmann et al., 2008].
Figure 6.
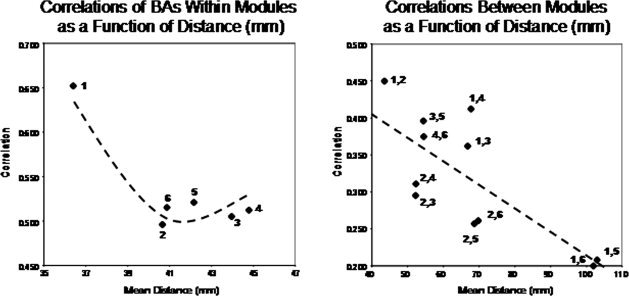
(A) are the within Module temporal source correlations and (B) between Module temporal source correlations using LORETA. The y‐axis is correlation and the x‐axis is the Euclidean distance in mm from a given reference Brodmann area within a Module in (A) and the Euclidean distance in mm between Modules in (B). A nonlinear quadratic function best describes the within Module correlations as a function of distance while the between Module correlations are linear as a function of distance.
Figure 1.
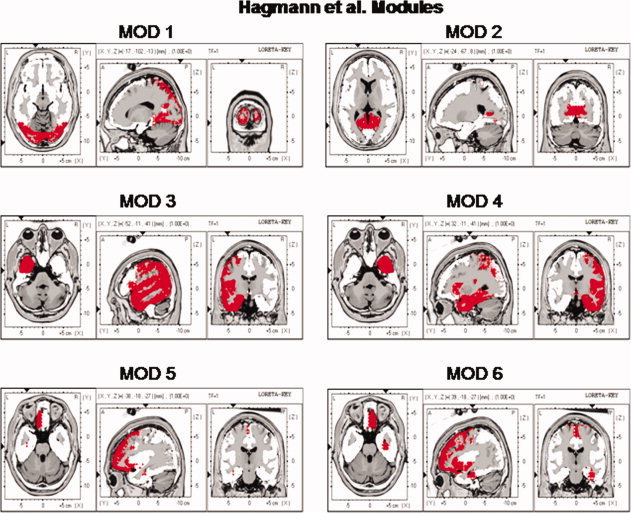
The locations of the six Hagmann et al. [2008] Modules as represented by the Key Institute LORETA voxels [Lancaster et al., 2000; Pascual‐Marqui, 2004]. As per Hagmann et al. [ 2008] Modules 3 and 4 are the same but from different hemispheres. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Neuroelectrical imaging methods such as LORETA share the ability to link synchronous neural activity registered to a common and standardized anatomical Talairach atlas [Lancaster et al., 2000; Michel et al., 2009; Towle et al., 1993]. LORETA is a maximally smooth inverse solution of the sources of the EEG by using a three‐dimensional Laplacian operator to weight the Lead Field to simultaneous distributed sources [Pascual‐Marqui, 1999; Pascual‐Marqui et al., 1994; Malmivuo and Plonsey, 1995]. Because local synchrony of neurons is necessary to produce a recordable scalp EEG, another constraint on the Lead Field is that the density of synapses in clusters of pyramidal neurons is positively related to current source density in a given volume of the brain. Cross‐correlation of LORETA spectral amplitudes over wide brain regions is a measure of the spatial‐temporal synchrony of neurons located in different regions of interest (ROIs) and in different Brodmann areas [Hoechstetter et al., 2004; Pascual‐Marqui et al., 2001; Teipel et al., 2008; Thatcher, 1995; Thatcher et al., 1994, 2007].
Several studies have used coherence and correlations to investigate the normalized covariance of electrical activity in different Brodmann areas [Hoechstetter et al., 2004; Pascual‐Marqui et al., 2001; Thatcher et al., 1994]. Thatcher et al. [ 1994] recorded EEG during voluntary finger movements and derived three dipoles in the sensory‐motor cortical regions that accounted for approximately 97% of the variance of the surface EEG and were validated using PET and MRI. A pseudo‐inverse procedure was then used to derive three different time series from each of the three dipoles, and coherence and phase delays were computed between the various combinations of dipole time series. Stable but rapid changes in coherence between sources were shown to be time locked to voluntary motor movements in the supplemental motor cortex and the contra‐lateral motor cortex and long phase delays eliminated volume conduction. Hoechstetter et al. [ 2004] used a multiple dipole source solution for scalp EEG electrical potentials and then used coherence to compute the correlation between the three‐dimensional current sources and demonstrated changes in the correlation between current sources related to different tasks. Pascual‐Marqui et al. [ 2001] used low resolution electromagnetic tomography (LORETA) to compute current sources and then used a correlation coefficient to explore differences in source correlations between a normal control group and a group of schizophrenic patients. Thatcher et al. [ 2007] used essentially the same methods as published by Pascual‐Marqui et al. [ 2001], i.e., LORETA source correlations and demonstrated spatial undulations and regular spacing of correlations as a function of distance. Because of the spatial heterogeneity of correlations volume conduction could not explain the findings in any of these studies.
All of these studies revealed interesting and reproducible relations between current sources and network connectivity that is independent of volume conduction and provide a deeper understanding of the surface EEG dynamics. For example, in the Thatcher et al. [2007] study regions that had the highest neuron packing density exhibited the highest nearest neighbor source correlations and a model of a “U” shaped cortico‐cortical fiber system fit the spatial patters of source correlations [Braitenberg, 1994; Braitenberg and Schüz, 1998].
There are over 795 peer reviewed studies using LORETA including cross‐validations with PET, fMRI and SPECT [Thatcher, 2010] and a listing at: http://www.uzh.ch/keyinst/NewLORETA/QuoteLORETA/PapersThatQuoteLORETA05.htm). Given the large scientific literature in support of accurate EEG source localization, it is reasonable to hypothesize that there is a linkage between DSI and LORETA because diffusion weighted images reflect anatomical connectivity (axons) and anatomical connectivity is the basis for effective connectivity, (one region influencing another), therefore, it follows that DSI should predict synchrony between distant brain regions as measured by LORETA. In other words, one would expect a relationship between the density of synaptic connections as measured by DSI Modules and EEG currents generated within and between DSI defined Modules. Therefore this paper is a test of the null‐hypothesis that LORETA current sources exhibit a random clustering and random ranking of correlations that are not like the anatomical clusters or Modules measured by DSI in the Hagmann et al. [ 2008] study.
METHODS
Subjects
A total of 71 right handed normal adults ranging in age from 13 to 42 (male = 41, mean = 16.13, SD = 4.63, range = 13.01–41.51) were included in this study. The subjects in the study were selected based on no history of neurological disorders such as epilepsy, head injuries and reported normal development and successful school performance. None of the subjects had taken any medications prior to EEG recording. Only subjects with both a eyes open and eyes closed EEG are included in this study and therefore the subjects in this study are a subset of the 97 subjects from the previous LORETA source correlation analyses [Thatcher el al, 2007].
EEG Recording
The EEG was recorded from 19 scalp locations based on the International 10/20 System of electrode placement, using linked ears as a reference. Each EEG record was plotted and visually examined and then edited to remove artifact. The amplifier bandwidths were nominally 0.5–30 Hz, the outputs being 3 db down at these frequencies, and the sample rate was 128 Hz. Split‐half and test–retest reliability measures were conducted on the edited EEG segments and only records with >95% test–retest reliability were entered into the spectral analyses where the first half of the edited EEG selections were used to predict the 2nd half of the selections [Ferguson, 1973]. EEG was acquired in the eyes closed conditions and record lengths varied from 58.6 s to 120 s.
Cross‐Spectral Analysis and LORETA Computation
The edited EEG samples were divided into successive 2‐s epochs of 256 sample points of the edited EEG and then a FFT cross‐spectral analysis with a cosine taper window was used according to standard procedures for Low Resolution Electromagnetic Tomography (LORETA) frequency analyses (Gomez and Thatcher, 2001; Pascual‐Margui, 1999; Pascual‐Marqui et al., 1994; 2001; Thatcher et al., 2005a, 2005b]. LORETA is a distributed EEG inverse solution where the currents at three‐dimensional gray matter voxels J are a linear combination of the signal S recorded at a scalp electrode:
Where T is a minimum norm three‐dimensional matrix of 2,394 gray matter voxels with x, y, and z coordinates in a generalized inverse that weights the solution to sources that are synchronous in local volumes or regions using the three‐dimensional Laplacian Operator [Pasqual‐Marqui, 1999; Pasqual‐Marqui et al., 1994]. The T matrix is mathematically defined as:
Where B is the discrete Laplacian Operator and W is a weighting matrix (inv indicates inverse) and pinv(X) is the Moore‐Penrouse pseudoinverse of X [Menke, 1984].
The Talairach Atlas coordinates of the Montreal Neurological Institute's MRI average of 305 brains [Lancaster et al., 2000; Pascual‐Marqui, 1999] and the linkage to standard anatomical 7 mm × 7 mm × 7 mm voxels each with a distinct Talairach Atlas Coordinate. Groups of voxels are also defined by the clear anatomical landmarks established by von Brodmann in 1909 and referred to as Brodmann areas. Importantly, Brodmann areas were largely defined by the same clear anatomical landmarks as used by Hagmann et al. [ 2008]. The resultant current source vector at each voxel was computed as the square root of the sum of the squares for the x, y, and z source moments for each 0.5 Hz frequency band. To reduce the number of variables, adjacent frequency 0.5 Hz bins were averaged to produce nine different frequency bands: delta (1–4 Hz); theta (4–7 Hz); alpha1 (8–10 Hz); alpha2 (10–12 Hz); beta1 (12–15 Hz); beta2 (15–18 Hz); beta3 (18–25 Hz), and hi‐beta (25–30 Hz) for each of the 2,394 gray matter voxels.
Groupings of ROI According to DSI Modules
The anatomical names and Brodmann areas that correspond to each of the 2,394 gray matter voxels in Talairach Atlas coordinates was provided by Lancaster et al. [2000] and Pascual‐Marqui [ 1999, 2004]. The first best match to a given ROI was used for both Brodmann area values and anatomical names. However, the Hagmann et al. [ 2008] Modules are not organized according to Brodmann areas and have similar but not exactly the same anatomical names as are commonly used in LORETA studies. Nevertheless, there was high overlap in most of the anatomical labels and anatomical regions in DSI and EEG neuroimaging using LORETA. Table I shows the groupings of LORETA ROIs that correspond to each of the six DSI Modules [Hagmann et al., 2008].
Table I.
The Modules listed in Figure 6 of the Hagmann et al [2008] DSI study and the corresponding ROIs with Talairach atlas coordinates used in LORETA
| Hagmann's modules | Loreta anatomical regions | x‐tal | y‐tal | z‐tal |
|---|---|---|---|---|
| 1 | L_Cuneus | −9 | −82 | 17 |
| L_Inferior Occipital Gyrus | −36 | −81 | −5 | |
| L_Lingual Gyrus | −11 | −73 | −1 | |
| L_Middle Occipital Gyrus | −38 | −81 | 7 | |
| L_Precuneus | −14 | −64 | 43 | |
| L_Superior Occipital Gyrus | −36 | −82 | 28 | |
| L_Superior Parietal Lobule | −25 | −59 | 55 | |
| R_Cuneus | 9 | −77 | 19 | |
| R_Inferior Occipital Gyrus | 36 | −84 | −5 | |
| R_Lingual Gyrus | 12 | −70 | −1 | |
| R_Middle Occipital Gyrus | 40 | −78 | 9 | |
| R_Precuneus | 13 | −63 | 42 | |
| R_Superior Occipital Gyrus | 36 | −82 | 28 | |
| R_Superior Parietal Lobule | 27 | −60 | 54 | |
| 2 | L_Cingulate Gyrus | −5 | −13 | 35 |
| L_Paracentral Lobule | −5 | −32 | 55 | |
| L_Posterior Cingulate | −9 | −57 | 15 | |
| R_Cingulate Gyrus | 6 | −11 | 35 | |
| R_Paracentral Lobule | 6 | −31 | 53 | |
| R_Posterior Cingulate | 10 | −55 | 15 | |
| 3 | L_Angular Gyrus | −47 | −65 | 32 |
| L_Fusiform Gyrus | −43 | −43 | −15 | |
| L_Inferior Parietal Lobule | −48 | −42 | 42 | |
| L_Inferior Temporal Gyrus | −52 | −27 | −20 | |
| L_Insula | −39 | −8 | 7 | |
| L_Middle Temporal Gyrus | −54 | −35 | −2 | |
| L_Parahippocampal Gyrus | −25 | −24 | −12 | |
| L_Postcentral Gyrus | −49 | −25 | 38 | |
| L_Precentral Gyrus | −50 | −2 | 30 | |
| L_Subcallosal Gyrus | −10 | 8 | −11 | |
| L_Superior Temporal Gyrus | −50 | −18 | 1 | |
| L_Supramarginal Gyrus | −57 | −47 | 30 | |
| L_Transverse Temporal Gyrus | −55 | −19 | 13 | |
| L_Uncus | −27 | −6 | −28 | |
| 4 | R_Angular Gyrus | 46 | −65 | 34 |
| R_Fusiform Gyrus | 45 | −41 | −16 | |
| R_Inferior Parietal Lobule | 50 | −42 | 40 | |
| R_Inferior Temporal Gyrus | 53 | −28 | −19 | |
| R_Insula | 40 | −6 | 9 | |
| R_Middle Temporal Gyrus | 53 | −33 | −3 | |
| R_Parahippocampal Gyrus | 25 | −26 | −10 | |
| R_Postcentral Gyrus | 48 | −26 | 41 | |
| R_Precentral Gyrus | 52 | −1 | 27 | |
| R_Subcallosal Gyrus | 11 | 8 | −11 | |
| R_Superior Temporal Gyrus | 51 | −17 | 1 | |
| R_Supramarginal Gyrus | 58 | −48 | 30 | |
| R_Transverse Temporal Gyrus | 61 | −12 | 14 | |
| R_Uncus | 26 | −4 | −28 | |
| 5 | L_Anterior Cingulate | −5 | 29 | 8 |
| L_Extra‐Nuclear | −36 | 10 | −6 | |
| L_Inferior Frontal Gyrus | −40 | 24 | −1 | |
| L_Medial Frontal Gyrus | −6 | 31 | 19 | |
| L_Middle Frontal Gyrus | −35 | 31 | 24 | |
| L_Orbital Gyrus | −7 | 50 | −21 | |
| L_Rectal Gyrus | −7 | 30 | −22 | |
| L_Sub‐Gyral | −35 | −23 | 0 | |
| L_Superior Frontal Gyrus | −17 | 38 | 31 | |
| 6 | R_Anterior Cingulate | 6 | 30 | 7 |
| R_Extra‐Nuclear | 37 | 12 | −6 | |
| R_Inferior Frontal Gyrus | 42 | 24 | 1 | |
| R_Medial Frontal Gyrus | 6 | 33 | 16 | |
| R_Middle Frontal Gyrus | 36 | 30 | 26 | |
| R_Orbital Gyrus | 8 | 43 | −22 | |
| R_Rectal Gyrus | 7 | 32 | −23 | |
| R_Sub‐Gyral | 36 | −21 | −4 | |
| R_Superior Frontal Gyrus | 18 | 41 | 26 |
Tal, talairach.
Examination of the six modules shows that there was reasonable correspondence between the anatomical labeling in the Hagmann et al. [2008] study and the anatomical labeling used by the Human Brain Map nomenclature that was used in the LORETA computations [Lancaster et al., 2000; Pascual‐Marqui, 1999, 2004]. Figure one shows the ROIs in LORETA corresponding to the Hagmann et al. Modules that correspond to the voxels colored red in Figure 1. The listing of regions of interests and the anatomical nomenclature is in Table I.
Distance Metric of Modules and ROIs
A Euclidean distance metric was computed for each ROI that corresponded to the six Hagmann et al. [2008] modules in two steps. Step one computed a separate average of the x, y, and z Talairach atlas coordinates of each voxel within a ROI. Step two involved computing the square root of the sum of the squares of absolute distance between the average x, y, and z coordinates of a reference ROI with respect to a different ROI. The computation of the absolute distance is the difference between the average X of a reference ROI or Module (i.e., X1) and the average X coordinate of a second ROI or Module (i.e., X2) and the same for the Y and Z coordinates. The difference between the x, y, and z coordinates is then squared and the square root computed. Table II shows the Talairach atlas coordinates for the center of each Hagmann et al. [ 2008] Module. Table III shows the Euclidean distances between Brodmann areas within a Module as well as the Euclidean distance between the centers of each Module.
Table II.
Talairach coordinates of the center of the six Hagmann et al (2006). Modules based on the Key Institute LORETA program (Pascual‐Marqui, 1999; 2004)
| Modules | x‐tal | y‐tal | z‐tal |
|---|---|---|---|
| Hagmann's center average coordinates | |||
| Module 1 | 0 | −74 | 21 |
| Module 2 | 1 | −33 | 35 |
| Module 3 | −43 | −25 | 8 |
| Module 4 | 44 | −24 | 8 |
| Module 5 | −21 | 24 | 4 |
| Module 6 | 22 | 25 | 2 |
Tal, Talairach atlas coordinates.
Table III.
(A) The average Euclidean distances between Brodmann areas within a module in millimeters and (B) the average Euclidean distance between the centers of each module in millimeters
| Hagmann's module distances | ||
|---|---|---|
| A | Within modules | Distances (mm) |
| Module1 | 36.40 | |
| Module2 | 40.66 | |
| Module3 | 43.96 | |
| Module4 | 44.78 | |
| Module5 | 42.16 | |
| Module6 | 40.88 | |
| B | Between modules | Distances (mm) |
| Module1 ‐ Module2 | 43.54 | |
| Module1 ‐ Module3 | 66.81 | |
| Module1 ‐ Module4 | 67.75 | |
| Module1 ‐ Module5 | 101.99 | |
| Module1 ‐ Module6 | 102.96 | |
| Module2 ‐ Module3 | 52.26 | |
| Module2 ‐ Module4 | 52.31 | |
| Module2 ‐ Module5 | 68.67 | |
| Module2 ‐ Module6 | 69.70 | |
| Module3 ‐ Module4* | 87.61 | |
| Module3 ‐ Module5 | 54.44 | |
| Module3 ‐ Module6* | 82.18 | |
| Module4 ‐ Module5* | 81.25 | |
| Module4 ‐ Module6 | 54.46 | |
| Module5 ‐ Module6* | 42.39 | |
Between hemisphere distances that were no used in Figure 6.
Spatial‐Temporal Source Correlations or Comodulation
To reduce the total number of possible mathematical combinations of 2,394 × 2,394 to a more manageable size a “Reference Region of Interest” was computed as the average current density within the ROI and each voxel in the selected ROI was replaced with the average current density value. A Pearson Product correlation coefficient was computed between the average reference ROI current density value and the average current density values in the remaining 32 ROIs in a given hemisphere over successive two‐second EEG epochs. In other words, the spatial‐temporal correlation was computed over the time series of 2‐s epochs between the reference ROI and the remaining ROIs. This procedure was repeated for each of the 66 ROIs (33 ROIs for the left hemisphere and 33 for the right hemisphere). To be consistent with Hagmann et al.'s [2008] procedures, only correlations between all combinations of the 33 ROIs within a hemisphere were computed. The statistical significance level of the spatio‐temporal correlations were determined by the number of degrees of freedom or the total number of 2‐s epochs that span a given time series minus two. The spatial‐temporal correlation between all pairs of ROIs within each hemisphere were computed, then averaged across subjects, sorted, and rank ordered.
RESULTS
Correlations Between Hagmann Modules and LORETA Brodmann Areas
Figure 2 are contour maps of all possible LORETA source correlations in the eyes closed (EC) and eyes open (EO) conditions summed for all frequency bands. The diagonal is the correlation of each ROI with itself (r = 1.0). The null hypothesis is that the off‐diagonal elements are randomly scattered and not spatially organized. In stead, it can be seen that there is a strong ordering of correlations between the LORETA ROIs that correspond to the Hagmann et al. [2008] Module organization. For example, temporal correlations between the ROIs that correspond to Hagmann et al.'s Module‐1 are higher for Module‐1 than for any of the between Module correlations. Hagmann et al. [ 2008] Module‐2 is correlated most strongly with LORETA ROIs that correspond to Module‐2 and similarly “Module‐3,” “Module‐4,” “Module‐5,” and “Module‐6” all exhibit the highest correlation to the matching Hagmann ROIs and not to noncorresponding ROIs in different Modules. The red and orange colors represent high correlations and the blue represent low correlations.
Figure 2.
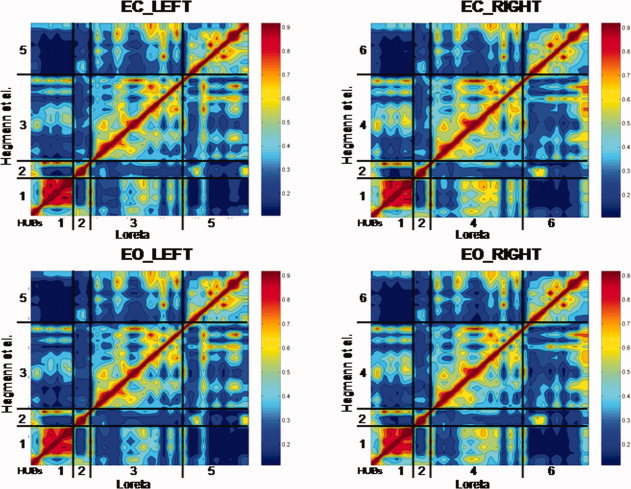
Contour maps of showing the results of the temporal correlation analysis between all possible combinations of the 33 LORETA ROIs in each hemisphere. The y‐axis are the six Hagmann et al. [2008] Modules and the x‐axis are the LORETA ROIs corresponding to the Hagmann Modules shown in Table I. The diagonal is the correlation of ROIs with themselves [r = 1.0]. The null‐hypothesis is that the off‐diagonal elements are randomly correlated and do not show any ordering. Instead the off‐diagonal elements show a strong correspondence to the six Hagmann et al. [ 2008] Modules using LORETA. The color scale to the right of each contour plot is the magnitude of temporal source correlation between LORETA ROIs. Example is from the theta frequency band and the numerical results are shown in Table IV. EC, eyes closed; EO, eyes open conditions. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Table IV shows the average correlation between the ROIs for each of the six LORETA derived Modules that correspond to the six different Hagmann et al. [2008] Modules for eyes closed and eyes open conditions. It can be seen that LORETA source correlations exhibited the same intra‐Module rankings as was reported by Hagamann et al. [ 2008] based on the density of connections. That is, LORETA Module 1 exhibited the highest correlation with ROIs that correspond to the Hagmann et al. [ 2008] Module #1 and lower correlations between ROIs that comprise the other Modules. Similarly, LORETA Module 2 exhibited the highest temporal correlation between ROIs that correspond to the Hagmann et al. [ 2008] Module #2 and lower correlations between ROIs that comprise the other Modules, etc.
Table IV.
Rank ordered LORETA correlations to Hagmann et al., DSI modules
| MOD 1 Both hemispheres visual | MOD 2 Both hemispheres cingulate volitional motor attention, wkmem | MOD 3 Left hemisphere anditory/language memory | MOD 4 Right hemisphere auditory/language memory | MOD 5 Left hemisphere executive sequential plan social skills | MOD 6 Right hemisphere executive sequential plan social skills | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EC NORMs_n = 71_Theta Loteta Source Corrs_Hagmann's MODULES | |||||||||||
| Eyes closed | |||||||||||
| MOD 1 | 0.666 | MOD 2 | 0.495 | MOD 3 | 0.514 | MOD 4 | 0.532 | MOD 5 | 0.537 | MOD 6 | 0.520 |
| MOD 2 | 0.450 | MOD 1 | 0.458 | MOD 1 | 0.408 | MOD 1 | 0.466 | MOD 3 | 0.398 | MOD 4 | 0.387 |
| MOD 4 | 0.412 | MOD 4 | 0.311 | MOD 5 | 0.396 | MOD 6 | 0.375 | MOD 2 | 0.299 | MOD 2 | 0.305 |
| MOD 3 | 0.362 | MOD 3 | 0.295 | MOD 2 | 0.309 | MOD 2 | 0.320 | MOD 1 | 0.214 | MOD 1 | 0.229 |
| MOD 6 | 0.208 | MOD 6 | 0.261 | MOD 4 | n/a | MOD 3 | n/a | MOD 4 | n/a | MOD 3 | n/a |
| MOD 5 | 0.200 | MOD 5 | 0.257 | MOD 6 | n/a | MOD 5 | n/a | MOD 6 | n/a | MOD 5 | n/a |
| Eyes opened | |||||||||||
| MOD 1 | 0.652 | MOD 2 | 0.496 | MOD 3 | 0.505 | MOD 4 | 0.512 | MOD 5 | 0.521 | MOD 6 | 0.515 |
| MOD 2 | 0.446 | MOD 1 | 0.445 | MOD 5 | 0.385 | MOD 1 | 0.439 | MOD 3 | 0.387 | MOD 4 | 0.381 |
| MOD 4 | 0.392 | MOD 4 | 0.297 | MOD 1 | 0.378 | MOD 6 | 0.373 | MOD 2 | 0.291 | MOD 2 | 0.301 |
| MOD 3 | 0.342 | MOD 3 | 0.269 | MOD 2 | 0.281 | MOD 2 | 0.307 | MOD 1 | 0.210 | MOD 1 | 0.229 |
| MOD 6 | 0.207 | MOD 6 | 0.256 | MOD 4 | n/a | MOD 3 | n/a | MOD 4 | n/a | MOD 3 | n/a |
| MOD 5 | 0.193 | MOD 5 | 0.249 | MOD 6 | n/a | MOD 5 | n/a | MOD 6 | n/a | MOD 5 | n/a |
A Chi Square statistical test of the fit between the DSI Modules and the LORETA Modules based on the fact that there are six DSI Modules and six LORETA Modules. Therefore the probability for a single match is 1/36. A Chi square test of the expected vs. observed frequency distribution match between the Hagmann and LORETA maximal values = 250; P < 0.00001. The Chi square was statistically significant (P < 0.0001) for the eyes open and eyes closed conditions and for all frequency bands. The Chi Square was also significant for all nine frequency bands and for eyes open and eyes closed conditions which shows that there is a strong effect size.
The stability and robustness of the match between LORETA Brodmann areas and Hagmann et al. Modules was assessed by determining how many of the 71 subjects showed the highest correlation between EEG LORETA Brodmann areas that make up each Hagmann et al. Module, i.e., how many subjects showed the highest correlation between LORETA Brodmann areas for Hagmann Module 1 compared with any other module, or the LORETA Brodmann areas for Hagmann Module 2 compared with any other module, etc. Table V shows the results of this analysis in which the highest values were 71 out of 71 subjects for Modules 5 and 6 in the eyes closed condition and the lowest was 48 out of 71 for Module 2 in the eyes open condition. On the basis of the null hypothesis a random number of ranked orderings expected by chance alone is N = 35.5 It can be seen in Table V that the χ2 = 142.47 and P < 0.000001 for the eyes closed condition and 153.0 and P < 0.000001 for the eyes open condition and thus the effect size is moderate to strong and can be detected in single subjects for some of the Modules.
Table V.
Observed number of Subjects Per Top Ordered Ranking. 35.5 are expected by chance alone
| Modules: | Eyes closed | Eyes opened |
|---|---|---|
| MOD1 | 70 | 70 |
| MOD2 | 51 | 48 |
| MOD3 | 60 | 61 |
| MOD4 | 58 | 69 |
| MOD5 | 71 | 70 |
| MOD6 | 71 | 69 |
| X2 = | 142.5 | 153.0 |
| P < | 0.000001 | 0.000001 |
Frequency Spectrum of LORETA Current Source Density in Hagmann et al. Modules
Figures 3 and 4 shows the power spectrum of LORETA current source density from the six Hagmann Modules for the eyes closed and eyes open conditions. It can be seen that eyes open (dashed lines) exhibits reduced power in comparison to the eyes closed condition (solid lines) in all frequencies. The alpha frequency bands were dominate in posterior Modules 1 and 2 and alpha was weakest in the frontal Modules 5 and 6. The frequency spectra in Modules 1 and 2 are similar but not identical. The high similarity is likely due to the high relative connectivity between the precuneus in Module 1 and the posterior cingulate in Module 2.
Figure 3.
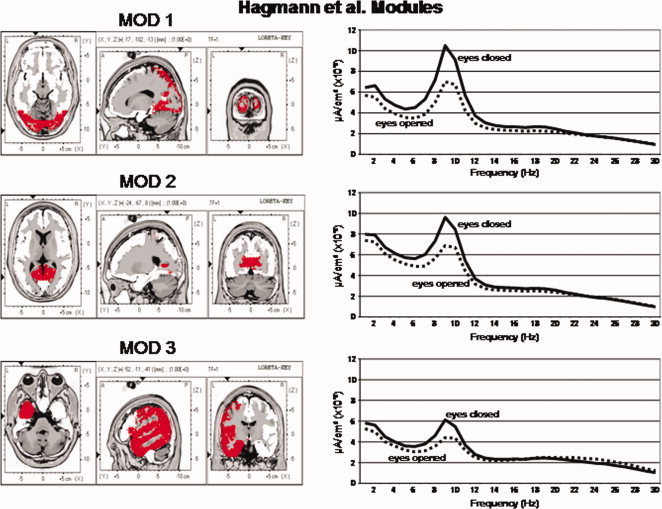
Left are the voxel locations of the Hagmann et al. [ 2008] Modules 1 to 3 as shown in Figure 1. Right are the power spectra of the average LORETA currents from the ROIs constituting Hagmann Modules 1 to 3. The y‐axis is current in uA/cm2 and the x‐axis is frequency from 1 to 30 Hz. The solid lines are the eyes closed condition and the dashed lines are the eyes open condition. Solid lines = eyes closed condition and dashed lines = eyes open. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Figure 4.
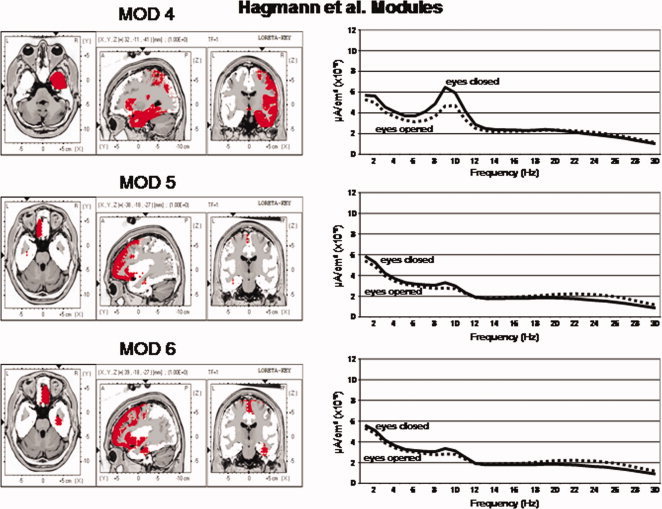
Left are the voxel locations of the Hagmann et al. [ 2008] Modules 4 to 6 as shown in Figure 1. Right are the power spectra of the average LORETA currents from the ROIs constituting Hagmann Modules 4 to 6. The y‐axis is current in uA/cm2 and the x‐axis is frequency from 1 to 30 Hz. The solid lines are the eyes closed condition and the dashed lines are the eyes open condition. Solid lines = eyes closed condition and dashed lines = eyes open. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Magnitude of LORETA Source Correlations
Figure 5 shows the magnitude of the temporal source correlations within each of the six Hagmann et al. [ 2008] Modules for each frequency band for the eyes open and eyes closed condition. The y‐axis = average correlation between LORETA ROIs and Hagmann et al. [ 2008] anatomical Modules. The x‐axis are frequency bands. The solid lines are the eyes closed condition and the dashed lines are the eyes open condition. Solid lines = eyes closed condition and dashed lines = eyes open. It can be seen that the alpha frequency band exhibits the highest within Module correlation between ROIs for Modules 1 to 4 and that the hi‐beta frequency band exhibits the highest within Module correlation between ROIs constituting Modules 5 and 6.
Figure 5.
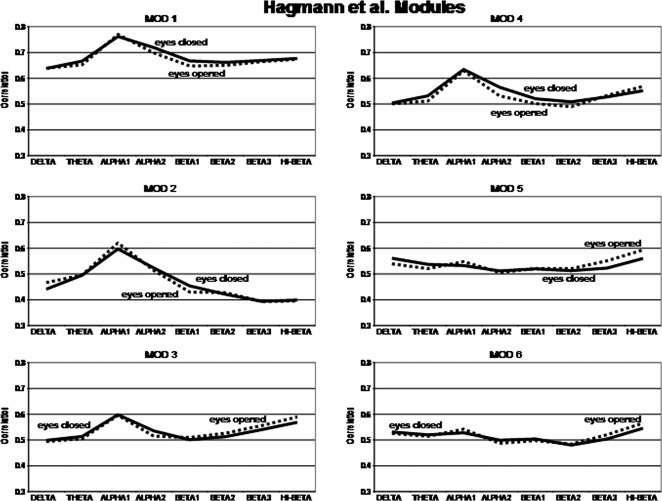
Magnitude of the temporal source correlations using LORETA ROIs within each of the six Hagmann et al. [ 2008] Modules for each frequency band and for the eyes open and eyes closed condition. The y‐axis = average correlation between LORETA ROIs and Hagmann et al. [ 2008] anatomical Modules. The x‐axis are frequency bands. The solid lines are the eyes closed condition and the dashed lines are the eyes open condition. Solid lines = eyes closed condition and dashed lines = eyes open.
Within Module vs. Between Module Brodmann Area Distances
Many anatomical studies demonstrate a raid decrease in synaptic connection density as a function of distance from any group or cluster of pyramidal neurons [Braitenberg, 1978; Braitenberg and Schüz, 1998; Binzigger et al., 2010; Sholl, 1959]. In order to explore distance affects, correlations were compared between Brodmann areas within a DSI Module vs. Brodmann areas between the centers of the DSI Modules. Table III shows the average Euclidean distance in millimeters between Brodmann areas within a DSI Module. The average within Module Euclidean distance ranged from 36.4 mm (Mod1) to 44.8 mm (Mod4). Table III shows the average between module distance in millimeters from the center of the intrahemispheric Brodmann areas. The average between Module Euclidean distance ranged from 42.4 mm (Mod5 to Mod6) to 103 mm (Mod1 to Mod6). The within module connection prediction based on Sholl [ 1959] and Braitenberg [ 1978] is that correlations decrease rapidly as a function of distance between Brodmann areas within a module. The between module prediction is that the more distant Modules will exhibit lower correlations than the less distant Modules because connections decrease with distance from any Module. It can be seen in Figure 6A that there is a significant nonlinear quadratic function that best describes the change in temporal correlations as a function of within Module distance, with Module 1 showing the highest correlations (R 2 = 95.3%, P < 0.01). If Module 1 is excluded then there is a slight increase in correlation with increased within Module distance in the remaining five within Module correlations and, in fact, the correlation is higher for Mod 4 than it is for Mod 2 even though the within Module distance is higher for Mod4 (44.78 mm) than Mod 2 (40.66 mm). This finding is the opposite of that predicted by volume conduction.
Figure 6B shows the relationship between distances as shown in Table III and the magnitude of correlation of current densities between Modules. Unlike the within Module analyses, a statistically significant linear relationship was present (R 2 = 66.1%, P < 0.02). That is, the greater the distance from a given Module then the lower the temporal LORETA current density correlations.
DISCUSSION
The results of this study demonstrated a spatial correspondence between electroencephalographic source analysis and the anatomical density of connectivity as measured by diffusion spectral imaging (DSI) [Hagmann et al., 2008]. The spatial “clustering” of EEG source correlations was not random and instead was the same as observed with diffusion spectral imaging (DSI) [Hagmann et al., 2008]. Overall, the eyes closed and eyes open conditions served as a replication since the EEG that was measured at different periods of time and under different conditions and produced the same cross‐correlation Module structures (Table IV and Fig. 2). The null‐hypothesis is rejected that the LORETA spatial relations are random and do not cluster in the same manner as observed in the Hagmann et al. [ 2008] study. A simple explanation of why EEG source correlations are spatially “clustered” in the same manner as DSI is because the same synaptic densities are measured by both DSI and EEG source analyses. EEG differs from DSI by higher temporal resolution and measures of synchrony between sources, however, the basic six anatomical “clusters” are present in the two different measurement domains thereby demonstrating a linkage between structural DSI and dynamical EEG. This is important because it provides another cross‐modality validation of Electrical Neuroimaging as a neurophysiologically useful measure of the sources of the human EEG. The Hagmann et al. [ 2008] Modules are also functional modules in that each involves different specialized brain regions clustered in functional groups. By co‐registration of EEG sources to the Hagmann et al. [ 2008] anatomical clusters allows for a spatial reference by which phase dynamics and fine temporal coherence within and between Modules can be analyzed.
Volume Conduction vs. Connectivity
Volume conduction occurs because synchronous electrical sources produce an electrical field with zero phase lag that falls off smoothly and rapidly with distance. It is also known that the greater the connectivity between neurons then the higher the amplitude of EEG because connectivity is necessary for synchrony. Anatomical studies also demonstrate a smooth decrease in connectivity as a function of distance from any collection of neurons [Braitenberg, 1978; Braitenberg and Schüz, 1998; Binzegger et al., 2010; Sholl, 1959]. Thus, electrical volume conduction and connection density are confounded to some extent, especially in the short distance domain. Schulz and Braitenberg [ 2002] showed that there are three categories of cortico‐cortical connections in the human brain: (1) intracortical connections which represent the majority of cortical connections and are on the order of 1 mm to ∼5 mm and involve collateral axonal connections that do not enter the cerebral white matter; (2) “U” shaped myelinated fibers representing the majority of the cerebral white matter that connect cortical gyri and sulci and are on the order of 3 mm to 3 cm and, (3) deeply located long distance fiber systems referred to as fasciculi with connections from ∼3 to 15 cm that represent approximately 4% of the cerebral white matter. The intracortical fiber system is too short at 1–3 mm for 19 lead or even 512 lead EEG to resolve connectivity differences at the scalp surface [Nunez, 1981]. Nonetheless, the effects of the intracortical system on the amplitude of the EEG are strong because fiber bundles carry action potentials that produce somadendritic excitatory post synaptic potentials and thereby synchronize large groups of neurons [Nunez, 1981, 1994].
LORETA source correlation studies have demonstrated spatial heterogeneity consistent with the studies by Schulz and Braitenberg [ 2002], especially in the longer distances and these studies can not be explained by volume conduction [Pascual et al., 2001; Thatcher et al., 2007]. For example, Figure 7 is an example of increases and decreases in source correlations as a function of distance in a subject in this study with a pattern consistent with the Schulz and Braitenberg [ 2002] cortico‐cortical connection model which can not be explained by volume conduction. All of the subjects in the present study showed essentially the same spatially heterogeneous source correlations as those in Figure 7.
Figure 7.
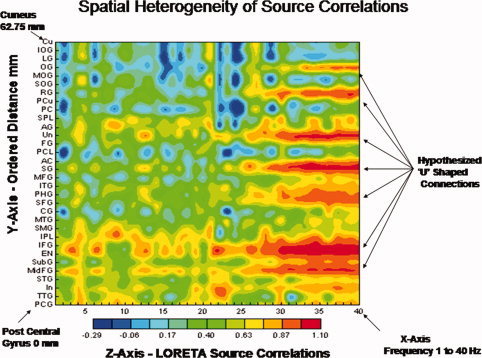
From Thatcher et al. [ 2007] and an exemplar of one of the subjects in this study demonstrating spatial heterogeneity of LORETA source correlations which can not be explained by volume conduction. All subjects in this study exhibited similar spatially heterogeneous LORETA source correlations [see Thatcher et al., 2007 for further details]. The two‐dimensional contour map of the LORETA source correlations are ordered as a function of distance from a reference Brodmann area. The regions of interest (ROIs) are ordered from the left post central gyrus (Brodmann area (1) to the left cuneus (Brodmann area 17 that is 62.75 mm distant). The x‐axis is frequency (1–40 Hz), the y‐axis are regions of interest (ROIs) and the regions of interest are ordered as a function of distance from the post central gyrus. The z‐axis is the magnitude of the LORETA source correlation as represented by the color bar of the contour map. PCA, posterior pentral gyrus; TTG, transverse temporal gyrus; In, insula; STG, superior temporal gyrus; MdFG, middle frontal gyrus; Sub G, sub gyral region; EN, extra‐nuclear frontal gyrus; IFG, inferior frontal gyrus; IPL, inferior parietal lobule, SMG, supramaginal gyrus; MTG, middle temporal gyrus; CG, cingulate gyrus; SFG, superior frontal gyrus; PHG, parahippocampal gyrus; ITG, inferior temporal gyrus; MFG, medial frontal gyrus; SG, subcallosal gyrus; AC, anterior cingulate; PCL, paracentral lobule; FG, fusiform gyrus; UN, uncus; AG, angular gyrus; PC, posterior cingulate; PCu, precuneus; RG, rectal gyrus; SOG, superior occipital gyrus; MOG, middle occipital gyus; OG, orbital gyrus; LG, lingual gyrus; IOG, inferior occipital gyrus; Cu, cuneus. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
In addition to LORETA spatial heterogeneity the lack of a systematic relationship between within Module distance and the magnitude of temporal correlation also argues against volume conduction as a significant source of variance in the present study (Fig. 6A). For example, Module 4 exhibited a higher correlation than Module 2 which is the opposite of what is expected if volume conduction was operating (see Fig. 6A). A more definitive analysis of the connectivity relations between source covariance and distance will require the use of coherence and phase differences because when phase differences are greater than zero then volume conduction is ruled out by definition. A word of caution is necessary because zero phase lag relations exist across wide domains of the cerebral cortex due to the thalamus which is centrally located and can simultaneously activate neurons in distant cortical regions [Steriade, 2006]. Therefore, just because phase difference = 0 does not mean that volume conduction explains the results, an underlying thalamic input to two or more locations can also explain the results. A method to distinguish zero phase lag due to volume conduction vs zero phase lag due to network connectivity is by phase reset measures that precisely define the onset and offset of phase shift which is by definition independent of volume conduction [Buzsaki, 2006; Freeman et al., 2003, 2006; Thatcher et al., 2008c, 2009].
Frequency and Connectivity
Although the alpha frequency power was dominant, nonetheless, different power spectra were present in each of the six Modules (see Figs. 4 and 5). Eyes closed and eyes open conditions exhibited similar power spectra in each of the Modules with the eyes open condition resulting in an attenuation of power especially in the 10–13 Hz frequency range. Alpha1 exhibited the highest correlations in Modules 1 to 2 which include posterior cortical regions known to generate alpha rhythms. Module 5 and 6 exhibited greater power in the lower frequency bands than the other Modules. Alpha was the dominant frequency in Modules 1 to 4 which is expected due to the predominance of posterior cortical regions included in these Modules. Less alpha in frontal ROIs was observed which is also expected given the fact that there is typically less alpha power in frontal regions than in posterior regions. Also, there was greater power in the hi‐beta frequency band in frontal regions in comparison to posterior regions.
Electrical Neuroimaging Network Analysis
Structural network analysis is a new discipline used to quantify the topologies of large connection datasets and has its origins in the mathematics of networks known as graph theory. Network analyses of structural and functional connectivity are used to quantify brain networks with a small number of meaningful and computable measures [Achard et al., 2006; Sporns and Zwi, 2004]. Recently, Rubinov and Sporns [2009] reviewed a common set of concepts and measures shared by a variety of Neuroimaging modalities such as PET, fMRI, DTI, DSI, and EEG/MEG. Each neuroimage modality produces somewhat different Module structures. For example, Chen et al. [ 2008] used cortical thickness and network analyses to demonstrate six basic Modules and He et al. [ 2009] used fMRI and graph theory and demonstrated five basic Modules. The He et al. [ 2009] and Chen et al. [ 2008] Modules shared some similarities to Hagmann et al. [ 2008]; however, there also were differences in the make up of the Modules. The lack of perfect agreement between anatomical DSI Modules vs fMRI Modules are in part due to differences in the experimental measures themselves (e.g., blood flow vs tissue thickness vs axon connections, etc.) [Deuker et al., 2009].
In the present study a hypothesis was first posed based on the fact that EEG current density is related to the density of synchronous synapses on the dendrites and soma of pyramidal neurons, therefore, LORETA source correlations should reflect the same “Modular” synaptic density as measured by Hagmann et al. [ 2008] using DSI. The choice of an anatomical measure of connection density rather than other modularity studies was based on the importance of a structural synaptic reference as the basis for comparisons between functional Modules, anatomical synaptic density and Electrical Neuroimaging [Michel et al., 2009]. The results of this study demonstrate that the linkage between structure and function is relevant to the understanding of the temporal coupling of current sources in different anatomical Modules in the millisecond time domain.
REFERENCES
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E ( 2006): A resilient, low‐ frequency, small‐world human brain functional network with highly connected association cortical Modules. J Neurosci 26: 63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achard S, Bullmore E ( 2007): Efficiency and cost of economical brain functional networks. PLoS Comput Biol 3: e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binzegger T, Douglas RJ, Martin KA ( 2010): An axonal perspective on cortical circuits In: Feldmeyer D, Lubkep JHR, editors. New Aspects of Axonal Structure. New York: Springer; pp 117–140. [Google Scholar]
- Braitenberg V ( 1978): Cortical architectonics: General and areal In: Brazier MAB, Petsche H, editors. Architectonics of the Cerebral Cortex. New York: Raven Press, pp 443–465. [Google Scholar]
- Braitenberg V, Schüz, A ( 1998): Cortex: Statistics and Geometry of Neuronal Connections, 2nd ed. Heidelberg: Springer. [Google Scholar]
- Brodmann VK ( 1909): Localization in the cerebral cortex: The principles of comparative localisation in the cerebral cortex based on cytoarchitectonics, Translated by L. J. Garey, London: Springer, 1994. [Google Scholar]
- Bullmore E, Sporns O ( 2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10: 186–198. [DOI] [PubMed] [Google Scholar]
- Buzski G ( 2006): Rhythms of the Brain. MA: Oxford University Press. [Google Scholar]
- Chen ZJ, He Y, Rosa‐Neto P, Germann J, Evans AC ( 2008): Revealing modular architecture of human brain structural networks by using cortical thickness from MRI. Cerebral Cortex 18: 2374–2381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deuker L, Bullmore ET, Smith M, Christensen S, Nathan PJ, Rockstroh B, Bassett DS ( 2009): Reproducibility of graph metrics of human brain functional networks. NeuroImage 47: 1460–1468. [DOI] [PubMed] [Google Scholar]
- Ferguson R ( 1973): Statistics for Behavioral Science. New York: Wiley. [Google Scholar]
- Freeman WJ, Burke BC, Homes MD ( 2003). Aperiodic phase re‐setting in scalp EEG of beta‐gamma oscillations by state transitions at alpha‐theta rates. Hum Brain Mapp 19: 248–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman WJ, Homes MD, West GA, Vanhatlo S ( 2006): Fine spatiotemporal structure of phase in human intracranial EEG. Clin Neurophysiol 117: 1228–1243. [DOI] [PubMed] [Google Scholar]
- Gomez J, Thatcher RW ( 2001): Frequency domain equivalence between potentials and currents using LORETA. Int J Neurosci 107: 161–171. [DOI] [PubMed] [Google Scholar]
- Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O ( 2008): Mapping the structural core of human cerebral cortex. PLoS Biol 6: e159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Wang J, Wang L, Chen ZJ, Yan C, Yang H, Tang H, Zhu C, Gong Q, Zang Y, Evans AC ( 2009): Uncovering intrinsic modular organization of spontaneous brain activity in humans. PLoS ONE 4: e5226. doi:10.1371/journal.pone.0005226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoechstetter K, Bornfleth H, Weckesser D, Ille N, Berg P, Scherg M ( 2004): BESA source coherence: A new method to study cortical oscillatory coupling. Brain Topogr 16: 233–238. [DOI] [PubMed] [Google Scholar]
- Lancaster JL, Woldorff MG, Parsons LM, Liotti M, Freitas CS, Rainey L ( 2000): Automatice Talairach atlas labels for functional brain mapping. Human Brain Mapp 10: 120–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee WH, Kim TS, Kim AT, Lee SY ( 2008): 3‐D diffusion tensor MRI anisotropy content‐adaptive finite element head model generation for bioelectromagnetic imaging. IEEE Eng Med Biol Soc 4003–64006. [DOI] [PubMed] [Google Scholar]
- Malmivuo J, Plonsey R ( 1995): Bioelectromagnetism. New York, NY: Oxford University Press. [Google Scholar]
- Menke W ( 1984): Geophysical Data Analysis: Discrete Inverse Theory. Orlando, FL: Academic Press. [Google Scholar]
- Michel CM, Koenig T, Brandeis D, Gianotti LR, Waxkerman J ( 2009): Electrical Neuroimaging. New York: Cambridge University Press. [Google Scholar]
- Pascual‐Marqui RD, Michel CM, Lehmann D ( 1994): Low resolution electromagnetic tomography: A new method for localizing electrical activity in the brain. Int J Psychophysiol 18: 49–65. [DOI] [PubMed] [Google Scholar]
- Pascual‐Marqui RD, Koukkou M, Lehmann D, Kochi K ( 2001): Functional localization and functional connectivity with LORETA comparison of normal controls and first episode drug naïve schizophrenics. J Neurotherapy 4: 35–37. [Google Scholar]
- Pascual‐Marqui, RD ( 1999): Review of methods for solving the EEG inverse problem. Int J Bioelectromagnetism 1: 75–86. [Google Scholar]
- Pascual‐Margui RD ( 2004): Free software and documentation from the Key Institute that was downloaded from http://www.unizh.ch/keyinst/NewLORETA/Software/Software.htm.
- Scannell JW, Burns GA, Hilgetag CC, O'Neil MA, Young MP ( 1999): The connectional organization of the cortico‐thalamic system of the cat. Cereb Cortex 9: 277–299. [DOI] [PubMed] [Google Scholar]
- Schulz A, Braintenberg V ( 2002): The human cortical white matter: quantitative aspects of cortico‐cortical long‐range connectivity In: Schultz A, Miller R. editors. Cortical Areas: Unity and Diversity. London: Conceptual Advances in Brain Research, pp 377–386. [Google Scholar]
- Sholl DA ( 1959): A comparative study of the neuronal packing density in the cerebral cortex. J Anat 93: 143–158. [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Chialvo D, Kaiser M, Hilgetag CC ( 2004): Organization, development and function of complex brain networks. Trends Cogn Sci 8: 418–425. [DOI] [PubMed] [Google Scholar]
- Sporns O, Zwi JD ( 2004): The small world of the cerebral cortex. Neuroinformatics 2: 715, 145–162. [DOI] [PubMed] [Google Scholar]
- Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P ( 2007): Small‐world 723 networks and functional connectivity in Alzheimer's disease. Cereb Cortex 17: 724, 92–99. [DOI] [PubMed] [Google Scholar]
- Stam CJ, de Haan W, Daffertshofer A, Jones BF, Manshanden I, van Cappellen van Walsum AM, Montez T, Verbunt JP, de Munck JC, van Dijk BW, 727 Berendse HW, Scheltens P ( 2009): Graph theoretical analysis of magnetoen‐ 728. cephalographic functional connectivity in Alzheimer's disease. Brain 132: 213–224. [DOI] [PubMed] [Google Scholar]
- Steriade M ( 2006): Grouping of brain rhythms in corticothalamic systems. Neuroscience 137: 1087–1106. [DOI] [PubMed] [Google Scholar]
- Talairach J, Tournoux P ( 1988): Co‐Planar Stereotaxic Atlas of the Human Brain. Stuttgart: Thieme. [Google Scholar]
- Teipel SJ, Pogarell O, Meindl T, Dietrich O, Sydykova D, Hunklinger U, Georgii B, Mulert C, Reiser MF, Möller HJ, Hampel H ( 2009): Regional networks underlying interhemispheric connectivity: An EEG and DTI study in healthy ageing and amnestic mild cognitive impairment. Hum Brain Mapp 30: 2098–2119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thatcher RW ( 1995): Tomographic EEG/MEG. J Neuroimaging 5: 35–45. [DOI] [PubMed] [Google Scholar]
- Thatcher RW ( 2010): Validity and reliability of quantitative electroencephalography. J Neurotherapy 14: 122–152. [Google Scholar]
- Thatcher R, Wang B, Toro C, Hallett M ( 1994): Human neural network dynamics using multimodal registration of EEG, PET and MRI In: Thatcher R, Hallett M, Zeffiro T, John E, Huerta M, editors. Functional Neuroimaging: Technical Foundations. Academic Press: New York. [Google Scholar]
- Thatcher RW, Biver CJ, North D ( 2007): Spatial‐temporal current source correlations and cortical connectivity, Clin EEG Neurosci 38: 35–48. [DOI] [PubMed] [Google Scholar]
- Thatcher RW, North D, Biver C ( 2005a): EEG inverse solutions and parametric vs. non‐parametric statistics of Low Resolution Electromagnetic Tomography (LORETA). Clin EEG Neurosci 36: 1–9. [DOI] [PubMed] [Google Scholar]
- Thatcher RW, North D, Biver C ( 2005b): Evaluation and validity of a LORETA normative EEG database. Clin EEG Neurosci 36: 116–122. [DOI] [PubMed] [Google Scholar]
- Thatcher RW, Biver CJ, North D ( 2008a): Intelligence and EEG current density using low resolution electromagnetic tomogaphy. Hum Brain Mapp 28: 118–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thatcher RW, North D, Biver C ( 2008b): Development of cortical connectivity as measured by EEG coherence and phase. Hum Brain Mapp 29: 1400–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thatcher RW, North D, Biver C ( 2008c): Intelligence and EEG phase reset: A two‐compartmental model of phase shift and lock, NeuroImage 42: 1639–1653. [DOI] [PubMed] [Google Scholar]
- Thatcher RW, North D, Biver C ( 2009): Self organized criticality and the development of EEG phase reset. Hum Brain Mapp 30: 553–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towle VL, Bolanos J, Suarez D, Tan K, Grzeszczuk R, Levin DN, Cakmur R, Frank SA, Spire JP ( 1993): The spatial location of EEG electrodes: Locating the best‐fitting sphere relative to cortical anatomy. Electroencephalography Clin Neurophysiol 86: 1–6. [DOI] [PubMed] [Google Scholar]


