Abstract
Auditory functional magnetic resonance imaging (fMRI) was used to assess neural activation in the human auditory brainstem (AB) and cortex (AC) as a function of bandwidth (BW). We recorded brain activation of 22 normal hearing listeners induced by band pass filtered pink noise stimuli with equal sound pressure level of 70 dB SPL. Tested bandwidths were 50, 500, 1,500, 3,000, 6,000, and 8,000 Hz. The center frequency was 4,000 Hz. Categorical loudness scaling had been performed in a silent booth with all of these stimuli. Loudness as a function of bandwidth followed a concave‐shaped curve which reflected the influence of spectral loudness summation (SLS) for higher BW and the influence of large amplitude fluctuations for very low BW, which itself could be explained by peak‐listening. While neural activation of the AB, as measured by the percent signal change from baseline (PSC), was tuned to the physical BW of the stimuli in a straight linear fashion, the trend of perceived loudness as a function of BW was reflected in several aspects by corresponding neural activation in the primary auditory cortex (PAC). Finally, from the absolute differences of the PSC between PAC and AB, gains in perceived loudness associated with SLS and the effect of large amplitude fluctuations could be predicted with an accuracy of 1–2 dB for the whole group of participants. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.
Keywords: loudness, bandwidth, critical bands, auditory filter, fMRI
INTRODUCTION
Loudness is the perceptual correlate of the physical parameter sound intensity [Moore, 2003]. In addition to the sound pressure level (SPL), several other physical parameters like spectral bandwidth, duration, and modulation of an acoustic stimulus are affecting its perceived loudness. Spectral bandwidth also has an influence on several other perceptual measures of a sound like its pitch, timbre, and fluctuation strength. For a certain range of bandwidths, it is known that the perceived loudness of sounds increases with increasing bandwidth even if the sound pressure level remains constant. This phenomenon is called spectral loudness summation and has been explained within the concept of critical bands [Fletcher, 1940; Scharf, 1961; Zwicker and Stevens, 1957]. One can think of a critical band as a frequency selective auditory channel of psychoacoustic processing. It is assumed that the overall loudness is determined by some integral of the partial loudness across such auditory channels and that each single channel is compressive, viz. a change in the output is smaller than a change in the input [Appell, 2002; Leibold and Jesteadt, 2007; Moore and Glasberg, 2004]. This would explain SLS along the line that if the sound energy is distributed over a sum of such bands, perceived loudness is larger as when the sound energy is restricted to one band only. The concept of critical bands has proved to be very important in psychoacoustics and had a high impact on many theories and models of the auditory system over decades of hearing research. Critical bands were also referred to a specific area on the basilar membrane, an elongated thin sheet of fibers located in the inner ear, on which each channel is assumed to cover a length of about 0.9 mm [Greenwood, 1990; Moore, 2003]. If critical bands are associated with modeling the basilar membrane as a bank of overlapping band pass filters, the question would be at what stage in the auditory pathway beyond the cochlea the final summation of loudness across the initially independent channels takes place. We hypothesize that the integration of auditory channels to form a unified loudness percept is not completed before cortex for two reasons. First, the tonotopic organization of the neurons in the auditory nerve is maintained throughout the auditory pathway up to the stage of the primary auditory cortex by means of orderly projections between auditory nuclei [Merzenich and Brugge, 1973; Morel et al., 1993], although the arrangement of frequencies in the cortex might have a more complex shape [Formisano et al., 2003]. Second, a loudness judgment is certainly a cognitive task and it has been shown that there are other auditory and nonauditory factors that also have an effect. Auditory factors include the kind of presentation, stimulus duration, and temporal fluctuations [Epstein and Florentine, 2009; Grimm et al., 2002; Verhey and Uhlemann, 2008; Zhang and Zeng, 1997]. Examples for nonauditory factors are context effects and personality traits like anxiety [Algom and Marks, 1990; Gabriel et al., 1997; Menzel et al., 2008; Stephens, 1970]. Furthermore, to our knowledge, there is no empirical evidence from physiological data, which indicates that spectral loudness summation is completed at a stage before cortex.
Neuroimaging techniques may help to find an answer to the question of where within the auditory pathway loudness coding and SLS, in particular, take place. Using fMRI, Langers et al. [ 2007b] compared the BOLD‐signal intensity as a function of sound pressure level of normal hearing subjects against hearing impaired subjects. The results of this study suggest that neural activity in AC is related to loudness rather than to sound intensity. In another recent fMRI‐study performed by our laboratory, it was demonstrated that, for normal hearing subjects, perceived loudness is reflected by corresponding neural activation in the auditory cortex, but not in the auditory brainstem [Röhl and Uppenkamp, 2009]. The BOLD‐signal intensity induced by pink noise at an equal SPL was significantly correlated to the individual loudness judgments in those cortical voxels that were sensitive to sound, while AC and AB exhibited a linear and similar response with sound intensity when averaged across listeners. For several auditory brainstem nuclei, Hawley et al. [ 2005], using fMRI and cardiac gating, found that activation increases monotonically with increasing bandwidth when either stimulus spectrum level or energy is held constant. Combining these statements about the neural processing of bandwidth, sound intensity and loudness, we formulate the hypothesis that SLS takes place in the auditory cortex: If the bandwidth is increased, activity in the AB will increase monotonously according to Hawley et al. We would expect that the response in AC is similar to the brainstem response as long as the bandwidth is smaller than one critical band according to Röhl and Uppenkamp [ 2009]. If the critical bandwidth is exceeded, i.e. spectral loudness summation comes into play, the activity in the AB will still follow the bandwidth only. Contrary to that, in the auditory cortex, the increase of perceived loudness due to SLS will be superimposed onto the received input of the brainstem. Although there is strong evidence from our previous study that the transformation of intensity to loudness takes place in the auditory cortex and not in the brainstem [Röhl and Uppenkamp, 2009], a direct verification of the SLS cortex hypothesis is still required. To our knowledge, there has been no fMRI‐study so far that has investigated activation in the human auditory cortex as a function of bandwidth at fixed SPL. Studies using other neuroimaging methods like MEG have come up with ambiguous results. Using MEG and band pass noise at different center frequencies, Soeta et al. [ 2005] reported that the peak amplitude of N1m decreased with increasing bandwidth of the band pass noise. In a second study the same authors, using two‐tone complexes, described an increase of N1m amplitudes with increasing frequency separation or total bandwidth, when these were greater than the critical bandwidth [Soeta and Nakagawa, 2006]. This was interpreted as an MEG correlate of critical band‐like behavior. The apparent contradiction between the results of these two studies could probably be resolved if all findings were related not only to bandwidth, but also to perceived loudness, which had not been assessed by psychoacoustic measurements. Therefore, in this fMRI‐study, BOLD‐responses are analyzed with respect to bandwidth and to loudness assessed by categorical loudness scaling.
METHODS
The full experiment for each of the 22 listeners consisted of two separate appointments. The first session took place in an insulated sound booth (IAC GmbH, Type 403A). During this session, standard audiometry and categorical loudness scaling were performed for all the stimuli used throughout this study. The second session took place in the MRI scanner. During this session, brain activity was recorded as induced by all experimental stimuli at a fixed sound pressure level.
Participants
Participants were recruited through advertizements placed on the notice‐board at the university. Inclusion criteria were the following: age between 18 and 30; normal hearing, i.e. audiometric thresholds better than 20 dB HL for all frequencies except 8 kHz, where up to 35 dB HL was accepted. Exclusion criteria were psychiatric or neurological disorders and any contraindication for MRI. All volunteers (15 males, 7 females) gave written informed consent to the study, which was approved by the ethics committee of the University of Oldenburg.
Stimuli
Band pass filtered uncorrelated continuous pink noise with a duration of 5 s was used as acoustic stimulus throughout this study. The center frequency of the band pass filter was 4,000 Hz. The following bandwidths were tested: 50; 500; 1,500; 3,000; 6,000; and 8,000 Hz. The stimuli with the lowest bandwidth of 50 Hz had a pitch‐like sound‐quality (similar to a sinusoid at 4,000 Hz) because of its very limited bandwidth. This narrow bandwidth also resulted in distinct random amplitude fluctuations of the signal that are known to affect loudness [Chalupper and Fastl, 2002; Zhang and Zeng, 1997; Zwicker and Fastl, 1999]. Zwicker and Fastl suggested that in such cases the perceived loudness is bonded to the maximum rather than the mean sound pressure level. With increasing bandwidth, these fluctuations decrease. For a bandwidth of 500 Hz, this effect is already largely reduced. The probability density distributions (PDF) of the differences between SPL estimated within 50 ms time windows and the mean SPL are depicted in Figure 1. PDFs were estimated with a kernel‐smoothing method [Bowman and Azzalini, 1997]. Figure 1 illustrates that for the 50 Hz BW stimulus, the sound intensity fluctuates in a way that reflects the difference between its maximum and mean value, D MAX‐MEAN, of 6.1 dB. Note that D MAX‐MEAN is different from the crest factor or peak‐to‐average ratio of a signal which is defined by the ratio of the peak amplitude of the waveform relative to its RMS.
Figure 1.
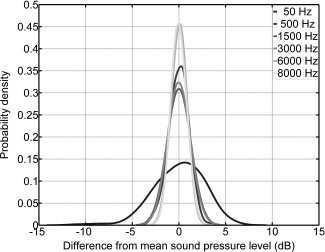
Probability density distribution of sound pressure levels estimated within 50 ms time frames relative to the mean sound pressure level of the 5 s stimuli. Note that the stimulus with the smallest bandwidth of 50 Hz has pronounced amplitude fluctuations.
In the sound booth, the stimuli were presented dichotically via headphones (Sennheiser HDA 200), which were calibrated with a condenser microphone (model 4134, Brüel & Kjær GmbH) and a coupler (artificial ear model 4153, Brüel & Kjær GmbH). In the MRI, the stimuli were also played dichotically via dynamic headphones (MR confon GmbH, Magdeburg, Germany) with a sampling rate of 44.1 kHz. The headphones were calibrated with a fiber‐optic microphone (Sennheiser GmbH & Co. KG, Wedemark, Germany) and a custom‐made MRI compatible acoustic coupler that conforms to the IEC 60318‐3:1998 standard. This coupler was manufactured by the scientific workshop of the University. The accuracy of calibration of the MRI sound delivery system was within 2–3 dB.
Categorical Loudness Scaling
Categorical loudness scaling is a psychoacoustic measurement procedure that registers individual subjective loudness perception [Heller, 1985; Kollmeier, 1997]. During the procedure, subjects give their rating on a response scale with eleven response alternatives. The response scale includes five named loudness categories, “very soft ‐ soft ‐ medium ‐ loud ‐ very loud,” four numbered intermediate response alternatives, and two named limiting categories, “inaudible” and “too loud.” These categories were transformed into numbers from 0 categorical units (cu) to 50 cu in steps of 5 cu. Acoustic stimuli were presented in random order in relation to bandwidth and sound intensity, where the level of two successive presentations always differed by at least 10 dB and less than 50 dB. For each bandwidth, the lowest presentation level was 0 dB SPL (inaudible to all listeners). The highest presentation level was limited to the individual uncomfortable loudness level (UCL) for a 1‐kHz sinusoid. The UCL was determined during the audiometric measurement. We used an ascending stimulus level sequence beginning at 60 dB HL with a step size of 5 dB. The listener's task was to press the response button as soon as the stimulus was perceived as too loud. To avoid harmful sounds, the sequence stopped at 120 dB HL if the listener had not pressed the response button by then. Before the actual experimental run, participants were introduced to the categorical loudness scale (on a paper version) and they were instructed to press the response button only when the sound was perceived as “too loud,” rather than “loud” or “very loud.” In most cases, the maximum presentation level for the band pass filtered pink noise was about 92 dB SPL. For sound pressure levels below 70 dB SPL, sounds were presented in increments of 5 dB. The increment size was reduced to 3 dB for levels above 70 dB SPL and reduced again to 2 dB for levels from 10 dB below the individual UCL and onwards. This reduction was introduced since the loudness curve was expected to show a steeper slope at higher presentation levels. Therefore, the reduction of the step size enabled a balanced sampling with comparable steps on the loudness scale. Listeners gave their ratings by a simple mouse click on a response scale displayed on a computer screen. One session lasted for about 15 min. It was repeated if the categorical loudness rating “too loud” had not been reached for at least one of the bandwidths tested. Categorical loudness scaling was not repeated in the MRI scanner for this study. In a previous study, it was shown that for a pink noise stimulus with a bandwidth of 8,000 Hz, the differences in perceived loudness between the sound booth and fMRI setting within the sparse imaging paradigm can be disregarded [Röhl and Uppenkamp, 2009]. The scanner sequences for the fMRI data acquisition, and therefore the acoustic environment, were the same in both studies.
Functional Magnetic Resonance Imaging
Measurements were performed on a MRI scanner SIEMENS Sonata 1.5T, equipped with a standard single channel head coil. Twenty‐one transversal slices of 3.9 mm thickness angled away from the eyes and centered at the posterior commissure were acquired encompassing the superior temporal lobes, including the primary and secondary auditory cortices (SAC).
Functional MRI using echo planar imaging (EPI) sequences (TE: 63 ms; volume acquisition time: 2.7 s; flip angle: 90°; matrix size: 64 × 64; field of view: 192 × 192 mm2) was performed in a sparse imaging paradigm employing clustered‐volume acquisition [Edmister et al., 1999; Hall et al., 1999] at a fixed time of repeat (TR) of 7.7 s. The sparse temporal sampling technique was demonstrated to deliver an increased hemodynamic response signal in auditory areas as compared to conventional fMRI designs, e.g. continuous scanning [Gaab et al., 2007a, b; Schmidt et al., 2008]. Images were acquired at the end of a 5‐s stimulus interval en bloc; this ensured that the presentation of the auditory stimuli was not masked by the scanner noise. This recording technique allows for an estimation of the accumulated strength of activation, but not for an estimation of the time course of the hemodynamic response. All acoustic stimuli were presented in random order at a fixed sound pressure level of 70 dB SPL. One experimental session was split into four runs, with about 2 min of rest in between. Each stimulus condition, including the silence, was presented 12 times during one run, resulting in 336 scans per subject. A simple detection task was employed to ensure that the participants were attending to the acoustic stimuli. Deviants in this task differed from standard stimuli that their intensity was not kept constant, but after 2 s decreased slowly by 10 dB for a short period of 330 ms. Participants were instructed to count the number of deviants within each run. A maximum of six deviants was randomly distributed over each run. The participants were asked after each of the four runs for the number of counted deviants. The performance on this task was good. The mean number of missed deviants across all listeners was smaller than one per run, indicating that the subjects stayed on the task. A T1 weighted structural image with a resolution of 1 × 1 × 1 mm3 was also acquired after the fMRI scan to obtain individual anatomical landmarks.
Data Analysis
The fMRI data were analyzed with SPM5 (Wellcome Department of Cognitive Neurology). Standard preprocessing steps, including realignment, normalization to Talairach space, interpolation to 2 × 2 × 2 mm3, smoothing with 6 mm FWHM Gaussian filter were carried out. Two different types of a general linear model were used. A high‐pass filter with a cut‐off frequency of 1/128 s and a first‐order autoregressive model were used to handle the physiological and nonphysiological low‐frequency noise characteristics of fMRI time series.
In Model 1, each condition (different bandwidths and silence) was modeled as an individual regressor. Neural activation was determined using one sample t‐test. Statistical maps were generated by contrasting each condition of bandwidth against the silence baseline, including a general sound against silence contrast. These 7 × 22 first‐level contrast images were then entered into a second‐level random effects analysis (RFX) to allow for population‐level inferences. The threshold for significance was at P < 0.05 with a correction for multiple comparisons by the family‐wise error rate (FWE) for this and all later second‐level analyses. Model 1 was used to pursue the general trend of sound‐induced activation as characterized by the spatial location and volume of activation. In Model 2, a linear systems analysis was employed. In this analysis, one of the two regressors modeled the silence condition and the other one the different conditions of the sound stimuli, each of which had a different bandwidth. The bandwidth was coded by parametric modulation. The highest order modeled in the linear systems analysis was two. Linear and quadratic components were extracted from one sample t‐tests by first and second‐order parametric modulation regressors. The resulting 2 × 22 first‐level contrast images were then entered into two separate second‐level analyses computing the one sample group mean. Model 2 was used to track the response (PSC) of the voxels which followed the underlying linear or nonlinear trends of the acoustic stimulus with a high accuracy. Pilot investigations suggested that the PSC of those voxels showing a general sound‐related activation changes only slightly with bandwidth. In the analysis, we distinguish between the auditory cortex and auditory brainstem areas by boundaries defined in the Talairach coordinate system. The coordinates of the ROI surrounding the auditory cortex were |x| > 20 mm, |y| < 50 mm, and −20 mm < z < 50 mm. The coordinates of the ROI surrounding the auditory brainstem were |x| < 20 mm, 0 mm < y < 50 mm, and −30 mm < z < 10 mm. These boundaries were defined with respect to the variability across listeners of sound‐induced activation. The main motivation was a rough separation of activation in the left AC, right AC, and brainstem structures. This comparatively generous definition of the ROI also ensures that no functional activation in auditory areas is missed, even if it does not necessarily overlap with textbook anatomical landmarks. Activation in the primary auditory cortex was distinguished from secondary auditory areas by means of probability maps of the PAC as reported by Rademacher et al. [ 2001].
RESULTS
Categorical Loudness Scaling
For each bandwidth and each participant, a loudness curve was fitted to the data which consisted of 24 ± 1 loudness ratings depending on the individual UCL. Loudness curves representing the group were then derived by averaging across individual loudness curves for each bandwidth.
Fitting the loudness curves
First, the degrees of freedom were estimated which were necessary to fit a proper loudness curve to the individual ratings. For this purpose, we tested polynomials of degree n (n = 1…4), whereby no offset was included. The mean R 2 for a linear regression of the loudness curve for all bandwidths was 0.85. Including the quadratic component yielded a significant improvement for the R 2 for all bandwidths with a mean R 2 of 0.91. Including a third‐order component improved the fitting for the curves from 500 to 6,000 Hz BW and yielded a mean R 2 of 0.94 ranging from 0.92 to 0.95. A fourth‐order term did not improve the goodness of fit. Therefore, three degrees of freedom were regarded as optimal.
Loudness curves
Loudness curves representing the group are depicted in Figure 2. Categorical loudness as a function of sound pressure level increased monotonously for all bandwidths. The nonlinearity of the curve increased for bandwidths from 50 to 1,500 Hz, and then decreased again with increasing bandwidth. At 8,000 Hz BW the loudness curve is nearly linear.
Figure 2.

Categorical loudness of the pink noise stimuli as a function of sound pressure level for all six bandwidths tested. The shading shows the standard deviation across listeners. Note that the nonlinearity in perceived loudness is at its maximum for the stimulus with a medium bandwidth of 1,500 Hz. The pictograms in each plot show sections of 200 ms duration of the corresponding signal.
The estimated categorical loudness for the presentation level later used in fMRI (70 dB SPL) is depicted in the left panel of Figure 3. The mean loudness ratings were arranged along a concave‐shaped curve, with a minimum at 1,500 Hz for the perceived loudness. Determining the bandwidth for which the perceived loudness at a sound pressure level of 70 dB SPL was at its minimum, for each participant individually, yielded a value of 1.6 ± 1.1 kHz. The underlying functional relation of perceived loudness and bandwidth was, therefore, not linear. A good fit was obtained by a second‐order polynomial (R 2 = 0.93). The total categorical loudness curve for the acoustic stimulus used throughout the fMRI experiment can, therefore, be separated into a linear and a nonlinear (quadratic) component (R 2 = 0.78). The nonlinear component was determined by subtracting the estimates of a linear regression from the total response. The ratio between the nonlinear and linear growth coefficients of the respective curves, Q NL/L, was 0.28 ± 0.39 averaged across listeners.
Figure 3.
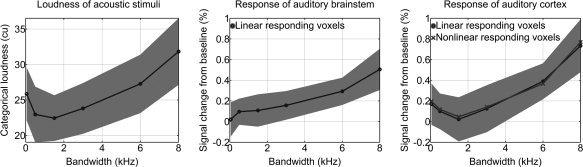
Left: Perceived loudness of acoustic stimuli as measured by psychoacoustic loudness scaling. Percent signal change from baseline of those voxels in AB (middle) and PAC (right), for which the underlying BOLD‐signal as a function of bandwidth had a significant linear (AB and PAC) or nonlinear (quadratic, PAC) component. Note that the response in the auditory cortex reflects the perceived loudness to a larger extent than the response in the brainstem does.
The initial decrease in the loudness curve (as depicted in the left panel of Fig. 3) of 2.9 cu from 50 to 500 Hz bandwidth was significant (P = 0.02). The subsequent decrease of 0.5 cu from 500 to 1,500 Hz was not significant. The initial decrease could be explained along the line that the amplitude fluctuations which are known to result in a gain of perceived loudness decrease with increasing bandwidth of the stimuli. The amplitude fluctuations were assessed by the maximum difference, D MAX‐MEAN, between the sound pressure levels estimated within 50 ms time frames and the mean sound pressure level of the 5 s stimuli. A D MAX‐MEAN of 6.1 dB (3.5 dB) was observed for the stimulus with a bandwidth of 50 Hz (500 Hz). This level difference was corrected for the D MAX‐MEAN of 1.7 dB, which was estimated for the stimulus with a bandwidth of 1,500 Hz. This corrected value was then added to the mean sound pressure level of 70 dB SPL and transformed to perceived loudness using the loudness curve for the stimulus with a bandwidth of 1,500 Hz for which amplitude fluctuations can be disregarded. Using this approach, a difference in the expected perceived loudness of 3.4 cu (0.5 cu) was calculated for the stimulus with a bandwidth of 50 Hz (500 Hz). These predictions match the measured difference between the perceived loudness of the 50 Hz (500 Hz) BW stimulus and the 1,500 Hz BW stimulus of 3.3 cu (1.3 cu).
For bandwidths greater than 1,500 Hz, the perceived loudness (as depicted in the left upper panel of Fig. 3) increased linearly (R 2 = 0.96) by 1.4 ± 0.5 cu/kHz BW. As Figure 4 shows, this increase depends on the sound pressure level. SLS has its maximum at 65 dB SPL. It decreased for lower and higher SPLs. At sound pressure levels below 20 dB, a slight decrease was observed. A similar trend was observed for the effect of large amplitude fluctuations, e.g. when comparing the perceived loudness for the 50 Hz BW stimulus with the mean perceived loudness of the 1,500 Hz BW stimulus. The maximum increase of 3.8 ± 2.5 cu was seen at an intermediate sound pressure level of 62 dB SPL; while for lower sound pressure levels, the increase vanished completely and turned into a decrease at SPLs above 86 dB. However, the effect of −1.6 ± 5.5 cu for a sound pressure level of 90 dB was very small as compared to the interindividual variability.
Figure 4.
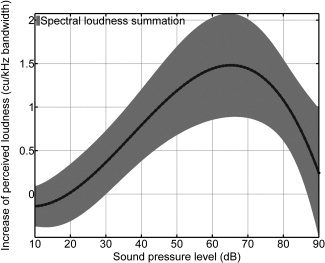
Increase of perceived loudness with bandwidth as a function of sound pressure level. The shading shows the standard deviation across listeners. Note that the increase (spectral loudness summation) is greatest for medium sound pressure levels.
Functional Magnetic Resonance Imaging
Neural activation in response to sound presentation
Second level RFX analysis of first‐level sound versus silence contrast images as derived by Model 1 are illustrated in Figure 5. The image shows three axial slices, one through the auditory brainstem (z = −10 mm) and two through the auditory cortex (z = 0 mm and z = 10 mm). The minimum t‐value at threshold was 5.06. Statistical parametric maps (SPM) were overlaid on the mean T1 scan of the group. Activation was detected in the auditory cortex for all six bandwidths tested. The volume of activation as listed in Table I initially decreased for a bandwidth of up to 1,500 Hz, but increased again afterwards (except for 6 kHz in the right auditory cortex). Activation in the brainstem with more than ten connected voxels was present at bandwidths of 6,000 and 8,000 Hz only.
Figure 5.

Sound‐induced activation of the 70 dB SPL pink noise stimuli for all six bandwidths tested overlaid on the group mean T1 image. The contrasts as derived on a second‐level‐RFX analysis were thresholded at P < 0.05 (FWE). Note that activation in the auditory cortex is at its minimum for the stimulus with a bandwidth of 1,500 Hz.
Table I.
Volume of activation and center of mass of sound‐induced activation of the 70 dB SPL pink noise stimuli for all six bandwidths tested
| BW | Left auditory cortex | Auditory brainstem | Right auditory cortex | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Voxel | x | y | z | Voxel | x | y | z | Voxel | x | y | z | |
| 50 | 811 | −40 | −28 | 9 | 0 | – | – | – | 533 | 43 | −22 | 7 |
| 500 | 396 | −36 | −27 | 11 | 1 | −4 | −50 | −16 | 269 | 40 | −22 | 9 |
| 1,500 | 303 | −36 | −27 | 10 | 0 | – | – | – | 190 | 39 | −23 | 9 |
| 3,000 | 410 | −36 | −26 | 10 | 7 | −1 | −40 | −16 | 467 | 41 | −23 | 8 |
| 6,000 | 855 | −42 | −24 | 9 | 132 | 0 | −35 | −10 | 276 | 40 | −22 | 9 |
| 8,000 | 858 | −46 | −21 | 9 | 490 | −1 | −34 | −11 | 562 | 49 | −17 | 6 |
The contrasts as derived on a second‐level‐RFX analysis were thresholded at P < 0.05 (FWE). Note that the volume of activation and the spatial shift of the x‐coordinates of the activation foci have an almost common reversal point at 1,500 Hz in the auditory cortex. Each voxel has a volume of 2 × 2 × 2 mm3.
The centers of activation foci (weighted by the t‐values of the SPM) for the left, right, and medial regions of interest are also listed in Table I. A systematic unidirectional shift (from posterior to anterior) was only present for the y‐coordinates of the left activation foci in the auditory cortex. For the x‐ and z‐coordinate the shift was almost coherent, from inferior‐lateral to superior‐medial and back to inferior‐lateral. The most superior‐medial location was found for a bandwidth of about 1,500 Hz.
The shift of the x‐ and y‐ coordinates for stimuli with bandwidths between 1,500 and 8,000 Hz, that is, for stimuli with more or less flat signal envelope and no large fluctuations in amplitude, was subject to a further analysis. The shift from medial to lateral by 10 mm in both hemispheres, comparing the center of activation induced by the 1,500 Hz BW stimulus—with predominantly high frequencies and a brighter timbre—and the 8,000 Hz BW stimulus—with more energy at lower frequencies and a darker timbre—can be analyzed with respect to the tonotopic mapping in AC. An analysis of variance showed that the effect of bandwidth on the x‐coordinate of the center of activation was significant for the left [F(3,79) = 7.92, p = 1.2 e–4], but not for the right hemisphere [F(3,73) = 3.01, p = 0.036] when considering multiple testing. The second shift from posterior to anterior of 6 mm was less pronounced. An analysis of variance showed that the effect of bandwidth on the y‐coordinate of the center of mass was significant for the right [F(3,73) = 4.81, P = 0.004], but not for the left hemisphere [F(3,79) = 2.77, P = 0.048] when considering multiple testing. This statistical analysis was performed on the x‐ and y‐coordinates of the center of activation as estimated from first‐level statistical parametric maps. The threshold for significance was chosen at P < 0.05, using the false discovery rate (FDR) to correct for multiple comparisons. The mean centers of activation estimated from first‐level SPM were similar to that estimated from second‐level SPM for the x‐coordinates [r = 0.998, P = 9.0 e–14], with a mean difference of 1 mm, and for the y‐coordinates [r = 0.93, P = 1.2 e–5], with a mean difference of 2 mm.
Change of neural activation caused by a change of bandwidth
First‐level contrast images using Model 1 and comparing activation of the stimuli with the full bandwidth of 8,000 Hz against those with a lower bandwidth, e.g. 1,500 Hz (here denoted as C8000‐1500), were analyzed. The corresponding five contrast images of each listener were then entered into a second‐level RFX analysis. Statistical parametric maps reflecting a change of neural activation caused by a change of bandwidth were estimated using a threshold for significance of 5% (FWE, t min = 5.17). The activated volume for a differential contrast image, like C8000‐1500, was denoted as differential volume (DV). In general, the analysis of the DV as a function of difference in bandwidth, e.g. 6,500 Hz for the contrast C8000‐1500, revealed results corresponding to those outlined in the previous section. In the auditory brainstem, DV increased monotonously and almost linearly with 0.5 cm3/kHz with difference in bandwidth (R 2 = 0.80). The mean DV was 1.8 cm3 (averaged over the five conditions from 50 to 6,000 Hz BW). In the left auditory cortex, the DV increased up to the stimulus with a bandwidth of 1,500 Hz and decreased thereafter. The mean DV was 1.2 cm3. In the right auditory cortex, the DV showed the weakest sensitivity to a difference in bandwidth with an almost linear increase (R 2 = 0.84) of 0.1 cm3/kHz. The mean DV was 0.2 cm3. In general, reversed contrasts did not yield any suprathreshold voxels—with one exception—C50‐8000, for which suprathreshold voxels were found in secondary auditory areas. In the left hemisphere, these were at x = −44 mm, y = −14 mm, z = −4 mm anterior of HG (20 voxels, t = 6.34, Z = 5.82, P = 3.0 e–9) and at x = −38 mm, y = −36 mm, z = 16 mm posterior of HG (10 voxels, t = 6.18, Z = 5.69, P = 6.2 e–9). In the right hemisphere, they were at x = 60 mm, y = −26 mm, z = 6 mm posterior and lateral of HG (11 voxels, t = 5.70, Z = 5.31, P = 5.6 e−8). Instead, suprathreshold voxels corresponding to the DV of the contrast C8000‐50 were found in the inferior colliculi [Griffiths et al., 2001] at x = 2 mm, y = −36 mm, z = −8 mm (404 voxels, t = 11.96, Z = Inf, P = 4.4 e−16) and in the left primary auditory cortex at x = −46 mm, y = −22 mm, z = 8 mm (101 voxels, t = 8.49, Z = 7.39, P = 7.2 e−14). Statistically less satisfying results were found in the right primary auditory cortex at x = 50 mm, y = −20 mm, z = 4 mm (6 voxels, t = 5.59, Z = 5.22, p = 8.9 e−8).
Activation as derived from linear systems analysis
Results of a second‐level RFX analysis using contrast images from Model 2 are depicted in Table II. The threshold for significance was 5% (FWE, t min = 6.94, extent threshold of five connected voxels). Voxels that show a linear relation between their BOLD‐signal intensity and the bandwidth of the stimuli were primarily located in AB and—to a weaker extent—in PAC, where they were lateralized to the left hemisphere. Suprathreshold voxels that show a nonlinear (quadratic, U‐shaped) response were present in the PAC only, again with a lateralization to the left hemisphere. These voxels also showed a significant linear response and were, therefore, also a part of the linearly responding voxels. Inverted trends were not observed in auditory regions.
Table II.
Statistical results of linear systems analysis
| Trend | Voxel | t‐Value | z‐Value | P‐value | Talairach coordinates | ||
|---|---|---|---|---|---|---|---|
| x | y | z | |||||
| Linear | 173 | 12.94 | 6.72 | 8.9 e−12 | 4 | −34 | −8 |
| 57 | 9.05 | 5.72 | 5.4 e−9 | −48 | −22 | 6 | |
| 6 | 8.30 | 5.47 | 2.3 e−8 | 12 | −22 | −8 | |
| Quadratic | 6 | 8.37 | 5.49 | 2.0 e−8 | −46 | −22 | 8 |
The table lists the volume of activation and the corresponding t‐, Z‐, and P‐values of voxel clusters for which the underlying BOLD‐signal as a function of bandwidth had a significant linear or quadratic (nonlinear, U‐shaped) component. The threshold for significance was 5% (FWE, extent threshold of five connected voxels). The statistically most satisfying linear response was found in the auditory brainstem. Note that all trends were positive. Each voxel has a volume of 2 × 2 × 2 mm3.
The middle and right panels of Figure 3 depict the corresponding percent signal change from baseline for the linearly responding voxels of the left PAC and AB. The total response of the six quadratically responding voxels found in the left PAC was almost identical with that of the linearly responding voxels (r = 0.997, P = 1.3 e–5]. This is illustrated in the right panel of Figure 3. Therefore, without loss of generality, the further analysis was restricted to the linearly responding voxels. However, although they were identified by the linear systems analysis as responding in a linear way, their response may not be purely linear, but may rather be comprised of a significantly linear component. The total responses in AB and PAC were, therefore, segregated into their linear and nonlinear components as done previously for the perceived loudness curve. The goodness of a second‐order polynomial curve fit for the nonlinear component was acceptable for the PAC (R 2 = 0.92), but not for the AB (R 2 = 0.55), for which the total response followed a straight linear trend (R 2 = 0.95). This reflects solely the identification of nonlinearly responding voxels by means of the linear sytems analysis in the PAC. The mean increase of the total response for BW for which SLS has been observed (between 1,500 and 8,000 Hz) was 0.06% ± 0.02%/kHz BW in the AB, and 0.11% ± 0.05%/kHz BW in the PAC. The difference was significant (p = 4.8 e−4).The mean increase of the linear component was 0.05% ± 0.02%/kHz BW in the AB, and 0.07% ± 0.04%/kHz BW in the PAC. The difference was significant (P = 0.02). The ratio between the nonlinear and linear growth coefficients of the respective curves, Q NL/L, was 0.10 ± 0.20 in the AB, and 0.33 ± 0.40 in the PAC. The difference was significant (P = 0.009). In addition, the value of Q NL/L found for the PAC was close to the ratio of 0.28 ± 0.39, which was found for the loudness curve. This clearly reveals the similarities between the loudness of acoustic stimuli and the PSC as detected in the primary auditory cortex.
Predicting spectral loudness summation by neuroimaging data
To separate the input to the auditory cortex which it receives from the auditory brainstem, the total response as detected in AB was subtracted from the total response as detected in the PAC (PSCs, as depicted in the middle and right panels of Fig. 3). To transform these PSC values into the psychophysical measure of perceived loudness, the loudness as measured by categorical loudness scaling for the stimulus with the full BW of 31.8 ± 4.7 cu was divided by the corresponding PSC in the PAC of 0.73% ± 0.26%. This yielded a calibration factor of 43.4 ± 12.8 cu/%. With this calibration factor, the difference of the PSC between PAC and AB of 0.23% would be transformed to a difference in perceived loudness of 9.9 cu. This value is very close to 9.4 cu which was measured by categorical loudness scaling for the mean difference between the stimulus with the full bandwidth and that exhibiting the lowest perceived loudness (1,500 Hz bandwidth). This calculation has been applied for all other bandwidths. The results are depicted in Figure 6. The correlation between the fMRI model predictions and the psychoacoustic scaling estimates was significant (r = 0.92, P = 0.01). The mean difference between both was 0.7 ± 2.4 cu, corresponding to a difference in sound pressure level smaller than 2 ± 7 dB.
Figure 6.
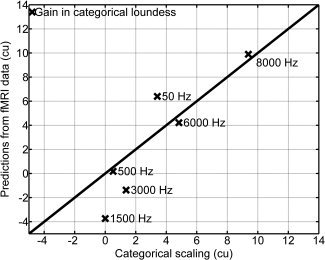
Loudness gain relative to the stimulus with the lowest perceived categorical loudness at 1,500 Hz BW as determined by categorical loudness scaling and predicted from neuroimaging data. The predictions are based on the comparison of the PSC between those PAC‐ and AB‐voxels for which the underlying BOLD‐signal as a function of bandwidth had a significant linear component.
Similar results were obtained for the six voxels which responded nonlinearly, as identified by the means of the linear systems analysis. From these six voxels, a calibration factor of 41.4 ± 12.2 cu/% was determined. Model predictions based on this factor result in similar outcomes. Again, a significant correlation between model predictions and psychoacoustic data was observed (r = 0.90, P = 0.02). The mean difference between neuroimaging model predictions and psychoacoustic scaling results was 0.1 ± 2.5 cu.
DISCUSSION
This study investigated the representation of bandwidth in auditory fMRI activation maps and its relation to loudness judgments using continuous pink noise. The stimuli were centered at 4,000 Hz and had a fixed sound pressure level of 70 dB SPL. Tested bandwidths ranged from 50 to 8,000 Hz. The main findings of this study were as follows: (1) Perceived loudness follows a nonlinear trend that is influenced by SLS for higher BW and by peak‐listening for lower BW, for which large fluctuations in amplitude become pronounced. (2) Both SLS and peak‐listening were most pronounced for medium sound pressure levels around 65 dB SPL. (3) Stimuli with a darker timbre activated the PAC more in lateral and anterior regions, while stimuli with a brighter timbre activated the PAC more in medial and posterior regions. (4) While the nonlinear trend of the perceptual measure of loudness was reflected by corresponding neural activation in the PAC in several aspects, the linear trend of the physical measure of bandwidth was reflected by corresponding neural activation in the auditory brainstem.
Perceived Loudness as a Function of Bandwidth and Sound Pressure Level
In this study, categorical loudness scaling was performed prior to the fMRI experiment to assess the influence of bandwidth on loudness. Most psychoacoustic measurements that investigated loudness with respect to bandwidth were designed as loudness balancing procedures where participants were required to adjust the level of a test stimulus to match the loudness of a given reference stimulus. To avoid biasing effects due to the choice of the reference stimulus, we used categorical scaling to track the effects of bandwidth on loudness. The scaling revealed that perceived loudness as a function of BW for a sound pressure level of 70 dB SPL (fMRI stimulus) had a minimum at 1,500 Hz, after which it was linearly increasing. Below 1,500 Hz, a significant increase of perceived loudness was observed, comparing stimuli with the bandwidths of 50 and 1,500 Hz. It has been suggested that the loudness of a sound that has large fluctuations in amplitude—such as the 50 Hz BW stimulus—is determined by the peak value of the sound pressure level rather than by its mean [Zwicker and Fastl, 1999]. Also, Zhang et al. [ 1997] report that stimuli with greater temporal fluctuations can produce a significantly louder sensation. While Zwicker et al. suggested that the effect of large amplitude fluctuations on loudness is determined by temporal integration with a time constant of about 100 ms, Zhang et al. assumed that the effect is determined by the absolute temporal resolution with a time constant one to two orders of magnitude lower. Since probably both temporal integration and temporal resolution may have an effect, a duration of 50 ms was used in the current study for the time window for which corresponding sound pressure levels were calculated. Using this window duration, the effect of large amplitude fluctuations could be predicted accurately. However, the difference between measured and predicted differences in perceived loudness was acceptably small (smaller than 1.5 cu) for a broad range of window durations from 2 to 160 ms. Therefore, an accurate estimate for the duration of the analysis windows for loudness judgments in relation to peak‐listening, discriminating the effects of temporal integration, and temporal resolution, appears to be difficult.
The increase of the loudness function beyond 1,500 Hz reflects the phenomenon of spectral loudness summation. SLS has been explained by the concept of the critical bands [Fletcher, 1940; Zwicker and Stevens, 1957]. Fletcher assumed that the peripheral auditory system behaves as if it contains a bank of overlapping bandpass filters. A typical measure of such an auditory filter is the equivalent rectangular bandwidth (ERB). The ERB at 4,000 Hz center frequency is estimated at 456 Hz [Glasberg and Moore, 1990]. The step sizes of bandwidths were comparatively large in this study, since it was not designed to yield an exact estimate of the ERB. However, the effect of modulation can almost be ruled out at or just slightly above 500 Hz, since the decrease of perceived loudness from 500 to 1,500 Hz is very small (smaller than 1 cu) and not significant. A further observation was that spectral loudness summation varies with overall sound pressure level, with the largest effect for medium levels. This finding is in line with the literature [Garnier et al., 1999; Zwicker and Stevens, 1957]. The finding that the effect of loudness summation is reversed and the perceived loudness decreases with increasing bandwidth at lower sound pressure levels has also been reported in the book of Zwicker and Fastl [ 1999]. When approaching the absolute threshold, the energy density gets too small to make the sound audible when the bandwidth is increased. A quite similar trend as observed for the gain due to SLS—as a function of sound pressure level—was observed for the effect of large amplitude fluctuations. Peak‐listening was most pronounced for medium sound pressure levels as well.
General Trend of Neural Activation
The almost common trend of the volume of activation and the location of the foci of activation in the auditory cortex were the first neural correlates derived from statistical parametric maps which suggested, that at least one acoustical feature other than bandwidth might be represented in the neural activation pattern. Neither of the two correlates followed the overall physical bandwidth monotonously, but merely the perceived loudness which had a reversal point at 1,500 Hz as well. This left open the question of whether neural activation below 1,500 Hz is additionally affected by modulation directly, or by loudness and, therefore, only indirectly by modulation. However, beyond 500 Hz, the effect of modulation, e.g. the large amplitude fluctuations, was negligible and, therefore, the influence of bandwidth on the location of activation foci was further investigated. The shift of the activation foci from medial to lateral, which was observed for stimuli with a bandwidth greater than 500 Hz, and which was significant in the left hemisphere, is in line with the concept of tonotopy. Because of the logarithmic frequency scaling of the basilar membrane, one would presume that an equal increase of bandwidth towards both sides of the center frequency places more energy in the low‐frequency range as compared to the high‐frequency range. This gives the stimuli a darker timbre when their bandwidth is increased. Therefore, stimuli with increasing bandwidth should strongly activate those regions with a higher sensitivity to low‐frequency stimuli. A tonotopic organization of the human auditory cortex with a low‐ to high‐frequency gradient oriented along HG in anterolateral to posteromedial direction has been described by several fMRI studies [Bilecen et al., 1998; Langers et al., 2007a; Schönwiesner et al., 2002; Talavage et al., 2000; Wessinger et al., 1997]. These are in line with our findings about the shift of the activation foci with timbre, e.g. bandwidth. More recent studies identified two mirror‐symmetric [Formisano et al., 2003] or even more gradients [Humphries et al., 2010; Talavage et al., 2004], with different orientations, that, in some cases, differ from the long axis of HG. Formisano et al. and Humphries et al. offered among others two plausible reasons for the apparent variability between studies: One reason might be the analysis procedure employed, e.g. volume‐based versus surface‐based data analysis. The second reason might be the different choice of the low‐ and high‐frequency endpoints of the investigated range.
While the influences of bandwidth, loudness and modulation could not be distinguished in the very first step of analysis, for lower BWs in particular, the comparison of activation induced by the stimulus with the full bandwidth against those which had a smaller one (and vice versa), allows for some further insight. For the bandwidth of 50 Hz, we found significantly more activation in the secondary auditory cortex as compared to the stimulus with the full BW. These findings are in line with Giraud et al. [ 2000]. They reported that nonprimary auditory areas respond more to dynamic and spectrally complex stimuli. A similar observation was made by Wessinger et al. [ 2001]. They reported that pure tone stimuli activate only a core region of the auditory cortex, whereas surrounding belt areas are only activated by narrow‐band noise bursts. This suggests that, restricting the analysis to areas in the primary auditory cortex, a region is investigated where bandwidth and loudness rather than modulation matter, although the effect of modulation on loudness might still be represented in the activation of the PAC. This was also the reason why the verification of the concept of tonotopy (in the PAC) was restricted to those cases (BW above 500 Hz) for which the stimuli activated mainly the PAC, but not the SAC.
Activation in the Auditory Brainstem
The first direct hint that the auditory brainstem is less prone to acoustical features other than bandwidth—like loudness or modulation—came from the analysis of the differential bandwidth volume. The observed trend suggested that the auditory brainstem responds more or less monotonously to increasing bandwidth. Although AB is smaller in size, it has shown not only the most systematic linear trend, but also the largest changes in the DV with increasing difference in bandwidth. A second direct hint came from linear systems analysis of the fMRI data. Here, it was found that the auditory brainstem was not only the region which showed the most statistically satisfying linear response, but also exhibited no significant nonlinear response at all. Activation in the auditory brainstem has been investigated by the means of auditory fMRI with cardiac‐gating by Hawley et al. [ 2005]. The authors report that neural activation increased monotonously with bandwidth in all brainstem nuclei (cochlear nucleus, superior olivary complex, and inferior colliculus), when stimulus spectrum or energy level was held constant. The region denoted as auditory brainstem in the present study refers mostly to the inferior colliculi. Our findings are therefore in line with Hawley et al., but we can specify that the increase of activation is indeed linearly related to bandwidth.
Activation in the Primary Auditory Cortex
Linear systems analysis allowed for an identification of those voxels for which the underlying BOLD‐signal as a function of bandwidth had a significant linear or quadratic (nonlinear) component. In contrast to AB, in PAC the PSC of those voxels reflected the trend of perceived loudness in several aspects: (1) The PSC comprised a significant nonlinear component, similar as the perceived loudness, in PAC only. (2) The total response in PAC had a similar Q NL/L of 0.33 as the perceived loudness for which Q NL/L was 0.28. (3) The PSC increased significantly stronger with bandwidth in PAC as compared to AB reflecting the increase of loudness with bandwidth due to SLS. These results give strong evidence that SLS may not be completed before PAC, while the effect of large amplitude fluctuations on loudness—the peak‐listening—appears to take place in PAC only. The remaining influence of the periphery on perceived loudness, especially SLS, could be excluded in further analysis. Here, just a simple rule of three has been applied. By means of the absolute differences of the PSC between PAC and AB, SLS and the effect of large amplitude fluctuations on perceived loudness could be predicted with a high accuracy of 1–2 dB for the whole group of participants. This simple calculation suggests that SLS may not only be incomplete before PAC, but rather that it takes place in PAC only.
One additional factor that should be taken into consideration when comparing neural activation between different brain areas (like PAC‐ and AB‐voxels in this study), is the efficiency of the neurovascular coupling [Logothetis and Wandell, 2004]. If this hemodynamic efficiency would be greater in the PAC as compared to the AB, our predictions based on a subtraction procedure would overestimate the effect of spectral loudness summation. In a recent study on loudness [Röhl and Uppenkamp, 2009], we observed a similar activation of auditory cortex and brainstem for the general effect of sound presentation. This can be interpreted as an indication that the hemodynamic efficiency is similar between both areas. Recent results on the time course of the BOLD response in cortical and subcortical structures in nonhuman primates by Baumann et al. [ 2010] can also be interpreted as an indication that the hemodynamic efficiency is similar for PAC and AB.
To our knowledge, there have been no fMRI‐studies investigating the effects of bandwidth in the human auditory cortex so far. Langers et al. [ 2007b] investigated the effect of loudness and intensity. They report that, for an area of the auditory cortex in which the correlation between the BOLD‐signal intensity and loudness level is strong, the BOLD‐signal intensity is almost linearly related to perceived loudness and sound intensity. Comparing the results of normal‐hearing and hearing‐impaired listeners, Langers et al. conclude that the BOLD‐signal is related to loudness rather than physical sound intensity. In a previous study, we also found for normal hearing listeners that in the AC, but not in the AB, the PSC of those voxels that were sensitive to sound was significantly correlated to the perceived loudness of acoustic stimuli [Röhl and Uppenkamp, 2009]. In that study, pink noise stimuli of 8,000 Hz BW were used at different SPLs. Combining the results of Hawley et al., Langer et al. and Röhl et al., the most simple interpretation would be, that AC is fed by the PSC of the auditory brainstem according to the sound pressure level and the bandwidth of the stimuli, and an additional component is added which is linearly related to the perceived loudness. This is exactly what was found for the voxels in the AC for which the BOLD‐intensity was tuned to bandwidth (either linear or nonlinear).
From this point of view, the striking results of Soeta et al. [ 2006, 2005] can also be interpreted: In their studies, psychoacoustic measurements on the perceived loudness had not been performed, but rather a simple model of spectral loudness summation was used—although acknowledging that subjects not necessarily perceive corresponding loudness increases when the critical bandwidth is exceeded. In Soeta et al. [ 2005], spectral loudness summation was probably outperformed by the effect of the large amplitude fluctuations on loudness for their very narrow band stimuli having a bandwidth between 1 and 320 Hz; In Soeta et al. [ 2006], stimuli were used that had bandwidths between 20 Hz and 1,000 Hz which fell in the critical range for SLS. Therefore, N1m amplitudes in the 2005 study possibly decreased with bandwidth, because amplitude fluctuations decreased with increasing bandwidth and thus the perceived loudness as well. Corresponding to that, N1m amplitudes in the 2006 study increased with bandwidth, reflecting SLS. However, varying pitch strength of all narrow‐band stimuli or problems with sound presentation associated with the use of plastic tubes also might be issues of concern.
A common problem of many parametric studies in psychophysics including this one is that it is difficult to change a sound along one parameter axis without influencing other psychoacoustical parameters that can act as confounders on the dependent variable. In our case, we were interested in the effect of spectral bandwidth and the related change in perceived loudness on neural activation. Confounders can be addressed either directly by collecting additional data on it, or by considering possible effects on the dependent variable that are already known when interpreting the results. Two confounds can be identified in our design. The first is the additional change of timbre with the additional involvement of low frequencies. The second is the additional effect of amplitude modulation at the very narrow bandwidth condition.
Possible effects of a change in timbre on neural activation could only be considered during the interpretation of the results because of the current study design. Another strategy would be to center the noise bands on a logarithmic scale rather than a linear scale throughout the experiment. The difference between these strategies in the design of the band‐widening experiment is comparatively small for bandwidths up to about 3 kHz. For larger bandwidths, however, the linearly and logarithmically centered frequency bands will sound somewhat different. Nevertheless, both these strategies will equally result in a wide band signal with a pronounced change of timbre relative to the narrowband conditions.
One way to avoid possible confounding effects of the amplitude modulation in the small bandwidth conditions might have been to employ a similar modulation also in the conditions with the wider bandwidths. However, it is not clear whether this strategy would introduce an additional confound due to a possible interaction between bandwidth and amplitude modulation. Therefore, to keep it simple and to ensure methodological comparability with previous studies on loudness [Röhl and Uppenkamp, 2009, 2010], the stimuli were, in their majority, chosen not to be modulated. This allowed us to compare the full bandwidth conditions across both studies (N 1 = 44/45, N 2 = 22). There was no significant difference in the 70 dB SPL conditions between both studies.
CONCLUSION
Gains in perceived loudness due to SLS and the effect of large amplitude fluctuations on loudness are reflected by differences in neural activation between the PAC and the AB. While neural activation in the auditory brainstem reflects physical bandwidth in a linear fashion, a link between perceived loudness and neural activation could be solely observed in the PAC.
Acknowledgements
We thank all volunteers for participating in this study.
REFERENCES
- Algom D, Marks LE ( 1990): Range and regression, loudness scales, and loudness processing: Toward a context‐bound psychophysics. J Exp Psychol Hum Percept Perform 16: 706–727. [DOI] [PubMed] [Google Scholar]
- Appell JE ( 2002): Loudness Models for Rehabilitative Audiology. Oldenburg: University of Oldenburg. [Google Scholar]
- Baumann S, Griffiths TD, Rees A, Hunter D, Sun L, Thiele A. ( 2010): Characterisation of the BOLD response time course at different levels of the auditory pathway in non‐human primates. 50: 1099–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bilecen D, Scheffler K, Schmid N, Tschopp K, Seelig J ( 1998): Tonotopic organization of the human auditory cortex as detected by BOLD‐FMRI. Hearing Res 126: 19–27. [DOI] [PubMed] [Google Scholar]
- Bowman AW, Azzalini A ( 1997): Applied Smoothing Techniques for Data Analysis. Oxford University Press. [Google Scholar]
- Chalupper J, Fastl H ( 2002): Dynamic loudness model (DLM) for normal and hearing‐impaired listeners. Acta Acustica United with Acustica 88: 378–386. [Google Scholar]
- Edmister WB, Talavage TM, Ledden PJ, Weisskoff RM ( 1999): Improved auditory cortex imaging using clustered volume acquisitions. Hum Brain Mapp 7: 89–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein M, Florentine M ( 2009): Binaural loudness summation for speech and tones presented via earphones and loudspeakers. Ear Hear 30: 234–237. [DOI] [PubMed] [Google Scholar]
- Fletcher H ( 1940): Auditory patterns. Rev Modern Phys 12: 47. [Google Scholar]
- Formisano E, Kim DS, Di Salle F, van de Moortele PF, Ugurbil K, Goebel R ( 2003): Mirror‐symmetric tonotopic maps in human primary auditory cortex. Neuron 40: 859–869. [DOI] [PubMed] [Google Scholar]
- Gaab N, Gabrieli JD, Glover GH ( 2007a): Assessing the influence of scanner background noise on auditory processing. I. An fMRI study comparing three experimental designs with varying degrees of scanner noise. Hum Brain Mapp 28: 703–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaab N, Gabrieli JD, Glover GH ( 2007b): Assessing the influence of scanner background noise on auditory processing. II. An fMRI study comparing auditory processing in the absence and presence of recorded scanner noise using a sparse design. Hum Brain Mapp 28: 721–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel B, Kollmeier B, Mellert V ( 1997): Influence of individual listener, measurement room and choice of test‐tone levels on the shape of equal‐loudness level contours. Acta Acustica United with Acustica 83: 670–683. [Google Scholar]
- Garnier S, Micheyl C, Arthaud P, Berger‐Vachon C, Collet L ( 1999): Temporal loudness integration and spectral loudness summation in normal‐hearing and hearing‐impaired listeners. Acta Otolaryngol 119: 154–157. [DOI] [PubMed] [Google Scholar]
- Giraud AL, Lorenzi C, Ashburner J, Wable J, Johnsrude I, Frackowiak R, Kleinschmidt A ( 2000): Representation of the temporal envelope of sounds in the human brain. J Neurophysiol 84: 1588–1598. [DOI] [PubMed] [Google Scholar]
- Glasberg BR, Moore BCJ ( 1990): Derivation of auditory filter shapes from notched‐noise data. Hear Res 47: 103–138. [DOI] [PubMed] [Google Scholar]
- Greenwood DD ( 1990): A cochlear frequency‐position function for several species – 29 years later. J Acoust Soc Am 87: 2592–2605. [DOI] [PubMed] [Google Scholar]
- Griffiths TD, Uppenkamp S, Johnsrude I, Josephs O, Patterson RD ( 2001): Encoding of the temporal regularity of sound in the human brainstem. Nature Neurosci 4: 633–637. [DOI] [PubMed] [Google Scholar]
- Grimm G, Hohmann V, Verhey JL ( 2002): Loudness of fluctuating sounds. Acta Acustica United with Acustica 88: 359–368. [Google Scholar]
- Hall DA, Haggard MP, Akeroyd MA, Palmer AR, Summerfield AQ, Elliott MP, Gurney EM, Bowtell RW ( 1999): Sparse temporal sampling in auditory fMRI. Hum Brain Mapp 7: 213–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawley ML, Melcher JR, Fullerton BC ( 2005): Effects of sound bandwidth on fMRI activation in human auditory brainstem nuclei. Hear Res 204: 101–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heller O ( 1985): Hörfeldaudiometrie mit dem Verfahren der Kategorienunterteilung. Psychologische Beiträge 27: 478–493. [Google Scholar]
- Humphries C, Liebenthal E, Binder JR ( 2010): Tonotopic organization of human auditory cortex. NeuroImage 50: 1202–1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kollmeier B ( 1997): Hörflächenskalierung—Grundlagen und Anwendungen der kategorialen Lautheitsskalierung für Hördiagnostik und Hörgeräte‐Versorgung. Heidelberg: median‐verlag Killisch‐Horn GmbH. [Google Scholar]
- Langers DRM, Backes WH, van Dijk P ( 2007a): Representation of lateralization and tonotopy in primary versus secondary human auditory cortex. NeuroImage 34: 264–273. [DOI] [PubMed] [Google Scholar]
- Langers DRM, van Dijk P, Schoenmaker ES, Backes WH ( 2007b): fMRI activation in relation to sound intensity and loudness. NeuroImage 35: 709–718. [DOI] [PubMed] [Google Scholar]
- Leibold LJ, Jesteadt W ( 2007): Use of perceptual weights to test a model of loudness summation. J Acoust Soc Am 122: EL69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Wandell BA ( 2004): Interpreting the BOLD signal. Annu Rev Physiol 66: 735–769. [DOI] [PubMed] [Google Scholar]
- Menzel D, Fastl H, Graf R, Hellbrück J ( 2008): Influence of vehicle color on loudness judgments. J Acoust Soc Am 123: 2477–2479. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Brugge JF ( 1973): Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res 50: 275–296. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Glasberg BR ( 2004): A revised model of loudness perception applied to cochlear hearing loss. Hear Res 188: 70–88. [DOI] [PubMed] [Google Scholar]
- Moore BCJ ( 2003): An Introduction to the Psychology of Hearing. London: Academic Press. [Google Scholar]
- Morel A, Garraghty PE, Kaas JH ( 1993): Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol 335: 437–459. [DOI] [PubMed] [Google Scholar]
- Rademacher J, Morosan P, Schormann T, Schleicher A, Werner C, Freund HJ, Zilles K ( 2001): Probabilistic mapping and volume measurement of human primary auditory cortex. Neuroimage 13: 669–683. [DOI] [PubMed] [Google Scholar]
- Röhl M, Uppenkamp S ( 2009): A Detailed view at FMRI activation maps in relation to sound intensity and loudness In: PA Santi, editor. Assoc Res Otolaryngol Abs 32: 293–294. [Google Scholar]
- Röhl M, Uppenkamp S ( 2010): An auditory fMRI correlate of impulsivity. Psychiatry Res 181: 145–150. [DOI] [PubMed] [Google Scholar]
- Scharf B ( 1961): Complex sounds and critical bands. Psychol Bull 58: 205–217. [DOI] [PubMed] [Google Scholar]
- Schmidt CF, Zaehle T, Meyer M, Geiser E, Boesiger P, Jancke L ( 2008): Silent and continuous fMRI scanning differentially modulate activation in an auditory language comprehension task. Hum Brain Mapp 29: 46–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schönwiesner M, von Cramon DY, Rübsamen R ( 2002): Is it tonotopy after all? NeuroImage 17: 1144–1161. [DOI] [PubMed] [Google Scholar]
- Soeta Y, Nakagawa S ( 2006): Complex tone processing and critical band in the human auditory cortex. Hear Res 222: 125–132. [DOI] [PubMed] [Google Scholar]
- Soeta Y, Nakagawa S, Tonoike M ( 2005): Auditory evoked magnetic fields in relation to bandwidth variations of bandpass noise. Hear Res 202: 47–54. [DOI] [PubMed] [Google Scholar]
- Stephens SD ( 1970): Personality and the slope of loudness function. Q J Exp Psychol 22: 9–13. [DOI] [PubMed] [Google Scholar]
- Talavage TM, Ledden PJ, Benson RR, Rosen BR, Melcher JR ( 2000): Frequency‐dependent responses exhibited by multiple regions in human auditory cortex. Hearing Res 150: 225–244. [DOI] [PubMed] [Google Scholar]
- Talavage TM, Sereno MI, Melcher JR, Ledden PJ, Rosen BR, Dale AM ( 2004): Tonotopic organization in human auditory cortex revealed by progressions of frequency sensitivity. J Neurophysiol 91: 1282–1296. [DOI] [PubMed] [Google Scholar]
- Verhey JL, Uhlemann M ( 2008): Spectral loudness summation for sequences of short noise bursts. J Acoust Soc Am 123: 925–934. [DOI] [PubMed] [Google Scholar]
- Wessinger CM, Buonocore MH, Kussmaul CL, Mangun GR ( 1997): Tonotopy in human auditory cortex examined with functional magnetic resonance imaging. Hum Brain Mapp 5: 18–25. [DOI] [PubMed] [Google Scholar]
- Wessinger CM, Tian B, van Lare J, Pekar J, Rauschecker JP ( 2001): Hierarchical organization of the human auditory cortex revealed by functional magnetic resonance imaging. J Cogn Neurosci 13: 1–7. [DOI] [PubMed] [Google Scholar]
- Zhang C, Zeng FG ( 1997): Loudness of dynamic stimuli in acoustic and electric hearing. J Acoust Soc Am 102: 2925–2934. [DOI] [PubMed] [Google Scholar]
- Zwicker E, Fastl H ( 1999): Psychoacoustics. Heidelberg: Springer‐Verlag. [Google Scholar]
- Zwicker E, Flottorp G, Stevens SS ( 1957): Critical bandwidths in loudness summation. J Acoust Soc Am 29: 548–557. [Google Scholar]


