Abstract
This work presents a novel method of mapping the brain's response to single stimuli in space and time without prior knowledge of the paradigm timing: paradigm free mapping (PFM). This method is based on deconvolution of the hemodynamic response from the voxel time series assuming a linear response and using a ridge‐regression algorithm. Statistical inference is performed by defining a spatio‐temporal t‐statistic and by controlling for multiple comparisons using the false discovery rate procedure. The methodology was validated on five subjects who performed self‐paced and visually cued finger tapping at 7 Tesla, with moderate (TR = 2 s) and high (TR = 0.4 s) temporal resolution. The results demonstrate that detection of single‐trial BOLD events is feasible without a priori information on the stimulus paradigm. The proposed method opens up the possibility of designing temporally unconstrained paradigms to study the cortical response to unpredictable mental events. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.
Keywords: brain mapping, MRI, event‐related, single‐trial analysis, deconvolution, motor cortex
INTRODUCTION
Mapping the cortical response to a single mental event in both space and time is essential to improve our understanding of the basis of human perception and cognition. fMRI paradigms typically use event‐related (ER) designs [Humberstone et al.,1997] to study individual cognitive events and to analyze the cortical response to isolated trials. The traditional approach in ER‐fMRI analysis is to average across several single trial responses to improve estimation of the hemodynamic response parameters [Bellgowan et al.,2003], but this assumes that the hemodynamic response amplitude and shape is constant across trials [Buckner et al.,1996]. It is generally assumed that this improvement is proportional to the square root of the number of trials averaged. However, there is intrinsic variability in the observed hemodynamic response function (HRF) between successive trials (inter‐trial variability) and across subjects (inter‐subject variability) [Aguirre et al.,1998; Duann et al.,2002; Handwerker et al.,2004], which may arise not only from physiological effects, motion, and systematic confounds such as magnetic field inhomogeneities but also from uncontrolled changes in the subject's attention or performance. Although averaging responses across trials improves sensitivity to the basic response to a task, it removes sensitivity to the variability in the response to a task, which may be important for understanding finer aspects of mental processing, such as learning or adaptation, or in pharmacological studies [Bingel et al.,2002; Gonzalo et al.,2000]. Furthermore, in many studies, an exact temporal model of the expected BOLD signal change cannot be predicted in advance and in this case paradigm‐free methods may be helpful, for example, in studies of hallucinations in schizophrenia or interictal discharges in epilepsy, or cognitive paradigms which involve switching in the subject's perception such as visual priming or binocular rivalry, and where the subject's behavioral response is difficult to be recorded accurately. In addition, unpredicted activation may provide novel information about task‐unrelated brain activity during resting periods. Therefore, there is a critical need for alternative approaches to fMRI analysis which do not require the onsets of cortical responses to be specified, and which allow the use of more unconstrained experimental paradigms [Faisan et al.,2007; Hutchinson et al.,2009; Lindquist et al.,2007].
Ultrahigh field fMRI provides sufficient BOLD contrast to noise ratio to allow the detection of the response to single trials in fMRI paradigms [Pfeuffer et al.,2002; Ugurbil et al.,1999]. Single trial fMRI was initially used to describe the sequence of activations related to single motor [Richter et al.,1997a], mental rotation [Richter et al.,1997b,2000], and visual tasks [Menon et al.,1998], but has been extended to study more complex cognitive tasks, such as the observation of one's own and other's actions [Cunnington et al.,2006] or pain processing [Bingel et al.,2002]. Nevertheless, these studies have used prior knowledge of the stimulus or paradigm timing.
If there is no information on when the activation occurs or the shape of the HRF, data‐driven analysis approaches such as clustering [Fadili et al.,2000; Goutte et al.,1999; Richter et al.,2000], principal component analysis (PCA) [Andersen et al.,1999; Baumgarter et al.,2000], independent component analysis (ICA) [Beckmann and Smith,2004; Calhoun and Adali,2006; McKeown et al.,1998], and Temporal Clustering Analysis (TCA) [Liu et al.,2000; Morgan et al.,2008] can be used. However, these analysis techniques require the researcher to estimate a priori the number of components or clusters, and then to select and interpret the relevant components or clusters. These methods can be useful in the search for voxels showing consistent spatial or temporal patterns or when decomposing the data into components to be used as regressors in a general linear model analysis. Nevertheless, in searching for cortical responses, these methods couple voxels together based on some feature (e.g., based on the time of their first activation in TCA), and so this approach would not be useful if the same regions were activated in response to two different stimuli [Morgan et al.,2008].
Model‐based approaches have also previously been developed to analyze data with no timing constraints. Probabilistic frameworks based on Hidden Markov modes [Faisan et al.,2007; Hutchinson et al., 2009] have enabled spatio‐temporal mapping of the response but have not been used for single trial analysis. Alternatively, change point theory methods have been proposed to estimate the onsets and durations of activations by modeling the voxel time series as a mixture of two Gaussian distributions (baseline and activation) [Lindquist et al.,2007]. Before fitting the Gaussian mixture model, Lindquist et al. [2007] suggested first temporally smoothing the voxel time series with an Exponentially Weighted Moving Average (EWMA) filter and then testing for significant changes in the filtered time series by using a Hotelling T 2‐test comparing to a baseline state. However, change point theory methods have only been used to detect activation associated with single‐epoch paradigms with prolonged activations.
Here, we present a novel method, Paradigm Free Mapping (PFM), which aims to detect and characterize the cortical response to single‐trial events or actions with no prior information about the timing or location of the events. This method is based on the mathematical deconvolution of the HRF from the voxel time series by means of ridge‐regression estimation [Hastie et al.,2001; Hoerl and Kennard,1970], the definition of temporal t‐statistics to detect points of significant change [Lindquist et al.,2007] in the deconvolved signal, and multiple hypothesis correction by the false discovery rate (FDR) procedure [Benjamini and Hochberg,1995; Genovese et al.,2002]. The output of the proposed method is a temporal sequence of t‐maps, which depict the spatial and temporal extent of brain activity associated with single trial events in a simple and exploratory manner, without any knowledge of the paradigm timing.
THEORY
The proposed method is a two‐stage approach. The first stage is based on the voxel‐wise deconvolution of the HRF from the time series by means of the ridge regression estimator, assuming linearity [Boyton et al.,1996; Gitelman et al.,2003]. Statistical noise characterization is performed voxel‐wise and is based on an autoregressive model whose parameters are estimated using Levinson‐Durbin recursion prior to deconvolution of the HRF. The second stage involves calculating a temporal t‐statistic from the deconvolved signal at each voxel, similar to Lindquist et al. [2007], and then statistically assessing the significance of activations using an FDR procedure to account for multiple hypothesis testing [Genovese et al.,2002].
Ridge Regression Deconvolution
In the absence of noise and assuming a linear, time‐invariant model, the measured BOLD fMRI time series, y(t), can be modeled as the convolution of an input signal, s(t), and the HRF, h(t),
| (1) |
where L is the discrete‐time length of the HRF. This discrete time model can be rewritten in matrix formulation as
| (2) |
where y and s are column vectors of length N (N being the number of time points of the fMRI time series), and H is the convolution (Toeplitz) matrix of dimension N × N defined from the HRF. In this work we used the canonical HRF from Statistical Parametric Mapping (SPM), which is based on two gamma variate functions [Friston et al.,1998]. The goal is to compute an estimate of the input signal, s.
In practice, however, the fMRI signal also includes physiological and other fluctuations which can be incorporated in the signal model as an additive, global noise term, ε,
| (3) |
Here, the noise is assumed to be a stationary, stochastic, normal process with zero mean, variance σ2 and temporal covariance matrix Σ, that is, ε ∼ N(0, σ2 Σ), and this covariance matrix is assumed to be voxel dependent to take account of variations in the noise characteristics observed across regions and tissues [Woolrich et al.,2001].
Assuming normally distributed noise with a fixed general covariance matrix Σ, the generalized least squares (GLS) estimator yields the maximum likelihood estimator of s. However, since the columns of the convolution matrix, H, are highly correlated, the GLS estimates can become poorly determined and exhibit high variance [Gitelman et al.,2003; Hastie et al.,2001]. In addition, GLS estimators can fail to calculate accurate estimates when there is error in the model formulation, such as a mismatch between the canonical HRF used in the model and the true HRF of the data. One solution to these problems is to impose a regularization term on (penalization of) the coefficient estimates [Hastie et al.,2001]. The ridge regression (RR) algorithm [Hoerl and Kennard,1970], also known as regularized least squares, computes an estimate of s (s RR) by simultaneously minimizing the variance of the residuals and the power (i.e., L2‐norm) of the resulting estimate of the input signal s:
| (4) |
where λ is the regularization parameter which controls the trade off between both terms. The RR estimate is then given by
| (5) |
When λ
 0, the RR estimator reduces to the GLS estimator (we denote the solution with λ = 0 as ŝGLS). The choice of λ is important to ensure that the RR algorithm computes reasonable estimates. Here, we used the following expression for the regularization parameter [Selén et al.,2008],
0, the RR estimator reduces to the GLS estimator (we denote the solution with λ = 0 as ŝGLS). The choice of λ is important to ensure that the RR algorithm computes reasonable estimates. Here, we used the following expression for the regularization parameter [Selén et al.,2008],
| (6) |
where
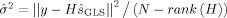 is the variance of the residuals after fitting the GLS estimate, ŝ
GLS (note that the rank of H is N−1 and therefore the denominator is equal to 1). Thus the regularization parameter was the quotient of estimates of the variances of the noise and the input signal. Alternative selection criteria for the regularization parameter could be considered such as L‐curve [Hansen and O'Leary,1993], cross‐validation methods [Hastie et al.,2001], or Empirical Bayes algorithms [Gitelman et al.,2003].
is the variance of the residuals after fitting the GLS estimate, ŝ
GLS (note that the rank of H is N−1 and therefore the denominator is equal to 1). Thus the regularization parameter was the quotient of estimates of the variances of the noise and the input signal. Alternative selection criteria for the regularization parameter could be considered such as L‐curve [Hansen and O'Leary,1993], cross‐validation methods [Hastie et al.,2001], or Empirical Bayes algorithms [Gitelman et al.,2003].
Noise Autocorrelation Estimation
To improve robustness of the temporal covariance estimation, the noise, ε, was modeled as an auto‐regressive, stochastic process of order p, AR(p) [Stoica and Moses,2005; Woolrich et al.,2001]. The noise covariance matrix was estimated from a set of baseline volumes, B, acquired at the start of the time series while the subjects were instructed to remain at rest (see Fig. 1a). Voxelwise estimation of the autocorrelation coefficients, r(i), was performed before deconvolution of the hemodynamic response, considering a set of K neighboring voxels, so that spatial information about the noise is incorporated into the model:
| (7) |
where y k is the vector of baseline observations for the kth voxel. From those coefficients, the AR model parameters for each candidate order p (a i, i = 1,…, p) were computed recursively using the Levinson‐Durbin (LD) algorithm [Stoica and Moses,2005]. The final choice of the model order, p̂, was based on the finite sample Minimum Description Length (MDL) criterion [De Ridder et al.,2005]:
| (8) |
where
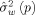 is the residual variance estimated by the LD algorithm for order p. The covariance matrix Σ was then calculated from the AR parameters corresponding to the optimal model order, p̂ [Stoica and Moses,2005].
is the residual variance estimated by the LD algorithm for order p. The covariance matrix Σ was then calculated from the AR parameters corresponding to the optimal model order, p̂ [Stoica and Moses,2005].
Figure 1.
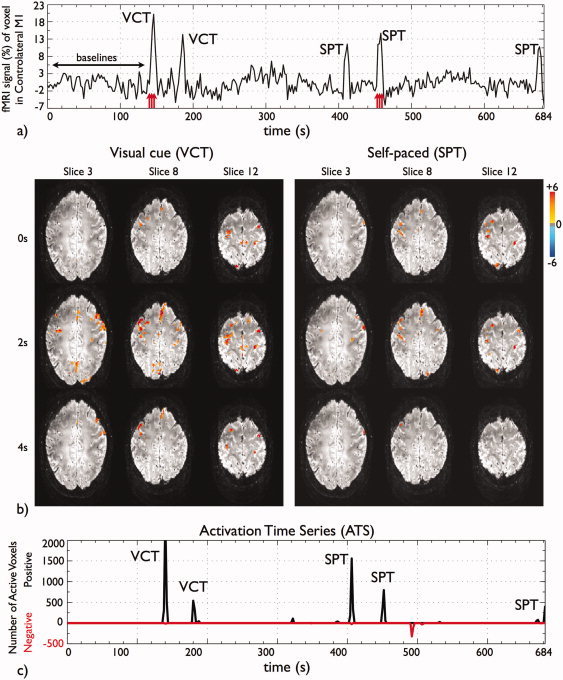
Data for subject A and dataset of TR 2 s (a) pre‐processed and normalized fMRI time series of a voxel located in the contralateral primary motor cortex. The figure illustrates the initial baseline volumes B used to estimate the noise covariance matrix and to compute the statistics and the VCT and SPT events; (b) time course of t‐maps of the second VCT and SPT trials, as indicated by the red arrows in Figure 1a. The times shown on the left are relative to the movement onset as recorded by the EMG signals. Activity is detected (P value < 0.05, FDR‐corrected) in SMA, bilateral PM, M1 and S1, inferior and superior parietal cortex and visual cortex; (c) fMRI ATS showing the number of voxels exceeding threshold (P value < 0.05, FDR‐corrected) per time point. Note that all finger tapping events are detected. In addition, the subject performed an additional finger‐tapping of approximately 2 s close to the end of the scanning period, contrary to given instructions, which was confirmed by questioning post‐scanning. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Statistical Inference
To test for the presence of activation statistically, a t‐statistic time course was defined from the RR estimates given in Eq. (5), comparing the signal at each time point to the mean of the corresponding baseline for each voxel [Lindquist et al.,2007]. Significant deviation from the mean estimated during the baselines would cause the null hypothesis of non‐activation to be rejected for this voxel and time point. For each time point i after the baseline period, the t‐statistic time series was computed over the L nearest neighboring voxels as
| (9) |
where ŝ
(i) was the spatial mean of the ridge regression estimates at voxel k at time i, and
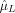 and
and
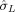 are the mean and variability of the baseline period (1 ≤ i ≤ B) taking into account the correlation of the deconvolved time series, all calculated over the neighboring L voxels. Note that the t‐statistics are not independent in time. Each temporal t‐statistic has a marginal Student's t distribution with B−1 degrees of freedom assuming the observations in the baseline are independent of that at time point i (i > B) (see Appendix for full details). Then, P values were computed from the t‐statistics at each voxel and at each time point.
are the mean and variability of the baseline period (1 ≤ i ≤ B) taking into account the correlation of the deconvolved time series, all calculated over the neighboring L voxels. Note that the t‐statistics are not independent in time. Each temporal t‐statistic has a marginal Student's t distribution with B−1 degrees of freedom assuming the observations in the baseline are independent of that at time point i (i > B) (see Appendix for full details). Then, P values were computed from the t‐statistics at each voxel and at each time point.
The total number of tests was equal to the number of voxels being tested, multiplied by the number of time points, and was much greater than conventional statistical parametric approaches where a single statistic is computed per voxel. Because of the large amount of spatial and temporal correlation of the P values, correcting in both space and time would considerably reduce the sensitivity of the method. Therefore, to deal with multiple hypothesis testing, the P values were corrected in space for each time point individually by means of the FDR procedure [Benjamini and Hochberg,1995; Genovese et al.,2002]. Given an FDR rate, a time series was computed with the t‐threshold for each time point.
METHODS
Experiments were conducted with approval from the University of Nottingham ethics committee and informed consent was obtained from all participants.
Experimental Paradigm
Six subjects (five male and one female, age 24–32 years, five right‐handed and one left‐handed) were scanned. Experiments were performed with BOLD acquisition at repetition times (TR) of 2 s and 0.4 s. Each scan started with an initial baseline (rest) period of 140 s. This resulted in B = 70 baseline time points for TR 2 s and B = 345 baseline time points for TR 0.4 s. After this initial baseline, the subjects were visually cued to perform two trials of finger tapping (VCT) at 140 s and 180 s, each finger tapping trial being 4 s in duration. After 384 s, a message (“TAP at will”) was projected onto the screen indicating the start of the second period during which subjects were asked to carry out freely two trials of self‐paced finger tapping (SPT) of similar duration to the VCT task. Throughout the scan duration, subjects were instructed to fixate on a cross projected onto the screen when no other instruction was presented. Subjects were instructed about the paradigm prior to the scanning session. The visual instructions were projected from an LCD projector onto a screen located inside the scanner room, which subjects viewed through prism glasses with angle mirrors. The total scan duration was 684 s (342 scans for TR 2 s, after five scans discarded to achieve steady‐state magnetization, and 1710 scans for TR 0.4 s, after 30 scans discarded).
MR Data Acquisition
MR images were acquired on a Philips 7T Achieva scanner (Best, Netherlands) using a 16‐channel head coil (Nova Medical, MA). Subjects' heads were secured in place using foam pads to minimize head motion. Cardiac and respiratory data were recorded throughout the fMRI acquisition using a respiratory belt and a pulse oximeter to allow physiological noise correction of the data. Datasets were acquired using single‐shot, gradient echo EPI (TE 30 ms, in‐plane resolution 2 × 2 mm2, slice thickness 2 mm, SENSE factor 1.5) with 20 slices for the TR 2 s and six slices for TR 0.4 s. The flip angle was set to 80° or 40°, which approximated the Ernst angle for each TR, respectively. At TR 2 s, the imaging slices were positioned at approximately +15° to the canto‐meatal line above the corpus callosum, to cover the supplementary motor area (SMA), premotor (PM) and primary motor (M1) cortices, parietal cortex, and the calcarine fissure. At TR 0.4 s, a more tilted angle and 1 mm gap between slices was used to cover approximately the same brain regions in fewer slices. Following the fMRI acquisition, high‐resolution 1 mm isotropic resolution 3D anatomical T1‐weighted (MPRAGE sequence) and T2*‐weighted (spoiled‐FLASH sequence) images were acquired to aid the localization of brain regions.
Surface Electromyography Recording and Analysis
Surface electromyography (EMG) was used to monitor the muscle activity in both hands during the fMRI experiment. Active electrode pairs were positioned on the left extensor (LE), right extensor (RE), and right flexor (RF) digitorum with paired electrode wires twisted to minimize the differential effect of the magnetic field on the EMG leads [van Rootselaar et al.,2007]. Ground and reference electrodes were positioned on bony parts of the wrist. Although subjects were instructed to perform finger tapping with their dominant hand (five right‐hand subjects and one left‐hand subject), EMG signals from both hands were recorded. EMG recording was performed using a Brain Vision recorder and a MR compatible BrainAmp amplifier (Brain Products, Munich, Germany). The amplifier was placed at the foot of the scanner bed on foam to minimize the effects of vibration. EMG signals were transmitted via an optical cable and recorded on a PC outside the scanner room. Data were sampled at 5000 Hz/channel and EMG analysis performed using Brain Vision Analyzer software. The quality of the EMG signals was checked visually prior to scanning and during the fMRI acquisition. EMG data were corrected for scanner artifacts using the average artefact subtraction method [Allen et al.,2000]. The differential signal between each active electrode pair was then calculated, a high pass filter with a 10 Hz cut‐off frequency applied and EMG signals rectified [Francis et al.,2009; van Rootselaar et al.,2007].
fMRI Data Analysis
fMRI datasets were motion corrected and the realignment parameters were visually assessed for task‐related movements, particularly at the times of the finger tapping events. This resulted in two datasets from one subject (left‐handed) being discarded due to significant motion during the self‐paced finger tapping period. The remaining five subjects' 10 datasets were corrected for physiological noise using RETROICOR [Glover et al.,2000]. In‐brain, non‐CSF voxels were then masked for further analysis. Detrending was performed by deconvolving the voxel time series with up to 4th‐order Legendre polynomials, and the sine and cosine signals with one cycle over the scan duration. These steps were performed using AFNI [NIMH/NIH, Cox,1996]. Each voxel time series was then normalized to the mean value of its baseline volumes to compute the percentage signal change.
Each dataset was then analyzed using the PFM method described in the Theory section, implemented using in‐house software written in Matlab (The Mathworks, Natick, MA). The autocorrelation matrix was estimated from the baseline volumes (see Fig. 1a). In contrast to other approaches that assume a constant autocorrelation matrix across the whole brain, here we computed it on a voxelwise basis, and then averaged it over the three‐dimensional nearest neighbors (K = 27), although smaller kernels were used at mask boundaries (minimum K = 6). In the subsequent voxel‐wise calculation of the AR coefficients, candidate orders in the range 0–3rd were considered since it was observed that for the finite‐sample minimum description length (MDL) criterion selection [De Ridder et al.,2005] voxels with model order higher than 3 were mainly located on large veins and CSF regions. Ridge regression (RR) deconvolution was performed using a two gamma‐variate HRF with standard SPM (FIL/UCL) parameters [Friston et al.,1998] sampled at the corresponding TR. To increase the speed of the algorithm, the deconvolution based on the RR algorithm was performed in blocks of 50 scans (TR 2 s) and 150 scans (TR 0.4 s) with the regularization parameter computed from the first block. To validate this procedure, the analysis was repeated for several block lengths, and block length was found to have negligible effect on the results provided that the duration of the block was longer than the HRF. Following the RR deconvolution, t‐statistics were computed using the five closest in‐plane voxels (L = 5) and t‐maps were then thresholded at a P value of 0.05 (FDR‐corrected). Finally, spatial clustering was applied to the thresholded maps with a minimum 3D cluster size of 5 voxels. The resulting t‐maps were then overlaid on the T1‐weighted and T2*‐weighted anatomical images which were resampled to EPI space using a 12‐parameter affine spatial transformation.
A problem with paradigm‐free fMRI analysis is that the whole data set must be explored to determine when interesting cortical events occur; two methods were developed to address this. First, an activation movie was created from the time series of thresholded t‐maps to allow qualitative visualization of when coordinated activation occurred across the cortex. Second, an activation time series (ATS) was created to compress this 4D data set (the movie) into a 1D plot that highlighted periods when coordinated activation occurred across the cortex (see Fig. 1c). This diagram contains two lines to separate positive and negative BOLD events: the positive going line (black) plots the number of voxels exceeding the t‐threshold with positive signal amplitude at each time point, whereas the negative going line (red) similarly plots voxels with negative signal amplitude.
Two further statistical maps were generated for each activation event: a “Statistical Map” and a “Delay Map.” All activation events involving more than 100 voxels on the ATS were investigated, including events associated with a finger tap and events detected during apparent periods of rest. The Statistical Map showed the statistical significance of the activation in each event and was created by condensing the t‐map time course relevant to each event into one volume, where the value for each voxel was the maximum of the time course of t‐maps' at that activation event. The number of t‐maps included in each activation event was determined according to the width of the corresponding peak in the ATS. The Delay Map displayed the time when the maximum statistically significant activation occurred for each activation event, relative to the movement onset recorded by the EMG. In addition, for those voxels declared active in each trial, the time series of percent BOLD signal changes were measured from 5 s before to 25 s after movement onset, and filtered with a low pass FIR filter (Hamming window) with cut‐off frequency of 0.3 Hz, to denoise the hemodynamic response estimate.
Finally, to summarize and combine the results for all subjects, the number of times a functionally interesting ROI exceeded threshold at an expected event for each TR and each type of trial (cued and self‐paced) was found, to calculate its frequency of activation. For the paradigms used here, functionally interesting ROIs were identified following relevant publications [Cunnington et al.,2002; Witt et al.,2008] and included the supplementary motor area [medial region of the Brodmann Area (BA) 6], bilateral lateral premotor cortex (lateral BA 6), bilateral primary motor cortex (BA 4), bilateral primary somatosensory cortex (BA 1, 2, and 3), superior parietal cortex (BA 5 and 7), inferior parietal cortex (BA 39 and 40), secondary and primary visual cortex.
Evaluation of PFM Method
Three methods were used to evaluate the proposed PFM method: (i) the EMG time‐series of the hand movements were compared to the onset of activated regions by means of a nonparametric test of the correlation between the ATS and the EMG signals, (ii) the spatial extent of activated regions was compared qualitatively to statistical maps generated using the traditional GLM analysis approach, using the timing information from the EMG signals as the stimulus onsets of the model, and (iii) the spatial extent of activated regions was compared qualitatively to the results of the Probabilistic Independent Component Analysis algorithm [Beckmann and Smith,2004] included in FSL.
(i) EMG‐activation time series
The Spearman's rank correlation coefficient between the EMG amplitude time series of the LE, RE, and RF and the fMRI ATS (positive and negative lines summed) were calculated using the Matlab Statistical Toolbox (The Mathworks, Natick, MA), along with the corresponding P values for the non‐correlation hypothesis. The EMG signals were first decimated to have the same number of time points as the ATS and then thresholded at an amplitude z‐score of 4, that is, four times the standard deviation from the EMG time course mean. The decimation was performed using the decimate function in the Matlab Signal Processing Toolbox (The Mathworks, Natick, MA). This function applies a Chebyshev Type I filter with normalized cut‐off frequency 0.8/r, where r is the decimation factor, and 0.05 dB of passband ripple. The correlation coefficients were computed to assess the accuracy of PFM in detecting significant movements (outliers) recorded in the EMG. Note that in case of no movement in the decimated time series, the Spearman's rank correlation cannot be defined.
(ii) Traditional GLM analysis
A GLM‐based model was formed with the regressors in the design matrix calculated from the convolution of the stimulus time series for both tasks modeled as delta functions at the times of onset of tapping as detected by EMG, with the SPM‐canonical HRF and its first temporal derivative [Friston et al.,1998]. GLM‐based analysis was done using the 3dREMLfit function in AFNI, and the corresponding statistics (F‐test) were FDR corrected and thresholded at P value < 0.05 and minimum cluster size of 5 voxels. GLM‐based statistical maps were also computed for any activation events detected during periods of rest, but in this case using the onset times estimated from the ATS to define a single event in the time series.
To examine agreement between the GLM and PFM maps, we calculated the number of overlapping voxels in both maps for each of the tapping events (PFM ∩ GLM), and the percentage of overlapping voxels relative to the number of detected voxels with PFM (% PFM in GLM = PFM ∩ GLM/PFM).
(ii) Independent component analysis
The datasets were analyzed with the Probabilistic ICA [Beckmann and Smith,2004] algorithm available in the FSL software (MELODIC, http://www.fmrib.ox.ac.uk/fsl). First PCA was performed, and then a model selection criterion, based on a Laplace approximation to the posterior distribution of the model evidence (LAP), was used for dimensionality reduction. The spatial independent components, or sources, were then computed with the FastICA algorithm [Hyvärinen,1999], which maximizes the non‐Gaussianity of the spatial sources. Finally, the spatial maps were transformed into Z‐score maps by dividing by the voxelwise estimated standard error of the residual noise [Beckmann and Smith,2004]. To identify relevant components, we computed the Pearson correlation coefficients between the time course of each spatial component and a reference time course, which was generated by the convolution of the decimated right‐flexor EMG signal with the canonical HRF from SPM (EMG regressor). Spatial components with correlation coefficient larger than 0.3 were labeled as relevant independent components. For illustration, the Z‐score maps were thresholded at Z > 3.0 and minimum cluster size of 5 voxels.
RESULTS
Figure 1a illustrates the pre‐processed (i.e., corrected for motion, linear and quadratic trends, and physiological fluctuations), normalized BOLD signal time course of a voxel located in the contralateral primary motor cortex for a representative subject at TR 2 s. Figure 1b shows the corresponding sequence of t‐maps (P value < 0.05, FDR‐corrected) for the first visually cued tapping (VCT) and the second self‐paced tapping (SPT) produced using the PFM method. These are shown for three different slices, for three consecutive time points (TR 2 s) labeled relative to the onset of movement as recorded by the EMG signals. Figure 1c shows the corresponding fMRI ATS that summarizes the significant activation detected across the whole brain at each time point. In this plot, positive activations are shown as positive peaks (black) and negative activations are shown as negative peaks (red). The complete movie of t‐maps for this experiment, illustrating the evolution of brain activity throughout the scan is available as Supporting Information.
The single‐trial detection sensitivity of the PFM method was assessed by comparing the fMRI ATS to the LE and RF EMG signals (the RF and RE EMG signals were similar). Figure 2 plots the EMG and fMRI ATS of the same subject as Figure 1 at each repetition time (TR 2 s and 0.4 s). It can be seen that temporal clusters of activation detected as peaks in the ATS (without any knowledge of the EMG data in the fMRI analysis) are in synchrony with the finger‐tapping events detected from the EMG signals or precede them by a maximum of 1 time point for the TR 2 s data and 4 time points for the TR 0.4 s data. Earlier activations were observed in the SMA (see Fig. 3), an area involved in the initiation of movement along with primary sensorimotor regions (pre‐ and post‐central sulcus). These peaks in the ATS were used to generate the Statistical Maps based on a number of t‐maps that depended on the length of the response and the TR of the dataset. The plots with the EMG and ATS corresponding to the rest of subjects are available as Supporting Information. Although subjects were instructed to perform finger tapping only with the dominant hand, EMG activity was recorded in the left extensor in synchrony with the right hand finger tapping in all but one subject (subject F, see Table I and Supporting Information figure). In addition, two subjects did not exactly follow the instructions: Subject A performed an additional finger‐tapping of 2 s at the end of the scanning period in the TR 2 s dataset (top left of Fig. 2), which was confirmed by post‐scanning questioning and by EMG, whilst subject B performed four SPT trials rather than the instructed two trials for both TR 2 s and 0.4 s datasets (see Supporting Information figure). These additional responses were detected with the PFM approach. The PFM method was able to detect 7 out of 10 (7/10) VCT events at TR 2 s, 11/13 SPT at TR 2 s. All finger tapping events were detected with PFM at TR 0.4 s (see Supporting Information for the EMG and ATS plots). For trials where activations were not detected there was always large variability in the baseline period. Along with the visually cued and self paced events, all EMG measurements showed sporadic spikes of muscle activity in both hands at times correlated with peaks in the fMRI ATS. Furthermore the ATS also showed task‐unrelated events, that is, sporadic, spatio‐temporal clusters of cortical activation occurring during the rest periods.
Figure 2.
EMG‐fMRI plots for subject A for both datasets of TR 2 s (left) and 0.4 s (right). Each plot shows the fMRI ATS (P value < 0.05, FDR‐corrected) (bottom) and the EMG time series corresponding to the left extensor (LE) (top) and right flexor (middle) to capture upper limb movements. To facilitate the interpretation of the result, the ATS differentiates between positive activations (black, positive y‐axis) and negative activations (red, negative y‐axis). The dark box indicates the baseline period. ATS were used to detect periods of significant brain activation. As illustrated, all main finger tapping events are detected at the times recorded by the EMG. In addition, sporadic clusters of activation were detected during periods at rest which may correspond to small body movements or mental tasks. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Figure 3.
Time courses of t‐maps (P value < 0.05, FDR‐corrected) showing the activation for the first VCT (top) and first SPT (bottom) for subject A at TR 0.4 s. In addition, the corresponding statistical parametric maps (F‐test, P value < 0.05, FDR‐corrected) after fitting a GLM model with the canonical HRF and the first derivative are shown at the right bottom of each slice sequence (white box). The times are relative to the onset of the tapping as recorded by the EMG signals. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Table I.
Spearman's rank correlation coefficients between the decimated and thresholded EMG signals and the activation time series for datasets of TR 2 s with 342 time points (a) and TR 0.4 s with 1710 time points (b)
| Spearman's correlation (ATS‐EMG) | Left extensor | Right extensor | Right flexor |
|---|---|---|---|
| (a) TR 2 s | |||
| Subject A | 0.342* | 0.483* | 0.417* |
| Subject B | 0.110 | 0.444* | 0.262* |
| Subject C | 0.242* | 0.100 | 0.101 |
| Subject D | 0.620* | 0.645* | 0.444* |
| Subject F | −0.002 | 0.273* | 0.446* |
| (b) TR 0.4 s | |||
| Subject A | 0.175* | 0.326* | 0.269* |
| Subject B | 0.138* | 0.251* | 0.377* |
| Subject C | −0.011 | 0.103* | 0.342* |
| Subject D | 0.341* | 0.427* | 0.382* |
| Subject F | NaN | NaN | 0.133* |
The asterisks indicate that the correlation coefficient is statistically significant (non‐parametric P value < 0.001). Note that all correlation coefficients are significant except for the right‐hand extensor (RE) and flexor (RF) of subject C at TR 2 s (both VCTs undetected); left‐hand extensor (LE) of subject B at TR 2 s (second VCT, second SPT and third SPT undetected and artifactual EMG signal); and the LE of subject C at TR 0.4 s, LE of subject F at TR 2 s, and for both the LE and RE of subject F at TR 0.4 s (EMG signals showed reduced or no significant movements at all).
The Spearman's rank correlation coefficients between the fMRI ATS and the EMG signals are shown in Table I for TRs 2 s and 0.4 s. At both TRs, the fMRI ATS and EMG time courses were significantly correlated (P < 0.001) at 23 of the 30 possible combinations (EMG‐dataset). The causes for no correlation between the fMRI signal and the EMG were: no detection of events in the ATS (RE and RF of subject C at TR 2 s); artifactual EMG acquisition (LE of subject B at TR 2 s); and reduced or no significant movement recorded by the EMG (LE of subject C at TR 0.4 s, LE of subject F at TR 2 s, LE and RE of subject F at TR 0.4 s).
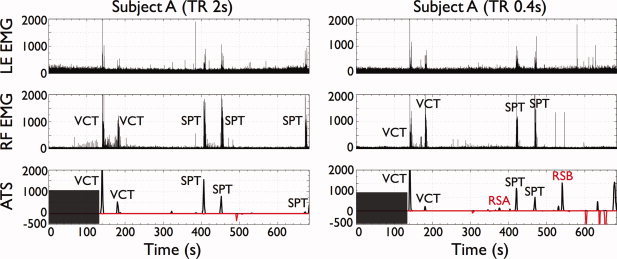
Figure 3 illustrates the time courses of t‐maps (P value < 0.05, FDR‐corrected) during the first visually cued trial and the first self paced trial for one slice of subject A (TR 0.4 s), overlaid onto the corresponding T2*‐weighted anatomical image. The statistical map created by condensing the time course of t‐maps is also shown and labeled PFM. The time shown in the t‐maps is relative to the onset of movement execution as recorded by the EMG signals. Since the t‐maps are generated following deconvolution of the canonical HRF from the signal time course, the timing of events in the t‐map time series does not directly reflect the delay of the hemodynamic response. A movie of the t‐maps for the complete scan of this dataset is available as Supporting Information. For comparison, the statistical map (F‐test, P value < 0.05, FDR‐corrected) using the traditional GLM approach is also depicted in a box at the bottom right of each time sequence of t‐maps in Figure 3. It can be observed that both PFM and GLM depict activations in overlapping regions. Averaging across all finger tapping events and all subjects (except the first VCT of Subject C at TR 2 s where no activated voxels were shown in both maps), we observed that 70% of the voxels identified as active in the PFM maps were also present in the GLM maps, with higher rate at TR 0.4 s (75%) than at TR 2 s (64%). The average value of %PFM in GLM at TR 2 s increased to 83% if the five events not detected with PFM at TR 2 s were discarded.
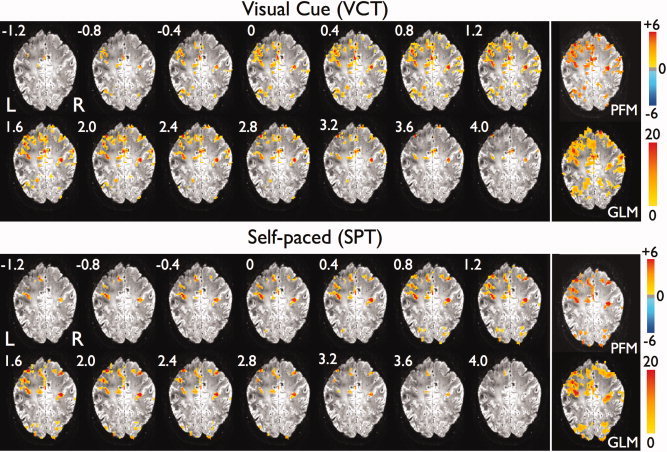
Figure 4 illustrates the six spatial probabilistic ICA maps selected as relevant (i.e., correlation coefficient with EMG‐reference function > 0.3) and their associated time series for the same dataset as Figure 3. Probabilistic ICA is also able to map the cortical activation in areas of the primary sensorimotor cortex, although the temporal information provided directly by PFM was spread across several spatial ICA components and associated time courses. In addition, some areas are simultaneously active in several components, for example, voxels of the contralateral postcentral gyrus in components 2 and 3. The total number of components identified from probabilistic ICA using the LAP criterion, the percentage of the variability of the dataset described by these components, and the number of relevant components (i.e., those whose correlation coefficient with EMG‐reference function > 0.3) are shown in Table II. It can be seen that a large number of components were extracted from the probabilistic ICA analysis for the datasets acquired with high temporal resolution (TR 0.4 s). There was considerable variability between subjects in the number of components identified as relevant. For the components shown in Figure 4, the ICA responses were more unilateral than the responses detected with either PFM or GLM, and the EMG indicated that there was actually movement of both hands (except for one subject). In fact, ICA also detected bilateral activation in the motor cortex as illustrated in components IC2 and IC3. However Figure 4 only plots those components that are highly correlated with the EMG‐regressor (correlation coefficient > 0.3), suggesting that the correlation between the components corresponding to the bilateral activation were not highly correlated with the EMG.
Figure 4.
Spatial probabilistic ICA maps and associated time courses of the relevant components (i.e., those whose correlation coefficient with EMG regressor is > 0.3) for the dataset of subject A at TR 0.4 s (same as Figures 3 and 5). All maps represent Z‐scores (thresholded at Z > 3.0) after normalization of the spatial components with the voxelwise estimated standard error of the residual noise. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Table II.
Total number of ICs identified with probabilistic ICA using the criterion which maximizes the Laplace approximation of the posterior distribution of the model evidence (LAP), the percentage of the variability of the data retained with these components, and the number of relevant ICs (correlation coefficient with EMG regressor > 0.3)
| TR 2 s | TR 0.4 s | |||
|---|---|---|---|---|
| # ICs (% variability) | # Relevant ICs | # ICs (% variability) | # Relevant ICs | |
| Subject A | 134 (82.0) | 11 | 431 (72.3) | 6 |
| Subject B | 119 (79.9) | 2 | 298 (63.7) | 6 |
| Subject C | 124 (82.8) | 12 | 556 (78.3) | 33 |
| Subject D | 125 (82.6) | 11 | 549 (77.0) | 16 |
| Subject F | 113 (78.2) | 2 | 561 (75.6) | 4 |
The t‐maps in Figures 1 and 3 illustrate that activation for the finger tapping trials was found in areas of sensorimotor execution and processing of motor movements as expected. The relative timing of the different cortical responses was generally quite variable between events. However, for the visually cued tap shown in Figure 3, initial activity occurred in regions close to the contralateral central sulcus extending into the contralateral primary motor and primary somatosensory cortices, cingulate gyrus, ipsilateral postcentral sulcus, ipsilateral supramarginal gyrus and bilaterally in the lateral occipital gyrus and intraparietal sulcus. Later, activation extended into a larger network of areas including the cingulate gyrus and posterior SMA (paracentral lobule), bilateral primary sensorimotor (M1 and S1) cortices, superior frontal gyrus and superior parietal lobule. Posteriorly, activation was also seen in the ipsilateral primary motor and bilateral premotor cortices, along with draining veins. Activation was found in similar regions for the self‐paced tap shown in Figure 3, although ipsilateral premotor areas showed earlier activation in the self‐paced tap than for the visually cued tap. Interestingly, BOLD responses were seen in areas of the occipital lobe not only in the visually cued task but also in the self paced trial (no visual cue). Notably, for this particular dataset, no independent component with correlation with the EMG regressor larger than 0.3 accounted for the activation found in the visual cortex and superior parietal lobule in the PFM and GLM maps.
Figure 5a shows the PFM delay maps for voxels exceeding the threshold (P value < 0.05, FDR‐corrected), and illustrates the variability in the timing of the response across voxels both within and between functional areas. Figure 5b illustrates the single trial hemodynamic response without temporal or spatial averaging of individual voxels located in the posterior part of the contralateral M1 (contM1), contralateral SMA and anterior part of ipsilateral M1 (ipsM1) (location shown in Fig. 5a), chosen to avoid any veins (detected by low signal in the underlying T2* weighted image).
Figure 5.
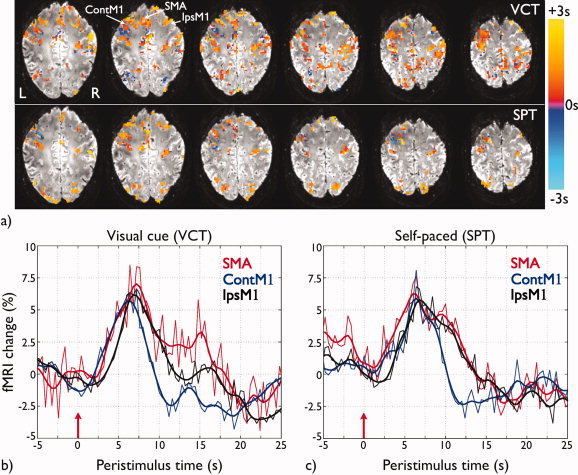
(a) Delay maps of voxels exceeding threshold (P value < 0.05, FDR‐corrected) for each trial for the same slices as shown in Figure 3. The delay is computed as the time when the maximum statistically significant activation occurred, defined relative to the movement onset recorded by the EMG signals; (b) Hemodynamic responses for three voxels in SMA (red), contralateral M1 (contM1, blue), and ipsilateral M1 (ipsM1, black), with location indicated in Figure 5a for the first VCT; and (c) for the first SPT for subject A and dataset of TR 0.4 s, both shown in Figure 3. The red arrows at time 0 s are at the movement onsets as recorded by the EMG signals. The thick lines correspond to the smoothed version of the voxel time series (thin lines) by filtering with a Hamming low pass filter with cut‐off frequency 0.3 Hz. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Both statistical and delay maps (Figs. 1, 3, and 5a) demonstrate variability in the spatial extent and delay of activation across individual trials. Variability was also observed between subjects. Table III lists the frequency of detection of events across subjects and trials, for both VCT and SPT tasks at both TRs. Datasets showed consistent activations (frequency of activation > 0.70) across subjects and tapping tasks in the SMA, bilateral M1 and bilateral S1 regions. It was also observed that contralateral M1 and S1 areas showed the most repeatable patterns of activation across trials (i.e., same voxels consistently activated), followed by ipsilateral S1 and M1. It should be noted that coverage of the lateral PM in both hemispheres was limited by the tilt of the slices, especially for the datasets of TR 0.4 s, which had fewer slices. In addition, the primary visual cortex was not covered in subject B for both TRs, and in subject C for TR 0.4 s.
Table III.
Frequency of activation in regions of interest
| TR 2 s | TR 0.4 s | |||
|---|---|---|---|---|
| VCT | SPT | VCT | SPT | |
| SMA | 0.7 | 0.7 | 0.9 | 1 |
| Contralateral PM | 0.7 | 0.35 | 0.8 | 0.66 |
| Contralateral M1 | 0.7 | 0.7 | 0.9 | 1 |
| Contralateral S1 | 0.7 | 0.7 | 0.9 | 1 |
| Cont. Inf. Parietal | 0.7 | 0.4 | 0.9 | 1 |
| Cont. Sup. Parietal | 0.56 | 0.53 | 0.72 | 0.75 |
| Ipsilateral PM | 0.56 | 0.43 | 0.75 | 0.7 |
| Ipsilateral M1 | 0.7 | 0.6 | 0.9 | 1 |
| Ipsilateral S1 | 0.63 | 0.53 | 0.9 | 1 |
| Ips. Inf. Parietal | 0.56 | 0.53 | 0.9 | 1 |
| Ips. Sup. Parietal | 0.5 | 0.47 | 0.8 | 0.75 |
| Primary Visual | 0.45 | 0.53 | 0.75 | 0.83 |
| Secondary Visual | 0.56 | 0.4 | 0.8 | 0.5 |
This value is defined as the number of events the ROI was found active divided by the number of times (tasks and subjects) for which this area was scanned.
Figure 6 illustrates the PFM Statistical Maps (P value < 0.05, FDR‐corrected) for two task‐unrelated activations (at points RSA and RSB in Fig. 2) detected during the periods of rest for the dataset of subject A at TR 0.4 s. For comparison, the corresponding statistical maps obtained with the GLM analysis (F‐test, P value < 0.05, FDR‐corrected) are also displayed at the bottom of each map. These GLM statistical maps were computed using the time of the peak in the ATS to define the onset time for these task‐unrelated events. There was excellent agreement between the GLM statistical parameteric maps and the PFM Statistical Maps. These task‐unrelated activations did not show a specific recurring pattern or a consistent spatio‐temporal pattern between subjects. For instance, Statistical Map RSA shows cortical activity in the posterior cingulate cortex, precuneus, and lateral inferior parietal cortex, whereas Statistical Map RSB shows activation in both primary sensorimotor areas (PM, M1 and S1, anterior cingulate cortex and SMA) and visual areas, and is related to task‐independent hand movement (confirmed by the EMG).
Figure 6.
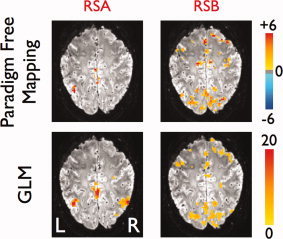
Statistical maps obtained with PFM (P value < 0.05, FDR corrected) (top) and GLM (F‐test, P value < 0.05, FDR‐corrected) (bottom) corresponding to the time points of activations shown at the ATS of subject A at TR 0.4 in Figure 2. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
DISCUSSION
We have described a new Paradigm Free Mapping method for the analysis of fMRI data and shown that using this method it is possible to detect individual (single‐trial) BOLD responses to motor activity at high field without any prior knowledge of the paradigm timing. Other fMRI analysis methods have previously been proposed to study single‐trial responses [Kruggel and Von Crammon,1999; Richter et al.,1997a,1997b,2000; Svensen et al.,2000], but these approaches assumed prior knowledge of the onset times of the evoked stimuli. Using the method presented here, it was possible to observe the temporal processing of single trial events in a simple and unsupervised manner with no knowledge of the stimulus timing. The output of the PFM analysis method is a time course of t‐maps. Brain activation movies have previously been used to display the cortical response to stimulus processing [Windischberger et al.,2008], but based on a finite impulse response (FIR) model approach where the onsets of the stimuli were known a priori. Furthermore, we have also introduced the ATS as a method of reducing the dimensionality of the data to make the results easier to interpret.
The PFM method is based on voxelwise deconvolution of the HRF under a linear model using the ridge regression algorithm and autoregressive noise characterization assuming that the hemodynamic response conforms to a two‐gamma variates with the standard SPM parameters, to include a post stimulus undershoot [Friston et al.,1998]. Despite the variability in the shape of the HRF [Aguirre et al.,1998; Duann et al.,2002; Handwerker et al.,2004], the ridge regression estimation has previously demonstrated high robustness against model mismatches [Selén et al.,2008] due to the L2‐norm regularization term. It should be noted that the Ridge Regression deconvolution is equivalent to a Bayesian deconvolution assuming Gaussian priors for the noise and the signal coefficients, and Gitelman et al. [2003] proposed estimation of the regularization parameter via an empirical Bayes approach using the Restricted Maximum Likelihood (ReML) and expectation maximization (EM) algorithms. Here, generalized least square (GLS) estimates of the noise and coefficient variances were used to compute the regularization parameter, which increases computational speed with a negligible decrease in robustness against model mismatch [Selén et al.,2008]. Notably, the use of Gaussian priors has been previously proposed but using a Finite Impulse Response (FIR) model which, in contrast to PFM, aims to deconvolve or estimate the HRF shape assuming a predetermined paradigm [Goutte et al.,2000; Marralec et al.,2003]. Alternatively, to increase the accuracy of the estimation with less penalty on the active responses, deconvolution models based on sparse estimation techniques, such as the LASSO or the Dantzig Selector, might be used assuming that cortical activity is localized sparsely in time [Caballero‐Gaudes et al.,2009]. Our current formulation performs the deconvolution on a voxel‐by‐voxel basis, but there is certainly correlation in the response between neighboring voxels. The PFM approach could be extended to use a spatio‐temporal deconvolution [Harrison et al.,2007] to improve the detection of single‐trial responses and to characterize the variability in the HRF between neighboring voxels.
An AR model was adopted for the statistical characterization of the noise because the numerical algorithms used to estimate the model parameters, such as the LD algorithm, exhibit higher robustness than those for ARMA or MA models [Stoica and Moses,2005]. In addition, isotropic spatial smoothing was used to reduce the variance of the autocorrelation estimates, but non‐isotropic spatial filters could be employed to further improve this estimate across brain‐air and tissue boundaries [Woolrich et al.,2001].
The datasets were corrected for motion and physiological fluctuations with RETROICOR [Glover et al.,2000]. Alternative methods to reduce physiological noise components could also be used, such as regressing out the convolution of measured respiratory and cardiac variations with empirical, pre‐determined response functions [Birn et al.,2008; Chang et al.,2009] and ultimately, the PFM approach could also be extended to incorporate a non‐stationary noise characterization [Fadili and Bullmore,2005; Long et al.,2005].
The statistical significance of the activations was evaluated after FDR thresholding of the temporal t‐statistic. Similar to Lindquist et al. [2007], the t‐statistics were computed as the deviance of the estimated signal time series for each voxel from its estimated baseline signal. However, in PFM the test statistics are based on filtering the fMRI time series with a filter based on the deconvolution of the HRF, whereas Lindquist et al. [2007] used an exponentially weighted moving averaged (EWMA) filter. Consequently, there is a noticeable difference between the interpretation of the EWMA statistics and PFM since the latter is directly related to the signal which drives the fMRI BOLD response. Setting baseline periods involves making the assumption that no hemodynamic event of neural origin occurred in those periods and our own results have illustrated the presence of significant and coherent activations during periods of rest different from the initial baseline. In a few datasets this might have lead to loss of sensitivity to some responses. This could be overcome by eliminating baseline periods with obvious neural‐related signal changes.
The baseline period needs to include a sufficient number of time points (B) to be able to allow the mean amplitude and variance of the baseline state to be estimated. In addition, the degrees of freedom will reduce with fewer baseline time points. In our experiments, we used large values of B, but in practice we could use fewer number since the Student's t‐distribution does not change considerably providing B is large enough (∼>30). The baseline period also needs to be of sufficient length (∼>60 s) to include several cycles of baseline fluctuations. However, we are currently working on an alternative formulation of the PFM which removes the need of a baseline period for which the statistical inference is performed by formulating multiple generative models with different number of events and then choosing the one with largest evidence according to model selection criteria, such as AIC or BIC.
We used the traditional BH [Benjamini and Hochberg,1995] approach to control the false discovery rate for each of the time points separately. No temporal correction was performed because the spatial and temporal correlation of the statistics led to a significant reduction in the spatial (but not temporal) sensitivity of PFM to the main events. Future work will address the investigation of spatio‐temporal cluster inference methods in a PFM formulation, for example, based in adaptive FDR procedures [Schwartzman et al.,2009] or current cluster thresholding methods [Chumbley et al.,2010; Smith and Nichols,2009] to account for the spatial and temporal smoothness of the PFM statistics and increase the sensitivity of the technique in a four‐dimensional correction.
The performance of the PFM method was evaluated using a paradigm where subjects performed dominant‐hand finger‐tapping, visually cued or self paced. Nonparametric P values based on the Spearman's rank correlation coefficient demonstrated significant correlation between the EMG signal time course and fMRI ATS, confirming the feasibility of paradigm free detection of single trial motor movements. We observed a higher probability in the detection of the events at TR 0.4 s (22 out of 22 events) than at TR 2 s (18 out of 23 events), which results from the higher sampling rate of the HRF, despite lower contrast‐to‐noise ratio existing at TR 0.4 s. In some cases, the onset and peak of the ATS preceded the EMG onset by up to one time point for data with TR 2 s or four time points for the TR 0.4 s data. This earlier onset may have arisen due to cortical activity associated with preparation and planning, or may indicate a mismatch between the canonical HRF and the actual HRF. Once the activations have been detected with PFM, a posteriori fitting of the HRF parameters could be helpful to understand the origins of any difference [Lindquist et al.,2009].
The PFM technique consistently detected significant activation in brain regions known to be involved in the initiation and processing of a motor task [Witt et al.,2008], including SMA [Cunnington et al.,2002,2003], bilateral PM [Halsband et al.,1993; Harrington et al.,2000; Passingham,1985], bilateral M1 [Cunnington et al.,2002; Richter et al.,1997a], bilateral S1 [Porro et al.,1996; Rao et al.,1993], bilateral inferior parietal (supramarginal gyrus) [Harrington et al.,2000], superior posterior parietal areas [Gordon et al.,1998; Schubert et al.,1998]. In addition, activation was also observed in the intraparietal sulcus and superior frontal areas in some subjects (see Fig. 3), areas shown to be involved in the processing of visuo‐motor tasks and spatial attention [Corbetta and Shulman,2002]. Primary and secondary visual cortex (V1 and V2) activity was observed for VCT and interestingly, activation in V1 was also observed during the SPT trials (Table III), possibly due to the mental visualization of the visual cue associated with the previous finger tapping events [Pascual‐Leone et al.,2005]. Table III shows that primary sensorimotor areas (SMA, M1, and S1) were the most consistently active areas within and across subjects, whereas sensory association areas not primarily implicated in the task demonstrated a larger variability [Duann et al.,2002; Richter et al.,1997]. Note that due to the tilt of the slices only the superior part of the premotor cortex was scanned and much of the PM area was missed for some subjects.
Ipsilateral activation in the PM and M1 cortices was detected for all subjects (Table III). The EMG signals indicated that all subjects, except subject F, had significant movement of the non‐dominant hand during the uni‐manual finger tapping task. However, even in the case of this subject where no activity in the non‐dominant hand was recorded by the EMG, activity in ipsilateral sensorimotor areas was detected, supporting indications that the ipsilateral hemisphere also plays an important role in the planning, execution and control of unimanual motor tasks [Kawashima et al.,1994; Porro et al.,2000].
For validation of PFM, we compared the results obtained with GLM and Probabilistic ICA [Beckmann and Smith,2004]. As illustrated in Figure 3, the PFM activation maps showed large correspondence with the GLM maps, especially at the main clusters of activation. In general, the PFM areas were smaller than the GLM areas but lay within the GLM areas with a high degree of overlap (%PFM area in GLM area: 75.5% for TR 0.4 s and 64.2% for TR 2 s) suggesting that PFM maps had a higher specificity (i.e., were more stringently thresholded) than the GLM maps. On the other hand, both PFM and ICA successfully detected time points and areas of activation associated to the finger tapping responses without prior knowledge of the paradigm, but there are several differences between both approaches. PFM is based on the deconvolution of an assumed model of the HRF, whereas ICA is a completely model‐free approach. The component decomposition obtained with some ICA algorithms, such as Fast‐ICA or Infomax, is sensitive to their initialization [Himberg et al.,2004], whereas this is not a problem for PFM. In addition, an important consideration is that ICA requires the number of components to be extracted from the data to be determined, either manually or by using selection criteria (LAP, MDL, or AIC). One of the most compelling aspects of PFM is the observation of spatio‐temporally coordinated activation in the activation movie. In comparison each ICA component describes the behavior of a number of voxels acting in synchrony, and so voxels with slightly different time courses end up in different components which need to be appropriately combined to recover the temporal information that is immediately available from PFM. For a long dataset, such as our datasets acquired at TR 0.4 s, ICA requires a large number of components to describe the variability in the data (see Table II) and functionally significant information is spread across several components (e.g., see areas of the postcentral gyrus which are included in the components IC2 and IC3 of Fig. 4). In this study, we selected the relevant independent components based on the correlation between the ICA component timecourse and the EMG signal. This allowed us to identify spatial components including the SMA and bilateral primary somatosensory areas, but there were some areas, such as the visual cortex and superior parietal lobule, which were not detected in the components selected by correlation with the EMG, but which were significantly active with both PFM and GLM (compare Figs. 3 and 4). This does not imply that there are no components to account for these responses, but finding them may be very difficult in a real paradigm free mapping scenario and would involve cross‐validation, or visualization and clustering of the components [Himberg et al.,2004] which would be computationally intensive for long datasets. In fact, the PFM activation time course might prove a useful signature with which to identify relevant components. It is worth noting that PFM only detects discrete, temporally sparse events, and therefore would not be able to characterize slow‐frequency oscillations, for example, as described in resting state data, which can be detected with other techniques, such as ICA, PCA, or seed‐voxel correlation [Damoiseaux et al.,2006].
This work was performed at 7T to take advantage of the improved BOLD contrast to noise ratio (CNR) at 7T which makes routine single trial fMRI feasible [Pfeuffer et al.,2002]. The TR = 0.4 and TR = 2.0 s data were both acquired at the same TE and the ratio of the measured tSNR was ∼1.3, but the technique was still able to detect activation at the shorter TR (see Fig. 2), suggesting PFM would also be applicable for less robust responses and data acquired at lower field strengths [Triantafyllou et al.,2005], but further work is required to determine the ultimate limit to sensitivity.
Once a response had been detected with the PFM method, the high CNR available from 7T data allowed the amplitude and timing of the HRF to be studied on a trial‐by‐trial and voxel‐by‐voxel basis (see Fig. 5) with no temporal averaging. Amplitudes and delays were shown to vary considerably not only between voxels of different sensory areas but also within the same area as shown previously [Duann et al.,2002; Pfeuffer et al.,2002]. This variability could be due to variations in task performance, coherent spontaneous activity [Fox et al.,2007] or underlying baseline trends which were not completely removed with temporal detrending in the preprocessing [Tanabe et al.,2002]. The spatio‐temporal mapping provided by the PFM will enable the source of this variability to be investigated by studying the relationship between HRF duration and relative delay, physiological measures (e.g., phase of the cardiac cycle) and amplitude of activation, on a trial by trial basis, across brain regions and between subjects.
This novel Paradigm Free Mapping technique may provide the possibility of designing a new class of neuroimaging paradigms which make use of single trial fMRI, including the study of learning and adaptation [Bingel et al.,2002; Gonzalo et al.,2000], or other paradigms where timing information of the brain response cannot be hypothesized in advance [Faisan et al.,2007; Hutchinson et al.,2009]. Beyond this, the block‐by‐block deconvolution used to increase the speed of the algorithm opens the door to a real‐time implementation of PFM which would allow experiments to be designed where the paradigm is modified in the light of cortical response [deCharms,2008].
Interestingly, PFM enabled the unsupervised detection of significant transient, task‐unrelated spatio‐temporal patterns of brain activity across the cortex during periods of apparent rest (Figs. 2 and 6). These activation events could be related to unconstrained behavior in the scanner, such as small body movements, or may relate to other mental tasks such as changes in attention [Corbetta et al.,2002] or somatic perception [Felician and Romaiguère,2008]. Using the ATS, the temporal locations of these events were determined, and these events could subsequently be detected and further assessed using GLM analysis (Fig. 6). PFM could be used to identify spurious extreme fluctuations that would affect other statistical analyses. Information about the task‐unrelated events extracted using PFM will complement the information obtained with other analysis techniques of resting‐state BOLD fMRI. Future work will focus on assessing the functional significance of these activations and studying the factors giving rise to these task‐unrelated or spontaneous events and their effects on cortical networks [Petridou et al.,2009].
Supporting information
Additional Supporting Information may be found in the online version of this article.
Supporting Figure 1A
Supporting Figure 1B
Supporting Movie 1
Supporting Movie 2
Acknowledgements
The authors thank Samia Aboushoushah and Peter Wright for their assistance during the EMG acquisition.
Let s k(i) be the observation (ridge regression estimate) at voxel k at time i, and write
| (A1) |
for the arithmetic mean at time i over the neighborhood N(k) of voxel k which consists of L voxels (i =1,…, N; k = 1, …, L). Hereinafter we do not consider the superscript index k to simplify the notation. Consider the model where s L are jointly multivariate normal with marginal distributions during the baseline period given by
| (A2) |
and the correlation matrix during the baseline period is the B × B matrix ΣL. In addition, after the baseline period the marginal distribution at time i is
| (A3) |
which is independent of the values in the baseline period.
We wish to test
| (A4) |
Let
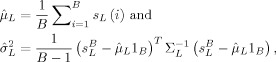 |
be the baseline mean and variance estimates respectively, where s = (s L(1), …, s L(B))T is the B‐vector of the spatially averaged deconvolved time series for the baseline and 1B is the B‐vector of ones. The correlation matrix ΣL is estimated by standardizing the spatial average of the covariance matrices of the ridge regression estimates for each baseline, that is, we estimate the correlation matrix ΣL by standardizing (to unit diagonal elements)
| (A5) |
and λl is the regularization parameter for voxel l.
Under H 0 we have, for i > B,
| (A6) |
and independently
| (A7) |
treating ΣL as known (Hogg and Craig,1995). Hence, it can be written that
| (A8) |
if H
0 is true, where t
v is the Student's t distribution with v degrees of freedom. Here, we used the definition of the t‐statistic such that if two random variables X and Y are independently distributed as N(0,1) and χ, then
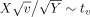 .
.
References
- Aguirre GK, Zarahn E, D'Esposito M ( 1998): The variability of human, BOLD hemodynamic responses. Neuroimage 8: 360–369. [DOI] [PubMed] [Google Scholar]
- Allen PJ, Josephs O, Turner R ( 2000): A method for removing imaging artifact from continuous EEG recorded during functional MRI. Neuroimage 12: 230–239. [DOI] [PubMed] [Google Scholar]
- Andersen AH, Gash DM, Avison MJ ( 1999): Principal component analysis of the dynamic response measured by fMRI: A generalized linear systems framework. Magn Reson Imaging 17: 795–815. [DOI] [PubMed] [Google Scholar]
- Baumgartner R, Ryner L, Richter W, Summers R, Jarmasz M, Somorjai R ( 2000): Comparison of two exploratory data analysis methods for fMRI: Fuzzy clustering vs. principal component analysis. Magn Reson Imaging 18: 89–94. [DOI] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM ( 2004): Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans Med Imaging 23: 137–152. [DOI] [PubMed] [Google Scholar]
- Bellgowan PSF, Saad ZS, Bandettini PA ( 2003): Understanding neural system dynamics through task modulation and measurement of functional MRI amplitude, latency, and width. Proc Natl Acad Sci USA 100: 1415–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y ( 1995): Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Stat Soc Series B Stat Methodol 57: 289–300. [Google Scholar]
- Bingel U, Quante M, Knab R, Bromm B, Weiller C, Büchel C ( 2002): Subcortical structures involved in pain processing: Evidence from single‐trial fMRI. Pain 99: 313–321. [DOI] [PubMed] [Google Scholar]
- Birn RM, Smith MA, Jones TB, Bandettini PA ( 2008): The respiration response function: The temporal dynamics of fMRI signal fluctuations related to changes in respiration. Neuroimage 40: 644–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ ( 1996): Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci 16: 4207–4221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Bandettini PA, O'Craven KM, Savoy RL, Petersen SE, Raichle ME, Rosen BR ( 1996): Detection of cortical activation during averaged single trials of cognitive task using functional magnetic resonance imaging. Proc Natl Acad Sci USA 93: 14878–14883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero‐Gaudes C, Petridou N, Francis S, Dryden I, Gowland P ( 2009): Sparse Estimation Using the Dantzig Selector Algorithm Automatically Detects Single‐Trial BOLD Responses in Space and Time. 15th Annual Meeting of the Organization for Human Brain Mapping, San Francisco, CA.
- Calhoun VD, Adali T ( 2006): Unmixing fMRI with independent component analysis. IEEE Eng Med Biol Mag 25: 79–90. [DOI] [PubMed] [Google Scholar]
- Chang C, Cunningham JP, Glover GH ( 2009): Influence of heart rate on the BOLD signal: The cardiac response function. Neuroimage 44: 857–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chumbley J, Worsley K, Flandin G, Friston K ( 2010): Topological FDR for neuroimaging. Neuroimage 49: 3057–3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta M, Shulman GL ( 2002): Control of goal‐directed and stimulus‐driven attention in the brain. Nat Rev Neurosci 3: 201–215. [DOI] [PubMed] [Google Scholar]
- Cox RW ( 1996): AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res 29: 162–173. [DOI] [PubMed] [Google Scholar]
- Cunnington R, Windischberger C, Deecke L, Moser E ( 2002): The preparation and execution of self‐initiated and externally triggered movement: A study of event‐related fMRI. Neuroimage 15: 373–385. [DOI] [PubMed] [Google Scholar]
- Cunnington R, Windischberger C, Deecke L, Moser E ( 2003): The preparation and readiness for voluntary movement: A high‐field event‐related study of the Bereitschafts‐BOLD response. Neuroimage 20: 404–412. [DOI] [PubMed] [Google Scholar]
- Cunnington R, Windischberger C, Robinson S, Moser E ( 2006): The selection of intended actions and the observation of other's actions: A time‐resolved fMRI study. Neuroimage 29: 1294–1302. [DOI] [PubMed] [Google Scholar]
- Damoiseaux JS, Rombouts SA, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF ( 2006): Consistent resting‐state networks across healthy subjects. Proc Natl Acad Sci USA 103: 13848–13853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- deCharms RC ( 2008): Applications of real‐time fMRI. Nat Rev Neurosci 9: 720–729. [DOI] [PubMed] [Google Scholar]
- De Ridder F, Pintelon R, Schoukens J, Gillikin DP ( 2005): Modified AIC and MDL model selection criteria for short data records. IEEE Trans Instrum Meas 54: 144–149. [Google Scholar]
- Duann JR, Jung TP, Kuo WJ, Yeh TC, Makeig S, Hsieh JC, Sejnowski TJ ( 2002): Single‐trial variability in event‐related BOLD signals. Neuroimage 15: 823–835. [DOI] [PubMed] [Google Scholar]
- Fadili MJ, Ruan S, Bloyet D, Mazoyer B ( 2000): A multistep unsupervised fuzzy clustering analysis of fMRI time series. Hum Brain Mapp 10: 160–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fadili MJ, Bullmore ET ( 2005). Penalized partially linear models using sparse representations with an application to fMRI time series. IEEE Trans Signal Process 53: 3436–3448. [Google Scholar]
- Faisan S, Thoroval L, Armspach J, Heitz F ( 2007): Hidden Markov multiple event sequence models: A paradigm for the spatio‐temporal analysis of fMRI data. Med Image Anal 11: 1–20. [DOI] [PubMed] [Google Scholar]
- Felician O, Romaiguère P ( 2008): Your body and mine: A neuropsychological perspective. Neurophysiol Clin 38: 183–187. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Raichle ME ( 2007): Intrinsic fluctuations within cortical systems account for intertrial variability in human behavior. Neuron 56: 171–184. [DOI] [PubMed] [Google Scholar]
- Francis S, Lin X, Aboushoushah S, White TP, Philips M, Bowtell R, Constantinescu CS ( 2009): fMRI analysis of active, passive and electrically stimulated ankle dorsiflexion. Neuroimage 44: 469–479. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Fletcher P, Josephs O, Holmes A, Rugg MD, Turner R ( 1998): Event‐related fMRI: Characterizing differential responses. Neuroimage 7: 30–40. [DOI] [PubMed] [Google Scholar]
- Genovese CR, Lazar NA, Nichols T ( 2002): Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage 15: 870–878. [DOI] [PubMed] [Google Scholar]
- Gitelman DR, Penny WD, Ashburner J, Friston KJ ( 2003): Modeling regional and psychophysiologic interactions in fMRI: The importance of hemodynamic deconvolution. Neuroimage 19: 200–207. [DOI] [PubMed] [Google Scholar]
- Glover GH, Li TQ, Ress D ( 2000): Image‐based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn Reson Med 44: 162–167. [DOI] [PubMed] [Google Scholar]
- Gonzalo D, Shallice T, Dolan R ( 2000): Time‐dependent changes in learning audiovisual associations: A single‐trial fMRI study. Neuroimage 11: 243–255. [DOI] [PubMed] [Google Scholar]
- Gordon AM, Lee JH, Flament D, Ugurbil K, Ebner TJ ( 1998): Functional magnetic resonance imaging of motor, sensory, and posterior parietal cortical areas during performance of sequential typing movements. Exp Brain Res 121: 153–166. [DOI] [PubMed] [Google Scholar]
- Goutte C, Toft P, Rostrup E, Nielsen F, Hansen LK ( 1999): On clustering fMRI time series. Neuroimage 9: 298–310. [DOI] [PubMed] [Google Scholar]
- Goutte C, Arup Nielsen F, Hansen LK ( 2000): Modeling the hemodynamic response in fMRI using smooth FIR filters. IEEE Trans Med Imag 19: 1188–1201. [DOI] [PubMed] [Google Scholar]
- Halsband U, Ito N, Tanji J, Freund HJ ( 1993): The role of premotor cortex and the supplementary motor area in the temporal control of movement in man. Brain 116: 243–266. [DOI] [PubMed] [Google Scholar]
- Handwerker DA, Ollinger JM, D'Esposito M ( 2004): Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage 21: 1639–1651. [DOI] [PubMed] [Google Scholar]
- Hansen PC, O'Leary DP ( 1993): The use of the L‐curve in the regularization of discrete ill‐posed problems. SIAM J Sci Comput 14: 1487–1503. [Google Scholar]
- Harrington DL, Rao SM, Haaland KY, Bobholz JA, Mayer AR, Binder JR, Cox RW ( 2000): Specialized neural systems underlying representations of sequential movements. J Cogn Neurosci 12: 56–77. [DOI] [PubMed] [Google Scholar]
- Harrison LM, Penny W, Ashburner J, Trujillo‐Barreto N, Friston KJ ( 2007): Diffusion‐based spatial priors for imaging. Neuroimage 38: 677–695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman J ( 2001): The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 1st ed. New York: Springer. [Google Scholar]
- Himberg J, Hyvrinen A, Esposito F ( 2004): Validating the independent components of neuroimaging time‐series via clustering and visualization. NeuroImage 22: 1214–1222. [DOI] [PubMed] [Google Scholar]
- Hoerl AE, Kennard RW ( 1970): Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 12: 55–67. [Google Scholar]
- Hogg RV, Craig AT ( 1995): Introduction to Mathematical Statistics, 5th ed. Englewood Cliffs, NJ: Prentice‐Hall. [Google Scholar]
- Humberstone M, Sawle GV, Clare S, Hykin J, Coxon R, Bowtell R, Macdonald IA, Morris PG ( 1997): Functional magnetic resonance imaging of single motor events reveals human presupplementary motor area. Ann Neurol 42: 632–637. [DOI] [PubMed] [Google Scholar]
- Hutchinson RA, Niculescu RS, Keller TA, Rustandi I, Mitchell TM ( 2009): Modeling fMRI data generated by overlapping cognitive processes with unknown onsets uding Hidden Process Models. Neuroimage 46: 87–104. [DOI] [PubMed] [Google Scholar]
- Hyvrinen A ( 1999): Fast and robust fixed‐point algorithms for independent component analysis. IEEE Trans Neural Netw 10: 626–634. [DOI] [PubMed] [Google Scholar]
- Kawashima R, Roland PE, O'Sullivan BT ( 1994): Activity in the human primary motor cortex related to ipsilateral hand movements. Brain Res 663: 251–256. [DOI] [PubMed] [Google Scholar]
- Kruggel F, von Cramon DY ( 1999): Modeling the hemodynamic response in single‐trial functional MRI experiments. Magn Reson Med 42: 787–797. [DOI] [PubMed] [Google Scholar]
- Lindquist MA, Meng Loh J, Atlas LY, Wager TD ( 2009): Modeling the hemodynamic response function in fMRI: Efficiency, bias and mis‐modeling. Neuroimage 45: S187–S198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindquist MA, Waugh C, Wager TD ( 2007): Modeling state‐related fMRI activity using change‐point theory. Neuroimage 35: 1125–1141. [DOI] [PubMed] [Google Scholar]
- Liu Y, Gao JH, Liu HL, Fox PT ( 2000): The temporal response of the brain after eating revealed by functional MRI. Nature 405: 1058–1062. [DOI] [PubMed] [Google Scholar]
- Long CJ, Brown EN, Triantafyllou C, Aharon I, Wald LL, Solo V ( 2005): Nonstationary noise estimation in functional MRI. NeuroImage 28: 890–903. [DOI] [PubMed] [Google Scholar]
- Marrelec G, Benali H, Ciuciu P, Pélegrini‐Issac M, Poline JB ( 2003): Robust bayesian estimation of the hemodynamic response function in event related BOLD fMRI using basic physiological information. Hum Brain Mapp 19: 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, Sejnowski TJ ( 1998): Analysis of fMRI data by blind separation into independent spatial components. Hum Brain Mapp 6: 160–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon RS, Luknowsky DC, Gati JS ( 1998): Mental chronometry using latency‐resolved functional MRI. Proc Natl Acad Sci USA 95: 10902–10907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan VL, Li Y, Abou‐Khalil B, Gore JC ( 2008): Development of 2dTCA for the detection of irregular, transient BOLD activity. Hum Brain Mapp 29: 57–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual‐Leone A, Amedi A, Fregni F, Merabet LB ( 2005): The plastic human brain cortex. Annu Rev Neurosci 28: 377–401. [DOI] [PubMed] [Google Scholar]
- Passingham RE ( 1985): Premotor cortex: Sensory cues and movement. Behav Brain Res 18: 175–185. [DOI] [PubMed] [Google Scholar]
- Petridou N, Caballero‐Gaudes C, Dryden I, Francis S, Gowland P ( 2009): Spatiotemporally Coordinated Activation Detected During Apparent Rest in fMRI. 15th Annual Meeting of the Organization for Human Brain Mapping, San Francisco, CA.
- Pfeuffer J, van de Moortele PF, Yacoub E, Shmuel A, Adrianny G, Andersen P, Merkle H, Garwood M, Urgurbil K, Hu X ( 2002): Zoomed functional imaging in the human brain at 7 Tesla with simultaneous high spatial and high temporal resolution. Neuroimage 17: 272–286. [DOI] [PubMed] [Google Scholar]
- Porro CA, Cettolo V, Francescato MP, Baraldi P ( 2000): Ipsilateral involvement of primary motor cortex during motor imagery. Eur J Neurosci 12: 3059–3063. [DOI] [PubMed] [Google Scholar]
- Porro CA, Francescato MP, Cettolo V, Diamond ME, Baraldi P, Zuiani C, Bazzochi M, di Prampero PE ( 1996): Primary motor and sensory cortex activation during motor performance and motor imagery: A functional magnetic resonance study. J Neurosci 16: 7688–7698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao SM, Binder JR, Bandettini PA, Hammeke TA, Yetkin FZ, Jaesmanowicz A, Lisk LM, Morris GL, Mueller WM, Estkowski LD ( 1993): Functional magnetic resonance imaging of complex human movements. Neurology 43: 2311–2318. [DOI] [PubMed] [Google Scholar]
- Richter W, Andersen PM, Georgopoulos AP, Kim SG ( 1997a): Sequential activity in human motor areas during a delayed cued finger movement task studied by time‐resolved fMRI. Neuroreport 8: 1257–1261. [DOI] [PubMed] [Google Scholar]
- Richter W, Ugurbil K, Georgopoulus AP, Kim SG ( 1997b): Time‐resolved fMRI of mental rotation. Neuroreport 8: 3697–3702. [DOI] [PubMed] [Google Scholar]
- Richter W, Somorjai R, Summers R, Jarzmasz M, Menon RV, Gati JS, Georgopoulus AP, Tegeler C, Ugurbil K, Kim SG ( 2000): Motor area activity during mental rotation studied by time‐resolved single‐trail fMRI. J Cogn Neurosci 12: 310–320. [DOI] [PubMed] [Google Scholar]
- Schubert T, von Cramon DY, Niendorf T, Pollmann S, Bublak P ( 1998): Cortical areas and the control of self‐determined finger movements: an fMRI study. Neuroreport 9: 3171–3176. [DOI] [PubMed] [Google Scholar]
- Schwartzman A, Dougherty RF, Lee J, Ghahremani D, Taylor JE ( 2009): Empirical null and false discovery rate analysis in neuroimaging. Neuroimage 44: 71–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selén Y, Abrahamsson R, Stoica P ( 2008): Automatic robust adaptive beamforming via ridge regression. Signal Processing 88: 33–49. [Google Scholar]
- Smith SM, Nichols TE ( 2009): Threshold‐free cluster enhancement: Addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neuroimage 44: 83–98. [DOI] [PubMed] [Google Scholar]
- Stoica P, Moses RL ( 2005): Spectral Analysis of Signals. Englewood Cliffs, NJ: Prentice‐Hall. [Google Scholar]
- Svensen M, Kruggel F, von Cramon DY ( 2000): Probabilistic modeling of single‐trial fMRI data. IEEE Trans Med Imaging 19: 25–35. [DOI] [PubMed] [Google Scholar]
- Tanabe J, Miller D, Tregellas J, Freedman R, Meyer FG ( 2002): Comparison of detrending methods for optimal fMRI preprocessing. Neuroimage 15: 902–907. [DOI] [PubMed] [Google Scholar]
- Tryantafyllou C, Hoge RD, Krueger G, Wiggins DJ, Potthast A, Wiggins GC, Wald LL ( 2005): Comparison of physiological noise at 1.5T, 3T and 7T and optimization of fMRI acquisition parameters. Neuroimage 26: 243–250. [DOI] [PubMed] [Google Scholar]
- Ugurbil K, Xiaoping H, Wei C, Zhu XH, Kim SG, Georgopoulos A ( 1999): Functional mapping in the human brain using high magnetic fields. Philos Trans R Soc Lond B 354: 1195–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Rootselaar AF, Renken R, de Jong BM, Hoogduin JM, Tijssen MA, Maurits NM ( 2007): fMRI analysis for motor paradigms using EMG‐based designs: A validation study. Hum Brain Mapp 28: 1117–1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Windischberger C, Cunnington R, Lamm C, Lanzenberger R, Langerberger H, Deecke L, Bauer H, Moser E ( 2008): Time‐resolved analysis of fMRI signal changes using brain activation movies. J Neurosci Methods 169: 222–230. [DOI] [PubMed] [Google Scholar]
- Witt ST, Laird AR, Meyerand ME ( 2008): Functional neuroimaging correlates of finger‐tapping task variations: An ALE meta‐analysis. Neuroimage 42: 343–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolrich M, Ripley BD, Brady M, Smith SM ( 2001): Temporal autocorrelation in univariate linear modeling of fMRI data. Neuroimage 14: 1370–1386. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found in the online version of this article.
Supporting Figure 1A
Supporting Figure 1B
Supporting Movie 1
Supporting Movie 2


