Age‐related changes in topological organization of structural brain networks in healthy individuals

Abstract

The aim of this study was to examine structural brain networks using regional gray matter volume, as well as to investigate changes in small‐world and modular organization with normal aging. We constructed structural brain networks composed of 90 regions in young, middle, and old age groups. We randomly selected 350 healthy subjects for each group from a Japanese magnetic resonance image database. Structural brain networks in three age groups showed economical small‐world properties, providing high global and local efficiency for parallel information processing at low connection cost. The small‐world efficiency and node betweenness varied significantly and revealed a U‐ or inverted U‐curve model tendency among three age groups. Results also demonstrated that structural brain networks exhibited a modular organization in which the connections between regions are much denser within modules than between them. The modular organization of structural brain networks was similar between the young and middle age groups, but quite different from the old group. In particular, the old group showed a notable decrease in the connector ratio and the intermodule connections. Combining the results of small‐world efficiency, node betweenness and modular organization, we concluded that the brain network changed slightly, developing into a more distributed organization from young to middle age. The organization eventually altered greatly, shifting to a more localized organization in old age. Our findings provided quantitative insights into topological principles of structural brain networks and changes related to normal aging. Hum Brain Mapp, 2012. © 2011 Wiley Periodicals, Inc.

INTRODUCTION

New advances in the quantitative analysis of complex networks, based largely on graph theory, have been rapidly applied to studies of brain network topological organization. The structural and functional systems of the human brain show topological properties of complex networks, such as small‐world properties, highly connected hubs, and modularity [Bullmore and Sporns,2009]. Significant discoveries related to human brain functional networks have indicated that the brain exhibits small‐world properties characterized by a high clustering index and a short average distance between any two regions [Latora and Marchiori,2001; Watts and Strogatz,1998], using modern neuroimaging techniques such as functional magnetic resonance imaging (fMRI), and electroencephalogram (EEG) [Achard and Bullmore,2007; Achard et al.,2006; Bassett et al.,2006; Eguiluz et al.,2005; Ferri et al.,2007; Micheloyannis et al.,2006; Salvador et al.,2005]. It has been verified that structural networks of the human brain revealed by measurements of cortical thickness or regional gray matter volume (RGMV) have small‐world properties [Bassett et al.,2008; He et al.,2007,2008,2009a]. Moreover, the small‐world properties were confirmed in human brain structural networks using diffusion MRI technique [Gong et al.,2009b; Hagmann et al.,2007; Iturria‐Medina et al.,2008]. Achard and Bullmore were the first to demonstrate economical small‐world properties in brain functional networks, which provide high global and local efficiency for parallel information processing at a low wiring cost [Achard and Bullmore,2007]. Efficiency metrics have also provided a new measure to quantify differences between patient groups and appropriate comparison groups [He et al.,2009a; Liu et al.,2008; Wang et al.,2009b].

Modularity is thought to be one of the main organizing principles in most complex systems, including biological, social, and economical networks [Girvan and Newman,2002; Guimerà et al.,2005; Hartwell et al.,1999; Newman,2006a]. A key advantage of modular organization is that it favors evolutionary and developmental optimization of multiple or changing selection criteria: a modular‐organized network can evolve or grow one module at a time, without risking loss of function in other modules [Kashtan and Alon,2005; Redies and Puelles,2001]. Defining and characterizing modular organization in the human brain can help us to identify a set of modules structurally or functionally associated with components that perform specific biological functions. This investigation will also provide us with rich quantitative insights into structural–functional mapping. The modular organization of structural and functional networks in human brain has been demonstrated by several previous studies [Chen et al.,2008; Ferrarini et al.,2009; Hagmann et al.,2008; He et al.,2009b; Meunier et al.,2009a,b; Robinson et al.,2009; Valencia et al.,2009].

Normal processes of brain maturation and senescence might be reflected as quantifiable changes in structural and functional network topological properties [Bullmore and Sporns,2009; Micheloyannis et al.,2009]. A previous study on functional brain networks indicated that an older age group had significantly reduced cost efficiency in comparison to a younger group [Achard and Bullmore,2007]. Normal aging might thus be associated with changes in the economical small‐world properties of brain functional networks. Furthermore, normal aging had been proven to be associated with changes in modular organization of human brain functional networks [Meunier et al.,2009a]. A recent study reported that the organization of multiple functional brain networks shifts from a local anatomical emphasis in children to a more distributed organization in young adults [Fair et al.,2009]. The study also demonstrated that community detection by modularity optimization reveals stable communities within the graphs that are clearly different between young children and young adults [Fair et al.,2009]. A recent study also reported that the development of large‐scale brain networks is characterized by weakening of short‐range functional connectivity and strengthening of long‐range functional connectivity, comparing the children group (7–9 years) with the young‐adults group (19–22 years), [Supekar et al.,2009]. However, few studies have analyzed the influences on both small‐world and modular organization with normal aging. The main purpose of this study is to clarify topological properties in structural brain networks among different age groups. We hypothesized that the economical small‐world properties and the modular organization of structural brain networks would be altered with normal aging.

In the present study, we divided all healthy subjects into three groups by age. Study participants were selected from a large‐scale brain MRI database of normal Japanese (1421 subjects, ages from 18 to 80 years), [Sato et al.,2003]. The structural connectivity in the human brain consisting of 90 regions was constructed by computing the correlation matrix of RGMV across subjects within each group. Efficiency metrics were applied to investigate whether structural brain networks show economical small‐world attributes and whether significant differences exist in properties of brain networks among three age‐specific groups. We investigated the regional nodal characteristics of brain networks and compared the between‐group differences in node betweenness. Furthermore, we examined the modular organization of structural brain networks and identified several modules of the brain network in each age‐specific group. To clarify differences on the modular organization of brain networks among three groups, we compared the constitution of modules and computed attributes using, for example, the connector ratio and the distribution efficiency.

MATERIALS AND METHODS

Subjects

The subjects were all community‐dwelling normal Japanese subjects recruited by two projects; the Aoba Brain Imaging Project, Sendai, Japan and the Tsurugaya Project, Sendai, Japan. The Aoba Brain Imaging Project was performed to create a database of normal Japanese brain images [Sato et al.,2003]. To perform this, we obtained 1,637 brain MR images from normal Japanese volunteers who were living in and around Sendai City, Japan. The Tsurugaya Project study is a comprehensive geriatric assessment (CGA) of the elderly population. It involved 1,179 subjects aged 70 years or older in 2002 who were living in Tsurugaya district, Sendai City, Japan. We selected 210 subjects by random sampling from subjects who would be willing to undergo brain MRI and submitted these patients to MRI. The subjects of the two projects were all healthy and had neither present illness nor a history of neurological disease, psychiatric disease, brain tumor, or head injury. Prior to the acquisition of MR images, all subjects enrolled in the two projects were interviewed by medical doctors for screening to determine whether he/she was normal and to obtain clinical data. In both projects, we excluded in advance those subjects who had past or present history of malignant tumors, head traumas, cerebrovascular diseases, epilepsy, or psychiatric diseases. After the interview, brain MR images were obtained from each subject. The MR images were inspected by two to three well‐trained radiologists. Images with the following findings were excluded from this study: head injuries, brain tumors, hemorrhage, major and lacunar infarctions, and moderate to severe white matter hyperintensities. We did not exclude the images with mild spotty white matter hyperintensities.

We collected brain images of 1,483 subjects in this study (mean ± S.D.; age, 46.30 ± 16.98 years; range: 18–80 years). To investigate the topological properties and organization of structural brain networks with normal aging, we divided all subjects into three groups by age (young, 18–40 years; middle, 41–60 years; old, 61–80 years), without regard to sex. Group ID naming and characteristics of the subjects are shown in Table I.

Table I.

Characteristics of the subjects

Group ID	Age range	Number of subjects	Age (mean ± SD)
Young (Y)	18–40	551 (F: 231/M: 320)	27.42 ± 6.77
		350 (F: 158/M: 192)	27.31 ± 6.65
Middle (M)	41–60	560 (F: 331/M: 229)	50.94 ± 5.22
		350 (F: 196/M: 154)	51.07 ± 5.26
Old (O)	61–80	372 (F: 198/M: 174)	68.32 ± 4.58
		350 (F: 188/M: 162)	68.17 ± 4.03

The italic and bold characters indicate the characteristics of 350 subjects randomly selected for each group.

MRI data acquisition and the use of them for the studies by Fukuda H (the last author of the study) were approved by the Institutional Review Board of Tohoku University School of Medicine. Informed consent was obtained from each subject after a full explanation of the purpose and procedures of the study, according to the Declaration of Helsinki (1991), prior to MR image scanning.

Image Acquisition

Brain images were obtained from each subject using two 0.5 T MR scanners (Sigma contour, GE‐Yokogawa Medical Systems, Tokyo) with two different pulse sequences: (1) 124 contiguous, 1.5‐mm thick axial planes of three dimensional T1‐weighted images (spoiled gradient recalled acquisition in steady state: repetition time (TR), 40 ms; echo time (TE), 7 ms; flip angle (FA), 30°; voxel size, 1.02 mm × 1.02 mm × 1.5 mm); (2) 63 contiguous, 3 mm‐thick axial planes of gapless (using interleaving) proton density‐weighted images/T2‐weighted images (dual echo fast spin echo: TR, 2,860 ms; TE, 15/120 ms; voxel size, 1.02 mm × 1.02 mm × 3 mm). T1 images were used for the present analysis and all three images were used to exclude those MRIs with abnormalities, as described above.

Measurements of Regional Gray Matter Volume

After the image acquisition, RGMV for each subject was measured by using statistical parametric mapping 2 (SPM2) (Wellcome Department of Cognitive Neurology, London, UK) [Friston et al.,1995] in Matlab (Math Works, Natick, MA). First, T1‐weighted MR images were transformed to the same stereotactic space by registering each of the images to the ICBM 152 template (Montreal Neurological Institute, Montreal, Canada), which approximates the Talairach space [Jean Talairach,1988]. Then, tissue segmentation from the raw images to the gray matter, white matter, cerebrospinal fluid space, and non‐brain tissue was performed using the SPM2 default segmentation procedure. We applied these processes using the MATLAB file “cg_vbm_optimized” (http://dbm.neuro.uni-jena.de/vbm.html). WFU_PickAtlas software was employed to label the regions in the gray matter images, which provided a method for generating ROI masks based on the Talairach Daemon database [Lancaster et al.,2000; Maldjian et al.,2003,2004]. We parcellated the entire gray matter into 45 separate regions for each hemisphere (90 regions in total, see Supporting Information Table SI) defined by the Automated Anatomical Labeling (AAL) atlas [Tzourio‐Mazoyer et al.,2002] to calculate the RGMV for each subject.

Construction of Brain Structural Connection Matrix

To study the topological properties of structural brain networks among three age‐specific groups, we examined the correlation matrices using graph‐theoretical analysis: GroupIDs were Young, Middle, and Old. Since there was a large difference in the number of subjects in each group, we randomly selected 350 subjects for each age group (the original group) (Table I) to reduce the influence due to varying degrees of freedom for each group in computing inter‐regional correlation across subjects. We also repeated this randomly‐selected grouping method 20 times in each age group to examine whether subject characteristics were significantly changed. As a result, the characteristics of 350 subjects randomly selected for each age group were not significantly different from those of the original group. We used a linear regression analysis to remove the effects from total gray matter volume and sex, so that the residuals of this regression were employed as the substitute for the raw RGMV, denoted as corrected RGMV (cRGMV). To analyze the structural brain network by using RGMV, we first applied the method introduced by He et al. to construct the structural connection matrix [He et al.,2007]. We computed the Pearson correlation coefficient between cRGMV across 350 subjects randomly chosen from each group to construct the interregional correlation matrix (N × N, where N is the number of gray matter regions, here N = 90) for each group. Each connection matrix can be converted to a binarized and undirected graph (network) G by using a correlation or cost threshold. Then the networks were analyzed by using graph theoretical methods. All topological parameters of the networks calculated in this study and their implications are shown in Table II.

Table II.

Topological parameters of structural brain networks used in this study

Network properties	Characters	Descriptions
Economical small‐world properties	Cost	The cost or the sparsity to construct a network.
	Eloc	The local efficiency measures how efficient are the network to exchange the information at the clustering level.
	Eglob	The global efficiency measures how efficient are the network to exchange the information at the global level.
	I Eloc	The integrated local efficiency is the integrals of the local efficiency curves over the preselected range of cost threshold.
	I Eglob	The integrated global efficiency is the integrals of the global efficiency curves over the preselected range of cost threshold.
Nodal characteristics	BC	The normalized betweenness measures the ability of a node relative to information flow between other nodes throughout the network.
	I BC	The integrated normalized betweenness is the integrated normalized betweenness over the preselected range of cost threshold.
Modularity	B	The modularity measures how the network is organized into modules with high level of local clustering.
	sBC	The within‐module betweenness centrality measures the importance of a node relative to the information flow between other nodes in the module.
	PC	The participant coefficient measures the ability of a node to maintain the communication between its own module and the other modules.

Small‐World Properties

Small‐world properties (clustering coefficient, C _p and characteristic path length, L _p) were originally defined by Wattz and Strogatz [1998]. In addition to the conventional small‐world parameters (C _p and L _p), more biologically sensible properties of brain networks are the efficiency metrics (global efficiency, E _glob and local efficiency, E _loc), which measure the capability of the network with regard to information transmission at the global and local levels, respectively [Latora and Marchiori,2001]. In several recent studies, the efficiency metrics have been applied to human brain functional [Achard and Bullmore,2007; Wang et al.,2009a,b] and structural [He et al.,2009a; Iturria‐Medina et al.,2008] network studies. For a graph G with N nodes and K edges, the global efficiency of G can be computed as [Latora and Marchiori,2001]:

(1)

where d _ij is the shortest path length between node i and node j in G. The local efficiency of G is defined as [Latora and Marchiori,2001]:

(2)

where E _glob(G _i) is the global efficiency of G _i, the sub‐graph of the neighbors of node i. In this study, we generated a population (n = 1,000) of regular networks and random networks that preserved the same number of nodes and edges, respectively. The efficiency metrics (E _glob and E _loc) of real brain networks (G) were compared with those of regular graphs (G _reg) and random graphs (G _rand), respectively. The real brain network G is considered to be a small‐world network if it meets the following criteria [Latora and Marchiori,2001]:

(3)

In this study, we applied a cost threshold to investigate economical small‐world properties of networks. Such a thresholding approach can normalize all networks to have the same number of edges or wiring cost and thus provide an avenue to detect changes in topological organization with aging [Achard and Bullmore,2007; He et al.,2009a]. To estimate the small‐world properties of structural brain networks and to define a small‐world regime, we first applied a broad cost threshold range (0.05 ≤ cost ≤0.5, increased by 0.01) to all the connection matrices. The cost (or sparsity) was computed as the ratio of the number of actual connections divided by the maximum possible number of connections in the network. We then adopted the following complementary approaches to choose the small‐world regime: (1) the small‐world properties were estimable (K > log(N) = 4.5, N = 90) [Watts and Strogatz,1998], (2) all brain networks were fully connected, and (3) the resulting brain networks have sparse properties and distinguishable properties in comparison to the degree‐matched random networks [Bassett et al.,2008; Liu et al.,2008; Wang et al.,2009a]. Finally, we selected the small‐world regime as a range of cost threshold (0.11 ≤ cost ≤0.25, step = 0.01). These thresholds were also used for the following calculation of regional nodal characteristics and modularity.

Regional Nodal Characteristics

In this study, we examined the node betweenness in the networks. The betweenness bc_i of a node i is defined as the number of shortest paths between any two nodes that run through node i [Freeman,1977]. We defined the normalized betweenness as BC_i = bc_i/<bc_i>, where <bc_i> was the average betweenness of all nodes. Thus, the normalized betweenness of BC_i measures the ability of a node relative to information flow between other nodes throughout the network. Finally, we averaged the normalized betweenness across the range of cost threshold (0.11 ≤ cost ≤0.25). Regions with a higher value of 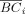(> mean + SD) were identified as global hubs in the brain network [Sporns et al.,2007].

Modularity and Regional Role

A module can be generally defined as a subset of nodes in the graph that are more densely connected to the other nodes in the same module than to nodes outside the module [Radicchi et al.,2004]. Several algorithms have been proposed to define the modular decomposition of an undirected graph [Clauset et al.,2004; Danon et al.,2005; Guimerà and Amaral,2005a,2005b; Guimerà et al.,2004; Newman2006a,2006b,2004; Newman and Girvan,2004; Reichardt and Bornholdt,2006]. Despite the many interesting alternative methods, it should be noted that the problem of community finding remains a challenge because no single method is fast and sensitive enough to ensure ideal results for general, large networks, a problem that is compounded by the lack of a clear definition of communities. Here, we adopted the spectral algorithm [Guimerà and Amaral,2005b; Guimerà et al.,2004; Newman,2006a] for community detection, which is believed to be the most precise and be able to find a division with the highest value of modularity for many networks [Costa et al.,2007]. This algorithm reformulates the modularity concept in terms of the eigenvectors of a new characteristic matrix for the network, called the modularity matrix [Newman,2006a].

For each subgraph g, its modularity matrix B ^(g) has elements

(4)

for vertices i and j in g. In Eq. (4), the actual number of edges falling between a particular pair of vertices i and j is aij; k _i is the degree of a vertex i; δ_ij = 1 if i = j and 0 otherwise. Thus, to split the network in communities, the modularity matrix is constructed and its most positive eigenvalue and corresponding eigenvector are determined. According to the signs of the elements of this vector, the network is divided in two parts (vertices with positive elements are assigned to one community and vertices with negative elements to another). Next, the process is repeated recursively to each community until a split that makes a zero or negative contribution to total modularity is reached. Similarly, Newman proposed a new definition of communities as indivisible subgraphs, i.e., subgraphs whose division would not increase the modularity.

In this study, we detected the community structure for the structural brain networks of three groups, which were thresholded by a specific cost threshold (cost = 0.11). With this threshold, we can capture the structural connectivity backbone underlying the modular organization of the most sparse and fully‐connected brain networks. To further distinguish the roles of nodes in terms of their intra‐ and inter‐module connectivity patterns, the two measurements, the within‐module betweenness centrality, sBC and the participant coefficient (PC) were applied [Guimerà and Amaral,2005a; Guimerà et al., 2005]. The sBC (i) of a node i is the betweenness centrality, but is calculated only within the module s to which it belongs. This parameter measures the importance of a node relative to the information flow between other nodes in the module. The PC(i) of a node i is defined as

where N _M is the number of modules, k _is is the number of links of node i to nodes in module s and k _i is the total degree of node i. The PC(i) tends to 1 if node i has a homogeneous connection distribution with all the modules and to 0 if it does not have any inter‐module connections. PC measures the ability of a node to maintain the communication between its own module and the other modules. A high PC value for a given node usually means the node has many inter‐module connections. Depending on the sBC, the nodes in the brain functional network were classified as modular hubs (sBC >mean + std) or non‐hubs (sBC ≤mean + std), respectively. In terms of the PC, the hub nodes were further subdivided into R1 connector hubs (PC > 0.25) and R2 provincial hubs (PC ≤ 0.25), and non‐hub nodes were divided into R3 connector non‐hubs (PC > 0.25) and R4 peripheral non‐hubs (PC ≤ 0.25) [Guimerà and Amaral,2005a; Guimerà, 2005].

Statistical Analysis

To analyze statistical significance of between‐group differences with regard to the efficiency metrics (local and global efficiency) among three age‐specific groups, a nonparametric permutation test method was applied in the small‐world regime defined above (0.11 ≤cost ≤0.25, step = 0.01), [Bullmore et al.,1999; He et al.,2008]. Thus, we can explore the between‐group differences in efficiency metrics at each threshold level. Here, we performed three comparisons (Z _I, Z _II, Z _III) including the young versus middle (Y vs. M), the middle versus old (M vs. O), and the young versus old (Y vs. O), respectively. For each comparison, the efficiency metrics of binarized graphs at a given threshold were computed separately for each group. Then one randomization procedure of the permutation test yielded two new groups that were generalized by randomly reallocating each subject's set of cRGMV measures from previous groups. The correlation matrices for new groups were recomputed and binarized by thresholding to achieve the same threshold as in the real networks. The efficiency metrics of corresponding binarized graphs and their between‐group differences were calculated. This permutation test randomization procedure was repeated 1,000 times at each threshold, consistent with the real networks. Finally, the 95th percentile points of each distribution were used as the critical values for a one‐tailed test of the null hypothesis with a probability of Type I error of 0.05. Moreover, we calculated the integrals of the efficiency metrics curves as the integrated metrics (I _Eloc, the integrated local efficiency; I _Eglob, the integrated global efficiency) over the preselected range of cost threshold. Between‐group significances of three comparisons on the integrated metrics were also estimated by 1,000 permutation tests. For the investigation of node betweenness, we also computed the between‐group significance of two comparisons (Y vs. M and M vs. O) on the integrated normalized betweenness (I _BCi) over the cost threshold range, using 1,000 permutation tests. To adjust for the multiple comparisons, a false discovery rate (FDR) procedure was applied at a q value of 0.05 [Genovese et al.,2002]. We also calculated the ratio of intermodule connections under a cost threshold range (0.11 ≤ cost ≤0.25, step = 0.01) with the modular organization by the cost of 0.11. An ANOVA analysis was applied to test the between‐group significance of the ratio of intermodule connections.

RESULTS

Economical Small‐World Properties and Age‐Related Changes

We used a range for cost threshold (0.11 ≤ cost ≤0.25, step = 0.01) to verify the properties of structural brain networks from three age‐specific groups (Young, 18–40 years; Middle, 41–60 years; Old, 61–80 years). With the cost thresholding strategy, both the local and global efficiency curves of structural brain networks in three groups were intermediate compared with those of the matched random and regular networks (Fig. 1A,B). The structural brain networks in three age‐specific groups exhibited economical small‐world properties, indicated by higher local and global efficiency than comparable random and regular networks, respectively [Latora and Marchiori,2001].

Figure 1.

Economical small‐world properties and age‐related changes. Left: The local and global efficiency of brain networks as a function of cost threshold. Right: The trend for the integrated efficiency metrics in age‐specific groups. A: Local efficiency calculated under the cost threshold range of 0.11–0.25. B: Global efficiency calculated under the cost threshold range of 0.11–0.25. Significant differences between age groups were tested by permutation test under uncorrected conditions (P < 0.05). ▴; Y vs. M, ×; Y vs. M, ♦; Y vs. O. C: Integrated local efficiency. D: Integrated global efficiency. Three comparisons were performed as follows: Z _I (Young vs. Middle), Z _II (Middle vs. Old), and Z _III (Young vs. Old).

As shown in Figure 1A, the local efficiency in the young group was significantly larger than those of the middle and old groups, whereas no significant difference was found between the middle and old groups. The global efficiency of the young group was significantly lower than that of the middle and old groups, and the old group had significant lower values than the middle group (Fig. 1B). Using the integrated efficiency metrics over the small‐world regime, we defined a U‐curve model to clarify the trend of topological properties of structural brain networks with normal aging. The integrated local and global efficiency showed a U‐curve and an inverted‐U‐curve, respectively (Fig. 1C,D).

Regional Nodal Characteristics and Age‐Related Changes

To identify the global hubs in structural brain networks, we averaged the normalized node betweenness centrality BC_i of each region over the cost threshold regime. The regions with higher (> mean + sd) were identified as the global hubs (Table III). In the young group, 16 regions were designated as the global hubs, specifically 14 association regions and 2 limbic/paralimbic regions. In the middle group, 14 regions were identified as the global hubs, specifically 10 association regions and 4 limbic/paralimbic regions. In the old group, 14 regions were identified as the global hubs, specifically 10 association regions, 3 limbic/paralimbic regions and 1 subcortical region. Among the identified global hubs, 12 of 16 regions in the young group, 9 of 14 regions in the middle group, and 7 of 14 regions in the old group were frontal and parietal regions. Results also indicated that 10 out of all 14 global hubs in the middle group and 6 out of all 14 global hubs in the old group were also identified as the global hubs in the young group. To further clarify the alteration of regional nodal characteristics, we applied 1,000 permutation tests to compute the significance of between‐group differences in node betweenness (P < 0.001, FDR‐corrected). The results indicated that six regions in the dorsal frontal‐parietal junction [IFGoperc.L, SFGmed.L, SFGmed.R, SFGdor.L, IPL.L, PCUN.L; for abbreviation see Supporting Information Table SI] showed decreased node betweenness from young to middle age, whereas only three regions in the ventral frontal and temporal lobes [ORBinf.L, ORBinf.R, STG.L] revealed increased node betweenness (see Supporting Information Table SII). For the period from middle to old age, five ventral lateral cortices in the frontal and temporal lobes [ORBinf.L, ORBinf.R, ORBmed.R, MTG.L, MTG.R] showed decreased node betweenness, whereas nine regions mostly in the lateral occipital‐parietal junction [MOG.L, MOG.R, ANG.L, ANG.R] and the paralimbic/subcortical area [PHG.R, AMYG.R, CAU.L, THA.L] revealed increased node betweenness (see Supporting Information Table SIII). The global hubs and the significant age‐related changes in node betweenness were visualized by surface representations of structural brain networks using the Caret software [Van Essen,2005], (see Fig. 2).

Table III.

The global hubs of the structural brain networks

Abbreviations	Class	Young			Middle			Old			Reference
		N bc(i)	Module	Role	N bc(i)	Module	Role	N bc(i)	Module	Role
SFGmed. L	Association	4.559	IV	R2				4.762	IV	R3	E
MTG. L	Association	4.305	V	R3	3.543	V	R3				B, C, E, F, G
SFGmed. R	Association	3.698	IV	R4							A, C, D, E
MOG. R	Association	3.569	I	R3				2.737	II	R3	A, G
ORBmed. R	Paralimbic	2.876	V	R3	3.451	V	R3
LING. R	Association	2.865	III	R3	1.945	II	R3				B, G
SMG. L	Association	2.846	I	R3	2.579	I	R3	1.997	I	R3	B
SMG. R	Association	2.496	III	R3	1.853	IV	R3	2.249	I	R3	C
PCUN. L	Association	2.442	III	R3							A, D, G
IFGtriang. R	Association	2.321	I	R3	2.610	I	R3	2.999	I	R3	E, G
ORBmed. L	Paralimbic	2.289	V	R3	2.009	V	R3				C
SFGdor. L	Association	2.261	IV	R2							A, D, E, G
MTG. R	Association	2.162	V	R3	3.631	V	R3				B, C, E, F, G
IFGtriang. L	Association	2.086	I	R3	1.854	I	R3	2.689	I	R3	E, G
PCUN. R	Association	2.050	III	R1							A, D, G
SFGdor. R	Association	2.028	IV	R4	1.941	IV	R2				A, C, D, E, F, G
ANG. R	Association							3.431	II	R3	B
AMYG. R	Paralimbic							3.389	V	R3
PHG. R	Paralimbic							2.760	V	R2	E, F
STG. R	Association				2.986	I	R3	2.665	I	R4	B, C, G
ANG. L	Association							2.318	II	R3	B
INS. L	Paralimbic							2.211	I	R2	D
MOG. L	Association							2.016	II	R3	A, G
THA. L	Subcortical							1.948	I	R3
STG. L	Association				1.991	I	R1				B, G
ORBinf. L	Paralimbic				3.037	V	R1				B, C
ORBinf. R	Paralimbic				3.018	V	R3				B

The hub regions (normalized node betweenness, Nbc(i)>mean + SD) in structural brain networks of three age groups are listed in decreasing order of the node betweenness in the young group. The regions are classified as association, primary, limbic/paralimbic or subcortical regions as described by Mesulam [2000]. The module column indicates the anatomical modules that the hub regions belong to, and the role column indicates the roles that the hub regions play in terms of their intra‐ and inter‐module connectivity patterns; connector hub (R1), provincial hub (R2), connector non‐hub (R3), and provincial non‐hub (see Materials and Methods). R: right; L: left. For the description of the abbreviations, see supplementary Table S1.

The reference column indicates the hub regions previously identified in human brain structural (A, B, C, D, E), or functional (F, G) networks. A; Gong et al. [2009], B; He et al. [2008], C; Chen et al. [2008], D; Iturria‐Medina [2008], E; He et al. [2007], F; He et al. [2009b], G; Achard et al. [2006].

Figure 2.

Surface representations for global hubs and the significant age‐related changes in node betweenness. Top: The global hubs in the young group. Middle: The global hubs in the middle group and the significant age‐related changes in node betweenness from young to middle age. Bottom: The global hubs in the old group and the significant age‐related changes in node betweenness from middle to old age. The global hubs and non‐hubs are indicated by spheres in big and small size, respectively. The nodes with significant decreased and increased age‐related changes are indicated by green and red spheres, respectively. The nodes without significant age‐related change are indicated by blue spheres.

Modularity and Age‐Related Changes

Maximum modularity (M) of brain networks decreased as a function of increasing cost threshold (see Supporting Information Fig. S1). It is generally accepted that M ≥ 0.3 are indicative of nonrandom community structure [Newman and Girvan,2004]. In this study, as the values of modularity were all larger than 0.3 over the preselected cost threshold range, and structural brain networks were consistently modularly organized in three age groups. However, there was no significant difference in modularity among the age‐specific groups. Using the fixed cost threshold (cost = 0.11), the obtained brain networks that captured the structural connectivity backbone underlying the principal topological organization were separated into modules according to the spectral method proposed by Newman [2006a]. As a result, the brain networks were separated into five, six, and five modules in young, middle, and old groups, respectively (Table IV, see Supporting Information Table SIV). The brain regions included in modules with three age groups were described in Supporting Information Text S1. The surface representations for modules in structural brain networks are shown in Figure 3. Moreover, the modular organization of structural brain networks shown here was also reproduced by using different specific cost thresholds (cost = 0.15 and 0.20), (see Supporting Information Fig. S2). We showed the modular organization of the structural brain networks in topological spaces (Fig. 4A–C). The topological representations were drawn by the Pajek software package (http://vlado.fmf.uni-lj.si/pub/networks/pajek) using a Kamada‐Kawai algorithm [Kamada Kawai,1989]. With this algorithm, the geometric distance between two brain regions on the drawing space approximates the shortest path length between them.

Table IV.

The distribution of connectors and inter‐module connections in each module

Module	Young			Middle			Old
	Regions	Connector	Intermodule	Regions	Connector	Intermodule	Regions	Connector	Intermodule
I	16	11(0.69)	80(0.37)	13	9(0.69)	49(0.25)	26	7(0.27)	51(0.36)
II	21	8(0.38)	16(0.07)	18	6(0.33)	25(0.13)	10	4(0.40)	43(0.30)
III	14	12(0.86)	43(0.20)	18	12(0.67)	35(0.18)	8	4(0.50)	12(0.09)
IV	20	3(0.15)	10(0.05)	19	6(0.32)	16(0.08)	18	6(0.33)	19(0.13)
V	19	15(0.79)	69(0.32)	14	11(0.79)	58(0.30)	28	3(0.11)	13(0.09)
VI				8	5(0.63)	15(0.08)
Total number	90	49	109	90	49	99	90	24	69

The “Connector” column indicates the numbers of connector nodes in each module and its ratio to the total number of regions in the module (in parentheses). The “Intermodule” column indicates the numbers of intermodule connections in each module and its ratio to the total number of intermodule connections in the whole network (in parentheses). The bold and italic characters indicate the values of the connector‐module in each age group, with both the higher connector ratio (>0.6) and the higher ratio of intermodule connections (larger than <1/number of modules>).

Figure 3.

Surface representations for modules in structural brain networks. All of 90 brain regions are plotted by different colored spheres (different colors represent distinct network modules) and further mapped onto the cortical surfaces at the lateral and medial views, respectively.

Figure 4.

Modular organization of structural brain networks. Left: The modular organization of young (A), middle (B), and old (C) brain networks visualized by minimizing free energy using a Kamada‐Kawaki layout algorithm. The global hubs and non‐hubs are represented by the bigger and smaller circles, respectively. The regions are represented by the module color. The intramodule and intermodule connections are represented by the light gray and black lines, respectively. Right: The regional node roles in brain modules for young (D), middle (E), and old (F) brain networks, with connector nodes located in a central ring to highlight intermodule connections. The intramodule and intermodule connections are shown in colored and black lines, respectively.

In this study, according to the patterns of intra‐ and inter‐module connections, the four possible roles of regions were defined as connector hub (R1), provincial hub (R2), connector non‐hub (R3), and provincial non‐hub (R4). To show the node roles of regions in each module, we arranged the connector nodes (R1 and R3) in a central ring. In the young and middle group, 49 regions (8 R1 and 41 R3) and 49 regions (7 R1 and 42 R3) were identified as connector nodes (Table IV, Fig. 4D,E). However, only 28 regions (3 R1 and 25 R3) were defined as the connectors (Table IV, Fig. 4F). Most global hubs (Young, 12/16; Middle, 13/14; Old, 11/14) played R1 or R3 (connector) roles, with numerous inter‐module connections executing a critical impact on the coordination of information flow through the whole network (Table III).

In addition to discrepancies in the composition and numbers of modules, we also found differences in the topological roles of the modules in the brain networks of three groups. We defined the connector‐module as the module that had both a high connector ratio (the ratio of the connectors to the regions in the module was larger than 0.6) and a high ratio of intermodule connections (the ratio of the intermodule connections in the modules to that in the whole network was larger than <1/numbers of modules>) (Table IV). In both the young and the middle group, Modules I, III, and V were identified as the connector‐modules (Table IV). The young brain network was observed to have dense inter‐module connections between Module I and V (53/109), as well as between Module I and III (25/109) (see Supporting Information Table SV). In the middle group, the inter‐module connections spread around modules and abundant connections existed only between Modules I and V (28/99) (see Supporting Information Table SVI). Although no module was recognized as the connector‐module in the old group, there were relatively dense inter‐module connections between Modules I and II (32/69) (see Supporting Information Table SVII). Furthermore, the young and middle groups showed significantly higher proportions of intermodule connections than did the old group (ANOVA, P = 0.007), (Fig. 5).

Figure 5.

The ratio of intermodule connections.

DISCUSSION

This is the first study, to our knowledge, to investigate both small‐world properties and modularity of structural brain networks in healthy individuals across a broad age range. We found that structural brain networks exhibited economical small‐world properties in three age‐specific groups. We defined the global hubs to account for higher node betweenness in each group. In particular, the small‐world properties and node betweenness showed significant changes with normal aging. Moreover, our results demonstrated that structural brain networks showed modular organization in three groups and changed greatly in the old age group. Structural brain networks developed into a more distributed organization from young to middle age, then organized into a localized organization with substantial alterations in old age. Thus, understanding changes in topological properties in structural brain networks may help elucidate normal processes of brain maturation and senescence.

Economical Small‐World Properties and Age‐Related Changes

In this study, structural brain networks exhibited economical small‐world properties in all age‐specific groups, as determined using RGMV with MR images. Our findings of high global and local efficiency in structural brain networks with three age‐specific groups were compatible with previous functional and structural brain networks studies [Achard and Bullmore,2007; Bassett et al.,2008; He et al.,2008,2009a; Wang et al.,2009b]. Computational modeling simulations [Sporns et al.,2000] and experimental studies [Chen et al.,2008] have also suggested the emergence of small‐world topology when networks are evolved for the great complexity of dynamic behavior, defined as an optimal balance between local specialization and global integration [Strogatz,2001]. Thus, our results provided further support for the standpoint that brain networks might have evolved to maximize the cost efficiency of parallel information processing.

We also noted age‐related changes in efficiency metrics of structural brain networks. First, the structural brain network may develop into a more distributed organization from young to middle age, accompanied by significant decreases in local efficiency and robust increases in global efficiency. The reduction of local efficiency might be related to that healthy aging is associated with a regionally distributed pattern of gray matter atrophy [Bergfield et al.,2010]. Moreover, a previous study suggests that high global efficiency assures effective integrity or rapid transfers of information between and across remote regions that are believed to constitute the basis of cognitive process [Sporns and Zwi,2004]. Recent studies also demonstrate a positive correlation between the global efficiency of brain networks and intellectual performance, indicating a more efficient parallel information transfer in the human brain [Li et al.,2009; van den Heuvel et al.,2009]. Thus, the period from young to middle age may reflect a maturation process in the structural brain network. This finding was also in accordance with that the age‐related cognitive changes involved in the age‐related loss of gray matter volume [Hedden and Gabrieli,2004; Resnick et al.,2003; Tisserand et al.,2004]. Second, the structural brain network may evolve into a more local organization from middle to old age. The local efficiency did not differ significantly between the middle and old groups (Fig. 1A), whereas the integrated local efficiency increased significantly (Fig. 1C). Besides, the global efficiency and the integrated global efficiency decreased significantly (Fig. 1B,D). This phenomenon may indicate a degeneration process in the structural brain network with normal aging. It has been suggested the regular networks have a slow signal propagation speed and synchronizability in comparison to small‐world networks [Strogatz,2001]. The regular configuration that upsets the optimal balance of a small‐world network was related to many neurological and psychiatric disorders described as dysconnectivity syndromes [Catani and ffytche,2005]. Many previous studies have reported the regular configuration of brain networks in patients with diseases such as schizophrenia or AD, derived from fMRI, EEG or structural MRI data [Bassett et al.,2008; He et al.,2008; Stam et al.,2007]. There seems to be convergent evidence from methodologically disparate studies that both AD and schizophrenia are associated with abnormal topological organization of structural and functional brain networks [Bullmore and Sporns,2009]. Thus, our results suggested that aging has high risk for dysconnectivity syndromes. Third, the U‐curve model defined in this study indicated a quadratic curve‐like tendency of structural brain networks with normal aging. Our recent study demonstrated that gray matter volume declined with age in healthy community‐dwelling individuals, whereas the white matter ratio (WMR) had an inverted‐U curve trajectory with age. WMR increased until around 50 years of age and then decreased in each gender [Taki et al., in press]. This increase in the WMR is thought to represent maturational changes such as myelination, which may continue until middle adulthood. There are other supporting evidences that both gray and white matter magnetization transfer ratio (MTR) histograms follow quadratic curves: in both cases, they increase up until middle adulthood and then decline significantly, as determined by a study that assessed age‐related MTR histogram measurements in healthy subjects (54 healthy volunteers Aged 20–86 years), [Ge et al.,2002a,b]. Brain maturation includes both regressive cellular events (such as synaptic pruning) and progressive cellular events (such as myelination), which could result in the appearance of regional gray matter volume decline or cortical thinning on MR images [Sowell et al.,2003,2004]. It has been noted that brain maturational change continues to about the fifth decade of age [Sowell et al.,2003], which may account for the maturation of structural brain networks.

In addition to the above findings, we observed that the young group showed higher local efficiency (Fig. 1A,C) but lower global efficiency (Fig. 1B,D) as compared with the old group. This finding was different from the results of a previous study [Achard and Bullmore,2007], in which the young group (N = 15; mean age = 24.7 years) showed higher values in the relative global efficiency and no significant difference in the relative local efficiency compared with the old group (N = 11; mean age = 66.5 years). The discrepancies could be attributed to different network modalities (structural vs. functional) and population size (350 vs. 11/15).

Regional Nodal Characteristics and Age‐Related Changes

Node betweenness is an important metric that can be used to determine the relative importance of a node with a network and identify the pivotal nodes in the complex network. As indicated by the higher values of node betweenness, 16, 14, and 14 global hubs that are crucial to efficient communication were identified in the young, middle, and old groups, respectively. These global hub regions were mainly composed of recently evolved association and primitive limbic/paralimbic regions. Association regions have proven to contribute to the integrity of multiple functional systems, such as attention and memory systems [Mesulam,1998], and tend to be hubs of the brain functional network regardless of age [Achard and Bullmore,2007]. Limbic/paralimbic regions have been shown to be highly interconnected with the prefrontal regions and subcortical regions, and are mainly involved in emotional processing and the maintenance of a conscious state of mind [Mesulam,1998]. In this study, most global hubs were frontal and parietal regions, especially in the young (12 of 16) and middle (9 of 14) groups. Previous studies have also demonstrated that identified global hubs were mainly prefrontal and parietal regions, providing a potential explanation for their well‐documented activation by many cognitive functions [Bullmore and Sporns,2009]. Moreover, although the identified global hubs varied among three age‐specific groups, most of these regions were found to show high regional efficiency or node betweenness in the structural [Chen et al.,2008; Gong et al.,2009b; He et al.,2007,2008; Iturria‐Medina et al.,2008] and functional [Achard et al.,2006; He et al.,2009b] human brain networks (Table III). It was noted that the substantial discrepancies of identified global hubs between this study and the previous studies could be due to the different neuroimaging modalities, subjects' characteristics and computational methods.

We also found significant changes in node betweenness with decreasing and increasing in both periods (see Fig. 2). This finding was consistent with a previous study which indicates both negative and positive age effects on the regional efficiency in cortical regions [Gong et al.,2009a]. The most of these identified regions were association cortices (7 out of 9) in the period from young to middle age. From middle to old age, the regions were association (7 out of 14) and paralimbic/subcortical (7 out of 14) regions. These results supported the view that age‐related changes are mainly characteristic of association cortex as opposed to primary cortex [Albert and Knoefel,1994]. Our results were also similar to the result by a previous study that old age is associated with significantly reduced nodal efficiency in several regions of the frontal and temporal neocortex [Achard and Bullmore,2007]. We also tried to interpret this phenomenon by previous results in the dynamic course of brain maturation. A previous study indicates that relative regional differences in cortical GM volume with age occur in the frontal, parietal and temporal lobes [Smith et al.,2007]. Importantly, the discrepancies in node betweenness between middle and old groups were more notable than those between young and middle groups (see Fig. 2). Thus, our results suggested that the organization of structural brain networks changed slightly from young to middle age, whereas it altered greatly from middle to old age.

Modularity and Age‐Related Changes

Our results indicated the existence of modular organization in the structural brain networks in three age‐specific groups. The organization consisted of modules of tightly connected brain regions. Each module in a network has intramodule connections that are denser than its intermodule connections. High local clustering represents a general organizational principle throughout many larger‐scale brain networks and may contribute to the balance between brain functional segregation and integration while conserving connection length, efficient recurrent processing within modules, and efficient information exchange between modules [Bassett and Bullmore,2006; Chen et al.,2008; Latora and Marchiori,2001; Sporns et al.,2000]. Thus, this finding of modular organization in structural brain networks was consistent with the pre‐stated results of economical small‐world attributes, indicated by higher local and global efficiency than comparable random and regular networks, respectively. Moreover, we noted that the structural brain networks were organized with topological modules that closely overlap known functional domains such as auditory and language (Module I in young and middle), memory and emotion processing (Module II in young and middle), visual and “default” network (Module III in young and middle), motor and somatosensory (Module IV in young, middle, and old), cognitive processing and learning (Module V in young), and decision‐making (Module V in middle). The modules in the old group were quite different from those in the young and middle groups. Specially, Module I was primarily associated with memory, as well as auditory and language functions; Module II was mainly involved in the visual system; Module III was involved with emotion formation and processing; Module V was similar to Modules II and V in the middle group, which were mainly associated with memory, emotion, and cognitive processing. These results were also in accordance with several recent studies on the modular organization of human brain that utilized structural and functional network analyses [Chen et al.,2008; Hagmann et al.,2008; He et al.,2009b]. For the full discussion, see Supporting Information Text S1.

We also found no significant difference with regard to the modularity of the global brain networks among three age‐specific groups [see Supporting Information Fig. S1]. This finding was consistent with that of a previous study, in which no significant difference was found between the young and old groups with regard to modularity, implying that modular organization is conserved over the adult age range considered [Meunier et al.,2009a]. Nonetheless, there were notable discrepancies in the composition and topological roles of modules among brain networks in this study. First, comparing the composition of the modules among three age groups, we found that the modular organization of the young and middle groups were very similar but quite different from that of the old group (Figs. 3 and 4). A new module (Module VI) in the old group represented the separation of all subcortical regions from the areas known as Modules I and V in the young group. The constitution of the modules in the middle group resembled that in the young group (see Fig. 4). However, the regions in the old group were assembled more densely, leading to the overnumbered regions in modules (see Fig. 4). This finding may indicate that the modular organization of structural brain networks changes greatly until old age. Second, the number of connectors in the old group was also less than that in the young and middle groups (Table IV). The connectors were crucial for the global coordination of information flow in the brain networks and were of great importance for maintaining network integrity [He et al.,2009b; Sporns et al.,2007]. Moreover, the modules in the old group seemed to be more locally organized, resulting in fewer intermodule connections as compared with the numbers in the young and middle group (see Fig. 5). The intermodule connections facilitate communication between different modules and contribute to the network bridges that serve as pivotal connections for the information flow of the whole brain network [Chen et al.,2008; He et al.,2009b]. This finding was in accordance with a previous study on age‐related changes in modular organization of human brain functional networks, in which the number of intermodule connections to frontal modular regions was significantly reduced in an old group [Meunier et al.,2009a]. As a result, three connector‐modules were identified in both the young and middle groups, whereas no connector‐module was found in the old group (Table IV). The connector‐module may play a critical role in coordinating activity across the brain network as a whole and in mediating interactions between modules [Meunier et al.,2009a]. Combined with the findings in the small‐world properties and node betweenness, these results may reveal that the structural brain network changed slightly, shifting into a more distributed organization during the transition from young to middle age, and then organizing into a localized organization with great alteration in old age. Our findings were also in agreement with a recent study on functional brain networks, which indicated the organization of multiple functional networks shifts from a local anatomical emphasis in children to a more “distributed” organization in young adults over development [Fair et al.,2009].

METHODOLOGY

The human brain structural network was first constructed by using cortical thickness measurements [He et al.,2007], because of strong correlations between regions that are axonally connected [Lerch et al.,2006]. We used the measurement of RGMV to construct structural brain networks, as applied first by a previous study on the hierarchical organization of human cortical networks [Bassett et al.,2008]. Although there is still no direct proof that correlations of gray matter volume across subjects are indicative of axonal connectivity via white matter tracts, strong correlations between brain regions known to be anatomically connected have been observed in previous optimized voxel‐based morphometry studies [Mechelli et al.,2005; Pezawas et al.,2005]. Thus, the RGMV as the measurement of structural connectivity is currently considered as exploratory and should be investigated further in future studies. Salvador et al. showed that regional volume had a positive correlation which its mutual information that measured the functional connectivity between the region and the rest brain regions [Salvador et al.,2008]. A previous study also indicates that network properties (e.g., small‐worldness and degree distribution) change with the alterations of topological organization introduced by the different parcellation schemes [Wang et al.,2009a]. Thus, the comparison of network parameters across studies must be made with reference to the spatial scale of the parcellation schemes [Zalesky et al.,2010]. While this study was a cross‐sectional study, a longitudinal analysis would also be useful to investigate the change in structural brain networks with normal aging. Because all subjects in this study were more than 20 years old, young and adolescent subjects are expected to be included in future studies of brain network development. It is also important to investigate the topological properties and modular organization of human brain networks with normal aging, in combination with functional and structural studies.

CONCLUSION

In this study, we quantitatively analyzed the changes in small‐world properties and modularity of structural brain networks with normal aging, using the structural MRI. Our results indicated that normal aging had a notable effect on the topological organization of structural brain networks. These findings were compatible with previous studies on the small‐world and modular organization of brain functional and structural networks, thus enhancing our understanding of the underlying physiology of normal aging in the human brain.

Supporting information

Additional Supporting Information may be found in the online version of this article.

Supporting information