Abstract
Although the brain areas in the default‐mode network (DMN) act in a coordinated way during rest, the activity levels in the individual areas of the DMN are highly heterogeneous. The relation between the activity levels and the pattern of causal interaction among the DMN areas remains unknown. In the present fMRI study, seven nodes of the DMN were identified and their activity levels were rank‐ordered based on a power spectral analysis of the resting blood oxygenation level‐dependent (BOLD) signals. Furthermore, the direction of information flow among these DMN nodes was determined using Granger causality analysis and graph‐theoretic methods. We found that the activity levels in these seven DMN nodes had a highly consistent hierarchical distribution, with the highest activity level in the posterior cingulate/precuneus cortices, followed by ventral medial prefrontal cortex and dorsal medial prefrontal cortex, and with the lowest level in the left inferior temporal gyrus. Importantly, a significant correlation was found between the activity levels and the In‐Out degrees of information flow across the DMN nodes, suggesting that Granger causal influences can be used to predict BOLD activity levels. These findings shed light on the dynamical organization of cortical neuronal networks and may provide the basis for characterizing network disruption by brain disorders. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.
Keywords: spontaneous neuronal activity, default‐mode network, Granger causality analysis, power, information flow
INTRODUCTION
The default mode network (DMN) is comprised of a set of cortical and subcortical regions, including the posterior cingulate/precuneus cortices (PCC/PrCC), medial prefrontal cortex (MPFC), orbital frontal gyrus, anterior cingulate gyrus, inferotemporal cortex, and lateral parietal cortex [Fox et al.,2005; Fransson,2005; Greicius et al.,2003; Gusnard and Raichle,2001; Raichle et al.,2001]. At rest, activity levels in different areas of the DMN, characterized by the magnitude of the low frequency (0.01–0.08 Hz) blood oxygenation level‐dependent (BOLD) fluctuations, are highly heterogeneous. They are particularly strong in the PCC/precuneus area and MPFC, but relatively weak in the dorsolateral prefrontal cortex, parietal and occipital lobes [Fransson,2005]. Different resting conditions such as “eye‐opening” and “eye‐closing” are known to modulate BOLD activities in the PCC and MPFC [Yan et al.,2009].
The low frequency fluctuations of the BOLD signals in different regions of the DMN are shown to be correlated even when the brain is free from any externally imposed tasks [Fox et al.,2005; Fransson,2005; Greicius et al.,2003]. These synchronous spontaneous signal changes are thought to arise mainly from concurrent fluctuations in metabolic demands in different parts of the resting brain [Fransson,2005]. The patterns of interactions between regions of DMN and other brain networks are heterogeneous [Uddin et al.,2009]. While the ventromedial prefrontal cortex (vMPFC) and PCC exert greater influence on their anticorrelated networks than the other way around [Uddin et al.,2009], these same regions received significant influences from right fronto‐insular cortex and right posterior parietal cortex, respectively [Sridharan et al.,2008]. However, no studies to date have directly assessed the causal interactions among the nodes within the DMN. Moreover, the relationship between the brain BOLD activity levels and the pattern of causal interaction among the DMN nodes remains unknown.
The activities in the resting DMN can be quantified by a number of measures, including the amplitude of the low frequency fluctuation (ALFF) [Zang et al.,2007; Zuo et al.,2009], the power spectrum [Duff et al.,2008; Fransson,2006], and the root mean square [Li et al.,2000]. In the present study, the power over the frequency band (0.01–0.08 Hz) was used to characterize the activity level in each of the DMN regions. The issue of heterogeneity in DMN activity levels is examined from the perspective of causal interactions between the cortical regions in the DMN. In particular, we sought to extend the previous studies by addressing whether there is correlation between the resting activity level and the direction of causal information flow within the network. Specific analyses performed include: (a) the activity level ordering of different regions within the DMN, including the PCC/PrCC, dMPFC, vMPFC, bilateral parietal and temporal cortices, according to the power of lower frequency BOLD signal fluctuations, (b) the directionality and strength of causal influence between the seven cortical regions within the DMN, and (c) the relationship between the spontaneous neuronal activity level and the causal information flow character of each DMN region using network analysis.
MATERIALS AND METHODS
Participants
Thirty (21.0 ± 2.5‐years old; nine females) healthy, right‐handed subjects participated in the study. All subjects were free of psychiatric disorders or neurological illness. All examinations were carried out according to the ethical guidelines and declarations of the Declaration of Helsinki. Written informed consent was obtained from all participating subjects. The research protocol was approved by the local Medical Ethics Committee in Jinling Hospital, Nanjing University School of Medicine.
MRI Data Acquisition and Protocol
Imaging data were acquired using a 1.5 T scanner (GE‐Signa, Milwaukee, WI) in the department of Medical Imaging, Jinling Hospital. Subjects were instructed to relax with their eyes closed and keep their heads still during MRI scanning, without falling asleep [Fransson,2005]. Axial anatomical images were acquired using a T1‐FLAIR sequence (TR/TE = 2,200 ms/24ms, matrix = 512 × 512, FOV = 24 × 24 cm2, slice thickness/gap = 4.0 mm/0.5 mm, 23 slices covered the whole brain) for image registration and functional localization. Functional images were subsequently collected in the same slice orientation with a GRE‐EPI sequence (TR/TE = 2,000 ms/40 ms, FA= 80°, matrix = 64 × 64, FOV = 24 × 24 cm2) to yield 250 brain volumes.
Image Preprocessing
Imaging data were preprocessed using SPM2 (http://www.fil.ion.ucl.ac.uk/spm). The data underwent slice‐timing correction and realignment for head motion correction. Three subjects whose head motion exceeded 1 mm or rotation exceeded 1° during scanning were excluded. The data from the remaining 27 subjects (n = 27) were subjected to further analysis. The standard Montreal Neurological Institute (MNI) template provided by SPM was used in normalization with resampling voxel size of 3 × 3 × 3 mm3. After linear trends were removed, the data were bandpass filtered between 0.01 and 0.08 Hz to remove the effects of very‐low‐frequency drift and high frequency noise by using custom‐made software. Images were spatially smoothed with FWHM of 8 mm.
Independent Component Analysis and Identification of DMN
In accordance with one of our previous studies [Zhang et al.,2009], spatial independent component analysis (ICA) was conducted to decompose the data from each individual into components using the GIFT software (http://icatb.sourceforge.net/). The number of components was determined by a dimension estimation procedure using a minimum description length criterion that has been modified to account for spatial correlation [Li et al.,2007]. The independent components (ICs) corresponding to the DMN were extracted based on the templates described previously [Mantini et al.,2007]. On average, 30 components were identified for each subject. After the ICA separation, the templates of the DMN were then used to select the low‐frequency components in each subject using a best‐fit procedure [Greicius et al.,2004]. Briefly, a template‐matching procedure was used by taking the average z‐score of voxels falling within the template minus the average z‐score of voxels outside the template and selecting the component in which this difference (the goodness‐of‐fit) was the greatest. The z‐scores used here reflect the degree to which a given voxel's time series correlates with the time series corresponding to a specific ICA component, scaled by the standard deviation of the error term. The ICs corresponding to the DMN were extracted from all the subjects. The z‐maps of DMN were then generated for a random‐effect analysis using a one‐sample t‐test. Thresholds were set at P < 0.05 (correction using the false discovery rate (FDR) criterion).
Defining the Regions of Interest
In the present study, the regions of interest (ROIs) for the key DMN nodes were determined by using the Marsbar software package (http://marsbar.sourceforge.net), in which spherical ROIs were defined as the sets of voxels included in 8‐mm spheres centered on the local maximum activation clusters extracted from ICA. The averaged resting BOLD signal over the voxels in each ROI along the 250 TRs was considered as the time course of the ROI.
Definition and Ordering of Activity Levels
For each subject, the band power in the range (0.01, 0.08 Hz) was calculated to represent the activity level of the low‐frequency BOLD fluctuation for the ROI. The activity level in each DMN region was averaged across subjects and sorted in an ascending order. Both Page's L test [Page,1963; Siegel and Castellan,1988] (see Supporting Information “Materials and Methods” for details) and Kendall's W test were used to test whether the ordering is consistent across subjects. In light of the observation that the changes of BOLD signal, relative spiking frequency of a neuronal ensemble, cerebral blood flow, and cerebral blood volume share similar patterns, it is possible to relate this order to the different degrees of energy metabolism in different regions of the resting brain DMN [Hyder et al.,2002; Maandag et al.,2007].
Granger Causality Analysis
Granger causality (GC) was originally developed to evaluate causal relations between two time series in the economic sciences [Granger,1969]. Recently, the GC method has begun to find increasing applications in the analysis of biomedical data including electroencephalography (EEG) data [Chen et al.,2006; Kaminski et al.,2001] and fMRI data [Bressler et al.,2008; Goebel et al.,2003; Liao et al.,2009; Roebroeck et al.,2005]. Mathematically, the GC analysis is based on the concept of predictability; briefly, a signal y is said to causally influence a signal x if the future course of x is more accurately predicted based on the history of signals x and y compared to that based on the history of the signal x alone [Granger,1969]. Following this principle of predictability, Granger causality is often estimated using vector autoregressive (VAR) models [Weiss et al.,2008]. In addition to the time domain expression, the Granger causality may also be expressed in the frequency domain by time series decomposition techniques [Geweke,1984].
Using the equations described in [Ding et al.,2006] (see Supporting Information “Materials and Methods” for details), the GC values between two time series from two cortical regions were obtained. An order‐one VAR model was used to assess causal influence between the ROIs in a pairwise manner. For any two ROI time series x and y, the following Granger causality components at frequency ω were evaluated: the causal influence from x to y (f x→y(ω)) and the causal influence from y to x (f y→x(ω)). Integrating the spectrum over frequencies between 0.01 and 0.08 Hz we obtain their time domain counterparts, F x→y and F y→x, from which the difference of directional influence term dF = F y→x − F x→y was derived to assess the relative causal influence between the two time series. Positive values of this difference term point to a greater directional influence from y to x, whereas negative values indicate a greater directional influence from x to y.
Statistical inference was performed in the context of the bootstrap technique [Efron and Tibshirani,1993] and significance thresholds were obtained within a previously established framework [Roebroeck et al.,2005] (see Supporting Information “Materials and Methods” for details). A causal connectivity graph was constructed with those links for which the dF is significantly different from the null distribution (Wilcoxon signed rank test, P < 0.05). To further quantify the causal interactions among the DMN nodes, graph‐theoretic network analyses were performed across all the subjects (n = 27). For each subject, the significant connections were used for computing the In‐Out degree described below.
Definition of In‐Out Degree From GC Analysis
Several metrics of traditional graph‐theoretic analyses [Seth,2005] were used to describe the interactions between brain regions in the causal connectivity network. In‐degree of a node in a GC causal connectivity network means the number of causal in‐flow connections to the node from any of the other nodes in the network. Out‐degree of a node means the number of causal out‐flow connections from the node to any of the other nodes in the network. The In‐Out degree of a node is then defined as the difference between its In‐degree and Out‐degree. In‐Out degree can identify nodes that have distinctive causal effects on network dynamics. Specifically, a node with a relatively high positive In‐Out degree is regarded as a causal target, whereas a node with a relatively high negative In‐Out degree is a causal source. The In‐Out degrees were averaged over the subjects for each DMN region and sorted in an ascending order. The averaged In‐Out degrees as a function of DMN regions were shown in the mean ± standard error (SE) format (Fig. 2B). The Page's L test and the Kendall's W test were used to assess how consistent the order is across subjects.
Figure 2.
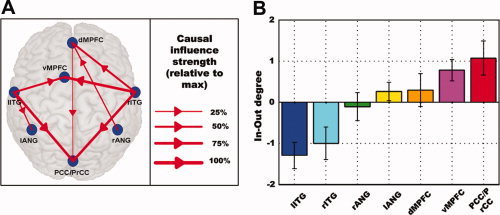
The Granger causality (GC) results for the seven ROIs in the DMN. A: Network diagram showing significant difference Granger causality (dF) among seven regions at a group level (P < 0.05). The blue dots refer to the seven ROIs. The arrow indicates the direction of significant relative causal influence. After normalization by the maximum dF‐value, the strength of the relative causal connections was divided into four grades and expressed by the thickness of the red line. B: The In‐Out degrees in the seven nodes as an index for the relative information flow in the GC network. Error bars denote standard error of the mean (SEM) across subjects (n = 27). The In‐Out degree level of each ROI is expressed by the same color scheme as that of Figure 1B.
Correlation Between Activity Level and Causal Influence
The BOLD activity level at each DMN node was plotted as a function of its In‐Out degree for each of the 27 subjects. A Spearman rank correlation coefficient was then calculated to assess the association between the two variables. At the individual level, the correlation coefficients of all the subjects obtained from the same analysis were transformed into z scores by a Z‐transform. A random effect analysis on the z score was then performed at a group level. The confidence interval of the ensemble correlation coefficient was estimated by an inverse Z‐transform.
RESULTS
In the DMN extracted from ICA, seven cortical regions were chosen for further analysis, including PCC/PrCC, vMPFC, dMPFC, left angular gyrus (lANG), right angular gyrus (rANG), right inferior temporal gyrus (rITG), left inferior temporal gyrus (lITG) (Fig. 1A).
Figure 1.
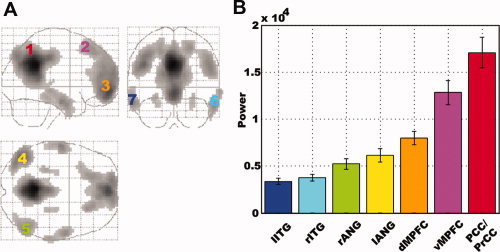
The default mode network (DMN) and activity level distribution. A: DMN extracted from ICA. The numbers denote the seven cortical regions of interest (ROIs) in the DMN. ROI 1: posterior cingulate/precuneus cortices (PCC/PrCC); ROI 2: dorsal medial prefrontal cortex (dMPFC); ROI 3: ventral medial prefrontal cortex (vMPFC); ROI 4: left angular gyrus (lANG); ROI 5: right angular gyrus (rANG); ROI 6: right inferior temporal gyrus (rITG); and ROI 7: left inferior temporal gyrus (lITG). B: The distribution of activity levels in the seven ROIs according to the power of low frequency (0.01–0.08 Hz) BOLD signal fluctuations. Error bars denote standard error of the mean (SEM) across subjects (n = 27). The location of each ROI and the BOLD signal power level of each ROI are expressed using the same color scheme.
The activity levels measured by the power of low frequency BOLD fluctuations varied across the regions of interest in the DMN. These regions can be ordered according to their average activity levels in an ascending fashion: lITG < rITG < rANG < lANG < dMPFC < vMPFC < PCC/PrCC (Fig. 1B). To test how consistent this order is across subjects, the Page test statistic L was calculated [Page,1963], and the quantity of 3,645 was obtained. From the Table of L values, this quantity is significant at the P < 0.001 significance level, meaning that the ordering above is highly consistent across subjects. This ordering was further confirmed by Kendall's W test (W = 0.5026, P < 0.001).
Granger causality analysis was applied to elucidate the dynamic interactions among the seven nodes of the DMN. A causal connectivity network graph was constructed using the arrow‐headed lines of varying thickness to indicate the direction and strength of the causal influences (Fig. 2A). Those links that showed significant Granger causal connectivity at the group level (Wilcoxon signed rank test, P < 0.05) were shown in red. The strength and direction of causal influences coming into or going from each node were seen to be different across the network, indicating that the causal influence between the seven regions of the DMN was not spatially homogeneous. In particular, the PCC/PrCC and vMPFC regions were primarily the targets of incoming causal influences. The dMPFC region, while receiving dominant incoming influences, also exerted weak outgoing influences on the PCC. In contrast, both the left and right inferotemporal gyri were strong drivers of network activity, exerting strong outgoing influences on the other regions of the DMN network. Based upon the results from Figure 2, the seven DMN nodes were rank‐ordered according to their In‐Out degrees in the ascending fashion (Fig. 2B). The consistency of this ordering across subjects was again tested using the Page test statistic which yielded a significant value of 3277.5 (P < 0.05) and the Kendall's W test with a coefficient of concordance of 0.095 (P < 0.05).
From Figures 1B and 2B, it can be seen that among the seven DMN regions, PCC/PrCC had the highest activity level and strongest causal inflow, whereas lITG showed the lowest activity level and strongest causal outflow, suggesting a relationship between neuronal activity levels and causal flow characteristics within the DMN. A random effect model was applied to examine the correlation between activity level and In‐Out degree at the individual subject level. Given a significance level of 0.05, the null hypothesis that there is no correlation between the two variables can be rejected at P = 6.50E−05. The 95% confidence interval of the ensemble correlation coefficient is [0.33213, 0.73428]. This effect was further described by plotting activity level as a function of In‐Out degree for each subject in Figure 3. The fitted line showed that the power and the In‐Out degree were significantly correlated. In other words, the nodes with lowest activity levels exert causal influences on other nodes in the DMN network, whereas the nodes with highest activity levels receive causal influences from other nodes in the DMN network.
Figure 3.
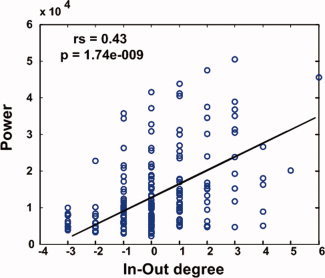
Relation between BOLD signal power and In‐Out degree. For each of the seven nodes in the DMN, the low frequency BOLD power is plotted as a function of the In‐Out degree for all subjects (n = 27). The solid line represents the median regression fit. Spearman rank correlation coefficient (rs) and P value are indicated.
DISCUSSION
Previous resting‐state fMRI studies suggest that the low‐frequency fluctuations of BOLD signals [Biswal et al.,1995; Hampson et al.,2006; Lowe et al.,1998; Xiong et al.,1999] were not distributed evenly throughout the brain [Fransson,2005]. In agreement with these prior findings, our results provided further evidence supporting heterogeneity of the resting brain activities in the default mode network. In addition, a new finding was reported which indicated that there is a rank‐order among the seven cortical nodes of the DMN according to the resting activity levels characterized by the power of low frequency BOLD fluctuations (Fig. 1B). This ordering, lITG < rITG < rANG < lANG < dMPFC < vMPFC < PCC/PrCC, was found to be highly consistent across subjects.
By applying graph‐theoretic concepts to Granger causality analysis, we found that the PCC/PrCC and MPFC were both driven by the other nodes in the DMN, with the PCC/PrCC being the primary target of causal influences. This observation is consistent with the notion that the DMN is composed of interconnected subsystems converging on the key hubs with the PCC and MPFC being the first and the second key hubs of the DMN [Buckner et al.,2008]. A comparison of each DMN node's standing in the activity level ranking (Fig. 1B) and the same node's standing in the In‐Out degree ranking (Fig. 2B) led to our most important finding that the power of the BOLD signal and In‐Out degree of the directional influence are positively correlated (see Fig. 3). Among the seven DMN nodes, the region with a larger In‐Out degree tends to exhibit a higher level of activity, suggesting a hitherto unknown connection between the activity level of a DMN node and its pattern of interaction with the other DMN nodes. Such a relationship (as shown in Fig. 3) can be understood from a casual power perspective based on the theory of time series analysis. According to Ding et al. [2006], the power of a time series is the sum of intrinsic power and causal power (see Supporting Information “Materials and Methods” for details). Increased causal influence from y to x leads to higher causal power which in turn leads to increased total power of x which can be measured by the power spectral method. In the present study, the In‐Out degree of a node may be regarded as the measure of relative causal contributions, while the activity level shown in Figure 1B represents the total power of a time series. For each node, the increase of In‐Out degree indicates higher incoming causal influences, which in turn leads to increased power of the BOLD signal. This causal power‐based interpretation of the results in Figure 3 could be understood in terms of brain's metabolic activity. Specifically, signal communication in the mammalian cerebral cortex is an expensive process that has energetic demands tightly coupled to the information encoding by the neuronal ensembles [Smith et al.,2002]. A large fraction of the energy is spent to support the activities of rapid signaling neurons for intracortical signaling across different regions of the brain [Maandag et al.,2007].
We make several observations. First, Granger causality analysis for fMRI data relies on the measurements of the temporal relation between different BOLD time series. Spurious influences might be obtained because the hemodynamic activity is known to have differential delays with respect to the underlying neuronal activity in different brain structures [Roebroeck et al.,2005]. However, the impact of such variable hemodynamic delays may not be as severe when the sampling interval is as long as 2 s, which is often the case in fMRI studies [Deshpande et al.,2008]. Moreover, for the purpose of obviating the effects of the spatial variability of the hemodynamic response and getting accurate results, the summed time series over a region of interest may be used to analyze the causal influences among different brain regions instead of raw voxel‐level time series [Deshpande et al.,2009].
Second, within a pairwise analysis framework, as is the case here, the directional influence from brain region X to region Y does not take into account the possibility that this influence is mediated by a third region. This situation could be addressed by conditional Granger causality analysis [Ding et al.,2006; Granger,1969]. Of primary concern in this case may be the rational choice of the third region which could simply be the combination of all the other brain regions in a network besides X and Y. Recent work has suggested the use of principal component analysis in conjunction with conditional Granger causality analysis as a viable approach to overcome this problem [Zhou et al.,2009].
Third, it is worth noting that our ICA analysis have identified bilateral hippocampal formations as components of the DMN network. However, the relationship between the BOLD power and In‐Out degree in these two regions was found to not follow the same pattern as the other seven cortical regions studied here. Previous work has shown that hippocampal involvement in the default mode network was weak relative to other areas of the DMN in terms of the BOLD effect size [Damoiseaux et al.,2006]. Susceptibility artifacts in these two areas of the brain [Laird et al.,2009], including effects from cerebrospinal fluids and white matte, are thought to be the underlying reason. These artifacts may also help to explain why these two areas behave differently in our analysis of the relationship between activity level and In‐Our degree in the DMN.
Fourth, abnormalities in the DMN have been implicated in a number of cognitive deficits such as those found in Alzheimer's disease [Greicius et al.,2004] and anxiety disorders [Zhao et al.,2007]. An analysis of the strength and directionality changes of causal information flow and their relation to the abnormal energy consumption pattern within DMN may provide significant insights into the regions of the network that are compromised in clinically impaired individuals. This strategy of linking the activity levels in individual brain areas with directional influences among these brain areas may offer a new avenue to better understand the altered dynamics of neuronal networks underlying myriad brain disorders.
CONCLUSIONS
In this study, we combined three approaches: (1) power spectral analysis, (2) Ganger causality analysis, and (3) graph‐theoretic concepts, to investigate the spatiotemporal dynamics of the default mode network during rest. Similar rank orders were found for the seven key DMN regions in terms of the activity level measured by low frequency BOLD signal power and the In‐Out degree of Granger causal influence. Importantly, there is a significant positive correlation between these two variables. Namely, a causal target in the neuronal activity propagation process among the DMN regions tends to have a higher level of BOLD signal power, implying that the causal influence patterns may help to predict neuronal activity levels in the DMN network. These findings suggest that apprehending the relation between activity levels in individual brain areas and directions of information flow among these areas constitute the next logical step towards understanding the dynamic organization of a neuronal network and its disruption under pathological conditions.
Supporting information
Additional Supporting Information may be found in the online version of this article.
Supporting Information
REFERENCES
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS ( 1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magn Reson Med 34: 537–541. [DOI] [PubMed] [Google Scholar]
- Bressler SL, Tang W, Sylvester CM, Shulman GL, Corbetta M ( 2008): Top‐down control of human visual cortex by frontal and parietal cortex in anticipatory visual spatial attention. J Neurosci 28: 10056–10061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Andrews‐Hanna JR, Schacter DL ( 2008): The brain's default network: anatomy, function, and relevance to disease. Ann N Y Acad Sci 1124: 1–38. [DOI] [PubMed] [Google Scholar]
- Chen Y, Bressler SL, Ding M ( 2006): Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J Neurosci Methods 150: 228–237. [DOI] [PubMed] [Google Scholar]
- Damoiseaux JS, Rombouts SA, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF ( 2006): Consistent resting‐state networks across healthy subjects. Proc Natl Acad Sci USA 103: 13848–13853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, Hu X, Stilla R, Sathian K ( 2008): Effective connectivity during haptic perception: A study using Granger causality analysis of functional magnetic resonance imaging data. Neuroimage 40: 1807–1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, LaConte S, James GA, Peltier S, Hu X ( 2009): Multivariate Granger causality analysis of fMRI data. Hum Brain Mapp 30: 1361–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding M, Chen Y, Bressler SL ( 2006): Granger causality basic theory and application to neuroscience In: Schelter B, Winterhalder M, Timmer J, editors. Handbook of Time Series Analysis, Berlin: Wiley‐VCH Verlage; pp 451–474. [Google Scholar]
- Duff EP, Johnston LA, Xiong J, Fox PT, Mareels I, Egan GF ( 2008): The power of spectral density analysis for mapping endogenous BOLD signal fluctuations. Hum Brain Mapp 29: 778–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ ( 1993): An Introduction to the Bootstrap. Boca Raton, FL: Chapman & Hall/CRC. [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME ( 2005): The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA 102: 9673–9678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransson P ( 2005): Spontaneous low‐frequency BOLD signal fluctuations: an fMRI investigation of the resting‐state default mode of brain function hypothesis. Hum Brain Mapp 26: 15–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransson P ( 2006): How default is the default mode of brain function? Further evidence from intrinsic BOLD signal fluctuations. Neuropsychologia 44: 2836–2845. [DOI] [PubMed] [Google Scholar]
- Geweke JF ( 1984): Measures of conditional linear dependence and feedback between time Series. J Am Stat Assoc 79: 907–915. [Google Scholar]
- Goebel R, Roebroeck A, Kim DS, Formisano E ( 2003): Investigating directed cortical interactions in time‐resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magn Reson Imaging 21: 1251–1261. [DOI] [PubMed] [Google Scholar]
- Granger CWJ ( 1969): Investigating causal relations by econometric models and cross‐spectral methods. Econometrica 37: 424–438. [Google Scholar]
- Greicius MD, Krasnow B, Reiss AL, Menon V ( 2003): Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proc Natl Acad Sci USA 100: 253–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V ( 2004): Default‐mode network activity distinguishes Alzheimer's disease from healthy aging: evidence from functional MRI. Proc Natl Acad Sci USA 101: 4637–4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusnard DA, Raichle ME ( 2001): Searching for a baseline: Functional imaging and the resting human brain. Nat Rev Neurosci 2: 685–694. [DOI] [PubMed] [Google Scholar]
- Hampson M, Driesen NR, Skudlarski P, Gore JC, Constable RT ( 2006): Brain connectivity related to working memory performance. J Neurosci 26: 13338–13343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyder F, Rothman DL, Shulman RG ( 2002): Total neuroenergetics support localized brain activity: implications for the interpretation of fMRI. Proc Natl Acad Sci USA 99: 10771–10776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaminski M, Ding M, Truccolo WA, Bressler SL ( 2001): Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol Cybern 85: 145–157. [DOI] [PubMed] [Google Scholar]
- Laird AR, Eickhoff SB, Li K, Robin DA, Glahn DC, Fox PT ( 2009): Investigating the functional heterogeneity of the default mode network using coordinate‐based meta‐analytic modeling. J Neurosci 29: 14496–14505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li SJ, Biswal B, Li Z, Risinger R, Rainey C, Cho JK, Salmeron BJ, Stein EA ( 2000): Cocaine administration decreases functional connectivity in human primary visual and motor cortex as detected by functional MRI. Magn Reson Med 43: 45–51. [DOI] [PubMed] [Google Scholar]
- Li YO, Adali T, Calhoun VD ( 2007): Estimating the number of independent components for functional magnetic resonance imaging data. Hum Brain Mapp 28: 1251–1266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao W, Mantini D, Zhang Z, Pan Z, Ding J, Gong Q, Yang Y, Chen H ( 2009): Evaluating the effective connectivity of resting state networks using conditional Granger causality. Biol Cybern 102: 57–69. [DOI] [PubMed] [Google Scholar]
- Lowe MJ, Mock BJ, Sorenson JA ( 1998): Functional connectivity in single and multislice echoplanar imaging using resting‐state fluctuations. NeuroImage 7: 119–132. [DOI] [PubMed] [Google Scholar]
- Maandag NJ, Coman D, Sanganahalli BG, Herman P, Smith AJ, Blumenfeld H, Shulman RG, Hyder F ( 2007): Energetics of neuronal signaling and fMRI activity. Proc Natl Acad Sci USA 104: 20546–20551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantini D, Perrucci MG, Del Gratta C, Romani GL, Corbetta M ( 2007): Electrophysiological signatures of resting state networks in the human brain. Proc Natl Acad Sci USA 104: 13170–13175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Page EB ( 1963): Ordered hypotheses for multiple treatments: A significance test for linear ranks. J Am Stat Assoc 58: 216–230. [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL ( 2001): A default mode of brain function. Proc Natl Acad Sci USA 98: 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R ( 2005): Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage 25: 230–242. [DOI] [PubMed] [Google Scholar]
- Seth AK ( 2005): Causal connectivity of evolved neural networks during behavior. Network 16: 35–54. [DOI] [PubMed] [Google Scholar]
- Siegel S, Castellan N ( 1988): Nonparametric Statistics for the Behavioral Sciences. New York: McGraw‐Hill; pp 184–190. [Google Scholar]
- Smith AJ, Blumenfeld H, Behar KL, Rothman DL, Shulman RG, Hyder F ( 2002): Cerebral energetics and spiking frequency: The neurophysiological basis of fMRI. Proc Natl Acad Sci USA 99: 10765–10770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridharan D, Levitin DJ, Menon V ( 2008): A critical role for the right fronto‐insular cortex in switching between central‐executive and default‐mode networks. Proc Natl Acad Sci USA 105: 12569–12574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin LQ, Kelly AM, Biswal BB, Xavier Castellanos F, Milham MP ( 2009): Functional connectivity of default mode network components: Correlation, anticorrelation, and causality. Hum Brain Mapp 30: 625–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss T, Hesse W, Ungureanu M, Hecht H, Leistritz L, Witte H, Miltner WH ( 2008): How do brain areas communicate during the processing of noxious stimuli? An analysis of laser‐evoked event‐related potentials using the Granger causality index. J Neurophysiol 99: 2220–2231. [DOI] [PubMed] [Google Scholar]
- Xiong J, Parsons LM, Gao JH, Fox PT ( 1999): Interregional connectivity to primary motor cortex revealed using MRI resting state images. Hum Brain Mapp 8: 151–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan C, Liu D, He Y, Zou Q, Zhu C, Zuo X, Long X, Zang Y ( 2009): Spontaneous brain activity in the default mode network is sensitive to different resting‐state conditions with limited cognitive load. PLoS ONE 4: e5473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zang YF, He Y, Zhu CZ, Cao QJ, Sui MQ, Liang M, Tian LX, Jiang TZ, Wang YF ( 2007): Altered baseline brain activity in children with ADHD revealed by resting‐state functional MRI. Brain Dev 29: 83–91. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Lu G, Zhong Y, Tan Q, Yang Z, Liao W, Chen Z, Shi J, Liu Y ( 2009): Impaired attention network in temporal lobe epilepsy: A resting FMRI study. Neurosci Lett 458: 97–101. [DOI] [PubMed] [Google Scholar]
- Zhao XH, Wang PJ, Li CB, Hu ZH, Xi Q, Wu WY, Tang XW ( 2007): Altered default mode network activity in patient with anxiety disorders: An fMRI study. Eur J Radiol 63: 373–378. [DOI] [PubMed] [Google Scholar]
- Zhou Z, Chen Y, Ding M, Wright P, Lu Z, Liu Y ( 2009): Analyzing brain networks with PCA and conditional Granger causality. Hum Brain Mapp 30: 2197–2206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo XN, Di Martino A, Kelly C, Shehzad ZE, Gee DG, Klein DF, Castellanos FX, Biswal BB, Milham MP ( 2009): The oscillating brain: complex and reliable. NeuroImage 49: 1432–1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found in the online version of this article.
Supporting Information


