Temporal dynamics of reward processing revealed by magnetoencephalography

Abstract

Monetary gains and losses in gambling situations are associated with a distinct electroencephalographic signature: in the event‐related potentials (ERPs), a mediofrontal feedback‐related negativity (FRN) is seen for losses, whereas oscillatory activity shows a burst of in the θ‐range for losses and in the β‐range for gains. We used whole‐head magnetoencephalography to pinpoint the magnetic counterparts of these effects in young healthy adults and explore their evolution over time. On each trial, participants bet on one of two visually presented numbers (25 or 5) by button‐press. Both numbers changed color: if the chosen number turned green (red), it indicated a gain (loss) of the corresponding sum in Euro cent. For losses, we found the magnetic correlate of the FRN extending between 230 and 465 ms. Source localization with low‐resolution electromagnetic tomography indicated a first generator in posterior cingulate cortex with subsequent activity in the anterior cingulate cortex. Importantly, this effect was sensitive to the magnitude of the monetary loss (25 cent > 5 cent). Later activation was also found in the right insula. Time‐frequency analysis revealed a number of oscillatory components in the theta, alpha, and high‐beta/low‐gamma bands associated to gains, and in the high‐beta band, associated to the magnitude of the loss. All together, these effects provide a more fine‐grained picture of the temporal dynamics of the processing of monetary rewards and losses in the brain. Hum Brain Mapp, 2011. © 2011 Wiley Periodicals, Inc.

INTRODUCTION

External feedback can be used to optimize behavior and thus presents a powerful learning signal. Events as simple as the bitter taste of a fruit that has gone bad or as complex as a driver being fined after making a forbidden turn will affect how we react the next time in a similar situation. Numerous studies in animals and humans have demonstrated that such learning from feedback (reinforcement learning) involves structures that are important for the processing of rewards [see e.g. Bussey et al.,1997; Holroyd and Coles,2002; Kennerley et al.,2006; Khamassi et al.,2008; Robbins and Everitt,1996; Schultz et al.,2000; van der Helden et al.,2009].

In 1997, Miltner et al. [1997] were the first to describe a component in the human event‐related potential (ERP) associated to external negative feedback, which they labeled feedback‐related negativity (FRN). These authors postulated that the FRN is generated by the same generic mechanism that is also reflected by the response‐locked error‐related negativity (ERN; [Falkenstein et al.,1990; Gehring et al.,1993]) found for performance errors. Subsequent studies have further refined the definition of the FRN as a negative deflection in the ERP, which has a frontocentral scalp distribution and peaks between 250 and 400 ms that has been demonstrated most often following a negative feedback stimulus [Gehring and Willoughby,2002; Holroyd et al.,2006; Müller et al.,2005; Nieuwenhuis et al.,2004a; van Drongelen et al.,1996], but exceptions have been reported [Cohen et al.,2007; Holroyd et al., 2009].

Although there is a general consensus that the FRN is sensitive to the valence of the feedback, there is diverging evidence regarding the question whether it is also sensitive to its magnitude, for example, the amount of money lost. Some studies have indeed found that the FRN is modulated by both valence and magnitude of the feedback [Wu and Zhou,2009], while others have assessed the effect of the magnitude by comparing the difference waves between the gain‐loss conditions in higher and lower gambles, observing apparent differences, which failed to be statistically significant [Goyer et al.,2008; Hewig et al.,2007]. However, other researchers have failed to find an effect of the magnitude of the loss and/or have found a comparably large FRN even to neutral feedback, but have observed an effect of magnitude on the P300 that follows the FRN [Nieuwenhuis et al.,2004b; Yeung and Sanfey,2004]. This has led them to suggest that the FRN categorizes outcomes in a binary fashion, compiling negative and neutral stimuli into one category [Hajcak et al.,2006; Holroyd et al.,2006; Yeung and Sanfey,2004]. Thus, the question regarding the sensitivity of the FRN to reward magnitude is still open.

More recently, attention has been drawn toward other factors that might be modulating the FRN, such as predictability and risk, posing new questions, which are yet to be fully answered. On this matter, most studies have observed that the amplitude of the FRN increases when the punishment is less probable and/or more unexpected [Bellebaum and Daum,2008; Holroyd and Krigolson,2007; Moser and Simons,2009; Wu and Zhou,2009], although others have found no influence of predictability on the FRN but rather on the ERP following reward [Cohen et al.,2007] or on an earlier P200 component [Polezzi et al.,2008]. Regarding the influence of risk, it has been observed that participants who tend to make riskier gambles after losing display a greater FRN [Yeung and Sanfey,2004] and that the FRN is sensitive to the magnitude of the outcome in conditions where participants are less inclined toward taking risks [Polezzi et al.,2010]. Hence, there appears to be a number of factors influencing the amplitude of the FRN, most of which are probably yet to be explored.

It is generally considered that there is no specific component in the averaged ERP indexing positive feedback such as monetary gains, whereas wavelet‐based time‐frequency analysis of single‐trial EEG data has revealed a distinct beta component (20–30 Hz) associated with monetary gains in addition to an increase in theta power (4–8 Hz) for losses [Marco‐Pallarés et al.,2008]. This finding is consistent with the increase in beta power associated to winning described by Cohen et al. [2007] in a reinforcement learning task and suggests that the beta oscillatory response could be decisive in the processing of rewards.

With regard to the localization of the neurophysiological responses to gains and losses, source localization of the FRN using dipole analysis implied generators in the anterior cingulate cortex (ACC) and the supplementary motor area [Gehring and Willoughby,2002; Miltner et al.,1997], whereas other authors have described sources also in the right superior frontal gyrus, striatum, and/or posterior cingulate cortex (PCC) [Müller et al.,2005; Nieuwenhuis et al.,2005]. Thus, there is currently no consensus as to the generators involved in the FRN. Moreover, these studies have not explored the temporal evolution of the neural processing of feedback, hereby not taking full advantage of the high‐temporal resolution of electrophysiological techniques. Numerous fMRI studies have highlighted the network involved in the processing of positive and negative feedback, which includes amygdala, nucleus accumbens, ventral striatum, insula, ACC, prefrontal cortex, and PCC [Carter et al.,1998; Delgado et al.,2000; Fujiwara et al.,2009; Holroyd et al.,2004; Liu et al.,2007; Marco‐Pallarés et al.,2007; Menon et al.,2001; Nieuwenhuis et al.,2005]. This suggests that dipole models, where the number of sources has to be known a priori to estimate an appropriate solution, may not be entirely adequate to determine the sources of the FRN [Näätänen et al.,1994; Rippon,2006] and distributed source models, such as minimum‐norm least‐squares [Hämäläinen and Ilmoniemi,1984], minimum current estimates [Uutela et al.,1999], low‐resolution electromagnetic tomography (LORETA; [Pascual‐Marqui et al.,1994]), or beamformer models [van Drongelen et al.,1996] may be more suitable, because these provide a bias‐free estimate of activity.

Nonetheless, it cannot be disregarded that there is no unique solution to the inverse problem and that distributed source models, though generally referred to as bias‐free, are not exempt from disadvantages. For instance, solutions such as the minimum‐norm least‐squares [Hämäläinen and Ilmoniemi,1984] tend to underestimate the depth of the sources [Bengtsson et al.,2009; Fuchs et al.,1999]. Therefore, it is still necessary to impose constraints, like weighting factors for depth and smoothness, in order to obtain better solutions. In the case of LORETA [Pascual‐Marqui et al.,1994], introducing a smoothness constraint makes it possible to accurately reconstruct more focal and deeper sources, although it still smears them spatially, and it can overestimate the source depths [Bengtsson et al.,2009; Fuchs et al.,1999; Pascual‐Marqui,1999]. Consequently, when looking at solutions to the inverse problem, it is important to keep in mind that these are merely models based on the information provided by external field measurements and are hence not totally accurate representations of the neural generators.

Taken together, in spite of considerable research on the neurophysiological correlates of the processing of positive and negative feedback, there are a number of open questions that were targeted with this study using magnetoencephalography (MEG). Thus, the first objective of our study was to ascertain whether a magnetic equivalent of the FRN existed and whether the magnitude of the gain or the loss modulated its amplitude. The neuromagnetic signal is originated almost solely by primary currents, whereas the electrophysiological signal recorded by EEG is composed both by primary and secondary currents [Bengtsson et al.,2009; Rippon,2006]. This makes MEG particularly suited to study discrepant results obtained in EEG, such as the effect of the magnitude of the reward or punishment.

As a second objective of the study, we sought to localize the generators of the magnetic counterpart of the FRN taking advantage of the higher spatial resolution of MEG [Bengtsson et al.,2009; Magno et al.,2006; Näätänen et al.,1994]. We also aimed to analyze the temporal dynamics of the neural processing of monetary gains and losses.

Finally, given the well‐known suitability of MEG for the identification of cortical oscillations [Hari and Salmelin,1997; Näätänen et al.,1994], our third objective was to find the oscillatory components elicited by the magnetic activity of the brain in response to monetary gains and losses. In accordance with the previous EEG studies, we expect a boost in power of the high‐beta band (20–30 Hz) associated to gains and a boost in theta power (4–8 Hz) associated to losses.

MATERIALS AND METHODS

Participants

Sixteen healthy adults (12 women, aged 22–29 years, M = 25.81, SD = 1.82) from the participant database at the Otto‐von‐Guericke‐Universität in Magdeburg took part in the study. They were required to be right‐handed and have normal or corrected‐to‐normal (with contact lenses) vision and no history of neurological disorder (assessed by questionnaire). Participants were asked to change into a hospital gown and remove make‐up and hair products. None wore any metallic implants or accessories. One female participant had to be removed from further analysis due to massive ocular artifacts. The study was approved by the ethics committee of the Otto‐von‐Guericke‐Universität, and all subjects gave written informed consent for their participation.

Stimuli and Procedure

A simplified version of the gambling task of Gehring and Willoughby [2002] was used, such that valence (monetary gain/loss) and correctness coincided. Following a fixation cue of 800–1,200 ms duration, the numbers [5] and [25] appeared in white at either side of it. Only two possible displays were presented, [5][25] or [25][5], each in 50% of the trials. The participants had to make an obligatory button response with the left or right index finger; feedback appeared 1,500 ms after this and stayed on the screen for 1,000 ms. If the participant's response was made within 1,000 ms of the appearance of the stimuli, one of the numbers turned green (indicating gain) and the other red (indicating loss); otherwise, both numbers turned gray. Gains and losses occurred randomly and could not be influenced by the participant's performance. The participant incurred the gain/loss displayed by the chosen number. The experiment comprised 800 trials, each lasting 4,300–4,700 ms, divided into eight blocks of 100 trials. After each block, the participant was informed about his/her current point status. Participants began with 500 points (1 point = 0.01€). The stimuli were presented using Presentation software (Neurobehavioral Systems) and visualized on a rear projection screen in the MEG chamber.

Data Acquisition

Data were acquired using a 148‐channel 4D Neuroimaging Magnes 2500 WH MEG scanner (Biomagnetic Technologies, San Diego, CA) and a Synamps amplifier (NeuroScan, Herndon, VA) at a sampling rate of 678.17 Hz and band‐pass filtered between 0.1 and 200 Hz.

Anatomical landmarks (left and right preauricular points, nasion, Cz, inion) were digitized by means of a Polhemus 3Space Fastrak system (Polhemus, Colchester, VT) and brought into reference with magnetic marker fields generated by five electrode coils mounted on an elastic cap on the participant's head. Eye movements were monitored by electrodes above and below the right eye and on the outer canthi of both eyes. Electrooculogram (EOG) impedances were kept below 5 kΩ.

Data Analysis

MEG signals were submitted to online and offline noise reduction [Robinson,1989], and artifacts were rejected with individual limits of between 3 and 5 pT for the MEG and a common limit of 100 μV for the EOG. Six sensors had to be removed from further analysis from all data sets due to considerable noise in several participants' data. A set of averaged evoked‐magnetic fields (EMFs) time‐locked to the onset of the feedback stimulus and baselined between −100 and 0 ms were calculated for each of the four conditions: maximum gain [+25], maximum loss [−25], minimum gain [+5], and minimum loss [−5].

Nonparametric permutation testing [Maris and Oostenveld,2007; Nichols and Holmes,2002] was used to compare the following pairs of conditions: maximum gain versus maximum loss ([+25] minus [−25]), minimum gain versus minimum loss ([+5] minus [−5]), maximum loss versus minimum loss ([−25] minus [−5]), and maximum gain versus minimum gain ([+25] minus [+5]). Exploring the temporal dynamics of feedback processing with MEG implies performing multiple statistical tests on all the time‐sensor points of interest, making it necessary to control the family‐wise error rate (FWER). Although unable to show interactions between factors, nonparametric permutation testing provides a way of solving the multiple comparisons problem by controlling the FWER, yet remaining more sensitive than approaches such as Bonferroni (for a detailed explanation of the statistical rationale, see Maris and Oostenveld [2007]). This technique has been successfully used on event‐related and time‐frequency data on both MEG and EEG [see e.g. Bearer et al.,2009; Solomyak and Marantz,2009; van Dijk et al.,2008].

To perform the nonparametric permutation testing, ad hoc tools were constructed using Matlab 7.2 [Mathworks, 2006]. First, paired t‐tests were computed for all time‐sensor points between 200 and 600 ms postfeedback to include the time window usually analyzed in FRN studies and the differences between conditions, which were visually apparent on the EMFs. Contiguous time‐sensor points exceeding the threshold were grouped into clusters and their cluster t‐value (sum of all the t‐values in the sample) calculated. Subsequently, 1,000 randomizations of the conditions were performed on the cluster with the greatest t _clus‐value, the cluster t _rand‐values were computed, and a histogram of the statistics was generated. This served as reference to which all the original t _clus‐values were compared: the null hypothesis was rejected for those clusters presenting a t _clus‐value greater than 95% of the distribution of t _rand. Also, significant clusters were only considered for further analysis if they were formed by at least 30 contiguous time points (i.e., 44 ms) and five neighboring sensors.

For the localization of the electromagnetic sources, differences between the abovementioned pairs of conditions were calculated and bandpass‐filtered between 1 and 30 Hz; a notch filter was used at 50 Hz. Source analysis was performed on the time windows that showed significant differences using LORETA [Pascual‐Marqui et al.,1994] with an interpolated Boundary Element Method model, as implemented in the multimodal neuroimaging software Curry 6.0 (Neuroscan), and projected on a standard brain model. The extent of the activations was defined, so that solutions that explained less than 85% of the largest current were suppressed.

To study time‐frequency behavior of the magnetic activity elicited by the feedback, single‐trial data (2,000‐ms pre‐ and postfeedback) were convoluted using a complex Morlet wavelet:

The relation 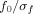(where 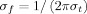) was set to 6.7. The 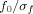parameter relates to the number of oscillations in the wavelet: reducing the number of oscillations would yield a higher temporal but lower frequential resolution and vice versa. The value of 6.7 used in this analysis has been successfully used in previous EEG studies using the complex Morlet wavelet transform [see e.g. Marco‐Pallarés et al.,2008; Tallon‐Baudry et al.,1997].

Changes in time varying energy (square of the convolution of wavelet and signal) in the studied frequencies (1–40 Hz, linear increase) with respect to a −100–0 ms baseline were computed for each trial and averaged for each subject before calculating a grand average. All four conditions were subsequently statistically compared within the 200–600 ms time segment. To avoid the multiple comparison problem (40 frequencies × 475 time points × 148 sensors), nonparametric permutation testing analogous to that performed on the EMFs was used, clustering sensor‐time‐frequency points [Maris and Oostenveld,2007]. For a cluster to be considered for further analysis, it had to be formed by at least three contiguous frequencies, thirty consecutive time points (i.e., 44 ms), and five neighboring sensors.

RESULTS

Behavioral Results

On average, participants received gain or loss feedback to 729 (SD = 67) of the 800 stimuli, ending the experiment with an average of 591 points (SD = 321). The other trials were lost due to time‐out errors. The frequency of choice of each response alternative and the corresponding reaction times can be seen in Table I.

Table I.

Mean (SD) number of times participants chose alternatives [25] and [5], RTs, and their respective statistical comparisons

	25	5	t	df	P
Choice	445 (97)	284 (89)	3.58	14	<0.01
RT	654 (135)	653 (140)	1.33	14	>0.05

Evoked Magnetic Fields

The nonparametric testing performed on the EMFs showed significant differences in several time windows for all the comparisons between conditions, with the exception of maximum gain versus minimum gain ([+25] minus [+5]). The time windows and sensor locations of the significant clusters as well as their t _clus‐ and P‐values are shown in Table II. These differences started earliest (230 ms) for the minimum gain [+5] versus minimum loss comparison [−5], and at 290 ms for both the maximum gain [+25] versus maximum loss [−25], and maximum loss [−25] versus minimum loss [−5] comparisons and were mainly found for central and posterior sensors. Moreover, late differences (between 520 and 575 ms) were found for bilateral peripheral sensors in both valence comparisons ([+25] minus [−25] and [+5] minus [−5]). Figure 1 shows the feedback‐locked EMFs at six representative sensors for the four conditions: minimum gain [+5], maximum gain [+25], minimum loss [−5], and maximum loss [−25].

Table II.

Results of the nonparametric permutation testing performed on the EMFs for the comparisons: positive and negative t _clus‐values indicate the positive (magnetic field lines entering the head) and negative (magnetic field lines exiting the head) surfaces of the magnetic field contours of the difference, respectively

Cluster	Time window (ms)	t clus	P
Maximum gain versus maximum loss
Right central	290–335	1167.58	<0.005
Left posterior	290–375	−2131.58	<0.001
Left central‐posterior	365–465	−2122.10	<0.001
Right peripheral	520–570	657.44	<0.07
Minimum gain versus minimum loss
Right posterior	230–320	−1264.27	<0.001
Left‐central anterior	355–420	−604.88	<0.001
Right peripheral	520–575	469.25	<0.001
Left peripheral	520–575	−887.69	<0.001
Maximum loss versus minimum loss
Right posterior	290–340	−1063.23	<0.001
Left central‐posterior	300–355	1363.40	<0.001
Right posterior	455–515	−608.55	<0.05
Maximum gain versus minimum gain
No significant differences found

Figure 1.

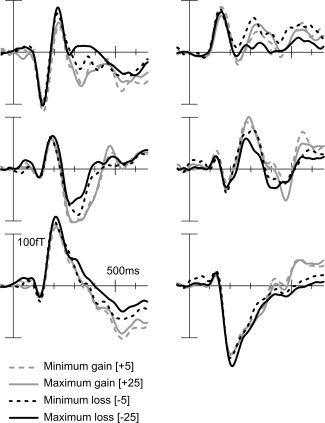
Feedback‐locked EMFs for minimum gain [+5] (gray‐dashed line), maximum gain [+25] (gray solid line), minimum loss [−5] (black dashed line), and maximum loss [−25] (black solid line) in six sensors that are part of significant clusters: left and right posterior (row 1), left and right central (row 2), and left and right peripheral (row 3). The EMFs are low‐passed filtered at 12 Hz for visualization purposes. For a depiction of all sensors and the exact location of these six, see the Supporting Information.

It is important to note that due to the fact that the magnetic fields form around neuronal currents, contrary to what happens in EEG, positive and negative t _clus‐values in Table II do not indicate the direction of the difference between conditions, but merely the positive (magnetic lines of flux entering the head) and negative (magnetic lines of flux exiting the head) surfaces of the magnetic field contours of the difference, respectively. This can be observed in Figure 2, which depicts the topographies of the differences between maximum gain [+25] and maximum loss [−25] (Fig. 2A), minimum gain [+5] and minimum loss [−5] (Fig. 2B), and maximum loss [−25] and minimum loss [−5] (Fig. 2C) at points in time at which sources were localized.

Figure 2.

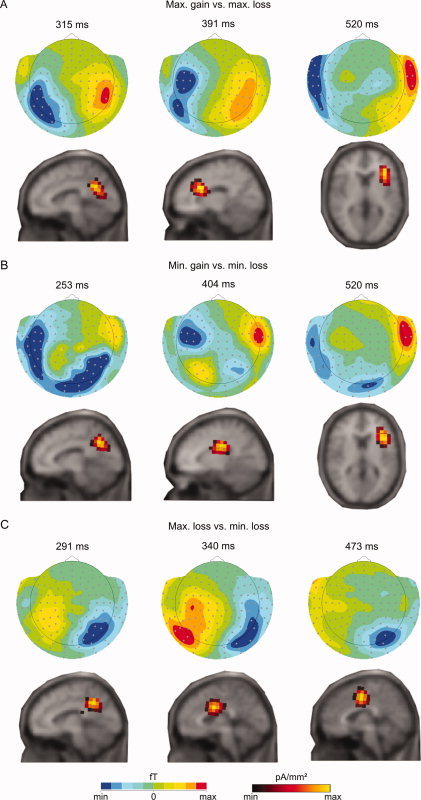
Difference evoked response plots and source density estimates of the difference between (A) maximum gain and maximum loss at 315 ms (−70–70 fT; 3.65–4.25 pA/mm²), 391 ms (−60–60 fT; 3.28–3.96 pA/mm²), and 520 ms (−50–50 fT; 3.95–4.70 pA/mm²); between (B) minimum gain and minimum loss at 253 ms (−30–30 fT; 2.12–2.65 pA/mm²), 404 ms (−45–45 fT; 4.59–5.40 pA/mm²), and 520 ms (−55–55 fT; 3.25–3.77 pA/mm²); and between (C) maximum and minimum loss at 291 ms (−45–45 fT; 2.05–2.38 pA/mm²), 340 ms (−40–40 fT; 2.24–2.80 pA/mm²), and 473 ms(−50–50 fT; 1.11–1.39 pA/mm²). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Source Analysis

Source analysis using LORETA [Pascual‐Marqui et al.,1994] evidenced activation of several different areas at different points in time. All three comparisons that had yielded significant differences in the EMFs initially showed a similar pattern of activation, which started in the PCC (250–315 ms), and was followed by the ACC and the medial cingulate gyrus (340–475 ms). However, a late difference was found for both valence comparisons, which was not found for the magnitude comparison ([−25] minus [−5]), and localized in the right anterior insular cortex (520 ms).

The difference between maximum gain [+25] and maximum loss [−25] was first localized in the dorsal PCC (BA 31; Talairach coordinates: 7, −56, 22; peak at 315 ms), followed by the posterior ACC (BA 24; Talairach: −13, 1, 29; peak at 391 ms). The marginally significant difference found at right peripheral sensors had its source in the right anterior insula (BA13; Talairach: 33, 9, 14; peak at 520 ms) (see Fig. 2A).

In the case of the comparison between minimum gain [+5] and minimum loss [−5], the timeline of source activations was dorsal PCC (BA 31; Talairach: 8, −58, 24; peak at 253 ms), ventral PCC (BA 23; Talairach: 11, −19, 26; peak at 404 ms), and right anterior insular cortex (BA 13; Talairach: 38, 5, 17; peak at 520 ms) (see Fig. 2B).

The sources of the comparison between maximum and minimum loss ([−25] minus [−5]) showed a similar pattern: dorsal PCC (BA31; Talairach: 7, −54, 26; peak at 291 ms) followed by posterior ACC (BA24; Talairach: 3, −9, 31; peaks at 340 and 473 ms) (see Fig. 2C).

Time‐Frequency Analysis

Power spectra of the differences between maximum gain [+25] and maximum loss [−25] showed two discernible increases in power between 5–15 Hz and 23–40 Hz in the analyzed segment (200–600 ms postfeedback) associated to the gain condition (Fig. 3A, first and second column). Additionally, the minimum gain [+5] versus minimum loss [−5] spectrum showed a similar increase in the lower frequencies for gains compared to losses, though constrained to the 5–9 Hz range (Fig. 3A, third column). Contrary to the initial hypothesis, there was no apparent increase in theta power for the losses. However, the spectrum of the difference between maximum loss [−25] and minimum loss [−5] evidenced an increase in power between 5 and 12 Hz starting around 150 ms postfeedback for minimum loss [−5] and an increase in beta/gamma power (21–35 Hz) for maximum loss [−25], which was more apparent from 450 ms postfeedback onwards (Fig. 3A, rightmost column).

Figure 3.

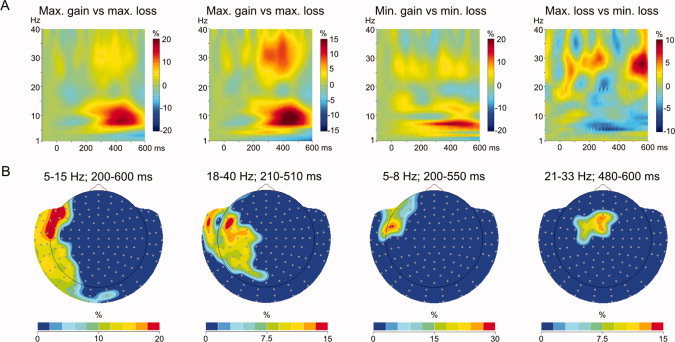
(A) Spectra of the significant time‐sensor clusters and (B) topographies of the significant time‐frequency‐sensor clusters of the difference between maximum gain versus maximum loss at left sensors between 200 and 600 ms (5–15 Hz, peak at 10 Hz) (column 1) and at left anterior sensors between 210 and 510 ms (18–40 Hz, peaks at 29 and 34 Hz) (column 2); minimum gain versus minimum loss at left anterior sensors between 200 and 550 ms (5–8 Hz, peak at 7 Hz) (column 3); and maximum loss versus minimum loss at central anterior sensors between 480 and 600 ms (21–33 Hz, peak at 28 Hz) (column 4). Both spectra and topographies represent the percentage of change in power with respect to baseline, but the spectra correspond to the average of all sensors in the cluster whereas the topographies represent each sensor individually, which explains the differences in the scales. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The nonparametric permutation testing performed on the time‐frequency data revealed significant differences in the 5–15 Hz and 18–40 Hz ranges when comparing the gain and loss conditions. Specifically, there were increases in power for the gains, but not for the losses, in the alpha (peak frequency at 10 Hz) and high‐beta/low‐gamma (peak frequencies at 29 and 34 Hz) bands between 200–600 ms and 210–510 ms postfeedback, respectively, for maximum gain [+25] versus maximum loss [−25], and in the theta (peak frequency at 7 Hz) band between 200 and 550 ms postfeedback for minimum gain [+5] versus minimum loss [−5]. The topographies of these three clusters showed that the peaks were localized around left anterior sensors (Fig. 3B, columns 1–3). Furthermore, as in the analysis of the EMFs, only the magnitude of the loss showed significant differences, which were found between 21 and 33 Hz, with its peak frequency at 28 Hz in the high‐beta band, whereas there was no effect of the magnitude of the gain. This significant cluster was also localized in anterior sensors, though its topography showed a more central distribution than for the other comparisons (Fig. 3B, rightmost column). The time windows, frequencies, and sensor locations of the significant clusters, as well as their t _clus‐ and P‐values, are shown in Table III.

Table III.

Results of the nonparametric permutation testing performed on the time‐frequency data for the comparisons

Cluster	Time window (ms)	Frequency window (Hz)	Peak frequency (Hz)	t clus	P
Maximum gain versus maximum loss
Left	200–600	5–15	10	15362.72	<0.001
Left anterior	210–510	18–40	29; 34	9783.38	<0.01
Minimum gain versus minimum loss
Left anterior	200–550	5–8	7	770.68	<0.001
Maximum loss versus minimum loss
Central anterior	480–600	21–33	28	1563.51	<0.001
Maximum gain versus minimum gain
No significant differences found

In this case, t _clus‐values indicate the direction of the difference.

DISCUSSION

Our findings demonstrate the existence of a magnetic equivalent of the FRN, which we have labeled mFRN. This magnetic component is sensitive to the magnitude of the negative feedback and can be localized in posterior, medial, and anterior cingulate cortices. Our observations also show a temporal evolution, indicating that part of the processing of monetary gains and losses takes place in the right anterior insula. Moreover, we have been able to identify distinct magnetic oscillatory components associated to the processing of monetary feedback.

Evoked Magnetic Fields and Sources: Effect of Valence

We have found significant differences between the magnetic neural responses to monetary gain and loss, which appear consistently in several clusters of sensors between 230 and 465 ms. Thus, the mFRN can be observed over a longer time window and a wider range of sensors than the FRN, as can be seen in the EMFs and the scalp topographies. At first glance, this might seem inconsistent with latencies reported in previous studies, but there are a few issues that should be taken into consideration.

The electrophysiological literature generally describes the FRN as peaking between 250 and 400 ms after a negative feedback stimulus [see e.g. Gehring and Willoughby,2002; Nieuwenhuis et al.,2004a] and being mounted on the P300 [see e.g. Nieuwenhuis et al.,2004b; Yeung and Sanfey,2004], which appears between 200 and 500 ms, and is also known to be sensitive to feedback [Sutton et al.,1978]. In contrast to our study, most ERP research reports peak latencies and defines a time window for statistical analysis around these. Hence it needs to be noted that we describe time windows in which all time points differ significantly, as identified by nonparametric permutation testing, and not merely peak latencies. Moreover, because our data do not allow us to differentiate precisely between the mFRN and a possible magnetic P300, hereupon we will only use the term mFRN.

The distinct spatiotemporal evolution of the mFRN translates into a timeline of source activations, which seem to reconcile the observations made by several previous studies that had identified the source of the FRN in either PCC or ACC/medial cingulate cortex or had attempted to explain more variance by placing dipoles in both areas [Gehring and Willoughby,2002; Miltner et al.,1997; Müller et al.,2005; Nieuwenhuis et al.,2005; Tom et al.,2007]. Activation of these areas has not only been found during the processing and monitoring of external feedback and internal error‐detection in human subjects [Badgaiyan and Posner,1998; Fujiwara et al.,2009; Menon et al.,2001; Müller et al.,2005]. Cell recordings performed on nonhuman primates have detected neurons in the ACC that have increased firing rates both after positive feedback and performance errors [Amiez et al.,2005; Kennerley et al.,2006; Niki and Watanabe,1979]. Similarly, other researchers have observed that some cells in this area respond differentially to rewarding and aversive outcomes [Nishijo et al.,1997; Quilodran et al.,2008]. However, in contrast to human research, most primate models define negative feedback as reward omission rather than punishment. The differential activation of the PCC for reward and punishment identified in humans has thus not been found in animal models, although McCoy et al. [2003] observed that neurons in this area of the macaque cortex do fire differently in response to reward and reward‐omission.

Our data indicate that the mFRN initially originates in the dorsal PCC (BA 31) and that the activation moves forward along the cingulate gyrus as time progresses, showing a more anterior distribution in the case of the maximum gain and maximum loss comparison. In addition to its relation to reward processes, increased activation in the PCC has also been understood as an indication of the evaluation and processing of emotionally salient stimuli [Maddock,1999; Maddock et al.,2003; Vogt et al.,1992], whereas activation in more anterior portions of the cingulate cortex has been associated to changes in response strategy in both human and animal models, highlighting its implication in selection and reinforcement of adaptive behavior [Bush et al.,2002; Holroyd and Coles,2002; Kennerley and Wallis,2009; Kennerley et al.,2006; O'Doherty et al.,2003; Paus,2001; Shima and Tanji,1998]. Hence, the timeline of activations we have found as a result of the effect of valence might be a reflection of a two stage processing of feedback: an initial, perhaps somewhat coarse, stage of emotional evaluation taking place in the dorsal PCC, followed by an assessment of possible changes in response strategy in more anterior areas of the cingulate gyrus.

One of the novel findings of our study is the right anterior insular activation (BA 13) found 520 ms after the onset of the feedback stimulus in both valence comparisons. Similar activations have been frequently described in fMRI studies examining error processing [Hester et al.,2004; Menon et al.,2001; Wittfoth et al.,2008] and punishing feedback [Liu et al.,2007; O'Doherty et al.,2003; Preuschoff et al.,2008; Wächter et al.,2009]. However, to our knowledge, this is the first time neurophysiological data that have shown insular activity following feedback.

The insular cortex is known to take part in the processing of risk‐taking behavior and frustration or emotional distress [Abler et al.,2005; Chua et al.,2009; Fishbein et al.,2005; Paulus et al.,2003; Sanfey et al.,2003] and to have anatomical and functional connections with areas implicated in reward processing, such as ACC, orbitofrontal cortex, nucleus accumbens, hippocampus, and amygdala [Càmara et al.,2008; Reynolds and Zahm,2005]. Our data suggest that the influence of risk on the processing of feedback needs to be explored further: the fact that the current density of the insular activation following higher gambles (i.e., [25]) is stronger than following smaller gables (i.e., [5]) could be an indication that the former are perceived as riskier than the latter.

Given the known anatomical and functional connections [Càmara et al.,2008; Reynolds and Zahm,2005], the timeline of activations we found in our study could be an indication that the cingulate areas activated in the earlier time windows and the insula are communicating when evaluating the outcome of reward and punishment as well as a sign of the processing of negative emotions following loss feedback. We thus posit there are two moments of affective processing associated to the effect of valence, which take place in the PCC and the insular cortex. As mentioned further earlier, we consider that the earlier processing that takes place in the PCC could be a reflection of a fast, and coarser processing designated to rapidly evaluate the value of the outcome to help it lead to a second stage in which strategic decisions are taken. Therefore, the late emotional processing taking place in the insula could be purely dealing with the more fine‐grained negative emotions derived from the monetary loss.

In our analysis, we have tried to take advantage of the excellent temporal resolution of MEG not only by merely examining responses that take place very early in time, but also by breaking down how the neural activations evolve over time. Our data indicate that the processing of feedback information is not limited to the earlier time windows, but that the emotional processing of these events continues after the appearance of the mFRN.

Evoked Magnetic Fields and Sources: Effect of Magnitude

We observed that the mFRN is sensitive to the magnitude of the loss, though not to the magnitude of the gain, and that the sources of these differences could be once more traced back to both dorsal PCC (BA 31) and posterior ACC (BA 24). As noted before, there has been diverging evidence concerning the sensitivity of the FRN to the amount lost [Hajcak et al.,2006; Holroyd and Coles,2002; Holroyd et al.,2002,2006; Nieuwenhuis et al.,2004a; Yeung and Sanfey,2004]. Also, animal models have shown that the firing rates of neurons in both PCC and ACC of the macaque brain are sensitive to the magnitude of rewards [Amiez et al.,2005; Hayden et al.,2008; Kennerley and Wallis,2009; McCoy et al.,2003], but then again these studies have not explored aversive outcomes. The mFRN appears to be reflecting a classification of punishing feedback along a bad‐worse dimension, which is in agreement with the postulates of the reinforcement learning theory of the FRN [Holroyd and Coles,2002; Holroyd et al.,2002; Nieuwenhuis et al.,2004a,b].

Once again, our MEG data reveal a distinct temporal evolution: our finding of a sequential activation of PCC and ACC could be evidencing that the first stage of evaluative processing of the feedback [Badgaiyan and Posner,1998; Maddock et al.,2003; Menon et al.,2001; Müller et al.,2005; Vogt et al.,1992] and the second stage of assessment of a possible shift in response strategy [Bush et al.,2002; Holroyd and Coles,2002; O'Doherty et al.,2003; Paus,2001] are different for larger and smaller monetary losses. This explanation is not only consistent with the fact that both areas are sensitive to the effect of valence of the feedback, but also that they are to the magnitude of the loss, but not the gain, which would obviously not require a shift in strategy.

Still, the question remains why the mFRN is not sensitive to the magnitude of positive feedback. We know from animal models that there are neurons in the cingulate cortex that react differently to gains and losses [Amiez et al.,2005; Hayden et al.,2008; Kennerley et al.,2006; McCoy et al.,2003]. However, human research has mostly found subcortical activation, mainly striatal, following rewarding feedback and which is sensitive to its magnitude [Knutson et al.,2003; Yacubian et al.,2006]. It is therefore possible that the processing of reward magnitude in humans has a larger subcortical than cortical contribution, which would make it difficult for certain MEG systems to detect, becasue these can be relatively insensitive to deeper sources [Singh,2006].

Oscillatory Responses: Effect of Valence

Our analysis of the oscillatory responses elicited by feedback shows a significant increase in power for maximum gain compared to maximum loss between 200 and 600 ms ranging from 5 to 15 Hz, comprising most of the theta (4–8 Hz) and alpha (8–12 Hz) bands, and peaking around 10 Hz between 380 and 450 ms. A boost in theta power (5–8 Hz) is also found between 200 and 550 ms associated to minimum gain compared to minimum loss. Although discrepant with some of the earlier research, which have found increases in power in the theta band (4–7 Hz) following negative feedback and in the high‐beta band (20–30 Hz) following positive feedback [Cohen et al.,2007; Gehring and Willoughby,2004; Marco‐Pallarés et al.,2008], our data are consistent with previous studies by Papo et al. [2007a,b], who have found increases in theta and alpha activity after positive feedback and have related these to activation in the ACC. Also, an increase in alpha power has too been observed to occur following correct responses compared to performance errors [Carp and Compton,2009].

Given the distribution of the significant theta and theta/alpha clusters in our study, ACC and also PCC could be the sources of the oscillations in our data, because the sensors largely coincide with the significant sensors, which yielded those sources in the previously described analyses. Although the oscillations from PCC remain, to our knowledge, generally unstudied, it has been observed that theta oscillations from the ACC are associated to adjustments in response strategy in nonhuman primates [Womelsdorf et al.,2010]. Moreover, both theta and alpha oscillations have been observed using paradigms that evoke a P300 response in the ERPs [Başar et al.,1997,2001] and have been associated to the processing of risk [Qin et al.,2009], among multiple other processes (for a review, see Başar et al. [2001]). Such explanations of the oscillations would harmonize with those of the evoked responses posited previously, yet further research is required to explain how or whether the temporal dynamics of the evoked responses relate to the temporal dynamics of the oscillatory responses.

We have further found a burst in power associated to maximum gain compared to maximum loss between 210 and 510 ms ranging from 18 to 40 Hz, hence spanning parts of the beta (12–30 Hz) and gamma (>30 Hz) bands. This cluster has two distinct peak frequencies around 29 Hz (250–290 ms) and 34 Hz (380–400 ms) and can therefore be linked to previous accounts of a boost in high beta/low gamma associated to positive feedback [Cohen et al.,2007; Marco‐Pallarés et al.,2008; Papo et al.,2007b]. It has been proposed that this beta activity might be synchronizing neural populations over long distances and therefore communicating different reward‐related structures [Marco‐Pallarés et al.,2008].

It should be noted that at least part of the differences between our study and previous research can be accounted for by differences in statistical methodology. Previous investigations [Cohen et al.,2007; Gehring and Willoughby,2004; Marco‐Pallarés et al.,2008] performed parametric statistics, that is, ANOVAs, on the averaged values of predefined frequency bands and electrodes, which could have overlooked other effects, whereas the nonparametric permutation testing we used in this study allowed us to explore each and every time point, frequency, and sensor.

Oscillatory Responses: Effect of Magnitude

Apart from the differential effect of valence, we found a significantly higher response for maximum loss compared to minimum loss between 480–600 ms in the 21–33 Hz range, more precisely peaking between 27–29 Hz and 520–580 ms, which interestingly is a later time window than that of the evoked responses. This is the first evidence of an effect of the magnitude of the punishment in oscillatory activity, as previous research only focused on the effect of valence [Cohen et al.,2007; Gehring and Willoughby,2004; Marco‐Pallarés et al.,2008; Papo et al.,2007a,b].

As with the EMFs, we have not found an effect of the magnitude of the gains in the oscillatory responses. As stated before, one of the reasons for this could again have to do with a possible greater contribution of subcortical oscillations. Nonetheless, we feel that further research is needed on the oscillatory responses to the magnitude of reward and punishment before venturing more elaborated explanations about their significance.

CONCLUSIONS

In this study, we have characterized the temporal dynamics of monetary feedback processing. We have shown a magnetic correlate of the well‐established FRN, which we have labeled mFRN, evidencing that MEG is a well‐suited technique for the study of the neural responses to feedback and that it provides complementary information to previous research performed with EEG. The mFRN is found in a range of sensors between 230 and 465 ms, is sensitive to the magnitude of the punishment, though not of the reward, and is localized at first in the dorsal PCC and later in time in more anterior portions of the cingulate cortex. Our data also show a late component associated to the differential processing of monetary gains and losses, which can be localized in the right anterior insula.

We have also shown a number of oscillatory components in the theta, alpha, and high‐beta/low‐gamma bands associated to gains compared to losses, and in the high beta band, associated to the magnitude of the loss. These results slightly diverge from some of the few previous studies that have dealt with the time‐frequency components of reward, suggesting that further, more detailed analyses of oscillations will lead to a better understanding of the neural processing of reward.

All in all, our study paints a dynamic picture of how the brain deals with reward and punishment. We have sought to exploit both the excellent temporal resolution of MEG and its higher spatial resolution compared to EEG by outlining the evolution over time of neural activations associated to the evoked components as well as by depicting a number of oscillatory components elicited by the processing of monetary wins and losses.

Supporting information

Additional Supporting Information may be found in the online version of this article.

Supporting Information