Geometric computation of human gyrification indexes from magnetic resonance images

Abstract

Human brains are highly convoluted surfaces with multiple folds. To characterize the complexity of these folds and their relationship with neurological and psychiatric conditions, different techniques have been developed to quantify the folding patterns, also known as the surface complexity or gyrification of the brain. In this study, the authors propose a new geometric approach to measure the gyrification of human brains from magnetic resonance images. This approach is based on intrinsic 3D measurements that relate the local brain surface area to the corresponding area of a tightly wrapped sheet. The authors also present an adaptation of this technique in which the geodesic depth is incorporated into the gyrification computation. These gyrification measures are efficiently and accurately computed by solving geometric partial differential equations. The presentation of the geometric framework is complemented with experimental results for brain complexity in typically developing children and adolescents. Using this novel approach, the authors provide evidence for a gradual decrease in brain surface complexity throughout childhood and adolescence. These developmental differences occur earlier in the occipital lobe and move anterior as children progress into young adulthood. Hum Brain Mapp, 2013. © 2012 Wiley Periodicals, Inc.

INTRODUCTION

The cortical surface of a human brain evolves from a smooth, lissencephalic surface to a highly convoluted surface during the third trimester of fetal life in a process known as gyrification [Welker, 1990]. By the time of birth, the brain of an infant, although smaller, has a morphological appearance that resembles an adult brain. Even though a cortical surface is considered to be a topological sphere, the gyri and sulci that form the fissures and folds can be complicated [Welker, 1990]. This is especially true for the human brain. It has been shown that a higher degree of folding of the cortical surface indicates a progressive evolution of cortical complexity in humans [Zilles et al., 1988]. The increased cortical folding associated with human phylogeny has produced a highly efficient mechanism to increase cortical gray matter while optimizing a smaller overall brain size.

Abbreviations

GI

gyrification index

ICV

intracranial volume

MRI

magnetic resonance images

ROI

region of interest

It is of great interest to characterize the surface morphology of the brain, since careful quantification can provide valuable information associated with alterations or differences related to development and pathology. The cortical complexity has been used to evaluate abnormalities of the brain's surface morphology in various neurological and psychiatric conditions and in disorders of cognition [White and Hilgetag, 2008]. For example, there have been a number of different studies finding aberrations in gyrification patterns in individuals with schizophrenia [for a review see White and Hilgetag, 2010]. Since there is a proposed connection between development and gyrification [Armstrong et al., 1995], and between gyrification and connectivity [Van Essen, 1997], these findings may help ascertain the underlying neurobiology of schizophrenia and other psychiatric and neurological disorders.

The mechanisms underlying gyrification are interesting and it is not yet known exactly how the brain develops its typical convoluted pattern. There are many questions surrounding the relationship between the degree of convolutions with brain function, age, gender, ethnicity, and health status. These mysteries of human brain development have prompted researchers to develop measures to quantify the degree of complexity of the cortical surface. The gyrification index (GI) proposed by Zilles et al. [ 1988] was one approach developed to quantify the degree of cortical folding. The GI is defined as the two‐dimensional ratio between the total outline (including sulcal folds) and the superficially exposed outline for each coronal section of postmortem brains. Initially these contours were manually delineated on postmortem brains and have been applied to study both the phylogeny [Zilles et al., 1988] and ontogeny [Armstrong et al., 1995] of cortical gyrification. Brains that have higher degrees of cortical folding relative to their brain size (i.e., increased cortical complexity) yield larger values of GI. The anterior to posterior maps of human GI have shown greater gyrification in the frontal, temporal, and parietal lobes of the brain [Zilles et al., 1988].

However, due to the 2D delineation of the traditional GI [Zilles et al., 1988], the intrinsic 3D nature of the brain surface is not taken into account and this GI does not completely avoid a biased estimate. For example, the GI may be altered if the slice orientation is slightly different within the same subject. Since surface morphology can be considered a two‐dimensional (2D) surface in three‐dimensional (3D) space, it is important to consider a fully 3D GI to eliminate the shortcomings of the coronal 2D approach. Furthermore, manual extraction of the contours is extremely time‐consuming and prone to human errors. Thus, fully automatic algorithms are important to reduce errors by manual delineation.

So far, 3D computational algorithms to measure gyrification are based on either curvature or surface area. Curvature‐based approaches evaluate the smoothed absolute mean curvature on parameterized cortical mesh models [Luders et al., 2006; Magnotta et al., 1999; Thompson et al., 1996; White et al., 2003]. These curvature‐based approaches have been shown to find differences that were not previously identified using traditional GI approaches. More recently, a localized 3D GI [Schaer et al., 2008] was developed and applied to a group of children affected by 22q11.2 Deletion Syndrome. This technique uses a 3D triangular mesh reconstruction of the cortical and outer hull surfaces and measures the amount of cortical surface buried in the sulci by constructing and relating this to nonintrinsic spheres. Schaer et al. [ 2008] used the approach developed by Kao et al. [ 2007] to generate the outer hull surface. With this surface, the localized GI for each point on the cortical surface was obtained through a depth‐weighted average of neighboring points.

Another 3D approach to measure gyrification is to use the surface ratio between the pial surface contained in a small sphere and that of a disk of the same radius, which approximates the surface area of that region if it were not folded [Toro et al., 2008]. In this approach, a triangular mesh is created and a nonintrinsic sphere with a suitable radius is then constructed at each cortex point. This method is less sensitive to the choice of different radii when compared with that by Schaer et al. [ 2008]. It has been applied to a sample of 314 subjects, 164 females, and 150 males. The study showed the disproportionate ratio of cortical surface area to brain size, similar to an earlier observation across species [Prothero and Sundsten, 1984]. In addition, the increase of the cortical folding in the prefrontal cortex is observed for in larger brains. Since this approach does not require the construction of an outer hull surface, it results in a simple and efficient algorithm when compared with the method proposed by Schaer et al. [ 2008].

In this article, the authors build upon their previous study [Kao et al., 2007] and propose a 3D‐geometric approach for the automatic computation of global and regional GIs of the human brain. By finding a novel geometrically corresponding region on the outer hull surface for any selected region of interest (ROI) on the cortical surface, the authors define a 3D‐regional GI as the area ratio between the selected region and the corresponding region of a tightly wrapped sheet around the cortical surface. Furthermore, the 3D GI can be weighted by local quantities, i.e., curvature or geodesic sulcal depth, and is fully intrinsic and different from the method proposed by Schaer et al. [ 2008] and Toro et al. [ 2008] in that it does not depend on a chosen radius and a corresponding nonintrinsic sphere to determine the regions used to calculate the localized GI. The incorporation of the robust sulcal depth computation developed in [Kao et al., 2007] as part of the GI measurement is the key to define the corresponding region on the outer hull surface for a ROI given on the cortical surface. The depth measurement is informative to characterize different levels of convolutions in human brains. Weighting by the geodesic depth is important to distinguish between a deep sulcal region and a shallow sulcal region when both sulcal regions have the same surface areas.

In “Materials and Methods,” the authors introduce the proposed novel algorithms to calculate 3D gyrification indices. Quantitative results for the proposed GIs, and comparison with previous approaches, are presented in “Experimental Results.” For this, the authors present the application of the algorithm to a population of typically developing children. Finally, the authors conclude the article in “Concluding Remarks and Discussion” by briefly describing the contributions and findings and proposing further lines of study in the area of computational approaches for measuring GI.

MATERIALS AND METHODS

A flow chart describing the main steps of the proposed 3D geometric GI computation algorithm is provided in Figure 1. A triangular mesh of cortical surface shown in Figure 1a is the input of the algorithm. First, an outer hull surface (see Figure 1b) covering the sulcal regions in a shrink‐wrap fashion is constructed. Second, the authors extract the geodesic depth (see Figure 1c) using an efficient fast sweeping algorithm [Kao et al., 2005; Tsai et al., 2003; Zhao, 2005]. Third, a region on the cortical surface (see Figure 1d) is selected and its boundary is extracted. Fourth, the corresponding part of the selected region (see Figure 1e) on the outer hull surface is computed. Fifth and finally, the authors define the regional GI as the ratio between the area of the region on the cortical surface and the area of the corresponding region on the outer hull surface. This ratio is calculated with and without weighting by the local sulcal depth. These steps are explained in detail in the subsequent sections.

Figure 1.

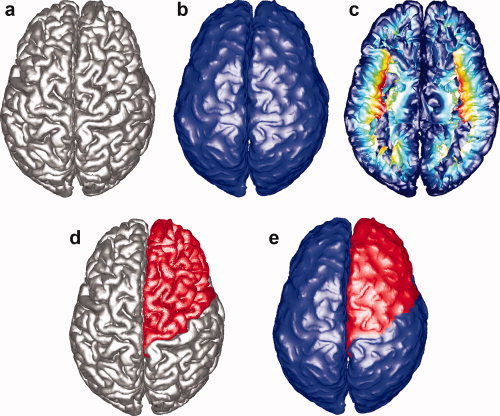
Flow chart of the main steps of the proposed GI computation algorithm. Each figure explains the major steps of the algorithm: (a) Triangular mesh of the pial surface. (b) Outer hull surface computation. (c) Geodesic depth computation: the color‐coding corresponds to the computed geodesic depth where shallow regions are colored in blue and deep regions are colored in red. (d) Region of interest on the pial surface selection: frontal lobe is selected (colored in red) in this demonstration. (e) Corresponding region on the outer hull surface computation: the corresponding region is computed (colored in red). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Surface Extraction and Depth Computation

There are a number of software packages available to obtain a triangular mesh of the cortical surface; e.g., Freesurfer [Dale et al., 1999]1, SurfRelax [Larsson, 2001]2, and BrainVisa [Han et al., 2004]3. In this article, the authors used the pial surface generated by Freesurfer. Meanwhile, total intracranial volume (ICV) was also calculated using the technique developed by Buckner et al. [ 2004]. By M, the authors denote a triangular mesh with faces f ₁,…,f _N; M is required to be a closed and orientable 2‐manifold in Euclidean 3‐space. The authors then apply a regular grid to derive an implicit representation of the pial surface by computing the signed distance function to the surface on a Cartesian grid [Kao et al., 2007]. Using a level set technique, the authors compute an outer hull surface that encloses the pial surface in a shrink‐wrap type fashion. The outer hull is such that one can still distinguish the gyri, but the sulcal regions are now “filled.” A depth measure is then defined for every point on the pial surface as the shortest distance that connects each cortical surface point to a point on the outer hull surface such that the connecting path remains inside the sulcal regions. The computational realization uses an efficient fast sweeping algorithm.

As shown in Figure 1a, once the authors have the explicit form M of the pial surface, the authors compute the signed distance function to the surface on a Cartesian grid. In the implicit form, the pial surface becomes the zero level set {ϕ = 0} of the signed distance function ϕ: R ³ → R [Osher and Sethian, 1988]. The details for obtaining this signed distance function can be found in [Kao et al., 2007].

After obtaining both an explicit triangular mesh representation and an implicit level set representation on a Cartesian grid, the authors compute the outer hull surface using a morphological closing operation applied to the level set function ϕ [Osher and Sethian, 1988]. That is, the authors first move the pial surface outward by a time parameter T, and then the authors move the surface inward by the same amount of time. The governing equation is:

where

Thus, the implicit representation of the outer hull surface is given by:

This minimization guarantees that the outer hull surface covers, but does not penetrate the pial surface. In the algorithm, the authors choose T = 10 (mm/unit time), since T needs to be large enough to fill/close the sulcal regions and also small enough to preserve the overall shape of the gyri. Even though the level set method cannot guarantee topology preservation, in the numerical implementation, the authors found that the restricted region {Ψ ≤ 0} is topology preserving. (In the case that there is a topology change, one can use the topology‐preserving level set method [Han et al., 2003]). In Figure 1b, the authors show the computed outer hull surface for the given pial surface shown in Figure 1a.

Once the authors generate the outer hull surface, the authors apply the fast sweeping method to calculate the geodesic depth for points on the pial surface. The defined geodesic depth corresponds to the shortest path from the given pial surface point to the computed outer hull, which does not cross the surface of the brain [Kao et al., 2007]. Thus, the authors apply the distance computation algorithm to the restricted (CSF) region between the outer hull and the pial surface {Ψ ≤ 0 and ϕ ≥ 0}. In Figure 1c, the authors show a top view of the bottom part of the pial surface. The color‐coding corresponds to the computed geodesic depth where shallow regions are colored in blue and deep regions are colored in red.

Corresponding Region on the Outer Hull Surface Computation

In this stage, the authors first select a ROI on the pial surface. The region can be chosen using several different algorithms and can involve any sulcus or gyrus of interest. Alternatively, implementing either a depth or curvature threshold can restrict this region. After obtaining the ROI on the pial surface, the corresponding region on the hull surface is computed in two steps.

In the first step, the boundary of the pial surface for the selected region is extracted. Then the authors sample points on this boundary and find the boundary points for the corresponding region on the computed outer hull surface. This is performed following the negative gradient of the previously computed sulcal depth. The authors extract the paths for each starting point situated on the boundary of the selected pial region by solving the following equations, and stop when the authors reach the previously computed outer hull surface:

where d is the geodesic depth defined in the authors computed in “Surface Extraction and Depth Computation,” B ${}_{\text{p}}^{\text{s}}$ is a point on the boundary of the selected region on the pial surface, and B ${}_{\text{h}}^{\text{s}}$ is then the corresponding boundary point on the outer hull surface. In this method, the authors obtain all the corresponding boundary points on the outer hull surface in an intrinsic and geometric fashion. This method of finding the corresponding points on the outer hull surface is novel and different from the previously proposed methods.

In the second step, these boundary points are connected to form the boundary of the corresponding region on the outer hull surface. It is achieved using the shortest distance along the edges of the triangles. An alternative choice would be to use the geodesic distance on the triangular mesh M [Peyre and Cohen, 2006]. Since M is a closed and orientable 2‐manifold in Euclidean 3‐space, the authors can march inside it and find the triangles restricted in the constructed boundary on the outer hull surface.4 The region defined by these restricted triangles corresponds, on the outer hull surface, to the selected pial ROI.

In Figure 1d, the authors demonstrate a selected region in red on the pial surface. In Figure 1e, the authors show the outer hull surface of the same region, also shown in red. Figure 2 illustrates the axial, coronal, and sagittal slices of the original magnetic resonance images (MRI) brain volume on which, the authors overlay the intersection curve of the pial and outer hull surfaces of one hemisphere (in blue) with the selected sulcal region on the pial surface and the computed corresponding region on the outer hull surface (in red).

Figure 2.

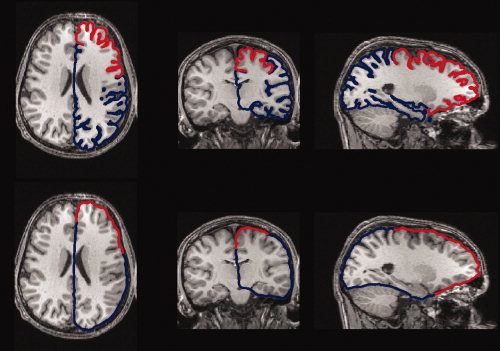
Axial (1^st column), coronal (2^nd column), and sagittal (3^rd column) slices of the MRI brain volume combined with the pial and outer hull surfaces of one hemisphere (blue lines). The red part on the curve is the intersection of the selected region (frontal lobe here) on the pial surface and the corresponding region on the outer hull surface. Top three slices correspond to Figure 1d (pial surface) and bottom three slices correspond to Figure 1e (outer hull). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

These geometric computations form the basis needed for the gyrification indices. In contrast to other 3D methods [Schaer et al., 2008; Toro et al., 2008], where the GI measurements rely on the selection of an extrinsic sphere with predefined radius, the computation of the corresponding outer hull region is completely form fitting to the geometry of the brain.

Gyrification Indexes

The most commonly used GI was proposed by Zilles et al. [ 1988], and was defined on each 2D slice i in the coronal section as the ratio of the length of the total cortical contour L ${}_{\text{T}}^{\text{i}}$ to the length of the superficially exposed cortical contour L ${}_{\text{S}}^{\text{i}}$, that is,

Notice that the correspondence between contours was determined manually in Zilles et al. [ 1988]. The mean GI of each hemisphere was then defined as:

where the sum ran over all the postmortem brain slices i. This 2D measurement does not allow for the assessment of localized properties. Different theories have postulated that active, localized growth of the cortical convolutions may lead to different brain structures, e.g., regions which are developing into gyri grow at a faster rate than areas destined to become sulci. Furthermore, research has demonstrated that the development of different regions of the brain are more susceptible to events occurring during prenatal life, e.g., the temporal lobe is more vulnerable in preterm births, with a resulting increased temporal lobe GI [Kesler et al., 2006]. Thus, reliable and accurate regional GIs are of great interest to better understand the complexity of brain folding.

Area‐based gyrification measurement

In the following, the authors will introduce several GI measurements. Using Freesurfer, each hemisphere is classified into 35 different sulcal and gyral regions and a complete labeling of these 35 regions can be obtained by the automated parcellation system. The authors grouped these ROIs into six anatomically defined regions (see a description of the regions in Table I). The authors utilized 33 of the 35 regions in defining the frontal lobe, parietal lobe, temporal lobe, medial temporal lobe, occipital lobe, and the cingulate gyrus.

Table I.

Average surface area ratio and average depth for each brain region

	Surface area ratio				Average depth
	Left hemisphere (pial surf)	Right hemisphere (pial surf)	Left hemisphere (hull surf)	Right emisphere (hull surf)	Left hemisphere	Right hemisphere
Frontal	0.3509	0.3533	0.3750	0.3777	0.1241	0.1230
Parietal	0.2265	0.2302	0.1937	0.1909	0.1613	0.1625
Temporal	0.1540	0.1482	0.1527	0.1489	0.1501	0.1507
Medial temporal	0.0484	0.0441	0.0634	0.0598	0.0800	0.0757
Occipital	0.1125	0.1164	0.1180	0.1261	0.1001	0.0986
Cingulate	0.0364	0.0380	0.0509	0.0507	0.0637	0.0649

The pial surface is the area that includes the sulci, whereas the hull surface reflects corresponding region on the brain surface. The average depth measure is the average depth of the sulci within each brain region, measured from points on the hull surface to the points within the sulci.

Freesurfer parcellated regions used to define each brain ROI. Frontal lobe – caudal middle frontal, lateral orbitofrontal, medial orbitofrontal, paracentral, parsopercularis, parsorbitalis, parstriangularis, precentral, rostral middle frontal, superior frontal, frontalpole.

Parietal lobe – inferior parietal, postcentral, precuneus, superiorparietal, supramarginal.

Temporal lobe – bankssts, inferior temporal, middle temporal, superior temporal, temporal pole, transverse temporal.

Medial temporal lobe – entorhinal, fusiform, parahippocampal.

Occipital lobe – cuneus, lateraloccipital, lingual, pericalcarine.

Cingulate cortex – caudal anterior cingulate, isthmus cingulate, posterior cingulate, rostral anterior cingulate.

Figure 3 shows the classification of the six regions on the left pial surface. The authors can successfully identify the corresponding six regions on the hull surface. For comparison, the authors also show the inflated left pial surface, which is obtained directly from Freesurfer.

Figure 3.

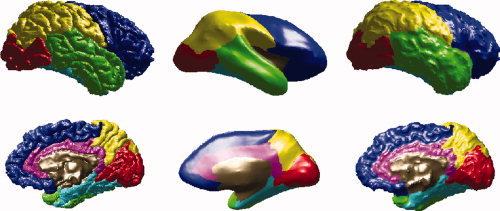
Six regions of interest on left pial surface (1^st column), inflated left pial surface (2^nd column), and the left hull surface (3^rd column). Frontal lobe is shown in blue, parietal lobe in yellow, temporal lobe in green, medial temporal lobe in cyan, occipital lobe in red, and cingulate cortex in magenta. The region which is not classified is shown in brown. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The region‐based GI GI${}_{\text{region}}^{\text{1}}$ at each lobe is then defined as the ratio between the area of the lobe on the pial surface and the area of the corresponding region on the outer hull surface,

where A ${}_{\text{p}}^{\text{s}}$ is the area of any selected lobe on the pial surface and A ${}_{\text{h}}^{\text{s}}$ is the corresponding area on the hull surface, computed as detailed in the previous section.

This regional GI GI${}_{\text{region}}^{\text{1}}$ has several key features:

• 1
  The corresponding region on the outer hull surface is naturally computed from the ROI on the pial surface, leading to a parameter‐free intrinsic GI. If the authors select the whole pial surface, the corresponding region is then the whole outer hull surface. The GI measurement becomes:

  

  where A _p is the area of the whole pial surface, and A _h is the area of the whole outer hull surface. If only a slice of the pial surface is considered the surface area in 3D becomes the slice perimeter in 2D. However, this reduction may still be different from the exact definition of Zilles et al. [ 1988], since the corresponding point on the outer hull surface may not be on the same plane any longer. From this point of view, powerful 3D GI computation is of great importance.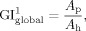
• 2Since all the triangles in the selected region on the pial surface are collected, all the sulcal information restricted to the selected area is considered.
• 3The selection of the region on the pial surface can be further parceled to determine GIs for different subregions. For instance, having calculated the depth information for each point on the pial surface, the authors can define a threshold d ₀ and choose a ROI as all the points with depth d ≥ d ₀. Other possible choices are to select one of the 35 sulcal or gyral regions as ROI.

Depth‐based gyrification measurement

Before the authors extend the GI${}_{\text{region}}^{\text{1}}$ to a weighted GI by adding the depth information of the pial surface, the authors introduce a normalization of the computed depth value.

Since the absolute depth significantly depends on brain size, it is reasonable to consider the relative depth. In this method, two brains with a similar morphology, but different volumes, would have comparable gyrification indices. The authors implement this using d _N instead of the absolute value d,

where the denominator 3V/A on the right hand side is a normalization factor based on volume V and area A [Rodriguez‐Carranza et al., 2008]. One can examine this normalization considering a sphere of radius R, then the normalized value for a certain depth d of folding becomes:

and if the radius is 2R and the depth is 2d, the normalized depth becomes:

While these two spheres have similar folding but different depths, the normalized depths are the same. See Figure 4 for an illustration.

Figure 4.

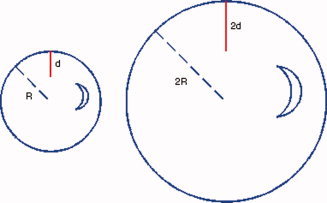
Two spheres with radius R and 2R and the depths d and 2d are shown respectively. The normalized depths d _N = (d/R) = (2d/2R) compensate the depth (size) differences in two structures with similar morphology. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Remark 1: The human brain is actually more like an ellipsoid elongated on the anterior–posterior direction. In this situation, the authors can fit the brain surface by an ellipsoid in a xyz‐Cartesian coordinate system and obtain the equatorial radii a and b (along the x and y axes) and the polar radius c (along the z‐axis). The approximate surface area formula (Knud Thomsen's formula) is:

with p ≈ 1.6075. The volume formula of an ellipsoid is:

Thus, the previously defined normalization factor becomes:

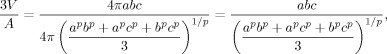and this is consistent with the situation of a sphere by redefining:

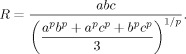The authors now define the depth‐based GI. For any region R _p selected on the pial surface, the corresponding region on the outer hull surface is denoted by R _h. A GI that considers the normalized depth information d _N can be defined as:

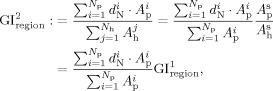where N _p and N _h are the total number of triangular vertices inside the regions R _p and R _h respectively, d ${}_{\text{N}}^{\mathit{\text{i}}}$ is the normalized depth of the vertex i (depth to the outer hull surface as detailed before [Kao et al., 2007]), A ${}_{\text{p}}^{\mathit{\text{i}}}$ is the area of the vertex _i in R _p, and A ${}_{\text{h}}^{\mathit{\text{j}}}$ is the area of the vertex j in R _h. Notice that A ${}_{\text{p}}^{\text{s}}$ and A ${}_{\text{h}}^{\text{s}}$ are defined as before in “Gyrification Indexes.” The area at a vertex i (see Figure 5, cyan colored vertex) is defined in the following method. For each neighboring triangle of vertex i, the authors find the centroid (see Figure 5, black colored) and for each neighboring ring of vertex i, find the middle point (see Figure 5, yellow colored). Then the area at vertex i is the area sum of all such triangles formed by the vertex i, the centroid of the neighboring triangle and the middle point of the neighboring ring in the same triangle. Figure 5 illustrates this.

Figure 5.

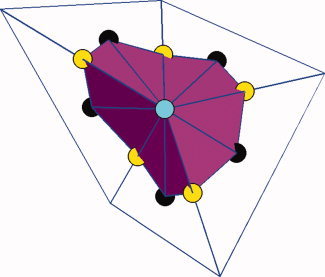
Area definition at a vertex. For the vertex at the center (cyan), the area is defined as the total area of the region shown in magenta, which is made up of all the triangles constructed by connecting the vertex (cyan), the centroid (black) of its neighboring triangle and the middle point (yellow) of its neighboring ring in the same triangle. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

By adding weights to the depth of the pial surface, GI${}_{\text{region}}^{\text{2}}$ is in fact a measurement of the average geodesic depth in the selected ROI on the pial surface scaled by the ratio of the area of the selected region on the pial surface to the area of the corresponding region on the outer hull surface, i.e., GI${}_{\text{region}}^{\text{1}}$. Similar to the previously defined GI, the global counterpart of GI${}_{\text{region}}^{\text{2}}$ becomes:

This is an approximation of the scaled average geodesic depth of the restricted (CSF) region between the outer hull and the pial surface {Ψ ≤ 0 and ϕ ≥ 0}.

The rationale behind a measure that is weighted by the normalized geodesic depth is to account for depth differences in the regions with the similar areas. In Figure 6, the inferior temporal gyrus and postcentral gyrus (colored in red and green, respectively) have similar surface areas. They are 30.17 and 27.44 cm², respectively, in this brain example. The depth measurement (shallow in blue and deep in red) shows that postcentral gyrus has much larger value in depth due the surrounding deep sulci. It turns out that the GI²/GI¹ for inferior temporal gyrus and postcentral gyrus are 0.09 and 0.21, respectively. Since the depth values used are normalized, the values are always smaller than 1. However, the GI² of postcentral gyrus is roughly twice as the one of inferior temporal gyrus. Thus GI² can be used to distinguish regions with similar surface areas but differences in average depth.

Figure 6.

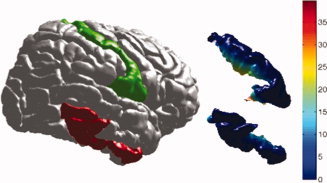
The inferior temporal gyrus and postcentral gyrus (colored in red and green respectively) have similar surface areas. They are 30.17 and 27.44 cm², respectively in this brain example. The depth measurement (shallow in blue and deep in red) shows that postcentral gyrus has much larger value in depth. The GI² /GI¹ for inferior temporal gyrus and postcentral gyrus are 0.09 and 0.21, respectively. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Remark 2: The localized GI proposed by Schaer et al. [ 2008] is obtained through a depth‐weighted average of localized GI of the neighboring points. Therefore, this pointwise GI is in fact still region‐based since the ROI is defined by the radius of the nonintrinsic sphere. In the approach, there is no need to choose a nonintrinsic sphere. The authors do not provide a point‐wise GI as it makes more sense to study gyrification of anatomical ROI on cortical surface.

Subjects

To test this approach, the authors applied the methods to a study of the development of gyrification in 26 typically developing children and adolescents [White et al., 2010]. Subjects were stratified into three age groups, which included children (8–12 years old), young adolescents (13–15 years old), and older adolescents (16–19 years of age). The demographic information for the children is provided in Table II. Socioeconomic status was determined using the Four Factor Index of Social Status [Hollingshead, 1975].

Table II.

Demographic information for the 26 typically developing children

	8–12 Year olds	13–15 Year olds	16–19 Year olds	P
Age	10.5 (1.6)	14.0 (0.87)	16.9 (1.2)
Sex (male/female)	4/2	6/3	4/7	n.s.
Socioeconomic status	50.7 (9.7)	49.7 (15.5)	51.1 (9.7)	n.s.

Statistical Analyses

Evaluation of the differences in demographics was assessed using one‐way ANOVAs or t‐tests for continuous data and chi‐square tests for categorical data. Paired t‐tests were used to assess lateralization of gyrification and cortical depth measures. If the gyrification of each hemisphere is independent, which is unlikely, then measures for the right and left hemispheres should not be pooled, even if they do not show lateralizing effects. If they are dependent, then they may or may not show lateralization. Since there were differences in lateralization, the authors did not pool data from the two hemispheres. An ANCOVA of the total sample (14 males and 12 females), with age and ICV as covariates, was used to evaluate sex effects of the sulcal depth measures. Measures of gyrification were evaluated between the three age groups using a one‐way ANOVA.

EXPERIMENTAL RESULTS

Demographics

There were no differences between the sex, socioeconomic status, or handedness between any of the three age groups (Table II). An ANCOVA with age as a covariate demonstrated sex differences in the total ICV (F _1,23 = 4.8, P = 0.04), however, there were no differences in ICV between the three age groups.

Data Analyses on the Pial Surface

The area ratio and average normalized depth for each lobe on the pial surface are shown in Figure 3, marked with different colors. Figure 7a plots the area ratio 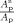and Figure 7b plots the normalized average depth 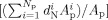for each lobe in both hemispheres for all subjects. In this study, the notations are the same as mentioned in “Materials and Methods.” Table I lists the mean value of the area ratio (columns 2 and 3) and the normalized average depth (columns 6 and 7) for all the subjects. They both show no significant intrinsic differences between the left and right hemispheres.

Figure 7.

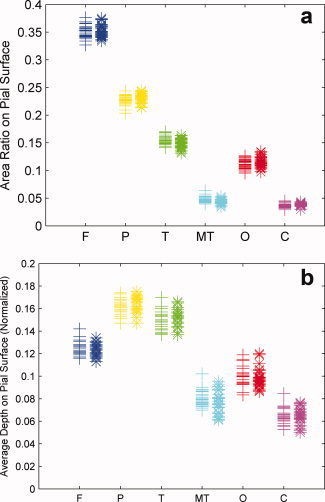
(a) Area ratio (area on the pial surface for ROI/pial surface area) of each region on both hemispheres for all subjects. Left hemisphere measurements are marked by “+,” and right hemisphere measurements are marked by “*.” (b) Normalized average depth [sum (normalized depth × area on the pial surface for ROI)/area on the pial surface for ROI] of each region on both hemispheres for all subjects. Left hemisphere measurements are marked by “+,” and right hemisphere measurements are marked by “*.” [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Data Analyses on the Outer Hull Surface

The area ratios 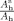for the corresponding regions of all lobes on the outer hull surface are shown in Figure 8 and Table I (columns 4 and 5). As expected, there are no significant differences between the hemispheres and the corresponding order is the same as for the pial surface. They are ordered from the largest to the smallest region: frontal lobe, parietal lobe, temporal lobe, occipital lobe, medial temporal lobe, and cingulate cortex. In Zilles et al. [ 1988], the anterior to posterior maps of human GI have also shown greater gyrification in the frontal, parietal, and temporal lobes of the brain.

Figure 8.

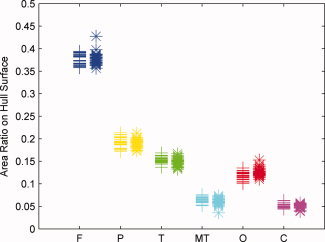
Area ratio of the corresponding region (area on the hull surface for corresponding ROI/hull surface area) for each region on both hemispheres for all subjects. Left hemisphere measurements are marked by “+,” and right hemisphere measurements are marked by “*.” [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Lateralization of Sulcal Depth and Gyrification Measures

A paired t‐test found that there was significant laterality for the maximum depth for many of the major sulci. These laterality differences are shown in Table III. As expected, the regions which demonstrate lateralizing effects are related to language regions in the temporal lobes, as well as specific sulci within the frontal and parietal lobes. Sulci that do not show lateralizing effects include areas related to primary sensory and motor functions (central sulcus and calcarine fissure). Due to these differences, lateralized measures were not pooled to assess for developmental differences in sulcal depth.

Table III.

Maximum depth (in mm) for the major sulci within each hemisphere and paired t‐test measures for differences in lateralization

Sulci	Maximum depth (left)	Maximum depth (right)	t/P
Central sulcus	29.8 (2.4)	30.1 (2.4)	n.s.
Lateral sulcus	34.1 (2.1)	33.5 (1.9)	2.5/0.02
Superior frontal	20.1 (1.6)	19.2 (2.2)	2.1/0.05
Superior temporal	22.6 (2.2)	24.8 (2.2)	−7.5/<0.0001
Middle temporal	14.2 (1.9)	15.5 (2.1)	−2.6/0.02
Intraparietal	26.0 (1.7)	26.0 (2.1)	n.s.
Transverse occipital	17.2 (1.9)	16.4 (2.3)	n.s.
Calcarine fissure	20.2 (3.2)	20.8 (3.5)	n.s.
Superior parietal	13.3 (1.7)	14.3 (1.3)	−2.9/0.008
Parieto‐occipital fissure	18.8 (2.6)	20.5 (2.6)	−2.9/0.007
Supramarginal	21.9 (2.2)	21.1 (3.6)	n.s.
Orbitofrontal	9.6 (1.3)	10.8 (1.0)	−4.7/<0.0001
Ant. ascending ramus	29.7 (2.8)	27.3 (2.2)	4.8/<0.0001
Ant. horizontal ramus	13.3 (1.7)	16.2 (3.3)	18.5/<0.0001

Specific brain regions show lateralization in function, such as language centers in the temporal lobe and visuospatial performance in the parietal lobe. In addition, hemispheric differences in gyrification have also been found in psychiatric disorders [Narr et al., 2001; Sallet et al., 2003]. The authors have tested whether differences in lateralization were also present in measures of gyrification. Paired t‐tests found no differences in either GI${}_{\text{region}}^{\text{1}}$ or GI${}_{\text{region}}^{\text{2}}$ between the left and right frontal and temporal lobes. However, there were significant laterality effects of both GI${}_{\text{region}}^{\text{1}}$ and GI${}_{\text{region}}^{\text{2}}$ in the parietal lobe (GI${}_{\text{region}}^{\text{1}}$: t = 4.8, df = 28, P < 0.0001; GI${}_{\text{region}}^{\text{2}}$: t = 2.9, df = 28, P = 0.007), the occipital lobe (GI${}_{\text{region}}^{\text{1}}$: t = 4.6, df = 28, P < 0.0001; GI${}_{\text{region}}^{\text{2}}$: t = 4.6, df = 28, P = 0.01), and the cingulate cortex (GI${}_{\text{region}}^{\text{1}}$: t = 3.3, df = 28, P = 0.004; GI${}_{\text{region}}^{\text{2}}$: t = 2.2, df = 28, P = 0.03). The parietal lobe had greater cortical complexity in the right hemisphere, whereas the occipital lobe and cingulate cortex had greater cortical complexity in the left hemisphere. In addition, laterality effects were found in the medial temporal lobes for GI${}_{\text{region}}^{\text{2}}$ (t = −2.4, df = 28, P = 0.02), with the left lobe having greater gyrification than the right. Due to these differences, gyrification measures were not pooled for the right and left hemispheres.

Developmental Differences in Sulcal Depth

There were relatively few differences in sulcal depth between the different age groups for the 15 major sulci that were evaluated. There were age‐related differences in the maximum depth of the right middle temporal sulcus (F _2,21 = 4.1, P = 0.03), right lateral sulcus (F _2,21 = 3.5, P = 0.05), and a trend for the right central sulcus (F _2,21 = 3.2, P = 0.06).

Developmental Differences in Gyrification

There were no differences in the measures of GI${}_{\text{region}}^{\text{1}}$ or GI${}_{\text{region}}^{\text{2}}$ between males and females in any of the regions of interest, thus males and females were pooled for the analyses. Age‐related differences in gyrification for both hemispheres using GI${}_{\text{region}}^{\text{1}}$ and GI${}_{\text{region}}^{\text{2}}$ analyses can be seen in Figure 9. The GI${}_{\text{region}}^{\text{1}}$ decreases with age in the left (F _2,24 = 4.6, P = 0.02) and right (F _2,24 = 4.9, P = 0.02) frontal lobe; left (F _2,24 = 4.2, P = 0.03) and right (F _2,24 = 6.8, P = 0.004) medial temporal lobe. In addition, there are trend decreases in the GI${}_{\text{region}}^{\text{1}}$ by age in the left (F _2,24 = 2.6, P = 0.09) and right parietal lobes (F _2,24 = 2.6, P = 0.09).

Figure 9.

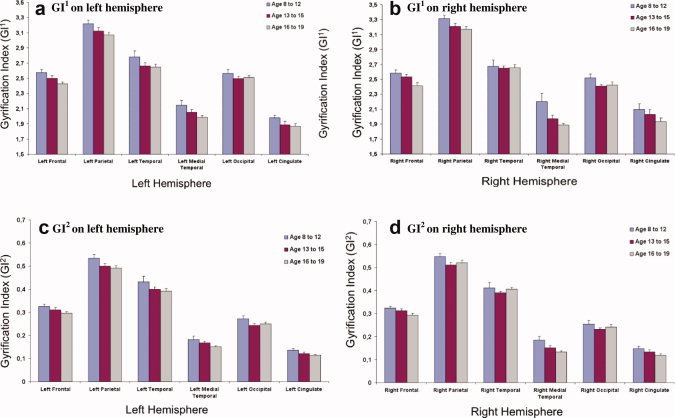
Developmental differences between gyrification indexes using both GI¹ and GI² within different brain regions for the left and right hemispheres. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Fewer age‐related differences were found using the gyrification measure that accounts for regional differences in sulcal depth (GI${}_{\text{region}}^{\text{2}}$). Age‐related differences were found in the left (F _2,24 = 4.1, P = 0.03) and right (F _2,24 = 6.5, P = 0.006) medial temporal lobe. In addition, trend differences were found in the left (F _2,24 = 3.1, P = 0.07) and right (F _2,24 = 2.8, P = 0.08) cingulate, left parietal lobe (F _2,24 = 2.7, P = 0.09), and the left (F _2,24 = 2.5, P = 0.10) and right (F _2,24 = 3.3, P = 0.06) frontal lobes.

Notice that the right and left cingulate cortex provides information on a more local measure of the approach due to its smaller pial surface area. Using this region, the GI${}_{\text{region}}^{\text{2}}$ measure demonstrates a smaller standard deviation within each of the age regions (see Figures 9a,b) for GI${}_{\text{region}}^{\text{1}}$ and Figures 9c,d for GI${}_{\text{region}}^{\text{2}}$). GI${}_{\text{region}}^{\text{2}}$ provides additional information to understand the nature of gyrification, however, we believe that it is additive information above GI‐1, rather than a stand‐alone approach. It may prove stronger in finding differences in clinical populations.

Comparison with Existing Techniques

In comparison with the recently proposed 3D GI measurements [Schaer et al., 2008; Toro et al., 2008], the proposed GI computation method is parameter‐free and defines the regional 3D GI directly on the pial surface. In the study by Schaer et al. [ 2008], the localized GI was determined for each point on the outer hull surface by quantifying the ratio of area containing in the pial surface and outer hull surface within a specified sphere. This index is then used to define the localized GI for each point on the pial surface via a weighted contribution of localized GI of the surrounding points on the outer hull surface. The weight is related to the distance between the vertex point on the pial surface and the involved vertex points on the outer hull surface. There are several possible disadvantages to this method: first, the outer hull surface is generated from the pial surface, and strictly speaking, there is no GI on the outer hull surface. Secondly, the extrinsic distance they use in the weighting is along the normal axis of the vertex to the outer hull surface, while the intrinsic distance is the computed geodesic depth [Kao et al., 2007], which is a more natural technique in defining the GI. In addition, after Schaer et al. [ 2008) extracted the perimeter on the ROI on the outer hull surface, they project this perimeter to the pial surface by taking the nearest point on the pial surface, whereas the correspondence relies once again on the natural geodesic depth direction. Finally, the results from a spherical mask [Schaer et al., 2008; Toro et al., 2008] will depend on the radius used. Smaller spheres will have greater variability secondary to anatomical differences, whereas larger spheres will not provide a localized measure of gyrification and will cross boundaries into alternate regions. Nevertheless, the approaches by Schaer et al. [ 2008] and Toro et al. [ 2008] are significant improvements over the previous 2D GI.

To compare the proposed technique with the localized GI proposed by Schaer et al. [ 2008] experimentally, the authors calculated localized GI values at different radii and averaged these values into the six defined brain regions. It turns out that localized GI is quite sensitive to the selection of the radius of the sphere. (Radii of 20, 25, 30, and 35 mm are tested.) With radii of less than 20 mm, not all data could be processed using Freesurfer with a resultant loss in the degrees of freedom. Table IV lists the one‐way ANOVA results for radius of 20, 25, 30, and 35 mm respectively.

Table IV.

Results from the one‐way ANOVAs that show developmental differences with the approach by Schaer et al. (2008) using different radii (mm) within different regions

Brain region	LGI r = 20		LGI r = 25		LGI r = 30		LGI r = 35
	Left F 2,23/P	Right F 2,22/P	Left F 2,24/P	Right F 2,24/P	Left F 2,24/P	Right F 2,24/P	Left F 2,24/P	Right F 2,24/P
Frontal	5.7/0.01	3.1/0.07	2.7/0.09	2.5/0.10	3.4/0.05	2.9/0.07	3.7/0.04	3.0/0.07
Parietal	9.1/0.001	5.2/0.01	7.7/0.003	3.0/0.07	6.1/0.007	4.4/0.02	6.3/0.006	4/0.03
Temporal	5.1/0.01	4.5/0.02	3.2/0.06	2.5/0.10	2.6/0.10	3.4/0.05	1.9/0.2	3.3/0.06
Medial temporal	0.4/0.7	4.5/0.02	0.3/0.7	1.6/0.2	0.5/0.6	1.5/0.2	0.3/0.8	1.1/0.3
Occipital	2.2/0.1	1.5/0.3	2.5/0.1	1.5/0.2	2.9/0.07	1.2/0.3	2.7/0.09	2.1/0.1
Cingulate	5.8/0.009	3.7/0.04	4.7/0.02	4.6/0.02	4.3/0.03	5.6/0.01	4.6/0.02	4.3/0.03

Note that there is instability in the significance levels dependent on the chosen radius

To illustrate this strong radii dependency, the authors ran a one‐way ANOVA test (Table V) to show the sensitivity. From Table V, the authors can observe significant differences between radii in the frontal, parietal, and temporal lobes in both hemispheres for the three age groups. More variability appeared when the authors ran analyses using gender as a covariate. The anatomically based measures of GI${}_{\text{region}}^{\text{1}}$ and GI${}_{\text{region}}^{\text{2}}$ are more stable. To have a more complete idea of the effects of the localized GI, the authors did a four‐radius by three‐age‐group by two‐region ANOVA test, which showed that there were significant effects due to radius (F _3,1271 = 44.61, P < 0.0001) and age group (F _2,1271 = 19.03, P < 0.0001), but no significant effects due to region (F _1,1271 = 1.11, P = 0.29).

Table V.

One‐way ANOVAs evaluating main effects of radius (r = 20, 25, 30, and 35 mm) within each age group in each region

Brain region	8–12 years		13–15 years		16–19 years
	Left F 3,20/P	Right F 3,20/P	Left F 3,35/P	Right F 3,35/P	Left F 3,40/P	Right F 3,39/P
Frontal	9.1/<0.001	11.5/<0.001	7.7/0.0004	8.1/0.0003	6.5/0.001	10.9/<0.001
Parietal	11.3/<0.001	6.4/0.003	5.8/0.002	10.0/<0.001	6.5/0.001	11.8/<0.001
Temporal	6.6/0.003	9.3/<0.001	6.9/0.001	9.96/<0.001	7.4/0.0005	19.8/<0.001
Medial Temporal	0.06/0.98	0.3/0.8	0.23/0.9	1.6/0.2	0.3/0.8	0.2/0.9
Occipital	1.8/0.2	1.0/0.4	0.13/0.9	2.1/0.1	0.49/0.7	0.5/0.7
Cingulate	1.5/0.3	0.76/0.5	0.98/0.4	1.3/0.3	2.3/0.1	2.1/0.1

Note that the effect of the choice of radius using the approach Schaer et al. (2008) is highly significant for most cortical regions. This shows that this approach to measure GI is less stable.

DISCUSSION

The authors utilized a novel GI computational technique to demonstrate developmental differences in gyrification in a cohort of typically developing children and adolescents. The proposed computational method used intrinsic 3D measurement to find GIs for a ROI. It is thus able to identify regional alterations in brain surface complexity. The regions are defined by the cortical lobes, although this method could also be applied to smaller cortical regions. Unlike the method introduced by Schaer et al. [ 2008], the proposed method makes use of specific anatomical regions rather than a set spherical region. While this may have the disadvantage of obtaining point‐by‐point gyrification measures, the variability in point‐by‐point measures resulting from structural variability between brains will be lessened by an atomically based approach.

The application of the proposed 3D GI results show that there is continued molding of the surface morphology of the brain through childhood and adolescence. This same time period has been shown to be associated with a decrease in surface GM and an associated increase in the surface cerebral spinal fluid [Giedd et al., 1999; Sowell et al., 2004]. It is not surprising that decreases in the underlying volume of GM would result in an associated decrease in cortical complexity, as has been demonstrated in typically developing adults [Magnotta et al., 1999]. The developmental differences in GI are localized to the later maturing structures, including the frontal and medial temporal lobes [Huttenlocher, 1982, 1990]. Regions that develop earlier, such as the occipital, parietal, and lateral temporal lobes, do not demonstrate the same level of developmental differences as the frontal and medial temporal regions [Huttenlocher and Courten, 1987].

The brain has reached its peak volume by 8 years of age and thus it is not surprising that there are not striking developmental differences in the depths of the major sulci. Indeed, the primary sulci are the first to develop and are associated with a greater heritability [Lohmann et al., 1999]. The secondary and tertiary sulci develop later, and are more linked to environmental factors. However, most of the primary and secondary sulci form during the third trimester of fetal life [Welker, 1990] and it is likely that restructuring and depth of the major sulci, including laterality differences, are fairly stable by 8 years of age. Future studies mapping the development of the sulci, gyri, and GI between birth and 8 years of age will be beneficial to assess alterations of these measures as language and other cognitive processes mature.

There are limitations to the current study. The authors had a relatively small sample size to evaluate for developmental differences. However, the fact that significant findings were present and were consistent across measures may reflect a relatively robust measure to assess developmental differences.

CONCLUDING REMARKS AND DISCUSSION

The proposed 3D geometric approach for defining the global and regional gyrification indices naturally extends the standard approach of defining the coronal 2D GI. In addition, the approach utilizes the intrinsic 3D nature of human cortical surface. Classifying the cortical surface into six different regions and defining a simple regional GI on each region as the area ratio of corresponding surfaces helps us to more carefully characterize the cortical complexity in each region and provides a better method to understand the effect of each region in brain functioning. Furthermore, applying the method in a developmental study, the proposed measurement of depth‐weighted regional gyrification turns out to be more robust in finding the developmental differences in children and adolescents, e.g., the authors observe significantly increased gyrification in the right parietal lobe and right cingulate cortex, as well as age‐rated differences in the left frontal, right parietal, and the right cingulate cortex. These findings provide references for future study of the relationship between gyrification and neurological and psychiatric conditions, in addition to the development of other more advanced techniques to quantify the gyrification of the human brain.

Since there is not one universally accepted definition for computational GI, and this is a relatively new and ongoing research area, the authors conclude this discussion with some possible alternatives that deserve further study.

From a statistical point of view, the 3D regional GI GI${}_{\text{region}}^{\text{2}}$ is essentially an estimation of the first moment of the area. This motivates the authors to consider higher order moments. For instance, a second central moment estimator:

where

is the average depth in the selected region and, evaluates the variance of the area distribution and the third central moment estimator will then help in evaluating the skewness of the area distribution.

The GI measurement does not necessarily need to be a scalar value, so one can also consider a vectorized GI measurement. For any selected region R _p on the pial surface and the corresponding region R _h on the outer hull surface, one can define (for example)

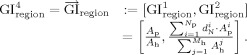With this expression, the authors can evaluate the local sulci information considering both the area ratio and the average depth of the selected region, narrowing the similarity between different regions and providing more information for analyzing the brain complexity.

In summary, the authors have reported a novel approach to measuring 3D gyrification of the human brain and have applied this measure to evaluate age‐related differences in typically developing adolescents. Developmental differences in gyrification were readily detected between childhood and young adulthood (Figure 9) as well as different trajectories between the different brain lobes. Future studies are needed that evaluating longitudinal assessments of gyrification may provide greater resolution of the age related changes. In addition, test–retest studies of individuals who are learning a specific task (i.e., playing a musical instrument) would be beneficial to determine if specific regions change with practice. It is possible that measures of GI are more sensitive to subtle changes in GM when compared with volume measures.

The use of lobar regions of interest that the authors applied can reduce the noise inherent in the structural variability when compared with the techniques which utilize voxel‐based moving‐average measures. Nevertheless, a “gold standard” measure for GI does not currently exist and a study performing a “head‐to‐head” assessment of the different approaches for measuring GI would be beneficial. The findings suggest that brain gyrification continues to change from childhood through young adulthood.