Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2010 Dec 14;32(1):80–93. doi: 10.1002/hbm.21000

A phase synchrony measure for quantifying dynamic functional integration in the brain

Selin Aviyente 1,✉, Edward M Bernat 2, Westley S Evans 1, Scott R Sponheim 3,4
PMCID: PMC6870375  PMID: 20336687

Abstract

The temporal coordination of neural activity within structural networks of the brain has been posited as a basis for cognition. Changes in the frequency and similarity of oscillating electrical potentials emitted by neuronal populations may reflect the means by which networks of the brain carry out functions critical for adaptive behavior. A computation of the phase relationship between signals recorded from separable brain regions is a method for characterizing the temporal interactions of neuronal populations. Recently, different phase estimation methods for quantifying the time‐varying and frequency‐dependent nature of neural synchronization have been proposed. The most common method for measuring the synchronization of signals through phase computations uses complex wavelet transforms of neural signals to estimate their instantaneous phase difference and locking. In this article, we extend this idea by introducing a new time‐varying phase synchrony measure based on Cohen's class of time–frequency distributions. This index offers improvements over existing synchrony measures by characterizing the similarity of signals from separable brain regions with uniformly high resolution across time and frequency. The proposed measure is applied to both synthesized signals and electroencephalography data to test its effectiveness in estimating phase changes and quantifying neural synchrony in the brain. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.

Keywords: EEG, phase, synchronization, time–frequency

INTRODUCTION

Quantifying neural coordination in the brain is a fundamental problem of neuroscience [Ansari‐Asl et al., 2005; Klein et al., 2006; Lachaux et al., 2002; Le Van Quyen et al., 2001; Sun et al., 2003; Varela et al., 2001]. The brain's cognitive functions are likely based on the coordinated interactions of neuronal sources that are distributed across specialized brain areas. Presumably, integration of neural activity across brain regions occurs at various spatial and temporal scales. The spatial and temporal scaling of neuronal interactions may well be dynamically adjusted to support adaptive behavior of an organism. Recent research provides evidence that neural integration plays an important role in a wide range of cognitive and executive processes, such as memory and attention, that are impaired in pathological brain states [Uhlhaas and Singer, 2006; Uhlhaas et al., 2006]. For example, current theories of schizophrenia emphasize that core aspects of the pathophysiology are due to deficits in the coordination of distributed processes that involve multiple cortical areas, rather than specific brain areas or neurotransmitter systems [Spencer et al., 2003, 2004; Uhlhaas et al., 2006]. Similarly, epilepsy, Alzheimer's disease and Parkinson's disease have been characterized in terms of abnormalities in neural integration across the brain [Brown, 2003; Netoff and Schiff, 2002; Stam et al., 2005]. Therefore, to characterize adaptive and pathological elements of neuronal synchrony, there is a growing need to quantify the interactions of brain regions during adaptive functioning of the organism.

Any mechanism for neural integration must involve interactions between functionally relevant local networks. The nature of such interactions remains a point of debate. It has been recently argued that networks of reciprocal interactions are key to integration [Varela et al., 2001]. Among various modes of reciprocal interactions, phase synchronization between the participating neuronal groups has been the most studied mechanism. To examine functional integration in the temporal frame in which the brain completes processes, there is a need to characterize the temporal dynamics of neural networks with millisecond accuracy [Friston, 2000]. Neuroimaging techniques with high temporal resolution, such as the electroencephalogram [Ansari‐Asl et al., 2005] and magnetoencephalogram (MEG), are the most appropriate tools for examining the dynamic interactions of neural networks.

Studies of visual binding provide direct evidence supporting phase synchrony as a basic mechanism for brain integration [Roskies, 1999] and suggest that visual objects are coded by cell assemblies that synchronously fire. Although visual binding refers to the “local” integration within neighboring cortical areas, synchronization of neural assemblies may span multiple spatial and temporal scales in the nervous system, ranging from local integration to large‐scale integration. Recent research provides evidence for the existence and significance of large‐scale synchronization. In the article by Rodriguez et al. [ 1999], for example, a consistent pattern of gamma frequency synchrony among occipital, parietal, and frontal areas during face recognition was shown. Similarly, others have observed increased beta and gamma range synchrony between auditory and visual regions of the brain during perception and increased synchrony between prefrontal and posterior association areas in the theta band during a working memory task [Sarnthein et al., 1998]. These findings point to the significance of large‐scale synchrony in the human brain during cognition and perception and provide evidence for synchrony within several frequency bands as well as across frequency bands [Palva et al., 2005]. In this article, we present an index of phase synchrony for quantifying large‐scale synchronization that affords consistently high resolution across time and frequency bands as reflected in electroencephalography (EEG) recordings.

Types of indices used for quantifying large‐scale synchrony can be broadly categorized into linear and nonlinear measures [Pereda et al., 2005]. Linear correlation measures include temporal correlation, spectral coherence, directed transfer function [Kaminski and Blinowska, 1991], partial directed coherence [Baccalá and Sameshima, 2001], and Granger causality [Granger, 1969; Kaminski et al., 2001], and attempt to quantify the degree of synchronization. These methods are closely related to each other and rely on a multivariate autoregressive model for describing the dynamics of multichannel EEG signals. The magnitude of the transfer function between different channels quantifies the connectivity between the different cortical sites. These measures have limitations for the following reasons. First of all, they rely on parametric modeling of EEG signals and thus suffer from some of the common problems with parametric models such as determination of the order and robustness of the parameters to perturbations. Second, they assume stationarity of the underlying signals by defining the transfer function solely in the frequency domain and the linearity of the interactions between different channels. This linearity assumption restricts the types of interactions that can be quantified to amplitude effects and does not allow the separation of the effects of amplitude and phase.

Nonlinear correlation measures, on the other hand, attempt to address this limitation of linear measures by quantifying temporal correlation through measures of phase synchrony [Damasio, 1990; Friston et al., 1997; Rosenblum et al., 1996; Tononi and Edelman, 1998; Varela, 1995; Varela et al., 2001] and generalized synchronization measures, including information theoretic measures [Breakspear, 2002; Breakspear and Terry, 2002; Chávez et al., 2003; Hinrichs et al., 2006; Stam, 2005]. A desirable phase synchrony measure should be able to separate the phase and amplitude effects from each other and take the nonstationary nature of brain activity into account. Two different measures for quantifying time‐varying phase synchrony have been proposed to address these issues. The first method uses the Hilbert transform of the signal to get an analytic form of the signal and estimates instantaneous phase directly from its analytic form [Tass et al., 1998]. To estimate the instantaneous phase of a signal from its analytic form, one has to ensure that the signal is composed of a narrowband of frequencies. Thus, the Hilbert transform method of computing phase synchrony requires first bandpass filtering of the signal around a frequency of interest and then applying the Hilbert transform to obtain the instantaneous phase. This is an indirect way of deriving the frequency‐dependent phase estimates and is prone to error especially in the case of noisy signals as noise tends to be wideband. The second approach computes a time‐varying complex energy spectrum using either the continuous wavelet transform with a complex Morlet wavelet [Lachaux et al., 2002] or the short‐time Fourier transform (STFT) [Li and Jung, 2000]. It has been observed that the two approaches are similar in their results with the time‐varying spectrum‐based methods giving higher resolution phase synchrony estimates over time and frequency, especially at the low frequency range [Le Van Quyen et al., 2001]. Although the wavelet‐ and STFT‐based phase synchrony estimates address the issue of nonstationarity, they suffer from a number of drawbacks. In the case of the wavelet transform, the nonuniform resolution across time and frequency results in biased energy representations and corresponding phase estimates. In the case of STFT, there is a tradeoff between time and frequency resolution because of the window function. For these reasons, there is a need for high time–frequency resolution phase distributions that can better track dynamic changes in the synchrony of neural signals.

In this article, we propose an enhanced characterization of neural synchrony using a new nonlinear phase estimation method based on bilinear time–frequency distributions (TFDs). This phase synchrony measure extends the current complex Morlet wavelet‐based phase synchrony measure, which will be referred to as the wavelet time–frequency phase synchrony (wavelet‐TFPS), by using a high‐resolution complex TFD. The proposed measure is based on a reduced interference Rihaczek (RID‐Rihaczek) distribution and will be referred to as RID‐TFPS.

It is important to note some current methodological issues with applying phase synchrony measures to EEG recordings. Perhaps, the most important one is volume conduction, which refers to activity that may come from a single source but is observed at multiple scalp electrodes. This problem is especially important in phase synchrony measures because data recorded from nearby electrodes are very likely to pick up activity from a common source causing spurious correlation between the electrodes. Synchrony measures could thus be artificially inflated to the degree of the volume conduction. Similarly, the bipolar recording channels used in EEG studies can introduce artifactual synchrony between electrodes as they share a common reference electrode [Guevara et al., 2005]. Several methods have been suggested for addressing the problem of volume conduction and bipolar recording channels, including source reconstruction and Laplacian filtering to deemphasize the effects of the common source [Lachaux et al., 1999; Nunez and Srinivasan, 2006; Nunez et al., 1997]. Measures such as phase lag index (PLI) have also been introduced to address volume conduction through isolating information in the correlation structure that is unlikely to be explained by common sources [Stam et al., 2007]. In this article, we do not aim to directly address or overcome such limitations. Instead, the focus is on introducing new time‐varying phase synchrony estimates that are of uniform resolution across the time–frequency spectrum, while acknowledging that such estimates are not immune to the effects of volume conduction.

MATERIALS AND METHODS

Simulated Data

To test the validity and evaluate the performance of the proposed phase synchrony measure, we generated three different simulations. In the following simulations, the frequency parameters of the signals were defined in terms of the normalized frequency [0,1], where 1 corresponds to half of the sampling frequency.

Example 1: Time‐varying phase tracking

The first simulation tested the performance of the proposed measure in tracking time‐varying phase differences. We considered two complex exponential signals with a time‐varying phase difference, x 1(t) = exp(jω1 t) and x 2(t) = exp(jω1(t−at 2)), where ω1 = 8π, a = 0.25 for the time range 0–1 s. The parameters ω1 and a were chosen such that the maximum phase difference between the two signals is less than or equal to 2π to prevent any ambiguity about the phase. The instantaneous phase difference at the frequency of interest, ω, was computed using the Rihaczek‐based phase estimation method and was compared to the theoretical phase difference, ω1 at 2.

Example 2: Comparison of the RID‐TFPS and the wavelet‐TFPS measures for linear chirp signal

In the second simulation example, we compared the performance of the RID‐TFPS measure to the wavelet‐TFPS measure for signals with time‐varying frequency content. The goal of this example was to illustrate how the two methods differ in the way they track phase synchrony across time and a range of frequencies. For this purpose, we considered two linear chirp signals with constant phase difference, that is, x 1(t) = exp(j(ω0 t + βt 2)) and x 2(t) = exp(j(ω0 t + βt 2 + θ)), where ω0 = 0.1, β = 0.001 in terms of the normalized frequency for 128 time samples. The parameters ω0 and β were chosen such that the signal covers a broad range of frequencies, that is, it is not narrowband, and that there is no aliasing in frequency. We considered 100 simulations of this signal model with uniformly distributed random phase difference θ ∈ [0,2π] and additive white Gaussian noise at a signal‐to‐noise ratio (SNR) of 14 dB.

Example 3: Performance of the RID‐TFPS and the wavelet‐TFPS measures in noise

In the third example, we evaluated the robustness of the RID‐TFPS measure in noise and compared it to the performance of the wavelet‐TFPS measure. To evaluate the robustness in noise, we considered two signal models: high synchrony and low synchrony signals in noise. In the first model, we considered two sinusoids with a constant phase difference in noise, x 1(t) = sin(16πt) + n 1(t), x 2(t) = sin(16πt + π/4) + n 2(t), where n 1(t) and n 2(t) are independent white Gaussian noise processes at different variance levels, with SNR varying in the range of −12 to 17 dB. In the second model, a pair of low synchrony signals was considered, that is, x 1(t) = sin(16πt) + n 1(t), x 2(t) = n 2(t) with n 1(t) and n 2(t) being independent white Gaussian noise processes in the same SNR range as above. For both models, we considered 200 simulations of 200 trials of the two signal models to evaluate the distribution of the synchrony values.

Biological Data: Error‐Related Negativity

To evaluate the proposed phase synchrony measure with biological data, the measure was applied to a set of EEG/ERP data containing the error‐related negativity (ERN also referred to as the error negativity Ne [Falkenstein et al., 1991; Gehring et al., 1993]). The ERN is a brain potential response that occurs following performance errors in a speeded reaction time task. The ERN has been characterized as a neurophysiological index of endogenous action monitoring the automatic capacity to monitor behavioral performance on‐line and to initiate corrective action as needed, either through detection of errors [Gehring et al., 1995] or detection of conflict among competing neural response pathways [Carter et al., 1998]. Evidence indicates that the primary neural generator of the ERN is the anterior cingulate cortex [Baccalá and Sameshima, 2001], and that it is maximal over midline‐frontal scalp sites (e.g., FCz) when recorded with EEG/ERP [Bush et al., 2000; Dehaene et al., 1994; Holroyd et al., 1998]. In terms of time–frequency representations, the ERN is known to involve increases in the theta range (3–7 Hz) for both amplitude (e.g., [Gehring and Willoughby, 2004; Hall et al., 2007]) and intertrial phase synchrony (e.g., [Trujillo and Allen, 2007]). Importantly for the current purposes, the ACC is understood to be coordinated with other brain regions involved in cognitive control processes [Holroyd and Coles, 2002; Miller and Cohen, 2001], for example, lateral prefrontal cortex and the primary motor areas. The ultimate utility of applying measures of phase synchrony to the ERN is in creating measures of how these regions coordinate and communicate to produce response modulation. The current application, however, is intended to evaluate the quality of the newly developed phase synchrony measure, rather than to make definitive statements about interactions among regions during the ERN.

The primary details of the task and data collection are given briefly here (see previous article for further detail [Hall et al., 2007]). EEG data from 62 channels were collected from 92 undergraduate students (34 male) from the University of Minnesota. Recordings were done in accordance with the 10/20 system on a Neuroscan Synamps2 system (Neuroscan). A speeded response flanker task was used, and error and correct response‐locked averages were computed for each subject. These averages served as the experimental data to which the new method was applied.

Cohen's Class of TFDs

Cohen's class of distributions are bilinear TFDs that are expressed as1 [Cohen, 1995]:

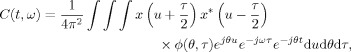equation image (1)

where the function ϕ(θ,τ) is the kernel function and x is the signal. TFDs represent the energy distribution of a signal over time and frequency, simultaneously. The kernel function completely determines the properties of its corresponding TFD. Some of the most desired properties of TFDs are the energy preservation, satisfying the marginals, and the reduced interference. Energy preservation and satisfying the marginals imply that the following equalities hold

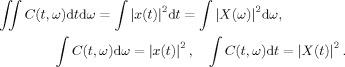equation image (2)

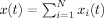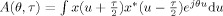For bilinear time–frequency energy distributions, crossterms or interference occur when the signal is multicomponent, that is, if Inline graphic then Inline graphic, where c  x i,x i and c  x i,x j refer to the autoterms and crossterms, respectively. The crossterms introduce time–frequency structures that do not correspond to the time–frequency spectrum of the actual signal. In the case of real life signals, such as the EEG, where the individual components may not be disjoint in the time–frequency plane, the crossterms will contaminate the spectrum of the autoterms directly. For this reason, there is a need for filtering out the crossterms using an appropriate kernel function. Any TFD given by Eq. (1) can be equivalently written as follows:

equation image (3)

where Inline graphic is the ambiguity function of the signal. This alternative representation of TFD is equivalent to multiplying the signal's autocorrelation function (ambiguity function) with a filter (kernel function) and then transforming it back to the time–frequency plane. As the ambiguity function tends to group the autoterms close to the θ–τ axis, the kernel function is usually designed as a lowpass filter. In this article, we will use reduced interference distributions (RIDs) to address the problem of crossterms, with |ϕ(θ,τ)| ≪ 1 for |θτ| ≫ 0, to concentrate the energy around the autoterms [Jeong and Williams, 1992].

The major differences between Cohen's class of TFDs compared to other time–frequency representations such as the wavelet transform are the nonlinearity of the distribution, energy preservation, and the uniform resolution over time and frequency. The wavelet transform provides a representation over time and scale where the frequency resolution is high at low frequencies and low at high frequencies. Although this property makes wavelet transform attractive in detecting high‐frequency transients in a given signal, it inherently imposes a nonuniform time–frequency tiling on the analyzed signal and thus results in biased energy representations. Cohen's class of bilinear TFDs on the other hand assumes uniform resolution over the entire time–frequency plane.

Most of the members of Cohen's class are real‐valued energy distributions such as the spectrogram and the Wigner distribution. These distributions are successful at describing the energy of the signal over time and frequency, simultaneously. However, they do not carry any information about the phase of the signal. For this reason, they cannot be directly used for describing the phase information in an individual signal and estimating the phase synchrony between two signals. Therefore, there is a need for high‐resolution complex‐valued TFDs that carry both the energy and the phase information of the underlying signals.

Rihaczek Distribution

Rihaczek derived the signal energy distribution in time and frequency by application of the complex signal notation. If we consider two complex signals at the same frequency, x 1(t) and x 2(t), where x 1(t) may be interpreted as the voltage and x 2(t) as the current generated in an impedance, the total complex energy is defined as ∫x 1(t)x  2*(t)dt. Rihaczek extended this idea for computing the interaction energy of a signal within some frequency band centered at a frequency of interest with the signal itself at a given time restricted to an infinitesimal time interval. This extension leads to the time–frequency energy density function, which is expressed as [Rihaczek, 1968]:

equation image (4)

and which measures the complex energy of a signal around time t and frequency ω. The complex energy density function provides a fuller appreciation of the properties of phase‐modulated signals that is not available with other TFDs. For example, with the short‐time Fourier transform or the wavelet transform, the time–frequency resolution is determined by the waveforms used to expand the signal. In the case of the STFT, the time–frequency resolution is uniform with the resolution being determined by the length of the window. For the Rihaczek distribution, on the other hand, the time–frequency resolution is determined by the rate of change of the instantaneous frequency, which provides better localization for phase‐modulated signals.

Like other members of Cohen's class of distributions, the Rihaczek distribution can also be shown to be a bilinear, time and frequency shift covariant TFD that satisfies the marginals, preserves the energy of the signal with strong time and frequency support properties, that is, the distribution is only nonzero when both the signal itself and its Fourier spectrum are nonzero. With these properties, the Rihaczek distribution provides both a time‐varying energy spectrum and a phase spectrum and offers good time–frequency localization for phase‐modulated signals, and thus is an appropriate choice for estimating the phase synchrony between EEG signals.

Reduced interference Rihaczek distribution

One of the disadvantages of the Rihaczek distribution is the existence of crossterms for multicomponent signals. For any signal, x(t) = x 1(t) + x 2(t), the Rihaczek distribution is as follows:

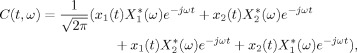equation image (5)

where the last two terms in the above expression are the crossterms. These crossterms are located at the same time and frequency locations as the original signals and will lead to biased energy and phase estimates.

To get rid of these crossterms, in this article, we propose a reduced interference version of the Rihaczek distribution by applying a kernel function such as the Choi‐Williams (CW) kernel with 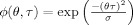Inline graphic to filter the crossterms in the ambiguity domain. Different kernel functions such as the Born‐Jordan kernel, binomial kernel can be used to address the issue of crossterms with similar results [Cohen, 1995]. The resulting distribution can be written in terms of the product of the CW kernel and the kernel for the Rihaczek distribution as follows:

equation image (6)

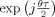where Inline graphic is the kernel function for the Rihaczek distribution, which can be obtained from the ratio 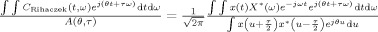Inline graphic, using Eq. (3) and the definition of the Rihaczek distribution. This new distribution, which will be referred to as RID‐Rihaczek distribution, still satisfies the marginals and preserves the energy and is a complex energy distribution at the same time. The value of σ can be adjusted to achieve a desired trade‐off between resolution and the amount of crossterms retained. Figure 1 illustrates the magnitudes of the original and the RID‐Rihaczek distributions for the sum of two signals to show the effect of filtering. In this article, the RID‐Rihaczek distribution will be used to define the phase synchrony between signals.

Figure 1.

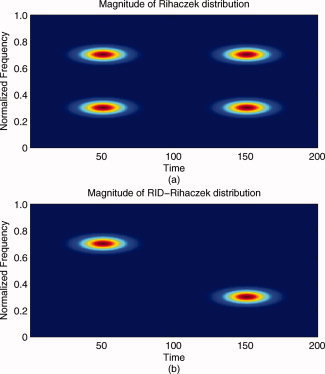
Figure 1

Open in a new tab

(a) Magnitude of Rihaczek distribution and (b) magnitude of RID‐Rihaczek distribution for the sum of two gabor logon signals, 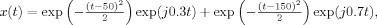Inline graphic computed with a Choi‐Williams kernel, 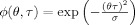Inline graphic, where σ = 0.001. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Time‐Varying Phase Spectrum and Phase Synchrony

Synchrony measures the relation between the temporal structures of the signals regardless of signal amplitude. Two signals are said to be synchronous if their rhythms coincide. The amount of synchrony between two signals is usually quantified by estimating the instantaneous phase of the individual signals around the frequency of interest. As mentioned earlier, the two main current approaches for isolating the instantaneous phase of the signal are Hilbert transform and complex wavelet transform. In the Hilbert transform method, the signal is first bandpass filtered around the frequency of interest and then the instantaneous phase is estimated from the analytic form of the signal. In the wavelet transform approach, the phase of the signal is extracted from the coefficients of the wavelet transform at the target frequency, which is basically equivalent to estimate the instantaneous spectrum around a frequency of interest. In both methods, the goal is to obtain an expression for the signal in terms of its instantaneous amplitude, a(t), and phase, ϕ(t), at the frequency of interest as follows:

equation image (7)

This formulation can be repeated for different frequencies, and the relationships between the temporal organization of two signals, x and y, can be observed by their instantaneous phase difference:

equation image (8)

where n and m are integers that indicate the ratios of possible frequency locking. Most studies focus on the case n = m = 1, that is, look at phase synchrony at a particular frequency of interest.

In neuroscience, the focus is on the case when the phase difference is bounded over a limited time window, that is, the weak locking condition [Rosenblum et al., 1996]. This is defined as a period of phase locking between two events and is an indicator of the dynamic phase relationship between two oscillatory neuronal sources independent of their amplitude.

After defining a high resolution, complex TFD, one can easily estimate the phase in the time–frequency plane. The time‐varying phase estimate is defined as follows:

equation image (9)

where C(t,ω) is the RID‐Rihaczek distribution given by Eq. (6). For the particular case of the Rihaczek distribution, where there is no smoothing, this expression simplifies to ϕ(t) − θ(ω) − ωt, where ϕ(t) and θ(ω) refer to the phase in the time and the frequency domains, respectively.

Once the time‐varying phase spectrum is defined, the phase difference between two signals, x 1(t) and x 2(t), can be computed as follows:

equation image (10)

For the actual Rihaczek distribution, this expression will reduce to (ϕ1(t − ϕ2(t)) + (θ2(ω) − (θ1(ω)), that is, the sum of the differences between the phases in the time and frequency domains.

It can be shown that for the Rihaczek distribution of a real‐valued signal, the phase between a signal x 1(t) and its shifted version x 1 (t − t 0) is given by:

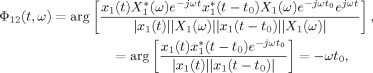equation image (11)

which is a linear function of frequency as expected.2 Similar expressions can be obtained for the RID‐Rihaczek distribution with the phase difference estimate being smoothed by the kernel function.

In most applications, the time‐varying phase spectrum is not directly useful for measuring the synchrony between the signals. To further quantify the synchrony between signals, we need to define a measure of phase synchrony based on the time‐varying phase spectrum estimate introduced above. In previous work, phase synchrony measures have been applied to measure both the intertrial phase synchrony and phase synchrony across electrodes. Although intertrial phase synchrony is effective at quantifying stimulus‐related synchronization [Tallon‐Baudry and Bertrand, 1999], in this article our focus will be on synchronization across electrodes to quantify functional integration. Similar to the definition given in [Lachaux et al., 2002], one can obtain the phase locking value (PLV). PLV is defined between two signals and is averaged over all realizations/trials. It measures the intertrial variability of the phase difference at time t and frequency ω and can quantify the consistency of response‐locked phase differences across trials as follows:

equation image (12)

where N is the number of trials and ϕ 12k(t,ω) is the time‐varying phase estimate between two electrodes for the kth trial. If the phase difference varies little across the trials, PLV is close to 1. In this article, we will use PLV based on the RID‐Rihaczek distribution to quantify the synchrony between electrode pairs and will refer to this measure as the RID‐TFPS measure or simply as PLV, interchangeably.

Phase synchrony measures represent the actual phase difference between two signals for a defined time and frequency. To more accurately measure transient changes in phase synchrony (instead of constant synchrony), we baseline correct the time–frequency phase‐synchrony values. For baseline correction, the average phase synchrony at each frequency for the prestimulus time range is subtracted from the poststimulus phase synchrony, as follows:

equation image (13)

Statistics of the Time–Frequency Phase Synchrony Measure

RID‐TFPS provides an estimate of the synchrony between two ensembles of signals for any time–frequency bin. Given a PLV, the natural question is whether the two signals are independent or not. For real data with limited numbers of trials, nonzero synchrony values can arise between independent signals by chance alone. Bias and variance of the RID‐TFPS for independent white signals would provide measures of how the synchrony value is affected by the number of trials as well as give an indication of the range of synchrony values for independent signals. A more detailed analysis of the performance of the RID‐TFPS as a phase synchrony estimator would require the computation of Cramer‐Rao lower bound, which is beyond the focus of this article.

In this article, the bias and variance of the RID‐TFPS are determined based on simulations with white noise time series as it is not possible to find an analytic expression for these quantities. Similar to the approach outlined in [Lachaux et al., 2002] for the wavelet‐TFPS, we generate independent white noise sequences, with length 64, and compute the bias and variance for different number of trials, N. We have observed that the bias and the variance are independent of the time and frequency bin as the RID‐Rihaczek distribution provides uniform resolution in the time–frequency plane. The mean and the range of RID‐TFPS values over a range of N are shown in Figure 2a. It can be seen that the bias and variance go to zero as N → ∞.

Figure 2.

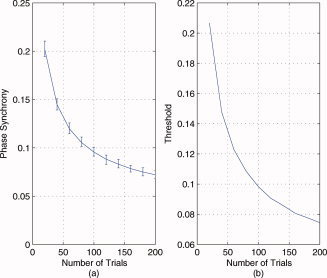
Figure 2

Open in a new tab

Statistical evaluation of the RID‐TFPS measure: (a) The bias and the range (minimum to maximum) of RID‐TFPS measure for 200 simulations of 200 white noise pairs as a function of the number of trials. (b) The significance threshold for the RID‐TFPS for P = 0.05 as a function of the number of trials. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Similarly, this procedure can be used to determine the statistical significance of the computed RID‐TFPS value. Determining the statistical significance involves hypothesis testing and requires the formation of a null hypothesis. In some cases, it may be possible to derive analytically the distribution of the given measure under a given null hypothesis. However, in the case of the RID‐TFPS this proves to be a very difficult problem, therefore this distribution is estimated by direct Monte Carlo simulations. For this purpose, an ensemble of surrogate data sets are generated [Theiler et al., 1992]. For each surrogate data set, the RID‐TFPS is computed and from this ensemble of statistics, the distribution is approximated. A robust way to define significance would be directly in terms of the P‐values with rank statistics. For example, if the observed time series has a synchrony value that is in the lower one percentile of all the surrogate statistics, then a P‐value of 0.01 could be quoted.

In this article, we use the null hypothesis that the observed data are independent. For this purpose, 200 surrogate data ensembles with N pairs of independent white noise signals with the same length as the original signals are generated, and the RID‐TFPS values are computed over these N trials. The mean RID‐TFPS value over time and frequency is computed for each surrogate data set, and the distribution of the synchrony values under the null hypothesis is formed. All time–frequency pairs are treated as independent points as we observed that the synchrony values for white noise are independent of time and frequency. The statistical test will compare the synchrony value obtained from the actual signals with this distribution obtained for independent signals. If the observed value is higher than a given proportion q of the distribution (e.g., 95%), then the two signals under consideration are said to be nonindependent with a probability p = 1 − q. In Figure 2b, we plot the significance thresholds for P = 0.05 as a function of the number of trials, N.

RESULTS

In this section, we will first test the validity of the RID‐TFPS measure on the set of simulated signals in section “simulated data” and then apply it to ERN ERP signals collected during a speeded response task.

Simulated Data

Example 1: Time‐varying phase tracking

In this example, the proposed Rihaczek distribution‐based phase estimation method is applied to compute the instantaneous phase difference between the two signals, x 1(t) = exp(jω1 t) and x 2(t) = exp(jω1(t − at 2)), shown in Figure 3a, using Eq. (10). In Figure 3b, we compare the theoretical phase difference, which is a second‐order polynomial, and the estimated one at the frequency of interest, ω1. From this figure, it is seen that the proposed method is successful at estimating the time‐varying phase difference with a mean square error of 1.1 × 10−30. This result is independent of the parameters, ω1 and a, as long as the maximum of ω1 at 2 is less than or equal to 2π.

Figure 3.

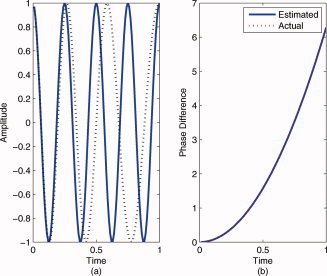
Figure 3

Open in a new tab

Comparison of the theoretical and estimated time‐varying phase difference between x 1(t) = exp(jw 1 t) and x 2(t) = exp(jw 1(t − at 2)), where ω1 = 8π, a = 0.25 for the time range 0–1 s using the proposed RID‐Rihaczek‐based phase estimation method: (a) The two signals and (b) the theoretical and the estimated phase differences. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Example 2: Comparison of the RID‐TFPS and the wavelet‐TFPS measures for linear chirp signal

In this example, we compared the performance of the RID‐TFPS and the wavelet‐TFPS measures for two linear chirp signals with a constant phase difference in white Gaussian noise. From Figure 4a, it can be seen that the RID‐TFPS is close to 1 around the instantaneous frequency (the maximum synchrony is equal to 0.9976) and smoothly tapers off as the frequency moves away from the instantaneous frequency. For the wavelet‐TFPS (Fig. 4b), the values do not taper off gradually but rather sharply and there is a larger bandwidth around the instantaneous frequency (the maximum synchrony is equal to 0.9672). The instantaneous frequency is defined as the derivative of the phase and is equal to ω0 + 2βt in this example, shown by the black lines in Figure 4a,b. The difference in the concentration of the phase synchrony values around the instantaneous frequency can be quantified by computing the mean squared error (MSE) between the ideal PLV profile and the computed ones. The ideal PLV profile is a time–frequency surface with ones at the instantaneous frequency and zeros everywhere else and can be easily obtained by computing the Wigner distribution and estimating the instantaneous frequency. For the RID‐TFPS, MSE is equal to 0.2138, whereas for the wavelet‐TFPS it is equal to 0.3015, indicating a larger deviation from the ideal case. It is also important to note that for the wavelet‐TFPS, the bandwidth around the instantaneous frequency increases as the instantaneous frequency increases. This is due to the fact that at high frequencies the wavelet transform has high time resolution at the expense of low frequency resolution.

Figure 4.

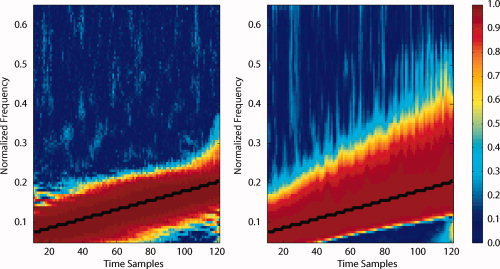
Figure 4

Open in a new tab

Average phase locking value for two chirp signals with a constant phase difference in noise, that is, x 1(t) = exp(j(ω0 t + βt 2)) and x 2(t) = exp(j(ω0 t + βt 2 + θ)) over 100 simulations: (a) RID‐TFPS and (b) wavelet‐TFPS.

Example 3: Performance of the RID‐TFPS and the wavelet‐TFPS measures in noise

In this example, we evaluated the robustness of the two TFPS measures in noise. To evaluate the robustness under noise, we considered two signal models in noise: A pair of high synchrony signals (two sinusoids with a constant phase difference) and a pair of low synchrony signals (a sinusoid and white Gaussian noise) described in section “simulated data.” In the first model, ideally, when the noise variance is small, that is, the SNR is high, the phase synchrony is expected to be close to 1. As the noise power increases, the phase synchrony should get smaller as the two signals are no longer perfectly in phase with each other. This phenomenon is illustrated for both the RID‐TFPS and the wavelet‐TFPS measures in Figure 5a. This figure illustrates that the RID‐TFPS measure remains higher for a larger range of SNR values compared with the wavelet‐TFPS measure and that the range (minimum to maximum) of the RID‐TFPS is smaller than that of the wavelet‐TFPS as observed through the error bars. The difference between the two synchrony measures is found to be statistically significant for all tested SNR values (t‐values are 160.2178, 154.15, 101.4, 48.86, 8.6, and 10.8). These results support the idea that the RID‐TFPS is more robust against noise than the wavelet‐TFPS. Moreover, the computed synchrony values are greater than the threshold computed in section “statistics of the time‐frequency phase synchrony measure” (0.0748) indicating that the null hypothesis that two signals are independent is rejected at the 95% confidence level. For the second model (Fig. 5b), both of the measures show low values of synchrony. The average phase synchrony is low for both methods indicating that the noise variance has little effect on the value of phase synchrony. Further, for all of the SNR values, the computed synchrony value is smaller than the threshold discussed in section “statistics of the time‐frequency phase synchrony measure” (0.0748) indicating that we fail to reject the null hypothesis that two signals are independent at the 95% confidence level. Despite the low and nonsignificant values for both the RID‐ and wavelet‐TFPS measures, it is worth observing (in Fig. 5b) that the SNR has an influence on the synchrony values for the RID‐TFPS, such that there is an increase in TFPS values at the highest SNR levels. This can be explained by the deterministic signal's amplitude interfering with the actual phase synchrony computation for high SNRs. Although this pattern is readily apparent for the RID‐TFPS, and significant, this same pattern is present in the wavelet‐TFPS implementation, although so small that the graph does not depict it clearly. Pearson correlation between the RID‐ and wavelet‐TFPS does reveal the correspondence (r = 0.38). We hypothesize that this effect is stronger for the RID‐TFPS because of the extensive filtering inherent in the wavelet‐TFPS and points to expectable ways in which background noise can influence phase synchrony computation.

Figure 5.

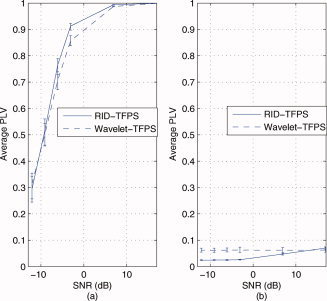
Figure 5

Open in a new tab

Comparison of robustness of the RID‐TFPS versus the wavelet‐TFPS in noise for a range of SNRs [−12 dB, 17 dB]. A total of 200 simulations with 200 trials are run for each SNR value and for the two types of signals (high synchrony pair and low synchrony pair). The mean and the range of synchrony values (minimum to maximum) over 200 simulations at 8 Hz are shown: (a) between two high synchrony signals (sinusoids in independent white Gaussian noise, x 1(t) = sin(16πt) + n 1(t), x 2(t) = sin(16πt + π/4) + n 2(t))) and (b) between two low synchrony signals (a sinusoid in white Gaussian noise and independent white Gaussian noise, x 1(t) = sin(16πt) + n 1(t), x 2(t) = n 2(t))). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Biological Data: ERN

Previous research suggests that the ERN ERP component is associated with increased intertrial synchrony in the theta range and that this synchrony is enhanced for error responses compared with correct responses [Trujillo and Allen, 2007]. Because the ERN generally has its amplitude and intertrial synchrony maximum around FCz, we hypothesized that measurable synchrony during the ERN would be observable between FCz and the other electrode sites on the scalp. We tested this hypothesis by computing the PLV between FCz and each of the remaining 61 electrodes. Phase synchrony was computed using Eq. (12) separately for error and correct trials across a wide range of frequencies (1–64 Hz) and from 1,000 ms before the stimulus to 2,000 ms after the stimulus. The number of error and correct trials varied across subjects, but accuracy was generally high (M = 90%, SD = 8.9%). Thus, correct trials greatly outnumbered error trials. To handle this, for each subject, a random subset of the correct trials was chosen to match the number of error trials (M = 24.83).

Comparisons of the RID‐TFPS to the wavelet‐TFPS for error and correct responses are presented in Figure 6. The first row contains the grand average time‐domain amplitude signal representation. The second and third rows contain the RID‐ and the wavelet‐TFPS measures, respectively. The left column contains data from error trials and the right from correct trials. The correlation between the average wavelet‐ and RID‐TFPS surfaces is 0.594 for error and 0.559 for correct trials, both of which are statistically significant (P < 0.001). This supports the view that the wavelet‐ and the RID‐TFPS measures evidence similar time–frequency structure and suggests that these measures are representing the same synchrony activity. For both trial types, however, the RID‐TFPS activity appears more localized and less smoothed on the surface relative to the wavelet‐TFPS. This is consistent with the smearing inherent in the wavelet tiles, which have reduced temporal support at low frequencies and reduced frequency support at higher frequencies. This difference is particularly apparent in the 100 ms just after the button press for both error [Hall et al., 2007] and correct trials, where the RID provides more structure and definition than the wavelets. For example, the wavelet contains activity during this window that looks much less differentiated from activity before and after that window. As described earlier (e.g., Fig. 2b), the synchrony values for both error and correct trials were significantly greater than for white noise indicating that the computed synchrony values are not due to chance. It is also worth noting that the TFPS for error trials was significantly greater than that for correct trials, broadly across the surfaces depicted in Figure 6. However, partly because of volume conduction and other potential confounds and partly in an attempt to remove global condition and frequency‐band TFPS differences, the error–correct comparisons are assessed using a baseline correction as follows.

Figure 6.

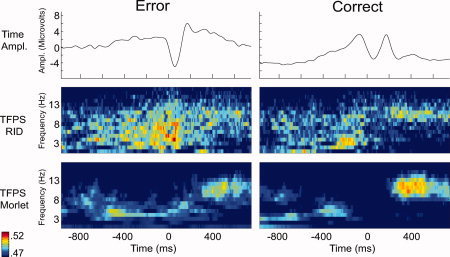
Figure 6

Open in a new tab

Comparison of the RID‐TFPS and the wavelet‐TFPS for error and correct trials. The first row shows the grand average of the response for error and correct trials in the time domain. The second and third rows show the RID‐ and the wavelet‐TFPS measures, respectively. The left column contains data from error trials and the right from correct trials.

In this article, we baseline corrected the time–frequency phase‐synchrony values before comparing TFPS from error and correct trials as described in section “time‐varying phase spectrum and phase synchrony.” Because the presented data are response locked, a great deal of additional stimulus‐related processing occurs just before the response. We thus chose a baseline by moving a 100 ms window from 1,000 ms before the response up to the response. We observed that baseline correction had the strongest effects just before the response, but the effects seemed to vary widely in the 500 ms before the response. In the late part of the 1,000 ms, on the other hand, the surface‐wide differences between error and correct were still removed, and the impact of the baseline varies less as a function of time, all suggesting this correction was an improvement over uncorrected measures. The baseline window selected with this approach was −1,000 to −900 ms, well before the stimulus was presented (e.g., range of mean reaction times in the experiment 618–741 ms).

In Figure 7, differences between error and correct trials are presented for the RID‐TFPS measure, now baseline corrected as described earlier. We illustrate the grand average time–frequency surfaces depicting variation of the PLVs between error and correct for a subset of electrodes. The time–frequency surfaces are obtained by averaging the error–correct difference synchrony values across subjects.

Figure 7.

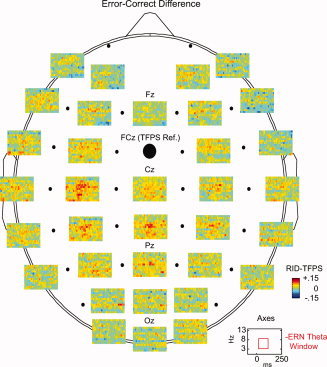
Figure 7

Open in a new tab

The spatial localization of the baseline corrected error–correct difference phase synchrony based on the RID‐TFPS. The average phase synchrony surfaces across subjects depicting variation of the error–correct difference phase locking values for a subset of electrodes are shown.

In Figure 8, we present the spatial localization of the differences between error and correct trials for both wavelet‐ and RID‐TFPS measures. The left side of the plot contains topographic representations of the grand error–correct difference in the ERN theta window (25–75 ms after the response and in the 4–8 Hz range). The right side depicts the statistical assessment of the differences using the Wilcoxon sign‐rank test. In these figures, increased synchrony for error trials relative to correct can be observed in central electrodes (proximal to primary motor areas). These differences are statistically significant, as detailed in the topographic map of Wilcoxon P‐values. This is notable in comparison to other regions, such as occipital and frontal, which have few apparent or significant differences. Topographic significance patterns between the wavelet and RID are similar, providing further support for the view that the two TFPS measures are indexing the same underlying synchrony. This offers some validation for the RID‐TFPS relative to the previously published wavelet‐TFPS approach, and thus provides motivation for future efforts to utilize the improved time–frequency support offered by the RID to better isolate the time–frequency attributes of biological signals (e.g., the ERN).

Figure 8.

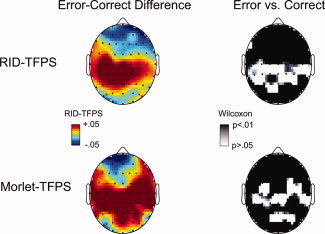
Figure 8

Open in a new tab

Comparison of the RID‐TFPS and the wavelet‐TFPS topographic maps for the error–correct difference in the ERN theta window. The right side of the plot depicts the statistical assessment of the differences using the Wilcoxon sign‐rank test.

DISCUSSION

In this article, we have introduced a new time‐varying measure of phase synchrony for quantifying large‐scale neural synchrony in the brain. The proposed measure is based on a complex‐valued TFD introduced by Rihaczek [ 1968]. The time‐varying phase and phase synchrony measures are defined based on this complex distribution. The effectiveness of the proposed measure in quantifying time‐varying phase synchrony was verified both through simulations and with EEG data recorded from human subjects.

The proposed RID‐TFPS measure is shown to provide higher time–frequency resolution and improved robustness under noise compared with the wavelet‐TFPS. The increased resolution is due to Rihaczek distribution being based directly on the signal and its Fourier transform and not involving a frequency‐dependent window function like the wavelet transform. Although the frequency‐dependent scaling property of the wavelet transform is useful for detecting high‐frequency transients, it inherently imposes a certain time–frequency structure on the underlying signal, which in turn results in bias in the phase synchrony estimates. This bias can be seen in both the increased bandwidth across the instantaneous frequency in Figure 4b and the reduced value of phase synchrony at high SNRs in Figure 5a.

Results based on the analysis of EEG signals collected during a study of ERN [Hall et al., 2007] revealed significant and expected differences in phase synchrony between error and correct responses. Statistically significant increases in phase synchrony for error responses, relative to correct, were observed 25–75 ms after the subject response and in the 4–8 Hz range corresponding to the ERN. The current analyses suggest that there is a topographically broad increase in interelectrode phase synchrony for error trials in the theta range. This is consistent with the idea that a number of regions become engaged together in the function of performance monitoring. In the current data, the phase synchrony differences are significant for central electrodes near the primary motor areas, suggesting that this measure may be indexing interactions between the ACC and motor areas during error processing. Although such inferences must be tentative, as suggested earlier, this pattern of results can be anticipated from the literature, suggesting that the new phase synchrony measure may appropriately index activity between regions understood to be implicated in the ERN.

The proposed RID‐TFPS method was also compared to the wavelet‐TFPS for ERN data. The two measures looked similar and were significantly correlated, suggesting that they index the same underlying activity. The current effort was intended to demonstrate stable behavior of the RID‐TFPS, rather than document specific gains in the time–frequency representation of ERN activity per se. Nevertheless, the effect of known limitations in the wavelets can be observed in the plots. Specifically, for both error and correct trial types, the RID‐TFPS index depicts activity that is more localized on the time–frequency surface (i.e., smaller and more distinct areas of activation), while the wavelet‐TFPS displays characteristic temporal smoothing at lower frequencies (see Fig. 6). These observations in biological data, combined with the assessment of the simulated data earlier, suggest that commonly understood limitations of wavelet transforms are present in the current wavelet‐TFPS implementations. This provides motivation for more detailed analysis of specific ERP phenomena, like the ERN, to evaluate whether the improvements offered by the RID‐TFPS produce significant gains in disaggregating such activity.

In this article, we have also proposed a methodology for determining the significance of the computed phase synchrony values both within a subject and across experimental conditions. To determine the significance of a computed synchrony value, we generated surrogate data ensembles consisting of independent white noise signals with the same length as the original signal. The distribution of the synchrony values under this null hypothesis was formed and statistical hypothesis testing was used to determine the significance of synchrony from real data. This approach tests whether the hypothesis that the actual signals are independent can be rejected with a given probability. It is possible to extend the formulation of the null hypothesis such that the surrogate data are generated from shifted trials of the original data. In previous work, it has been shown that both the white noise and shifted trials approaches yield similar test statistics for the wavelet‐TFPS [Lachaux et al., 2002]. We have observed a similar finding for the RID‐TFPS and focus on white noise approach for generating the surrogate data because of its generalizability and because it is more analogous to assessing synchronous brain regions within ongoing EEG.

One further difficulty in interpreting ERN phase synchrony observed in raw EEG/ERP (untransformed data recorded at the scalp) is that some of the observed synchrony will likely be due to volume conduction. As suggested earlier, this can happen when a neural source is observable at more than one electrode. When the phase synchrony between those two electrodes is computed, some degree of the synchrony would be due to that single source, instead of indexing two regions operating in synchrony, which is the goal of the analysis. The baseline correction helps to a degree by attenuating volume conduction‐driven phase synchrony that is more tonic in nature (e.g., consistently present in the baseline), although failing to address additional volume conduction associated with stimulus‐locked activity (e.g., ERN). Additional methods are available to attenuate volume conduction by localizing activity toward the cortical surface (e.g., Laplacian transforms) [Lachaux et al., 1999], but application of these methods to the data would likely limit characterization of activity from the deeper ACC source, where the ERN has its primary generators. In recent work by Stam et al. [ 2007], a new measure named the PLI has been introduced to address the problem of volume conduction and active reference electrodes in the assessment of functional connectivity. The PLI is a measure of the asymmetry of the distribution of phase differences between two signals and can separate consistent, nonzero phase difference from random phase differences due to noise. The PLI is not limited to any particular phase estimation method and can easily be adapted to the proposed RID‐TFPS to replace PLV. Thus, because our goal is to validate the behavior of the phase estimation method with expected patterns of phase synchrony, rather than make a definitive statement about phase synchrony and the ERN, further efforts to more completely isolate the regions of activity relative to volume conduction are left for future work.

Apart from addressing the problem of volume conduction, EEG source localization methods such as current dipole models and distributed models can be used to identify and isolate ERN activity [Michel et al., 2004]. Source localization methods can be used to identify ERN activity in areas of interest such as ACC (the known primary source of ERN), lateral‐PFC, and primary motor cortex. Once localized signal models are derived for these areas, the proposed phase synchrony measure can be applied directly to these source signals to identify functional integration at the neuronal source level.

In this article, the application of the phase synchrony measure focused on computing the connectivity with respect to a reference electrode, FCz. The proposed measure can also be applied to quantify all possible pairwise electrode interactions. This analysis would allow us to better identify the local networks responsible for ERN. Similarly, one can apply the proposed measure for quantifying intertrial synchrony as in [Tallon‐Baudry and Bertrand, 1999] to identify stimulus‐related synchronization.

Similar to other bivariate measures of functional connectivity, the proposed measure is limited in the sense that it can only quantify pairwise interactions between electrodes rather than identifying a group of electrodes or neuronal sources that are synchronized. Recent work suggests that it is possible to extend bivariate measures of phase synchrony to the multivariate case by using the relationship between instantaneous frequency and phase and estimating the instantaneous frequency locking in the time–frequency plane [Rudrauf et al., 2006]. Similar to the method proposed by [Rudrauf et al., 2006], one can use high‐resolution TFDs to estimate the instantaneous frequency of a group of electrodes and estimate the frequency locking/phase synchronization across trials and electrodes. This extension would offer improvements over the wavelet‐based multivariate measures due to the uniformly high time–frequency resolution provided by bilinear TFDs.

Footnotes

1

All integrals are from −∞ to ∞ unless otherwise stated.

2

ϕ12(t,ω) = −ωt 0 with modulus of π.

REFERENCES

  1. Ansari‐Asl K, Bellanger JJ, Bartolomei F, Wendling F, Senhadji L ( 2005): Time‐frequency characterization of interdependencies in nonstationary signals: Application to epileptic EEG. IEEE Trans Biomed Eng 52: 1218–1226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Baccalá LA, Sameshima K ( 2001): Partial directed coherence: A new concept in neural structure determination. Biol Cybern 84: 463–474. [DOI] [PubMed] [Google Scholar]
  3. Breakspear M ( 2002): Nonlinear phase desynchronization in human electroencephalographic data. Hum Brain Mapp 15: 175–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Breakspear M, Terry JR ( 2002): Nonlinear interdependence in neural systems: Motivation, theory, and relevance. Int J Neurosci 112: 1263–1284. [DOI] [PubMed] [Google Scholar]
  5. Brown P ( 2003): Oscillatory nature of human basal ganglia activity: Relationship to the pathophysiology of Parkinson's disease. Mov Disord 18: 357–363. [DOI] [PubMed] [Google Scholar]
  6. Bush G, Luu P, Posner MI ( 2000): Cognitive and emotional influences in anterior cingulate cortex. Trends Cogn Sci 4: 215–222. [DOI] [PubMed] [Google Scholar]
  7. Carter CS, Braver TS, Barch DM, Botvinick MM, Noll D, Cohen JD ( 1998): Anterior cingulate cortex, error detection, and the online monitoring of performance. Science 280: 747. [DOI] [PubMed] [Google Scholar]
  8. Chávez M, Martinerie J, Le Van Quyen M ( 2003): Statistical assessment of nonlinear causality: Application to epileptic EEG signals. J Neurosci Methods 124: 113–128. [DOI] [PubMed] [Google Scholar]
  9. Cohen L ( 1995): Time‐Frequency Analysis: Theory and Applications. New Jersey: Prentice Hall. [Google Scholar]
  10. Damasio AR ( 1990): Synchronous activation in multiple cortical regions: A mechanism for recall. Semin Neurosci 2: 287–296. [Google Scholar]
  11. Dehaene S, Posner MI, Tucker DM ( 1994): Localization of a neural system for error detection and compensation. Psychol Sci 5: 303–305. [Google Scholar]
  12. Falkenstein M, Hohnsbein J, Hoormann J, Blanke L ( 1991): Effects of crossmodal divided attention on late ERP components. II. Error processing in choice reaction tasks. Electroencephalogr Clin Neurophysiol 78: 447–455. [DOI] [PubMed] [Google Scholar]
  13. Friston KJ ( 2000): The labile brain. I. Neuronal transients and nonlinear coupling. Philos Trans R Soc Lond B Biol Sci 355: 215–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Friston KJ, Buechel C, Fink GR, Morris J, Rolls E, Dolan RJ ( 1997): Psychophysiological and modulatory interactions in neuroimaging. Neuroimage 6: 218–229. [DOI] [PubMed] [Google Scholar]
  15. Gehring WJ, Willoughby AR ( 2004): Are all medial frontal negativities created equal? Toward a richer empirical basis for theories of action monitoring In: Ullsperger M, Falkenstein M, (editors.), Errors, conflicts and the brain. Current opinions on performance monitoring. Leipzig: Max Planck Institute of Cognitive Neuroscience; pp. 14–20. [Google Scholar]
  16. Gehring WJ, Goss B, Coles MGH, Meyer DE, Donchin E ( 1993): A neural system for error detection and compensation. Psychol Sci 4: 385–390. [Google Scholar]
  17. Gehring WJ, Coles MG, Meyer DE, Donchin E ( 1995): A brain potential manifestation of error‐related processing. Electroencephalogr Clin Neurophysiol Suppl 44: 261–272. [PubMed] [Google Scholar]
  18. Granger CWJ ( 1969): Investigating causal relations by econometric models and cross‐spectral methods. Econometrica 37: 424–438. [Google Scholar]
  19. Guevara R, Velazquez JLP, Nenadovic V, Wennberg R, Senjanovic G, Dominguez LG ( 2005): Phase synchronization measurements using electroencephalographic recordings. Neuroinformatics 3: 301–313. [DOI] [PubMed] [Google Scholar]
  20. Hall JR, Bernat EM, Patrick CJ ( 2007): Externalizing psychopathology and the error‐related negativity. Psychol Sci 18: 326–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hinrichs H, Heinze HJ, Schoenfeld MA ( 2006): Causal visual interactions as revealed by an information theoretic measure and fMRI. Neuroimage 31: 1051–1060. [DOI] [PubMed] [Google Scholar]
  22. Holroyd CB, Coles MGH ( 2002): The neural basis of human error processing: Reinforcement learning, dopamine, and the error‐related negativity. Psychol Rev 109: 679–709. [DOI] [PubMed] [Google Scholar]
  23. Holroyd CB, Dien J, Coles MGH ( 1998): Error‐related scalp potentials elicited by hand and foot movements: Evidence for an output‐independent error‐processing system in humans. Neurosci Lett 242: 65–68. [DOI] [PubMed] [Google Scholar]
  24. Jeong J, Williams WJ ( 1992): Kernel design for reduced interference distributions. IEEE Trans Signal Process 40: 402–412. [Google Scholar]
  25. Kaminski MJ, Blinowska KJ ( 1991): A new method of the description of the information flow in the brain structures. Biol Cybern 65: 203–210. [DOI] [PubMed] [Google Scholar]
  26. Kaminski M, Ding M, Truccolo WA, Bressler SL ( 2001): Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol Cybern 85: 145–157. [DOI] [PubMed] [Google Scholar]
  27. Klein A, Sauer T, Jedynak A, Skrandies W ( 2006): Conventional and wavelet coherence applied to sensory‐evoked electrical brain activity. IEEE Trans Biomed Eng 53: 266–272. [DOI] [PubMed] [Google Scholar]
  28. Lachaux JP, Rodriguez E, Martinerie J, Varela FJ ( 1999): Measuring phase synchrony in brain signals. Hum Brain Mapp 8: 194–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lachaux JP, Lutz A, Rudrauf D, Cosmelli D, Le Van Quyen M, Martinerie J, Varela F ( 2002): Estimating the time‐course of coherence between single‐trial brain signals: An introduction to wavelet coherence. Neurophysiol Clin 32: 157–174. [DOI] [PubMed] [Google Scholar]
  30. Le Van Quyen M, Foucher J, Lachaux JP, Rodriguez E, Lutz A, Martinerie J, Varela FJ ( 2001): Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. J Neurosci Methods 111: 83–98. [DOI] [PubMed] [Google Scholar]
  31. Li D, Jung R ( 2000): Quantifying coevolution of nonstationary biomedical signals using time‐varying phase spectra. Ann Biomed Eng 28: 1101–1115. [DOI] [PubMed] [Google Scholar]
  32. Michel CM, Murray MM, Lantz G, Gonzalez S, Spinelli L, Grave de Peralta R ( 2004): EEG source imaging. Clin Neurophysiol 115: 2195–2222. [DOI] [PubMed] [Google Scholar]
  33. Miller EK, Cohen JD ( 2001): An integrative theory of prefrontal cortex function. Annu Rev Neurosci 24: 167–202. [DOI] [PubMed] [Google Scholar]
  34. Netoff TI, Schiff SJ ( 2002): Decreased neuronal synchronization during experimental seizures. J Neurosci 22: 7297–7307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Nunez PL, Srinivasan R ( 2006): Electric Fields of the Brain: The Neurophysics of EEG. New York: Oxford University Press. [Google Scholar]
  36. Nunez PL, Srinivasan R, Westdorp AF, Wijesinghe RS, Tucker DM, Silberstein RB, Cadusch PJ ( 1997): EEG coherency. I. Statistics, reference electrode, volume conduction, Laplacians, cortical imaging, and interpretation at multiple scales. Electroencephalogr Clin Neurophysiol 103: 499–515. [DOI] [PubMed] [Google Scholar]
  37. Palva JM, Palva S, Kaila K ( 2005): Phase synchrony among neuronal oscillations in the human cortex. J Neurosci 25: 3962–3972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pereda E, Quiroga RQ, Bhattacharya J ( 2005): Nonlinear multivariate analysis of neurophysiological signals. Prog Neurobiol 77: 1–37. [DOI] [PubMed] [Google Scholar]
  39. Rihaczek A ( 1968): Signal energy distribution in time and frequency. IEEE Trans Inform Theory 14: 369–374. [Google Scholar]
  40. Rodriguez E, George N, Lachaux JP, Martinerie J, Renault B, Varela FJ ( 1999): Perception's shadow: Long‐distance synchronization of human brain activity. Nature 397: 391–393. [DOI] [PubMed] [Google Scholar]
  41. Rosenblum MG, Pikovsky AS, Kurths J ( 1996): Phase synchronization of chaotic oscillators. Phys Rev Lett 76: 1804–1807. [DOI] [PubMed] [Google Scholar]
  42. Roskies AL ( 1999): The binding problem: Special issue. Neuron 24: 7–9. [DOI] [PubMed] [Google Scholar]
  43. Rudrauf D, Douiri A, Kovach C, Lachaux JP, Cosmelli D, Chavez M, Adam C, Renault B, Martinerie J, Le Van Quyen M ( 2006): Frequency flows and the time‐frequency dynamics of multivariate phase synchronization in brain signals. Neuroimage 31: 209–227. [DOI] [PubMed] [Google Scholar]
  44. Sarnthein J, Petsche H, Rappelsberger P, Shaw GL, von Stein A ( 1998): Synchronization between prefrontal and posterior association cortex during human working memory. Proc Natl Acad Sci USA 95: 7092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Spencer KM, Nestor PG, Niznikiewicz MA, Salisbury DF, Shenton ME, McCarley RW ( 2003): Abnormal neural synchrony in schizophrenia. J Neurosci 23: 7407–7411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Spencer KM, Nestor PG, Perlmutter R, Niznikiewicz MA, Klump MC, Frumin M, Shenton ME, McCarley RW ( 2004): Neural synchrony indexes disordered perception and cognition in schizophrenia. Proc Natl Acad Sci USA 101: 17288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Stam CJ ( 2005): Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin Neurophysiol 116: 2266–2301. [DOI] [PubMed] [Google Scholar]
  48. Stam CJ, Montez T, Jones BF, Rombouts S, van der Made Y, Pijnenburg YAL, Scheltens P ( 2005): Disturbed fluctuations of resting state EEG synchronization in Alzheimer's disease. Clin Neurophysiol 116: 708–715. [DOI] [PubMed] [Google Scholar]
  49. Stam CJ, Nolte G, Daffertshofer A ( 2007): Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum Brain Mapp 28: 1178–1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Sun LS, Shen MF, Ting KH, Chan FHY ( 2003): Analysis of time‐varying synchronization of multi‐channel EEG signals using wavelet coherence. Proceedings of the IEEE International Conference on Neural Networks and Signal Processing. pp 216–219.
  51. Tallon‐Baudry C, Bertrand O ( 1999): Oscillatory gamma activity in humans and its role in object representation. Trends Cogn Sci 3: 151–162. [DOI] [PubMed] [Google Scholar]
  52. Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, Schnitzler A, Freund HJ ( 1998): Detection of n: m phase locking from noisy data: Application to magnetoencephalography. Phys Rev Lett 81: 3291–3294. [Google Scholar]
  53. Theiler J, Galdrikian B, Longtin A, Eubank S, Farmer JD ( 1992): Testing for nonlinearity in time series: The method of surrogate data. Physica D 58: 77–94. [Google Scholar]
  54. Tononi G, Edelman GM ( 1998): Consciousness and complexity. Science 282: 1846. [DOI] [PubMed] [Google Scholar]
  55. Trujillo LT, Allen JJB ( 2007): Theta EEG dynamics of the error‐related negativity. Clin Neurophysiol 118: 645–668. [DOI] [PubMed] [Google Scholar]
  56. Uhlhaas PJ, Singer W ( 2006): Neural synchrony in brain disorders: Relevance for cognitive dysfunctions and pathophysiology. Neuron 52: 155–168. [DOI] [PubMed] [Google Scholar]
  57. Uhlhaas PJ, Linden DEJ, Singer W, Haenschel C, Lindner M, Maurer K, Rodriguez E ( 2006): Dysfunctional long‐range coordination of neural activity during gestalt perception in schizophrenia. J Neurosci 26: 8168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Varela FJ ( 1995): Resonant cell assemblies: A new approach to cognitive functions and neuronal synchrony. Biol Res 28: 81–95. [PubMed] [Google Scholar]
  59. Varela F, Lachaux JP, Rodriguez E, Martinerie J ( 2001): The brainweb: Phase synchronization and large‐scale integration. Nat Rev Neurosci 2: 229–239. [DOI] [PubMed] [Google Scholar]

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES