Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2011 Feb 8;32(12):2131–2140. doi: 10.1002/hbm.21174

Thickness profile generation for the corpus callosum using Laplace's equation

Christopher L Adamson 1, Amanda G Wood 1,2,3,✉, Jian Chen 1, Sarah Barton 1, David C Reutens 4, Christos Pantelis 5, Dennis Velakoulis 5,6, Mark Walterfang 5,6
PMCID: PMC6870377  PMID: 21305661

Abstract

The corpus callosum facilitates communication between the cerebral hemispheres. Morphological abnormalities of the corpus callosum have been identified in numerous psychiatric and neurological disorders. To quantitatively analyze the thickness profile of the corpus callosum, we adapted an automatic thickness measurement method, which was originally used on magnetic resonance (MR) images of the cerebral cortex (Hutton et al. [2008]: NeuroImage 40:1701–10; Jones et al. [2002]: Hum Brain Mapp 11:12–32; Schmitt and Böhme [2002]: NeuroImage 16:1103–9; Yezzi and Prince [2003]: IEEE Trans Med Imaging 22:1332–9), to MR images of the corpus callosum. The thickness model was derived by computing a solution to Laplace's equation evaluated on callosal voxels. The streamlines from this solution form non‐overlapping, cross‐sectional contours the lengths of which are modeled as the callosal thickness. Apart from the semi‐automated segmentation and endpoint selection procedures, the method is fully automated, robust, and reproducible. We compared the Laplace method with the orthogonal projection technique previously published (Walterfang et al. [2009a]: Psych Res Neuroimaging 173:77–82; Walterfang et al. [2008a]: Br J Psychiatry 192:429–34; Walterfang et al. [2008b]: Schizophr Res 103:1–10) on a cohort of 296 subjects, composed of 86 patients with chronic schizophrenia (CSZ), 110 individuals with first‐episode psychosis, 100 individuals at ultra‐high risk for psychosis (UHR; 27 of whom later developed psychosis, UHR‐P, and 73 who did not, UHR‐NP), and 55 control subjects (CTL). We report similar patterns of statistically significant differences in regional callosal thickness with respect to the comparisons CSZ vs. CTL, UHR vs. CTL, UHR‐P vs. UHR‐NP, and UHR vs. CTL. Hum Brain Mapp, 2011. © 2011 Wiley Periodicals, Inc.

Keywords: corpus callosum, Laplace, thickness measurements

INTRODUCTION

The corpus callosum (CC) is a white matter structure that facilitates communication between the cerebral hemispheres. The dense myelination of the axons within the CC makes it easily identifiable as hyperintense voxels in mid‐sagittal slices of T 1‐weighted magnetic resonance (MR) images. Morphological abnormalities, identified using thickness‐ or area‐based analysis of the CC in MR images, have been reported in degenerative disorders such as Alzheimer's disease [Hampel et al.,1998], vascular dementia [Pantel et al.,1998] and frontotemporal dementia [Yamauchi et al.,2000], neuropsychiatric illnesses, including schizophrenia [Bachmann et al.,2003; Downhill et al.,2000], autism [Vidal et al.,2006], and bipolar disorder (Brambilla et al.,2004), and other conditions such as traumatic brain injury [Beauchamp et al.,2009] and birth trauma [Benjak et al.,2008].

Recent studies have used descriptions of the CC based on regional thickness profiles constructed by measuring the lengths of line segments traversing the cross‐section of the callosum at predefined intervals from the genu to the splenium [Downhill et al.,2000; Peters et al.,2002; Walterfang et al.,2009b]. In Downhill et al. [2000] and Walterfang et al. [2009b], straight contours were produced via orthogonal projection outward from a midline that bisected the CC and connected two endpoints defined at the anterior tip of the genu and the end of the splenium. The endpoints divide the CC into superior and inferior boundaries, which are used as terminating points for the contours. The midlines were discretized into 30 and 39 equally spaced nodes by Walterfang et al. [2009b] and Downhill et al. [2000], respectively, from which the contours were instantiated. Peters et al. [2002] constructed straight contours by connecting 99 pairs of boundary points chosen to be equally spaced according to arc length parameterisations of the boundary contours.

Evidence from Schmitt and Böhme [2002], who investigated the similar problem of generating cross‐sectional traversals in images of the cerebral cortex, showed that overlapping contours were created by the orthogonal projection method in highly curved regions. Although the CC is generally not as severely curved as the sulci and gyri of the cerebral cortex, we demonstrate that overlapping contours are produced by the orthogonal projection method in curved callosal regions. This has implications for disorders in which the callosum typically exhibits increased degrees of curvature. For example, there is strong evidence that the callosum shows increased curvature in some disease states, such as schizophrenia [Casanova et al.,1990a; Casanova et al.,1990b; Frumin et al.,2002; Narr et al.,2000; Walterfang et al.,2008a], and a methodology which remains valid even in the presence of increased curvature is desirable when these disease states are compared against controls.

The presence of overlapping contours within a callosal thickness model renders the model invalid in terms of mathematical and anatomical aspects. Mathematically, at the point of intersection between two overlapping contours, the thickness function is multivalued, which is mathematically invalid. Anatomically, the fibres of the CC exhibit a predominantly homotopic organisation, which progresses along an anterior–posterior trajectory, that is mirrored in the cerebral cortex [Hofer and Frahm,2006]. Although crossing contours are not invalid in light of this topography, they do produce a contour ordering that disagrees with this organisation.

To address these issues for thickness measurements for the CC, we draw on methods that were developed for the related problem of cortical thickness measurement [Barta et al.,2005; Fischl and Dale,2000; Hutton et al.,2008; Jones et al.,2002; MacDonald et al.,2000; Schmitt and Böhme,2002; Yezzi and Prince,2003; Zeng et al.,1998]. The problem of cortical thickness measurement is more difficult at the segmentation stage due to segmentation uncertainties in the location of borders due to partial volume effects. These issues are not as problematic in the callosum as the boundaries are typically distinguishable from surrounding structures based on intensity alone. The thickness models proposed for the cortex, however, are directly transferable to the callosum.

A subset of the abovementioned methods modeled the cortical thickness using: signed distance functions [Zeng et al.,1998], minimal Euclidean distances between vertices located on mesh‐based estimates of each cortical surface [Fischl and Dale,2000; MacDonald et al.,2000] and orthogonal projection from the inner boundary to the outer boundary [Barta et al.,2005; MacDonald et al.,2000]. In the first and second cases, many‐to‐one mappings may be produced because a single node or voxel may be minimally distant to many nodes or voxels on the other surface. Application of the third method to the callosum, in 2D, would be prone to contour intersections as per the orthogonal projection method described previously.

In this article, we propose a thickness model for the corpus callosum that is based on the attractive mathematical properties of Laplace's equation [Hutton et al.,2008; Jones et al.,2002; Schmitt and Böhme,2002; Yezzi and Prince,2003]. In this heuristic, the cortical boundaries are assigned unique numeric potential values. The solution of Laplace's equation, obtained for all voxels within the cortex, possesses equipotential surfaces that make a smooth transition across the cortex. The cortical thickness of each cortical voxel is measured as the length of the streamline that passes through the voxel and intersects with each boundary. It can be shown that the streamlines are non‐overlapping, nominally parallel and intersect the boundary contours orthogonally. This model possesses the desirable qualities of being fully automated, being able to construct contours that are organised sequentially along an anterior–posterior trajectory akin to the organisation of the connections from the CC to the cortex [Hofer and Frahm,2006], and the mathematical properties of Laplace's equation guarantee valid thickness measurements.

We present a validation of the Laplace equation thickness model by reproducing the statistical analysis results of Walterfang et al. [Walterfang et al.,2008a,2008b,2009a], that demonstrated changes in global and/or regional callosal thickness across illness stages in schizophrenia. Thus, the main contribution of this article is to propose a robust, mostly automated and biologically plausible model to perform regional thickness analysis of the corpus callosum.

METHOD

Participants

The participants have been previously described in a series of analyses using the original straight‐line method for analyzing regional callosal thickness [Walterfang et al.,2008a,2008b,2009a]. In brief, we recruited 86 patients with chronic schizophrenia (CSZ), 110 individuals with first‐episode psychosis (FEP), 100 individuals at ultra‐high risk for psychosis (UHR; 27 of whom later developed psychosis, UHR‐P, and 73 who did not, UHR‐NP), and 55 control subjects (CTL). The chief analyses mirrored those previously published [Walterfang et al.,2008a,2008b,2009a], where we compared each patient group with the control group, and compared subgroups of the UHR group.

Image Acquisition

All subjects were scanned on a 1.5‐T GE Signa MRI machine. A three‐dimensional volumetric spoiled gradient recalled echo in the steady‐state sequence generated 124 contiguous, 1.5 mm coronal slices. Imaging parameters were TE, 3.3 ms; TR, 13.4 ms; flip angle, 30°; matrix size, 256 × 256; FOV, 24 × 24 cm matrix; voxel dimensions, 0.938 × 0.938 × 1.5 mm. Head movement was minimized by foam padding and Velcro straps across the forehead and chin. This scanner was calibrated fortnightly using the same proprietary phantom to ensure stability and accuracy of measurements. A numerical code was used to ensure blind analysis of data.

Image Analysis

We model the callosal thickness, for a point, x 0, inside the callosum, as the length of the contour that: (i) traverses the callosum from the superior to the inferior boundary; (ii) intersects both boundaries orthogonally; and (iii) passes through x 0. When measuring the thickness for multiple points inside the callosum, the collection of contours for these points must be non‐overlapping and be nominally parallel.

We segmented the callosum using a multistage algorithm. The acquired images were skull stripped using an automated method [Smith,2002]. Using the software package Automated Image Registration [Woods et al.,1998], images were registered to a template image comprising the average of 152 normal T1‐weighted MRI scans previously placed in stereotaxic coordinate space [Evans et al.,1993]. A nine‐parameter linear transformation was used which allowed translation, rotation and scaling along each of the three principal axes; this method accounts for brain size and the differential effect of gender and illness on the relationship between callosal and brain size [Bermudez and Zatorre,2001]. The midsagittal slice was then manually identified and the CC was segmented using a histogram method [Otsu,1979]. All segmentations were manually inspected to ensure that the fornix and pericallosal artery were not included. If these structures were still present, they were manually removed using the following manual editing protocol: (i) the fornix was excluded by following the inferior arc of the corpus callosum at the fornix‐callosal boundary, whereas the pericallosal artery was identified on some midsagittal slices and excluded by removing its characteristic curve adjacent to the genu.

A two‐step approach was used to construct the cross‐sectional contours. Initially, a user‐initialized iterative search, using the Nelder‐Mead simplex method for nonlinear, unconstrained optimisation [Lagarias et al.,1998], for optimum end points that maximised the length of the centre line of the callosum was performed. These subdivided the boundary contour into superior and inferior contours. The centre line was defined by first dividing the upper and lower surfaces of the callosum into 40 equidistant portions by 39 nodes. The centre line was made up of the line segments joining the endpoints and successive midpoints between corresponding nodes on the upper and lower surfaces. Once the end points had been identified by the local optimisation algorithm described previously, a smooth centre line was obtained with cubic spline interpolation between end points and successive midpoints. This curve was divided into 40 segments of equal lengths by 39 nodes. At each node, the distance of the line extending orthogonally to each boundary of the callosum represents the orthogonal projection callosal thickness.

In the method described in this article, we generate cross‐sectional contours, used to measure thickness, by solving Laplace's equation for all voxels inside the CC with prescribed boundary conditions on the superior and inferior contours. Formally, Laplace's equation is a second order partial differential equation that defines the scalar‐valued potential field, ϕ, defined for each voxel within the CC. The voxels of the CC are enclosed by the contours c superior, and c inferior, which denote the superior and inferior boundaries of the callosum, respectively. We use the Dirichlet problem form of Laplace's equation which is defined, in two dimensions, as,

equation image (1)

subject to the following boundary conditions

equation image (2)

where ϕsuperior and ϕinferior are predefined constants.

The boundary conditions at the endpoints of the contours require special treatment to ensure that ϕ remains single valued. The boundary contours are assumed to meet, but not intersect, so that 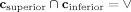Inline graphic. Then, we assume that linear segments, of infinitesimal size, join the boundary contours at their endpoints. Thus, the function ϕ makes linear transitions from ϕsuperior and ϕinferior along these linear segments. Therefore, endpoint‐originated streamlines will follow this linear trajectory, joining the endpoints. These assumptions ensure that ϕ remains single valued. Given that the callosum is discretized for computation, the endpoint segments will traverse the space between the voxels that represent the endpoints of the boundary contours.

For any point x 0 inside the callosum, we define the regional thickness, at that point, as the total arc length of the streamline that traverses the callosum from superior to inferior boundary and passes through x 0. Computationally, we construct each streamline as the concatenation of two parametric curves u(s) = (x(s), y(s)) and v(t) = (x(t), y(t)), with arc length parameters s and t, respectively, whose trajectories follow and oppose the normalised gradient of ϕ. Formally, we solve the following ordinary differential equation to construct the streamlines:

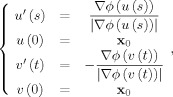equation image (3)

The directionality of these contours implies that ϕsuperior < ϕinferior. For convenience, we chose ϕsuperior = 0 and ϕinferior = 1.

The finite difference method (FDM) is used to discretize (1) and (2) to evaluate ϕ for each callosal voxel, using the standard 5‐point template to approximate the second derivatives,

equation image (4)

where ϕi,j denotes the value of (1) for voxel (i, j) and Δx and Δy denote the voxel width and height, respectively. Equation 4 was translated into a symmetric, positive‐definite system of linear equations that was solved using the iterative conjugate gradients method.

We used the first‐order Euler approximation to evaluate (3) numerically as follows

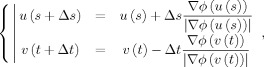equation image (5)

where Δs and Δt denote predefined step lengths. The gradient operators are approximated using first‐order linear interpolation. We select a collection of initial points by discretizing the equipotential contour, ϕ = (ϕsuperior + ϕinferior)/2, into 41 equally spaced nodes, of which the middle 39 are chosen for thickness measurements. The initial points must be chosen to lie on the same equipotential surface to ensure that contours overlap. The arc lengths of the curves formed by concatenating the u and u contours emanating from the midpoints is defined as the Laplace method callosal thickness profile.

To compare the orthogonal projection and Laplace equation methods in a valid way, the endpoints and boundary contours, generated from the preprocessing steps of the orthogonal projection method, were used for both methods in subsequent steps. Thus, the only difference between the methods lies in the construction of the cross‐sectional contours.

For analysis of between‐group differences with both methods, a non‐parametric permutation method of 20,000 randomisations was used for all group comparisons to examine for an effect of group, to account for non‐independence between adjacent thickness measurements and for multiple comparisons [Holmes et al.,1996]. Step‐down t testing to determine which regions showed significant change was planned to localise between‐group differences in regional callosal thickness. Statistical inference was based on the method of Holm, which controls for multiple comparisons of non‐independent measures by controlling the family‐wise error rate without assuming independence of adjacent callosal thickness measures [Holm,1979].

RESULTS

Figure 1 depicts the cross sectional contours generated by the Laplace equation method (A) and the orthogonal projection method (B) on an idealized corpus callosum using the Laplace equation method, whereas (C) and (D) compare the node positions and the resultant thickness profiles, respectively, constructed by both methods on the same callosal image. The contours labelled 36 and 37 in (B) are examples of overlapping contours produced by the orthogonal projection method, and (C) reveals that there are discrepancies between the nodal locations used by the two methods. The Laplace method midline seems to have smaller overall distance because of its geometry near the genu and splenium as illustrated in the inset in Figure 1(A). Therefore, the extreme nodes produced by the Laplace method are more advanced lengthwise along the callosum than their orthogonal projection method counterparts. Despite these disparities in nodal locations, these methods produce similar thickness profiles [Fig. 1(D)], suggesting that direct comparison of statistical analysis results produced by these methods is valid.

Figure 1.

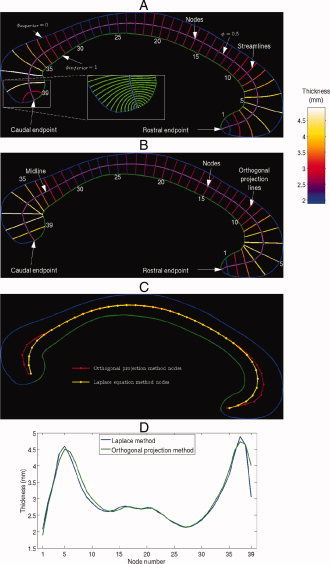
Figure 1

Open in a new tab

Laplace equation thickness model (A) and orthogonal projection method thickness model (B) shown on an idealized corpus callosum. The 39 sampled streamlines in (A) and (B) are colored according to callosal thickness and are annotated with their indices, which were chosen to increase caudally. (A) (Inset) Magnification of the streamlines (not colored according to callosal thickness), constructed from a denser sampling of the midline, near the splenium. A comparison of the node locations and resultant regional thickness profiles of the two methods are shown in (C) and (D), respectively.

As previously noted, the orthogonal projection method is prone to producing overlapping contours. Figure 2 quantitatively reveals that there are high concentrations of overlapping contours at the genu and splenium. This validates our earlier statement that the orthogonal projection method is prone to constructing crossing streamlines within regions of high curvature. Note that there are no occurrences of overlapping contours in the midbody of the callosum, which has limited curvature. In addition, crossing streamlines occur in a high number of cases, with the maximum proportions of callosi in which overlapping contours occur in these areas, across the entire dataset, are 64.16 and 31.66%, respectively.

Figure 2.

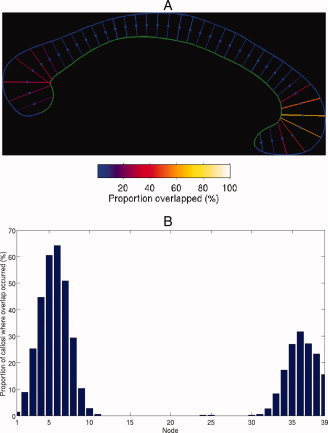
Figure 2

Open in a new tab

(A) Idealized callosum with the contours colored according to the number of callosi, as a percentage, in the dataset in which that contour intersected with at least one other contour. (B) Graphical representation of (A) with the non‐intersecting nodes, across the entire dataset, omitted.

Figure 3 shows a selection of particular callosi in which the effects of overlapping were particularly profound on callosal thickness measurements. Specifically, panels (A–C) contain callosi in which slices 37, 38, and 37 (indicated by the white arrows), respectively, located in the splenium, were constructed incorrectly. Rather than terminating within the inferior portion of the splenium, these streamlines penetrate into the midbody and intersect with multiple rostral neighbours. As a result, their callosal thicknesses are overestimated. The same slices in the Laplace equation terminate within the splenium. Figure 3(D) displays the typical overlapping pattern in the genu, where multiple streamlines converge on the highly curved segment of the inferior boundary, annotated by the white arrow. At the inferior boundary the streamlines of the orthogonal method overlap, resulting in overestimated thickness values, although the streamlines constructed by the Laplace equation method converge to similar locations, they do not overlap.

Figure 3.

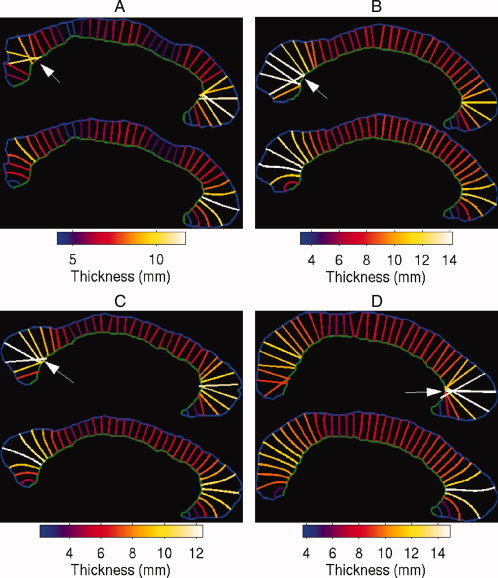
Figure 3

Open in a new tab

Four selected callosi with overlapping streamlines produced by the orthogonal projection method. In each figure, the top panel shows the streamlines produced by the orthogonal projection method, whereas the lower panel shows the streamlines produced by the Laplace equation method.

To further investigate the validity of comparing statistical analysis results between the two methods, Figure 4presents the nodal mean thicknesses and variances for the CTL cohort. The profile of the mean thickness is consistent across the two methods and the variance values are comparable, which provides further evidence that comparison of statistical analysis results of these methods is valid.

Figure 4.

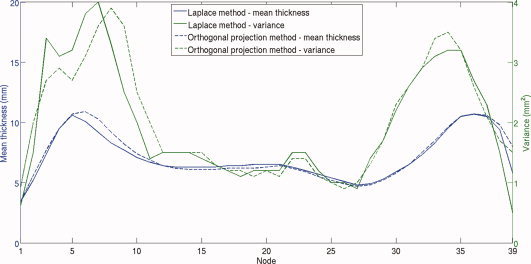
Figure 4

Open in a new tab

Mean thickness and variance values for the Laplace and Orthogonal projection thickness measurement methods for the CTL group. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

A comparison of group‐wise statistical analysis results generated by the straight‐line and Laplace methods can be seen in Figure 5, with significant regional between‐group changes mapped to a mean callosum. When CSZ were compared with CTL, a similar profile of significant reductions was seen in the anterior (Laplace: nodes 1–5, orthogonal projection: 1–5) and posterior genu (Laplace: 11 & 14–15, orthogonal projection: 11–18), and in the body and isthmus (Laplace: nodes 20–21 & 29, orthogonal projection: 20–21, 27–30), and were highly significant for both methods (Laplace: P < 0.005, orthogonal projection: P < 0.005). When the FEP and CTL groups were compared, reductions were again seen in the anterior genu (Laplace: 1‐2, orthogonal projection: 1‐4), which were at trend level for both methods (Laplace: P = 0.056, orthogonal projection: P = 0.053). When UHR and CTL groups were compared, no significant differences were detected using either method (P = 0.75 using the Laplace method, P = 0.64 using the straight‐line method). When the UHR‐P and UHR‐NP groups were compared, significant reductions were again seen at the level of the genu (Laplace: nodes 3‐4, orthogonal projection: nodes 1‐4) and were significant for both (Laplace: P < 0.01, orthogonal projection: P < 0.05). Although the statistically significant profiles were broadly in the same areas across these datasets, the Laplace method produced fewer regions of significant difference, particularly in the genu of the callosum, where curvature is greatest. Results using the Laplace methodology are broadly consistent with findings already published on this dataset [Walterfang et al.,2008a,2008b,2009a].

Figure 5.

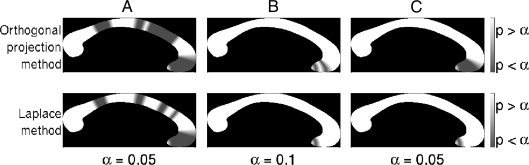
Figure 5

Open in a new tab

Comparison of statistical analysis results using the orthogonal projection callosal thickness measure (first row) and the Laplace method callosal thickness measure (second row). The columns of the figure denote the CSZ vs. CTL (A), FEP vs. CTL (B), and the UHR‐P vs. UHR‐NP (C) contrasts.

DISCUSSION

We used an adaptation of the method in [Hutton et al.,2008; Jones et al.,2002; Schmitt and Böhme,2002; Yezzi and Prince,2003], for measuring thickness between the superior and inferior surfaces of the corpus callosum. The Laplace equation thickness measurements produced similar results in between‐group comparisons to the straight‐line method across a large dataset in whom robust and meaningful differences have previously been demonstrated.

The primary motivation for developing the Laplace equation method was that the desirable properties of orthogonal boundary intersections and non‐overlapping contours were guaranteed. We do not claim that the Laplace method provides a more biologically valid thickness measure because current in vivo imaging techniques cannot be used to validate any method against the microscopic organisation of the fibres within the CC. In this sense, any subdivision method of the CC that is purely applied to MR data is heuristic in nature. However, the properties of Laplace's equation guarantee desirable mathematical and geometric properties of the thickness measurement contours.

Apart from the segmentation of the CC and the selection of the endpoints, which were performed semi‐automatically to validly compare results with the previous technique, the discretization of the callosum is fully automatic. The mathematical properties of the thickness model, derived from Laplace's equation, guarantee that the thickness measures are derived from non‐intersecting contours. As a result, our methodology avoids the potential limitation of methods that use orthogonal projections, where intersections may occur in areas of high curvature (such as at the genu or splenium). The Laplace equation thickness model thus avoids “crossing” thickness measures, and may be more suitable for a curved structure.

We found that using Laplace's equation yielded similar results to our original analysis using a thickness measurement derived from a straight line orthogonal to a calculated mid‐spline traversing the callosum, suggesting that applying the Laplace methodology to calculating callosal thickness has face validity in that it detects change in similar regions to those where change was detected using the straight‐line methodology. As seen in the CSZ vs. CTL comparisons, fewer slices in the genu are significantly different across groups, and in the FEP vs. CTL comparisons, no genu slices differ significantly; the findings in the UHR group are similar to the orthogonal projection method. Here, the foci of significant change appear in similar regions, but are less strongly positive. On the basis of the evidence that the orthogonal projection method produced overlapping contours in the genu, the Laplace equation method may reduce false positive results that occur in areas of high curvature, such as in the genu. This cannot be attributed to a more conservative statistical approach, as the permutation method used for each analysis was identical. It is also possible however that application of the Laplace equation method reduces sensitivity to detect change, resulting in a lack of detection of true differences.

This adaptation of Laplace's equation differs from the original cortical thickness description in a few key areas. Firstly, our application of this methodology to a mid‐sagittal callosal image occurs in two dimensions rather than three, although the Laplace equation is equally mathematically valid to describe a contour connecting two points in both circumstances, as the Laplace operator may be defined in any number of dimensions and the nested sublayers that are derived using Laplace's equation can occur in two or three dimensions. Furthermore, the robust measurement of cortical thickness requires the careful measurement of the inner cortical boundary, which requires careful segmentation of outer grey from inner white matter (usually based on voxel intensity), and errors in segmentation can result in incomplete surfaces. Due to the nature of the mid‐sagittal image of the callosum, with a large continuous region of high‐intensity white matter voxels with a well‐defined edge, the superior and inferior boundary of the callosum is very well‐defined using histogram segmentation.

One additional departure from [Hutton et al.,2008; Jones et al.,2002; Schmitt and Böhme,2002; Yezzi and Prince,2003], is that, unlike in the cerebral cortex, the superior and inferior boundaries of the corpus callosum do ultimately meet at its anterior and posterior endpoints. This raises the question of how to accurately measure thickness near the callosal endpoints. The inset of Figure 1(A) displays the behaviour of the streamlines near the endpoints, where a denser sampling of the midline was used to make the properties more obvious. Because the angle between the boundaries becomes obtuse, the streamlines must become increasingly curved and their endpoints must converge until ultimately colliding at the intersection between the boundaries. Arguably these streamlines do not make cross‐sectional traversals and, although these streamlines may be used in shape descriptors, therefore their lengths should not be interpreted as thickness measures. We used the 39‐point subdivision because the extreme contours were sufficiently distant from the endpoints to make cross‐sectional traversals. It is notable that no significant differences were found in thickness measures at the endpoints, positive findings in future analyses at these endpoints would need to be interpreted cautiously.

Attempts to improve the validity and robustness of neuroimaging methodologies are aimed at allowing researchers to enhance their capacity to detect true differences between diseased and healthy brains, and to monitor changes in brain structure and function with illness progression or in response to treatment.

Through utilization of the Laplace equation to robustly measure thickness of the callosum across its entire structure, including more highly curved regions near its endpoints, a more valid measure of regional callosal thickness may allow us to undertake more biologically meaningful and relevant analyses of regional callosal changes that occur in disease states.

The medial representation (M‐rep) method of Pizer et al. (2003) is an alternative technique to produce non‐overlapping, cross‐sectional contours for CC thickness measurements. For the CC, the thickness is measured using “spoke” contours that emanate from a medial axis, which bisects the CC from the genu to the splenium. This model was applied to the CC by Yushkevich et al. [2001] and the continuous version (cm‐reps) [Yushkevich et al.,2008], which uses the same “spoke” contours for thickness computation was applied by Sun et al. [2006]. However, although the contours emanating from the medial axis are linear, the cross‐sectional contours, formed by concatenating two “spoke” contours originating from the same node, is only piecewise‐linear. Nonetheless, both the M‐rep and the Laplace are computationally elegant models of thickness and do not necessarily reflect the underlying anatomy of the CC. Therefore, neither of these methods are inherently superior in calculating biologically valid thickness measurements.

The novel aspect of the recent work of Yushkevich et al. [2008] is that the callosal segmentation was extended laterally, beyond the midsagittal slice and this work examined the 3D callosal morphology. The Laplace equation thickness model is also applicable in this context. An avenue for future work is to investigate whether this extended definition of callosal geometry, using both thickness models, leads to a more informative description of disease states.

REFERENCES

  1. Bachmann S, Pantel J, Flender A, Bottmer C, Essig M, Schröder J ( 2003): Corpus callosum in first‐episode patients with schizophrenia—A magnetic resonance imaging study. Psychol Med 33: 1019–1027. [DOI] [PubMed] [Google Scholar]
  2. Barta P, Miller MI, Qiu A ( 2005): A stochastic model for studying the laminar structure of cortex from MRI. IEEE Trans Med Imaging 24: 728–742. [DOI] [PubMed] [Google Scholar]
  3. Beauchamp M, Anderson V, Catroppa C, Maller J, Godfrey C, Morse S, Rosenfeld J, Haritou F, Kean M ( 2009): Implications of reduced callosal area for social skills after severe traumatic brain injury in children. J Neurotrauma 26: 1645–1654. [DOI] [PubMed] [Google Scholar]
  4. Benjak V, Culjat M, Pavlovic M, Kostovic‐Srzentic M ( 2008): Changes of the corpus callosum in children who suffered perinatal injury of the periventricular crossroads of pathways. Coll Antropol 32: S25–S29. [PubMed] [Google Scholar]
  5. Bermudez P, Zatorre R ( 2001): Sexual dimorphism in the corpus callosum: Methodological considerations in MRI morphometry. Neuroimage 13: 1121–1130. [DOI] [PubMed] [Google Scholar]
  6. Brambilla P, Nicoletti M, Sassi R, Mallinger A, Frank E, Keshavan M, Soares J ( 2004): Corpus callosum signal intensity in patients with bipolar and unipolar disorder. J Neurol Neurosurg Psychiatry 75: 221–225. [PMC free article] [PubMed] [Google Scholar]
  7. Casanova M, Sanders R, Goldberg T, Bigelow L, Christison G, Torrey E, Weinberger D ( 1990a): Morphometry of the corpus callosum in monozygotic twins discordant for schizophrenia: A magnetic resonance imaging study. J Neurol Neurosurg Psychiatry 53: 416–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Casanova M, Zito M, Goldberg T, Suddath R ( 1990b): Corpus callosum curvature in schizophrenic twins. Biol Psychiatry 28: 83–84. [PubMed] [Google Scholar]
  9. Downhill JE, Buchsbaum MS, Wei T, Spiegel‐Cohen J, Hazlett EA, Haznedar MM, Silverman J, Siever LJ ( 2000): Shape and size of the corpus callosum in schizophrenia and schizotypal personality disorder. Schizophr Res 42: 193–208. [DOI] [PubMed] [Google Scholar]
  10. Evans AC, Collins DL, Mills SR, Brown ED, Kelly RL, Peters TM ( 1993): 3D Statistical Neuroanatomical Models From 305 MRI Volumes. Nuclear Science Symposium and Medical Imaging Conference, Vol. 3, 1993, 1993 IEEE Conference Record, p 1813–18 17.
  11. Fischl B, Dale AM ( 2000): Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA 97: 11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Frumin M, Golland P, Kikinis R, Hirayasu Y, Salisbury D, Hennen J, Dickey C, Anderson M, Jolesz F, Grimson W, McCarley R, Shenton M ( 2002): Shape differences in the corpus callosum in first‐episode schizophrenia and first‐episode psychotic affective disorder. Am J Psychiatry 159: 866–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hampel H, Teipel S, Alexander G, Horwitz B, Teichberg D, Schapiro M, Rapoport S ( 1998): Corpus callosum atrophy is a possible indicator of region‐ and cell type‐specific neuronal degeneration in Alzheimer disease: A magnetic resonance imaging analysis. Arch Neurol 55: 193–198. [DOI] [PubMed] [Google Scholar]
  14. Hofer S, Frahm J ( 2006): Topography of the human corpus callosum revisited—Comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. NeuroImage 32: 989–994. [DOI] [PubMed] [Google Scholar]
  15. Holm S ( 1979): A simple sequentially rejective multiple test procedure. Scand J Statist 6: 65–70. [Google Scholar]
  16. Holmes A, Blair R, Watson J, Ford I ( 1996): Nonparametric analysis of statistic images from functional mapping experiements. J Cereb Blood Flow Metab 16: 7–22. [DOI] [PubMed] [Google Scholar]
  17. Hutton C, De Vita E, Ashburner J, Deichmann R, Turner R ( 2008): Voxel‐based cortical thickness measurements in MRI. NeuroImage 40: 1701–1710. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Jones SE, Büchbinder BR, Aharon I ( 2002): Three‐dimensional mapping of cortical thickness using laplace's equation. Hum Brain Mapp 11: 12–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lagarias JC, Reeds JA, Wright MH, Wright PE ( 1998): Convergence properties of the Nelder‐‐Mead simplex method in low dimensions. SIAM J Optimization 9: 112–147. [Google Scholar]
  20. MacDonald D, Kabani N, Avis D, Evans AC ( 2000): Automated 3‐D extraction of inner and outer surfaces of cerebral cortex from MRI. NeuroImage 12: 340–356. [DOI] [PubMed] [Google Scholar]
  21. Narr K, Thompson P, Sharma T, Moussai J, Cannestra A, Toga A ( 2000): Mapping morphology of the corpus callosum in schizophrenia. Cereb Cortex 10: 40–49. [DOI] [PubMed] [Google Scholar]
  22. Otsu N ( 1979): A threshold selection method from gray‐level histograms. IEEE Trans Syst Man Cybernetics 9: 62–66. [Google Scholar]
  23. Pantel J, Schröder J, Essig M, Minakaran R, Schad L, Friedlinger M, Jauss M, Knopp M ( 1998): Corpus callosum in Alzheimer's disease and vascular dementia—A quantitative magnetic resonance study. J Neural Transm Suppl 54: 129–136. [DOI] [PubMed] [Google Scholar]
  24. Peters M, Oeltze S, Seminowicz D, Steinmetz H, Koeneke S, Jäncke L ( 2002): Division of the corpus callosum into subregions. Brain Cogn 50: 62–72. [DOI] [PubMed] [Google Scholar]
  25. Pizer SM, Fletcher PT, Joshi S, Thall A, Chen JZ, Fridman Y, Fritsch DS, Gash AG, Glotzer JM, Jiroutek MR, Lu C, Muller KE, Tracton G, Yushkevich P, Chaney EL ( 2003): Deformable M‐Reps for 3D medical image segmentation. Int J Comput Vision 55: 85–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Schmitt O, Böhme MA ( 2002): A robust transcortical profile scanner for generating 2‐D traverses in histological sections of richly curved cortical courses. NeuroImage 16: 1103–1109. [DOI] [PubMed] [Google Scholar]
  27. Smith SM ( 2002): Fast robust automated brain extraction. Hum Brain Mapp 17: 143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Sun H, Yushkevich PA, Hui Z, Cook PA, Dida JT, Simon TJ, Gee JC ( 2006): Shape‐based normalization of the corpus callosum for DTI connectivity analysis. IEEE Trans Med Imaging 26: 1166–1178. [DOI] [PubMed] [Google Scholar]
  29. Vidal CN, Nicolson R, DeVito TJ, Hayashi KM, Geaga JA, Drost DJ, Williamson PC, Rajakumar N, Sui Y, Dutton RA, Toga AW, Thompson PM ( 2006): Mapping corpus callosum deficits in autism: An index of aberrant cortical connectivity. Biol Psychiatry 60: 218–225. [DOI] [PubMed] [Google Scholar]
  30. Walterfang M, Wood A, Reutens D, Wood A, Chen J, Velakoulis D, McGorry P, Pantelis C ( 2009a): Corpus callosum size and shape in first‐episode affective and schizophrenia‐spectrum psychosis. Psych Res Neuroimaging 173: 77–82. [DOI] [PubMed] [Google Scholar]
  31. Walterfang M, Wood A, Reutens D, Wood S, Chen J, Velakoulis D, McGorry P, Pantelis C ( 2008a): Morphology of the corpus callosum at different stages of schizophrenia: Cross‐sectional study in first‐episode and chronic illness. Br J Psychiatry 192: 429–434. [DOI] [PubMed] [Google Scholar]
  32. Walterfang M, Yücel M, Barton S, Reutens D, Wood A, Chen J, Lorenzetti V, Velakoulis D, Pantelis C, Allen N ( 2009b): Corpus callosum size and shape in individuals with current and past depression. J Affect Disord 115: 411–420. [DOI] [PubMed] [Google Scholar]
  33. Walterfang M, Yung A, Wood A, Reutens D, Phillips L, Wood S, Chen J, Velakoulis D, McGorry P, Pantelis C ( 2008b): Corpus callosum shape alterations in individuals prior to the onset of psychosis. Schizophr Res 103: 1–10. [DOI] [PubMed] [Google Scholar]
  34. Woods R, Grafton S, Holmes C, Cherry S, Mazziotta J ( 1998): Automated image registration I: General methods and intrasubject, intramodality validation. J Comput Assist Tomogr 22: 155–165. [DOI] [PubMed] [Google Scholar]
  35. Yamauchi H, Fukuyama H, Nagahama Y, Katsumi Y, Hayashi T, Oyanagi C, Konishi J, Shio H ( 2000): Comparison of the pattern of atrophy of the corpus callosum in frontotemporal dementia, progressive supranuclear palsy, and Alzheimer's disease. J Neurol Neurosurg Psychiatry 69: 623–629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Yezzi AJ Jr, Prince JL ( 2003): An Eulerian PDE approach for computing tissue thickness. IEEE Trans Med Imaging 22: 1332–1339. [DOI] [PubMed] [Google Scholar]
  37. Yushkevich P, Pizer S, Joshi S, Marron JS ( 2001): Intuitive, Localized Analysis of Shape Variability. Information Processing in Medical Imaging. pp 402–408.
  38. Yushkevich PA, Zhang H, Simon TJ, Gee JC ( 2008): Structure‐specific statistical mapping of white matter tracts. NeuroImage 41: 448–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zeng X, Staib LH, Schultz RT, Duncan JS ( 1998): Segmentation and Measurement of the Cortex from 3D MR Images. MICCAI 1998 – LNCS 1496. pp 519–526. [DOI] [PubMed] [Google Scholar]

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES