Tracking children's mental states while solving algebra equations

Abstract

Behavioral and function magnetic resonance imagery (fMRI) data were combined to infer the mental states of students as they interacted with an intelligent tutoring system. Sixteen children interacted with a computer tutor for solving linear equations over a six‐day period (Days 0–5), with Days 1 and 5 occurring in an fMRI scanner. Hidden Markov model algorithms combined a model of student behavior with multi‐voxel imaging pattern data to predict the mental states of students. We separately assessed the algorithms' ability to predict which step in a problem‐solving sequence was performed and whether the step was performed correctly. For Day 1, the data patterns of other students were used to predict the mental states of a target student. These predictions were improved on Day 5 by adding information about the target student's behavioral and imaging data from Day 1. Successful tracking of mental states depended on using the combination of a behavioral model and multi‐voxel pattern analysis, illustrating the effectiveness of an integrated approach to tracking the cognition of individuals in real time as they perform complex tasks. Hum Brain Mapp, 2012. © 2011 Wiley Periodicals, Inc.

INTRODUCTION

This research reports an exploration of how multi‐voxel pattern analysis (MVPA) of fMRI data [e.g., Abdelnour and Huppert, 2009; Davatzikos et al., 2005; Haxby et al., 2001; Haynes et al., 2007; Haynes & Rees, 2005; Hutchinson et al., 2009; Mitchell et al., 2008; Norman et al., 2006] can be used to track the sequential structure of thought. Our particular application involves inferring the mental states of students learning mathematics. Diagnosing what a student is thinking is critical to the success of intelligent tutoring systems (e.g., cognitive tutors), which are computer‐based systems that have had some success in teaching mathematics to school children [Anderson et al., 1995; Koedinger et al., 1997; Ritter et al., 2007]. These tutors track students as they solve problems and make instructional decisions based on this tracking. The only information available to a typical tutoring system comes from the actions taken by students using the computer interface. Given that this surface behavior permits only limited inferences about what a student is thinking, it may be fruitful to consider how other types of data can be used to diagnose a student's mental state. In this article, we show how brain‐imaging data can be combined with a behavioral model to help solve this diagnosis problem.

Interpreting a student's mental state in the context of tutoring systems poses a problem not faced by many applications of MVPA. In typical MVPA, the scan sequence is already segregated into events to be classified. However, in a tutoring context, one has to infer how to break up a continuous stream of scans into events to be classified. This is similar to the problem of word identification in continuous speech, where both word boundaries and word identities must be determined simultaneously. The problem in speech recognition has been addressed with considerable success using hidden Markov model (HMM) algorithms [Rabiner, 1989]; therefore, we adapted the HMM approach to a tutoring context in order to simultaneously segment and classify events from scans of student problem solving. However, following Anderson et al. [ 2010], we argue that diagnosis of students' mental states requires augmenting MVPA techniques with a model of how students solve the problems. Continuing with the speech recognition analogy, this is akin to using a theory of grammar and lexical preferences to help narrow the choices that need to be made in processing speech signals. For the tutoring context studied here, we used a model of student behavior based on the information provided by the cognitive model in the tutor; namely, the likely steps involved in solving a problem and the relative difficulty of those steps.

The research reported here followed the general approach outlined in Anderson et al. [ 2010] and investigated whether it could be used to diagnose the mental states of children interacting with a tutoring system. We used the experimental tutoring system described in Anderson [ 2007] and Brunstein et al. [ 2009] that teaches a complete curriculum for solving linear equations based on the classic algebra text of Foerster [1990]. The tutoring system has a minimalist design to facilitate experimental control and detailed data collection. Nonetheless, it has the basic components of a cognitive tutor: instruction when new material is introduced, help upon request, and error flagging during problem solving. We were concerned with tracking students' mental states as they solved problems after receiving the initial instruction in a section of the curriculum1.

Figure 1 illustrates the solution of a simple problem in the curriculum: the linear equation x − 10 = 17. Students used a mouse for all tutor interactions—to select parts of the problem on which to operate, to select operations from a menu, and to enter values from a numeric keypad. Figure 1 illustrates the four‐step cycle in solving a problem: selecting a transformation, executing the transformation, selecting an evaluation, and executing the evaluation. Selecting refers to choosing both parts of the expression and an operation to perform on those parts. Executing refers to entering a new expression produced by the operation. These two steps are repeated in the transformation and the evaluation phases. Transformation refers to creating an algebraic re‐arrangement of the expression (e.g., converting x − 10 = 17 into x = 17 + 10). Evaluation refers to performing an arithmetic computation to simplify the transformed expression (e.g., evaluating 17 + 10 as 27). For the example in Figure 1, problem solving involves just one cycle of these four steps. More complex problems involved many cycles of these four steps.

Figure 1.

Each panel illustrates one of the four steps in a problem‐solving cycle with the tutor. The subpanels show the states of the tutor within a step. Each step starts with the last state of the previous step. The subpanels also indicate the minimal number of mouse clicks required to achieve that state for this specific problem. The first panel starts with the initial equation x − 10 = 17.

Step 1: The student selects a transformation to perform on this equation by clicking on the two sides of the equation (resulting in red highlighting) and choosing “Unwind” from the menu below. “Unwind” refers to undoing the operations surrounding the unknown; in this case undoing the “−10” by adding 10.

Step 2: The student expresses the result of the transformation by selecting a green box and entering 17 + 10. This results in the transformed equation x = 17 + 10.

Step 3: The student specifies that 17 + 10 is to be evaluated by clicking on this expression (resulting in the highlighting) and selecting “Evaluate” from the menu below.

Step 4: The student specifies the result of the evaluation by selecting a green box and entering 27. This creates the final answer x = 27. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The experiment involved students going through a sequence of such problems. We used brain‐imaging data in conjunction with a model of student behavior to address two goals associated with inferring students' mental states. First, we addressed the segmentation goal of determining which problem a student was solving and which step in the problem‐solving sequence the student was performing. Second, we addressed the diagnosis goal of determining whether a step was being performed correctly.

Students worked with the tutor over 6 days, which we refer to as Days 0–5, and were scanned on Days 1 and 5. We took slightly different approaches to interpreting the imaging data of students on these two days. On Day 1, we used the data from other students to interpret the brain activity of a particular student. On Day 5, we also used the data from that particular student on Day 1. Thus, Day 1 offers a test of how well the patterns of activity generalize across students while Day 5 provides evidence about how much more is added by knowledge of the particular student. This approach is similar to the deployment of computer tutors, where initially one must use the behavioral patterns of other students to interpret new students, but one can subsequently build up a model of the new students as they progress through the curriculum.

METHODS

Participants and Experimental Procedure

Sixteen right‐handed children (5 females and 11 males, 11–15 years old, mean = 13.1 years) were recruited by advertisement in a local Pittsburgh newspaper. Half were in pre‐algebra and the other half were beginning an algebra course. They were all relatively competent mathematically: 14 reported A's in their prior math course and the other two had B's.

The students went through a curriculum based on the sections in the Foerster [1990] text for transforming and solving linear equations. The experiment spanned six days. Figure 2 illustrates what happened over these days. On Day 0, students practiced the evaluation subsequence (Steps 3 and 4 in Fig. 1) and familiarized themselves with the tutoring system. On Day 1, three sections (described below) were completed in an fMRI scanner. On Days 2–4, they practiced more material from these sections and material from more advanced sections. On Day 5, the three sections used on Day 1 were repeated (but with new problems), again in the fMRI scanner. There were two problem sets for each of the three sections used on Days 1 and 5. Half of the students solved one problem set on Day 1 and the other set on Day 5; the other half had the opposite order. Instruction was provided at the start of each new section. Each section on Days 1 and 5 involved three scanning blocks during which the students solved 2–7 problems per block from the problem set for that section. The blocks were separated by breaks in the scanner sequence and were the major object of analysis. Continuing with the speech recognition analogy, the blocks were treated as “utterances” that we attempted to segment into a series of significant events that could be classified.

Figure 2.

Material presented over days and structure of scanning blocks on Days 1 and 5. The algebraic expressions are examples of what appeared in various sections on scanning days.

The three sections used on Days 1 and 5 covered three topics: solution of single‐operation equations (e.g., x − 10 = 17, illustrated in Fig. 1), the collection of constants in an expression (e.g., (7 + x) − 9), and the solution of two‐operation equations (e.g., 3x + 5 = 17). The first two sections involved one cycle of the four basic steps in Figure 1, whereas the third section involved two cycles and, therefore, eight steps. The more advanced sections completed on Days 2–4 (outside of the scanner) often involved many more than two cycles. Students solved the problems at their own pace. After a problem was solved, there was a 14‐s rest period (during which time a crosshair appeared onscreen) before the next problem was presented. In addition to the rest period after each problem, there was a 22‐s period at the start of each block during which a crosshair appeared.

Students interacted with the tutor using a mouse and clicking on parts of the equation to select them (these parts turned red when selected as illustrated in Fig. 1), to select operators from a set of buttons (selected buttons are boxed in Fig. 1), and to create expressions using a keypad displayed on the screen (as illustrated for “Execute Transformation” in Fig. 1). They used normal USB optical mouse that had its ferrous metal removed along with a signal booster on the interface cable to avoid interference.

Each new section began with some instruction but this was not scanned. Then the student went through a set of three scanning blocks for that section. The majority of the students' time was spent in these scanning blocks. If students made an error while solving a problem, it was signaled and they had to correct the error before they went on to the next step in the problem. They could request a hint at any point in time and the next step would be explained and the student was told the correct actions to perform in the interface2. In case the student made as many as five mistakes in a step, this explanation was automatically given to the student even if they did not ask for a hint.

FMRI Data Acquisition and Initial Analysis

Images were acquired using gradient echo‐planar imaging (EPI) on a Siemens 3T Allegra Scanner using a standard RF head coil (quadrature birdcage), with 2‐s repetition time (TR), 30‐ms echo time (TE), 70° flip angle, and 20‐cm field of view (FOV). We acquired 34 oblique‐axial slices on each full‐volume scan using a 3.2‐mm thick, 64 × 64 matrix. The anterior commissure–posterior commissure (AC‐PC) line was on the 11th slice from the bottom.

Acquired images were analyzed using the NIS system. Functional images were motion‐corrected using 6‐parameter 3D registration [AIR; Woods et al., 1998]. All images were then co‐registered to a common reference structural MRI by means of a 12‐parameter 3‐D registration [AIR; Woods et al., 1998] and smoothed with a 6‐mm full‐width‐half‐max 3‐D Gaussian filter to accommodate individual differences in anatomy.

A total of 408 regions were created by evenly distributing 4 × 4 × 4 voxel cubes over the 34 slices of the 64 × 64 acquisition matrix. Between‐region spacing was 1 voxel in the x‐ and y‐directions in the axial plane and one slice in the z‐direction. The final set of regions was acquired by applying a mask of the structural reference brain and excluding regions where less than 70% of the region's original 64 voxels survived.

Results3

Descriptive Behavioral Statistics

There were 144 blocks for each day (16 students × 3 sections × 3 blocks). Because of problems with the scanner, one block was lost for each of five students on Day 1 and for each of four students on Day 5, leaving 139 blocks to be analyzed for Day 1 and 140 for Day 5. The children solved 2–7 problems in each block, which took anywhere from 53 to 278 2‐s scans. Altogether, they solved 727 problems on Day 1, providing 19,376 scans of data, and 742 problems on Day 5, providing 15,614 scans of data. On Day 1, 12.8% of the steps involved errors and on Day 5, 6.6% involved errors. We defined an error as selection of the wrong part of an equation or a wrong operation in Steps 1 and 3 or entry of an incorrect result in Steps 2 and 4. Table I gives the statistics on time to execute a step (operationalized as number of scans involving that step and step accuracy). The two execution steps (2 and 4) took much longer (i.e., more scans) than the selection steps (1 and 3), whereas the two transformation steps (1 and 2) were more error‐prone than the evaluation steps (3 and 4). Students sped up more than 70% and their error rate dropped almost in half from Day 1 to Day 5.

Table I.

Behavioral statistics for the four steps

	Day 1			Day 5
	Mean scans	St.dev scans	Percent errors	Mean scans	St.dev scans	Percent errors
1. Select transformation	2.31	2.31	20.8%	1.47	0.94	10.5%
2. Execute transformation	7.10	5.05	20.6%	4.62	2.85	10.4%
3. Select evaluation	1.24	0.85	3.3%	0.76	0.64	0.8%
4. Execute evaluation	3.68	2.58	6.6%	2.99	2.37	6.6%

Behavioral Model

We developed both a behavioral model and an fMRI model to interpret the students' mental states and then combined the two approaches with an HMM. In this section, we describe the behavioral model. The fMRI model and the combined HMM models are described in later sections.

Predicting Day 1 behavior

We investigated how well the behavior of other students on a problem predicted the behavior of a particular student on that same problem. This is the kind of data used by a tutoring system. The target variable was the performance (either time or accuracy) of each student on each step of each problem. The predictor variable was the average performance of the other 15 students on the same steps of the problems. Predicting each student by using the data from the other 15 students is basically the leave‐one‐out methodology for cross‐validation [e.g., Peieira et al., 2009]. Thus, each student provides the target variables for himself and contributes to the predictor variables for the other students. Given that there were two problem sets for each section of the curriculum, with half of the students doing a particular set on Day 1 and the other half doing that same set on Day 5, the predictor observations for a particular problem came from both days. For each of the performance measures (time and accuracy), there were 3,560 predictor–target pairs (564 problems involving one cycle of four steps and 163 problems involving two cycles of four steps).

With respect to Day 1 time for a step, the predictor variable was the average of two median times—the median number of scans taken on that step by other students on Day 1 and the median for the same step on Day 54. This predictor variable correlates 0.695 with the target variable, which is the number of scans taken on that step by a particular student on Day 1. To illustrate this relationship, Figure 3 groups the problems into three categories of difficulty (based on time per step): easy (a median of two scans or less), middle (a median of three or four scans), and hard (greater than four scans). Parts (a) and (b) of Figure 3 are for Day 1 and show the systematic relationship that exists between the mean difficulty that a specific student experienced on a step of a problem and the mean difficulty that other students experienced. Comparing the distributions for correct and incorrect steps in Figure 3a,b, the latter is shifted toward longer times. There are no observations of errors being made and corrected in fewer than two scans. Figure 3 also shows gamma distributions fit to the data; for errors, the gammas were shifted to begin at scan 2.

Figure 3.

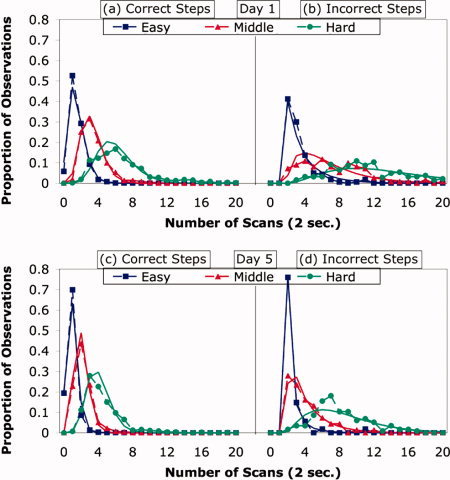
(a,b): Distribution of step times for a student on Day 1 as function of the difficulty other students experienced with that step. (c,d): Distribution of step times for a student on Day 5 as function of the difficulty other students experienced with that step and how slow that student was on Day 1. The points connected by dotted lines are the actual proportions of observations with different number of scans. The smooth lines are fitted gamma functions. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

With respect to Day 1 accuracy, the predictor variable was the average of the Day 1 and Day 5 error rates from the other students. Figure 4 illustrates the strong relationship between the probability that a specific student made an error on a step and the error rate of other students for that step. The predictor error rates were binned and the target probability of error for each bin was plotted in Figure 4. The correlation in the binned data is clearly strong (r = 0.999) and the best‐fitting linear function is Target = 0.04 + 0.87 × Predictor, indicating that any student's error probability is approximately equal to the error rate of the other students.

Figure 4.

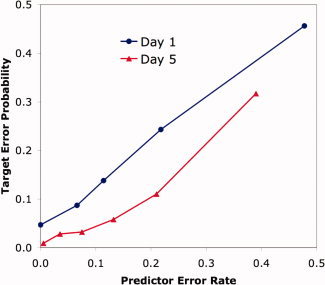
Probability that a student will make an error on a step as a function of the predictor error estimated from other data. Similar predictor error rates are aggregated to give different points on the figure. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

When interpreting the Day 1 data in Figures 3 and 4, it is important to recognize that we used the data from other students to predict a particular student whose data were not included in the average for prediction. Despite the strong relationship between the behavior of a particular student and that of other students, we found that it was not sufficient to predict the moment‐by‐moment behavior of a particular student, as will be shown in the later section on the performance of the algorithm.

Predicting Day 5 behavior

When predicting the times for a particular student on Day 5, we used that student's Day 1 data as well as the data from other students. This method of incorporating a student's earlier behavior is similar to how a typical tutor builds up a model of the student. The Day 5 predictor variables combined a student predictor, which was calculated from a student's Day 1 performance, with a problem predictor, which is the same predictor we used for Day 1 behavior. There were 3,612 predictor–target pairs for the Day 5 data (581 problems involving one cycle of four steps and 161 problems involving two cycles of four steps).

With respect to Day 5 time, the student predictor was the mean time each student took on each of the four steps on Day 1. These means, calculated separately for each particular student, correlated 0.626 with the target variable, which were the student's times on Day 5. The problem predictor correlated 0.696 with the target variable. The combined predictor was a 1/3 weighting of the student predictor and a 2/3 weighting the problem predictor5. This student‐by‐problem predictor correlated 0.711 with the target variable. Although the student‐by‐problem predictor yielded a relatively modest improvement over the problem predictor, the improvement is quite significant (t(3609) = 12.23). Thus, both the differences among students and the differences among steps contributed to predicting performance on Day 5. Figure 3c,d shows the systematic relationship that exists between the student‐by‐problem predictor and the time it took a student to perform the step on Day 5.

With respect to Day 5 accuracy, the student predictor was the average error rates of that particular student for the four types of steps. The student‐by‐problem predictor was again a 1/3 weighting of the student predictor and a 2/3 weighting of the problem predictor. Figure 4 also illustrates the relationship between this predictor and the Day 5 error rate. Again, the correlation is strong (r = 0.970) and the best‐fitting linear equation is Target = 0.72 × Predictor. The zero intercept, combined with a slope of less than 1, reflects the lower error rate on Day 5 than on Day 1, from which two‐thirds of the predictor observations came.

The problem predictors for Day 1 and the student‐by‐problem predictors for Day 5 represented the behavioral model that we combined with the imaging data to predict students' mental states. We used the gamma functions fit in Figure 3 for predicting times and we used the linear functions fit in Figure 4 for predicting error probabilities. However, before describing the integration of the behavioral model with the imaging data, we first describe how we processed the imaging data to get a complementary fMRI model.

Descriptive Imaging Analysis

To avoid overfitting and to make computation manageable, it was necessary to limit the number of regions for MVPA. Therefore, as described in the Methods section, we defined 408 regions that covered the entire brain, each region being approximately a cube with sides of 1.3 cm. Before describing the pattern analysis, we provide some statistics to characterize the response of these regions. To estimate the effects associated with the four steps (see Fig. 1), we created four boxcar functions that had values of 1 for scans occupied by these steps and 0 otherwise. We convolved these functions with the standard statistical parameter mapping (SPM) hemodynamic response function [Friston et al., 1998] to create four regressors. To estimate effects of errors, we added a fifth regressor created by convolving the hemodynamic response function with a boxcar function that had a value of 1 whenever an error was performed in a step. Finally, a set of regressors for a quadratic function was added for each block to correct for drift. This created a design matrix [Friston, 2006] that was regressed against the BOLD response in each region. For each subject and each region, we estimated three effects: an effect due to the difference between transformation and evaluation, (Steps 1 + 2) – (Steps 3 + 4); an effect due to the difference between selection and execution, (Steps 1 + 3) – (Steps 2 + 4); and an effect due to the difference between error steps and correct steps. These effects were evaluated with t‐tests for each region. We report only those regions with t values that exceeded the 2.13 threshold for two‐tailed significance given 15 degrees of freedom (16 subjects). Each of the three effects was associated with many more significant regions than the 0.05 × 408 = 20.4 regions expected by chance. Given that the goal of this analysis was descriptive rather than inferential (to provide context for understanding the results of the fMRI model—these analyses were not used in the fMRI model), we did not threshold these regions for multiple comparisons.

Figure 5a shows the 170 regions to reach significance for the error effect. Areas that showed increased activation in the presence of errors include the anterior cingulate cortex (ACC), lateral inferior prefrontal cortex (LIPFC), and the anterior insula. The ACC and anterior insula have been shown to be related to errors [e.g., Ullsperger et al., 2010]. In the ACT‐R model of algebra equation solving [Anderson, 2005], the ACC is associated with goal setting and the LIPFC with retrieval. In contrast to these regions, the left motor region controlling the right response hand showed decreased activation for errors, reflecting the slower rate of responding during an error period.

Figure 5.

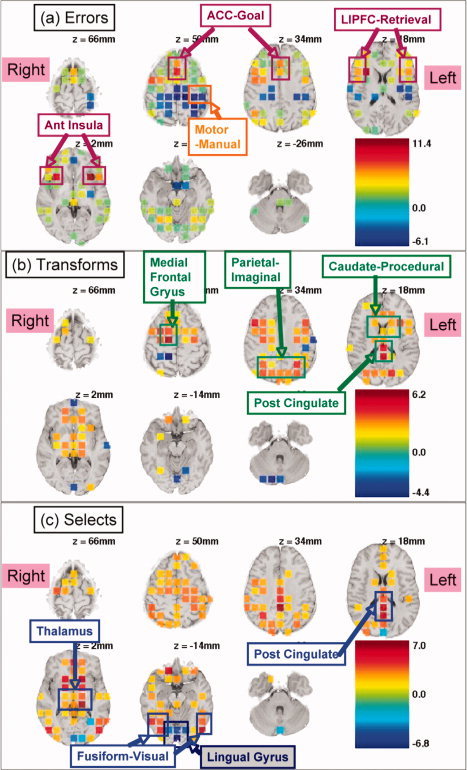
Regions showing significant effects of error (a), transformation versus evaluation (b), and selection versus execution (c). Refer to Figure 1 for illustration of transformation, evaluation, selection, and execution. Values indicated by color are t values.

Figure 5b shows the 103 regions with a significant difference between transformation steps and evaluation steps. Most of these regions showed greater activation for transformations. These regions include the medial frontal gyrus, the posterior parietal, the caudate, and the posterior cingulate. In the ACT‐R theory, the parietal region is associated with imagined transformations of algebraic equations and the caudate is associated with the procedural execution of such transformations.

Figure 5c shows the 149 regions with a significant difference between selection steps and execution steps. Most of these regions showed greater activation for selection. These regions include the posterior cingulate, the thalamus, and visual regions in the vicinity of the fusiform. The thalamic region also tended to be active for the contrasts in Figure 5a,b. In contrast, the lingual gyrus showed greater activation for execution.

We note that a region that showed more activation for one type of step than for another (e.g., more activation for selection than for execution) may have done so because of a positive effect for one type of step, a negative effect for the other type of step, or both. However, any of these cases were equally useful for discriminating between the two types of steps. The classification algorithm that is part of the fMRI model is simply looking for a linear combination of activation values that discriminates among categories.

FMRI Model

Our goal was to predict what a student was doing during each scan of a block. For each scan for each region, we calculated the percent change in the fMRI signal for that scan from a baseline defined as the average magnitude of all preceding scans in that block. Anderson et al. [ 2010] showed that the best classification of mental state during a scan is obtained by using the imaging data that occur two scans (4 s) after the event of interest because of the delayed nature of the hemodynamic response.

Excluding the first 11 warm‐up scans, a linear discriminant classifier [McLachlan, 2004] was trained to categorize the scans as coming from one of nine states. One state was the rest period between problems and the remaining eight were defined by the cross‐product of the four steps and whether they were correct or not. As with the behavioral data, we used the average data of all other students to classify the Day 1 scans for an individual student. To classify the Day 5 scans, we added 15 replications of that student's data from Day 1 (to match the other 15 students).

The linear discriminant analysis provided estimates of the conditional probabilities that the fMRI pattern in a scan came from each of the nine categories. We classified each scan as coming from the category with the highest conditional probability. Figure 6 shows the proportion of scans from each category assigned to the various categories. The classifier achieved almost 80% accuracy in labeling the rest scans. Its ability to label the other eight categories was considerably more modest. Nonetheless, the most common classification for each correct step was the proper assignment. In the case of an error step, the classifier most often assigned the step to the proper step position, but it was split nearly evenly between whether that step was performed correctly or not.

Figure 6.

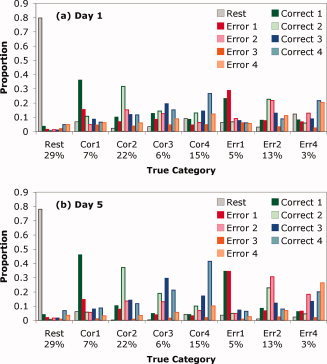
Ability of the linear discriminant function to distinguish among categories. The x‐axis gives the various categories and proportion of scans from that category. There were not enough observations of errors on step 3 to allow meaningful statistics (less than 0.5% on Day 1 and less than 0.2% on Day 5). The bars for each category show the proportion of scans in each category assigned to each of the nine possible categories.

Overall, 42.2% of the Day 1 scans and 52.9% of the Day 5 scans were correctly classified6. Chance was 15.6% for Day 1 and 18.9% for Day 57. Thus, the classifier was able to predict the data with much better than chance accuracy, even though its ability to discriminate among categories was somewhat short of what one might like. In the next section, we show that much better performance was achieved when the output of the classifier was combined with the behavioral model using HMM algorithms.

Adding the data from the specific student on Day 1 improved the accuracy of classification of that student on Day 5. Without the specific student's data, the accuracy was only 46.7%, which is a considerable drop from the 52.9% obtained with the student's data added in. On the other hand, accuracy was only 40.2% when we used only the specific student's Day 1 data and ignored the data from other students. These results indicate that patterns of brain activity generalize to some degree across students and across days, reinforcing the conclusions of previous research [e.g., Qin et al., 2003, 2004] that patterns of algebraic engagement generalize across participants and across changes produced by learning.

The linear combinations of the 408 regions used by the classifier are complex patterns. While we did not need all of these regions to achieve maximum accuracy, we found that accuracy started to decline when we used fewer than 200 regions. Thus, many regions carried some discriminative information8. Nonetheless, regions were differentially informative and, for illustrative purposes only, Figure 7 shows the 55 regions that produced 40.6% accuracy on Day 1 and 45.6% accuracy on Day 5, which is about 90% of the accuracy achieved with all 408 regions. These 55 regions were chosen on the basis of having the largest variance in weights9.

Figure 7.

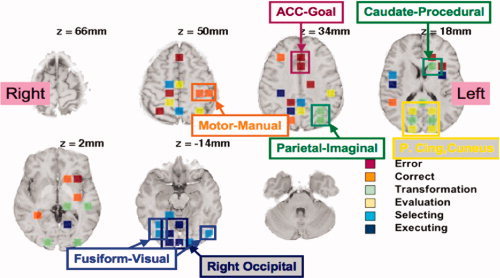
The 55 highly discriminative regions, labeled with the feature for which they were most active. Highlighted are the regions that are particularly striking and which suggest possible interpretations. They are labeled with their anatomical region and with the name of the ACT‐R module that they have been found to correlate with in past models of algebraic information processing [e.g., Anderson, 2005; Anderson et al., 2008].

Figure 7 shows these 55 regions and indicates how they discriminate among the eight steps (ignoring their contribution to discrimination from the rest state, which is relatively easy). The regions were labeled in terms of the three pairs of binary features that defined these eight categories: error versus correct, transformation versus evaluation, and selecting versus executing. We took the weights produced by the linear discriminant analysis for each of these eight categories and averaged them to get mean weights for these six binary features. For instance, for the transformation feature, we averaged the weights of the four kinds of transformation steps. We determined which feature had the largest positive value for a region and color‐coded the region accordingly in Figure 7 (although activity in all regions contributes to all discriminations, we coded each region based on the feature that its activity predominantly signaled). Because of the complex covariance structure of these regions, it does not follow that a region whose activity signals a feature will show a significant effect of that feature. Nonetheless, in 31 of the 55 cases in Figure 7, the region was associated with a significant effect for that dimension in Figure 5.

Although not all the regions can be readily interpreted, we identified a number of particularly regular patterns in Figure 7 that have quite reasonable interpretations:

• 1 Error. Particularly noteworthy are the two adjacent regions in the ACC that were most active during the error states. The anterior cingulate region has been associated with error detection and conflict monitoring [e.g., Carter et al., 1998].
• 2 Correct. Particularly striking are the two left motor regions, reflecting the slightly faster keying of answers (1.2 clicks per scan versus 0.9) because the student was less engaged in cognitive activity.
• 3 Transformation. The regions signaling transformations (Steps 1 and 2) included those in the parietal and caudate regions that we have found to be sensitive to operations on algebraic representations in other experiments [e.g., Qin et al., 2004].
• 4 Evaluation. There was a striking pattern of six bilaterally symmetric regions appearing from the posterior cingulate to the cuneus. The outer four of these regions were activated by evaluation (Steps 3 and 4) and the middle two regions were activated by transformation (Steps 1 and 2). It is not entirely clear how to interpret this pattern, although these regions are often active in memory tasks [e.g., Nielsen et al., 2005; Tulving et al., 1999] and in some studies of arithmetic [e.g., Fehr et al., 2007; Kesler et al., 2006]. This suggests that these regions were active during the retrieval of arithmetic facts in the evaluation step.
• 5 Selection. Regions overlapping and adjacent to the fusiform were active during the selection of the expression. This suggests their engagement in the detailed visual parsing of the expression.
• 6 Execution. When students were using the keypad there was activation in middle and right occipital regions. Assuming students were fixated on the center of the keypad, the expression they created would have appeared in the left visual field and should have projected to these regions.

To what degree could we actually predict states by simply looking at the number of mouse clicks occurring in a scan? Not surprisingly being a single dimensional feature, clicking rate alone is not able to discriminate among the full set of nine states. However, it does offer some accuracy in making binary discriminations. For instance, if asked to discriminate between rest states and non‐rest states, clicking rate can achieve 83.2% accuracy (averaging Day 1 and Day 5 performance) where chance would be 50%. Using brain‐imaging data, we do considerably better: 88.8%. Interestingly, had we combined the key data and the imaging data we would have done a better yet: 91.0%. This is evidence that performance can be improved merging data sources.

A more interesting binary discrimination is between non‐rest states that involve errors or no errors. Taking advantage of the slower keying in error states, clicking rate alone is able to achieve 55.6% accuracy. Again the imaging data produces considerably better performance: 64.7%. This time there is virtually no improvement combining the two sources of data: 64.8%. None of these scores for the discrimination of correct from error scans is particularly good. This discrimination will be considerably improved in our combined HMM Model.

Combined HMM Model

Figure 6 shows the success at classifying the state of a single scan using the fMRI data. A greater challenge was to link these single‐scan classifications together into a coherent interpretation of an entire block, which could involve hundreds of scans and many problems. Figure 8a shows the result of assigning each scan in a block to its most probable interpretation from the classifier. In this block, a student solved seven problems in 190 2‐s scans. The blue line indicates the student's progress through these problems. On the y‐axis, 0 indicates rest states and the integers 1–4 indicate the four steps. The green horizontal lines indicate when the steps were performed correctly and the red horizontal lines below them indicate when the steps were performed with an error. It can be seen that this student had one extended error episode on the second step of the first problem. The orange line indicates the classification of each scan by the fMRI model. This prediction line jumps around in a totally incoherent pattern. Scans from the rest periods were usually classified correctly, reflecting the relatively high discriminability of the rest periods, but even in this case the fMRI model assigned scans in the middle of the error episode to the rest category.

Figure 8.

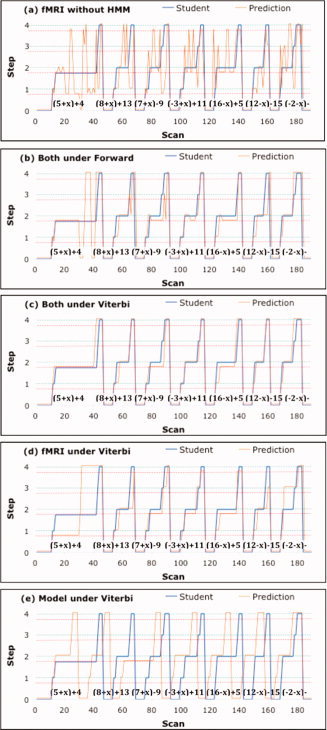
An example of an experimental block and various attempts to assign scans to stages of problem solving. The x‐axis gives the scan number and the y‐axis displays the progress of the student through seven problems (on Day 1, involving collection of constants—actual problems given in figure) starting in a rest state (0) and stepping through four states. The green dotted line indicates correctly performed steps and the red dotted line indicates incorrectly performed steps. The blue line displays the student's true trajectory and the orange line displays the assigned trajectory. (a) Scans are assigned to the most probable state based on the conditional probabilities from the linear discriminant analysis. (b) The behavioral model and imaging analysis are combined by the Forward HMM algorithm to make the best real‐time assignments. (c) The behavioral and imaging analyses are combined by the Viterbi HMM algorithm to make the best assignments after the block has ended. (d) Only fMRI data are used with the Viterbi Algorithm. (e) Only the behavioral model is used with the Viterbi Algorithm.

The behavioral model described earlier provides knowledge of the problem structure and the sequence of steps that the students had to take to get through the problems. Consequently, the behavioral model could be used to rule out the radical swings where, for instance, the fMRI model assigned one scan to Step 3 and the next scan to Step 1. Besides knowledge of the sequence of steps, the behavioral model provides the probability that any step will involve an error and the expected length of each step. Below we describe how we merged this behavioral model of the problem structure with the bottom‐up information from the fMRI model to identify the best interpretation of any scan or of any sequence of scans.

Our formal definition of an interpretation is an assignment of the first m scans to some sequence of the r states. For example, consider the interpretation of the first 100 scans in Figure 8. By the end of the block, the student must have gone through 36 states, reflecting the five states (four steps plus rest) for each of seven problems, plus the initial warm‐up, which we treated as a rest state. Because each step could be solved either with or without an error, there were 64 possible states (7 × 4 = 28 correct, 7 × 4 = 28 error, and 8 rest), but the student visited only 36 of these states. One interpretation of the first 100 scans would be that the student went through the first two problems without any errors and spent 10 scans in each of the 10 states, leaving unspecified how long it took the student to finish the rest of the problems. Using the naïve Bayes rule, the probability of any such interpretation, I, can be calculated as the product of the prior probability determined by the behavioral model and the conditional probabilities of the fMRI signals, given the assignment of scans to states:

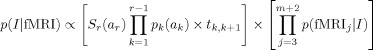The first term in the product is the prior probability (based on the behavioral model) and the second term involves the conditional probabilities (based on the linear discriminant analysis of the imaging data). The terms p _k(a _k) in the prior probability are the probabilities that the kth interval is of length a _k, and S _r(a _r) is the probability of the rth interval surviving at least as long as a _r. The terms t _{k ,k+1} are the probabilities of transitioning from state k to k + 1. Because the only nondeterminacy concerns whether the next step involves an error, the t _{k ,k+1} can be determined from the predicted error rates for that student (Fig. 4), as discussed in the behavioral model section. The duration probabilities, p _k(a _k) and S _r(a _r), can be determined from gamma distributions like those in Figure 3. The second term in the product contains p(fMRI_j|I), which are the probabilities of the fMRI signal on scan j+2, given I's assignment of scan j to a state. This is provided by the fMRI model.

Figure 9 illustrates how this can be conceived as a hidden semi‐Markov model. The figure shows the model for a fragment of a block that involves finishing a prior problem, transitioning to a rest state, stepping through one cycle of four steps to solve a problem, and returning to a rest state before the next problem. It is a semi‐Markov model because the number of scans in any state is variable. The distributions of state durations and the transition probabilities were determined from the behavioral model of step difficulty (Figs. 3 and 4). The fMRI data could be used for discrimination because they provided different probabilities of association with different states. We used the dynamic programming algorithms associated with HMMs [Rabiner, 1989] to efficiently calculate the probabilities of various interpretations. We used the Forward Algorithm to find the most probable interpretation of each state in real time, which would be appropriate for real‐time instruction in a tutoring system. We used the Viterbi Algorithm to find the most probable interpretation of the entire block after the block was completed, which would be appropriate for diagnosing the growth in a student's knowledge.

Figure 9.

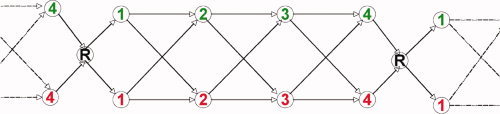
Representation of the behavioral model as a semi‐Markov process. States correspond to steps (green for correct, red for incorrect) and rest period (R).

Figure 8b shows that the Forward Algorithm recovered a much better interpretation than the fMRI model alone, although it was hardly perfect. For example, it showed a little vacillation toward the end of the very long error episode on problem 1. During this episode, even though it initially identified an error in the second step as its most probable interpretation, it jumped around toward the end of the episode because the likelihood of an error episode that long is quite low. However, it recovered by the end of the problem and did a fairly good job of tracking the student on the subsequent problems. It correctly identified 155 of the 190 scans, where 20 of the cases of misclassification involved being off by just one step. Since steps did not begin exactly on the scan boundaries for the student, there was some ambiguity about assigning states at these borders. Fifteen of the off‐by‐one‐step 20 cases were occurred at the boundaries between steps.

The Forward Algorithm in Figure 8b is appropriate for real‐time application, whereas the Viterbi Algorithm can be used after the block is finished to reconstruct the single most probable interpretation of the whole sequence of scans. Figure 8c shows the performance of the Viterbi Algorithm on this block. It was considerably more accurate, correctly identifying 170 of the 190 scans10. Note that the Viterbi Algorithm was constrained to produce a coherent interpretation of the entire sequence, so it did not produce the fluctuations seen with the Forward Algorithm in Figure 8b, which was trying to make its best assignments to each scan in real time.

One could ask how well one could do using the Viterbi Algorithm without the statistics of error probability or step length. To answer this question, we used the knowledge about legal transitions illustrated in Figure 9, but we treated all legal transitions among states and all step lengths as equally probable. Figure 8d shows the performance in this case. For this block, the algorithm correctly identified 131 of the 190 scans. Finally, one could ask how well one could do if one used the Viterbi Algorithm with just the behavioral model, ignoring the information from the fMRI model. This question can be answered by setting all conditional probabilities of the fMRI signals to be equal for all states. Figure 8e shows the results in this case. The algorithm correctly identified only 60 of the 190 scans, mainly at the beginning and the end of the block, where the Viterbi Algorithm is anchored.

Figure 8 shows the predictions for just one block from one student during Day 1. Table II summarizes how well the various approaches performed on all the blocks from Days 1 and 5. It gives measures of performance in identifying the step corresponding to a scan (the segmentation goal), identifying whether the scan came from a correct or error step (the diagnosis goal), and a final measure of whether it classified a scan accurately both with respect to step number and correctness (as in Fig. 6). With respect to the segmentation goal, the table indicates the proportion of scans assigned to the appropriate step and the mean error between the true step and the assigned step11. Figure 10 illustrates the segmentation performance of the Forward Algorithm using just the behavioral model, just the fMRI data, and both. The performance of the Forward Algorithm provides an estimate of how well the fMRI and behavioral models could do in real time at diagnosing what the student was thinking. The segmentation was much improved by combining both models. In that case, the majority of scans were accurately identified as to step, and most misassignments were just one step off.

Table II.

Performance statistics for the various algorithms as percentage of scansa

	Segmentation		Correct‐error discrimination			State
	Correct	Mean error	Hit rate	F Alarms	d‐prime	Accuracy
Day 1
fMRI without HMM	—	—	68.5%	48.3%	0.44	42.2%
Behavioral/Forward	30.4%	4.17	5.9%	1.1%	0.73	29.4%
Behavioral/Viterbi	43.5%	3.11	25.0%	6.7%	0.82	40.1%
fMRI/Forward	45.5%	3.83	38.7%	25.6%	0.37	38.7%
fMRI/Viterbi	60.9%	1.5	40.0%	24.0%	0.45	47.4%
Both/Forward	65.6%	1.83	27.4%	12.4%	0.55	54.7%
Both/Viterbi	75.9%	1.07	37.2%	13.4%	0.78	61.9%
Day 5
fMRI without HMM	—	—	69.6%	42.4%	0.70	52.9%
Behavioral/Forward	32.3%	4.15	0.5%	0.1%	0.51	36.7%
Behavioral/Viterbi	45.6%	3.68	27.8%	12.3%	0.57	42.3%
fMRI/Forward	42.5%	4.83	38.7%	21.0%	0.52	44.2%
fMRI/Viterbi	68.9%	0.97	45.2%	18.4%	0.78	58.3%
Both/Forward	75.0%	1.63	33.4%	10.1%	0.85	67.6%
Both/Viterbi	82.0%	0.66	54.9%	16.9%	1.08	71.9%

^aSegmentation statistics are calculated on all scans; other statistics exclude 11 warm‐up scans. “fMRI without HMM” is based on conditional probabilities only.

Figure 10.

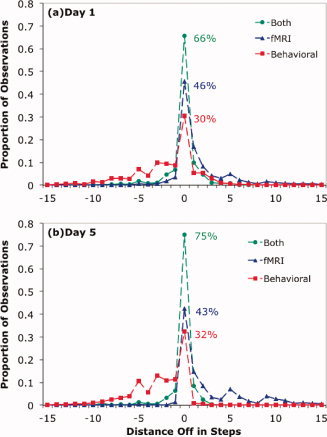
Performance of the Forward Algorithm with respect to the segmentation goal. The x‐axis gives the distance between the actual step and the predicted step: (a) Day 1 and (b) Day 5.

With respect to the diagnosis goal, Table II also provides hit rates (the percent of scans from error steps diagnosed as errors) and false alarm rates (the percent of scans from correct steps mistakenly diagnosed as errors), along with a d‐prime measure [Wickens, 2002] calculated from the combination. In the case of “fMRI without HMM,” we are using conditional probabilities and not passing them through an HMM to include base rate information. When the HMM is used parameterized with behavioral statistics, relatively low percentages of scans are classified as errors, reflecting the low base rates for errors (29.2% of the Day 1 non‐rest scans and just 16.1% of the Day 5 non‐rest scans were from error steps). Use of either the fMRI data or the Viterbi Algorithm increased the propensity for a scan to be labeled as an error, whereas the Forward Algorithm with just the behavioral model classified very few scans as coming from error steps. A potential problem with comparing d‐prime measures across the cases in Table II is that they can be misleading when the thresholds for error classification are so different.

As noted earlier, the Viterbi Algorithm, which is applied after the problem sequence is completed, is appropriate for diagnosing what a student has learned. From this perspective, there is really little reason to want to know whether a particular scan comes from an error step. The important issue is at a higher level of aggregation than a scan—diagnosing which steps involve errors. Therefore, we calculated how well the Viterbi Algorithm did at assessing the accuracy of a step, which involved the aggregation of multiple scans. These step‐based scores for the Viterbi Algorithm are displayed in Figure 11, which has the probability of accurately classifying an error step as an error on the y‐axis and the probability of mistakenly classifying a correct step as an error on the x‐axis. These diagnoses scores depend on accuracy of segmentation as well as accuracy of identifying error states. To the degree that steps are incorrectly segmented, the ability to diagnose whether they are being performed correctly will be compromised. We investigated how well we would do if we knew the correct segmentation and judged each step given the behavioral model and the fMRI model. We varied the threshold for error classification to create the receiver operator characteristic (ROC) curves in Figure 11. A measure of classification success is the area under these curves, which was 0.903 for Day 1 and 0.946 for Day 5. Comparing the “Both, Viterbi” data points with the curves gives a sense of how much was lost because of mistakes in segmentation. Because the Viterbi points are segmentation dependent, it is not really possible to draw out ROC curves for them. Changing the threshold for error classification from the current maximum‐likelihood values would produce worse segmentations and compromise discriminability.

Figure 11.

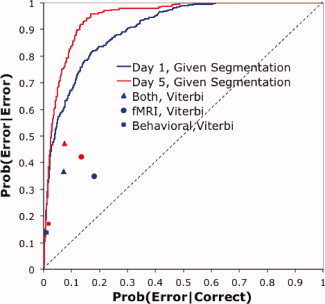
The performance on error classification of steps using the segmentation inferred by the Viterbi Algorithm from the various information sources. Blue is Day 1 performance and red is Day 5 performance. The ROC curves assume correct segmentation and use both the linear discriminant analysis of the imaging data and the behavioral model of the behavioral data.

CONCLUSIONS

This article has shown that it is possible to merge brain‐imaging data with a behavioral model of the student to provide a fairly accurate diagnosis of where a student is in problem‐solving episodes that last up to 10 min. Moreover, prediction accuracy using both information sources was substantially greater than using either source alone. The performance in Figures 10 and 11 should not be taken as the highest level of performance that could be achieved. Performance could be improved by enhancing the imaging data, by adding additional data sources, or by improving the behavioral model. We discuss these various possibilities below.

The current set of 408 regions for classification is almost certainly not optimal. Given the number of observations in our data, a set of 400–500 variables is about as many that can be used without running into problems of overfitting, which would result in better fits to the training data but worse prediction. However, there is no reason to suppose that the large‐sized regions we have defined covering the brain are the best set. Selection of appropriate predictors is probably the most critical aspect of successful MVPA.

Keeping the region set constant, we have examined a number of methods sometimes associated with improved performance in the literature, such as support vector machines (SVMs) with radial basis functions and other kernels. These methods did not help, perhaps because of the large number of regions and scans in our data set. Hsu et al. [ 2009] noted that SVMs do not give better results compared with linear classifiers when the number of features and instances are large. We also tried using multiple scans rather than a single scan to classify a target scan, but this resulted in overfitting the data.

Performance might be improved by adding data sources such as eye movements [e.g., Anderson & Gluck, 2001; Salvucci & Anderson, 2001]. Actually, we had a behavioral data source that would have allowed perfect classification: the identities of the mouse clicks. However, we used this as a basis for defining ground truth and held this information back from the algorithm. The eventual goal is to address issues that such behavioral data cannot diagnose, such as whether errors are due to slips or confusion, what strategy a student is trying, the degree of student engagement, frustration, and others. A challenge associated with all these issues is defining ground truth. There has been progress in using methods such as self‐rating to identify such mental states [e.g., Graesser et al., 2008].

While there are many directions for future progress, these results are an encouraging test of concept in terms of the potential for imaging data to address the challenge of diagnosis in intelligent tutoring systems. It is possible both to use information from other students to interpret a particular student and to grow a model of the particular student as information comes in. However, we expect that as we tackle more subtle diagnosis issues we will need to augment the fMRI data with a richer student model. The behavioral model seemed fairly adequate for the current task, but more refined tracking of mental states will probably need more detailed cognitive models of algebra problem solving, such as those described in Anderson [ 2007].

While this article has focused on tutoring, this general methodology provides a way to interpret fMRI data from individual participants as they perform many different tasks, although it is not appropriate for tasks taking only a few seconds. Also, while this article is concerned with using the HMM methods to interpret behavior, hidden Markov techniques have applications in model parameterization and comparison [Rabiner, 1989]. That is, they can be used to estimate parameters for models and to perform statistical comparison of alternative models. Their special power here is that rather than working with average data, they can work with single‐trial data and properly test assumptions about different strategies and points of processing breakdown.