Abstract
Studying the interaction between brain regions is important to increase our understanding of brain function. Magnetoencephalography (MEG) is well suited to investigate brain connectivity, because it provides measurements of activity of the whole brain at very high temporal resolution. Typically, brain activity is reconstructed from the sensor recordings with an inverse method such as a beamformer, and subsequently a connectivity metric is estimated between predefined reference regions‐of‐interest (ROIs) and the rest of the source space. Unfortunately, this approach relies on a robust estimate of the relevant reference regions and on a robust estimate of the activity in those reference regions, and is not generally applicable to a wide variety of cognitive paradigms. Here, we investigate the possibility to perform all‐to‐all pairwise connectivity analysis, thus removing the need to define ROIs. Particularly, we evaluate the effect of nonhomogeneous spatial smoothing of differential connectivity maps. This approach is inspired by the fact that the spatial resolution of source reconstructions is typically spatially nonhomogeneous. We use this property to reduce the spatial noise in the cerebro‐cerebral connectivity map, thus improving interpretability. Using extensive data simulations we show a superior detection rate and a substantial reduction in the number of spurious connections. We conclude that nonhomogeneous spatial smoothing of cerebro‐cerebral connectivity maps could be an important improvement of the existing analysis tools to study neuronal interactions noninvasively. Hum Brain Mapp, 2011. © 2010 Wiley‐Liss, Inc.
Keywords: connectivity, source localization, spatial smoothing, FWHM, magnetoencephalography
INTRODUCTION
The brain's remarkable property of being able to perform a huge amount of different cognitive operations critically depends on the coordinated interplay between functionally specialized brain regions. Interregional anatomical connections obviously provide the necessary pathways through which such interactions can occur. Yet, it is the dynamics of the activity within and between anatomically connected regions that eventually determines what we perceive, think, or do [Varela et al., 2001]. The study of connectivity has therefore received a lot of interest from the neuroscientific community recently. For this purpose, electroencephalography (EEG) and magnetoencephalography (MEG) have been employed, because these techniques can provide a whole‐brain estimate of brain activity in healthy human subjects, at a superior temporal resolution compared to functional magnetic resonance imaging (fMRI).
Analysis of connectivity from noninvasively obtained recordings of brain activity is severely complicated due to the fact that the electromagnetic field generated by a given neural source is measurable at multiple measurement sites [Schoffelen and Gross, 2009; Srinivasan et al., 2007]. Many commonly used connectivity measures are sensitive to this so‐called field spread, which complicates the interpretation of the results. To attenuate these effects, analysis of connectivity should ideally be done at the level of the underlying sources.
Typically this approach consists of two steps. In the first step, the activity of the underlying sources is reconstructed using an inverse method such as a beamformer [Van Veen et al., 1997] or a minimum norm estimate [Hämäläinen and Ilmoniemi, 1994]. This step yields either a three‐dimensional volumetric representation of estimated neuronal activity, or a two‐dimensional image in which the source elements are constrained to the cortical sheet, using anatomical information. The number of elements in the source reconstruction is usually in the order of a few thousand. From these activity maps regions‐of‐interest (ROIs) are selected based on specific criteria such as synchronization to an external reference channel [Gross et al., 2002; Jerbi et al., 2007; Schoffelen et al., 2008], or task‐dependent modulation in activity [Gross et al., 2004]. Alternatively, ROIs can be selected based on a connection density estimate (CDE) between each source element and all other elements [Kujala et al., 2007, 2008]. In the second step, connectivity is assessed between all pairs of ROIs, or between one or more reference ROIs and the elements of the whole source volume/cortical map. Statistical significance is inferred using a baseline condition, an experimental contrast, or shuffling the original time series [Pollok et al., 2005; Timmermann et al., 2003]. Any of these measures are necessary to account for spurious values of connectivity which are most pronounced in the vicinity of the reference ROI. Clearly, the validity of the interpretation of the results crucially depends on the adequate choice of the ROIs and on whether the spurious connectivity is properly accounted for.
Essentially, the ROI‐approach could be problematic because relevant nodes in the functionally connected neural network may be missed, or because identified nodes are falsely identified as such, due to unaccounted spatial structure in the activity maps or in spurious connectivity. As an alternative to the ROI‐approach one could simply compute connectivity between all pairs of source elements, which is nowadays feasible in a reasonable amount of time, even with a couple of thousand voxels. Connectivity maps between all pairs of source elements have been successfully utilized for ROI‐selection based on connection density estimates [Kujala et al., 2007]. Here, we propose to directly infer functional interactions from the full spatial structure in the connectivity maps. Results obtained this way are not dependent on the choice of the reference ROIs and it allows for a more thorough evaluation of the spatial structure of spurious connectivity. Yet, this all‐to‐all pairwise approach may suffer from its own interpretational problems. Because of the very high number of source element pairs there is a risk of obtaining false positive results, or sensitivity may be reduced when applying rigorous criteria to avoid false positives.
This article investigates the applicability of all‐to‐all pairwise connectivity mapping using simulated MEG‐data in combination with beamformers for inverse modeling. We used the correlation coefficient as a functional connectivity metric for computational efficiency, and evaluated the spatial structure of six‐dimensional differential connectivity maps. These differential maps were computed by subtracting source‐level connectivity maps obtained from simulated data in two conditions (connected sources versus unconnected sources). We identified hits and false positives based on the comparison between the locations of the interacting regions, identified from the reconstructed connectivity map, and the locations of the actual target sources. As a key step in our approach, we propose to apply nonhomogeneous spatial smoothing to the all‐to‐all pairwise connectivity maps, to account for excessive spatial noise in the reconstructed images. We show that nonhomogeneous spatial smoothing leads to superior detection sensitivity and a reduction in false positives under a variety of simulation conditions, as compared to unsmoothed connectivity maps. Yet, we show that the performance of this approach is decreased when the signal‐to‐noise ratio (SNR) of the sources fluctuates across the conditions.
MATERIALS AND METHODS
MEG Data Simulation
MEG sensor‐level covariance matrices were simulated for a 248‐sensor magnetometer array (4D Neuroimaging, San Diego). We used a realistic volume conductor model based on the brain surface of an anatomical MRI. The triangulated inner skull surface was projected inward by a distance of 1 cm. Of the 1,339 vertices of this mesh we selected 992 vertices as potential source locations, excluding locations at the base of the brain, the cerebellum, and the mesial surface. The coordinates of the candidate locations were rounded to the nearest grid point on an 8‐mm regular grid (to avoid spatial sampling issues in the beamformer analysis, see later). The orientation of the potential sources was constrained to be orthogonal to the local brain surface and pointing inward. Orientation constrained leadfields were computed using a quasi‐static approximation with the brain surface as a single shell [Nolte, 2003]. We simulated MEG sensor covariance matrices according to the following equation:
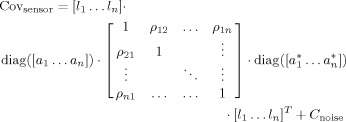 |
(1) |
in which [l 1…l n] denotes the concatenation of the columnar leadfield vectors corresponding to simulated sources 1 through n with fixed orientation, diag([a 1…a n]) is a diagonal matrix with the amplitudes of the sources on the main diagonal. The coefficients ρab represent the correlation coefficient between source a and source b, and C noise represents the sensor‐level noise covariance matrix.
A typical simulation consisted of simulating the activity of two dipoles in two conditions. In condition 1 the dipoles were correlated with a nonzero ρ12, and in condition 2 this parameter was set to 0, fixing the amplitudes a 1 and a 2 of both sources and both conditions at 1. The noise covariance matrix was scaled according to the frobenius norm of the noise‐free simulated sensor‐level covariance matrix with the simulated dipoles uncorrelated. For most of the simulations we assumed the noise to be white and equal for all sensors, which translates into C noise = λ·I. The parameter λ was kept constant across the conditions and determined the signal‐to‐noise ratio (SNR). The locations of the simulated dipoles were chosen such that the correlation coefficient between the leadfield vectors was within a range of 0.005 of a prespecified value. This set up allowed us to systematically vary the signal‐to‐noise ratio, the spatial correlation of the simulated sources (through simulating the sources at different pairs of locations, thus changing the leadfield correlation), and the temporal correlation between the sources (through the coefficient ρab). To account for variability introduced by the specific positions of the dipoles with respect to the sensor array we repeated the simulation for each parameter triplet (spatial correlation, temporal correlation, and SNR) 10 times.
The simulations described so far represent idealized situations and it would be important to verify the performance of all‐to‐all approach in more “realistic” simulations. First of all, the all‐to‐all pairwise approach to the differential connectivity maps may critically depend on the spatial structure in the noise. In real experimental data, noise is never spatially white due to finite measurement time and due to the fact that background brain activity and signals from non‐neural origin impose structure on the sensor‐covariance matrix which affects the properties of the spatial filters. Second, when using differential connectivity maps, one implicitly assumes that voxel pairs showing spurious values of connectivity in the active condition also show spurious connectivity to a similar extent in the control condition. This assumption may not always be valid, and depends on the spatial structure in the noise across the conditions compared. Important in this respect is also that changes in SNR caused by modulations in the amplitudes of the active sources may critically affect the spatial profile of the point spread function of the spatial filters and thus of the outcome of the analysis. We addressed these issues two additional sets of simulations.
We investigated the effect of more realistic noise by replacing the scaled identity matrix in the variable C noise (representing spatially white noise) with a covariance matrix obtained from real MEG‐data. The selected data were taken from 500 epochs in which a participant was fixating on a fixation cross on the screen. These epochs were of variable length with a range between 1 and 1.5 s, and digitized at 256 Hz. We randomly partitioned the 500 epochs into two sets of 250, and computed 2 covariance matrices, which we added to the correlated and uncorrelated simulation conditions respectively.
We also investigated the effect of a conditional change in SNR due to the active sources' amplitudes. For these simulations, we modulated the amplitude of the active sources in the uncorrelated condition with respect to their amplitude in the correlated condition by changing the parameters a 1 and a 2 from 0.8 to 1.2 in steps of 0.1. The amplitude of the sensor noise was kept constant across conditions.
Beamformer Analysis
The brain compartment was divided into a regularly spaced grid with a resolution of 8 mm, resulting in 3,371 locations. The leadfield at each of the grid locations was computed according to [Nolte, 2003]. Spatial filters were computed using a vectorized linearly constrained minimum variance (LCMV) algorithm [Van Veen et al., 1997], using the following formula:
where L r denotes the leadfield matrix for a dipolar source at location r, and Covsensor denotes the sensor level covariance matrix. No regularization was applied. We estimated the activity of the reconstructed sources in the orientation in which the output of the spatial filter W was maximized. To this end we performed an eigenvalue decomposition of the dipole covariance matrix W TCovsensor W, and the spatial filters were projected onto the orientation of the first eigenvalue.
All‐to‐All Pairwise Connectivity Analysis
We defined our connectivity metric to be the correlation coefficient between any pair of reconstructed source elements, which allowed for an efficient computation of all‐to‐all pairwise connectivity in the following way:
 |
where Covsensor represents the sensor‐level covariance matrix, and [w 1…w m] contains the spatial filters concatenated in the columns. Consequently, the matrix Covsource represents the source‐level covariance matrix, of which the elements c ij correspond with the covariance between a source at location i and a source at location j. The vector p source represents the power estimated at each of the grid locations, and is used in the normalization step to obtain the source‐level correlation matrix C source. The matrix C source contains a two‐dimensional representation of a six‐dimensional volume. Each of the rows/columns in the matrix corresponds with a volume representing the correlation between the estimated activity of a given reference location with the activity estimated at all other locations.
Because of spatial leakage of activity, spurious connectivity leads to a considerable spatial structure in estimated connectivity maps. In particular, voxels in the vicinity of the reference location show spuriously high connectivity values. To account for these artificially high values, rather than inferring “true” connectivity and statistical significance from the connectivity map directly, the difference in connectivity between an active condition and a control condition (baseline or experimental contrast) is usually computed. In the simulations we used a “control” condition in which the activity of the dipoles was temporally uncorrelated. We subtracted the connectivity map obtained from this control condition from the connectivity map computed for the active condition.
Nonhomogeneous Smoothing
Because of the high number of voxel pairs in the all‐to‐all pairwise connectivity map there may be false positives and/or sensitivity issues due to too stringent thresholding to account for false positives. To reduce the spatial noise underlying both potential confounds we analyzed the effect of nonhomogeneous smoothing of the six‐dimensional connectivity maps. This step is motivated by the fact that the point spread (or spatial leakage) of activity from a given location to neighboring locations is always present to some extent, and that the resulting spatial resolution is highly nonhomogeneous across the source reconstructed volume. Using beamformers as an inverse method, and provided the beamformer is capable at realistically “capturing” the true activity coming from a given region, a locally high spatial resolution is usually associated with neuronal activity in that region, whereas a locally low spatial resolution reflects the absence of neuronal activity in that region. The local spatial resolution of the inverse solution can be expressed in terms of the full width at half maximum (FWHM) of the spatial filter at each location [Barnes and Hillebrand, 2003; Gross et al., 2003]. We used these FWHM‐estimates to compute isotropic three‐dimensional Gaussian smoothing kernels for each source location and smoothed each element in the six‐dimensional connectivity map with the Gaussian kernels corresponding to the elements constituting that given voxel pair. The rationale for this approach is that spuriously high values of differential connectivity occurring between voxels in regions with relatively low spatial resolution (high FWHM) are smoothed to a greater extent than true high values of connectivity between voxels in active regions with relatively high spatial resolution (low FWHM). FWHM maps were computed according to Barnes and Hillebrand [2003] and for each grid point i we computed a three‐dimensional Gaussian kernel represented as a column vector k i, which was normalized such that the summed value of the elements was equal to 1. The connectivity maps were smoothed according to:
where the smoothing matrix K consists of a concatenation of the location‐specific Gaussian kernels, and the matrix C represents the source‐level correlation matrix. As a result, each element c consists of a weighted sum of the original connectivity matrix C, weighted with the voxel pair ij specific smoothing kernels.
We compared the effect of nonhomogeneous smoothing to the effect of homogeneous smoothing for a subset of the simulations by applying homogeneous smoothing kernels to the connectivity maps. This was achieved by computing smoothing matrices from fixed value FWHM maps.
Assessment of Performance with Six‐Dimensional Spatial Clustering
We analyzed the spatial structure in the differential connectivity maps by means of thresholding and spatial clustering.
Thresholding of the connectivity maps
The differential connectivity maps were thresholded to obtain binary maps. Our goal was to compare the sensitivity of the all‐to‐all approach with and without nonhomogeneous spatial smoothing. To be able to make an unbiased comparison between the smoothed and unsmoothed scenarios we applied thresholds such that a fixed number of voxel pairs exceeded this threshold, because the dynamic range in the differential connectivity was different for the unsmoothed and smoothed maps (see later). We assessed the effect of different thresholds on the outcome by varying the number of suprathreshold pairs. We applied a two‐sided test, which means that each map was thresholded and postprocessed twice, once with a positive threshold to assess the spatial structure in the binary map containing the voxel pairs with differential correlations larger than the threshold, and once with a negative threshold to assess the spatial structure in the binary map containing the voxel pairs with differential correlations smaller (more negative) than the threshold. The rationale for this two‐sided test was that although in our simulations the connectivity in the active condition always exceeded the connectivity in the control condition, in experimental data this can not generally be assumed. In practice, the differential correlation values at threshold were obtained by sorting (from large to small) the magnitude of the differential correlation values between all voxel pairs and taking the value at the Nth voxel pair as threshold, where N is the number of extra‐threshold pairs.
Suppression of spurious connections
To account for spurious connections between a given voxel and voxels in its vicinity, we removed these voxels from the binary maps by repeating the following procedure for each column of the binary map: the columnar vector i was reshaped into a three‐dimensional matrix to get a volumetric representation of the extrathreshold connectivity with respect to the ith voxel. The ith voxel was explicitly set to a value of 1, and a three‐dimensional spatial clustering algorithm was applied to identify those voxels spatially connected to the ith voxel. The identified voxels were subsequently set to 0, and the three‐dimensional matrix was reshaped into its equivalent columnar representation and placed back in the all‐to‐all binary map.
Six‐dimensional spatial clustering
The all‐to‐all binary map was then reshaped into a six‐dimensional matrix and we applied a six‐dimensional spatial clustering algorithm, yielding six‐dimensional clusters of functionally connected voxels. These clusters were finally analyzed in three‐dimensional space, and either consisted of two “blobs” of voxels in three‐dimensional space, representing two physically disconnected extrathreshold regions, or consisted of only one spatially contiguous “blob” of voxels.
Distance of clusters to target dipole locations
Finally, for each of the clusters we computed a distance metric to the simulated voxel pair, by summing the minimum Euclidean distance between each of the target dipole locations and the suprathreshold voxels. A six‐dimensional cluster consisting of two physically separated blobs of voxels was classified as a hit if the distance metric was below a certain threshold. We counted the total number of suprathreshold clusters, which in combination with the hitrate determined the number of false positives. The threshold distance was set to 2 cm, which allowed for clusters to be classified as a hit when the two blobs of voxels in three‐dimensional space were connected through a voxel pair consisting of neighbors of the actual target pair.
RESULTS
In all sets of simulations, we explored four dimensions of the parameter space: dipole correlation, leadfield correlation, SNR, and cluster threshold. Table I shows the values used on each of these dimensions for the first set of simulations. For each value of leadfield correlation we picked 10 dipole pairs with a leadfield correlation within 0.005 of the specified value and performed the simulation for all combinations of values on the other three dimensions. For each simulation and threshold we obtained a binary map from the thresholded (smoothed and unsmoothed) differential connectivity maps, representing the voxel pairs which were assumed to be functionally connected given the threshold. We spatially analyzed this binary map and obtained spatially clustered groups of voxels. If one of these six‐dimensional clusters was classified as a hit, the total number of false positives was the total number of six‐dimensional clusters minus 1, otherwise the number of false positives was set to the total number of six‐dimensional clusters. A cluster was considered to be a hit if the summed minimal euclidean distance of the two voxels in that six‐dimensional cluster (one in each of the blobs) to the target dipole pair, was less than 2 cm.
Table I.
Values of the parameters used for the simulations shown in Figure 2
| Parameter | Values used |
|---|---|
| Dipole correlation | −0.9, −0.5, −0.2, −0.1, −0.05, 0.05, 0.1, 0.2, 0.5, 0.9 |
| Leadfield correlation | −0.9, −0.5, −0.2, −0.1, −0.05, 0, 0.05, 0.1, 0.2, 0.5, 0.9 |
| Signal‐to‐noise ratio | 2, 5, 10, 15, 20 |
| Cluster threshold | 2,000, 1,000, 500, 200, 100, 50, 20, 10 |
Figure 1 shows the results of an illustrative example of a simulation. The simulation parameters used were a leadfield correlation of 0 and a dipole correlation of 0.05. Figure 1A shows a scatter plot of the differential correlation for all reconstructed dipole pairs as a function of the geometrical mean of the FWHM of the spatial filters at the voxels constituting the dipole pair. The black dots represent the results without nonhomogeneous smoothing, the red dots represent the nonhomogeneously smoothed case. The large gray and pink dot represent the reconstructed differential correlation value at the location of the simulated dipole pair in the unsmoothed and smoothed case, respectively. The SNR was set to a value of 10. The unsmoothed data show that (1) the reconstructed differential correlation value at the target dipole pair location is close to the simulated value (0.04 versus 0.05 in this case) (2) several dipole pairs have values of differential correlation exceeding the reconstructed value at the target dipole pair, and that (3) several dipole pairs actually show negative values of differential correlation which have a similar magnitude as the largest positive pairs. After application of nonhomogeneous smoothing the differential correlation values are generally closer to 0 and the reconstructed value at the simulated dipole pair is now one of the most extreme values in the distribution. The inset of Figure 1A shows the spatial structure in the 1/FWHM map. This so called roughness image shows a high roughness (locally low FWHM) in the vicinity of the simulated dipole pair. Figure 1B,C show the pairs of voxel clusters for the unsmoothed (B) and smoothed (C) case which are closest to the simulated dipole pair, as a function of SNR.
Figure 1.
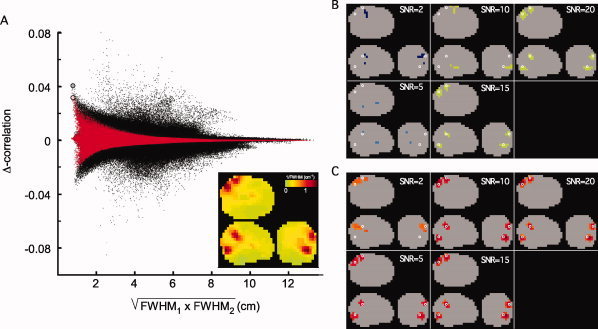
Example of the effects of nonhomogeneous smoothing on the differential all‐to‐all pairwise source correlations. (A) Scatterplot of differential correlation of all reconstructed dipole pairs as function of the geometric mean of the FWHM at the same locations. Black dots represent the unsmoothed differential correlation values, red dots represent the smoothed correlations. The thick dots represent the estimated differential correlation at the location of the simulated dipole pair, for the unsmoothed (gray) and smoothed case (pink). The inset shows a glass brain projection of 1/FWHM, highlighting the regions of high spatial resolution. (B, C) Glass brain projection of the pairs of voxel clusters closest to the simulated dipole pair (white circles), as a function of SNR, for the unsmoothed (B) and smoothed case (C).
Figure 2 summarizes the results of the 5,500 simulations that were carried out using the settings in Table I. Each graph shows the marginal means of the hitrate (left column) and of the number of false positives (middle column), for the unsmoothed (black bars) and smoothed (gray bars) connectivity maps, as a function of one of the dimensions of the simulated parameter space. The right column shows the pairwise significant differences for the hitrate and number of false positives, and for the smoothed and unsmoothed analyses separately. Overall, the nonhomogeneous smoothing resulted in a significantly higher hitrate and a lower number of false positives. The marginal mean hitrate as a function of the magnitude of the correlation between the target dipoles (Fig. 2A–C) ranged from 6.6 to 10% in the unsmoothed case, whereas it fluctuated between 50 and 60% in the smoothed case, and was maximal when the target dipole correlation was 0.5. The average number of false positives ranged from 7.2 to 15.6 in the unsmoothed case, and this value dropped to about 1.2 (range 1.0–1.4) in the smoothed case. Moreover, in the smoothed case, the number of false positives was not significantly modulated by the dipole correlation. An increase in the SNR (Fig 2D–F) led to an increased hitrate in both the smoothed (ranging from 21 to 72%) and the unsmoothed case (ranging from 0 to 26%). The number of false positives was slightly reduced at high SNR, dropping from 10.2 to 9.6, and from 1.6 to 1.0 in the unsmoothed and smoothed case, respectively. The effect of the spatial correlation between target dipoles (Fig. 2G–I) was quite variable. The marginal mean hitrate as a function of leadfield correlation ranged from 1.7 to 20% in the unsmoothed case, and from 20 to 75% in the smoothed case. The number of false positives ranged from 8.7 to 11.9 (unsmoothed), and 0.7 to 1.8 (smoothed). The inset in panel H shows the relation between the spatial correlation and the distance between the target dipoles. Increasing the cluster threshold (Fig. 2J–L) led to a decrease in both the hitrate and the number of false positives. The hitrate dropped from 21% to 2.5% in the unsmoothed case, and from 64% to 41% in the smoothed case. The number of false positives steeply declined from 25 to 1.7, and from 2.2 to 0.7 for the unsmoothed and smoothed cases, respectively.
Figure 2.
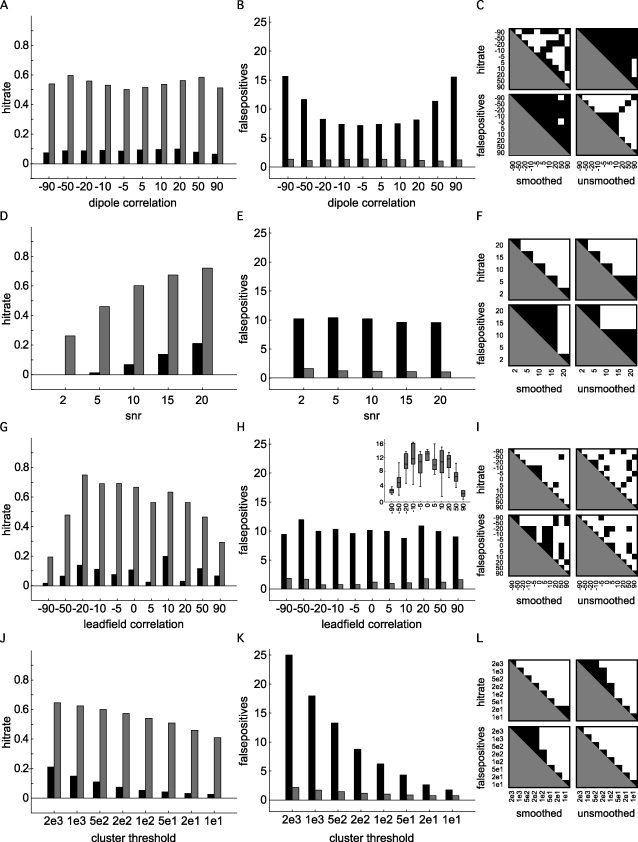
Results of 5,500 simulations showing the mean hit rate (left column), the average number of false positives (middle column), for the unsmoothed cases (black bars), and the smoothed cases (gray bars). The right column shows the pairwise significant differences for the hitrate and false positives, separately for the smoothed and unsmoothed cases [P < 0.05, corrected for multiple comparisons (Tukey‐Kramer test)]. A–C: Marginal mean hitrate, number of false positives and pairwise significant differences, as a function of simulated dipole correlation. D–F: Marginal mean hitrate, number of false positives and pairwise significant differences, as a function of signal‐to‐noise ratio. G–I: Marginal mean hitrate, number of false positives and pairwise significant differences, as a function of leadfield correlation of the simulated dipoles. The inset in panel H shows the relation between the leadfield correlation and the distance between the target dipoles. J–L: Marginal mean hitrate, number of false positives and pairwise significant differences, as a function of cluster threshold.
The overall increase in sensitivity after nonhomogeneous smoothing raises the question whether homogeneous smoothing in itself would lead to a similar improvement in detection rate and decrease in false positives. We tested this by applying homogeneous spatial smoothing to the connectivity maps, for a subset of the simulations described earlier. We smoothed the connectivity maps with homogeneous Gaussian convolution kernels with a FWHM of 1.2, 1.6, 2.4, and 4.0 cm. Figure 3 shows the marginal means for the hitrate and the number of false positives for a fixed cluster threshold (200) and SNR (15), averaged across a range of values for the dipole correlation and the leadfield correlation. Compared to the unsmoothed case, homogeneous smoothing led to a significant increase in hitrate and a significant decrease in the number of false positives, suggesting that in general homogeneous smoothing may be beneficial for the interpretability of the connectivity maps. Compared to the nonhomogeneously smoothed case, however, the hitrate was significantly reduced for all of the homogeneous smoothing schemes tested, and the number of false positives was significantly increased. Only with relatively high (4.0 cm FWHM) homogeneous smoothing the number of false positives was not significantly different from the nonhomogeneously smoothed case. Yet, the hitrate dropped from 70% with nonhomogeneous smoothing to about 20% with homogeneous smoothing.
Figure 3.
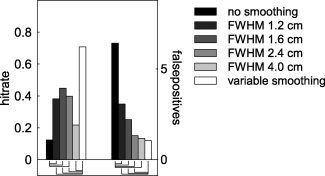
Comparison of hitrate and number of false positives for unsmoothed and nonhomogeneously smoothed cases, as well as for different homogeneous smoothing schemes. Significant differences between the unsmoothed (black bars) and the homogeneously smoothed, and between the nonhomogeneously smoothed (white bars) and the homogeneously smoothed are shown by the connecting lines underneath the bars.
We have shown so far that the interpretability of all‐to‐all pairwise connectivity maps constructed from “ideal” simulated data is improved when these maps are smoothed and that this improvement is optimized when data dependent nonhomogeneous smoothing kernels are applied. The following paragraphs describe the performance of our approach in more “realistic” simulations. Figure 4 shows the effect of adding “realistic noise” to the simulated covariance matrices. We repeated a subset of the simulations described earlier (see Table II for the parameter space searched), and added to the simulated sensor‐level covariance of any given unit amplitude dipole pair the covariance obtained from MEG‐data in which a subject was sitting in the MEG without a specific task. Figure 4A,B summarize the results of these 2,340 simulations, comparing the hitrate and average number of false positives with and without the addition of the realistic noise, as a function of SNR and averaged across the other dimensions of the simulation. Given the definition of SNR we used here, both the hitrate and the number of false positives were significantly increased. Compared to the same analysis using the unsmoothed connectivity maps, the performance after smoothing was still superior (results not shown).
Figure 4.
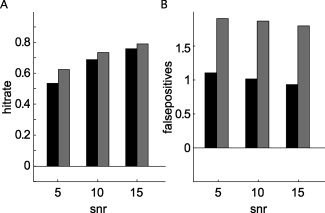
Performance of the all‐to‐all pairwise approach with nonhomogeneous smoothing in the presence of spatially correlated brain noise. Hitrate (A) and number of false positives (B) with spatially white (black bars), and with spatially correlated (gray bars) noise.
Table II.
| Parameter | Values used |
|---|---|
| Dipole correlation | −0.5, −0.2, −0.1, −0.05, 0.05, 0.1, 0.2, 0.5 |
| Leadfield correlation | −0.5, −0.2, −0.1, −0.05, 0, 0.05, 0.1, 0.2, 0.5 |
| Signal‐to‐noise ratio | 5, 10, 15 |
| Cluster threshold | 2,000, 1,000, 500, 200, 100, 50, 20, 10 |
The effect of a conditional change in SNR due to the active sources' amplitudes is shown in Figure 5. For these simulations, we modulated the amplitude of the active sources in the uncorrelated condition with respect to their amplitude in the correlated condition from 80 to 120%, in steps of 10%. The hitrate was decreased and the number of false positives was increased in the situations where the sources' amplitudes were modulated.
Figure 5.
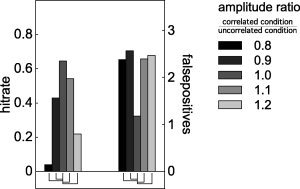
Comparison of hitrate and number of false positives after nonhomogeneous smoothing, when the amplitude of the simulated dipoles changes from the correlated to the uncorrelated condition. Significant differences between the unmodulated case (centre gray bar), and the modulated cases are shown by the connecting lines underneath the bars.
DISCUSSION
In this article, we explored the applicability of all‐to‐all pairwise connectivity analysis to noninvasively obtained electrophysiological data. In particular, we propose to apply nonhomogeneous smoothing to the obtained connectivity maps, as an essential step to reduce spurious connectivity. Results from extensive simulations show that nonhomogeneous smoothing leads to a significant increase in the hitrate and a significant decrease in the number of false positives, under a range of idealized simulation conditions.
The core of the simulations consisted of the estimation of differential connectivity maps and spatial postprocessing of these maps to obtain spatially disconnected clusters of voxels showing a modulation in connectivity. The application of nonhomogeneous smoothing to the connectivity maps proved to be an essential step in the all‐to‐all pairwise approach, in order to achieve a reasonably high hitrate and a low number of false positives. The rationale for the smoothing is based on the fact that the spatial resolution of source reconstructed images is relatively low and that this resolution is spatially nonuniform. This property of spatial filters is well known and has been investigated elsewhere in the context of beamformers as an inverse method [Barnes and Hillebrand, 2003; Gross et al., 2003]. Specifically, Barnes et al. use the estimated spatial nonuniformity to correct the statistical threshold for detecting univariate activations. Here, we actually manipulated the reconstructed images by applying spatial resolution dependent smoothing prior to postprocessing them. Moreover, the images were smoothed in a bivariate fashion, which means that for each voxel pair the all‐to‐all pairwise connectivity map was smoothed with a pair of filter kernels, with FWHM specific to that voxel pair. Essentially, the estimated FWHM for a spatial filter at a given voxel quantifies the volume into which the activity of a source at that location is spread out. Conversely, the estimated activity at a given voxel consists of the activity which truly comes from a source at that location, and of the activity which has “leaked” into that location from sources in other brain regions. Replacing any metric on the voxel level with an appropriately weighted average (i.e., nonhomogeneously smoothed) value of that metric therefore may lead to a reduction in spatial noise, which is smoothed to a greater extent than the underlying effect of interest. In this article, we present results indicating that this indeed seems to be the case for a simple bivariate metric (correlation coefficient) in simulated data, using beamformers for the inverse modeling. In general, we expect that this approach is applicable to other bivariate connectivity metrics as well, such as coherence, phase locking value, or directed measures of interaction. Moreover, it should be noted that nonhomogeneous smoothing may also have a beneficial effect on the statistical evaluation of reconstructed source images representing univariate metrics (such as T‐statistics between conditions). It remains to be seen however, to what extent other popular inverse methods will benefit from the nonhomogeneous smoothing. For example, minimum norm estimates are generally nonadaptive, which means that the local spatial resolution of the inverse solution is not that much dependent on the underlying spatial structure in the data. Therefore, the structure in the FWHM‐maps will not lead to a selective focal smoothing close to the active source locations, at the expense of a more vigorous smoothing in “silent” locations. Yet, it will probably not only depend on the actual values in the FHWM maps whether the all‐to‐all approach as such (with our without nonhomogeneous smoothing) will be feasible in these cases. Of course the quality of the all‐to‐all connectivity maps obtained with a particular inverse method will be an important determinant as well.
Another key element in the all‐to‐all pairwise approach is that we evaluated differential connectivity maps. The reason for this is that there is generally a distinct spatial structure in the leakage of estimated activity. This could lead to misinterpreting a distant local maximum as true connectivity if only a single condition were evaluated. Essentially, in a single condition the spatial structure of estimated connectivity with respect to a given reference location consists of a “mountain” of high connectivity values around the reference location and various spatial “sidelobes” reflecting the leakage of activity. The occurrence of sidelobes is a well‐known phenomenon in the application of beamformers in radar technology [Yu and Yeh, 1995], but in general any inverse method leads to spatial leakage [Lütkenhöner, 2003; Mitra and Maniar, 2006]. This can be taken into account by subtracting the connectivity map estimated from an appropriate baseline condition. Clearly, the implicit assumption is that the spatial structure of spurious connectivity is similar across the two conditions. We will refer to this assumption as the “equal bias assumption.” The reason for the low sensitivity of the all‐to‐all approach when the differential connectivity maps are not smoothed may well lie in the fact that the equal bias assumption is violated in many cases.
In our simulations, we explored the influence of different parameters on the outcome of the all‐to‐all connectivity analysis. These parameters either directly affected the quality of the simulated sensor‐level covariance matrices and thus the quality of the spatial filters (dipole correlation, leadfield correlation, and SNR), or influenced the outcome of an essential step in the postprocessing of the connectivity maps (cluster threshold). Overall, application of nonhomogeneous smoothing consistently improved the hitrate and the number of false positives (Fig. 2). Next to this, pairwise comparison of the different values of the simulation parameters revealed variable effects on the different outcome measures. In the following, we will briefly discuss the effects of the different parameters.
Effect of Correlation Strength
The marginal mean hitrate was significantly modulated by the temporal correlation between the activity of the underlying sources in the smoothed case, but not in the unsmoothed case. In our simulations, the maximal hitrate was achieved when the magnitude of the source correlation was 0.5. From a theoretical point of view, reconstructions of source activity using beamformers in the presence of correlated source activity are expected to be spatially blurred and temporally distorted [Sekihara et al., 2002; Van Veen et al., 1997]. Yet, it has been shown that beamformers are able to adequately reconstruct the magnitude of the simulated correlation up to a relatively high level of source correlation, and a relatively low SNR [Gross et al., 2001; Sekihara et al., 2002]. Next to this, from a practical point of view, it is hardly to be expected that the temporal correlation between brain sources in physiological data will be within the range as to cause significant distortion and spatial blurring such that the successful identification of interacting sources is hampered by the correlation. The present analysis relies on the fact that the beamformer is capable of retaining the spatial structure of the correlated sources in the differential connectivity map. Particularly, it relies on the fact that the reconstructed differential connectivity shows a local maximum at the location of the target dipole pair, and that the value of this local maximum survives the thresholding scheme. The fact that the smoothed hitrate was maximal at a dipole correlation of 0.5 may reflect the opposing effects of the magnitude of the correlation on the spatial distortion of the connectivity maps and on the elevation of the reconstructed connectivity at the simulated voxel pair beyond the noise threshold. The low unsmoothed hitrate in combination with the high number of false positives (which significantly increased with increasing magnitude of dipole correlation) most likely reflects the fact that the unsmoothed differential connectivity maps not only show a high number of spurious connections, but that the magnitude of the spurious correlations exceeds the magnitude at the target locations. The low hitrate does not mean, however, that the reconstructed differential connectivity at the target dipole pair is not adequately estimated in the unsmoothed case.
Effect of SNR
Increasing the SNR resulted in a systematic increase in hitrate without strongly affecting the number of false positives. This may be caused by the fact that an increased SNR leads to a more robust source reconstruction in the vicinity of the target source locations. The quality of the reconstruction outside these locations is not strongly affected, because those regions are “silent” to begin with. As a consequence of the better reconstruction of the target sources, the hitrate is increased, whereas the number of spurious connections is less affected by changes in SNR.
Effect of Spatial Correlation
Varying the spatial correlation between the underlying sources resulted in a considerably variable marginal hitrate and number of false positives, both in the unsmoothed and smoothed analysis. One likely explanation for this variability may be that only 10 dipole pairs per spatial correlation value were simulated, which in this case may be too low a number to smooth out random fluctuations. These fluctuations may be brought about by unaccounted variability introduced by factors such as spatial proximity of the target dipoles, and differences in the depth bias affecting the relative SNR of one dipole with respect to the other one. Irrespective of the underlying cause, our results indicate that the sensitivity of the all‐to‐all pairwise approach clearly depends on the locations of the interacting sources. This is an important finding for two reasons. First, it indicates that in simulation studies multiple source configurations should be assessed in order to evaluate a particular method. Second, true interactions may be missed in experimental data, depending on the relative locations of the interacting sources.
Effect of Threshold Selection
Increasing the cluster threshold (i.e., allowing fewer voxels to exceed the threshold) resulted in a reduction of both the hitrate and the number of false positives. This relative decline appeared to be steeper in the unsmoothed case. Admittedly, our choice for the cluster threshold is an arbitrary one, and it would be useful to investigate different ways of thresholding. We evaluated the connectivity maps by means of a six‐dimensional clustering algorithm, necessitating the generation of binary maps through the application of a threshold. In real data applications, this threshold could be determined based on statistical arguments. One potentially interesting approach would be to apply threshold‐free cluster enhancement (TFCE) [Smith and Nichols, 2009], which has been shown to be effective in boosting the sensitivity of three‐dimensional image analysis, and which does not rely on the a priori definition of a threshold. Essentially, the TFCE algorithm assigns to each voxel a value, which is the result of a weighted summation given a range of thresholds. For each threshold value, a measure of the difference between the metric at each location and the threshold is obtained and negative differences are set to 0. This difference is then weighted with a measure of the spatial extent of the cluster to which each suprathreshold voxel belongs. Typically, a range of thresholds is assessed, and the results are integrated.
Figure 3 compares the effect of nonhomogeneous smoothing to variable amounts of homogeneous smoothing. In general, homogeneous smoothing was found to be beneficial for the interpretability of the connectivity maps. There was a significant reduction in the number of false positives and a significant increase in the hitrate compared to the unsmoothed case, for all the homogeneous smoothing schemes tested. In particular, homogeneous smoothing with 1.6 and 2.4 cm FWHM smoothing kernels seem to offer a good trade off between achieving a reasonable hit rate and a relatively low number of false positives. Yet, nonhomogeneous smoothing offered an even better trade off between the hitrate and the number of false positives. This is most likely a consequence of the fact that homogeneous smoothing fails to strike an adequate balance between favoring the locations of interest, while simultaneously effectively smoothing the noise and sidelobes. For example, homogeneous smoothing with a high FWHM is effective in smoothing the spatial noise at locations of no interest (low number of false positives), but it reduces sensitivity because the true effect at the location of interest is buried in the smoothed noise.
The results discussed so far explored the applicability of all‐to‐all pairwise connectivity analysis arguably in “unrealistic” situations. The simulated sensor‐level covariance matrices represented ideal situations in which only two sources were active, and in which the background noise was spatially white (and reflecting infinite measurement time). Moreover, the amplitude of the sources between the correlated and uncorrelated condition was kept constant. We are fully aware that real experimental data is generally less well behaved, but we believe that the simulations presented so far are relevant for two reasons. First, simulating “ideal” sensor‐level covariance matrices allowed us to isolate the effects of different dimensions in the parameter space on the outcome. Second, it is important to evaluate the limitations of the method in the “ideal” case. However, we repeated a subset of the simulations in which we included noise estimated from an experimental recording, where a subject was fixating. The noise estimate in this case therefore contained both background brain activity and sensor noise. This resulted in a small increase in the hitrate and to a concurrent increase in the number of false positives. The increased hitrate may be caused by the fact that the magnitude of the spurious connections is less dramatic in the presence of realistic noise, as a consequence of which the voxels in the vicinity of the target locations survive the thresholding. The increased number of false positives is suggestive of the fact that the spurious connections are less clustered in space.
These findings seem to indicate that including more realistic noise affects the performance of the all‐to‐all pairwise approach to some extent, but that it does not lead to a dramatic reduction in sensitivity.
In a final set of simulations, we modulated the amplitudes of the active sources between the correlated and uncorrelated conditions. In contrast to the manipulations described earlier, the modulation of the sources' amplitude affected the sensitivity of the all‐to‐all pairwise approach. More precisely, a change in amplitude across the two conditions led to a substantial decrease in the hitrate and an approximate doubling of the number of false positives. This may be caused by the fact that the “equal bias assumption” is violated in the amplitude‐modulated case. It is conceivable that amplitude modulations lead to considerable nonrandom spatial structure in the differential connectivity maps which is not effectively dealt with by nonhomogeneous smoothing.
This finding is important for several reasons, and it affects not only the interpretability of the outcome of the all‐to‐all pairwise approach but it also affects the traditional region‐of‐interest approach. In real experimental data, the amplitudes of the interacting sources cannot be assumed to be more or less constant across the experimental conditions. As a matter of fact, one strategy often employed to identify reference regions‐of‐interest is using amplitude modulation as the selection criterion.
The confounding effect of amplitude modulations raises the question whether a conditional difference is appropriate to investigate connectivity, and whether other methods may be more appropriate to assess the spatial structure in the spurious connections. Surrogate data or data shuffling [Lachaux et al., 1999] is often used to assess the significance of interactions. Although these techniques may ensure amplitude constancy at the expense of destroying the true interactions, they also destroy spurious interactions due to spatial leakage, and therefore may not be sufficiently conservative. Alternatively, a stratification approach may be adopted when investigating an experimental contrast, in which for each reconstructed dipole pair the marginal distributions of the amplitudes are stratified across conditions after which the connectivity metric is computed from the trials remaining after stratification. A stratification approach may better preserve the spatial structure in the spurious connectivity while removing the confound of amplitude modulations. Yet, this will be a computationally very expensive approach, because each dipole pair has to be evaluated separately, potentially limiting its practical applicability.
The results presented so far were concerned with the situation in which a network of only two interacting nodes was simulated. It would be very relevant to investigate the applicability of the all‐to‐all approach to situations in which more “realistic” networks are simulated consisting of 3 or more interacting nodes. Although we expect that in such cases the all‐to‐all approach with nonhomogeneous smoothing will be able to extract meaningful structure from the data, more work is needed to investigate this.
CONCLUSIONS
Using extensive data simulations, we have shown that it is feasible to study all‐to‐all pairwise connectivity in MEG‐data. A crucial step in our approach is to apply nonhomogeneous smoothing to source reconstructions of connectivity. This is necessary to reduce the number of spurious connections at the benefit of the detectability of the truly interacting source regions. Amplitude changes of the interacting sources have been shown to limit the sensitivity of our approach. Future work needs to address this issue. We strongly believe that despite the current limitations the all‐to‐all pairwise approach is a viable one, which should be further developed in order to use it on experimental data.
REFERENCES
- Barnes GR, Hillebrand A ( 2003): Statistical flattening of MEG beamformer images. Hum Brain Mapp 18: 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Kujala J, Hämäläinen M, Timmermann L, Schnitzler A, Salmelin R ( 2001): Dynamic imaging of coherent sources: Studying neural interactions in the human brain. Proc Natl Acad Sci USA 98: 694–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Schmitz F, Schnitzler I, Kessler K, Shapiro K, Hommel B, Schnitzler A ( 2004): Modulation of long‐range neural synchrony reflects temporal limitations of visual attention in humans. Proc Natl Acad Sci USA 101: 13050–13055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Timmermann L, Kujala J, Dirks M, Schmitz F, Salmelin R, Schnitzler A ( 2002): The neural basis of intermittent motor control in humans. Proc Natl Acad Sci USA 99: 2299–2302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Timmermann L, Kujala J, Salmelin R, Schnitzler A ( 2003): Properties of MEG tomographic maps obtained with spatial filtering. Neuroimage 19: 1329–1336. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Ilmoniemi RJ ( 1994): Interpreting magnetic fields of the brain: Minimum norm estimates. Med Biol Eng Comput 32: 35–42. [DOI] [PubMed] [Google Scholar]
- Jerbi K, Lachaux JP, N'Diaye K, Pantazis D, Leahy RM, Garnero L, Baillet S ( 2007): Coherent neural representation of hand speed in humans revealed by MEG imaging. Proc Natl Acad Sci USA 104: 7676–7681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kujala J, Gross J, Salmelin R. ( 2008): Localization of correlated network activity at the cortical level with MEG. Neuroimage 39: 1706–1720. [DOI] [PubMed] [Google Scholar]
- Kujala J, Pammer K, Cornelissen P, Roebroeck A, Formisano E, Salmelin R ( 2007): Phase coupling in a cerebro‐cerebellar network at 8‐13 Hz during reading. Cereb Cortex 17: 1476–1485. [DOI] [PubMed] [Google Scholar]
- Lachaux JP, Rodriguez E, Martinerie J, Varela FJ ( 1999): Measuring phase synchrony in brain signals. Hum Brain Mapp 8: 194–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lütkenhöner B ( 2003): Magnetoencephalography and its Achilles' heel. J Physiol Paris 97: 641–658. [DOI] [PubMed] [Google Scholar]
- Mitra PP, Maniar H ( 2006): Concentration maximization and local basis expansions (LBEX) for linear inverse problems. IEEE Trans Biomed Eng 53: 1775–1782. [DOI] [PubMed] [Google Scholar]
- Nolte G ( 2003): The magnetic lead field theorem in the quasi‐static approximation and its use for magnetoencephalography forward calculation in realistic volume conductors. Phys Med Biol 48: 3637–3652. [DOI] [PubMed] [Google Scholar]
- Pollok B, Gross J, Muller K, Aschersleben G, Schnitzler A ( 2005): The cerebral oscillatory network associated with auditorily paced finger movements. Neuroimage 24: 646–655. [DOI] [PubMed] [Google Scholar]
- Schoffelen JM, Gross J ( 2009): Source connectivity analysis with MEG and EEG. Hum Brain Mapp 30: 1857–1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoffelen JM, Oostenveld R, Fries P ( 2008): Imaging the human motor system's beta‐band synchronization during isometric contraction. Neuroimage 41: 437–447. [DOI] [PubMed] [Google Scholar]
- Sekihara K, Nagarajan SS, Poeppel D, Marantz A ( 2002): Performance of an MEG adaptive‐beamformer technique in the presence of correlated neural activities: effects on signal intensity and time‐course estimates. IEEE Trans Biomed Eng 49( 12 Part 2): 1534–1546. [DOI] [PubMed] [Google Scholar]
- Smith SM, Nichols TE ( 2009): Threshold‐free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neuroimage 44: 83–98. [DOI] [PubMed] [Google Scholar]
- Srinivasan R, Winter WR, Ding J, Nunez PL ( 2007): EEG and MEG coherence: Measures of functional connectivity at distinct spatial scales of neocortical dynamics. J Neurosci Methods 166: 41–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timmermann L, Gross J, Butz M, Kircheis G, Haussinger D, Schnitzler A ( 2003): Mini‐asterixis in hepatic encephalopathy induced by pathologic thalamo‐motor‐cortical coupling. Neurology 61: 689–692. [DOI] [PubMed] [Google Scholar]
- Van Veen BD, van Drongelen W, Yuchtman M, Suzuki A ( 1997): Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Trans Biomed Eng 44: 867–880. [DOI] [PubMed] [Google Scholar]
- Varela F, Lachaux JP, Rodriguez E, Martinerie J ( 2001): The brainweb: Phase synchronization and large‐scale integration. Nat Rev Neurosci 2: 229–239. [DOI] [PubMed] [Google Scholar]
- Yu JL, Yeh CC ( 1995): Generalized eigenspace‐based beamformers. IEEE Trans Sign Proc 43: 2453–2461. [Google Scholar]


