Assessment of sire contribution and breed-of-origin of alleles in a three-way crossbred broiler dataset

ABSTRACT

Broiler breeding programs rely on crossbreeding. With genomic selection, widespread use of crossbred performance in breeding programs comes within reach. Commercial crossbreds, however, may have unknown pedigrees and their genomes may include DNA from 2 to 4 different breeds. Our aim was, for a broiler dataset with a limited number of sires having both purebred and crossbred offspring generated using natural mating, to rapidly derive parentage, assess the distribution of the sire contribution to the offspring generation, and to assess breed-of-origin of alleles in crossbreds. The dataset contained genotypes for 56,075 SNPs for 5,882 purebred and 10,943 3-way crossbred offspring generated by natural mating of 164 purebred sires to 1,016 purebred and 1,386 F1 crossbred hens. Using our algorithm FindParents, joint parentage derivation for the offspring and parent generations required only 1 m 29 s to retrieve parentage for 20,253 animals considering 4,504 possible parents. FindParents was similarly accurate as a maximum likelihood based method, apart from situations where settings of FindParents did not match the genotyping error rate in the data. Numbers of offspring per sire had a very skewed distribution, ranging from 1 to 270 crossbreds and 1 to 154 purebreds. Derivation of breed-of-origin of alleles relied on phasing all genotypes, including 8,205, 372, and 720 animals from the 3 pure lines involved, and allocating haplotypes in the crossbreds to purebred lines based on observed frequencies in the purebred lines. Breed-of-origin could be derived for 96.94% of the alleles of the 1,386 F1 crossbred hens and for 91.88% of the alleles of the 10,943 3-way crossbred offspring, of which 49.49% to the sire line. The achieved percentage of assignment to the sire line was sufficient to proceed with subsequent analyses requiring only the breed-of-origin of the paternal alleles to be known. Although required number of animals may be population dependent, to increase the total percentage of assigned alleles, it seems advisable to use at least approx. 1,000 genotyped purebred animals for each of the lines involved.

INTRODUCTION

Poultry and pig breeding programs make use of a breeding pyramid, where selection takes place in the top of the pyramid in the purebred (PB) parental lines. Genetic improvement realized in the PB parental lines arrives at commercial farms after a multiplier step, which involves several additional generations to increase the number of animals needed to supply all customers with animals. The breeding goal is to improve crossbred (CB) performance, but selection is generally based on PB performance. Basing selection on CB performance may ultimately yield higher genetic gain (Wei and Vanderwerf, 1994; Bijma and van Arendonk, 1998; Dekkers, 2007; van Grevenhof and van der Werf, 2015), but requires using phenotypic information of CB animals in the breeding program, which may be difficult using pedigree recording. Genotyping CB animals with available phenotypic information improves the accuracy of linking CB information back to PB selection candidates, and enables genomic prediction of PB selection candidates for CB performance (Ibanez-Escriche et al., 2009).

Genotyping of CB animals implies that CB information can be used in situations where no pedigree is available for the CB animals. Pedigree information of CB animals could be recovered from the genotype information, if genotypes for their ancestors are available, and this may be useful for several reasons. Firstly, genomic prediction models such as single-step GBLUP (Aguilar et al., 2010; Christensen and Lund, 2010) and single-step SNPBLUP (Liu et al., 2014; Fernando et al., 2016; Taskinen et al., 2017) that use information of genotyped and non-genotyped animals simultaneously require pedigree information on all genotyped animals. Secondly, if the CB animals are created through natural mating, there is no exact control over the contribution of each of the possible parents to the phenotyped animals, and precise contributions are unknown. Thirdly, pedigree information may be useful in any required genotype imputation.

Genomic prediction models for CB performance may model a single trait (e.g., body weight) as different correlated traits for each of the line compositions in the data. For example, considering a 3-way cross, created by mating a sire line to a cross of 2 dam lines, 5 correlated traits may be considered: 1 for each pure line, 1 for the 2-way CB dams, and 1 for the 3-way final cross. Different approaches have been proposed to model the genomic information required for such models: (1) ignore any differences between the lines involved, as well as between the PB and CB animals (Ibanez-Escriche et al., 2009); (2) the same as (1), but consider line-specific allele frequencies (Makgahlela et al., 2013; Hidalgo et al., 2016; Lourenco et al., 2016); or (3) model SNP effects separately for each PB line, basing relationships with CB animals only on alleles that the CB inherited from this line (Ibanez-Escriche et al., 2009; Christensen et al., 2014; Sevillano et al., 2017). The first 2 approaches only require that the line composition of each of the animals is known, whereas the third model requires that for each of the CB alleles the line-of-origin is known.

The objectives of this study were, for a large CB broiler dataset generated through natural mating, to 1) rapidly derive parentage, 2) investigate the difference in contribution of the sires to the offspring generation, and 3) derive breed-of-origin of alleles (BOA) for the CB animals in the dataset.

MATERIALS AND METHODS

Data recording and sample collection were conducted strictly in line with the Dutch law on the protection of animals (Gezondheids- en welzijnswet voor dieren).

Data

The data used in this study comprised 3 generations (Figure 1). Our analyses focus on the third generation, hereafter referred to as the offspring generation. The first and second generations contain possible parents and grandparents, and will hereafter be referred to as such. The offspring generation contained purebred line A animals, and A(BC) 3-way CB animals. The parent generation included possible line A sires, and line A and BC dams. The grandparent generation included possible line A grandparents, line B granddams, and line C grandsires. No pedigree information was available for any of the animals, because all animals in the parent and offspring generations were generated using natural mating.

Figure 1.

Design of the dataset used, including line A, B, and C grandparents (GP), A and BC parents (P), and A and A(BC) offspring (animals). The numbers in black represent total numbers per category, the italic numbers in brown indicate numbers being parents to both groups below, and the italic numbers in gray indicate numbers only being parents for one of the groups below. For instance, there is a total of 164 line A sires of the offspring generation; 144 have both A and A(BC) offspring, 8 have only A, and 12 have only A(BC) offspring.

The offspring generation was hatched in 5 different batches. Each batch was generated by housing approximately 100 purebred A males with either 1200 purebred A or 1200 crossbred BC breeder hens. After 2 hatches, males were swapped to ensure that the same males were mated with purebred A hens and crossbred BC hens. Resulting broiler progeny were wingbanded and blood sampled at hatch for genomic exploration. Broilers were raised in a commercial broiler house under conditions according to Cobb recommendations (found at www.cobb-vantress.com).

Animals from all 3 generations were genotyped using a Cobb custom Illumina 60k SNP chip (Groenen et al., 2011). The sex of broilers was derived from a selection of approximately 200 SNP genotypes (Cobb custom list of SNP) present on the Z and W chromosomes. In the offspring, parental, and grandparental generations, 27, 6, and 2 animals were not assigned to be male or female, respectively. Those 27 animals from the offspring generation were removed from the data, while those 6 parents and 2 grandparents were kept, as their sex could be derived later on from the derived pedigree. The data included 56,491 SNPs and 22,346 animals, after usual edits for call rate per animal (>95%) and SNP (>90%), and after removing SNPs with unknown position or located on the sex chromosomes, as well as mitochondrial SNPs. During the parent assignment, inconsistent genotypes between parent-offspring pairs were set to missing. A total of 416 SNPs were removed because they had more than 1% inconsistencies between offspring and derived parents. Any remaining missing genotypes were imputed using FImpute (Sargolzaei et al., 2014), considering the pedigree derived during the parent assignment. The final dataset included 56,075 SNPs. The 30 considered chromosomes and the distribution of the numbers of SNPs across those are shown in Table 1.

Table 1.

Per chromosome (Chrom.) the total numbers of SNPs and percentages of SNPs assigned to each of the lines for the A(BC) and BC crossbred animals.

			A(BC)				BC
Chrom.	Name	#SNPs	A	B	C	Total	B	C	Total
1	GGA1	9123	48.23	19.46	20.89	88.59	46.34	46.34	87.17
2	GGA2	6501	49.41	19.90	21.41	90.72	47.97	47.97	92.98
3	GGA3	5254	49.78	21.52	22.90	94.19	48.83	48.83	96.07
4	GGA4	4479	49.43	20.03	22.73	92.19	48.28	48.28	94.88
5	GGA5	3011	49.92	20.75	22.66	93.34	49.21	49.21	96.96
6	GGA6	2180	49.90	21.68	22.30	93.88	49.09	49.09	96.28
7	GGA7	2324	49.96	22.83	22.96	95.75	49.68	49.68	98.85
8	GGA8	1797	49.37	20.29	22.70	92.35	48.64	48.64	96.13
9	GGA9	1533	49.81	21.93	23.19	94.93	49.36	49.36	98.33
10	GGA10	1686	49.96	21.51	22.89	94.35	49.53	49.53	98.28
11	GGA11	1552	49.94	20.75	23.82	94.50	49.59	49.59	98.66
12	GGA12	1610	49.95	22.06	22.98	94.99	49.59	49.59	98.45
13	GGA13	1411	49.94	19.24	23.06	92.23	49.50	49.50	98.29
14	GGA14	1304	49.79	20.95	21.19	91.94	49.19	49.19	97.09
15	GGA15	1278	49.91	20.50	22.08	92.49	49.25	49.25	97.28
16	GGA16	94	49.83	18.50	20.02	88.35	45.98	45.98	88.85
17	GGA17	1136	49.89	18.06	23.13	91.08	49.45	49.45	98.18
18	GGA18	1120	49.88	22.43	22.09	94.40	49.60	49.60	98.43
19	GGA19	1101	49.93	20.78	24.10	94.81	49.71	49.71	98.87
20	GGA20	1791	49.75	20.33	22.73	92.82	48.69	48.69	96.56
21	GGA21	951	49.78	18.65	20.57	88.99	48.09	48.09	94.97
22	GGA22	486	49.97	21.37	21.92	93.26	49.62	49.62	98.75
23	GGA23	754	49.33	16.24	17.05	82.61	47.08	47.08	92.47
24	GGA24	913	49.89	19.96	20.75	90.60	49.25	49.25	97.44
25	GGA25	256	49.92	20.98	22.52	93.42	49.53	49.53	98.70
26	GGA26	880	49.69	17.12	20.30	87.11	48.50	48.50	95.35
27	GGA27	619	49.65	16.06	17.95	83.66	48.76	48.76	96.57
28	GGA28	805	49.87	18.84	21.30	90.00	49.19	49.19	97.09
29	LGE221	91	49.93	21.79	22.05	93.76	47.49	47.49	93.86
30	LGE64	35	49.81	18.91	22.43	91.15	46.35	46.35	91.88
Average2	-	56,075	49.49	20.34	22.05	91.88	48.47	48.47	96.94

¹Full name: LGE22C19W28_E50C23.

²Averages across all chromosomes, computed as weighted average using the number of SNPs as weights.

Derivation of Parentage

In genotype data, parent–offspring pairs can easily be detected by computing the number of opposing homozygotes (#OH) between any pair of individuals. The #OH of an individual and its parents is expected to be zero, or slightly higher to accommodate for genotyping errors (Calus et al., 2011; Hayes, 2011). Here we used a homemade algorithm that was implemented in Fortran 90, hereafter referred to as FindParents. FindParents used as input: a genotype file including autosomal SNPs, the sex of all the animals, a list of animals for which we wanted to assign parentage (comprising all animals from the offspring and parent generations), and a list of candidate parents (comprising all animals from the parent and grandparent generations). The algorithm implemented in FindParents involves the following steps:

1. Recode genotypes as 0 and 2 for the alternate homozygous genotypes, and 1 for heterozygous genotypes, and use 5 for missing genotypes.

2. Temporarily (i.e., only for use in step 3) replace all 1’s by 5, i.e., code the heterozygous genotypes as missing genotypes.

3. Count the #OH between any pair of individuals, avoiding comparing an individual with itself. This is achieved by counting per pair the number of SNPs where the sum of their genotypes was 2.

4. Sort candidate parents within individual based on increasing #OH. Retain per animal all candidate parents with #OH less than a threshold empirically derived from the data. Assuming that the distribution of the number of #OH across all combinations of offspring and possible parents is clearly a mixture of distributions, because it includes at least a distribution of #OH for non-related animals and a distribution for true parent–offspring pairs (Calus et al., 2011; Hayes, 2011), the #OH threshold was derived by visual inspection of the distribution of all #OH values.

5. From the shortlist generated in step 4, for offspring with at least 1 male and 1 female parent, and multiple possible pairs of parents, all possible pairs of male and female parents were evaluated using a trio approach. In this approach, when 1 of the 3 animals had a missing genotype, the genotypes of all 3 animals were replaced by a 1. This ensured that a trio did not fail the test for a specific SNP due to any missing genotypes. Then, for each locus the genotype of the offspring was subtracted from the sum of the genotypes of the parent pair. When the 3 genotypes match together, the result should be 0, 1, or 2, because the gametes “unused” by the offspring could give rise to another possible offspring genotype. Otherwise, the trio failed the test for this particular SNP. The percentage of SNP that failed the test were used for the parent assignment.

6. Assign the parents as follows:

   1. If only a single sire or a single dam matched with the genotypes of the offspring, then only this one parent was assigned.
   2. If there was only one possible parent pair identified, or only one of multiple possible parent pairs had a percentage of SNPs that failed the trio test smaller than a predefined threshold, then those 2 parents were assigned.
   3. In all other cases, including situations where multiple parent pairs matched with the genotypes of the offspring, multiple sires but no dams matched, or multiple dams but no sires matched, then no parents were assigned.

FindParents was applied twice. The first time all 56,075 SNPs were used. The second time, in steps 3 and 4 only a random subset of 1,000 SNPs was used. Then, step 4 was repeated using all 56,075 SNPs, considering for each individual only the parents that were retained based on the 1,000 SNPs. This approach was taken to try to speed up the process, as almost all computing time was used for step 3, and to investigate whether or not this affected the assigned parentage. To speed up the process further, the implemented program used parallel computing in step 3.

After the parent assignment, we retained all animals from the offspring generation for which both parents were assigned, as well as their assigned parents, and the assigned parents of those parents (i.e., assigned grandparents). Apparently not all grandparents were available in the data, as not all grandparents could be assigned. To complete as much as possible the grandparental generation for all offspring, we derived paternal haplotypes from the output of FImpute for any parents that had a known dam, but an unknown sire. We then computed between all these individuals the proportion of shared paternal alleles and transformed this into a distance measure by subtracting each proportion from 1. Based on visual inspection of a heatmap of the distance matrix, we estimated the apparent number of unknown sires by counting the number of observed clusters. Finally, the distance matrix was clustered using R-package “hclust” (R Core Team, 2016) to make a tree of the distance matrix that was then cut using the function “cutree” setting the number of desired groups equal to the apparent number of unknown sires. This process was repeated for any parents with known sire but unknown dam.

Validation of Parentage Derivation

To enable validation of the results obtained with FindParents, we simulated 100 A(BC) offspring of 100 randomly drawn line A sires and 1,000 randomly drawn line BC dams to mimic a situation where there are animals from the parental generation in the data that effectively do not have offspring. The offspring were generated by randomly matching simulated gametes of those sires and dams. Gametes were simulated from the phased data that were outputted by FImpute when imputing any missing genotypes. The probability that a recombination occurred between 2 neighboring SNPs was computed following Haldane's map function as 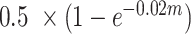(Haldane, 1919), where m is the distance in cM. The required distances between SNPs in cM were approximated by multiplying distances in base pairs by a factor of 3.15 × 10⁻⁶, obtained as the ratio between the physical (2996.2 cM) and genetic (952.4 Mb) size of the chicken genome (Groenen et al., 2009). The simulations were replicated 50 times. For each replicate, either the simulated genotypes were used as simulated or at random 1, 2, 3, 4, or 5% genotyping errors were introduced. If a simulated genotype was homozygous (0 or 2), a simulated genotype error resulted in replacing the genotype with a genotype 1 with a probability of 0.95, and in the remaining cases by replacing it with the alternate homozygote. If a simulated genotype was 1, a simulated genotype error resulted in replacing the genotype with genotypes 0 or 2, with equal probabilities. To compare the performance of FindParents, the simulated data were also analyzed using the R-package “SEQUOIA” version 1.3.1 (Huisman, 2017). As it was not possible to use all 56,075 SNPs in SEQUOIA, we ran it using 1,000 SNPs, obtained by selecting every 56th SNP. FindParents was also applied to those 1,000 SNPs as well as to all 56,075 SNPs. For SEQUOIA a genotyping error rate can be specified that is considered when deriving parentage. We analyzed all simulated datasets with SEQUOIA using assumed genotyping error rates of 0.5, 1, 2, 3, 4, and 5%. Likewise, we analyzed all simulated datasets with FindParents using #OH thresholds of 0.5, 1, 2, 3, 4, and 5%.

Derivation of BOA

For both the A(BC) offspring and the BC dams, the breed-of-origin for each of their alleles was derived, using the assigning BOA approach (Sevillano et al., 2016; Vandenplas et al., 2016). The BOA approach involved (1) simultaneously phasing genotypes of PB and CB animals using the (derived) pedigree information in AlphaPhase1.1 (Hickey et al., 2011); (2) building haplotype libraries for each line using phased haplotypes of PB animals; and (3) assigning BOA of CB animals based on their phased haplotypes, the frequencies of those haplotypes in each of the lines, and the line composition of CB animals (i.e., A(BC)). In the first step, AlphaPhase requires defining the number of consecutive SNPs to be phased simultaneously, denoted as core length, and the number of additional SNPs used on either end of the core, denoted as tail length, that are used in the process of phasing the SNPs in the core (Hickey et al., 2011). For each chromosome, 9 combinations of core and tail lengths were applied. Applied combinations of core and tail lengths (core length, tail length) were (150, 200), (200, 200), (250, 100), (250, 200), (300, 100), (300, 200), (350, 50), (350, 100), and (350, 200) for all chromosomes having more than 700 SNPs in the data. Used core and tail lengths for each chromosome are detailed in Supplementary Table S1. Each phasing analysis was performed twice considering either offset or non-offset analyses, resulting in 18 phasing analyses for each chromosome. Offset analyses were designed to create 50% overlap between cores of the offset and non-offset analyses by moving the beginning of each core to halfway along the first core of the non-offset analyses.

The data used for the BOA analysis included the A(BC) offspring and their assigned parents and grandparents, and any additional PB animals that were available in the data but not assigned to be parents or grandparents of the CB animals. The total numbers of PB animals included in the analyses were 8,205 for line A (including the PB offspring), 372 for line B, and 720 for line C.

RESULTS

Data Structure

To characterize the structure in the dataset, a genomic relationship matrix was computed using the first method of VanRaden (2008). A principal component analysis was performed on this genomic relationship. The first and second principal components clearly separated the animals with different line compositions (Figure 2). As expected, the BC dams were located in between the B and C purebred animals, and the A(BC) crossbred animals were located in between their A sires and BC dams.

Figure 2.

Principal component analysis of the genotype data.

Parent Assignment

The first step in the process of the parentage assignment is to derive the distribution of the #OH genotypes between any pair of individuals. This distribution showed multiple peaks, around 0, 4,100, 5,800, 7,600, 9,400, and 10,400 (Figure 3). The peaks at values greater than 0 likely represent different classes of relationships, including grandparent–grandchild relationships, as well as multiple peaks for pairs of unrelated animals originating from different combinations of the lines. Zooming in, on the range from 0 to 1,500 #OH, clearly revealed a peak at 0, with the lowest frequency around a value of 200 #OH, rapidly increasing after 500 #OH (Figure 4). Based on these results we used a threshold of 1% #OH, corresponding to 560 SNPs, to identify candidate parent–offspring pairs in the parentage assignment.

Figure 3.

Frequency of 0 to 20,000 opposing homozygotes between any pair of animals in the entire data.

Figure 4.

Frequency of 0 to 1,500 opposing homozygotes between any pair of animals in the entire data.

Derivation of parentage involved one analysis that used 8 threads and took 4 m 58 s wall clock time when using all SNPs in steps 3 and 4 of FindParents. When these steps were first performed using a random subset of 1,000 SNPs, the analyses finished in 1 m 29 s and yielded the same results. For the parentage assignment, 2 groups of animals were defined: 1) 20,253 animals for which we wanted to assign parentage, and 2) 4,504 possible parents of the first group. The first group included all A purebred and A(BC) offspring, and all A and BC animals from the parental generation. The second group included all A and BC animals from the parental generation, and all A, B, and C animals from the grandparental generation. Full parentage could be derived for 16,825 animals in the final offspring generation, including 5,882 purebred A and 10,943 A(BC) animals. At this stage, for the 5,882 purebred A offspring 78.9% of the paternal grandsires, 95.9% of the paternal granddams, 72.8% of the maternal grandsires, and 95.8% of the maternal granddams were assigned. For the 10,943 crossbred A(BC) offspring, 76.5% of the paternal grandsires, 94.4% of the paternal granddams, 80.0% of the maternal grandsires, and 91.3% of the maternal granddams were assigned. For all 443 parents with the dam assigned but not the sire, we clustered the derived paternal haplotypes, yielding 48 sires (Figure 5), of which 36 clustered with line A and 16 with line B. For all 27 parents with the sire assigned but not the dam, we clustered the derived maternal haplotypes, yielding 10 dams (Figure 6), of which 6 clustered with line A, 3 with line B, and 1 with line C. The 3 dams from line B were unexpected, as line B provided only sires in the cross used here. These animals were likely the result of sexing errors of the supposed line B males, and were together with their 49 offspring removed from the data.

Figure 5.

Heat map with dendrogram of the paternal haplotypes of animals of the parental generation with known dam but unknown sire.

Figure 6.

Heat map with dendrogram of the maternal haplotypes of animals of the parental generation with known sire but unknown dam.

After this final step, for 94.5% of the 5,882 purebred A offspring all grandparents were complete; for 2.4% the paternal grandparents were still unknown and for 3.2% the maternal grandparents were still unknown. For 90.6% of the 10,943 crossbred A(BC) offspring, all grandparents were complete; for 2.7% the paternal grandparents were still unknown and for 7.4% the maternal grandparents were still unknown.

Validation of Parentage Derivation

To investigate sensitivity of the assigned parents to the #OH threshold used, the parentage derivation step described above was repeated using an #OH threshold of 0.5% instead of 1%, i.e., 280 instead of 560 SNPs. Any observed differences in derived parentage were always such that a parent was assigned with one threshold, and no parent was assigned with the other threshold, or vice versa, meaning that using different thresholds never resulted in assigning a different parent. In the final generation containing 16,825 offspring, for only 19 animals differences were observed between the 2 #OH thresholds. Of these 19 animals, 15 and 16 had their sire assigned with #OH thresholds of 1 and 0.5%, respectively, with an overlap of 13 animals that had their sire assigned with both thresholds. In addition, 16 of those 19 animals had their dam assigned with a #OH threshold of 1%, but none with a threshold of 0.5%.

Results of the parentage derivation based on the simulated data are shown in Table 2. In all cases, any assigned parents were correct, e.g., no parents were incorrectly assigned. With FindParents using all SNPs and with SEQUOIA using 1,000 evenly spaced SNPs, the parentage assignment was in almost all cases 100% correct if the considered #OH threshold and SEQUOIA genotyping error rate, respectively, were equal or greater than the simulated error rate in the data. In the same cases, FindParents using 1,000 evenly spaced SNPs performed slightly worse when using a higher considered #OH threshold or when the simulated error rate in the data was greater. SEQUOIA was superior to FindParents, when the #OH threshold and SEQUOIA genotyping error rate were 0.5, and the simulated error rate was 2% or greater.

Table 2.

Percentage¹ of assigned parents² using FindParents or SEQUOIA.

		Simulated genotype error rate (%)
	Threshold3	0	1	2	3	4	5
FindParents	0.5	100	100	34.8	0.0	0.0	0.0
All SNPs	1	100	100	100	100	39.3	0.0
	2	100	100	100	100	100	100
	3	100	100	100	100	99.9	100
	4	99.9	100	100	100	100	85.9
	5	96.8	99.9	100	100	100	100
FindParents	0.5	100	100	88.2	39.7	12.1	2.3
1,000 SNPs	1	100	100	100	96.1	76.3	42.7
	2	100	100	99.9	99.9	99.9	99.6
	3	100	100	100	98.9	98.9	97.1
	4	99.2	99.9	100	99.9	95.0	95.0
	5	88.2	97.3	99.5	100	99.7	93.1
SEQUOIA	0.5	100	99.9	91.0	58.1	23.0	7.5
1,000 SNPs	1	100	100	99.9	97.0	77.6	45.3
	2	100	100	100	100	99.6	95.3
	3	100	100	100	100	100	99.5
	4	100	100	100	100	100	100
	5	100	100	100	100	100	100

¹Presented results are the averages across 50 replicates. Standard errors, computed as the standard deviation across replicates divided by , ranged from 0.0 to 0.8%.

²All assigned parents were correct.

³For FindParents, this is the #OH threshold; for SEQUOIA this is the specified genotyping error rate.

Parental Contributions

The numbers of identified individuals for each line composition for each of the 3 generations are shown in Figure 1. In total, 164 PB sires sired the entire offspring generation. The PB offspring had 152 sires, and the CB offspring had 156 sires, with 144 sires having both PB and CB offspring. The PB offspring had 1,016 PB dams, and the CB offspring had 1,386 F1 dams. The numbers of offspring per sire showed skewed distributions, ranging from 1 to 270 CB and from 1 to 154 PB (Figure 7). The numbers of PB and CB offspring per sire had a rank correlation of 0.70, which is for instance substantiated by the observation that the sire having the largest number of CB offspring was also the one with the second largest number of PB offspring (Figure 8). The numbers of offspring per dam ranged from 1 to 31 PB and 1 to 21 CB (Figure 9).

Figure 7.

Distribution of the number of purebred (A) and crossbred offspring (B) per sire.

Figure 8.

The number of crossbred vs. purebred offspring per sire.

Figure 9.

Distribution of the number of purebred (A) and crossbred offspring (B) per dam.

The 1,016 PB dams and 164 PB sires in total had 233 sires and 680 dams. Most of the line A grandparents that were the parents of line A sires in the parental generation were also parents of line A dams in the parental generation. Finally, the 1,386 BC dams had 226 line B sires and 678 line C dams.

Derivation of BOA

For the A(BC) animals, on average 49.49, 20.34, and 22.05% of the alleles could be assigned to lines A, B, and C, respectively (Table 1), yielding an average total assignment of 91.88%. For the BC animals, on average 48.47% of the alleles could be assigned to both lines B and C, yielding an average total assignment of 96.94%. The assignment percentage was exactly the same for lines B and C, because for a 2-way cross in the case only one allele can unambiguously be assigned to one line, the algorithm automatically assigns the other allele to the other line. The percentage of assigned alleles showed a clear relationship with the length of the chromosomes, as reflected in Figure 10 by the number of SNPs on a chromosome. In particular, the percentage of alleles of the A(BC) animals assigned to line A was close to the expected value of 50% and decreased for larger chromosomes, with a minimum value of 47.4% for the largest chromosome. A similar pattern for larger chromosomes was observed for assignment of alleles of BC animals, albeit that in this case the highest percentage of assigned alleles was achieved for chromosomes with intermediate length, with the lowest assignment percentage of approx. 44% observed for both the largest and one of the smallest chromosomes.

Figure 10.

The chromosome-wise percentage of assignment of alleles from A(BC) animals to line A and from BC animals to lines B and C vs. the number of SNPs per chromosome.

DISCUSSION

The objectives of this study were to rapidly reconstruct the pedigree in a large CB broiler dataset generated through natural mating, to evaluate the distribution of the number of offspring per sire, and to derive BOA for the CB animals in the dataset.

Parentage Assignment

The implemented algorithm FindParents very efficiently assigned parents for 2 generations of animals simultaneously. Here we provided FindParents with a list of animals for which the parents needed to be assigned, including animals from the offspring and parental generations, and a list of potential parents, including animals from the parental and grandparental generations. Alternatively, FindParents can retrieve parentage without providing any such list. In that case, however, it is important to note that an animal's offspring could incorrectly be assigned to be its parent. Thus, providing lists of possible offspring and parents may help to avoid such erroneous assignment, next to reducing the actual number of comparisons that has to be made, and is therefore recommended. When such lists are not provided, however, the trio approach helps to avoid assigning an offspring as an animal's parent, as the offspring combined with one of the parents or another offspring is expected to fail the trio test. Repeating the parentage assignment in our data without providing lists of offspring and potential parents gave exactly the same results, confirming that FindParents was able to distinguish for identified parent–offspring pairs which animal is the parent and which is the offspring. Analysis of the simulated datasets revealed that FindParents based on all approx. 50k SNPs is equally accurate as a maximum likelihood based method such as SEQUOIA based on 1,000 SNPs, provided that the used #OH threshold is similar to or somewhat greater than the genotyping error rate in the data. It should be noted that the simulated datasets were well structured as is expected to be the case in pigs and poultry breeding programs. Thus, FindParents provides an efficient and practical approach to derive parentage based on large numbers of SNPs, e.g., 50k such as included on common SNP chips use in livestock for genomic selection (Eggen, 2012), and can be integrated in pipelines for e.g., breeding value estimation without significantly increasing overall computing time.

Parental Contribution

The derivation of parentage showed that the distribution of the number of offspring of the sires was very skewed. There were sires that were allowed to breed but did not have any offspring, whereas the sire with the largest number of offspring had 270 CB and 152 PB offspring. This is one of the first studies that evaluated the differences in paternity for random mating systems where broiler breeder females are housed together with multiple broiler breeder males. In a previous study (Bilcik et al., 2005), 12 groups of 3 broiler breeder males and 12 females were housed for natural mating for 2 wk. Within those groups, the contribution of individual sires to the offspring ranged from 7 to 77%, and across groups the average of the minimum contribution was 15%, and the average of the maximum contribution was 55%. Although the group sizes were considerably smaller than in our data, the large difference in contributions by sires is in line with our results. In a study with laying hens (Jones and Mench, 1991), paternity was evaluated for 36 offspring of 6 different breeder males housed together with 57 females. The results also showed a skewed distribution in the offspring with 1, 2, 2, 5, 10, and 13 offspring per sire.

These results suggest that in practical breeding programs where in specific steps in the breeding pyramid natural mating may be employed, the contribution of males to the generated offspring may be highly variable. Deviations from the average contribution can affect the power of dedicated experiments, for instance to compute the PB-CB genetic correlation, because the data are not balanced in terms of the numbers of offspring per sire. Thus, in experimental set-ups using natural mating, depending on the specific research question addressed, optimization of the design should consider the possibly skewed contribution of sires to the offspring. Required formulas to predict the sampling variance of a genetic correlation exist, but all of them assume balanced designs (Tallis, 1959; Visscher, 1998; Bijma and Bastiaansen, 2014), and to our knowledge no formulas are available that take variance in contributions into consideration.

Derivation of BOA

The total percentage of assignment of alleles to the different breeds-of-origin was 91.9% for A(BC) animals. This is somewhat lower than the total percentage of assignment reported in previous studies. Reported assignment percentages for a 3-way cross were 94.3, 96.9, and 97.2%, respectively, for closely, distantly, and unrelated breeds in a simulation study (Vandenplas et al., 2016), and 95.2% for a 3-way cross in pigs (Sevillano et al., 2016). Considering the results per line showed a percentage of assignment of 49.5% to the sire line A, being very close the reported 49.6% assignment to the sire line in pigs (Sevillano et al., 2016). The 22.1% assigned to the maternal line C was close to reported values of 23.0 and 22.7% in pigs (Sevillano et al., 2016), whereas the 20.3% assigned to maternal line B was somewhat lower. These results are most likely due to the limited numbers of genotyped animals of line B used in the phasing analysis, being only 372, as opposed to 720 for line C. In the previous study on pigs, 4,179 and 7,183 animals were genotyped for the maternal lines, yielding only slightly higher assignment percentages than for our line C. The main step in the BOA procedure is phasing the haplotypes, and it has been shown that in phasing analyses for livestock data the accuracy of phasing within breed may be reduced if datasets include fewer than 1,000 genotyped individuals (Hickey et al., 2011). Therefore, in line with our results, it seems advisable in the procedure used to derive BOA to have at least 1,000 animals genotyped for each of the lines involved, as assignment percentages may be reduced otherwise.

The dataset used in our study was designed to enable estimating the PB-CB correlation for body weight (Duenk et al., 2019a), and to validate genomic prediction for CB performance, using either PB or CB performance for training the genomic prediction model (Duenk et al., 2019b). To ensure sufficient power to estimate the PB-CB correlation, the offspring generation was sired by a limited number of sires with both PB and CB offspring (Bijma and Bastiaansen, 2014). In this respect, it is especially important to be able to accurately model the relationships due to the sires. The achieved percentage of assignment to the sire line appeared sufficient to proceed with subsequent analyses requiring only the breed-of-origin of the paternal alleles to be known.

CONCLUSIONS

The implemented method FindParents to derive parentage was able to very rapidly retrieve the parents for approx. 20,000 animals from a total of approx. 4,500 possible parents. Results from simulations showed that for this particular dataset FindParents was as accurate as a maximum likelihood based method, provided that the #OH threshold used was similar to or somewhat greater than the genotyping error rate in the data, and that we used all approx. 50k SNPs rather than a subset of 1,000 SNPs. The derived parentage showed that the contribution of broiler breeder males to the offspring was very skewed, ranging from none to 270 offspring. Using the derived pedigree, and the available genotype data after phasing, enabled to assign breed-of-origin to the alleles of the CB offspring. The achieved percentage of assignment to the sire line was 49.5%, close to the maximum expected value of 50%, and sufficient to proceed with subsequent analyses requiring only the breed-of-origin of the paternal alleles to be known. The total percentage of assigned alleles was 91.9%; increasing this further requires adding more PB animals of the dam lines. For derivation of breed-of-origin for each line involved in a particular CB, it seems advisable to use at least 1,000 genotyped PB animals for each of the lines involved, although the required number of animals may be population dependent.

SUPPLEMENTARY DATA

Supplementary Material. Table S1. Per chromosome (Chr) the core and tail lengths used in the phasing analysis.