Source connectivity analysis with MEG and EEG

Abstract

Interactions between functionally specialized brain regions are crucial for normal brain function. Magnetoencephalography (MEG) and electroencephalography (EEG) are techniques suited to capture these interactions, because they provide whole head measurements of brain activity in the millisecond range. More than one sensor picks up the activity of an underlying source. This field spread severely limits the utility of connectivity measures computed directly between sensor recordings. Consequentially, neuronal interactions should be studied on the level of the reconstructed sources. This article reviews several methods that have been applied to investigate interactions between brain regions in source space. We will mainly focus on the different measures used to quantify connectivity, and on the different strategies adopted to identify regions of interest. Despite various successful accounts of MEG and EEG source connectivity, caution with respect to the interpretation of the results is still warranted. This is due to the fact that effects of field spread can never be completely abolished in source space. However, in this very exciting and developing field of research this cautionary note should not discourage researchers from further investigation into the connectivity between neuronal sources. Hum Brain Mapp 2009. © 2009 Wiley‐Liss, Inc.

INTRODUCTION

The goal of cognitive neuroscience is to understand how the brain is able to perceive, to think, and to behave. These processes rely on a coordinated interplay between various specialized brain regions. With the aim of identifying areas that subserve specific information processing tasks, the majority of neuroimaging studies have traditionally investigated task‐dependent changes in brain activity. The basic model justifying the study of such region‐specific changes in activity is based on the concept of functional segregation [Friston,1994]. However, to increase our knowledge of how the brain works, it does not suffice to study the activity and function of brain regions in isolation. Brain function also critically depends on functional integration, which relates to the pattern of interactions between brain regions.

Electroencephalography (EEG) and magnetoencephalography (MEG) are techniques that are ideally suited to study activity of the human brain on the time scale of cognitive processes. As these techniques provide measurements of brain activity by covering the whole head with a high number of sensors, they are increasingly used to study networks of interacting brain regions. The purpose of this mini‐review is to highlight some exciting recent methodological developments that enable researchers to study the interaction between brain regions based on noninvasively obtained electrophysiological measures of neuronal activity.

Interpretation of estimated connectivity from sensor level recordings is not straightforward, as these recordings are severely corrupted by effects of field spread. Source localization methods are constantly being refined, and offer the possibility of directly estimating the activity of the neuronal sources generating the sensor level data, attenuating the problem of field spread. In addition, neuroscientists have an ever increasing set of tools at their disposal to quantify interactions between neuronal signals. In this article, we will review different approaches that have been adopted for source level connectivity analysis. Bearing in mind that these approaches yield very promising results, we would like to emphasize the frequently overlooked issue that field spread is never completely abolished in source space. In our opinion, this calls for extreme caution in the interpretation of the results.

The structure of this review is as follows: first we will discuss the problems related to field spread in the context of connectivity analysis. Next, we will review the methods that are commonly used to analyze connectivity in source space; many different methods have been proposed, and we made an attempt to structure the literature by grouping the studies according to connectivity measures used. Following this, we will discuss the identification of regions of interest (ROIs), which is a crucial step in most studies. Subsequently, we will motivate the opinion that the interpretation of source level connectivity results should be done with care due to remaining effects of field spread. We will conclude this mini‐review with an outlook with respect to where we stand and what we should aim for in the future.

EFFECT OF FIELD SPREAD ON CONNECTIVITY RESULTS

A central issue in the interpretation of EEG and MEG data is the problem of field spread. Although it is a well‐known problem and described elsewhere [Nunez and Srinivasan,2006], it merits discussion in the context of connectivity analysis because it severely confounds many connectivity measures and therefore complicates the correct interpretation of the results. In the following section, we will briefly outline this problem in the context of connectivity analysis, and describe two strategies that attempt to diminish this problem: the analysis of experimental contrasts, and the use of connectivity measures that are less sensitive to field spread.

Field spread leads to a wide‐spread representation of any source at the sensors (Fig. 1A). This has severe consequences for the interpretability of connectivity measures estimated between pairs or sensors. To illustrate this, we simulated the activity of 10 temporally uncorrelated dipoles (gaussian noise), with an orientation parallel to the axis between the nasion and the midpoint of the interauricular line, and that were randomly distributed on the cortical sheet. Obviously, the orientations chosen are physiologically not meaningful, but are appropriate to demonstrate the effect of field spread on connectivity analysis. We simulated 100 s of data for a 248‐channel 4D neuroimaging magnetometer system, by using a realistically shaped volume conductor [Nolte,2003] and uncorrelated sensor noise. Figure 1B shows the absolute value of the correlation coefficient between all MEG sensor pairs as a function of their distance. Figure 1C shows the spatial topography of the absolute value of the correlation coefficient with respect to a reference sensor highlighted in white. These panels show that even though the underlying source activities are temporally uncorrelated, many sensor pairs show very high values of correlation. Moreover, the topography of correlation shows a distinct pattern with a spatially distant peak of correlation. This could be erroneously identified as a signature of two brain regions interacting.

Figure 1.

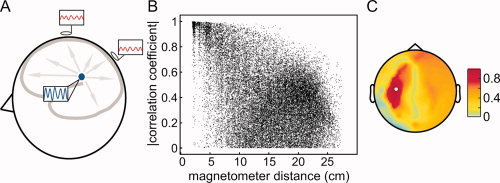
The effects of field spread confound sensor level estimates of connectivity measures. (A) Schematic representation of how the activity of a neuronal source is picked up by different sensors. (B) The absolute value of the correlation coefficient between all pairs of measured signals as a function of magnetometer distance. (C) Topographical representation of the correlation with respect to a reference sensor (highlighted in white).

To reduce the interpretational difficulties caused by field spread, one potential strategy could be to analyze changes in connectivity caused by an experimental manipulation, rather than the strength of the connectivity. The rationale for using experimental contrasts in this context is based on the assumption that the effects of field spread are identical across the experimental conditions and therefore subtract out. Unfortunately, these effects are highly dependent on the amplitude of the underlying (noise) sources. As a consequence, estimated modulations in connectivity do not necessarily reflect modulations in actual connectivity between relevant neuronal sources. This fact is illustrated in Figure 2.

Figure 2.

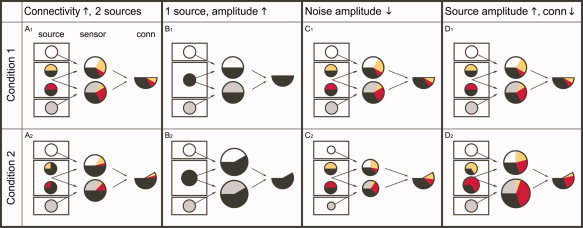
An estimated increase in connectivity may have different causes. The left column in each panel represents the sources, which are arranged in three compartments. Each circle represents a source, and these comprise the actual neural sources in the central “brain” compartment, and the irrelevant noise sources in the upper and lower compartments. The neural sources share a common component (a degree of connectivity), which is depicted as the black part of the circles. The circles in the middle column represent two sensor signals. Each of the sensors picks up a different mixture of the underlying sources. The partitioning of the sensor signals represents the relative contributions of the respective sources. The size of the circles represents the amplitude of the signal picked up at these sensors. The right column in each panel represents in the total area of the partitioned circle the degree of connectivity estimated between the two sensor signals. This degree of connectivity results from the total area of overlap between the colored partitions in the sensor signals. (A1, A2) Modulation of estimated connectivity due to a change in connectivity between neuronal sources of interest. The scenario A1 shows 4 sources (four circles in leftmost column). The different colors represent different uncorrelated signal components. The time series of the two sources in the middle contain a common component that makes up a specific part of their individual signal. Both sources are picked up by two sensors (circles in the middle column). Because of the noise sources only part of the sensor signals consists of signals of neural origin. This part is further subdivided into the different relative contributions of the two sources. Because of the fact that the upper sensor is closer to the upper source than to the lower source, it “sees” more of the upper source. Therefore, the yellow partition in the upper sensor is bigger than the red partition. The black part of the sensor signals represents the common component projected from the sources and has in fact been “diluted” by the noise sources. The degree of connectivity is derived by assessing the total overlap of colored partitions between the two sensors. Thus, it consists of the true common component picked up by the sensors (in black) and of the overlap in the colored partitions. In scenario A2, the common component in the activity of the neural sources is increased. Despite the diluting effect of the noise sources, an increase in the degree of connectivity can still be detected. (B1, B2) Modulation of estimated connectivity due to an increase in amplitude of a single neuronal source. (C1, C2) Modulation of estimated connectivity due to a decrease in amplitude of noise sources. (D1, D2) Modulation of estimated connectivity due to an increase in amplitude of the neuronal sources of interest, with a concurrent decrease of connectivity between them.

The figure schematically shows four simplified scenarios that give rise to identical modulations in estimated connectivity, which are caused by completely different changes in the underlying source configuration. Scenario A shows how an actual increase in source connectivity leads to an increase in estimated connectivity. However, the other three scenarios show that an apparent increase in connectivity (rightmost columns in the panels) can have different causes as well. Scenario B shows that even a single neuronal source that changes its amplitude can cause an increase in estimated connectivity. In scenario C, the signal‐to‐noise ratio changes due to a change in the amplitude of the noise sources. Scenario D shows that a decrease in connectivity between sources could actually lead to an estimated increase in connectivity, due to a concurrent increase in signal‐to‐noise ratio. The list of scenarios shown in Figure 2 is not exhaustive, but serves to illustrate that the interpretation of changes in estimated connectivity is not straightforward. This is an important point, and unless effects of field spread are completely suppressed or accounted for, the correct interpretation of the results of connectivity analysis is often ambiguous.

Field spread is an important motivation to perform the connectivity analysis at the source level. In addition to this, there are other important motivations to perform the analysis on the source level. First of all, there is a more direct indication of the anatomical location of the interacting brain regions. Second, source level analysis facilitates subsequent group analysis because the data can be averaged in a meaningful standardized space.

METHODS OF SOURCE CONNECTIVITY ANALYSIS

In this section, we will review the main methods that have been suggested for MEG source connectivity analysis. Most methods essentially adopt a two‐step procedure. First, an estimate of the activity of the neuronal sources is obtained by applying an inverse method (for a review, see [Baillet et al.,2001]). Second, an analysis of connectivity is performed, in which researchers usually restrict themselves to a set of prespecified ROIs. A notable exception to this two‐step approach is Dynamic Causal Modelling (DCM), which will be described in more detail below. It is beyond the scope of this review to present in a comprehensive discussion the advantages and disadvantages of all connectivity measures and inverse methods, and we will restrict ourselves to highlighting some applications of connectivity measures in source space. We will first describe the most commonly used connectivity measures and their application in source connectivity studies, followed by an overview of the strategies employed to identify ROIs.

Connectivity Measures

One key distinction that is often made in connectivity studies is that of functional versus effective connectivity [Friston,1994]. Measures of functional connectivity quantify statistical dependencies between neuronal signals, without explicitly addressing directed interactions. On the other hand, measures of effective connectivity quantify directed influence that one neuronal system exerts over another. Another key distinction is that between time and frequency domain measures of connectivity.

Measures of functional connectivity

Many source connectivity studies used coherence to quantify oscillatory interdependencies between brain areas [Gross et al.,2002; Hoechstetter et al.,2004; Pollok et al.,2004, 2005; Timmermann et al.,2003]. Coherence is the frequency domain analog of the cross‐correlation coefficient, and is usually computed using nonparametric spectral estimation techniques, such as the Fourier transform, or a wavelet transform. As such, coherence confounds the estimated consistency of a fixed phase difference with the correlation of the signals' amplitudes.

Amplitude effects can be disentangled from the consistency of the phase difference by means of the phase locking value (PLV). This measure can be obtained by normalizing the complex‐valued frequency domain single trial values with respect to their amplitudes, prior to estimating the interaction between the signals [Lachaux et al.,1999]. This phase synchronization analysis has been used in source connectivity analysis to complement traditional coherence analysis [Jerbi et al.,2007; Kujala et al.,2007; Lin et al.,2004]. Both coherence and PLV are symmetric measures and do not allow direct inference about directionality of information flow between areas. However, time delays can be estimated from the slope of the cross‐spectral densities between time series under favorable conditions [Halliday et al.,1995; Nolte et al.,2008].

Mutual information is a time domain measure to study linear and nonlinear dependencies between neuronal sources [Ioannides et al.,2000; Liu and Ioannides,2006]. The inverse method used in these studies was magnetic field tomography [Ioannides et al.,1990]. ROIs were identified from consistently activated areas across subjects. Time series of activation for each ROI were extracted and subjected to mutual information analysis. Mutual information was computed with a range of time lags between any pair of ROI. Although mutual information is a symmetric measure, application to time‐lagged signals can be useful to give insight into directionality.

Measures of effective connectivity

Frequency‐resolved estimates of directed interactions between brain areas can be obtained from parametric spectral estimators, using multivariate autoregressive models (MVAR‐models) [Schloegl and Supp,2006]. After fitting the MVAR‐model to the time courses of the estimated sources, directed interactions can be quantified by means of the directed transfer function (DTF) [Kaminski and Liang,2005], or the partial directed coherence [Baccala and Sameshima,2001; Kaminski and Blinowska,1991]. Essentially, these connectivity measures are designed as frequency domain analog of the concept of Granger causality [Granger,1969].

Granger causality analysis in source space has been performed by several groups [Astolfi et al.,2004, 2005; Gow et al.,2008; Kujala et al.,2007; Supp et al.,2007]. Astolfi et al. [2004, 2005] used structural equation modeling (SEM) in addition to DTF to infer effective connectivity from simulated and recorded high‐resolution EEG data. SEM and DTF analyses were applied to time courses of activation for anatomically defined ROIs computed from minimum norm solutions. The analysis was recently extended to allow the computation of time‐varying effective connectivity using adaptive MVAR‐models [Astolfi et al.,2008].

DCM is conceptually very different from the methods discussed so far [David and Friston,2003]. The key difference is that DCM aims to provide a biophysically plausible generative model of the measured data. The generative model specifies how input activates a system of prespecified interconnected neuronal populations, leading to the measured signal. As such DCM does not explicitly compute source waveforms separately, but provides an estimate of coupling parameters and source parameters in a single step [Kiebel et al.,2008]. In contrast with the two‐step procedures, DCM accounts for conditional dependencies between coupling parameters and source reconstruction parameters. DCM had originally been devised for the analysis of evoked responses [Garrido et al.,2007]. Recent developments have extended the functionality of this promising technique to induced responses [Chen et al.,2008] and steady‐state responses [Moran et al.,2007].

Identification of Regions of Interest

Almost all methods for MEG source connectivity analysis compute connectivity measures between every pair of a few selected ROIs, or between a few ROIs and the rest of the brain. The selection of ROIs obviously is a critical step as the quality of the estimated time courses in the ROIs determine the outcome of the connectivity analysis between them. Therefore, incorrect specification of ROIs could lead to erroneous results. Several strategies have been suggested.

A priori selection

ROIs can be selected based on a priori knowledge of their involvement in a given experimental task (e.g., from previous functional imaging studies) [Astolfi et al.,2004, 2005; Babiloni et al.,2005; Gross et al.,2001; Lin et al.,2004]. These areas can be identified in the individual anatomical MRI or coordinates in Talairach‐MNI space can be transformed into individual coordinates. Another approach has been used by Härle et al. [Härle et al.,2004]. They computed the minimum norm solution at 350 locations in the brain for steady‐state auditory responses. Connectivity was quantified by means of coherence. Using a priori selection, measures of connectivity can be computed between all possible pairs of ROIs although the locations may not be optimal or important regions may be missed.

Cortico‐peripheral coherence

This approach uses an estimate of coherence between a peripheral physiological signal and brain activity reconstructed at a discretized grid. It allows the identification of brain areas where the activity is modulated by rhythmic processes in the peripheral signal. This strategy has successfully been used for oscillatory components in movements as recorded with electromyography and movement tracking devices [Gross et al.,2001, 2002; Jerbi et al.,2007; Lin et al.,2004; Pollok et al.,2004; Schnitzler and Gross,2005; Schoffelen et al.,2008; Timmermann et al.,2003]. The areas of maximum cortico‐peripheral coherence can be used as reference areas for the analysis of cerebro‐cerebral coupling. A prerequisite for this strategy is of course the availability of a meaningful peripheral signal. Moreover, as one study showed, even in the presence of an adequate peripheral signal and a reliably identified reference area, subsequent cerebro‐cerebral coupling analysis does not always yield the expected results [Schoffelen et al.,2008].

Sensor coherence

Gross et al. reported the use of coherence between all sensor combinations for a MEG system with planar gradiometers. Long‐range coherences were identified and the underlying generators were localized iteratively [Gross et al.,2001]. Because of field spread outlined above, this strategy is not expected to work reliably in most cases.

Power maps

Possibly, the most widely used strategy is a selection of ROIs based on maps of neural activity. Brain areas showing strongest activity in an experimental task or strongest differences of activity between experimental conditions are selected for further connectivity analysis.

This approach was applied by David et al. They used a minimum norm estimate (MNE) to estimate the time courses of the sources of unaveraged data [David et al.,2002]. Significantly activated areas were then identified in relation to surrogate data. An iterative procedure was employed to reduce the number of active volume elements (voxels). This final selection of voxels was subsequently subjected to phase synchronization analysis. The technique has later been adjusted for the analysis of multitrial experiments [David et al.,2003]. A similar approach has been applied in a study investigating visuo‐motor coupling by Jerbi et al. [2007]. Subjects were instructed to manipulate a trackball to counter unpredictable rotations of a visually presented cube. The MNE was obtained for each sample on unaveraged data using a cortically constrained reconstruction with 12,000 points. For each of the locations power, and coherence and phase synchronization to trackball speed was computed. Individual results were spatially normalized to MNI space and corrected statistics were obtained from maximum statistics of randomly permuted data. The approach resulted in ROIs that were used as reference regions for cortico‐cortical coherence analysis. Selecting ROIs based on their activity (or modulation of activity) alone may not be optimal, since weakly activated or modulated brain areas could be missed even if they are strongly interacting with other areas.

Coherence‐based methods

Kujala et al. suggested a technique that identifies highly connected areas by computing the connection density throughout the brain [Kujala et al.,2007, 2008]. The connection density for a given voxel is defined as the number of long distance connections that exceed a certain coherence threshold. The connection density map can be thresholded and local maxima can be used as ROIs. Differences in the connection density map between conditions can be analyzed to identify task‐dependent connectivity changes.

Ideally, one would like to drop all assumptions and avoid arbitrary thresholds by computing the connectivity measure between all voxel combinations. Although already moderate voxel sizes lead to several million combinations, these big matrices can be handled by modern desktop computers. But, extracting useful information from this matrix is still a difficult problem.

Recently, a computationally efficient postprocessing of the voxel correlation matrix by means of a singular value decomposition (SVD) has been suggested [Dossevi et al.,2008]. Source activations were computed using MNE. The problem of computing the SVD of the (very big) source correlation matrix was reduced to the problem of computing the SVD of the inverse operator (that maps sensor signals to source space). The first eigenvectors were thresholded and taken as correlated areas. Applications to simulated data demonstrated some robustness to correlated sources. The suggested method is interesting since it does not rely on a priori information and makes no explicit use of source activity. Still, the choice of the number of relevant eigenvectors, the arbitrary thresholding for the eigenvectors, and the orthogonality constraint of the SVD are problematic and could be addressed in further developments.

LIMITATIONS

As mentioned before, one important motivation to perform connectivity analysis at the source level is the often implicit assumption that the effects of field spread are mitigated. However, unmixing of the sources is never perfect. This is illustrated in Figure 3. Using the simulated data as presented in Figure 1, we performed a source level connectivity analysis. We estimated the activity at 1,000 locations, distributed on the cortical sheet (without orientation constraint), and computed pairwise correlation coefficients between all estimated activities, using two commonly used inverse methods (Fig. 3A,B). It can be clearly seen that there is a massive number of dipole pairs showing spurious correlations. In this simulation, the linearly constrained minimum variance (LCMV) beamformer seems to perform somewhat better than the minimum‐norm estimate. The estimated correlation coefficients between the simulated uncorrelated dipoles are low, and the overall size of the spurious correlation coefficients is lower than in the minimum‐norm estimate. It is important to stress that the outcome of such a simulation is highly dependent on the parameters used for the simulation, and no conclusions should be drawn with respect to the performance of the different inverse methods from this example alone.

Figure 3.

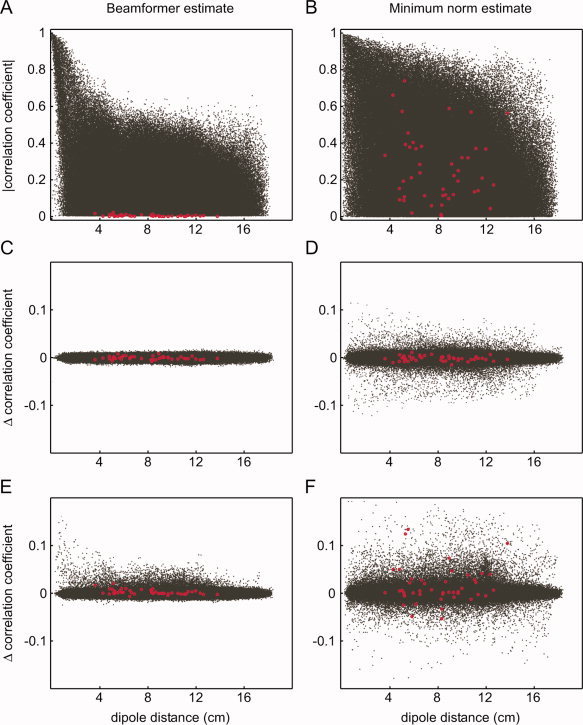
Effects of field spread are not totally abolished in source space. (A, B) Absolute value of the correlation coefficient as a function of dipole distance between the estimated activity at all pairs of 1,000 dipole locations on the cortical sheet (black), and between the estimated activity at all pairs of 10 of these locations at which activity was simulated (red). Two different inverse methods were used: an LCMV‐beamformer (A) and a minimum norm solution (B). The dipole orientations were unconstrained in both approaches. No regularization was applied. (C, D) The estimated difference in correlation between two “conditions” of simulated data, in which the signal‐to‐noise ratio was equal across conditions. Same conventions as in (A, B). (E, F) The estimated difference in correlation between two “conditions” of simulated data, in which the signal‐to‐noise ratio was about 30% lower in the second condition. Same conventions as in (A, B).

We will briefly discuss the reason why the outcome of connectivity analysis using experimental contrasts should be interpreted with care (in principle, the effects illustrated in Fig. 2 still hold for source connectivity analysis if sensors (middle columns) are replaced by estimates of source activity (virtual sensors)). Figure 3C,D show the difference in correlation between two simulated datasets, as a function of dipole distance. We simulated 10 uncorrelated dipoles with fixed location, orientation and amplitude, which were identical for both conditions. Also, the amplitude of the uncorrelated sensor noise was identical across conditions. The resulting difference in correlation between all pairs of simulated dipoles was close to 0. Moreover, the distribution of differential correlation coefficients across all dipole pairs was quite narrow, although the range was somewhat bigger for the minimum‐norm estimate. Figure 3E,F show the difference in correlation between two simulated datasets, in which the sensor noise was different across the two conditions (30% difference). The size of the spurious correlations between nonactive dipoles is substantially enhanced with both analysis methods. The estimated differential correlation between some of the simulated dipoles was also increased. These findings emphasize several problematic issues as follows:

• 1Even when focusing on the appropriate ROIs it could be that incorrect conclusions are drawn with respect to the underlying interactions.
• 2Inappropriately selected ROIs could lead to incorrect conclusions with respect to the underlying interactions.
• 3Condition‐specific fluctuations in signal‐to‐noise ratio due to amplitude changes of the brain signals could have effects similar to fluctuations in sensor noise. These effects are difficult to control and may confound the interpretation.

Interpretation of connectivity analysis on the source level is complicated by the confounding effects of field spread. This holds true irrespective of the connectivity measure used, provided a “traditional” inverse method has been used, prior to computing the connectivity measure. By traditional inverse methods we mean those methods that do not explicitly dissociate “interactions” due to field spread from true interactions between the underlying sources, and which comprise the beamformer, distributed source models, and the dipole fitting approaches discussed so far. Recently, two promising techniques have been proposed that are aimed at tackling the effects of field spread prior to performing the inversion step [Gomez‐Herrero et al.,2008; Marzetti et al.,2008]. One of these techniques uses the imaginary part of the sensor‐level cross‐spectral density matrix to identify spatial topographies of pairs of interacting neuronal sources [Marzetti et al.,2008]. Using an additional constraint of minimum overlap, the location of the interacting sources can be determined. The use of the imaginary part of the cross‐spectral density matrix ensures that the interaction cannot be explained by field spread [Nolte et al.,2004]. The authors were able to localize the generators of the μ‐rhythm and of the parieto‐occipital α‐rhythm in an example EEG dataset.

The other technique is based on the decomposition into independent components of the residuals of a MVAR‐model. The MVAR‐model is fitted to the sensor data, after an initial principal component analysis [Gomez‐Herrero et al.,2008]. The residuals of the fitted MVAR‐model contain the zero‐lag interactions between the sensors, and thus indirectly of the underlying sources. These zero‐lag interactions comprise the field spread. A subsequent independent component analysis (ICA) unmixes the residuals into a set of statistically independent time series. These components are assumed to be the residuals of the source level MVAR‐model. The ICA mixing matrix contains the spatial topographies of the interacting sources and can be used to determine their locations, as well as the MVAR‐coefficient matrices of these sources. This approach has been applied to EEG data to identify the directed interactions in an oscillatory network in the α frequency band.

CONCLUSION AND OUTLOOK

Recently, the importance of noninvasive functional connectivity analysis has been increasingly recognized. This has led to new methodological developments and an increasing number of connectivity studies. MEG, in particular, is a very promising tool for connectivity analysis due to its unique set of features (whole scalp coverage, good spatial and excellent temporal resolution). Connectivity analysis on sensor level recordings is very problematic due to effects of field spread. As illustrated above, a single activated brain area can lead to long‐range interdependencies between MEG/EEG sensors. Even contrasting connectivity results between experimental conditions at the sensor level does not provide an automatic cure for the problem of field spread. A detected change in coherence (or connectivity in general) between sensors could arise from many different scenarios. These scenarios may be caused by the complex interplay of changes of power (and coupling) of one or several brain areas and noise. Some of these scenarios may not involve any connectivity change between two brain areas or even the activity of two distinct brain areas in the first place. These complications lead to the recommendation to perform MEG/EEG connectivity analysis on the level of source activations.

The combined use of source localization techniques and connectivity analysis on source waveforms, and the recent development of a generative model as in DCM, open exciting possibilities in studying the transient interactions between brain areas, including the nature of these interactions and their directionality. The tools required for this type of analysis are readily implemented in commercial and open‐source software packages, and thus available to researchers at all levels of methodological expertise. Nevertheless, we hope we have presented some evidence to convince the reader that source connectivity analysis is far from trivial and that great care has to be taken during the analysis of MEG/EEG data and the interpretation of the results. Still, the high relevance of noninvasive connectivity analysis urges us to make every possible effort toward a validated methodology for connectivity analysis on the level of reconstructed brain sources. Our efforts need to address the following points:

• 1Although source connectivity analysis alleviates the problem of field spread to a certain extent, it does not provide a perfect solution. A quantification of field spread on source connectivity results is needed. This will most likely include the use of estimates of the spatial inhomogeneity of the source reconstructions. This inhomogeneity can be quantified by means of the full‐width half maximum (FWHM) of the inverse operator [Barnes et al.,2004; Gross et al.,2003] or by the resolution kernel [Backus and Gilbert,1968]. In addition, due to their potentially confounding effects, power changes between conditions should be routinely analyzed in connectivity studies and considered during interpretation of the results.
• 2The selection of ROIs often still requires interaction with the user and/or employs some arbitrarily chosen parameters. Ideally, the use of any a priori information in the selection of ROIs would be replaced by an evaluation of connectivity between all possible combinations of voxels (possibly preselected according to a FWHM‐estimate).
• 3A comprehensive and rigorous comparison of the performance of various combinations of source localization techniques and connectivity measures is missing and would represent an important step toward a common consensus about source connectivity methodology.

The ever increasing interest in noninvasive functional connectivity analyses with MEG/EEG and the rate of recent developments justify a fair degree of optimism regarding the future of this exciting area of research. MEG/EEG source connectivity analysis maximally exploits the unique capabilities of state‐of‐the‐art electromagnetic measurement systems and will undoubtedly lead to new fascinating insights into the complex relationship between the highly dynamic interactions of brain areas and human behavior.