Physical modeling of pulse artefact sources in simultaneous EEG/fMRI

Abstract

The collection of electroencephalography (EEG) data during simultaneous functional magnetic resonance imaging (fMRI) is impeded by large artefacts in the EEG recordings, with the pulse artefact (PA) being particularly challenging because of its persistence even after application of artefact correction algorithms. Despite several possible causes of the PA having been hypothesized, few studies have rigorously quantified the contributions from the different putative sources. This article presents analytic expressions and simulations describing two possible sources of the PA corresponding to different movements in the strong static field of the MR scanner: cardiac‐pulse‐driven head rotation and blood‐flow‐induced Hall voltages. Models of head rotation about a left–right axis and flow in a deep artery running in the anterior–posterior direction reproduced properties of the PA including the left/right spatial variation of polarity. Of these two sources, head rotation was shown to be the most likely source of the PA with simulated magnitudes of >200 μV being generated at 3 T, similar to the in vivo PA magnitudes, for an angular velocity of just 0.5°/s. Smaller artefact voltages of less than 10 μV were calculated for flow in a model artery with physical characteristics similar to the internal carotid artery. A deeper physical understanding of the PA is a key step in working toward production of higher fidelity EEG/fMRI data: analytic expressions for the artefact voltages can guide a redesign of the wiring layout on EEG caps to minimize intrinsic artefact pickup, while simulated artefact maps could be incorporated into selective filters. Hum Brain Mapp, 2010. © 2009 Wiley‐Liss, Inc.

INTRODUCTION

Simultaneous functional magnetic resonance imaging (fMRI) and electroencephalography (EEG) has become a widely used technique in studying brain activity, capitalizing on the high spatial resolution of the former and excellent temporal resolution of the latter [Debener et al.,2008; Laufs et al.,2008]. Two major artefacts corrupt EEG measurements made in an MR scanner during concurrent magnetic resonance imaging: the gradient artefact resulting from induced voltages due to the temporally varying magnetic field gradients used in MRI, and the pulse artefact (PA) caused by the pulsatile flow of blood. Since the temporal form of the gradient artefact is linked directly to the gradient waveforms, its timing is periodic and predictable. Usually, the gradient artefact can therefore be adequately suppressed via subtraction of an average artefact template [Allen et al.,2000]. In contrast, the PA does not display such consistency and the artefact can vary on time scales as short as consecutive heart beats [Bonmassar et al.,2002; Debener et al.,2007], as well as showing large variation across subjects [Huang‐Hellinger et al.,1995]. The maximum amplitude of neural activity detected by EEG seldom exceeds 50 μV and as such it may be completely obscured by the PA, whose amplitude can exceed 200 μV at 3 T [Debener et al.,2007]. The inability of current filtering methods to remove this artefact fully leads to significant degradation of the EEG data recorded in combined EEG/fMRI studies, since the frequency range of the PA coincides directly with the neuronal signals that are of interest in many EEG recordings [Bonmassar et al.,2002]. Thus, the accurate removal of the PA from simultaneous EEG/fMRI data is of paramount importance for collecting high fidelity EEG data in the MR scanner.

Various methods have been proposed for removal of such artefacts. The averaged artefact subtraction (AAS) algorithm pioneered by Allen et al. [1998] involves identification of the PA peaks, usually from a concurrently recorded electrocardiography (ECG) trace, and then averaging over an appropriate time window to generate an artefact template for each channel that is subsequently subtracted from the EEG data. The relative simplicity of this method means it is commonly used today, despite performance limitations resulting from a fundamental trade‐off: a longer averaging time risks producing an inadequate template due to the variations of the PA, whereas use of a shorter time risks filtering out the brain signals of interest as well as the PA. To improve upon AAS, more complex algorithms such as independent component analysis (ICA) [Briselli et al.,2006; Mantini et al.,2007; Nakamura et al.,2006], optimal basis set (OBS) analysis [Debener et al.,2007; Niazy et al.,2005], and spatial adaptive beamformer filtering [Brookes et al.,2008] have been used to produce promising results. The data‐driven focus of these methods however means that they give little insight into the physical origins of the PA; few studies have in fact attempted to quantify rigorously the source of this complex artefact.

Several possible mechanisms [Allen et al.,1998; Debener et al.,2008] by which cardiac pulsation could generate the PA in EEG recordings made in the strong uniform magnetic field of an MR scanner have been suggested. The most plausible of these are: (i) voltages induced by rotation of the head in the magnetic field—rotation that is driven by the momentum changes of blood as it is pumped by the heart and shunted into arteries in the head [Bonmassar et al.,2002; Huang‐Hellinger et al.,1995]; (ii) the pulsatile flow of blood, a conducting fluid, which in the presence of a magnetic field produces a separation of charge via the Hall effect [Tenforde et al.,1983] that gives rise to potential variation at the surface of the scalp [Muri et al.,1998]; and (iii) voltages generated by movement associated with pulse driven expansion of the scalp [Debener et al.,2008]. Here, we focused mainly on mechanisms (i) and (ii) (head rotation and blood flow) and used physical modeling to determine whether these mechanisms are realistic sources of the PA. This involved comparing the results of calculations with experimental measurements made on spherical agar phantoms and human subjects.

First, to provide a benchmark against which the candidate artefact causes can be assessed, we present measurements of the PA made in vivo at 3 T. The models of the artefact sources are then presented, beginning with analytic expressions for the voltage produced by head rotation, which are derived assuming that the human head can be modeled as a homogeneous sphere and that the EEG wires run along lines of longitude on the sphere's surface (Fig. 1a). This is followed by a numerical simulation incorporating the actual wirepaths of the EEG cap (Fig. 1b). The physics of our model were then verified by comparison to an experimental measurement made with an EEG cap placed on a spherical agar phantom that was manually rotated. The artefact arising from blood flow was also simulated, first via analytic calculation assuming the flow generated a point dipole in a homogeneous conducting sphere, and then with an experimental confirmation that involved collecting EEG data as an electrolytic solution flowed through a U‐shaped conduit in a conducting spherical phantom in a 3 T magnetic field.

Figure 1.

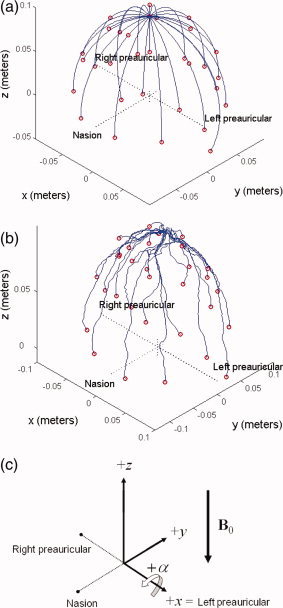
(a) Model 32‐channel EEG cap with purely meridional wires, which was used for the analytic calculations. The co‐ordinate system is defined so that the nasion and preauricular points lie along the principle axes. Electrodes are placed according to the Extended International 10–20 system. The +z‐axis points toward the top of the head, while the −y‐axis points toward the nasion and +x‐axis points toward the left preauricular point. The origin is defined by the intersection of a perpendicular from the nasion to the line between the left and right preauricular points. (b) Wirepaths from an actual EEG cap placed on a spherical phantom, digitized using a Polhemus Isotrak system. (c) Schematic of the coordinate system used in this article, including the direction of the B₀ field of the 3 T Philips Achieva MR scanner used for experimental measurements. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The aim of this work is to provide a deeper physical understanding of the PA. This is a key step in working toward production of higher fidelity EEG/fMRI data: analytic expressions for the artefact voltages can guide a redesign of the wiring layout on EEG caps to minimize intrinsic artefact pickup, while simulated artefact maps could be incorporated into selective filters. In particular, spatial and temporal maps generated by physical models of the PA could improve filtering methods by elucidating the characteristics that best differentiate signals resulting from neural activity from those linked to cardiac pulsation. For example, particular independent components and basis sets that are similar to known artefact signals may be identified and removed with greater confidence and accuracy, while feeding modeled spatiotemporal patterns of artefact voltage into an adaptive beamformer [Brookes et al.,2008; Wan et al.,2008] that can suppress particular spatial features in EEG recordings, could also allow improved elimination of the PA.

MATERIALS AND METHODS

Rotation Artefact

Theory and analytic calculations

The effect of head movements in a magnetic field on EEG recordings can be predicted using Faraday's law, which links changes in magnetic flux to induced potentials. Previous studies [Nakamura et al.,2006; Vasios et al.,2006] have modeled the EEG leads as closed wire loops (Fig. 2a) connected to a high‐impedance amplifier. This makes determining the induced voltages relatively easy as they can be calculated directly from the rate of change of flux enclosed by the wire loop using a surface integral

(1)

where B is the magnetic field.

Figure 2.

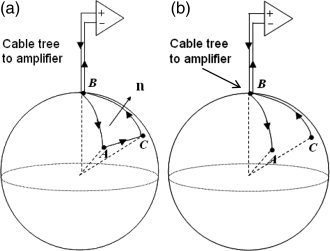
Wire loop configuration (a) versus situation that is relevant to EEG (b). In (b), there is not a single defined path from A to C through the conducting sphere, and thus we must calculate the spatially varying potential term induced by the temporally varying magnetic field in order to find the total artefact voltage.

Although this model is commonly used and provides an intuitively pleasing approach, it is nevertheless of limited utility in calculating the actual voltages that are generated at the amplifier by head rotation in an EEG recording, since the inclusion of a volume conductor in the circuit (Fig. 2b) means that it is not possible to define the relevant area over which the change in flux occurs. To do this, it is necessary to consider the spatially varying scalar electric potential, ϕ, induced in the volume conductor by charge redistribution resulting from the magnetic force acting on the moving charges, in addition to the potential directly induced through Faraday's Law in the EEG leads. The total potential difference at the amplifier is thus given by the sum of two terms: (1) the electrode contribution, given by the difference in scalar potential between electrodes on the surface of the volume conductor and (2) the lead contribution resulting from the voltage induced in the conducting wires as they move in the magnetic field [Glover and Bowtell,2007]. In general, this approach produces a different result than the surface integral [Eq. (1)], that is relevant for the closed loop case. We have recently used a similar approach successfully to model the gradient artefact [Yan et al.,2009].

Considering the scalar potential first, the spatially varying electric field, E′, induced in a region of a conducting object moving in a temporally invariant magnetic field, B, can be written as

(2)

[Lorrain,1990] where v is the local velocity in the frame where the magnetic field is stationary (v is spatially invariant in the case of translational motion, but will vary with position if rotation occurs). Here, the first term describes the electrostatic field while the second term is the electromotive field. A physical interpretation is that the magnetic force F = q v × B (where q is the test charge) redistributes the charges in a conductor moving in a magnetic field so that a new contribution to the electric field is produced, which can be described by the gradient of the scalar potential, ϕ. The electric field also generates a current density, J= σE′, but for the low values of σ|v × B| that are relevant for head movement in the static field of an MR scanner, we can assume that the magnetic field generated by the induced current density is negligible and that the charge redistribution is instantaneous.

In this quasi‐static regime, the normal component of J must be continuous across any boundary between regions of different conductivity in the object. This provides a boundary condition that can be used to solve for ϕ when the form of v × B is known. For the homogeneous conducting sphere considered here, this boundary condition means that the radial component of the electric field must be zero at the surface of the sphere:

(3)

In general, in an EEG recording the voltage measured at a data electrode (A) is compared to the voltage measured at a reference electrode (C). The electrode contribution to the potential difference measured at the amplifier inputs is then the difference in the values of ϕ at the positions of the two electrodes, which takes a value of V _Electrode = ϕ_A − ϕ_C.

The other contribution to the artefact voltage comes from movement of the conducting leads connecting the electrodes to the EEG amplifier. With the high impedance amplifiers used in EEG, we may assume that no current flows between the positive and negative terminals of the amplifier. The magnetic force thus acts to increase the potential energy, U, of charges in the wire rather than generating a current, and summing this along the wire gives:

(4)

where B and A are the start and end points of the wire, respectively, and dl is an infinitesimal length. Since electric potential can be defined as U = qV, the movement of the wires produces an artefact voltage contribution .

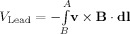Adding the voltages from the two sources together, the rotation artefact measured as the potential difference between the “data” electrode A and “reference” electrode C in Figure 2b is

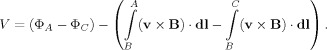(5)

For the analytic calculations, we assume that the EEG leads run along the meridians of the sphere in the θ‐direction, oriented such that the start of each lead is at the cable tree, positioned at the north pole of the sphere and the end is at the electrode (Fig. 1a). Another assumption is that the cable bundle connecting the cap and the amplifier remains stationary, so that the only contribution to the artefact comes from the leads on the EEG cap. Thus, the contribution of the wires to the artefact is given by the line integral on the surface of the sphere. For a lead at an azimuthal angle ϕ_E, running from polar angle 0 to θ_E on the surface of a sphere of radius, r, this is given by

(6)

with being the unit vector in the θ‐direction. To generate simple analytic expressions for the artefact voltage, we assume that the reference electrode is positioned at the north pole of the sphere (at the site of the cable tree).

In Appendix A, the approach described above is applied to evaluation of the artefact voltage produced by translation and by rotation about an axis that is parallel to the applied magnetic field. The analysis described therein indicates that both these types of motion generate no artefact voltage at the amplifier inputs. This is in agreement with the predictions of simple analysis based on consideration of changes in the flux linked by virtual loops formed by the leads and volume conductor. In the light of these findings, we focused our effort on analysis of the artefact voltages generated by rotation about an axis that is perpendicular to the applied field.

Effect of rotation about an axis that is perpendicular to the field

Initially, we consider the situation where the sphere rotates about the x‐axis with angular velocity, Ω, such that Ω = Ωi. This motion corresponds to a nod of the head. In most real situations, the head will not be positioned exactly at the iso‐center of the scanner and the orientation of the head and EEG cap arrangement with respect to the applied field may vary. Translations do not affect the voltage induced by rotation since the head is exposed to a homogeneous magnetic field. Angular offsets about the y and z axes, corresponding to roll and yaw of the head, respectively, are often relatively limited by the tight geometry of the RF receiver coil, but more substantial angular offsets about the x‐axis often occur in realistic subject positions [Yan et al.,2009] (see Fig. 1c). To investigate the effect of such an angulation, we rotate the B‐field orientation in the analytical calculations. Recognizing that the magnetic field in the Philips Achieva scanner points in the head to foot direction, we write the magnetic field in the frame of the rotated sphere as B = −B ₀ sin αj − B ₀ cos α k, so that +α corresponds to a nod forward of the head, as shown in Figure 1c.

The position dependent velocity produced by a rotation about the x‐axis can be written in the same frame as, v = Ω × r = Ω (−z j + y k) so that

(7)

We note that the divergence of v × B is zero under these circumstances, so we do not need to consider a space charge in the volume conductor [see Eq. (A6)], and consequently the scalar potential satisfies Laplace's equation, ∇² ϕ = 0. To solve for the scalar potential, ϕ, we apply the boundary condition that at the surface of the sphere, the net contribution from the radial electrostatic and electromotive fields in Eq. (2) must be zero in order to avoid an unrealistic flux of current out of the sphere. Focusing on the radial components of the different terms and evaluating at the surface of the sphere where r = a we find

(8)

Laplace's equation in spherical coordinates limits solutions of ϕ to a series of weighted spherical harmonics and in this simple case we can straightforwardly identify the appropriate solution as

(9)

The dependence of this expression on sin θ means that ϕ is zero at the pole of the sphere, where we assume that the reference electrode is positioned. Consequently for a sphere of radius, a, the potential difference between the reference electrode and a data electrode depends only on the position of the data electrode on the surface of the sphere, defined by spherical polar angles, θ_E and ϕ_E:

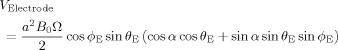(10)

For the line integral term, we assume that the wires of the EEG cap run along lines of longitude on the surface of the sphere, as shown in Figure 1a so that the integral along the lead from the pole to a data electrode at θ_E and ϕ_E, is given by

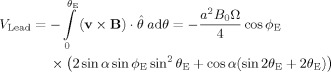(11)

Adding the two contributions together results in the cancellation of the scalar potential term, giving a total artefact voltage for a nodding motion of

(12)

By analogy, rotational motion about the y‐axis (roll) with the instantaneous position of the sphere corresponding to one in which the sphere starts with its z‐axis aligned with the magnet and then is rotated through angle, α, about the y‐axis is given by replacing the cosine term of Eq. (12) with a sine term.

Numerical calculations

A key shortcoming of the analytic model (Fig. 1a) is the assumption that the EEG leads follow lines of longitude. Thus, in the line integral of Eq. (5) only the θ‐component of v × B contributes despite the fact that the radial and azimuthal components are not necessarily zero. For a real cap whose leads often deviate substantially from meridional paths, all components of v × B may contribute to the artefact voltage. In addition, in a real system the reference electrode is generally not positioned at the site where the cable tree meets the head and the reference lead consequently contributes to the measured artefact. To produce a more accurate estimate of the artefact voltage produced by head rotation, we therefore evaluated the line integrals along digitized versions of the real wire paths from a 32‐channel BrainCap electrode cap (EasyCap, Herrsching, Germany) with 30 electrodes positioned according to the International Extended 10–20 system and a reference electrode positioned between Fz and Cz. The lead paths and electrode positions were measured on a human head using a Polhemus Isotrak motion tracking system that sampled the wire paths with ∼4 points per centimeter (Fig. 1b). The origin of the coordinate system in which the points were placed is at the center of the sphere of best fit to the scalp, as determined from anatomical MR images acquired from the subject [Yan et al.,2009]. Line integrals of v × B were calculated using a midpoint Riemann sum in Matlab (Mathworks, Natick, MA) over the digitized wire paths. The scalar potential contribution was found by evaluating ϕ at the position of the electrode. The total artefact was then calculated by subtracting the respective electrode and wire contributions of the digitized data and reference leads as in Eq. (5).

Experimental measurements

Experimental measurements allowed validation of the spatial form of the artefact generated by the analytical and numerical models. These measurements involved placing an EEG cap on a spherical agar phantom, which was then rotated in a static magnetic field. The phantom was constructed from 4% (by total weight) agar (Sigma Aldrich) in distilled water and 0.5% NaCl (corresponding to a conductivity of about 0.5 Ω⁻¹ m⁻¹) was added to mimic approximately the conductivity of tissues of the human head (blood ∼ 0.6 Ω⁻¹ m⁻¹ and gray/white matter ∼ 0.12 Ω⁻¹ m⁻¹ [Bencsik et al.,2007]). The mixture was boiled to make a viscous gel, which was then poured into a fiber‐glass mould with an inner radius of 0.095 m. After the agar had set, the mould was removed and three points representing the nasion and the left and right preauricular points were marked on the sphere (Fig. 1c). Three cylindrical, oil‐filled Vitamin E tablets wrapped in Parafilm were fixed at these fiducial positions.

The 32‐channel electrode cap was then fitted onto the phantom. This included channels for electrooculography (EOG) and ECG recordings. The former was attached between the left preauricular point and nasion, while the latter was not attached. This cap had two key features that made it particularly suitable for these experiments: first, the wires ran through the fabric of the cap, so that they largely conformed to the contours of the head/phantom and could be placed consistently from experiment to experiment. Second, the wires leading from the cap to the amplifier were twisted and tied together tightly at the top of the cap so that loose wires would not move in the magnetic field.

To simulate rotations of the head in a static magnetic field, we placed the phantom in the bore of a Philips Achieva 3.0 T MR Scanner atop of a roller platform specifically made to turn the phantom about its x‐axis (left–right) to mimic a nodding movement. Care was taken to orient the spherical phantom such that its z‐axis, running from the center to the North Pole (where the cable tree was positioned) was initially aligned with the B ₀‐field direction. In addition, the phantom's x‐axis was carefully aligned with the axis of rotation. This ensured that the experimental set‐up best represented the arrangement considered in the analytical and numerical models. The cable tree bundle was stretched straight along the longitudinal axis of the magnet to the back of the bore where it connected to the amplifier. The phantom was rotated at a rate of ∼30°/s, as later estimated from a rough measure of the angle of rotation and the duration of the rotational artefact on the EEG trace. The EEG data were recorded using Brain Vision Recorder software (Version 1.05) and a high input impedance BrainAmp MR EEG amplifier (Brain Products, Munich, Germany) that samples at 5 kHz and has hardware filters that limit the frequency range of the recorded signals to 0.016–1,000 Hz, with a roll‐off of 30 dB/octave at high frequency.

Blood Flow Artefact

Theory and analytic calculations

The ions in a conducting fluid, such as blood, experience a force when the fluid flows in an applied magnetic field. The force is given by F = q v × B, where q is the charge of the ion, v is the flow velocity, and B is the applied magnetic field. Thus any ion with a component of motion orthogonal to the magnetic field will experience a force whose direction is orthogonal to the plane containing both the velocity and magnetic field vectors. Positively and negatively charged particles move in opposite directions, accumulating on the vessel wall until equilibrium is established. When the vessel is embedded in a conducting medium the equilibrium charge distribution is that which ensures continuity of current flow across the vessel wall.

In addition to generating an electric field inside the vessel, the charge distribution on the vessel also produces an external field that causes current flow in the surrounding conducting tissue. A scalar potential is consequently produced at the surface of the body, which is picked up by surface electrodes as used in ECG and EEG measurements. The resulting potential is proportional to the blood velocity and so is expected to show a periodic variation through the cardiac cycle consistent with the form of the EEG PA. The flow artefact that is manifested in ECG measurements made inside an MR scanner is a well known consequence of this effect [Fischer et al.,1999].

Here, we use a simple model to estimate the magnitude and spatial form of the artefact voltages generated at the scalp by pulsatile blood flow in large arteries in the brain. In this analysis, which is described in Appendix B, we consider a blood vessel as a cylinder with a length, L, that is much greater than its radius, b, carrying blood flowing at a spatially uniform velocity, v, in an applied magnetic field, B, and show that when embedded in an infinite conducting medium the charge distribution at the vessel wall makes the vessel appear like a current dipole oriented perpendicular to the flow and magnetic field. The effective current dipole vector is shown in Appendix B to be

(13)

where σ is the conductivity of the medium. Using this estimated dipole strength, standard expressions for the scalar potential produced at the surface of a sphere by a dipole of known position, orientation, and strength could then be used to estimate the artefact voltage distribution that would result from blood flow in arteries of the brain. In particular the voltage generated at position, r, on the surface of a uniform conducting sphere of radius, a, by a vessel at the center of the sphere is given by

(14)

as derived in [Yao,2000]

Experimental measurements

To test the artefacts generated by pulsatile flow in a static magnetic field, a phantom of similar composition to that mentioned previously was constructed with an additional molded conduit that allowed a flowing fluid to be in contact with the conducting interior of the phantom. A 1‐cm diameter “U” shaped flow channel that enters at one side of the base of the phantom and runs axially to a point several centimeters from the top of the sphere before turning and exiting the other side of the base was formed inside the phantom, as shown schematically in Figure 3. A 64‐electrode MR‐compatible EEG cap (EasyCap, Herrsching, Germany) was used for these measurements. The reference electrode was positioned between Cz and Fz, with the software and hardware used for EEG collection otherwise being identical to that used for the phantom rotation experiment.

Figure 3.

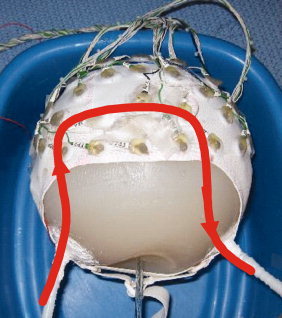
Schematic depicting the approximately U‐shaped conduit in the conducting spherical agar phantom through which saline solution was pumped for an experimental simulation of artefacts from blood flow. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

After placing the phantom in the bore of the MR scanner with the flow direction of the central section of the channel either in the anterior to posterior or right to left directions, 5 g/L saline solution was pumped through the channel at a velocity of ∼20 cm/s while EEG data were recorded. The flow was switched on for 10 s continuously so as to allow measurements to be taken after any effects of the initial momentum impulse due to the moving fluid arriving at the phantom had died out. This left a purely steady‐state flow artefact to be recorded.

In Vivo Artefact Measurements

EEG data were recorded on a healthy human volunteer (with the approval of the local ethics committee and informed consent of the subject) in the MR scanner. The subject was placed in the standard central location and supine position normally used in EEG/fMRI experiments, and rested before EEG data collection to achieve a normal resting state, with a heart rate of ∼70 beats per minute. Furthermore, the subject was instructed to keep his eyes open during the experiment in order to suppress alpha power. The EEG data were collected using identical software and hardware, and with the same 32‐channel cap as used in the rotation experiment on the agar phantom, but with the EOG and ECG channels connected in a conventional manner. Two measurements were made: (1) the intrinsic PA was measured with the subject in a resting state and (2) the subject nodded his head slowly to allow direct examination of the effects of head rotation in a magnetic field.

Analysis

For EEG analysis we used the Brain Vision Analyzer software (Brain Products GmbH, Munich, Germany), which provided a standardized platform across which numerical simulations and experimental data could be compared. For the simulations, the artefact magnitudes were first calculated in Matlab and then input into Analyzer. Agreement between the numerically calculated and experimentally measured artefacts was assessed by calculation of the correlation coefficient of the measured and calculated voltage patterns, and by evaluating the root‐mean‐square voltage difference between the results of the measurements and calculations.

RESULTS

In Vivo Pulse Artefact

The PA for the human head was measured first to provide a point of reference to which the results of the simulations could later be compared. A segment of the EEG and ECG data that were collected is shown in Figure 4. The EEG traces display an obvious PA that is time‐locked to the ECG peaks, and is made up of two distinct artefact peaks that follow each QRS complex. The first peak of the PA follows the R‐peak by ∼170 ms, while the second peak is delayed from the R‐peak by about 260 ms. The magnitude of the first peak is slightly higher than the second, with the range of values across electrodes for the former being [−300, 200] μV versus [−250, 150] μV for the latter. The largest artefact voltages occurred consistently at electrodes on the left/right sides of the head, such as F7 and F8. The spatial distributions of the PA at each of the two peaks in time are shown in Figure 5. Both maps show voltages with opposite polarity occurring over the electrodes of the right and left hemispheres, with a polarity inversion occurring between the first (Fig. 5a) and second temporal peaks (Fig. 5b). The properties of the PA, including the polarity reversal, magnitude, and temporal relationship to the ECG, all agree with Debener et al.'s findings in their systematic experimental study of this artefact [Debener et al.,2008]. Figure 5 thus shows the in vivo artefact maps that we aim to reproduce with the modeling.

Figure 4.

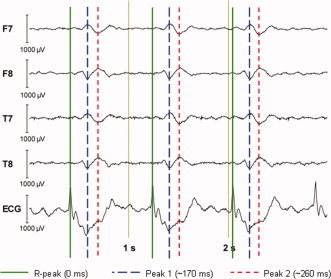
A representative 3‐s EEG trace displaying the BCG artefact measured on a 3 T Philips Achieva MRI scanner (with B ₀ field pointing from head to foot) and the timing relationship between the R‐peaks of the ECG and the two subsequent peaks in the individual EEG traces for which the spatial maps displayed in Figure 5. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 5.

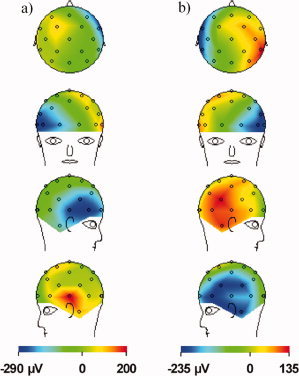
In vivo spatial voltage map of the BCG artefact measured for a human subject in the 3 T static magnetic field of a Philips Achieva MR Scanner, with the main magnetic field pointing in the head to foot direction. The artefacts are sampled at the two amplitude maxima shown in Figure 4 that follow each ECG R‐peak, with: (a) the first peak at ∼170 ms following the R‐peak and (b) the second peak at ∼260 ms. Note the left/right change in polarity between the maps formed at the two peaks. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Rotation Artefact

Analytical calculations

The analysis described in Appendix A shows that when the electrodes and leads of the EEG cap move with the volume conductor in a translation or in a rotation about the magnetic field direction, no measurable artefact voltage is measured at the amplifier input. In contrast, rotation of the head about an axis that is perpendicular to the field direction does generate a voltage at the amplifier. The form of this voltage artefact is described by Eq. (12) for the case of pitch (rotation about the x‐axis) for a conducting sphere on which the leads follow lines of longitude coming together at the pole of the sphere.

The relatively simple form of the analytical expressions provides basic physical insights into the spatial characteristics of the rotation artefact and its dependence on the measurement parameters. The magnitude scales with the static field strength, which corroborates the findings of Debener et al. [2008], and is also directly proportional to the angular velocity. In addition the artefact scales with the square of the radius of the spherical conductor, so that the artefact voltage would be expected to increase significantly with head size. Rotation about either x‐ or y‐axes generates an artefact voltage that increases linearly with θ_E, thus taking larger values for more inferior electrodes. In both cases, the pattern of the artefact voltage across electrodes is unaffected by rotating the field direction about the axis of rotational motion, but the overall amplitude is scaled by cos α, where α is the angle through which the field direction is rotated from alignment with the north–south axis of the sphere and cap arrangement.

The dependence on the azimuthal co‐ordinate is, however, different for rotation about the x‐ and y‐axes. The rotation about the x‐axis produces an artefact that is proportional to cos ϕ_E and so varies with the x‐co‐ordinate of the electrode on the surface of the sphere. The largest artefact voltages thus originate from electrodes on the extreme left and right positions on the phantom. In the case of rotation about the y‐axis, the artefact varies with sin ϕ_E and so depends on the y‐co‐ordinate. For this rolling motion, the artefact amplitude varies in the anterior–posterior direction. Inspection of the experimentally measured artefact indicates that it shows a dominant left–right spatial variation at the peaks in time (see Fig. 5). This shows a strong correspondence with the voltage pattern generated by the nodding motion (rotation about the x‐axis), which is shown in Figure 6 for a sphere of diameter 19 cm rotating at an angular velocity of 7.6 × 10⁻³ s⁻¹ (0.44°/s) in a 3 T field.

Figure 6.

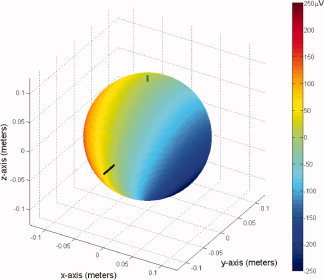
Analytic simulation of the artifacts generated by a forward nod of the head of angular velocity 0.44°/s for a 19‐cm diameter sphere, as predicted from a least‐squares fit to the in vivo BCG at the second peak. The long bar indicates the position of the nasion and the smaller bar marks the pole of the sphere, where the simulated “reference” electrode and cable tree are placed. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

To estimate approximately what magnitude of Ω is required to generate the artefacts, which were measured experimentally in the human subject, we evaluated a least‐squares fit for the angular velocity parameter, Ω, used in the analytic calculation to the experimentally measured artefact voltages at the two peaks plotted in Figure 5. The angular velocities that gave the best fit for the first and second peaks are Ω = −0.0072 s⁻¹ (−0.41°/s) and Ω = +0.0076 s⁻¹ (+0.44°/s), respectively, where the negative sign indicates a backward rotation of the head. The voltage range produced by a simulated rotation of a 19‐cm diameter sphere at 0.44°/s is approximately [−200, 200] μV for electrode positions spanning the whole surface of the sphere, as shown in Figure 6.

This calculation illustrates that relatively low rotation speeds can generate artefact voltages that are several hundred μV in magnitude, and that in the case of rotation about the x‐axis, the spatial pattern of the artefact voltage is similar to the PA measured in vivo. Furthermore, assuming that the PA results from head motion, associating the sign of the angular velocities with the timing of the two peaks gives some physical insight into the dynamics of the pulse‐driven head rotation. The first voltage peak occurs shortly after the fastest blood flow occurs in the aortic arch [Debener et al.,2008]. To reach the brain, rapidly moving blood flows through the carotid and vestibular arteries of the neck in a predominately axial direction and then is redirected into various smaller arteries. The forces required to redirect the blood generate an equal and opposite force on the head, leading to head motion characterized as the ballistocardiogram effect [Bonmassar et al.,2002]. The implication of the work described here is that the initial effect of the elevated flow following systole is a nodding backward of the head. This would be consistent with a greater force occurring on the anterior side of the point that the head pivots on, so that the net torque acts to tilt the head back. The subsequent restorative motion produces a forward nod with a positive angular velocity that would then create the voltage pattern of reversed polarity observed in the second peak of the in vivo PA.

Numerical and experimental results

Although the analytic solution provides useful physical insights into the artefact behavior, the simplified model of the wire paths is not representative of the actual lead distribution on the EEG cap. Thus, a numerical simulation using digitized traces of the real wire paths was carried out and the results compared to experimental measurements obtained from the phantom. In a previous publication [Yan et al.,2009], we showed that a numerical simulation of the gradient artefacts based on a digitized trace of the real wire patterns generated a spatial map of the artefact voltage that showed a significantly better correspondence to the experimental results than was the case when simulated results were generated using the simple meridional paths employed in the analytic calculations. In the case of the effect of rotation considered here, however, the improvement in correspondence between measured and simulated artefact patterns was negligible. Figure 7a,b show the artefact voltage calculated using the numerical approach; in Figure 7a it was assumed that the wires ran along meridional lines to electrode positions described by the Extended International 10–20 system, as in the simple model used to derive the analytic expression, and in Figure 7b the digitized wirepaths were used. Figure 7c shows the voltage pattern measured on the phantom when it was manually rotated about the x‐axis. The correlation coefficient calculated between the spatial map generated using the simple wirepaths (Figure 7a) and the experimental measurements made while rotating the phantom (Figure 7c) was 0.980. The correlation coefficient increased minimally to a value of 0.981 when the actual wirepaths were used in the modeling. Figure 7d shows the spatial map of the artefacts generated when the human subject nodded his head forward in the 3 T magnet bore. For these data, the correlation coefficient with calculated data obtained using the meridional wires is also high at 0.966, a value that improves to 0.989 when using the digitized wire paths. To evaluate further the agreement between the measured and modeled data, we calculated the value of Ω that minimized the sum over electrodes of the square of the difference between the measured and modeled artefact voltages. This yielded plausible angular velocities of 0.15 s⁻¹ (9°/s) and 0.23 s⁻¹ (13°/s), for the phantom rotation and head nod, respectively. Subtracting the modeled data from the measured voltage reduced the variance measured across electrodes to 8 and 9% of the original value in the experimental data in the two cases. Carrying out a similar procedure on the voltages measured at the second peak of the measured PA (Figs. 4 and 5) produced a reduction of the variance to 34% of its original measured value.

Figure 7.

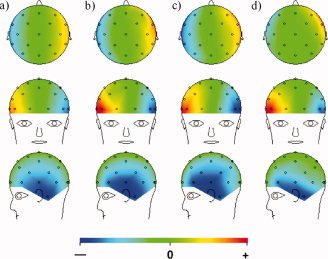
Comparison of numerically calculated and experimentally measured data for right‐handed rotation about the +x‐axis corresponding to a nod forward of the head: (a) numerical calculation based on leads following lines of longitude; (b) numerical calculation based on digitized real wirepaths; (c) experimental measurement on a conducting spherical agar phantom; (d) experimental measurement on the human head with the subject nodding his head forward. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Blood Flow Artefact

The simple analysis described in Appendix B indicates that the electrical potentials generated by flow in a section of a cylindrical vessel, whose length is greater than its diameter and that is exposed to a constant magnetic field, are dipolar in form and that the representative current dipole vector is characterized by Eq. (13). The form of this equation means that the direction of the effective dipole is perpendicular to the field and flow, and that its amplitude is proportional to the magnetic field, the vessel volume 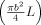, and the component of the velocity that is perpendicular to the applied magnetic field. Thus, large vessels in which blood flows rapidly in a direction perpendicular to the applied field produce the largest effects.

Potentials generated by constant flow are however not important when considering the time‐varying voltage that forms the PA. The relevant quantity to consider is the change in flow velocity through the cardiac cycle. It is expected that the highest relevant dipole strengths will be generated by large arteries in which the blood volume and pulsatile variation of velocity are greatest. Using values of 20 cm/s for the range of flow velocities and 0.1 cm² for the cross sectional area, which are representative of large arteries in the brain [Bammer et al.,2007] and a conductivity of 0.25 Ω⁻¹m⁻¹, yields a maximum effective dipole strength of 5 nAm per Tesla per centimeter of vessel length.

The exact form of the artefact voltage produced at the scalp surface clearly depends on the position and orientation of the effective dipole inside the head: a vessel that is close to the surface produces a larger, more localized potential, whereas a deeper vessel produces a more diffuse and weaker potential variation. Based on the widely distributed spatial form of the measured PA and the anatomical location of the large arteries of the brain, we consider the situation where the dipole is located at the center of a sphere. This allows us to use the relatively simple expression for the voltage at the sphere surface described by Eq. (14) to gain further insight into the spatial pattern of artefact voltages generated by flow. The form of this expression means that the flow‐related voltages scale linearly with magnetic field strength, consistent with previous experimental measurements of the PA at varying field strengths [Debener et al.,2008], but would be expected to decrease with increasing head size.

Figure 8 shows the voltage generated at the surface of a 19‐cm diameter sphere, for flow in the posterior‐to‐anterior (−y) direction with the magnetic field directed in the foot‐head (−z) direction as in the Philips 3 T magnet. Here flow of 12.6 cm/s velocity through a cylindrical vessel of 1 cm length and 0.5 cm radius was considered. These values are representative of the internal carotid artery, where the velocity represents the maximum deviation from the average value [Bammer et al.,2007]. For this geometry, the potential varies linearly with x‐co‐ordinate, and thus is largest at the left and right extremes of the sphere—a characteristic that is also evident in the measured PA. In particular, this posterior‐to‐anterior direction of flow generates a voltage that is positive on the left of the sphere which corresponds to the voltage pattern produced at the first temporal peak of the PA.

Figure 8.

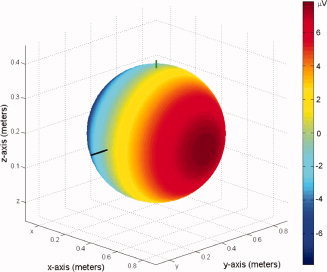
Analytic simulation of surface potentials generated at 3 T by flowing blood in the posterior‐to‐anterior direction through a vessel modeled after the internal carotid artery, given a 19‐cm sphere, cylindrical flow of 0.5 cm in diameter and 1 cm in length, and flow velocity of 12.6 cm/s in the posterior‐to‐anterior direction. Note that the model is for a Philips Achieva 3 T scanner with magnetic field pointing along the negative z‐axis. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The range of voltages produced is 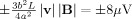for this situation where the field and velocity are perpendicular. It is evident from Eq. (14) that flow in the left–right (x) direction will generate a similar pattern rotated by 90° about the z‐axis, such that the voltage varies linearly with y‐position and is largest at the anterior and posterior extremes of the sphere.

An agar phantom was used to verify experimentally the pattern of voltage variation generated by the flow of a conductive fluid through a channel in a sphere in the presence of a static a magnetic field. Figure 9a,b show the effect of flowing saline solution through a U‐shaped conduit in the conducting spherical phantom in the anterior‐to‐posterior (AP) and the right‐to‐left (RL) directions, respectively. The perfect symmetry of the data generated using the dipole model (see Fig. 8) is not replicated by the experimental measurement due to the asymmetric construction of the conduit. Nevertheless, the general form of the spatial maps are in agreement with the predictions of Eq. (14), showing a predominantly left–right variation for AP flow and a variation in the anterior–posterior direction for RL flow. The polarity of Figure 9a is also correctly reversed relative to Figure 8 because the measurement was made for flow in the anterior–posterior direction, whereas Figure 8 was calculated for the opposite posterior‐to‐anterior direction of flow.

Figure 9.

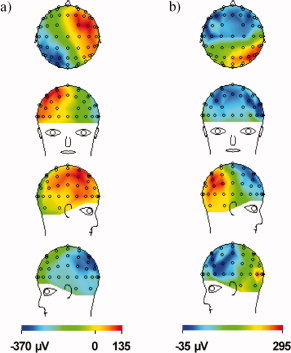
Spatial maps of EEG data for conductive fluid flowing through an approximately U‐shaped conduit inside a conductive spherical agar phantom. The measurement was conducted for continuous flow in the anterior‐to‐posterior (a) and right‐to‐left (b) directions and sampled 5 s after flow onset to avoid movement artefacts. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

DISCUSSION

We have described simple expressions that characterize the variation across different EEG leads of the artefact voltages produced by head rotation and blood flow in a static magnetic field. To do this, we have developed a new approach for evaluating the voltages produced by head movement in a uniform magnetic field and also derived a simple dipolar model of the Hall voltages produced by blood flow in a homogeneous magnetic field. Our analysis of the effect of head movement is restricted to rigid body motion and we have not therefore modeled the effect of pulse‐driven scalp expansion that is another potential source of the PA. We consider this effect in a more qualitative manner in the discussion below.

Rotational Artefact

The new method of analyzing the effect of motion involves summing the electrode contribution to the artefact voltage, resulting from the scalar potential generated at the surface of the head by the movement, and the lead contribution resulting from the integral of the movement‐induced electric field, −v × B, along the lead paths. In general, although the lead contribution can be calculated exactly for a properly characterized movement provided the lead paths are known, evaluation of the potential produced at the scalp surface is difficult and requires the use of finite or boundary element methods. To make progress, we therefore modeled the head as a conducting sphere, with the EEG leads following lines of longitude on the sphere's surface and initially showed that in a uniform field, translation and rotation about an axis that is parallel to the field direction generates no artefact voltage. Expressions for the voltages generated by rotation about an axis that is perpendicular to the field were also evaluated and a nodding rotation about the x‐axis (pitch) was shown to produce an artefact pattern that is similar in spatial form to that measured at the temporal peaks of the PA. In confirmatory experiments, it was shown that the artefact voltages recorded when a conducting agar sphere was manually rotated about the x‐axis in a 3 T field showed a similar spatial form to that predicted by the analytic expressions and seen in the real PA. Similar agreement was found with the pattern recorded when a subject nodded his head inside the 3 T magnet. It is worth noting that the expressions for the voltage are independent of the resistance of the leads and so approaches to artefact reduction based on increasing lead resistance are unlikely to work [Vasios et al.,2006].

The similarity of the spatial forms of the measured, in vivo PA and the voltage pattern calculated for a nodding motion using the simple analytical model is reflected in the correlation coefficient of 0.87 for the first temporal peak of the PA and in the reduction of the variance to 34% of its original measured value when the model data produced using an angular velocity of −0.0072 s⁻¹ was subtracted from the measurement. When comparing the physical nodding of the subject's head (Fig. 7d) with the in vivo PA recorded on the same subject (see Fig. 5), the spatial pattern formed by the first peak of the artefacts gave a correlation coefficient of 0.80. These high values indicate that a pulse‐related nodding motion is a plausible generator of the PA.

Using the analytic solutions, we were able to evaluate both the direction and magnitude of the angular velocity required to produce the artefact magnitudes observed for in vivo measurements of the PA. The directionality, reflected in the sign of the angular velocity, makes physical sense with the timing of pulse cycle and the twin peaks of each period of PA: the first peak corresponds to a nod backward of the head likely caused by the momentum transfer of fast flowing blood following the ventricular contraction, and the angular velocity direction for the second peak is reversed implying that restorative motion subsequently occurs. Additionally, the estimated magnitude of the angular velocity needed to produce the measured artefact is about 0.008 s⁻¹ (0.4°/s). Given that the duration of each of the two artefact peaks is around 100–200 ms, the change in angle of the head that would result from this rotation is less than 0.1°. These values are based on a single sphere model of the head, but the fact that the conductivity does not appear in the expressions for the artefact voltage [Eq. (12)] is an indication that the artefact voltage magnitude would not be greatly changed by incorporation of a low conductivity layer just below the surface of the sphere to represent the effect of the skull.

There was only a small improvement in the correlation of the simulated and measured voltage patterns when the actual digitized wirepaths were used in calculating the artefact voltage instead of the idealized partial lines of longitude. This finding is in contrast to previously described measurements of the gradient artefact [Yan et al.,2009], where a much improved correlation of measurements and simulations was obtained by using the real wirepaths. The difference must reflect the lower sensitivity of ∫(v × B) · dl to changes in the path of integration compared with the integral of 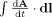, where A is the vector potential that characterizes an applied field gradient. This is unsurprising since the magnitude and direction of the vector field A needed to produce a field gradient has a much stronger spatial dependence than v × B in a rigid body rotation.

Blood Flow Artefact

Using the simple expression relating vessel geometry, blood velocity, and field direction to effective dipole strength, we have also been able to model the potentials produced at the surface of a conducting sphere by flow of a conducting fluid inside an internal vessel. The strong dependence of the relevant dipole strength on vessel size and variation of velocity across the cardiac cycle means that it is the large arteries that are most likely to produce significant time varying Hall voltages. Consequently, the argument that the pseudo‐random direction of blood flow in different vessel segments is likely to lead to a net cancellation of the voltage measured at the scalp surface [Bonmassar et al.,2002] is not particularly relevant since there is a definite directionality of flow in the network of large arteries. The spatial form of the measured PA is most consistent with the artefact voltage produced by flow in a vessel oriented in the posterior‐to‐anterior direction and located far from the surface, since such flow produces an artefact pattern that shows a predominant variation in the left‐to‐right direction and is diffusely spread over the whole surface of the head. Calculation of the correlation coefficient between the voltage pattern measured at the first temporal peak of the PA and that generated by a vessel section carrying blood flow in the y‐direction located at the center of a head‐sized sphere yields a value of 0.88. Although this high value of the correlation coefficient indicates a strong degree of similarity in spatial form of the artefact, the magnitude of the Hall voltages calculated for parameters that are typical of the large arteries in the brain [Bammer et al.,2007] are more than 20 times smaller than those measured in the PA. It should also be noted that these calculations assume that the vessel is embedded in a homogenous sphere whose conductivity is similar to that of blood. The calculated values of the artefact voltage would be considerably reduced if a triple sphere model [Zhang,1995], including a low conductivity layer representing the skull, was employed. It thus seems likely that blood flow in the large arteries in the brain makes only a relatively small contribution to the measured artefact, with the dominant contribution resulting from nodding motion that is driven by cardiac pulsation. The strong dependence on depth of the voltage generated by the effective dipole representing the effect of flow means that an artery close to the skin surface, such as the superficial temporal artery, could generate a much larger artefact voltage. However, a superficial dipole would be expected to generate a fairly localized voltage that decreases rapidly with distance from the vessel. Such a spatial variation of voltage is not obviously reflected in the measured artefact voltage pattern (see Fig. 5), so such flow also does not seem to make a large contribution to the measured PA.

Origin of the Pulse Artefact

The inference that the dominant cause of the PA is head movement is consistent with previous findings. For example, Anami et al. [2002] showed that it was possible to greatly reduce the PA in recordings made at 1.5 T by using a vacuum‐head fixation system. This indicates that it is head movement driven by cardiac pulsation that is the dominant cause of the PA. The same group [Nakamura et al.,2006] described experiments in which recordings were made inside and outside a magnet with a thin insulating sheet interposed between the electrodes and the scalp. The sheet was covered with a thin layer of conducting gel which ensured that there was good electrical contact between electrodes, but no contact to the scalp. Its presence thus meant that Hall voltages generated by blood flow in the head would not reach the EEG amplifiers, but induced voltages due to movement would still be present. Recordings made using this arrangement inside the magnet showed a significant increase in variance compared to those made at zero field, as a result of the presence of the PA. Thus, the PA was present even when the Hall voltages from flow were eliminated. The relative success of methods of correcting the PA based on measurements of voltages induced in a reference loop of wire fixed into the EEG cap [Masterton et al.,2007] is also indicative of the fact that there is significant movement of the head related to cardiac pulsation: Hall voltages due to flow will not register in a closed loop, while rotational motion in the field will induce a voltage. It is worth noting, however, that even if the wires forming the reference loops perfectly follow the EEG leads, the voltages generated at different locations over the head in such loops by head rotation show a different pattern of spatial variation to those produced in the EEG leads because of the effect of the volume conductor. Inductive reference loops [Masterton et al.,2007] can not therefore characterize the spatial variation of the artefact voltage, although they do provide a good representation of its temporal variation.

Another type of motion that could potentially contribute to the generation of the PA is cardiac driven expansion of the scalp as a result of blood rushing into surface arteries. The effect of this type of motion, which involves deformation, is harder to model than that of a rigid body rotation, but some insight can be gained by applying the approach to evaluating artefact voltages described above. If we model the head as a sphere with the EEG leads running along lines of longitude and the field running along the north–south axis of the sphere, the velocity of movement is radial in a uniform expansion of the sphere, so v × B is directed azimuthally and is therefore perpendicular to the lead paths and the normal to the sphere's surface. The latter implies that no scalar potential is needed to satisfy boundary conditions at the sphere's surface, leading to a zero electrode contribution to the artefact voltage, while the former means that the lead contribution, given by the line integral of −v × B along the relevant leads is also zero. We would therefore not expect such a uniform expansion to generate a significant artefact voltage. Although this expectation is based on a relatively qualitative argument, it is particularly hard to imagine from the symmetry of the field and wire paths that a uniform expansion could produce an artefact pattern showing a predominately left–right variation. It has however been previously shown in an experimental study that a localized expansion on the left and right sides of an EEG cap placed on a conducting spherical phantom, does generate a localized artefact with opposite polarity on the left and right sides of the phantom [Debener et al.,2008]. Simulation of such an expansion is beyond the scope of this article, but the broadly distributed nature of the voltage pattern measured at the peaks of the real PA lead the authors to believe that a localized expansion (e.g., near the temporal arteries) is probably not the dominant source of the PA. The effect of localized scalp expansion and flow in surface arteries may however explain why the correlation of the measured PA and the artefact produced by a head nod is 0.87 rather than being closer to unity.

Pulse Artefact Reduction

Accepting that the PA largely results from a cardiac‐driven, nodding head motion, the analytic expressions described here point toward methods that could be used to ameliorate the PA at source and to improve its correction via postprocessing methods. In particular, it is clear that limiting head motion [Anami et al.,2002; Nakamura et al.,2006] as much as is tolerable by the subject will help to reduce the size of the induced artefact.

It may also be possible to modify EEG cap designs so as to reduce the magnitude of the artefact voltage. The electrode contribution to the artefact voltage is obviously fixed by the positioning of the electrodes on the scalp surface, but the lead contribution can be varied by changing the wirepaths. Figure 10 shows the electrode and lead contributions for a nodding motion calculated using the digitized wirepaths, as used in the numerical model. This shows that the two contributions have opposite polarity and that the lead contribution is larger. Varying the lead voltage could therefore have a significant effect on the measured artefact voltage, while significantly, the opposite polarity of the two contributions suggests that optimized design of the leads can further reduce intrinsic artefact pickup through cancellation.

Figure 10.

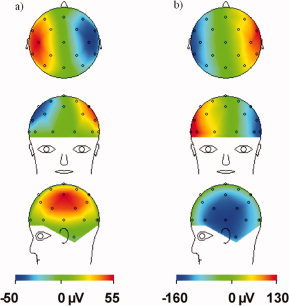
Decomposition of the rotation artefact (for right‐handed rotation about the x‐axis with an angular velocity of 0.44°/s in a field of 3 T) into contributions from (a) the electrodes and (b) the digitized leads as used in the numerical model. Note the opposite polarity of the two patterns. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Furthermore, Eq. (12) implies that by rotating the cable tree to the back of a spherical head, such that α = 90° the artefact voltage produced by a small rotation about the x‐axis could be completely eliminated. Clearly this is not an ideal position from an ergonomic point of view for the cable tree to emerge, and in the case of a real head shape the cancellation is likely to be more partial, but this sort of design should be tested. Other arrangements which produce lead voltages that largely cancel the electrode contributions generated during a nodding motion could also potentially be identified, consequently lowering the demands on postprocessing filters.

The modeling described here could also guide artefact correction algorithms. The spatial map of the rotation artefact could be incorporated into improved filtering techniques relying on spatial rather than temporal patterns such as the adaptive beamformer [Brookes et al.,2008]. Such methods allow the suppression of particular patterns that are known to be artefacts [Wan et al.,2008] and can potentially be targeted to remove a lesser proportion of true brain signals than the commonly used AAS algorithms. The analytic equations, in conjunction with better temporal modeling of head rotation could also be used to create temporal artefact waveforms that may help place a physical check on ICA [Nakamura et al.,2006] or OBS [Niazy et al.,2005] methods where the artefact components are currently identified by statistical methods. In addition, evaluation of head motion parameters produced during coregistration of fMRI image time series could allow the PA template to be adjusted in time based on calculation of changes in the form of the nodding artefact resulting from variation in average head orientation.

Relevance Beyond Understanding the Pulse Artefact

Although the focus of this article has been upon the spatial form of the PA, the approach used here could also be used to evaluate the voltages produced in EEG recordings by general head rotation. Again the motion parameters produced from fMRI time series could be used to identify the temporal variation of rotational velocity, which could form the basis of calculation of a predicted artefact voltage waveform on each channel. These artefact waveforms could then be subtracted from the recordings on each channel to improve data quality. The approach developed here for modeling the effect of Hall voltages produced by blood flow in a magnetic field in terms of a current dipole, could also be used in other areas of the body. In particular, it might be helpful in modeling the flow artefacts produced in ECG [Fischer et al.,1999] recordings made on the surface of the chest.

CONCLUSIONS

Using basic physical principles, we have modeled two potential causes of the PA, namely, rotation of the head and blood flow, and have shown that both are capable of matching the PA measured in vivo in spatial form. However, the Hall voltages produced at the scalp surface by pulsatile blood flow variation in large arteries in the brain are shown to be too small to be a significant cause of the measured PA. Conversely, it is shown that cardiac‐pulse‐induced nodding motion corresponding to an angular velocity of just 0.4°/s could generate the measured PA. The simple model of rotation can also help to explain features of the in vivo measurement such as the polarity reversal between the two peaks in time of the PA that are typically seen per cardiac cycle. Although we cannot exclude some contributions from scalp expansion and blood flow in superficial arteries, the work described here shows that head rotation is likely to be the dominant source of the PA. The analytic expressions and numerical simulations derived here should allow the design of improved EEG lead arrangements that lower the intrinsic artefact pick‐up, reducing the need for complex artefact correction. Greater understanding of the origin of the PA should also be of key value in developing more intelligent filtering algorithms for high fidelity, simultaneous EEG/fMRI data.

APPENDIX A: DERIVATION OF THE ARTEFACTS DUE TO MOVEMENT IN A STATIC FIELD

Here, we use the approach characterized by Eq. (5) to investigate the form of the artefact voltages generated in EEG recordings by translational motion and by rotation about an axis that is parallel to the applied field. The analysis indicates that both these motions generate no artefact voltage.

Translational Motion

In the case of translational motion, the electromotive field is spatially invariant so we can write,

(A1)

where 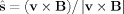. The boundary condition at the surface of the sphere is then satisfied by a scalar potential, which also satisfies Laplace's equation, of the form,

(A2)

where s describes the position in the ‐direction. The electrostatic force generated by this potential cancels the electromotive force everywhere inside the sphere, since v × B = ∇ϕ. Under these circumstances

(A3)

and simple inspection shows that the electrode and lead contributions to Eq. (5) are equal and opposite, so that the total artefact voltage is zero.

Rotation About an Axis Parallel to the Field

We now consider rotation about an axis that is parallel to the field direction, using the specific example where B = B ₀ k and Ω = Ωk, such that

(A4)

Substituting this expression into Eq. (2), and writing J = σE gives

(A5)

In the steady state, the current density must be divergence free so as to avoid unrealistic continuous charge accumulation. Consequently

(A6)

and using Eq. (A4) this yields

(A7)

The scalar potential thus obeys Poisson's equation such that a uniform space charge density of magnitude −2ε₀ΩB ₀ is formed inside the conductor [Lorrain, 1990]. This charge generates a radial electric field of magnitude −2ΩB ₀ r/3 inside the sphere and a contribution to the scalar potential ΩB ₀ r ²/3 that varies only with radial co‐ordinate and so is constant over the surface of the sphere. A second contribution to the scalar potential, ϕ′, comes from the charge density at the surface of the sphere. This is needed to ensure that the radial component of the current density is zero at the surface. Including the contribution of the space charge and v × B and applying the boundary condition at r = a gives

(A8)

The solution of this equation which also obeys Laplace's equation is

(A9)

The contribution of the electrodes to any artefact voltage is thus

(A10)

where θ_Data and θ_Reference describe the positions of the data and reference electrodes.

The contribution of the lead term depends on the line integral of v × B along the data and reference leads. However, the form of v × B given by Eq. (A4) can be described by the gradient of a scalar function

(A11)

so that the line integral only depends on the start and end points of the path of integration. The lead contribution to the artefact voltage is thus

(A12)

Summation of the electrode [Eq. (A10)] and lead contributions [Eq. (A12)] thus yields a total artefact voltage of zero for rotation about an axis that is parallel to the field.

Interestingly, if the electrodes and leads do not rotate with the conductor, a non‐zero voltage is measured from a conductor rotating about an axis parallel to the field. This effect forms the basis of the Faraday disk (and sphere) experiment [Lorrain, 1990].

APPENDIX B: EFFECT OF FLOW IN A UNIFORM CYLINDRICAL VESSEL

We consider a cylindrical vessel of radius, b, and length, L (≫ b), carrying blood of conductivity, σ, which flows at a uniform velocity, v, along the axis of the cylinder. The vessel is embedded in a infinite medium which also has conductivity, σ, and is exposed to a magnetic field, B. Inside the vessel, flowing ions experience a uniform effective electric field, v × B, which drives current flow across the vessel in the direction that is perpendicular to B. A charge distribution is consequently formed at the surface of the vessel and this in turn generates a scalar potential and an associated electric field. To find the form of the scalar potential and charge distribution, we apply the boundary condition that the normal component of the current density must be continuous across the vessel boundary. In addition, the scalar potential that is generated must be continuous across the boundary and must obey Laplace's equation everywhere except at the boundary. To simplify the mathematics we work in cylindrical polar co‐ordinates (ρ, ϕ, z) and define the direction of v × B as the x‐direction in the co‐ordinate frame of the cylindrical vessel. Working from the known solutions of Laplace's equation in cylindrical polar co‐ordinates, which show no variation with axial co‐ordinate (since we assume b ≪ L), we try a solution of the form

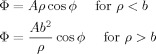(B1)

where A is a coefficient to be determined. The radial component of the current density, J = σE is then given by

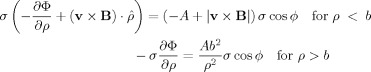(B2)

Equating the radial component of the current density on either side of the vessel wall at ρ = b gives

(B3)

By evaluating the change in 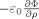on crossing the vessel wall it is straightforward to show that the surface charge density, q, required to generate this scalar potential is given by

(B4)

This corresponds to a positive charge density on the surface of the vessel reached by moving from the centre in the direction of v × B and a negative charge density on the opposite surface of the vessel. The symmetry of the charge distribution thus means that it has a zero total charge and a non‐zero dipole moment. Consequently, at a distance the electric field produced by a finite length of vessel, L, will be predominantly dipolar in form. We can find the electric dipole moment, P, of the charge distribution by using the standard integral

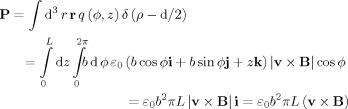(B5)

This is converted to an equivalent current dipole, Q, strength by multiplication by σ/ε₀ yielding

(B6)

We can thus estimate the scalar potential generated at the scalp by a blood flow in a vessel of finite length by representing its effect as that of a point dipole that is positioned at the center of the vessel and whose strength and direction is specified by Eq. (B6). The finite extent of the current distribution and deviation from the infinite cylinder approximation used here, mean that this only provides an approximate representation of the real effects.