Directed information flow—A model free measure to analyze causal interactions in event related EEG‐MEG‐experiments

Abstract

In a study that combined event related potential (ERP) and magnetic field (ERMF) data, we analyzed the timing and direction of information flow between striate (S) and extrastriate (ES) cortex by applying a generalized mutual information measure (DIT for “directed information transfer”) during a visual spatial attention task. ERP and ERMF recordings showed that selective attention to stimulus arrays in one visual field enhanced late responses (around 200 ms after the stimulus presentation) that were localized in S (ERMF) and ES (ERP) cortex. The results of the DIT analysis indicate there is a significant attention related increase in the flow of information back from ES to S cortex at around 220 ms, with an associated decrease in the flow of information forward from S cortex to ES cortex. These results support the hypothesis that a feedback mechanism guides attention‐related processing in primary visual cortex and provide evidence that DIT can by used to evaluate the direction of information flow between cortical areas. Hum Brain Mapp, 2008. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

Electroencephalography (EEG) and Magnetoencephalography (MEG) can be used to analyze the tempo‐spatial dynamics of neural activity underlying cognitive processes. One standard approach for analyzing event related potentials (ERPs)/ event related magnetic fields (EMRFs) assumes that distinct cortical regions will process different aspects of information at specific times. In addition to this approach, which primarily investigates the functional segregation of cognitive processing in time, the investigation of the functional connectivity between spatially distinct brain regions has recently also gained widespread attention [Friston, 1994; Friston et al., 1993 for a general overview of measures of connectivity]. Early approaches of functional connectivity relied on linear statistical measures like correlation and regression analyses in the time or frequency domains [Aertsen et al., 1989; Ahissar et al., 1992; Bressler and Kelso, 2001; Ding et al., 2000; Gerstein et al., 1978; Gross et al., 2001; Lachaux et al., 2002; Schack et al., 1999; Varela et al., 2001]. Because of their symmetric properties these measures are not able to identify the direction of any interregional interaction. This is also true for the mutual information measure [Papoulis, 1991; see Ioannides, 2001, for an application to MEG data], which is a generalization of the correlation technique. However, knowledge about the direction of connectivity is essential for understanding whether certain cognitive processes rely on a top‐down or bottom‐up mechanism. Arnhold et al. [1999] and Gross et al. [2002] (using Rosenblum's 2001 directionality index) have provided a partial solution to this problem by adapting algorithms from non linear dynamics, but only for the special case of coupled cortical oscillators.

A general definition of causal relations has been established by Granger [1969]. This approach assumes that a signal X is the cause of a signal Y if the predictability of Y is improved by the combination of the past of both X and Y rather than relying on the past of Y alone. This concept was applied by Freiwald et al. [1999], Sameshima and Baccala [1999] (focusing the Ganger causality to selected frequency bands by means of partial coherences), Kaminski et al. [2001], Hesse et al. [2003] and Bakardjian et al. [2006] to analyze causal interrelations between EEG‐signals using multivariate adaptive linear models as predictors. A similar procedure was applied by Brovelli et al. [2004] to analyze causal interactions among local field potentials (LFP) recorded from a group of cortical patches in monkeys. Moreover, David et al. [2006] quantified causal connectivity between different cortical areas based on a physiologically guided framework of neuronal interaction in conjunction with a Bayesian estimation scheme. A limitation inherent in all these approaches, however, is that they require the a priori assumptions of a model to describe the interaction mechanism. Since the required model parameters are usually unknown in neuroimaging studies, this requires model‐free measures of temporally varying causal interactions. Such a model free estimate should permit the detection of both linear and nonlinear couplings.

One model free approach was formulated by Saito and Harashima [1981] and further developed by Kamitake et al. [1984]. It is derived from information theory by generalizing the mutual entropy measure [see, for instance, Papoulis, 1991]. This approach has fewer formal restrictions than the approaches noted earlier. It does not simply quantify the information shared by two random variables at a certain time point, but rather evaluates two temporal sequences of random variables. The resulting “directed information transfer” (DIT) measure specifies the directed information flow between two signal sources using their multivariate nonparametric signal statistics. Liang et al. [2001] have used this method to infer causal interactions between cortical areas based on LFP. These LFPs were recorded invasively from a macaque brain during a visuomotor pattern discrimination task. A similar approach was recently used by Chavez et al. [2003] to identify the model free Granger causality (see earlier) between pairs of cortical and in‐depth EEG recordings with epileptic patients.

Recently, we showed [Hinrichs et al., 2006] how the DIT approach can be used to identify causal interactions between cerebral activations observed with functional magnetic resonance imaging (fMRI). Here, we adapt this technique for use with noninvasive event related EEG and MEG recordings. First we confirmed the efficacy of the DIT measure with data of this type using a simulated data set. Then we employed it to address the temporal dynamics of the causal interactions produced by visuo‐spatial attention in human visual cortex. In an experiment reported earlier by Noesselt et al. [2002], MEG‐ and EEG‐data sets were acquired simultaneously, while subjects performed a visual spatial attentional task. Because MEG‐recordings primarily pick up tangential sources, while EEG‐recordings measure a mixture of tangential and radial sources [Cohen and Cuffin, 1983], the combined MEG/EEG recordings allowed a dissociation between higher cortical sources picked up with EEG and primary cortical sources picked up with MEG (see later for details). We extend the observations made by Noesselt et al. [2002] by performing a DIT analysis on the combined EEG and MEG signals. The results of this analysis show that during the time interval from 180 to 280 ms “information” flows from ES to primary visual cortex. These results provide direct evidence that the primary visual cortex is subject to top‐down control, supporting earlier theoretical claims of attentional control from higher to lower cortical areas [Noesselt et al., 2002; Martinez et al., 1999, 2001].

MATERIALS AND METHODS

The Visual Attention Experiment [see Noesselt et al., 2002, for additional details]

ERP and ERMF were simultaneously acquired while subjects performed a visual spatial attention task. A centrally presented left or right arrow cue was followed by a sequence of 10 bilaterally presented 3 × 3 stimulus arrays. The arrays were made up of “plus” signs that were superimposed upon a globally and locally smoothed background checkerboard, with a central element that consisted of a letter T. In each array this T was randomly displayed either upright or inverted. The subject's task was to covertly direct attention to the array indicated by the initial arrow cue (ignoring the array in the opposite field), and report by pressing one of two buttons whether the center T of the attended array was upright or inverted. In a “neutral condition,” a central diamond was presented and subjects were required to push a button upon the appearance of the bilateral arrays with no discrimination required. Cue presentations lasted 500 ms, the cue‐array ISI was sometimes 0.5 but usually 3.5 s, array presentations lasted 200 ms, and the ISI between the arrays in each sequence was jittered between 800 and 4000 ms. Subjects were initially trained to a 75% correct criterion. Since the task was demanding, initial training required 0.5–2 h.

Subjects

Nine healthy adult subjects (6 male, age range 19–35 years, mean age = 25.7 years) with no psychiatric or neurological disorders participated in the combined EEG/MEG recordings after providing written informed consent.

MEG/EEG Recording

MEG data were acquired at a sampling rate of 255 Hz and a bandwidth of 0.0–50 Hz using a 148 magnetometer whole head system (Magnes 2500 WH, 4D‐Neuroimaging). EEG data were acquired simultaneously at the same sampling rate and bandwidth from 32 electrode sites (Fp1, Fp2, F7, F3, Fz, F4, F8, FC1, FC2, T7, C3, Cz, C4, T8, CP1, CP2, P7, P3, Pz, P4, P8, PO7, PO3, PO4, PO8, Oz, O9, Iz, and O10, left mastoid, right horizontal and vertical EOG; right mastoid serving as reference) according to the 10–20 system of the American Electroencephalographic Society. The MEG sensor coordinates were localized with respect to the subject's head using a spatial digitization device (Polhemus Fastrack). Coregistration of the MEG‐sensors with the individual structural MR images was accomplished by interactively localizing skull landmarks in the images. Eye movements were monitored using an infrared video device.

EEG‐/MEG Preprocessing

EEG

Stimulus related EEG‐epochs were selectively extracted for each attention condition (attend‐left, attend‐right, and neutral) using an epoch length of 1.230 s. To provide baseline data, sampling epochs started 200 ms prior to each array presentation. Accordingly, in the case of the shortest inter‐array interval of 800 ms (see earlier for the timing of the stimulus sequence) there the sampling epoch overlapped the presentation of the next array in a sequence by 230 ms. However, as explained later, all data analyses were performed on an epoch interval that ended prior to this overlap period. Artefacts were labeled and rejected if the maximum–minimum difference amplitude in an epoch exceeded a 100 μV peak‐to‐peak threshold (EEG and EOG). For the estimation of information flow the nonaveraged raw data epochs were evaluated, whereas the selectively averaged epochs (ERPs) were used for the topographical and temporal localization of the attention related effects [Noesselt et al., 2002]. In addition, we derived the global field power (GFP) of the ERP as the spatial standard deviation of the EEG amplitudes including all EEG‐electrodes.

MEG

Environmental noise was removed by subtracting an individually weighed sum of MEG reference signals from each of the MEG channels [Robinson, 1989]. Artefact labeling was done in the manner described for the EEG (amplitude criterion of 5 pT). MEG epochs that were recorded during eye movements, as indicated by the EOG (amplitude threshold 100 μV) were discarded. Again, raw and averaged data were used, respectively, to estimate information flow, to localize signals and to determine the GFP in the manner described for the EEG.

Selection of Latency Range and Sensors for Causal Analysis

Unlike data derived with functional imaging techniques (fMRI, positron emission tomography), superficially recorded EEG and MEG signals cannot be directly attributed to one restricted brain area. This is the case because EEG and MEG sensors pick up the combined activity from a number of concurrently active areas. Therefore, it can be difficult to attribute the results of connectivity analyses performed on the raw‐data gathered with these techniques to interactions between specific brain structures. Bearing this in mind, we restricted our analysis to a latency range in which previous source analyses [Noesselt et al., 2002] have indicated that the EEG‐ and MEG signals picked up by certain occipital sensors on average reflect neural activity that is predominantly extrastriate (ES) (EEG) or striate (S) (MEG) in origin. This source specificity can be attributed to the tangential dipole orientation of the S and the radial source orientation of ES generator observed with MEG and EEG, respectively. The dominant ES effects as seen in the ERPs may have obscured the S component in this modality. In contrast, the MEG for physical reasons is blind with respect to radial sources thus reflecting only the S activity. Accordingly, only a minor increase in the goodness of fit was observed when adding the source locations derived from the MEG‐analysis in the EEG‐fit and vice versa. This suggests that the raw‐waveforms we recorded were suitable for use in the information‐flow analysis without further preprocessing. Alternatively, one could argue that the analysis of the single trial dipole waveforms might be the best way to derive the flow of information. However, the low number of dipoles modeling the average ERP‐activity and ERMF is hardly suitable to adequately describe the much more complex structure of the spontaneous nonaveraged EEG and MEG [Michel et al., 2004], which is required to estimate the information flow (see appendix).

Attributing ERP‐ and ERMF‐activity to S and ES cortex was further supported by functional imaging (fMRI) data obtained in the same study by Noesselt et al. [2002]. This data showed a modulation in primary and lateral occipital cortices contralateral to the attended hemifield. This effect was observed in six out of six subjects in both the left and right hemisphere. The contralateral attentional enhancement was not only observed when comparing attend left with the attend right condition, but also when comparing the attend left/right conditions with the unfocused attention condition.

The latency range selected for our EEG‐/MEG‐ analysis was 180–280 ms. Within this time window, the source model of dipoles located in S and ES cortex explained more than 90% of the variance in the observed data in the combined ERMF and ERP source analysis. Moreover, the explained variance never fell below 85% if the ERP‐ and EMRF‐source models were independently estimated with two bilateral dipoles in the ES cortex for the ERPs and one dipole in S cortex (very close to midline) for the MEG. A second dipole in right temporo‐parietal cortex was needed to model unspecific MEG activity.

While we observed a significant contralaterality of the attentional effect in both ES and S cortex, the attentional effect in the ERMF‐data was even more robust when the focused attentional conditions were compared with the unfocused attention condition [Noesselt et al., 2002]. Here, we again observed a modulation in lateral occipital and S areas for the combined ERP/ERMF data as described earlier. We therefore used this comparison when conducting the causal analysis.

For each experimental condition (i.e., attend left, attend right, neutral), the causal analysis was conducted with the signals obtained as the average over three sensors in regions where the ERP and fields exhibited the strongest attention related modulations. For the EEG, two topographically symmetric regions, each represented by three electrodes (P3, PO7, PO3 and P4, PO8, PO4 in the 10‐20‐system, Fig. 3) were selected. The topographical distribution of the attention related ERMF component only varied a little between the attention conditions. Consequently, the strongest attention related ERMF‐amplitudes were observed at identical sensor sites in these two conditions. Three sensors (Fig. 3) located at the center of right hemisphere dipolar field distribution were, therefore, selected to represent the magnetic S activity in both attention conditions. As outlined in the appendix, the calculation of the flow measures in both directions (i.e., S to ES and ES to S) included both the EEG and MEG signals. After artefact rejection the number of combined EEG‐ MEG‐epochs per subject and condition averaged 558 with a standard deviation of 152.

Figure 3.

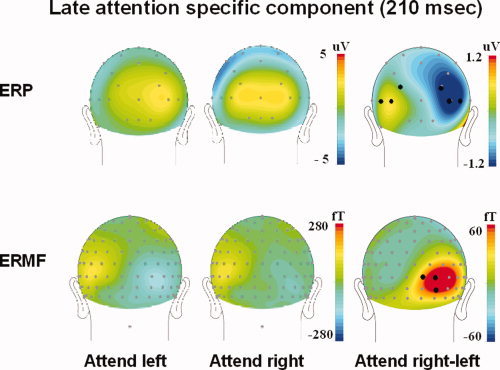
ERP‐ and ERMF‐scalp topography (grand average, spline interpolation) of the late attention effect. The signals analyzed in the present study were acquired from the sensors marked by black dots.

Application of the Information Flow Measure to ERP and ERMF

The methodological details of the information flow measure are described in the appendix. As outlined there, the flow from a signal at time k to another signal at a future time k+m is estimated taking into account N preceding samples of each signal. In the current experiment the information flow from ES to S and vice versa is estimated by a measure that combines the raw EEG‐ and MEG‐data using the sequence of event related single trials.

Basically, the estimation of the information flow applies a generalized version of the mutual information (MI) measure, which is the average information (“entropy”) shared by two signals. In contrast to the standard definition of the MI [Gallager, 1968] this generalization is non symmetric. This is a prerequisite for identifying the direction of interactions between two signals. Our measure is similar to the formalism of the Granger causality (GC) in that both quantify the influence of a signal's past on future values. However, while GC is based on an assumption of linear predictability that is usually model dependent [see for instance Hesse et al., 2003], the information flow measure quantifies model‐free information shared by a signals' past and the future). Like the similar approach of Chavez et al. [2003], the DIT approach may be interpreted as a model‐free nonlinear extension of the GC. Moreover, in contrast to GC, the information flow measure is able to include future values beyond the immediate successor the current time point, making it more suitable for identifying delayed interactions.

Numerically DIT measurements require the estimation of several multivariate covariance matrices. In the context of ERPs and ERMFs, an analysis of the flow of information over time requires that multivariate covariance matrices be calculated individually for each time point k (latency with respect to stimulus onset). These matrices must include N preceding samples of both signals and the future sample that the flow is targeting.

The information flow starting at a latency k extends in principle into an unlimited future, i.e., k+m, with m = 1,2,… (see appendix for a detailed description of the information flow measure). However, recent literature [Callaway, 1998; Van Essen et al., 1992] suggests that the delay between subsequent processing pathways within the occipital visual cortex is limited by only a few synapses. With an estimated maximum delay between S and ES sources of 40 ms in anesthetized animals [Lee et al., 1998; Schmolesky et al., 1998], or 25 ms in awake macaques [Chen et al., 2006; Lamme and Roelfsema, 2000; Ledberg et al., 2007] we considered a maximum delay of 40 ms as sufficient to describe the temporal dynamics of interconnections that might exist between the various S and ES structures, and restricted our analysis to a maximum delay of D = 10 samples at the sampling rate of 255 Hz.

With the goal of estimating the total information flow between the two time series involved, at each latency k we cumulated the flow over this 40 ms period according to the following equation.

Determination of the Direction

The main direction of interaction (i.e., the driver–responder relation) can be identified by taking the difference (subsequently labeled as the difference flow) between the flows obtained for the two opposite directions as follows:

If CDI(k) is significantly greater than 0 for a certain k, then the series X(k) may be interpreted as the driver of Y(k) at time k and vice versa. However, entropy rates may differ between the signals thus causing an intrinsic asymmetry in information flow [Schreiber, 2000]. This could render the interpretation in terms of a driver–responder‐relation debatable. Therefore, following usual principles of ERP evaluation, we evaluated the differential task related flow modulations, i.e., the contrast CDI_attended (k) versus CDI_neutral (k) with “attended” and “neutral” indicating the different task conditions.

In addition to the cumulated flow the temporal details of the flow at a certain latency k can be further analyzed by looking at the noncumulative difference flow values defined as

Here, the temporal distance M will be referred to as delay. Each differential flow of information is thus indexed by the latency k and delay M over, which the information flow will be assessed.

Method for Determining the Number of Past Samples to be Included

In “real‐world” applications of this method the number of past samples to be included (i.e., N) needs to be defined. Anderson [2004] has shown, that criteria to find the appropriate model order for linear models may well serve to define the order of general, i.e., both linear and non linear models. Consequently, we applied Schwarz's [1978] Bayesian information criterion as implemented in the ARFIT‐MATLAB‐package [Neumaier and Schneider, 2001]. The BIC penalizes large model orders p by a term 2p/L (L denoting the sample size), whereas the popular Akaike information criterion accounts for large model orders p by a term p*ln(L)/L, which produces a tendency to overestimate the model order in cases of large samples sizes [Hannan and Rissanen, 1982]. Using the BIC we estimated the appropriate order p as the average over the order values derived independently for each signal included in the analysis. From this, N was derived as p‐1 because the DIT‐formula combines N predecessors plus the actual value).

Influence of the Reference Electrode

It is known, that connectivity measures like coherence [Nunez et al., 1999] and Granger causality [Kaminski et al., 2001] are not entirely independent of the choice of the reference electrode. We wished to test for a potential influence of the reference electrode on the measure of DIT. We therefore re‐referenced the three EEG signals obtained in the left hemisphere (P3, PO7, PO3, acquired with right mastoid as reference) to the left mastoid. As a consequence signals that potentially carried spurious left attention specific activity (see the map in Fig. 3) as well as uncorrelated activity was subtracted from the original EEG signals. One would therefore expect that the ratio of uncorrelated to attention specific EEG activity would be reduced. Accordingly, the information shared between the EEG and MEG sensors should be decreased. Bearing the definition of the information flow measure in mind, one would therefore expect a reduced attention related flow from ES (EEG) to S (MEG) cortex. To check this expectation we calculated the cumulated flow from ES to S under the attend right condition based on the modified signal for all subjects and compared these values to the original ones.

Statistical Evaluation

Simulated data

Since only one simulated data set is available (see later), analytical analyses carried out over a group of data sets cannot be applied here. The statistical evaluation of a single data set is hampered by the fact that, to the best of our knowledge, the statistical distribution of I_XY, I_YX for uncoupled processes (corresponding to the null‐hypothesis) is unknown. Therefore, we empirically determined thresholds representing the level of information flow above which values had less than a 5% and 1% probability of occurring by chance. For this purpose each pair of simulated time series was used to generate 3000 independent pairs of surrogate time series, as proposed by Theiler et al. [1992]. In accordance with this method, each data set was independently transformed by a Fourier transform. The resulting complex spectrum was modified by adding random phase values uniformly distributed over the interval (0…2π) [using the random number generator provided by MATLAB V. 6.0 (The Mathworks company)]. Finally, the spectrum was transformed back to the time domain. This procedure keeps both the original amplitude distribution and the autocorrelation structure of each series but destroys the relation between the two time series. For each of these pairs of randomized time series we derived the I_XY and I_YX as well as the difference values as specified above. Finally, the thresholds required to exceed by chance with probabilities of P < 0.1, 0.05, and 0.01 were derived from these pairs of data sets by determining the 5% and 1%, quantiles of the sorted I_XY and I_YX and difference series.

Experimental data

All amplitude values were averaged over a 4 sample‐/16 ms‐interval before being subjected to further analysis. Since the flow values are positive by definition they were logarithmically transformed prior to statistical analyses to approximate a normal distribution [Bland and Altman, 1996]. Statistical comparisons of the information flows values were based on one or two way repeated measures analyses of variance (RANOVA).

In all analyses the significance threshold was set to P < 0.05.

Simulated Data

For a general test of the ability of the method to identify directed interactions within various delays we simulated a data set using a modified version of a linear model first proposed by Saito and Harashima [1981]:

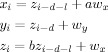Here, w_x and w_y are zero mean white noise processes with standard deviation of 1 and 0.5, respectively, and a = 0.5, b = 0.8. In this model, x leads y through the intermediate variable z and should therefore give rise to an information flow from x to y with delay d. As shown by Saito and Harashima [1981], a cross‐correlation analysis detects the interaction between x and y but fails to identify the direction, since it exhibit peaks of almost identical strength with both positive and negative lags. We generated 400 realizations (i.e., 400 trials), each with a length of 150 samples. For the 1st, 2nd, and 3rd sets of 50 samples the delay was set to d = 1, d = 2, and d = 3, respectively.

RESULTS

Simulated Data

The information flow as well as the cross correlation were estimated separately for each sample of the simulated time series. According to the Schwarz‐criterion, the estimated mean model order averaged over all trials was 5.9 with a standard deviation of 2.4. Therefore, we set N to 7. As is shown in Figure 1, the cross correlation is characterized by peaks of almost identical amplitude with the positive and negative lags. The data demonstrate what theory predicts: This measure is not suitable for determining the direction of an interaction. In contrast, the information flow measure (i.e., I_XY(k,I) and I_YX(k,I)) shows a clear asymmetry in favor of a flow from x to y (Fig. 2). In detail, there is a flow from x towards y, which is most pronounced at a delay of 1, 2, and 3 for the first, second and third sets of 50 samples, respectively, whereas almost no flow occurs in the opposite direction (i.e., y→x), which is in accord with the generating model. Surrogate based statistics showed that the calculated flow x→y at lag 1, 2, and 3, respectively, as well as the difference between the flow in the two directions, is significantly (P < 0.01) greater than zero. In contrast, in no case does the flow in opposite direction differ significantly from zero (P > 0.1). This analysis demonstrates that the new measure is reasonably sensitive to directional information.

Figure 1.

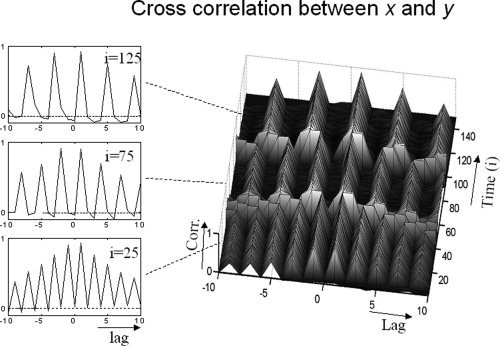
Left: Cross correlation between the simulated data sets (x and y, see methods section) at selected time points (see index) for a lag (delay) of ±10 sampling intervals. Right: Comprehensive overview for the whole period.

Figure 2.

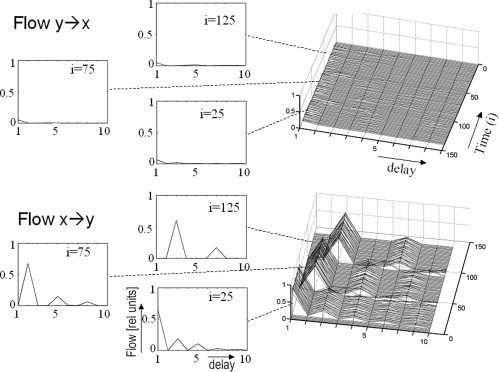
Information flow estimated for the simulated data sets (x and y). Upper row: Flow from y to x. Left: Temporal distribution of the flow at individual time points up to a delay (lag) of 10 sample intervals. Right: Comprehensive overview for the whole period Lower row: Same but for opposite flow direction, i.e., x to y.

Replacing sequence x by z yields a virtually identical result except for a slightly larger strength of flow towards y (0.65 on average for x→y but 0.8 for z→y). In contrast, no flow in either direction occurs between x and z.

Experimental Data

ERP and ERMF‐results

First, we briefly revisit the ERP‐and ERMF‐findings for the attention experiment previously reported by Noesselt et al. [2002]. When the attend left visual field (LVF) and attend right visual field (RVF) conditions are compared, the earliest significant attentional ERP‐modulation is observed over occipital sensors contralateral to the attended hemifield starting at a latency of around 90 ms post stimulus. Please note, that an initial response starting around 50 ms poststimulus was not modulated by attention. Using an equivalent current dipole model, the corresponding sources could be located in contralateral ES cortex. fMRI‐activations could be observed in virtually identical lateral occipital visual areas contralateral to the side of attention. In the same area, a subsequent attention specific component (latency >150 ms, peaking at about 230 ms) was elicited that had similar contralateral topographical distribution (Fig. 3). The dipole model indicates this component was generated by a second modulation of the ES area. An attention specific component with a similar late latency was also observed in the ERMF, but peaked slightly later around 250 ms. Here, the dipole fit revealed a S source but no lateral occipital activity. The lack of ERMF‐evidence for an ES modulation might be due to the mainly radial dipole orientation in this area [Cohen and Cuffin, 1983]. On the basis of the combined results from MEG, EEG, and fMRI, we speculated that the observed “late” attention‐related S modulation could be due to feedback connections from ES cortical areas.

Results of the causal analysis

Number of preceding samples for the estimation of information flow.

Using the Schwarz‐criterion, we determined the appropriate number of predecessors to be included for the 180–280 ms latency range separately for each trial and each subject, both in the selected EEG and MEG channels. The mean value was 5.2 with a standard deviation of 0.4. Consequently we included N = 5 preceding samples in all calculations.

Task specific modulations of the cumulated information flow.

As indicated in Figure 3, the visual attention effect is most prominent in the cortical hemisphere contralateral to the attended visual hemifield. In Figure 4A, we show the escalation in the cumulated information flow from contralateral ES to S cortical areas over the flow in the reverse direction [reflected by the CDI(k)‐values] for the attend left versus neutral, attend right versus neutral, and collapsed attend left + right versus neutral conditions. In all cases, throughout the latency range under consideration a flow enhancement of up to 80% occurs in the direction ES to S during the attend condition relative to the neutral condition, peaking around 220 ms. In contrast, during the neutral condition no such excess in favor of the direction ES→S is observed. As shown in Figure 4B, the superior flow from ES to S at this latency can be observed in almost all subjects for both the attend left and the attend right condition.

Figure 4.

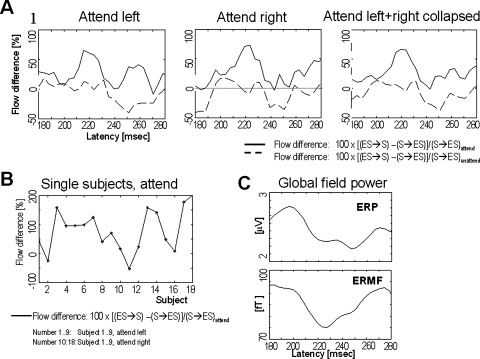
A: The enhanced cumulated information flow from contralateral extrastriate (ES) to striate (S) cortical areas, related to the flow (S→ES) under the “attend” and the “neutral” condition. Both the EEG and MEG data were included when deriving the flow values (see methods section for details). All data were low pass filtered at 24 Hz cut off frequency. B: Single subject data of the contralateral flow form extrastriate to striate versus the flow from striate to extrastriate cortex. Same normalization as in subfigure A. C: Global field power for the event related potentials (ERP) and the event related magnetic fields (ERMF). The data reflect the attend left + right collapsed condition.

We validated this observation in three steps: First, the cumulated flow values (i.e., CI) from ES→S and S→ES as observed during the attend condition around 220 ms were evaluated to test if the flow in the two opposite directions differs significantly. A two way RANOVA of these flow values with factors direction (ES→S vs. S→ES) and hemisphere (left vs. right) showed a significant direction [F(1,8) = 7.37, P < 0.027) and hemisphere [F(1,8) = 8.91, P < 0.018] main effect but no direction × hemisphere interaction (P > 0.1). This result indicates the enhanced flow towards S cortex during the attend task is statistically reliable. In the framework of Granger causality, one could thus conclude that ES Granger causes S during the attend condition. In addition, the hemisphere‐effect confirms the different strengths of this flow enhancement in the two hemispheres, as can be seen in Figure 4A.

A subsequent analysis aimed at validating a significant task related modulation of the flow difference, i.e., of the CDI (k) values. Therefore, we conducted a two way RANOVA of the difference flow values at 220 ms with factors hemisphere (left vs. right) and condition (attend vs. neutral). The CDI values are modulated by condition [F(1,8) = 10.4614, P < 0.0120] but not by hemisphere (P > 0.1), and there is no condition × hemisphere‐ interaction (P > 0.1).

Finally, a two‐way RANOVA with factors hemisphere (left vs. right) and direction (ES→S vs. S→ES) was conducted at 220 ms for the flow values [i.e., CI_XY(k) and CI_YX(k)] in the neutral condition. The only significant effect was a main effect of hemisphere (P < 0.05). There was no main effect of direction and no direction × hemisphere interaction (P > 0.1). Figure 4 suggests a larger flow from S→ES in the neutral condition around 250 ms, but this difference also does not reach statistical significance (P > 0.1).

Together, these analyses suggest that attention generates an increased flow of information from contralateral ES cortex towards S cortex.

To investigate the temporal dynamics of the ES–S coupling observed around 220 ms, we analyzed the noncumulated difference in the information flow [i.e., DI(k,m)] over the delay period of 1 to 10 samples (4 –40 ms) at that latency. As shown in Figure 5, the largest difference flow towards S was observed for delay values between 8 and 28 ms, peaking around 15 ms in the attend‐condition. A one way RANOVA with factor direction (ES→S vs. S→ES) was conducted individually for each delay. This analysis confirmed significant differences (P < 0.05, see Figure 5 for the normalized difference values) during the period of 8–28 ms. The difference at latencies from 12 to 28 ms remain significant (P < 0.05) even after a Bonferroni correction for the 10 concurrent tests.

Figure 5.

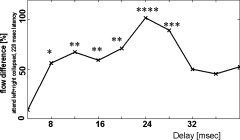
Excess of cumulated information flow towards striate areas (see Fig. 4 for the normalization) at various delays of interaction between contralateral extrastriate (ES) and striate (S) areas under the “attend” condition. The curve was derived at a latency of 220 ms where the cumulated difference flow between ES and S is largest under the “attend” condition. Levels of significance: “*” = P < 0.05, “**” = P < 0.01, “***” = P < 0.005, “****” = P < 0.001.

The observed modulation of the difference flow between ES and S could be due to either an increased flow from ES→S or a decreased flow from S→ES or to a combination of both. We analyzed the two flow directions separately to disentangle these possibilities. Comparing the flow CI_XY from ES→S (collapsed over both hemispheres) for the two conditions shows an attention related increase around 220 ms (Fig. 6 for the normalized values). This modulation was validated by a one way RANOVA with the factor condition (attend vs. neutral) [F(1,17) = 4.5792, P < 0.047]. In contrast, the inverse flow CI_YX(k) (i.e., S→ES, Fig. 6) decreases at the same latency when the subjects switch from the neutral to attend condition. The corresponding RANOVA shows that this difference is significant [F(1,17) = 4.5792, P < 0.013]. However, this decrease only reaches its maximum around 250 ms [F(1,17) = 9.0475, P < 0.0079]. Thus, both an attention related (ES→S) increase and a more pronounced S→ES decrease contribute to the observed CDI effect, but they do so at different latencies.

Figure 6.

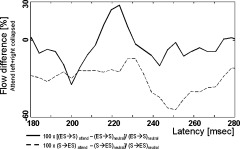
Difference between cumulated flow of information (both ES→S and S→ES observed under the “attend” and the “neutral” condition. All values are related to the flow obtained at the neutral condition. The data were low pass filtered at 24 Hz cut off frequency.

To test the contralaterality of this differential attention effect we also calculated the CDI values between ES and S under the attend‐condition for the hemisphere ipsilateral to the attended field at 220 ms. A two‐way RANOVA with factors hemisphere (left vs. right) and attention (left vs. right) revealed no significant main effects (P > 0.1) but a strong attention × hemisphere interaction [F(1,8) = 48.1943, P < 0.0002], suggesting a contralateral preference at the latency where the modulation of the flow from ES to S cortex is strongest.

Influence of the reference electrode.

The flow from ES to S at the attend right condition decreased in the left hemisphere from 0.0275 ± 0.0095 (averaged over all nine subjects) to 0.0186 ± 0.0130 after re‐referencing to the left mastoid. This is in accordance with the assumption of a reduction of attention specific activity and/or an increase in uncorrelated activity because of the subtraction of the left mastoid reference signal from the left hemispheric EEG. This outcome confirms that the DIT measure is sensitive to reference chosen.

DISCUSSION

The goal of this study was to demonstrate that a measure derived from mutual entropy theory, the DIT, can identify the time course, strength and direction of the functional coupling between cortical regions measured with combined EEG‐ and MEG recordings. To do this, we reanalyzed data from a visual spatial attention experiment by Noesselt et al. [2002]. On the basis of their original analysis of these data, Noesselt et al. [2002] concluded that ES structures might act on S cortex by means of a recurrent mechanism. This view was supported by the fact that S cortex showed a late activation following an initial attention specific modulation in ES regions. While this conclusion seems reasonable, the results provide only indirect evidence for the proposed feedback‐mechanism. Here, we assessed the neural interaction directly using DIT. The algorithm employed allows (i) an analysis of the temporal modulation of the flow of information from one area to another at specific latencies with a temporal resolution in the ms‐range (determined by the sampling rate), and (ii) the calculation of the directed connectivity without the need to specify an underlying model. Moreover, the new approach is capable of detecting both linear and non‐linear interactions. In the present study, however, we restricted the analysis to linear relations to limit the computational load. The results obtained with this analysis confirmed Noesselt et al.'s [2002] earlier conclusion that the S cortex is modulated by ES areas.

In principle, the DIT measure computes the generalized mutual information between two time series, thereby estimating the joint information in the actual samples of one series and future samples of the other series, given the past of both series. As shown by Liang et al. [2001] this information flow is not symmetrical between the two series, so that the driver–responder relationship can be detected. By calculating this measure individually for each member of a set of future time points (termed “delay” earlier), the detailed temporal structure of the directed connectivity can be resolved. The total flow at a certain latency is estimated using the cumulated flow values over the delay period. Thus, the DIT measure allows for a detailed connectivity analysis, which goes beyond standard correlation measures [see for instance Peled et al., 2001; Winterer et al., 2003], since these are restricted to the analysis of the strength of interactions. Structural equation modeling (SEM) is a variant of the correlation method that is also able to provide directional information between the nodes of a network model predefined by the user. However, it can neither derive the direction in case of a single pair of signals, nor track the temporally varying strengths and directions of interactions. Moreover, measures such as SEM are by definition restricted to linear relations. A recent non linear connectivity measure proposed by Gross et al. [2002] is capable of detecting directed dependencies between pairs of oscillatory signals, but does not consider the timing of an interaction.

Using simulated data, the difference with respect to directional information between DIT and correlation coefficients is obvious. The cross correlation function shows a decaying sequence of almost identical correlation coefficients for positive and negative lags. From this analysis, it is impossible to draw any conclusion regarding the direction. In contrast, the DIT measure shows a clear asymmetrical flow of information that accords with the driver– responder relation imposed by the linear model used for generating the data. In addition, the temporal delay at which the flow occurs precisely matches the lag imposed by the data‐generating model.

When calculating the total flow at a specified latency, one needs to address the question of the delay across, which flow values should be cumulated. That is, one has to decide what temporal distance from the latency of the signal generating the flow it is appropriate to investigate. A “shotgun” approach would be to cumulate over all flow values after the current latency, but this would lead to an accumulation over many delay values where no real interaction occurs, which could obscure the genuine interactions. In the present study, we tried to derive an upper bound for the temporal delay of interaction from some physiological considerations.

Our results reveal that the S activation observed in the MEG in the latency range from about 180 ms up to 280 ms after stimulus onset is driven by a statistically significant flow of information from ES to S cortex, peaking around 220 ms but extending over a much larger temporal range. This feedback flow shows a contralateral preference at a slightly later then about 250 ms (where the flow from S to ES cortex is minimal, see later), which suggests it is associated with an attentional control mechanism. Significant interactions between ES and S sensors extended over a delay range of 8–28 ms, and were largest at a delay of 24–28 ms. This compares with the mean latency difference of 20 ms between neural activity in V4 and V1 which Schmolesky et al. [1998] observed in intracerebral recordings of anesthetized macaques. Moreover, other studies on awake monkeys have reported onset latencies of 30 (V1) and 40 (V4) ms, respectively, for visual stimulation [Chen et al., 2006]. Applying the 3/5 rule [Schroeder et al., 1995] to account for the human‐simian latency differences an V1–V4 latency of roughly 17 ms can be expected in humans.

The slightly longer latencies we observed suggest that the feedback mechanism observed in our experiment might be mediated by two synaptic connections. In an experiment investigating visual pattern discrimination in macaques by means of invasively recorded LFP, Liang et al. [2000] observed a Granger causal influence, which was mainly directed from S to ES cortex at early latencies but subsequently changed to the opposite direction. Taking into account the 3/5 rule (see earlier) to compare latencies between the different species, the timing of the feedback activity largely resembles our result. From this it would have been interesting to analyze the flow of information in our data in an earlier time window where one would expect an enhancement of the information flow in opposite direction (S→ES). However, given the results of the dipole based source analysis [Noesselt et al., 2002], at latencies below 180 ms the ERP and ERMF cannot be attributed uniquely to ES and S cortex. Below 180 ms, there is too much overlap in sensor space to be able to define a subgroup of electrodes/sensors that reflects activity arising primarily in S or ES cortices, so the direction of the information flow cannot be clearly specified. The observed time window of 180–280 ms is nonetheless in accord with previous monkey studies [Metha et al., 2000] in which the authors reported an effect in V4 starting around 100 ms. Furthermore, Ledberg et al. [2007] reported that the earliest stimulus‐specific processing effects occur around 100 ms poststimulus. In humans such an effect should be observable at around 180 ms. Most studies have also failed to find an effect on the initial response in V1, suggesting that the first feedforward sweep is not modified by top‐down processes [see e.g., Lamme and Roelfsema, 2000 for a review].

One could argue that the modulation of the information flow might mainly reflect the course of signal‐to‐noise‐ratio in the underlying ERPs and ERMF. However, the fact that the peak of the directed flow values occurs at a latency of about 220 ms, which is clearly after the ERP‐ and before the ERMF‐GFP‐peak‐values (200 and 270 ms, respectively, Fig. 4C), argues against this view. Comparing the ERP‐/ERMF‐ and the DIT‐waveform one might in fact consider them as orthogonal measures.

Re‐referencing the left hemispheric EEG to the left mastoid led to a drop of the corresponding flow from ES to S in this hemisphere of about 30% under the attend condition. This observation indicates that the choice of reference must be taken into account when interpreting flow values derived from EEG data. In particular, the fact that the right hemispheric flow from ES to S observed under the attend left condition is lower than the corresponding flow for the attend right condition (observed with the original signals) in the left hemisphere (Fig. 4) may be due to this effect since the right hemispheric electrodes are located closer to the reference used during acquisition. However, unless the reference electrode does not reflect another concurrent mental process it will only lead to a degradation of the ability to find a directional bias in the information flow rather than creating an imbalance when there is none.

We found the attention specific increase in the difference flow between ES and S can be attributed to both to an increase in flow from ES to S and a subsequent decrease of flow from S to ES. This observation is in line with the hypothesis that the feedback from ES to S guides the spotlight of attention, and the consequent increase in spatial selectivity leads to a reduced flow from S to ES. The combined data give rise to the following hypothesis: The flow of information from ES back to S cortex guides a S neural selection process (reflected in the EMRF), which reduces the forward data stream by limiting processing outside the “refocused” spotlight of attention, enabling more efficient processing of detailed features within the spotlight at higher processing stages. This kind of mechanism has been proposed, for instance, by Vidyasagar [1999], Deco and Zihl [2001], and Roelfsema et al. [1998] [see also Hopf et al., 2005 for review]. Lateral interactions because of local processing routines are unlikely to have caused the effect, because those interactions should not be reflected in a modulation in the DIT‐measure bearing in mind that the DIT measure only accounts for interactions between areas but not within one area.

Regarding general applications of the reported method to the field of EEG‐ and MEG‐analysis, the method (like other connectivity measures) requires a pair of signals, which reflect activity in different cerebral structures, so that the driver and responder functions can be uniquely defined with respect to these structures. This requirement is usually met by functional imaging data as long as the corresponding voxels are separated by more than the full width half maximum distance. However, in case of electrophysiological data, additional criteria are needed to ensure that the two signals represent different brain structures. As demonstrated in this study, source analysis of the averaged ERP and fields is one way to provide this information. Alternatively, given a sufficient signal to noise ratio, a source analysis of the raw (nonaveraged) signals (obtained, for instance, with beamforming techniques) with the DIT analysis applied to the resulting epoch based source strength might provide a data set suitable for a DIT analysis of epochs of source strength. A similar approach was recently presented by Bakardjian et al. [2006] for a causal EEG analysis. As a side effect this method would circumvent the problem of choosing the appropriate reference electrode.

In conclusion, the measure of information flow reported here is an asymmetrical data‐driven measure capable of extracting the direction of information flow from combined ERP/EMRF data. The only a priori constraint, which has to be applied to the analysis is the window length in which the cross‐regional interaction occurs. The results from the reported visual attention experiment support the view that the attentional modulation of primary visual cortex is associated with a flow of information from higher visual cortices into the primary visual cortex.