Functional source separation applied to induced visual gamma activity

Abstract

Objective of this work was to explore the performance of a recently introduced source extraction method, FSS (Functional Source Separation), in recovering induced oscillatory change responses from extra‐cephalic magnetoencephalographic (MEG) signals. Unlike algorithms used to solve the inverse problem, FSS does not make any assumption about the underlying biophysical source model; instead, it makes use of task‐related features (functional constraints) to estimate source/s of interest. FSS was compared with blind source separation (BSS) approaches such as Principal and Independent Component Analysis, PCA and ICA, which are not subject to any explicit forward solution or functional constraint, but require source uncorrelatedness (PCA), or independence (ICA). A visual MEG experiment with signals recorded from six subjects viewing a set of static horizontal black/white square‐wave grating patterns at different spatial frequencies was analyzed. The beamforming technique Synthetic Aperture Magnetometry (SAM) was applied to localize task‐related sources; obtained spatial filters were used to automatically select BSS and FSS components in the spatial area of interest. Source spectral properties were investigated by using Morlet‐wavelet time‐frequency representations and significant task‐induced changes were evaluated by means of a resampling technique; the resulting spectral behaviours in the gamma frequency band of interest (20–70 Hz), as well as the spatial frequency‐dependent gamma reactivity, were quantified and compared among methods. Among the tested approaches, only FSS was able to estimate the expected sustained gamma activity enhancement in primary visual cortex, throughout the whole duration of the stimulus presentation for all subjects, and to obtain sources comparable to invasively recorded data. Hum Brain Mapp 29:131–141, 2008. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

The recordings of electric potentials and magnetic fields produced by the brain are possible thanks to Electro‐ and Magneto‐encephalography (EEG and MEG) with optimal temporal resolution for non‐invasive brain imaging. The underlying neural ensembles, also called generators or sources, are mixed with background activity and noise in the recorded external signals, thus it is difficult to identify and study their dynamic activity at the electrode/sensor space level.

To date, the main approach has been to apply procedures enhancing the signal‐to‐noise ratio, SNR (typically employing time‐domain averaging to obtain event‐related potentials/fields, ERP/ERF), and to solve the so‐called ‘inverse problem’, i.e., to calculate the spatial distribution of the intra‐cerebral currents by starting from the recorded external signals. This problem—being by definition ‘ill‐posed’—does not admit a unique solution, that is, it can be solved only by making considerable assumptions about the brain function or by constraining the solution. Despite the huge number of different techniques addressing the inverse problem [single and multiple dipoles—Scherg and Berg, 1991, MUSIC—Mosher et al., 1992, RAP‐MUSIC—Mosher and Leahy, 1999; minimum norm estimates—Hämäläinen and Ilmoniemi, 1994, LORETA—Pascual‐Marqui et al., 1995], and the complementary class of beamforming algorithms [Synthetic Aperture Magnetometry, SAM—Vrba and Robinson, 2001], up to date no universally accepted criteria exist to define adequate models nor to validate the results; perhaps, such validation can be performed only through explicit comparisons with the invasive data obtained in similar experimental settings [Crone et al., 1998; Hall et al., 2005].

The last decade has seen a great development of the source separation approaches based on exploiting the statistical properties of generators composed in the observed signals, without any assumption about the underlying biophysical generator model. To tackle such task, Blind Source Separation (BSS) [Cichocki and Amari, 2002] and, particularly, Independent Component Analysis (ICA) [Comon, 1994; Hyvärinen et al., 2001] were proposed. These techniques have been shown to be valid in isolating instrumental and physiological artifacts, thus considerably improving the SNR level [Barbati et al., 2004; Ikeda and Toyama, 2000; Makeig et al., 1996; Vigario et al., 2000]. Also, they have been successfully applied to extract single‐trial ERP/ERF (in this way avoiding the need to apply the standard averaging approach that could filter out information regarding interdependency between ongoing processes and salient event‐related features) [Makeig et al., 2004]. Noteworthily, on one hand BSS and ICA algorithms do not solve the inverse problem, but on the other hand they estimate complete source time courses for task‐related features description. They also provide information that could be used to recover the source position in a successive step, so as to improve the quality of localization results [Tang et al., 2000; Zhukov et al., 2000].

In a preceding paper [Barbati et al., 2006], a novel ‘informed’ source‐estimation method was introduced (Functional Source Separation, FSS) which adds a functional reactivity constraint to a basic ICA model. This procedure optimizes a cost function where a task‐related constraint is added to the non‐gaussianity maximization of the standard ICA model to bias the extraction towards the cerebral source of interest. A single source—corresponding to the global maximum of the multi‐objective optimization problem—is obtained at each time. In that work, two cortical sources describing the thumb and the little finger somatosensory evoked responses were obtained, and adequate description of the highly interconnected and temporally overlapping primary hand cortical network was achieved. The proposed procedure was demonstrated to significantly improve the quality of the extraction with respect to a standard ICA algorithm [fastICA, Hyvärinen et al., 2001].

In the present work, the objective was to explore the performance of Functional Source Separation (FSS) in reconstructing induced activity and, thus, the modulation of ongoing brain rhythms because of external events. These induced activity changes are often quantified as stimulus/task‐related variations in cortical oscillatory power [Pfurtscheller and Lopes da Silva, 1999]. Although such induced activity changes are statistically robust phenomena, they are not strictly time‐locked to the stimulus/task onset, and therefore do not result in a strong average evoked response. Importantly, whereas time‐averaged evoked responses corresponding to stereotypical events of fixed latency and waveform are likely to reflect primarily the properties of the external stimulation (i.e., the strength and the timing of the stimulus), induced responses exhibit substantial variation and latency jitter, and may provide complementary information on the internal self‐organization of the brain (i.e., on to what extent the spontaneous brain activity is perturbed by the stimulus/task). Since induced responses have been shown to play an important role in almost every aspect of the brain function [Arieli et al., 1996; Karakas et al., 2000; Pfurtscheller and Lopes da Silva, 1999], it is far from necessary to underline the importance for a source separation technique of being able to identify these non‐phase‐locked dynamics.

We therefore set out to investigate if FSS was able to extract ongoing cerebral activity with enough SNR to describe the induced responses, and explored this idea by reanalyzing a MEG dataset of a visual spatial frequency tuning paradigm [Hadjipapas et al., 2006, in press], by using FSS and by comparing it to conventional data‐driven, blind statistical approaches such as Principal Component Analysis, PCA, and ICA, which are not subject to any explicit source model or functional constraint. To design the task‐related constraint for the FSS application, we made use of the well‐documented functional aspect of a robust and temporally sustained stimulus‐induced power increase of gamma activity in the visual cortex [Adjamian et al., 2004a; Friedman‐Hill et al., 2000; Fries et al., 2001; Hall et al., 2005; Henrie and Shapley, 2005; Logothetis et al., 2001]. The magnetic field distributions of the extracted sources were compared with those obtained by a widely known spatial filtering technique [SAM, Vrba and Robinson 2001], which has been demonstrated to be a valid approach to reconstruct induced phenomena [Hillebrand and Barnes, 2005].

The extracted source power spectral characteristics were analyzed by means of the Morlet‐Wavelet time‐frequency representation; the spatial frequency‐dependent spectral reactivity was also quantified and compared among methods.

MATERIALS AND METHODS

Experimental Setup

A dataset from a visual MEG experiment, presented recently by some of the authors [Hadjipapas et al., 2006, submitted for publication], was used. Six subjects (four males, two females, aged between 25 and 40) participated in the study after giving their informed consent. All participants had normal or corrected‐to‐normal vision and no history of neurological disorders. They viewed a set of static horizontal black/white square‐wave grating patterns of maximum Michelson contrast at a viewing distance of 2 m for 4.5 s (experimental condition referred to as ‘Stimulus’), followed by 4.5 s of a uniform field of the same mean luminance (control condition or passive period referred to as ‘No‐Stimulus’). The spatial frequency (SF) of the gratings was set to 0.5, 3 or 6 cycles per degree (cpd). The stimuli of the three different SF were pseudo‐randomly interleaved within a single recording session. Each sequence of active and passive states was repeated 30 times for each grating SF. This was a passive viewing paradigm (the subject was not required to make a response).

Recordings

MEG data were recorded by using a 275‐channel system (CTF Systems, a subsidiary of VSM MedTech) utilizing 3rd‐order gradiometer configuration, at a sample rate of 600 Hz. Individual MEG data were then co‐registered with each subjects' anatomical MRI [Adjamian et al., 2004b], to prepare them for source localization procedures.

Source Separation Algorithms

The blind source separation techniques of PCA and ICA [fastICA, Hyvarinen et al., 2001] were compared with the novel introduced technique of FSS [Barbati et al., 2006].

PCA

PCA is a classical technique—stemming from the early work of Pearson [1901]—in statistical data analysis, feature extraction and data compression. Given a set of multivariate measurements, its purpose is to find a (possibly) smaller set of variables with less redundancy that would give as good a representation as possible. No generative model or explicit assumptions on the probability density of the data are made. A solution is found such that a single source will contribute as much of the signal variance as possible, by finding a rotated orthogonal coordinate system such that the elements of the original data matrix in the new coordinates become uncorrelated. Principal components (PC) were computed as follows:

(1)

where the matrix Q is the product of the inverse square root of Λ, the N × N diagonal eigenvalue matrix of the MEG data X—N being the number of sensors—and P, the corresponding orthogonal projection matrix, i.e., the eigenvector matrix. PCs were computed in the following two ways: first, by starting from the original MEG data matrix (case indicated as ‘PCA’) and, second, by deriving them from the MEG data filtered in the γ (gamma, 20–70 Hz) frequency band (case indicated as ‘PCA filt’), to facilitate the recovering of the signal of interest. In the latter case, the PC were obtained by multiplying the weight vectors from filtered data by the unfiltered signals, so as to allow a more complete signal reconstruction over a broader frequency range. In both cases, the number of components to be estimated was chosen to explain at least the 95% of the total data variance.

ICA

ICA [Comon, 1994] is a generative ‘latent variable’ model that describes how the observed data are generated by a process of mixing the underlying unknown sources; the sources (ICs) are assumed to be statistically independent and non‐gaussian. Since the observed mixed signals will tend to have more gaussian amplitude distributions, ICA strives to find a separation matrix that minimizes the gaussianity of the results, thus optimally separating the signals. The set of MEG signals X are assumed to be obtained as a linear combination (through an unknown mixing matrix A) of statistically independent non‐gaussian sources S (at most, one gaussian source):

(2)

Sources S are estimated (up to arbitrary scaling and permutation) by independent components (IC) as:

(3)

where the unmixing matrix W is estimated along with the components. In this application, the fastICA algorithm [Hyvarinen et al., 2001] was applied to the unfiltered MEG data matrix (case indicated as ‘ICA’) and to the data filtered in the γ (gamma, 20–70 Hz) frequency band (case indicated as ‘ICA filt’); this time, too, in the second case, the components were obtained by multiplying the weight vectors from filtered data by the original ones. In both cases, the initial number of components to be extracted was chosen to explain at least 95% of the total data variance.

FSS

As in the ICA approach, FSS starts from an additive hidden source model of the type X = AS, where X represent the observed MEG data, S are the underlying unknown sources and A is the source‐sensor coupling matrix to be estimated. Additional information to a standard ICA model is used to bias the decomposition algorithm towards solutions that satisfy physiological assumptions, by means of a multi‐objective cost function:

(4)

where J is the non‐gaussianity measure generally used in ICA (for example, kurtosis), λ is a parameter to weigh the two parts of the contrast function, and R accounts for the prior information we used to extract sources. In this application, as detailed in the Appendix A, the FSs were estimated with λ = 1,000 in all subjects.

If different R are employed for different source extractions and orthogonality between different sources is not required, the algorithm starts each time from the original data matrix; this means that the extracted sources (FSs) are not required to be independent.

In the present work, accordingly with the gamma activity under investigation, the following ad‐hoc functional constraint R was introduced:

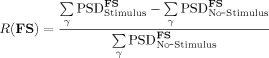(5)

by computing the power spectrum density (PSD) area difference of the source (FS) between Stimulus (from 0 to 4.5 s of each trial, t = 0 corresponding to the stimulus onset) and No‐Stimulus (from −4.5 to 0 s of each trial) in the γ (gamma, 20–70 Hz) frequency band. This difference was then standardized with respect to the gamma activity level at No‐Stimulus.

Orthogonal FSS extraction scheme.

According to the optimization technique adopted in the FSS procedure (simulated annealing, [Kirkpatrick et al., 1983]), the cost function can have any form (e.g., it does not need to be differentiable), and the algorithm, if properly set, reaches the global maximum of the cost function. To check this crucial aspect, an orthogonal FSS extraction scheme was implemented, in a way analogous to the deflation version of the fastICA algorithm. For each subject, a certain number of FSs were extracted in a single‐unit approach—by maximizing the cost function (4) with the constraint (5)—and each new component was decorrelated from the subspace generated by the components already found. The stop rule was determined by the following procedure: at every kth step of the extraction (by starting from k = 1, i.e., from the first FS estimated), the retro‐projected MEG data were computed, by multiplying the estimated mixing matrix by the corresponding FS:

(6)

Then, the discrepancy matrix was obtained as the difference between the original MEG data and the retro‐projected ones [Barbati et al., 2004]:

(7)

A mean R index, i.e., the mean value across the sensors of the functional constraint defined in Eq. (5) was obtained as the ratio between the mean R computed on the discrepancy matrix and the mean R across the original MEG sensors:

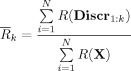(8)

N being the number of sensors. The starting assumption being that the original sensor space contains all the gamma reactivity information, even if hidden in the sensors mixture, the index in the above Eq. (8) tends to zero, as the number of extracted FSs increases. The extraction stopped when the percentage change between R _k and R _{k + 1} was negligible, in other words: when the fact of estimating a successive component added no more information about gamma reactivity. Details of this procedure are given in Appendix B.

BSS and FSS algorithms were applied to the data down sampled at 138 sensors and 31 trials (details of the machine we used are given in Appendix A).

Synthetic Aperture Magnetometry

The spatial filtering (‘beamformer’) technique known as Synthetic Aperture Magnetometry [SAM, Barnes and Hillebrand, 2003; Robinson and Vrba, 1999; Van Veen et al., 1997] was used to localize task‐related sources. The frequency range of interest (20–70 Hz) in the gamma band and the entire duration of the trial (including both Stimulus and No‐Stimulus periods) were used to define the covariance time window that determined the spatial filter properties of the beamformer [Barnes and Hillebrand, 2003]. For each subject, the SAM spatial filters, W ${}_{\text{θ}}^{\text{T}}$, were obtained as follows:

(9)

where L _θ is the lead field vector for the source θ (a single current dipole model) and C is the data covariance matrix computed over the selected time window; by multiplying the MEG data X by the estimated spatial filter, an estimate of the source activity could be obtained (S _θ), termed the ‘virtual electrode’. The standard pseudo‐t measure from the CTF SAM software was then computed from measures of power spectral change across all pairs of Stimulus vs. No‐Stimulus periods (contrast windows), for each voxel of a pre‐defined source space—in a grid of 5 mm—by using data pooled across all stimulus conditions. A volumetric Statistical Parametric Map (SPM) was thus obtained by estimating this index of change in neuronal activity, and the maxima of the pseudo‐t provided information on locations of the cortical sources of stimulus‐related activity. For each subject, the global SPM maxima in the selected gamma range—and, therefore, the location of the largest significant power changes—were estimated. The corresponding spatial filters, W ${}_{\text{θ}}^{\text{T}}$ in terms of Eq. (9), were taken into account for comparisons with BSS and FSS methods.

Extracted Source Performance Evaluation

Generated magnetic field distributions

As a first criterion to evaluate the ability of the extracted components of representing visually induced gamma activity, the correlation coefficients between the weight vectors of the estimated sources and the SAM spatial filters were computed. For PCA, ICA, and FSS, each column of the estimated mixing matrix summarizes the relative projection strengths of a component at the individual sensors, but no explicit information about the localization of the corresponding source is present; for SAM, each virtual electrode weight vector or spatial filter represents a map describing the topography of a well‐localized activity, selective for dipolar generators with a corresponding explicit coordinate. Such property was used to automatically select BSS and FSS components in the spatial area of interest. The significance of the correlation coefficients was assessed by means of a bootstrap procedure; the correlation coefficient distribution under the null hypothesis of no association was obtained by randomly resampling the extracted source weight vectors (number of bootstrap samples set at 1,000) and by computing the correlation coefficients with SAM filters for each one of the bootstrap samples, so as to obtain a significance threshold set as the 95th percentile of the obtained bootstrapped null distribution [Davison and Hinkley, 1997].

Induced Gamma Activity

Once the components had been selected for each method in the area of interest, the Morlet‐Wavelet time‐frequency representation was used to analyze the time‐frequency behaviour of source activity in relation to the grating pattern. Evidence from invasive neurophysiological local field potential (LFP) recordings in primary visual cortex, which—in contrast to MEG extracranial signals—are not subject to an inverse problem, suggests that the presentation of high‐contrast grating stimuli induces strong and sustained broadband γ‐band activity, which is temporally contingent in the presence of the stimulus in the visual field [Henrie and Shapley, 2005; Logothetis et al., 2001]. Therefore, it was a key point to evaluate the reconstruction of gamma activity throughout the whole duration of the stimulus presentation. Also in this case, significant power changes from the No‐Stimulus to the Stimulus periods were assessed by using a resampling bootstrap technique, and thresholded at P = 0.05, whereas non‐significant changes were set to 0.

To statistically compare spectrogram characteristics among methods, the mean value of the gamma reactivity across subjects, which was averaged in one‐second time windows in the Stimulus period (i.e., four windows, each one of 600 sample points), was computed and used as the dependent variable in an ANOVA model, with Method as the five‐level factor (PCA, PCA filt, ICA, ICA filt, FSS), and Time as a covariate.

Finally, to evaluate the induced gamma behaviour across different spatial frequencies of the gratings (0.5, 3 and 6 cpd), separately for each SF a set of three reactivity measures, following the functional constraint formula defined in Eq. (5), were computed for the subset of selected sources, and compared across methods (R_0.5, R_3 and R_6, respectively).

RESULTS AND DISCUSSION

To satisfy the required criterion to explain at least the 95% of the total variance of the MEG data, a number of components between 18 and 42 were found (Table I). It is to be noted that for ICA the final number of estimated sources could be smaller than the required one, due to the non‐convergence of the independence rotation after the orthogonal projection. The FSS procedure provides a single source that maximizes the cost function. This property was further confirmed in the present work by proving that in the orthogonal space with respect to the first extracted source, no significant task‐related activity could be found in the spatial area of interest (except for one out of six subjects, with an adjunctive selected source).

Table I.

Source magnetic field distributions

Subject	Hem	x	y	z	SAM pseudo‐t	FSS	BSS
							ICA	ICA filt	PCA	PCA filt
AH	L	−15	−86.4	−5.7	6.6	1/1 (100)	1/18 (5.6)	3/18 (16.7)	2/18 (11.1)	2/18 (11)
	R	16.6	−79.7	−3.1	8.7
EF	L	−13.5	−83.5	−18	6	1/1 (100)	0/8 (0)	2/28 (7.1)	10/31 (32.3)	11/31 (35)
	R	13.5	−93.5	−10.9	5.5
GB	L	−13.6	−90.6	−3.4	8.6	1/1 (100)	3/27 (11)	4/23 (17.4)	7/27 (26)	7/27 (26)
	R	16.3	−93.6	−5.1	7.2
KK	L	−29.8	−72.9	0.5	2.8	1/1 (100)	1/28 (3.6)	3/27 (11.1)	5/32 (15.6)	8/32 (25)
	R	10.8	−73.5	14.4	4.3
MS	L	−7.1	−78	−2.9	6.1	1/7 (14.3)	0/16 (0)	3/17 (17.6)	5/26 (19.2)	4/26 (15)
SW	L	−5.4	−86.9	−10.7	18.9	2/4 (50)	0/8 (0)	1/8 (12.5)	9/42 (21.4)	11/42 (26)

For each subject, Thalairach coordinates and pseudo t‐values of the voxels—corresponding to the largest peaks of SAM‐SPM—based on data pooled across all spatial frequencies, for one or both hemispheres (Hem). These correspond to the locations of virtual electrodes whose corresponding weight vectors were used for subsequent correlation analyses. The number of sources correlated with SAM spatial filters on the total number of estimated sources is reported for each FSS/BSS method; the ratio expressed as a percentage is shown in brackets. For ICA and PCA, the total number of sources to be extracted was chosen to explain at least the 95% of total variance of the MEG data (see Methods); it is to be noted that—for ICA—the final estimated number of components could be smaller than the required number of sources, because of the non‐convergence of the independence rotation after the orthogonal one.

Generated Magnetic Field Distributions

Looking for power changes in the 20–70 Hz band, we found the global SAM‐SPM maxima in locations consistent with the primary visual cortex in all subjects. In four out of six subjects there was evidence for bihemispheric activity, with the existence of two strong sources, one for each hemisphere.

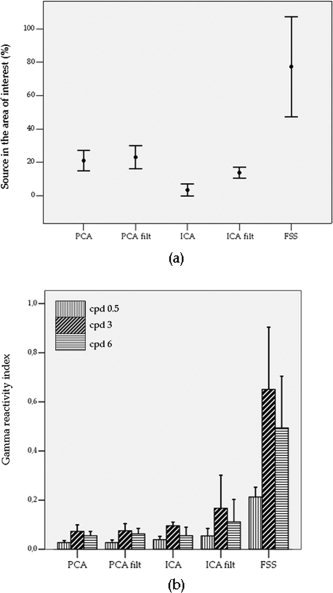
For each subject and source separation method, a component was selected if at least one of the correlation coefficients with SAM weight vectors was significant (Table I, Fig. 1a). Such selection produced a number of sources between 2 and 11 for PCA, and between 0 and 4 for ICA. In fact, for 3 out of the 6 tested subjects, ICA applied on unfiltered MEG data did not find any component in the area of interest (Table I). In all subjects, the first FS extracted was selected; in 4 cases, it was the only solution, whereas in the subject SW also the second extracted source was found in the area of interest. No significant differences between ICA filt, PCA and PCA filt correlation results were present; the worst spatial selectivity performance was found for ICA (paired Wilcoxon test on correlation percentages, ICA vs. [PCA; PCA filt; ICA filt], P < 0.05). The significantly higher percentage of sources in the area of interest was displayed by FSS (FSS vs. BSS, P < 0.05; Table I, Fig. 1a). An interesting finding was that a significant inverse relationship between the kurtosis of the components and ‘good’ map characteristics was present (Spearman ρ = −0.13, P = 0.002), in the sense that low kurtosis values were associated with the selected components. Moreover, no significant differences in kurtosis between the selected components across methods were found; kurtosis values of the retained components were about the same as that of a gaussian signal, with the median value equal to 0.3 (0 for the gaussian) and the inter‐quartile kurtosis range [0.13–0.5].

Figure 1.

(a) Error bars (mean ± 2*standard error) of the percentage (%) of source maps in the area of interest across subjects for each method; (b) Bars representing the mean +2*standard error of the spatial frequency‐related gamma reactivity index of the selected sources across subjects for each method. This index being the relative normalized variation between Stimulus and No‐Stimulus power spectral density (computed separately for each SF), the y‐axis scale units are not shown.

Induced Gamma Activity

The time‐frequency characteristics of the extracted source activities were compared across source separation methods. For the BSS algorithms, the ‘best’ component among those in the area of interest (2–11 for PCA, 0–4 for ICA; Table I) was chosen for the comparison. Such ‘best’ component was defined as the one showing the maximum amount of spectral changes between Stimulus and No‐Stimulus, as evaluated by summing the non‐zero points in the Morlet‐wavelet time‐frequency representation of the gamma band during the Stimulus period. The sustained increase in gamma activity throughout the whole duration of the stimulus presentation was consistently present in the FSS sources for all subjects. On the contrary, PCA, in both unfiltered and filtered cases, showed almost no significant activity in the spectral band of interest in all subjects, but SW. ICA of unfiltered MEG data had the worst performance, with the selected components present in only three out of six subjects. Furthermore, these three subjects showed almost no significant spectral feature of interest. ICA sources from filtered data had a better performance in depicting significant gamma activity in two out of the six tested subjects; the ‘best’ ICA component estimated for the ‘best’ subject (SW) showed activation in the gamma band for the entire duration of the stimuli and, in the subject EF, gamma spectral reactivity was found during the first second after the stimulus onset (Fig. 2).

Figure 2.

Time‐frequency plots: Time‐frequency analyses of the source signals for each subject and method. The y‐axis scale units that correspond to frequency (Hz) and the x‐axis that correspond to time are reported in the down‐right corner of the figure. The points after 0 correspond to the time when a static pattern was presented on the screen (Stimulus), and the points before 0 correspond to the time in which no pattern was present (No‐Stimulus), but the subject viewed a uniform field of the same average luminance as the pattern. The colour code represents significant changes in average power (across epochs) as a function of time and frequency represented as a percentage change from the power for a given frequency bin averaged across the No‐Stimulus period. The colour scale being symmetric, only maximum values are reported. Significant power changes from the Stimulus to the No‐Stimulus period were assessed by using a bootstrap technique, and thresholded at P = 0.05, whereas non‐significant changes were set to 0. Note for all subjects the sustained increase in gamma activity throughout the whole duration of the stimulus presentation of the FSS sources compared with the BSS ones, with the only exception of the subject SW, for whom it was possible to find a significant level of induced gamma activity for all the tested methods, except ICA. Noteworthily, SW was also the only subject with two FSs in the area of interest (indicated as ‘SW₁’ and ‘SW₂’).

From the ANOVA analysis, a significant higher mean gamma reactivity of FSS was obtained compared with the BSS algorithms (Method effect F(4, 102) = 15.5, P < 0.0001, all contrasts P < 0.0001), whereas the Time effect, as expected in the case of sustained induced responses, was not significant. Among the BSS methods, ICA filt showed the best performance (ICA filt vs. [PCA, PCA filt, ICA], P < 0.002); no significant differences were found among PCA, PCA filt and ICA.

It is to be noted that, in terms of effect size, the invasively recorded data [Henrie and Shapley, 2005] show exceptionally large changes reaching almost 600% of the baseline value in the maximal case. The corresponding effects observed across subjects in the FSS sources are generally somewhat smaller, the same being comprised between 200 and 500%, but—given the fact that these source signals are estimated from noninvasive measurements of the magnetic fields outside the head—such a result seems very encouraging, and gives confidence in the neurophysiologic meaningfulness of the procedure.

Further confirmation of the better performance of FSS with respect to the BSS methods in catching the functional characteristics of gamma reactivity was provided when the responsiveness to the three different stimulus spatial frequencies was considered. In fact, from the analysis of all paired comparisons between spatial frequency‐related reactivity indices (R_0.5, R_3 and R_6) for FSS and PCA on filtered and unfiltered data, significantly 0.5 cpd resulted to produce the lowest reactivity, as generally expected; but a significant higher reactivity was also present in 3 cpd vs. 6 cpd for the FSS sources alone (paired t‐test P value = 0.01, see Fig. 1b). This was in agreement with what observed in previous works, i.e., that the maximal cortical power within the gamma range in the primary visual cortex is produced in response to patterns of 2–4 cycles per degree, peaking at three cycles per degree, where the peak of mean illusions and discomfort is also maximal [Adjamian et al., 2004a; Hadjipapas et al., 2006, submitted for publication].

CONCLUSIONS

In the present work, we applied the recently introduced FSS algorithm to a dataset from a visual MEG experiment involving grating stimuli of varying spatial frequencies, with the aim to explore the ability of FSS in recovering induced responses.

In our previous work [Barbati et al., 2006], we had shown the interesting network properties of sources extracted by applying simple functional criteria, i.e., responsiveness described via well‐known evoked field characteristics. In the present study, we wanted to investigate if FSS was also effective when induced activity changes—much more variable than evoked responses, but possibly more informative brain phenomena that can occur at considerable time jitters with respect to the stimulus onset—were analyzed. To achieve this aim, we chose a very general but well‐described functional constraint, namely, that high‐contrast grating stimuli give rise to strong and sustained power increases in magnetoencephalographic γ‐band activity localized to the primary visual cortex [Adjamian, 2004a, Hall et al., 2005]. Moreover, we chose to investigate induced gamma activity because of the existence of extensive invasive neurophysiological data, which are not subject to an inverse problem, and could therefore be used to validate the results [Henrie and Shapley, 2005; Logothetis et al., 2001].

We compared FSS with two widely employed blind source separation algorithms, i.e., Principal and Independent Component Analyses. The common feature of these approaches (FSS and BSS) is that they both do not use any assumption about the biophysical generator source model underlying the recorded signals. This is a very important difference with respect to any source localization or beamforming algorithm, all ultimately (and critically) relying on the chosen source‐conductor model, whose validity depends on the processing step, and whose universally‐accepted selection criteria are difficult to define.

BSS techniques make use exclusively of statistical assumptions about the source properties, in terms of maximal explained variance and uncorrelatedness, PCA, or maximal source independence realized in searching for maximally non‐gaussian sources (ICA).

The FSS approach has been conceived as a multi‐objective framework that simultaneously exploits statistical features and functional task‐related properties of the source of interest, and adjusts the relative influence of these two aspects on the specific dataset in hand.

Results showed that the assumptions behind BSS models seem to be no longer suitable to fully describe induced responses; in particular, the source non‐gaussianity, synthesized by the kurtosis value of the estimated sources, was inversely related to the features of interest. In the comparison between weights estimated from unfiltered and filtered data in the frequency band under study, the criterion of explained variance also did not produce a relevant difference in the PCA case. FSS, in exploiting functional spectral differences between Stimulus and No‐Stimulus periods, was instead able to extract gamma activity in the area of interest, displaying sufficiently high signal‐to‐noise ratio to facilitate comparisons with invasively recorded LFP signals in the primate for all the recorded subjects.

The magnetic field distributions of the FSS sources across subjects displayed a significantly higher percentage of spatial selectivity with respect to the BSS ones, in the comparison with the beamformer spatial filters obtained by using both a‐priori frequency‐specific knowledge and biophysical assumptions about the underlying signal‐generating model. If on one side the FSS/BSS approaches offer the general advantage of not constraining the solution by a specific forward model, on the other side a successive localization step is needed, if the explicit source position coordinates are the principal aim of the study. Nevertheless, since the main strengths of MEG/EEG techniques are their good temporal—more than spatial—resolutions, the achievement of an accurate representation of the signal of high SNR perhaps is often more crucial than source localization.

It is to be noted that, to be successfully applied, FSS requires that some a priori hypothesis on the source (e.g., frequency range, or time course characteristics, and so on) and its variation according to the experimental conditions is identified; this information could not be always available, especially when completely new oscillatory phenomena are studied.

A current technical limitation of FSS is the number of sensors/time samples that could be used for computations, mainly because of the global optimization technique of simulated annealing that is adopted; work is in progress to improve these computational aspects, so as to allow an increasing number of sensors/time samples to be processed.

In a general case of multiple oscillatory sources, possibly with different timing and overlap, FSS could be applied with different constraints, each one reflecting the characteristics of the source of interest to be estimated. The extraction scheme for more than one source could be performed in an orthogonal or in a non‐orthogonal way. In the first case, the source extraction ordering is relevant [Barbati et al., 2006]. In the second case, each extraction starts from the original data matrix, by changing the functional constraint to be maximized.

In summary, from a general perspective of functional connectivity and neural integration studies, FSS appears to be a valid and flexible approach admitting the possibility to include different functional constraints to estimate different sources and not using any biophysical forward source model, nor requiring the uncorrelatedness or independence of the estimated sources. Therefore, it may provide a suitable, comprehensive framework to study some integrative aspects of the brain network processing.

APPENDIX A.

FSS Contrast Function Settings

In this appendix we specify how the values of the parameter λ in Eq. (4) was determined in the present application. It is to be noted that we did not use the constrained optimization procedure adopted in [Barbati et al., 2006], that included also the fixation of an additional parameter measuring the required minimum response, but instead a multi‐objective optimization scheme was adopted, considering together kurtosis and functional constraint to reach the optimum configuration. Such choice was made to simplify the automatization of the algorithm.

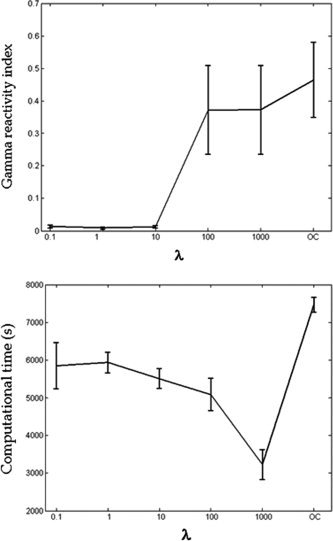
The parameter λ was selected by means of the following procedure: an initial grid was fixed with five different λ values (λ = 0.01; 1; 10; 100; 1000), and a last condition with λ = 1, but only activating the functional constraint in Eq. (4), i.e., removing the J part of the contrast function (only constraint, OC). Keeping trace of the computational times, we applied the FSS extraction method for each subject and for every condition of the grid. The gamma reactivity index R of Eq. (5) was then evaluated for each estimated source. λ was chosen to both maximize the functional constraint and minimize computational times. As to the first FS extracted (see Appendix B), for all subjects no significant increment was reliably reached in the value of R indices for λ ≥ 100 (Fig. A1, top). With respect to the computational time distribution (Fig. A1, bottom), the λ value minimizing the computational effort for the sources was λ = 1,000. The computational time was estimated for a computer with 3.2 GHz CPU and 1.0 GB RAM, for a data matrix of 138 channels and 31 trials (sampling frequency = 600 Hz, 1,67,400 sample points).

Figure A1.

Means and standard errors of the gamma reactivity index across subjects for the tested λ values; this index being a relative normalized variation between Stimulus and No‐Stimulus power spectral density, the y‐axis scale units are not reported (top). Means and standard errors of the computational times in seconds (scale units of the y‐axis) for the first FS extractions (bottom).

APPENDIX B.

Orthogonal FSS Extraction Scheme

In this appendix we specify how the stop rule of the orthogonal extraction scheme was applied. For each subject and each condition of the grid (see Appendix A), the FSS extraction stopped at the kth component when the following index:

(B1)

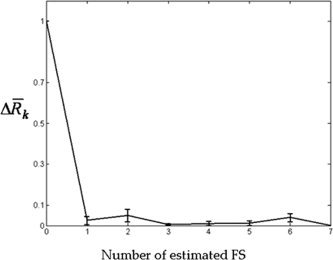
was under a threshold fixed at 0.01. The Δ R _k value was initialized at 1 for k = 0; for all subjects the extraction stopped at the first FS (k = 1) for the first three conditions of the grid (λ = 0.01; 1; 10); a number of FSs comprised between 1 and 7 was obtained in the remaining cases (λ = [100; 1,000]; OC). In Figure B1, means and standard errors across subjects for Δ R _k values (y‐axis), in function of the number k of FSs estimated (x‐axis) for the selected condition (λ = 1,000) are depicted. It is to be noted that, after the first component (i.e., for k > 1), Δ R _k values were consistently under 0.1, and the corresponding FS weights were not located in the spatial area of interest, the only exception being the subject SW (k = 2), in whom the first two FSs were found in the spatial area of interest.

Figure B1.

Means and standard errors across subjects for Δ R _k values (y‐axis) in function of the number k of FSs estimated (x‐axis) for the selected condition (λ = 1,000). Δ R _k is an a‐dimensional index, therefore the y‐axis scale units are not shown. As the stop rule was fixed at 0.01, the maximum estimated number of FSs was 7 (subject MS). After the first component (k > 1), all Δ R _k values were consistently under 0.1, and the corresponding FSs did not significantly correlate with SAM weights for all subjects but one (SW).