Blind identification of evoked human brain activity with independent component analysis of optical data

Abstract

Diffuse optical tomography (DOT) methods observe hemodynamics in the brain by measuring light transmission through the scalp, skull, and brain. Thus, separating signals due to heart pulsations, breathing movements, and systemic blood flow fluctuations from the desired brain functional responses is critical to the fidelity of the derived maps. Herein, we applied independent component analysis (ICA) to temporal signals obtained from a high‐density DOT system used for functional mapping of the visual cortex. DOT measurements were taken over the occipital cortex of human adult subjects while they viewed stimuli designed to activate two spatially distinct areas of the visual cortex. ICA was able to extract clean functional hemodynamic signals and separate brain activity sources from hemodynamic fluctuations related to heart and breathing without knowledge of the stimulus paradigm. Furthermore, independent components were found defining distinct functional responses to each stimulus type. Images generated from single ICA components were comparable, with regard to spatial extent and resolution, to images from block averaging (with knowledge of the block stimulus paradigm). Both images and estimated time‐series signals demonstrated that ICA was superior to principal component analysis in extracting the true event‐evoked response signals. Our results suggest that ICA can extract the time courses and the corresponding spatial extent of functional responses in DOT imaging. Hum Brain Mapp, 2009. © 2009 Wiley‐Liss, Inc.

INTRODUCTION

Diffuse optical tomography (DOT) is an emerging method for functional neuroimaging, with advantages complimentary to those of functional magnetic resonance imaging (fMRI) with blood oxygenation‐level dependent (BOLD) contrast. DOT uses a wearable imaging cap and portable equipment, giving it potential as an important tool for subjects not amenable to large, fixed scanner geometries, such as intensive care patients and young children. In addition, the ability to simultaneously image multiple hemodynamic contrasts (DOT can measure oxy‐, deoxy‐, and total hemoglobin concentrations, whereas BOLD is most sensitive to deoxyhemoglobin) allows the study of developing and diseased brains, where the neurovascular coupling is unknown or altered.

DOT is an advancement relative to previous optical neuroimaging techniques, often referred to as near‐infrared spectroscopy (NIRS) or diffuse optical imaging. While NIRS systems create two‐dimensional images from arrangements of isolated single source–detector pair (SD‐pair) measurements, DOT encapsulates various methods to synthesize overlapping measurements into higher‐quality three‐dimensional images. One DOT method that can provide high‐quality images while maintaining system simplicity is high‐density DOT, which uses an interleaved grid of sources and detectors with measurements at multiple distances to sample different tissue depths. These measurements can be reconstructed into images using a model of light transport in tissue and data inversion routines.

As with NIRS systems, DOT observes hemodynamics in the brain by measuring light that has been transmitted through the scalp, skull, and brain. Thus, superficial and global signals, such as those due to heart pulsations, breathing movements, and systemic blood flow fluctuations, must be removed from the composite measured response if accurate maps of brain hemodynamics are to be made. We have previously reported the development of a high‐performance DOT system [Zeff et al., 2007]. Using this system we demonstrated advances in imaging cortical responses to visual stimuli, improving upon previous noninvasive optical reports. In this study, we demonstrate the use of independent component analysis (ICA) with DOT hemodynamic data to isolate the temporal and spatial components of evoked responses in adult visual cortex.

ICA has proven useful for analysis of many types of biomedical images [James and Hesse, 2005] and has been particularly successful when applied to studies of the brain by electroencephalographic (EEG) recordings, by fMRI, or by simultaneous EEG‐fMRI recordings [e.g., Calhoun and Adali, 2006; Jung et al., 2001; Mantini et al., 2007b; Onton et al., 2006]. With EEG data, temporal ICA is frequently employed to remove artifacts in time‐series data [Grouiller et al., 2007; Mantini et al., 2007a]. With fMRI data, ICA is frequently used to determine the location of responses [Calhoun and Adali, 2006; Correa et al., 2007; McKeown et al., 1998] and to investigate functional connectivity or resting‐state brain networks [Beckmann et al., 2005; Damoiseaux et al., 2006; Jafri et al., 2008; van de Ven et al., 2004]. Recent studies have applied ICA to combined EEG‐fMRI studies [Eichele et al., 2008; Moosmann et al., 2008] to characterize the spatiotemporal aspects of functional responses.

Very few studies have applied ICA to optical data obtained from humans. Invasive imaging studies of optical intrinsic signals from animals have used extended spatial decorrelation, a method similar to ICA, to analyze two‐dimensional video recordings [Schiessl et al., 2000, 2008]. The invasive signal recordings in these studies would not have all of the contaminating factors from superficial physiology found in noninvasive recordings. A NIRS study in humans [Morren et al., 2004] used a special ICA algorithm, SOBI [Belouchrani et al., 1997], to detect fast (range of milliseconds) signals from neuronal scattering in the motor cortex (related to a finger‐tapping exercise). ICA was applied to the intensity signals to separate the fast scattering signals from noise, but only after filtering of the data to remove cardiac and respiratory cycles. ICA has also been applied to functional NIRS data to remove a signal correlated to skin blood flow, as determined with laser Doppler [Kohno et al., 2007]. To the best of our knowledge, ICA has neither been used with tomographic optical image reconstructions nor to separate noninvasive optical hemodynamic imaging signals into distinct brain functions.

We describe here our preliminary studies undertaken to investigate the usefulness of ICA for DOT measurements of functional responses in the brain to various stimuli. ICA was applied to DOT data obtained in a visual cortex mapping study of adult human subjects. We tested ICA against two previous standards—principal component analysis (PCA, a classical method for separating data into uncorrelated components) and block averaging—in their ability to extract event‐evoked responses from obscuring signals. We show that ICA is able to extract brain activity from highly contaminated, raw time‐series data, to discriminate between brain activity and other physiological signals, to characterize the temporal and spatial features of activity, and to differentiate between different brain activities, all without the knowledge of the stimulus design.

MATERIALS AND METHODS

Subjects

Data from three healthy adult subjects (one male and two females, ages 25–26) were used to evaluate the feasibility of temporal ICA. The study was approved by the Human Research Protection Office of the Washington University School of Medicine, and informed consent was obtained from all subjects prior to scanning.

DOT Data Acquisition

The imaging system is a continuous wave high‐density DOT imager with 24 source positions (near‐infrared wavelengths of 750 nm and 850 nm) and 28 detectors interleaved in a high‐density array (Fig. 1a) [Zeff et al., 2007]. Subjects were seated in an adjustable chair facing a 19‐in. liquid crystal display at a 70‐cm viewing distance. The DOT imaging cap was positioned with the optode array on the back of the head (Fig. 1a). The cap was centered horizontally, with the center of the imaging array near the inion.

Figure 1.

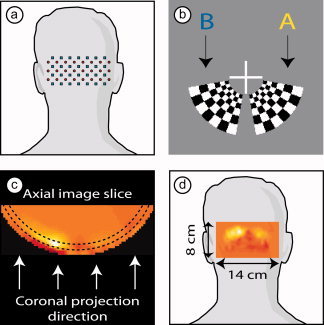
Experimental setup. (a) A schematic of the visual cortex imaging pad placed over the occipital cortex. Red dots are sources; blue squares are detectors. (b) Closeup of the two visual stimuli. Both extend over a polar angle of 70° and have an eccentricity of 0.5–1.7°. Checkerboards reversed at 10 Hz were presented for 10 s, and were separated by 31 s of 50% gray screen. (c) An axial image slice with a cortical activation. In this article, images are displayed as two‐dimensional coronal projections [as in (d)] of a cortical shell covering a depth 10 ± 5 mm below the scalp surface (the region between dotted lines with arrows showing direction of view). (d) Schematic showing placement of an activation image on a human subject. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The visual stimuli were radial, reversing, black‐and‐white grids (10‐Hz reversal) on a 50% gray background. The paradigm consisted of blocks of a 10‐s stimulus followed by a 31‐s 50% gray screen. Two types of stimuli, designated as A and B, were presented (Fig. 1b). The central lower‐right stimulus (A) extended over a polar angle of 70° and a radial angle of 0.5–1.7°; the central lower‐left stimulus (B) mirrored stimulus A. Stimuli were presented in a predetermined pseudorandom order, with eight presentations each of A and B stimuli, with a gray screen presented 15 s before and after the stimulus sequence. In addition, synchronization signals were obtained from a separate channel, marking the beginning of each stimulus presentation. The complete data set consisted of 11 min of recordings at 10.8 Hz, for a total of 7,080 time‐series points. This data (x) is used as the input for further analysis.

Data Preprocessing

SD‐pair data for 850 nm were converted to log‐ratio data. No temporal filtering was applied before ICA. The measurements from the first‐ and second‐nearest neighbor SD‐pairs were included for a total of 212 SD‐pair measurements. First‐nearest neighbor measurements consisted of sources and detectors separated by 1.3 cm, sampling superficial tissues, whereas the second‐nearest neighbor measurements had a SD separation of 3 cm, which samples both brain and superficial tissues. Block‐averaged time traces for each stimulus type were generated for later comparison with the results of ICA. Each segment (block) for block averaging consists of 430 points (40 s). The mean of data points in the interval 12–14 s after onset of stimulus (the peak of the hemodynamic response) for each of the 212 observed signals is used as the measurement metric (y _meas) for imaging, as described later.

DOT Imaging

For image reconstruction, a two‐layer, hemispheric head model (radius = 80 mm) is used with finite‐element, forward light modeling [NIRFAST, Dehghani et al., 2003] to obtain a sensitivity matrix for the optode array. The regularized and inverted sensitivity matrix is used to convert measurement data into images of the differential absorption within the head model. With the measurement data represented as a vector y _meas, the voxel image data represented as a vector v, and the inverted sensitivity matrix as S ^#, the linear, least‐squares solution for the image is given by

(1)

as described in Zeff et al. [ 2007]. From this three‐dimensionalimage, a cortical shell is selected for viewing (Fig. 1c). All images are shown as posterior coronal projections of this cortical shell (Fig. 1d).

We note parenthetically that in our previous publications we often use an alternative notation in which the DOT sensitivity matrix is represented by A and the vector of voxel data by x. In this article, we have changed the notation to allow us to use the notations typically used for ICA, in which x is a matrix of observed signals and A is the mixing matrix as in Eq. (2) mentioned later.

Images for both ICA and PCA components can be computed similarly. For a single component, the matrix column representing the mapping from the component to the 212‐measurement space can be used as the measurement metric (y _meas) to compute the image (with arbitrary scale) using the linear, least‐squares equation shown in Eq. (1).

Independent Component Analysis

ICA can be applied to either temporal or spatial data. For this study, we used temporal ICA, assuming independence of the unknown temporal sources or signals. ICA assumes that the mixture components follow a Gaussian distribution and that the source components are non‐Gaussian, usually super‐Gaussian. The measured or mixture signal data (x) are assumed to be a linear mixture of mutually statistically independent source components (s) as indicated by

(2)

where the matrix A is the mixing matrix and each row of x represents the temporal signal for one SD pair, and each row of s represents the temporal signal for a source component. The mixture data, x, has dimensions of m × n, where m is the number of SD‐pair measurements and n is the number of time samples.

The estimated sources () are computed using the unmixing matrix W

(3)

where the number of sources, k, may be less than the number of mixture signals. Thus, the dimensions of the source matrix are k × n and the dimensions of the W matrix are k × m. For our data, 20–40 source components (i.e., time courses) were estimated in preliminary processing to determine the number of components required.

There are several different ICA algorithms available. For analyses of biological data, one or more of three algorithms are usually applied: Infomax [Bell and Sejnowski, 1995; Lee et al., 1999], JADE [Cardoso and Souloumiac, 1993], and FastICA [Hyvärinen, 1999; Hyvärinen and Oja, 1997, 2000]. The success of ICA may depend on the algorithm and the evaluation measures used, as well as the statistical properties of the data. An early comparison of the Infomax and FastICA algorithms for fMRI data showed that both algorithms were accurate, but that each was best under certain evaluation criteria [Esposito et al., 2002]. A recent study has shown that all these three algorithms yield reliable and consistent results when applied to fMRI data [Correa et al., 2007].

For this study, we used the FastICA algorithm (version 2.5) available from http://www.cis.hut.fi/projects/ica/fastica/index.shtml [Hyvärinen, 1999; Hyvärinen and Oja, 1997 ]. We chose to use this algorithm as it is a recent version that is easy to use. The FastICA algorithm performs the following preprocessing steps: centering the data (subtracting the mean of each row), reducing the dimensionality of the problem with PCA, and whitening the data. FastICA also makes adjustments to the results of the analysis required to compensate for these preprocessing steps. The independent components (ICs) are estimated by maximizing the non‐Gaussianity of the estimated source signals using one of the four nonlinear contrast functions included in the algorithm. We selected the “skew” option for the nonlinearity function for our processing, as examination of the measured signals showed that some signals had a bimodal or skewed distribution, although many of the measured time‐series signals were approximately Gaussian. Also, the evoked‐response signals have a nonsymmetric distribution so that at least two estimated source components should have skewed distributions.

Given the estimated ICs, the mapping back to the original measurement space of a desired subset of components can be computed by

(4)

where the k × k diagonal matrix C has a value of 1 for diagonal elements corresponding to the IC to be included and 0 for elements elsewhere. The m × k matrix A is the estimate of the mixing matrix shown in Eq. (2). The measurement data corresponding to an IC can then be used to generate an image as described in the DOT imaging section. The ICs that were highly correlated (correlation magnitude >0.5) with the A or B response templates (see response template calculation mentioned later) were used to generate images of the scanned area. Note that these components are also easily detected by visual inspection as their shape is characteristic of functional responses.

Principal Component Analysis

Each data set x was also analyzed by PCA to select the same number of uncorrelated or principal components (PCs) as the number of ICs estimated by ICA. PCA was performed (following subtraction of each row mean) by using the singular value decomposition of x,

(5)

The Matlab command “svd(x, ‘econ’)” was used to perform the decomposition. Then, the resulting k PCs in rows of Y are given by

(6)

where the n × k matrix 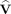contains the first k columns of V and the diagonal matrix 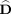is a k × k subset of the original D matrix containing the corresponding singular values.

The mapping from a single PC (or several PCs) to the measurement space of 212 signals is given by

(7)

where the matrix C is a k × k diagonal matrix with diagonal elements corresponding to the PCs to be retained set equal to 1, and the matrix M _x contains the row means (small for our data) that were subtracted from the data prior to PCA. The m × m U matrix is reduced to k columns for the modified matrix in the equation.

The measurement data corresponding to a PC is reconstructed as an image as described in the DOT imaging section. PCs that were highly correlated with the A or B response templates (see response template calculation mentioned later) were used to generate images of the scanned regions.

Response Template Construction

To objectively judge the ICA and PCA results, we created canonical hemodynamic time courses for each of the A and B stimulus temporal patterns. An extracted component that represents a response to stimulus A should show a hemodynamic response following the temporal pattern of the A event design, and similarly a component that represents a response to stimulus B should follow the temporal pattern of the B event design. To create such templates, we need to convolve each event design with a hemodynamic response function. One could use a hemodynamic response function from the literature. However, since hemodynamic responses can vary across cortical regions and stimulus paradigms, we calculated a hemodynamic response function directly from the measured, block‐averaged data.

A block‐averaged activation image was obtained for each subject and stimulus (Fig. 2a). Then, the pixel containing the maximum value in the image was used as the center pixel to define a 5 pixel × 5 pixel (1 cm × 1 cm) region. A temporal profile of this region was obtained. This procedure was repeated for all three subjects and both stimulus responses (Fig. 2b, red lines). To provide a single consistent response with high signal‐to‐noise ratio, the average of all responses was used as a standard response curve. To further reduce the noise in the response curve, two functions were fit piecewise to the data (Fig. 2b, blue line). This smoothing technique does not imply any underlying functional form for the hemodynamic response.

Figure 2.

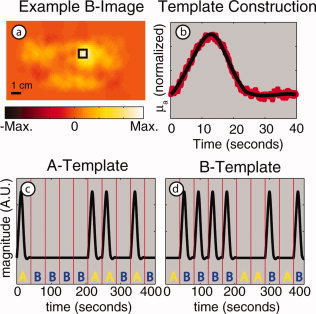
Steps in the calculation of response templates. (a) An image of an evoked response from stimulus B using block‐averaged raw data. The black box delineates the region selected for response B profile generation. (b) Averaged response from all subjects and all stimuli (red dots) along with a smoothed fitted curve (black solid line). (c,d) Templates for responses to stimuli A and B for one subject's presentation sequence. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

To create the fully synchronized reference patterns for the expected hemodynamic responses to both the A and B stimulus patterns, we inserted our smoothed standard hemodynamic response curve into the appropriate intervals of the presentation sequence for each subject. Since the subject viewed alternating presentations of stimulus A and B in one session, the two templates are synchronized to the known start of the entire pseudorandom sequence. Figure 2c,d show the two templates for one particular sequence of stimulus presentation.

Correlation Coefficients

To test the ICA and PCA components, temporal correlation coefficients were computed between each component and the template response curves for both stimuli. These coefficients were calculated for each of the three subjects. Only the magnitudes (absolute values) of the correlation coefficients were evaluated further as the sign of the ICA and PCA components is not uniquely determined.

RESULTS AND DISCUSSION

Independent Components

The time course of the average of the 212 original measured signals (Fig. 3a, Subject 1; for clarity, only 400 s of data are shown) is obviously a mixture of many different source signals in different frequency regimes (Fig. 3b), with low‐ and high‐frequency contaminants obscuring any functional response signal. Cardiac pulses, respiration, biological noise, and measurement instrument noise are all components in the final measured signal. After ICA, components typical of several important physiologic processes can be seen (shown with the sign convention that functional responses increase signal amplitude, although the estimated components may have been originally inverted as ICA cannot determine a multiplicative constant). The evoked response for each stimulus is found in a separate IC (Fig. 3c shows one of two such components), with the Fourier transform (FT) demonstrating prominent low‐frequency components (Fig. 3d). This IC conforms with the expected response to stimulus B and is highly correlated to the template signal for response B with a correlation coefficient of 0.81. Distinct ICs are found that correspond to different physiologic confounds. For example, an IC was found with a strong FT peak at about 1.3 Hz, most likely corresponding to heart pulsation (Fig. 3e,f), and an IC with a FT peak at about 0.3 Hz most likely is due to respiration (Fig. 3g,h). Other estimated ICA components (not shown) correspond to baseline drifts, sudden changes in the baseline, or artifacts of unknown origin.

Figure 3.

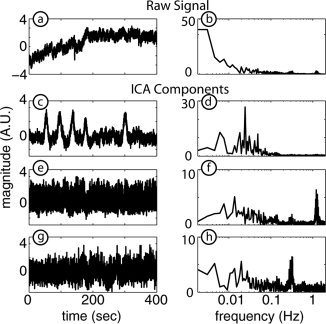
Representative ICA components and their Fourier transforms for Subject 1. (a) The average of all 212 measurement signals. (b) Fourier transform of (a) showing components occurring at many frequencies. (c) IC corresponding to a hemodynamic response for stimulus B. (d) Fourier transform of (c) with prominent low‐frequency content. (e) IC corresponding to cardiac pulse. (f) Fourier transform of (e) showing a strong frequency contribution at about 1.3 Hz. (g) IC corresponding to respiration. (h) Fourier transform of (g) with a strong frequency contribution at about 0.3 Hz.

ICA was able to distinguish the hemodynamic responses for both A and B stimulus types in all three subjects (Fig. 4a,b, Subject 2). The two components in Figure 4a,b are highly correlated to the response templates with correlation coefficients of 0.83 (stimulus A) and 0.86 (stimulus B). These responses generate images (Fig. 4c,d) that compare favorably with those from block‐averaged raw data (Fig. 4e,f). (Responses occur in the hemisphere contralateral to that of the visual stimulus.) The images generated from the ICA components qualitatively appear to have better spatial localization than the images from the block‐averaged raw data, and the background for the ICA images is also qualitatively flatter than that in the block‐averaged images.

Figure 4.

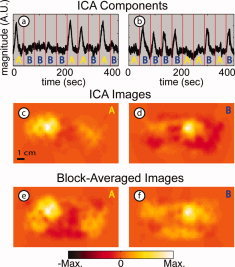
Results of ICA: Isolation of multiple stimulus responses for Subject 2 (arranged in two columns: A, B). (a) IC corresponding to the A stimulus type (r = 0.83 with template A) with the distinctive shape of a functional response. Red vertical lines represent stimulus onset, with letters showing which stimulus was presented in that interval (see Fig. 1). (b) IC corresponding to the B stimulus type (r = 0.86 with template B). (c,d) Images obtained for each IC. (e,f) Images obtained from block‐averaged raw signals. The two rows of images are similar with slightly less background activity in the ICA images. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The number of estimated ICs was selected as the minimum at which two estimated components clearly represented the stimulus responses. For the three subjects, 30, 24, and 35 components, respectively, were estimated from the 212 measurement signals. The variance in the reduced data set generated by PCA, as calculated from the eigenvalues, was greater than 98% for all three subjects. Alternatively, the number of components could be determined by setting a lower threshold for the percent variance represented by the PCA reduced data.

These ICA temporal response results were reproduced in all three subjects (Fig. 5a–c, stimulus B). Correlation coefficients for the three components are 0.81, 0.86, and 0.58 for Subjects 1, 2, and 3, respectively. The corresponding images generated from the ICs all show the expected localization and have high contrast‐to‐noise ratio (CNR; Fig. 5d–f). In all three subjects, the IC images qualitatively appear to have better resolution (smaller response regions) and lower noise than those from block‐averaged raw data (Fig. 5g–i).

Figure 5.

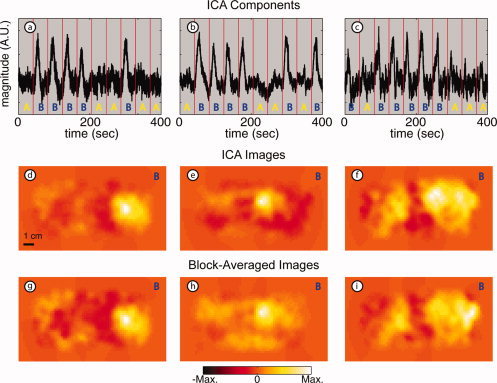
Results of ICA: Stimulus B in multiple subjects (arranged in three columns by subject). (a–c) ICs corresponding to stimulus B found in three subjects (r = 0.81, 0.86, 0.58). Red vertical lines represent stimulus onset with letters showing which stimulus was presented in that interval. Note that the hemodynamic responses are easily distinguishable in each subject. (d–f) Images obtained for each IC. (g–i) Images obtained from block‐averaged raw signals. Note the similarity between images in the two rows with less noise in the background for ICA images. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The ICs shown in the first row of Figures 4 and 5 have the distinctive shape of the stimulus response with varying degrees of contaminating signals. The contaminants appear to be mostly noise, and there appears to be no mixing of the two responses. For all three subjects, two response components, corresponding to the A and B stimuli, were isolated from the physiologic components (heart rate and breathing), and all six of these components have correlation coefficients greater than 0.58.

Principal Component Analysis

With our data and neuroimaging application, we find that, in contrast to ICA, PCA was unable, in any subject, to distinguish functional hemodynamic activations with good signal‐to‐noise ratio. The three PCs with the highest correlation to the B response for each subject (Fig. 6a–c) have much higher noise than the comparable IC (compare with Fig. 5a–c). Qualitatively, the functional evoked responses are distinguished by eye only with difficulty. Quantitatively, the correlation coefficients for these components are 0.44, 0.49, and 0.21, respectively (all much lower than even the worst result from ICA). The images generated from the PCs (Fig. 6d–f) show much higher noise than either those from ICA or block‐averaged raw data (compare with Fig. 5d–i). For Subject 1, the image from PCA has localized the activation to the subject's left hemisphere, while ICA places the activation correctly in the right hemisphere. For Subject 2, the temporal PC component appears to be a mixture of both the A and B responses with one response inverted (Fig. 6b). In fact, this PC has a correlation of 0.68 relative to the A template and a correlation of 0.49 relative to the B template, the two highest correlation coefficients among all subjects' PCs. The image from this PC (Fig. 6e) reflects this inability to separate the two functional responses, as we see an activation with the correct localization for a B response (compare with Fig. 4d) as well as a deactivation (inverted response) where we expect to see an A response (compare with Fig. 4c). For Subject 3, functional responses cannot be distinguished at all (the correlation coefficient is only 0.21). Rather, PCA localizes a small region to the far right of the imaging pad, possibly an artifact from optode motion (Fig. 6f).

Figure 6.

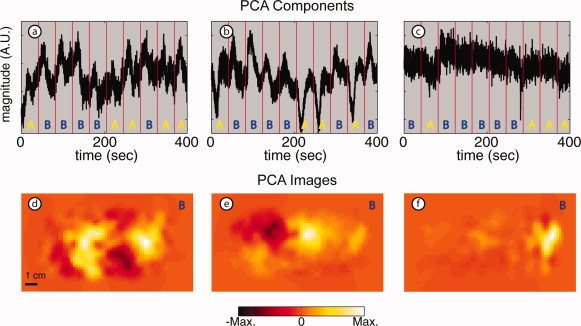
Results of PCA: stimulus B in multiple subjects (arranged in three columns by subject). (a–c) PCs with strongest correlation relative to stimulus B in each of the three subjects (r = 0.44, 0.49, 0.21). Amplitudes are arbitrary. Red vertical lines represent stimulus onset with letters, showing which stimulus was presented in that interval. Note that the signals are mixtures of stimulus responses and contaminants. (d–f) Images obtained for each PC. The images also show a mixture of different components; compare with images shown in Figure 5. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Correlation Coefficients

A more comprehensive assessment of the ICA and PCA approaches can be obtained by computing the correlation coefficients between every temporal component and the response template signals. As an example, from among all subjects, the IC (Fig. 7b) and the PC (Fig. 7c) with the highest correlation to a template for response A (Fig. 7a), have values of r = 0.83 and r = 0.68, respectively. If we examine the correlation coefficient for all ICs for this subject relative to the B template, we see a clear dichotomy between a single component that matches the expected response and low correlation values for all other components (Fig. 7d, black squares). However with the PCs (Fig. 7d, red triangles), there is no clear distinction between PCs that correlate and those that do not correlate. The results are similar when we plot the 178 correlation coefficients for the ICA and PCA components for all subjects with both response templates (recall the template is specific to each subject). Again, the ICs can easily be visually characterized with six components (two each for three subjects) that correlate with the stimuli (r > 0.58) and all the rest with very low correlation values (r < 0.24) (Fig. 7e, black squares). In contrast, the PCs exist in a spectrum with no clear distinction between those that correlate (only one correlation coefficient greater than 0.5) and those that do not (Fig. 7e, red triangles). For the PCs, there are many intermediate values (0.2–0.5) of the correlation coefficients. This suggests that the PCA components remain as a mixture of signals, with the evoked responses disseminated among many components.

Figure 7.

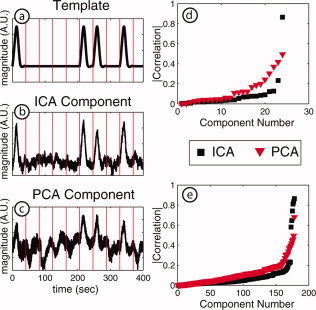
Correlation coefficients. (a) The template for the response to stimulus (for Subject 2). (b) The IC with the highest correlation (0.83) to the template. (c) The PC with the highest correlation (0.68) to the template. (d) The plot of all correlations for Subject 2 and stimulus B; correlations were computed for all 24 ICs and all 24 PCs. ICs show a clear dichotomy between the functional response component (r = 0.86) and other components. (e). Correlation coefficients for all three subjects and both stimuli; correlation coefficients were computed for all ICs and PCs relative to both stimuli resulting in 178 values for each method. For ICA, the six stimulus response components have high correlation values (>0.58), whereas the remaining components have low values (<0.24). In contrast, only one PC has a high correlation value (r = 0.68). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Thus, while PCA is useful for reduction of dimensionality before ICA, the PCs do not reflect the functional response to the stimuli for this data as accurately as do the ICs. These graphs (Fig. 7d,e) clearly demonstrate the superiority of ICA over PCA for this DOT application. In addition, the close correlation of the estimated functional response ICs to the expected evoked‐responses offers a way to automate the selection of components for imaging or further processing, automatically removing the noise components from the signal.

Discussion of Methodology

In this study, we applied ICA to the measured time‐series (x) data for a single optical wavelength without any preprocessing or filtering of the data. It is worth noting that several alternative temporal and spatiotemporal analysis methods have been proposed for improving the stimulus activation/background ratios (CNR) in NIRS measurements. For example, low‐pass filters (t > ∼ 2 s) are typically used to suppress cardiac pulsations and high‐pass filters to suppress long‐term fluctuations (t < ∼ 30 s) [Boas et al., 2001; Jasdzewski et al., 2003]. In addition, efforts have been made to remove specific cardiac and respiration signals [Gratton and Corballis, 1995; Nolte et al., 1998]. However, the spectrum of hemodynamic fluctuations is quite broad and densely populated, with contributions not only from pulse [Franceschini et al., 1999; Madsen and Secher, 1999] and breathing [Franceschini et al., 2002], but also from slower oscillations [Taga et al., 2000] in systemic and cerebral hemodynamics. Though less common, multichannel regression methods including an eigenvector analysis [Zhang et al., 2005] and a linear regression approach [Saager and Berger, 2005; Zeff et al., 2007] have also been used. For optimal ICA processing, it may be advantageous to perform some preprocessing to remove artifacts or signals with large amplitudes before the application of ICA as other investigators have found [Mantini et al., 2007a, b; Morren et al., 2004].

To benchmark the relevance of ICA to DOT data, we performed a quantitative comparison to PCA, a classical method for representing observed data as a sum of uncorrelated components. In previous reports, ICA has not always performed better than PCA, as the success of either approach depends on the type of data and the purpose of the study. For instance, a study that compared PCA and ICA for face recognition concluded that the optimal method is data‐dependent [Delac et al., 2005]. However, in most instances, ICA has significant advantages over PCA. For example, Bugli and Lambert [ 2007] found that, in application to EEG data, ICA could extract two event‐related potential signals, whereas PCA extracted only a mixture of two signals. Similar results have also been reported for other types of biomedical signals [Reidl et al., 2007; Tresch et al., 2006]. Our study finds that PCA, at best, detected a mixture of two different evoked signals and did not differentiate between functional activations and background physiology. ICA produced significantly better results, suggesting that the independence criteria are a meaningful approach to decompose DOT data sets.

The judgments about the success of the various methods were made using solely temporal criteria: a component (either from ICA or PCA) that corresponds to stimulus A should show a response when A is presented, but not B. It could happen that the component that correlates most highly temporally with stimulus A shows a spatial pattern that would be unexpected based on known retinotopy (i.e., the visual field mapping to contralateral cortex). This was not seen with any of the data‐processing methods. Both block averaging and ICA methods showed the expected spatial activation patterns. And, with the PCA component that appeared as a mixture of the two temporal hemodynamic responses, we also saw a spatial mixture of A and B; this latter conclusion being secondary, was based on reference to earlier ICA and block‐averaged images and not on a preconceived notion of the expected retinotopy. Future work should include further spatial analysis, including the correlation of their spatial patterns to expected brain localization. Establishing the spatial confidence of ICA mapping will be especially important in order to move the method toward more naturalistic settings (complex mixtures of stimuli) and fields where there is no expected brain localization to use as a reference.

In this study, we applied ICA to the SD‐pair time‐series signals derived from a high‐density DOT system as opposed to the more traditional sparse NIRS imaging systems. An advantage of the current data set is that many SD‐pairs sample the same tissue volume with different weightings. Thus, the DOT data set presents the ICA algorithm with a classical unmixing problem in which focal neural responses are projected on to a number of SD pairs. The spatial oversampling of the DOT data may provide an advantage over sparse NIRS data for ICA data processing.

We note that there are a number of other possible approaches for applying ICA to DOT data. The DOT inversion process provides model‐based “unmixing” of the data. ICA, either temporal or spatial, applied to the reconstructed image series may produce better results. Furthermore, DOT uses multiple wavelength data and spectral unmixing to distinguish changes in oxygenated hemoglobin, deoxygenated hemoglobin, and total hemoglobin concentrations. Since these variables are tightly coupled to physiology, ICA may perform better when applied to hemoglobin contrasts instead of the single wavelength data used in the present study. Such ICA of hemodynamic variables could also be combined with simultaneous monitoring of the subject's physiology (e.g., of pulse, breathing rate, and end tidal CO₂), which could be used for automatic sorting of the components. Future studies are needed to evaluate the performance of these alternate approaches to the temporal, spectral, and spatial aspects of DOT data analysis.

CONCLUSIONS

DOT can be used to investigate activity of the brain cortex similar to fMRI studies, with the added advantages of portability, simplicity of data acquisition and equipment, fewer restrictions on subjects, and comprehensive hemoglobin contrasts. However, since the DOT measurements are made with light entering and exiting through the scalp and skull, the measurements of light attenuation due to brain activity are highly contaminated by signals due to superficial and global hemodynamic fluctuations.

As shown herein, ICA is able to extract multiple hemodynamic functional responses initially obscured in DOT measurements by background physiology. Furthermore, we have shown that it is possible to extract functional responses from our DOT data without prior temporal filtering or processing based on frequency content. The images from ICA are comparable in spatial resolution to those from block‐averaged raw data and are obtained without a priori information about the nature of the stimuli. Thus, studies of task‐related responses to events without access to event design [e.g., Bartels and Zeki, 2004, 2005] can be analyzed with minor modifications to the techniques described here.

In conclusion, this report demonstrates the usefulness of ICA applied to unprocessed DOT data for blind identification of event‐evoked responses in the visual cortex of human brain. By improving sensitivity and identification, the application of ICA can potentially increase the impact of DOT methods in a wide range of basic research and clinical applications.