Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2010 Nov 16;31(12):2003–2014. doi: 10.1002/hbm.20993

Overall brain connectivity maps show cortico‐subcortical abnormalities in schizophrenia

Raymond Salvador 1,✉, Salvador Sarró 1, Jesús J Gomar 1, Jordi Ortiz‐Gil 1, Fidel Vila 2, Antoni Capdevila 2,4, Ed Bullmore 3, Peter J McKenna 1, Edith Pomarol‐Clotet 1
PMCID: PMC6870792  PMID: 20225222

Abstract

Abnormal interactions between areas of the brain have been pointed as possible causes for schizophrenia. However, the nature of these disturbances and the anatomical location of the regions involved are still unclear. Here, we describe a method to estimate maps of net levels of connectivity in the resting brain, and we apply it to look for differential patterns of connectivity in schizophrenia. This method uses partial coherences as a basic measure of covariability, and it minimises the effect of major physiological noise. When overall (net) connectivity maps of a sample of 40 patients with schizophrenia were compared with the maps from a matched sample of 40 controls, a single area of abnormality was found. It is an area of patient hyper‐connectivity and is located frontally, in medial and orbital structures, clearly overlapping the anterior node of the default mode network (DMN). When this area is used as a region of interest in a second‐level analysis, it shows functional hyper‐connections with several cortical and subcortical structures. Interestingly, the most significant abnormality is found with the caudate, which has a bilateral pattern of abnormality, pointing to a possible DMN–striatum deviant relation in schizophrenia. However, hyper‐connectivity observed with other regions (right hippocampus and amygdala, and other cortical structures) suggests a more pervasive alteration of brain connectivity in this disease. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.

Keywords: magnetic resonance imaging, resting state, functional connectivity, default mode network, caudate nucleus, basal ganglia, cerebral cortex

INTRODUCTION

The psychotic disorder schizophrenia is widely believed to be due to a disturbance of brain function, but the nature of this disturbance and which anatomical regions are affected still remains uncertain. Since the early 90s, different authors have argued for dysfunction in different areas and sets of regions, including frontal [Frith, 1992], fronto‐temporal [Friston and Frith, 1995; Liddle, 2001], fronto‐hippocampal [Gray et al., 1991; Weinberger and Lipska, 1995], fronto‐temporal‐striatal [Robbins, 1990] and fronto‐striato‐cerebellar [Andreasen, 1999] systems.

More recently, attention has also been focused on potential disturbances in a set of regions known as the default mode network (DMN) [e.g., Bluhm et al., 2007; Garrity et al., 2007; Pomarol‐Clotet et al., 2008]. This network is known to be active when the brain is not engaged in any specific task [Greicius et al., 2003; Mazoyer et al., 2001; Raichle et al., 2001], and it includes areas of the medial prefrontal cortex, the posterior cingulate and the inferior parietal lobule as main components. Implicit in this and all the previous hypotheses is the idea that the connectivity between brain regions is abnormal in patients with schizophrenia [Bullmore et al., 1997], echoing Bleuler [1911], who originally coined the term schizophrenia to refer to a putative fragmentation and discoordination of cerebral function.

Functional magnetic resonance imaging (fMRI) has been applied to explore connectivity anomalies in schizophrenia using different methodological approaches. Early studies selected, a priori, a set of regions of interest (ROI) based on previous results or models, and looked for differences in correlation coefficients or other multivariate association measures [e.g., Lawrie, 2002; Menon et al., 2001; Salvador et al., 2007; Schlösser et al., 2003]. Similarly, differences in correlations between a ROI and the remaining voxels of the brain have been reported. Although these methods can be very useful and they are still widely used, they only relate to connections involving the selected ROI.

Alternatively, less directed and more open analyses have been carried out either by making extensive connectivity analyses based on complete parcellations of the brain [Foucher et al., 2005; Liang et al., 2006; Liu et al., 2008] or by performing studies based on components extracted by non‐supervised methods [Demirci et al., 2009; Jafri et al., 2008; Kim et al., 2009]. In general, though, results reported by these and other studies are not entirely consistent. While in some cases major findings point to disconnection [e.g. Bluhm et al., 2007; Liang et al., 2006], other studies suggest the opposite [e.g., Jafri et al., 2008; Salvador et al., 2007], and in some instances, both disconnection and hyper‐connectivity are similarly related to the disease [e.g., Schlösser et al., 2003; Wolf et al., 2007]. To some extent, this heterogeneity in results is due to the usage of different cognitive tasks, involving different dynamics in different regions of the brain. In that sense, the increasingly common use of resting‐state fMRI may lead to more homogeneous connectivity results.

Here, we propose a new methodology, based on an exhaustive parcellation of the brain, which delivers general (overall) connectivity maps in a similar way to Salvador et al. [2008] but at the voxel level. The method is applied to explore differences in net levels of connectivity between a sample of patients with schizophrenia and a matched sample of controls scanned while being at rest. The method uses partial coherences as a main connectivity measure [Salvador et al., 2005a; Sun et al., 2004] and it controls for gross physiological noise.

METHODS

Subjects

Chronic patients with a diagnosis of schizophrenia according to DSM‐IV criteria were recruited from Benito Menni Hospital (Sant Boi, Barcelona, Spain). Inclusion criteria included right‐handedness, being intellectually preserved (WAIS III IQ > 85) and without reported alcohol/substance abuse within 12 months prior to participation. After rejection for excess of movement in the MRI scanner, a final sample of 40 patients (14 females and 26 males) with a mean age of 41.45 ± 12.9 (SD) years was used in the study.

All patients, but one, were taking antipsychotic medication (23 individuals had atypical neuroleptics, 3 subjects had typical neuroleptics and 13 had both). Doses ranged from 100 to 2,740 equiv of mg/day of chlorpromazine (median = 578, first and third quartiles = 300, 808). The duration of illness in the sample of patients ranged from 3 to 31 years (median = 20 years, first and third quartiles = 11, 24 years).

Healthy volunteers with no previous history of neurological or psychiatric illness were recruited by advertisement within the local community. Using the same inclusion/rejection criteria as in patients, a matched sample of 40 controls was finally available for the study [14 females and 26 males, with a mean age of 41.33 ± 13.08 (SD) years]. All participants gave written informed consent prior to involvement in accordance to the Declaration of Helsinki, and the research protocol was approved by the local ethics committee of the Benito Menni Hospital.

Image Acquisition and Pre‐processing

Each individual in the study underwent a single scanning session in which 266 volumes were acquired from a 1.5‐T GE Signa scanner, using a gradient echo echo‐planar (EPI) sequence depicting the blood‐oxygenation‐level‐dependent (BOLD) contrast. Each volume contained 16 axial planes acquired with the following parameters: TR = 2,000 ms, TE = 40 ms, flip angle = 70°, section thickness = 7 mm, section skip = 0.7 mm, in‐plane resolution = 3 mm × 3 mm. The first 10 volumes were discarded to avoid T1 saturation effects. Individuals were scanned while lying quietly (in a “resting state” condition). However, they were instructed to keep their eyes open to avoid high inter‐individual variability in self‐generated drowsiness or wakefulness states.

Several pre‐processing steps were carried out on the original images. Most of them used functions of the FSL software (reviewed in Smith et al. [2004]). The bet and mcflirt functions were applied for skull extraction and rigid‐body coregistration. To minimise movement artefacts, all individuals with an estimated maximum absolute movement over 3.0 mm, or an average absolute movement higher than 0.3 mm, were discarded from the study. In the remaining individuals, movement effects were reduced by fitting linear models to the time series of coregistered images. These models included the six movement parameters and their temporal differences (12 independent variables). Next, images were directly normalised to a reference standard brain image (flirt function) without any intermediate fitting to a structural high‐resolution image and were spatially smoothed with a Gaussian filter (SD = 3 mm [FWHM = 7 mm]). Finally, a binary mask based on the same standard brain was applied to the images. In the normalisation step, we used the T1 MNI template re‐sampled to 2 mm to perform an affine transformation with 12 degrees of freedom applying a correlation ratio cost function.

Characterisation of Gross Physiological Noise

MRI‐related artefacts and physiological noise account for a large part of the variance observed in fMRI time series [Huettel et al., 2004]. As shown through an example in Figure 1A, voxels with highest standard deviations are located in the edges of the brain, areas with large blood vessels and areas with CSF. Noise related to cardiac and respiratory processes induce cyclic patterns in different points of the brain, and its presence is usually analysed in the frequency domain. A frequency‐based principal component analysis [Brillinger, 1981] on the 6% of voxels with highest variances in the image of Figure 1A reveals very high levels of redundancy (Fig. 1B,C), suggesting strong coherence of gross noise in fMRI sequences, with possibly non‐synchronous dynamics.

Figure 1.

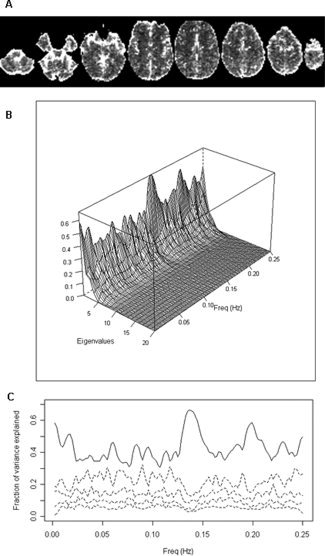
Figure 1

Open in a new tab

(A) Image of standard deviations from an fMRI sequence of a single individual. Highest variability is found at the edges of the brain, voxels including large blood vessels and voxels with CSF. (B) Proportion of variance explained by the largest eigenvalues from a principal component analysis in the frequency domain carried out on the 1,100 voxels (6% of voxels) with highest values in (A). Diagonalisation was performed on estimated coherence matrices. Variability is explained by a small number of components along the frequency spectrum, showing very high levels of redundancy. (C) 2D version of previous plot only showing the power spectra for the first principal component (solid line) and four following components (dashed lines).

To characterise the dynamics of this major noise, we visually explored the images of standard deviation of controls, looking for a subset of points with large variances but with low levels of redundancy. This selection process was made through several steps. First, standard deviation images for each healthy control were obtained from their normalised and spatially filtered volumes. Next, a single averaged standard deviation image was derived from all these individual images (Fig. 2A). From this image, an initial set of candidate points (voxels) containing local peaks (highest variances) was selected through visual inspection. Then, points with high levels of redundancy were sequentially discarded (redundancy was obtained by estimating multiple coherences between a point and the rest of the set in the time series of pre‐processed images). This led to the final selection of a group of five points located outside the brain parenchyma (Fig. 2A): (1) Superior sagittal sinus [MNI: 0,0,68], (2) Anterior cerebral artery [MNI: 0,30,12], (3) Cisterna superior [MNI: 0,−44,0], (4) Left Middle cerebral artery [MNI: −34,8,−22] and (5) Straight sinus [MNI: 0,−86,−16]. Time series of voxels located in these coordinates (one voxel per selected point) were extracted from the normalised and filtered fMRI volumes, and they were later used to reduce the contribution of gross noise in the covariability between brain areas (see next subsection). Averaged power spectra and coherence functions for the five selected points and the global brain time series are shown in Figure 2B,C.

Figure 2.

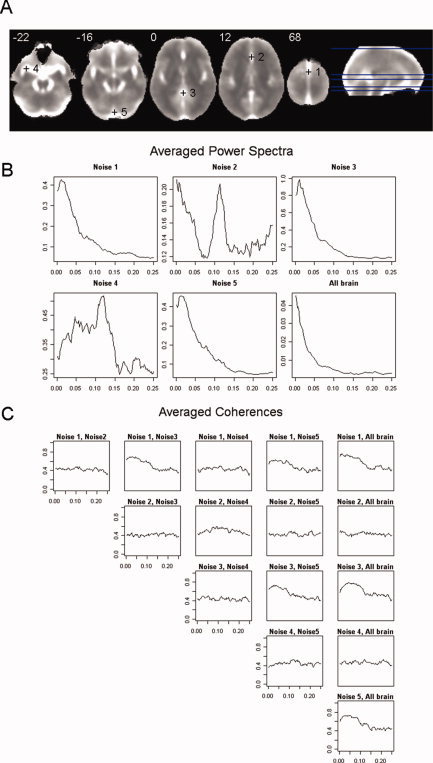
Figure 2

Open in a new tab

(A) Anatomical location of the five points finally chosen to characterise major physiological noise. The background image is an average of the individual standard deviation images taken from the normalised and filtered fMRI sequences from the healthy subjects. Left side of image is left side of brain. (B) Averages of power spectra for the five selected points and the global brain time series taken from the sample of healthy controls. (C) Averages of coherence functions between the time series of the five selected points and the global mean taken from the sample of controls. In both (B) and (C), frequencies are given in Hertz. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

ROI‐Based Partial Coherence Maps

Overall connectivity maps proposed here are based on averaging data from seed‐based connectivity maps from each one of the ROIs of an exhaustive parcellation of the brain. Instead of using standard seed correlation maps, though, we propose using partial coherence functions in the frequency domain. Specifically, given an average time series of a ROI, we estimated its partial coherence function in the frequency domain with each one of the voxels outside the ROI, using the set of time series with high variance, selected earlier, as nuisance covariates. All time series (including ROI mean time series) were extracted from the normalised and spatially filtered volumes.

Formally, given a time series from a ROI (X(t)ROI), a time series from a voxel (X(t)voxel) and a vector of time series with high variance (X(t)noise), the partial coherence between the first two, given the later, at frequency λ, is [Brillinger, 1981]

equation image (1)

where f(X ROI, X voxel|X noise)[λ] is the partial cross‐spectrum of (X(t)ROI) and (X(t)voxel) after removing the linear effects of (X(t)noise), and both f(X ROI|X noise)[λ] and f(X voxel|X noise)[λ] are partial spectrums conditioned for the same noise (see Dahlhaus [2000] for a definition of partial cross‐spectrums in terms of linear predictors). An examination of Eq. (1) reveals the analogy between partial coherences and partial correlations. However, partial coherences are complex quantities, containing information on both intensity and phase, and their modulus (a non‐negative value in the [0,1] interval) is usually reported instead. An alternative formula for Eq. (1) is given in Sun et al. [2004].

Inference on partial coherences is based on non‐parametric estimates of the cross‐spectral density matrices [matrices containing the estimates of the cross‐spectrums for all pairs of time series involved in Eq. (1)]. Obtaining these matrices from time series of the normalised and filtered images require several steps (Fig. 3A contains an example where intermediate results for each of these steps are shown). First, (1) time series were standardised (divided by their sample standard deviation) to reduce numerical inaccuracies in later calculations. Next, (2) a Bartlett window was applied to all time series to reduce leakage, and (3) a FFT algorithm was used, without any further re‐sampling, to obtain their Fourier coefficients. Then, (4) an initial estimate of the cross‐spectrum between each pair of time series was obtained by multiplying the Fourier coefficients at each Fourier frequency. And, finally, (5) a computationally efficient estimate of the cross‐spectrum was derived by averaging the previous estimates over a range of frequencies [Shumway and Stoffer, 2000] (here, we took averages over 10 Fourier frequencies).

Figure 3.

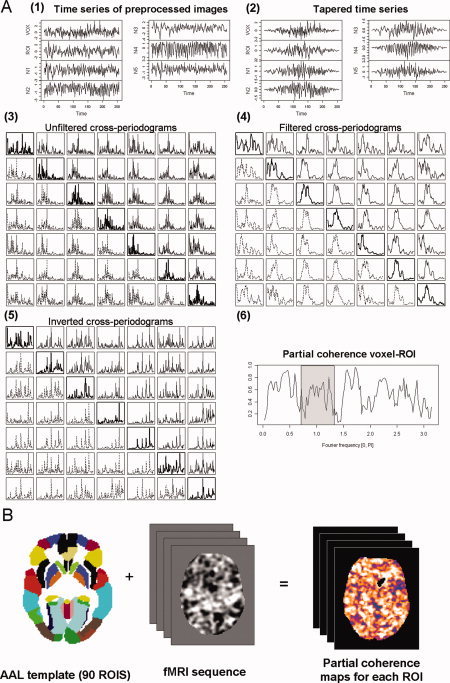
Figure 3

Open in a new tab

(A) Example showing the intermediate results from the calculations of the partial coherence between the mean time series of a ROI (left caudate) and a single voxel in the right frontal gyrus in a healthy control. (1) Extracted time series for the voxel, ROI, and five points with gross physiological noise. (2) The same time series after applying the Bartlett taper. (3) Cross‐periodograms obtained by multiplying the Fourier coefficients from a FFT applied on the tapered time series. (4) Cross‐periodograms after filtering with a simple mean filter. (5) Output from the inversion of the matrices containing the values of the filtered cross‐periodograms at each Fourier frequency. (6) Modulus of the partial coherence function obtained through Eq. (2) (main text) using data from the inverted matrices. Usually, an average of this function over a frequency band (grey window) will be finally stored. (B) All these steps will be performed for each of the 90 ROIs of the AAL template and on all voxels of the fMRI time series, leading to 90 partial coherence maps (one for each ROI). These maps will be eventually averaged to obtain the overall connectivity map for the individual. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Now, if we define X(t) as {X(t)ROI, X(t)voxel, X(t)noise}, 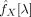Inline graphic as the estimate of the spectral density matrix of X(t) at frequency λ and 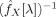Inline graphic as its inverse, we can estimate the partial coherence between X(t)ROI and X(t)voxel through [Dahlhaus, 2000]

equation image (2)

where numerical sub‐indices point to different elements in 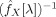Inline graphic, which in turn relate to the order of the elements in X(t) (1: X(t)ROI, 2: X(t)voxel).

We focused on the modulus of the estimates given by Eq. (2), which quantified intensity of covariability of X(t)ROI and X(t)voxel. A variance stabilising tanh−1 transformation [Brillinger, 1981] was applied when performing parametric tests at the group level.

The inversion of 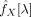Inline graphic is the most sensitive step in the inference of partial coherences. The quality of estimates will strongly depend on the absence of redundancies before inverting matrices. While moderate levels of redundancy will lead to valid but inaccurate (high variance) estimates, strong collinearity will deliver invalid and meaningless values (the matrix may not even be invertible). Special care should be taken in the selection of points with large physiological noise (see previous subsection) and in the spatial filtering of normalised images, as both steps may lead to unacceptable levels of redundancy in 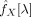Inline graphic. If an excess of spatial filtering in the normalised images is the major cause of redundancy, one can alternatively use a filter over the maps of estimated partial coherences. This will have the additional benefit of improving these estimates by reducing their variance [we applied a second Gaussian filter (SD = 3 mm) on the partial coherence images to reduce their noise]. Furthermore, before each matrix inversion, we performed a diagonalisation of 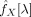Inline graphic and monitored collinearity levels with the ratio between the largest and smallest eigenvalues. A maximum value of 106 was used as a threshold for this ratio in all matrices, but this threshold was hardly ever reached.

Following the trend in resting‐state studies, we focused on connectivity patterns in the low frequencies [0.1–0.025 Hz], and we summarised partial coherence functions by taking averages on estimates in this frequency band. All computational steps explained in this section were performed with self‐written C programs, which made use of functions from the GNU scientific library (http://www.gnu.org/software/gsl/) for the diagonalisation and inversion of complex matrices.

Overall Connectivity Maps

Using the procedures described earlier, we obtained ROI‐based partial coherence images, at the individual level, for the 90 regions included in the AAL template (Fig. 3B). The AAL template divides each cerebral hemisphere into 45 anatomical regions of different sizes, including both grey mater cortical areas and subcortical nuclei, in a way that each region in one hemisphere has its homologous region in the other hemisphere (see Tzourio‐Mazoyer et al. [2002] for a detailed description of this template and the regions involved).

Next, we averaged these images for all the ROIs, producing whole brain net (overall) connectivity maps for every individual. Each voxel in these maps contained mean values of connectivity with the remaining 89 regions (i.e., excluding the region where the voxel was located, as we did not consider connectivity values between a ROI and each voxel within it). Voxels not located inside any ROI (e.g., white matter voxels) reported averages of connectivity from all 90 regions.

Group Analysis on Overall Maps and Second‐Level ROI Analyses

Overall connectivity maps for the 40 patients with schizophrenia were compared with overall maps from the matched sample of controls by means of standard linear models. Cluster‐based Gaussian random field methods available as part of the FSL software (smoothest and cluster tools) were applied to deliver maps of significant differences with a threshold of P = 0.05 corrected and a z of 2.5 to create the initial clusters. These maps showed areas where patients had abnormal levels of net connectivity (either disconnection or hyper‐connectivity). Clusters found to be significantly different between both groups were used as ROIs in a second‐level comparison (using the same P = 0.05 threshold but a more restrictive z of 3.8). This comparison reported on more specific abnormalities in connectivity patterns.

Finally, to evaluate the possible effects of medication or duration of illness on the overall connectivity maps, we fitted two regression models on the sample of 40 patients. One of them used chlorpromazine equivalents as the independent variable, and the other model used years of illness. Here, we applied the same threshold value of z = 2.5 but a less conservative P‐value of 0.1 to generate maps with brain areas showing significant correlations with both confounding variables.

RESULTS

A general view of overall connectivity maps is given in Figure 4. These show diffuse patterns of higher net connectivity in cortical regions, including the insula, and in some subcortical structures such as the thalami, whereas areas with lower values are usually found in white matter regions and ventricles. Reported connectivities are based on the modulus of estimated partial coherences, which are always positive. Hence, all values of overall connectivity are positive.

Figure 4.

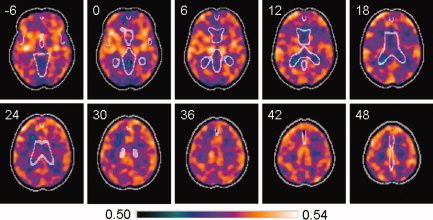
Figure 4

Open in a new tab

Averaged image of overall connectivity maps from a sample of 40 healthy controls, based on partial coherences in the [0.1–0.025 Hz] interval. Areas with higher net values of connectivity (shown in orange) are largely located in the cortex and other grey matter structures, whereas low connectivity (shown in blue) is generally found in white matter. A mask with CSF boundaries is shown in light grey. The z MNI coordinates are given for each slice. Left side of the image is left side of the brain. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

When the comparison in overall connectivity between patients with schizophrenia and controls was performed, a single cluster of increased connectivity (hyper‐connectivity) was found in patients (Fig. 5). This cluster included, bilaterally, frontomedial regions and parts of the anterior cingulate. It then stretched down on the right side to orbitofrontal areas, the anterior insula and ventral amygdala. Cluster peak differences in net connectivity were found in MNI coordinates (20, 18, −16; max z = 3.54) inside Brodmann area (BA) 11, with a probability of 0.00485 for the whole cluster. At these coordinates, the observed mean difference in overall connectivity between patients and controls was 0.0281.

Figure 5.

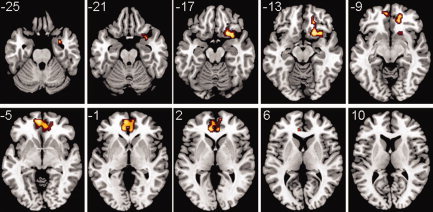
Figure 5

Open in a new tab

When comparing overall connectivity maps between patients with schizophrenia and controls, a single cluster of hyper‐connectivity is found in the patients. This cluster contains regions within the anterior node of the default mode network and other right ventral structures (orbitofrontal cortex, anterior insula and ventral amygdala). Overall connectivities were estimated in the [0.1–0.025 Hz] interval, and a corrected P = 0.05 threshold was used in the statistical analyses. The z MNI coordinates are given for each slice. Left side of the image is left side of the brain. A T1 template was used as a background. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

A second‐level connectivity analysis, taking the previous cluster as a ROI, found abnormally increased connectivity of this cluster with several cortical and subcortical regions (Fig. 6). Interestingly, strongest hyper‐connectivity was found with the left caudate nucleus (peak difference in [−16, 12, 8; max z = 4.8], cluster P = 0.00247, mean difference in partial coherences (pcoh) at peak = 0.0861), reaching the anterior left putamen. This abnormality was bilateral, as it was also found in the right caudate (peak difference in [10, 14, 0; max z = 4.32], cluster P = 0.0175, mean difference in pcoh at peak = 0.0789).

Figure 6.

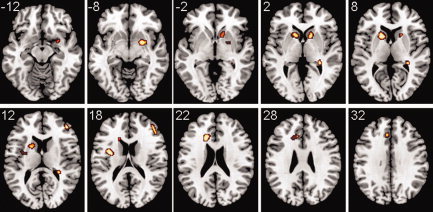
Figure 6

Open in a new tab

Images showing areas that had a significantly anomalous connectivity with the cluster in Figure 5 (which was taken as a ROI in a second‐level analysis). All regions were hyper‐connected in the patients. Abnormalities involved several subcortical structures; most notably the caudate bilaterally, parts of both left and right putamens, and right pallidum, amygdala and posterior hippocampus. Cortical hyper‐connected areas were found in the left insula, left dorsal anterior cingulate and right dorsolateral prefrontal cortex. Partial coherences were estimated in the [0.1–0.025 Hz] interval, and a corrected P = 0.05 threshold was used in the statistical analyses. The z MNI coordinates are given for each slice. Left side of the image is left side of the brain. A T1 template was used as a background. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

A third cluster with abnormally high connectivity with the area of Figure 5 included sections of the right putamen, pallidum and dorsal amygdala (coordinates of peak [22, 2, −8; max z = 4.58], cluster P = 0.0193, mean difference in pcoh at peak = 0.0793), and another one was located in the right posterior hippocampus (coordinates of peak [30, −34, 2; max z = 4.59], cluster P = 0.0327, mean difference in pcoh at peak = 0.0594).

Finally, three other hyper‐connected clusters included cortical areas. One small cluster was found in the right dorsolateral prefrontal cortex (peak difference in [44, 44, 14; max z = 4.6], BA45, cluster P = 0.0295, mean difference in pcoh at peak = 0.0804), another in the left dorsal anterior cingulate and neighbouring white matter (coordinates of peak [−16, 24, 22; max z = 4.61], cluster P = 0.0064, mean difference in pcoh at peak = 0.0816) and yet another in the left insula, reaching parts of the left putamen (coordinates of peak [−34, −2, 18; max z = 4.86], BA48, cluster P = 0.0205, mean difference in pcoh at peak = 0.0664).

The two regression analyses performed on the overall connectivity maps of patients, assessing the potential effect of medication dose and of duration of illness, did not report any significant cluster.

DISCUSSION

Overall connectivity maps for the whole brain have been derived through a new method that combines connectivity values of ROIs from a comprehensive parcellation of the brain. Although the method shares the same objective and has some similarities with the technique previously proposed in Salvador et al. [2008], it delivers global maps at the voxel level and it minimises the effect of gross physiological fluctuations.

When the method was applied to explore differences in net levels of connectivity between patients with schizophrenia and healthy controls scanned while being at rest, a single area of anomalous hyper‐connectivity was found in medial and orbital parts of the frontal cortex. Strikingly, this area overlaps with the anterior node of the DMN, bringing new evidence of the implication of this network in schizophrenia. Although other studies have found abnormal functional connectivity in this anatomical area [e.g., Bluhm et al., 2007; Garrity et al., 2007; Whitfield‐Gabrieli et al., 2009], many of them were set to look for specific differences in the DMN. In that sense, the strength of our work relies on the global, non‐directed nature of findings through the overall connectivity maps.

A second‐level analysis using this abnormal area as a ROI found anomalous hyper‐connectivity with several cortical and subcortical structures. Most remarkably, both caudate nuclei showed substantial hyper‐connection with the medial orbital prefrontal cortex in patients. This result gives further support to previous hypotheses of schizophrenia including the striatum [e.g., Robbins, 1990; Andreasen, 1999], but it would mainly suggest a DMN–basal ganglia hyper‐connection as a major disturbance in the disease. In that sense, an abnormal functioning of the cortico‐striato‐thalamic loop involving medial and ventral frontal regions could explain, non‐motor, cognitive deficits observed in patients. In relation to this, our reported fronto‐striatal alteration could be underlying the previously described ‘failure to deactivate’ of the anterior node of the DMN in working memory tasks [Pomarol‐Clotet et al., 2008; Whitfield‐Gabrieli et al., 2009]. However, beyond this central basal ganglia–DMN abnormality, hyper‐connectivity found with right hippocampus, amygdala and other cortical regions would point to a more pervasive alteration of brain connectivity in schizophrenia.

On the other hand, though, the coarse temporal and spatial resolutions of fMRI sequences do not bring much information on the direct mechanistic processes underlying the observed abnormalities, and we can only make suggestions, on this subject, based on other data. Possibly, structural alteration on any of the components of the fronto‐striatal circuit might have triggered these differences in connectivity. In that sense, converging evidence on grey matter volume changes in medial frontal regions [see reviews by Glahn et al., 2008; Honea et al., 2005; Ellison‐Wright et al., 2008] would point to these areas as potential primary loci of alteration. Still, structural anomalies in other regions of the brain, including white matter tracts, could also lay behind the reported findings. Alternatively, our results may be the consequence of dysregulation in related brain systems such as the dopaminergic pathways, which involve small midbrain nuclei and have connections to the basal ganglia and cortical structures. Dysfunction in these dopamine synaptic connections has long been proposed as one possible primary cause of the disease (see, for instance, the recent review by Howes and Kapur [2009]).

While the resting‐state condition analysed here may be seen as too ambiguous [Morcom and Fletcher, 2007], finding consistent patterns of abnormality in schizophrenia at rest may lead to a more straightforward characterisation of this pathology, avoiding problems related to task specification and differential performance. We should acknowledge, however, that proving the neural nature of connectivity patterns found in resting‐state studies is a complex task, requiring supplementary work from other modalities and techniques. Yet, this is a weakness shared as well with more standard fMRI studies [Sirotin and Das, 2009].

Results found in the comparison between patients and controls may have been influenced by other clinical factors than illness itself. Some previous studies point to changes in volume of brain structures with antipsychotic medication, specially the basal ganglia [e.g., Chakos et al., 1994; Corson et al., 1999; Lieberman et al., 2005] possibly leading to changes in connectivity patterns as well. Other studies, though, find that if present, structural changes are of a less extent than those linked to the evolution of disease (see review of Hulshoff and Kahn [2008]). Indeed, duration of illness and chronicity are other aspects that have been related to brain changes in schizophrenia [e.g., Lappin et al., 2006; Takahashi et al., 2007].

Here, we failed to find any significant relation between neuroleptic dose (given in chlorpromazine equivalents), illness duration and the proposed overall connectivity measure. Both confounding variables were analysed on a reasonably big sample (40 patients), having a significant amount of variability (with a range of 100 to 2,740 mg/day for medication and 3 to 31 years for illness duration) and using a rather permissive P‐value of 0.1. Hence, negative results found here would not suggest a primary role of these two confounding variables on shaping overall connectivity levels. However, future studies on unmedicated patients and on first‐episode cases may be needed to ratify our current results.

The connectivity methods described here are based on association measures in the frequency domain (mainly coherences and partial coherences). Such measures may be seen as extensions of the more usual correlations or partial correlations [e.g., Biswal et al., 1995, Fox et al., 2006; Salvador et al., 2005b], and they are natural alternatives for these standard methods when applied with predefined seeds or ROIs. Conversely, instead of using partial coherences, in this study we could have averaged standard correlation or partial correlation maps of all regions of the parcellation to obtain a simplified version of the overall connectivity maps.

Yet, we have chosen to use frequency domain measures for several reasons. On one hand, the dynamics of different sources of physiological noise (mainly respiration and heart pulses) are better characterised in this domain. Furthermore, apart from the possibility of describing time dynamics at different scales (i.e., at various frequency bands), frequency based measures of association allow quantifying non‐instantaneous relations. Most crucially, what in standard analyses are described as positive or negative correlations appear as just two specific cases in a continuum of possibly non‐synchronous dynamics. In that sense, although the information relating to the phase may be relevant to understand the nature of the relations studied, the primary interest of a connectivity analysis performed in the frequency domain will be on the modulus of (partial) coherences. The modulus quantifies the levels of covariability between time series regardless of their phase.

As shown by recent research on the spatiotemporal dynamics of the BOLD signal in rodents [Majeed et al., 2009], both low‐frequency cortical propagating waves and physiological noise lead to dephased time signals in different areas of the brain. While such non‐synchronous relations will be hardly detected or just plainly missed by standard association measures like correlations, frequency‐based association measures may describe them adequately.

Values reported in overall connectivity maps, though, will depend in some degree on the parcellation used. The boundaries of each region in the template and its relative size will condition its weight on the connectivity measure. In previous works [Salvador et al., 2007, 2008], we already described biases in connectivity due to size and number of regions considered. However, the fact that results are now reported at the voxel level and that calculations for each voxel are based on the same ROIs will avoid the spatial inconsistencies described previously. Further analyses comparing outcomes from different whole brain parcellations (in a similar way to Wang et al. [2009]) may help in evaluating the sensitivity of the method. Additional work may explore, as well, connectivity levels in frequency bands other than the 0.1–0.025 Hz interval, or the selection of new points of high variance for a better characterisation of physiological noise.

Finally, it should be recalled that, in essence, the overall measure proposed here is an arithmetic mean. Hence, it only reports on net or averaged levels of connectivity, being non‐informative on the specific connections involved (a second‐level analysis as the one carried out in this study will be required to obtain such information). In that sense, it is possible to find similar values of overall connectivity concealing significant differences in regional connectivity patterns, just because on average they level off. However, devising an alternative scalar measure, which could both summarise mean levels of connectivity and disambiguate these differences, seems challenging.

CONCLUSIONS

In summary, we have derived overall connectivity maps for the whole brain through a new method that combines connectivity values of ROIs from an exhaustive parcellation of the brain. The main results obtained from applying this new methodology on a sample of patients with schizophrenia suggest a model for the disease where malfunction in the anterior node of the DMN would be linked to a subcortical abnormality. More specifically, the outcome of this study would give further support for a fronto‐striatal hypothesis of schizophrenia. However, significant results found in other areas would indicate a more pervasive alteration of brain connectivity in this pathology. New studies with first episode and drug free patients will be needed to consolidate the findings.

REFERENCES

  1. Andreasen NC ( 1999): A unitary model of schizophrenia: Bleuler's “fragmented phrene” as schizencephaly. Arch Gen Psychiatry 56: 781–787. [DOI] [PubMed] [Google Scholar]
  2. Biswal B, Yetkin FZ, Haughton VM, Hyde JS ( 1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magn Reson Med 34: 537–541. [DOI] [PubMed] [Google Scholar]
  3. Bluhm RL, Miller J, Lanius RA, Osuch EA, Boksman K, Neufeld RW, Théberge J, Schaefer B, Williamson P ( 2007): Spontaneous low‐frequency fluctuations in the BOLD signal in schizophrenic patients: Anomalies in the default network. Schizophr Bull 33: 1004–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bleuler E ( 1911): Dementia praecox oder Gruppe der Schizophrenien. Leipzig und Wien: F. Deuticke. [Google Scholar]
  5. Brillinger DR ( 1981): Time Series Data Analysis and Theory. San Francisco: Holden Day; 540 p. [Google Scholar]
  6. Bullmore ET, Frangou S, Murray RM ( 1997): The dysplastic net hypothesis: An integration of developmental and dysconnectivity models of schizophrenia. Schizophr Res 28: 143–156. [DOI] [PubMed] [Google Scholar]
  7. Chakos MH, Lieberman JA, Bilder RM, Borenstein M, Lerner G, Bogerts B, Wu H, Kinon B, Ashtari M ( 1994): Increase in caudate nuclei volumes of first‐episode schizophrenic patients taking antipsychotic drugs. Am J Psychiatry 151: 1430–1436. [DOI] [PubMed] [Google Scholar]
  8. Corson PW, Nopoulos P, Miller DD, Arndt S, Andreasen NC ( 1999): Change in basal ganglia volume over 2 years in patients with schizophrenia: Typical versus atypical neuroleptics. Am J Psychiatry 156: 1200–1204. [DOI] [PubMed] [Google Scholar]
  9. Dahlhaus R ( 2000): Graphical interaction models for multivariate time series. Metrika 51: 157–172. [Google Scholar]
  10. Demirci O, Stevens MC, Andreasen NC, Michael A, Liu J, White T, Pearlson GD, Clark VP, Calhoun VD ( 2009): Investigation of relationships between fMRI brain networks in the spectral domain using ICA and Granger causality reveals distinct differences between schizophrenia patients and healthy controls. Neuroimage 46: 419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ellison‐Wright I, Glahn DC, Laird AR, Thelen SM, Bullmore E ( 2008): The anatomy of first‐episode and chronic schizophrenia: An anatomical likelihood estimation meta‐analysis. Am J Psychiatry 165: 1015–1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Foucher JR, Vidailhet P, Chanraud S, Gounot D, Grucker D, Pins D, Damsa C, Danion JM ( 2005): Functional integration in schizophrenia: Too little or too much? Preliminary results on fMRI data. Neuroimage 26: 374–388. [DOI] [PubMed] [Google Scholar]
  13. Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME ( 2006): Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc Natl Acad Sci USA 103: 10046–10051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Friston KJ, Frith CD ( 1995): Schizophrenia: A disconnection syndrome? Clin Neurosci 3: 89–97. [PubMed] [Google Scholar]
  15. Frith CD ( 1992): The Cognitive Neuropsychology of Schizophrenia. Hove, Erlbaum (UK): Taylor & Francis; 163 p. [Google Scholar]
  16. Garrity AG, Pearlson GD, McKiernan K, Lloyd D, Kiehl KA, Calhoun VD ( 2007): Aberrant “default mode” functional connectivity in schizophrenia. Am J Psychiatry 164: 450–457. [DOI] [PubMed] [Google Scholar]
  17. Glahn DC, Laird AR, Ellison‐Wright I, Thelen SM, Robinson JL, Lancaster JL, Bullmore E, Fox PT ( 2008): Meta‐analysis of gray matter anomalies in schizophrenia: Application of anatomic likelihood estimation and network analysis. Biol Psychiatry 64: 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gray JA, Feldon J, Rawlins JNP, Hemsley DR, Smith AD ( 1991): The neuropsychology of schizophrenia. Behav Brain Sci 14: 1–20. [Google Scholar]
  19. Greicius MD, Krasnow B, Reiss AL, Menon V ( 2003): Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proc Natl Acad Sci USA 100: 253–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Honea R, Crow TJ, Passingham D, Mackay CE ( 2005): Regional deficits in brain volume in schizophrenia: A meta‐analysis of voxel‐based morphometry studies. Am J Psychiatry 162: 2233–2245. [DOI] [PubMed] [Google Scholar]
  21. Howes OD, Kapur S ( 2009): The dopamine hypothesis of schizophrenia: Version III—The final common pathway. Schizophr Bull 35: 549–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Huettel SA, Song AW, McCarthy G ( 2004): Functional Magnetic Resonance Imaging. Sunderland, Massachusetts: Sinauer; 492 p. [Google Scholar]
  23. Hulshoff Pol HE, Kahn RS ( 2008): What happens after the first episode? A review of progressive brain changes in chronically ill patients with schizophrenia. Schizophr Bull 34: 354–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jafri MJ, Pearlson GD, Stevens M, Calhoun VD ( 2008): A method for functional network connectivity among spatially independent resting‐state components in schizophrenia. Neuroimage 39: 1666–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kim DI, Mathalon DH, Ford JM, Mannell M, Turner JA, Brown GG, Belger A, Gollub R, Lauriello J, Wible C, O'Leary D, Lim K, Toga A, Potkin SG, Birn F, Calhoun VD ( 2009): Auditory oddball deficits in schizophrenia: An independent component analysis of the fMRI multisite function BIRN study. Schizophr Bull 35: 67–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lappin JM, Morgan K, Morgan C, Hutchison G, Chitnis X, Suckling J, Fearon P, McGuire PK, Jones PB, Leff J, Murray RM, Dazzan P ( 2006): Gray matter abnormalities associated with duration of untreated psychosis. Schizophr Res 83: 145–153. [DOI] [PubMed] [Google Scholar]
  27. Lawrie SM, Buechel C, Whalley HC, Frith CD, Friston KJ, Johnstone EC ( 2002): Reduced frontotemporal functional connectivity in schizophrenia associated with auditory hallucinations. Biol Psychiatry 51: 1008–1011. [DOI] [PubMed] [Google Scholar]
  28. Liang M, Zhou Y, Jiang T, Liu Z, Tian L, Liu H, Hao Y ( 2006): Widespread functional disconnectivity in schizophrenia with resting‐state functional magnetic resonance imaging. Neuroreport 17: 209–213. [DOI] [PubMed] [Google Scholar]
  29. Liddle PF ( 2001): Disordered Mind and Brain. London: Gaskell; 301 p. [Google Scholar]
  30. Lieberman JA, Tollefson GD, Charles C, Zipursky R, Sharma T, Kahn RS, Keefe RS, Green AI, Gur RE, McEvoy J, Perkins D, Hamer RM, Gu H, Tohen M ( 2005): Antipsychotic drug effects on brain morphology in first‐episode psychosis. Arch Gen Psychiatry 62: 361–370. [DOI] [PubMed] [Google Scholar]
  31. Liu Y, Liang M, Zhou Y, He Y, Hao Y, Song M, Yu C, Liu H, Liu Z, Jiang T ( 2008): Disrupted small‐world networks in schizophrenia. Brain 131: 945–961. [DOI] [PubMed] [Google Scholar]
  32. Majeed W, Magnuson M, Keilholz SD ( 2009): Spatiotemporal dynamics of low frequency fluctuations in BOLD fMRI of the rat. J Magn Reson Imaging 30: 384–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Mazoyer B, Zago L, Mellet E, Bricogne S, Etard O, Houdé O, Crivello F, Joliot M, Petit L, Tzourio‐Mazoyer N ( 2001): Cortical networks for working memory and executive functions sustain the conscious resting state in man. Brain Res Bull 54: 287–298. [DOI] [PubMed] [Google Scholar]
  34. Menon V, Anagnoson RT, Glover GH, Pfefferbaum A ( 2001): Functional magnetic resonance imaging evidence for disrupted basal ganglia function in schizophrenia. Am J Psychiatry 158: 646–649. [DOI] [PubMed] [Google Scholar]
  35. Morcom AM, Fletcher PC ( 2007): Does the brain have a baseline? Why we should be resisting a rest. Neuroimage 37: 1073–1082. [DOI] [PubMed] [Google Scholar]
  36. Pomarol‐Clotet E, Salvador R, Sarró S, Gomar J, Vila F, Martínez A, Guerrero A, Ortiz‐Gil J, Sans‐Sansa B, Capdevila A, Cebamanos JM, McKenna PJ ( 2008): Failure to deactivate in the prefrontal cortex in schizophrenia: Dysfunction of the default mode network? Psychol Med 38: 1185–1193. [DOI] [PubMed] [Google Scholar]
  37. Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL ( 2001): A default mode of brain function. Proc Natl Acad Sci USA 98: 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Robbins TW ( 1990): The case of frontostriatal dysfunction in schizophrenia. Schizophr Bull 16: 391–402. [DOI] [PubMed] [Google Scholar]
  39. Salvador R, Suckling J, Schwarzbauer C, Bullmore E ( 2005a) Undirected graphs of frequency‐dependent functional connectivity in whole brain networks. Philos Trans R Soc Lond B Biol Sci 360: 937–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Salvador R, Suckling J, Coleman MR, Pickard JD, Menon D, Bullmore E ( 2005b) Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb Cortex 15: 1332–1342. [DOI] [PubMed] [Google Scholar]
  41. Salvador R, Martínez A, Pomarol‐Clotet E, Sarró S, Suckling J, Bullmore E ( 2007): Frequency based mutual information measures between clusters of brain regions in functional magnetic resonance imaging. Neuroimage 35: 83–88. [DOI] [PubMed] [Google Scholar]
  42. Salvador R, Martínez A, Pomarol‐Clotet E, Gomar J, Vila F, Sarró S, Capdevila A, Bullmore E ( 2008): A simple view of the brain through a frequency‐specific functional connectivity measure. Neuroimage 39: 279–289. [DOI] [PubMed] [Google Scholar]
  43. Schlösser R, Gesierich T, Kaufmann B, Vucurevic G, Hunsche S, Gawehn J, Stoeter P ( 2003): Altered effective connectivity during working memory performance in schizophrenia: A study with fMRI and structural equation modeling. Neuroimage 19: 751–763. [DOI] [PubMed] [Google Scholar]
  44. Shumway H, Stoffer DS ( 2000): Time Series Analysis and Its Applications. New York: Springer; 549 p. [Google Scholar]
  45. Sirotin YB, Das A ( 2009): Anticipatory haemodynamic signals in sensory cortex not predicted by local neuronal activity. Nature 457: 475–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen‐Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy R, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM ( 2004): Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23 ( Suppl 1): 208–219. [DOI] [PubMed] [Google Scholar]
  47. Sun FT, Miller LM, D'Esposito M ( 2004): Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. Neuroimage 21: 647–658. [DOI] [PubMed] [Google Scholar]
  48. Takahashi T, Suzuki M, Tanino R, Zhou SY, Hagino H, Niu L, Kawasaki Y, Seto H, Kurachi M ( 2007): Volume reduction of the left planum temporale gray matter associated with long duration of untreated psychosis in schizophrenia: A preliminary report. Psychiatry Res 154: 209–219. [DOI] [PubMed] [Google Scholar]
  49. Tzourio‐Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M ( 2002): Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single‐subject brain. Neuroimage 15: 273–289. [DOI] [PubMed] [Google Scholar]
  50. Wang J, Wang L, Zang Y, Yang H, Tang H, Gong Q, Chen Z, Zhu C, He Y ( 2009): Parcellation‐dependent small‐world brain functional networks: A resting‐state fMRI study. Hum Brain Mapp 30: 1511–1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Weinberger DR, Lipska BK ( 1995): Cortical maldevelopment, anti‐psychotic drugs, and schizophrenia: A search for common ground. Schizophr Res 16: 87–110. [DOI] [PubMed] [Google Scholar]
  52. Whitfield‐Gabrieli S, Thermenos HW, Milanovic S, Tsuang MT, Faraone SV, McCarley RW, Shenton ME, Green AI, Nieto‐Castanon A, LaViolette P, Wojcik J, Gabrieli JD, Seidman LJ ( 2009): Hyperactivity and hyperconnectivity of the default network in schizophrenia and in first‐degree relatives of persons with schizophrenia. Proc Natl Acad Sci USA 106: 1279–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Wolf DH, Gur RC, Valdez JN, Loughead J, Elliott MA, Gur RE, Ragland JD ( 2007): Alterations of fronto‐temporal connectivity during word encoding in schizophrenia. Psychiatry Res 154: 221–232. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES