Abstract
After errors in reaction tasks, a sharp negative wave emerges in the event‐related potential (ERP), the error (related) negativity (Ne or ERN). However, also after correct trials, an Ne‐like wave is seen, called CRN or Nc, which is much smaller than the Ne. This study tested the hypothesis whether Ne and Nc reflect the same functional process, and whether this process is linked to online response control. For this purpose, independent component analysis (ICA) was utilized with the EEG data of two types of reaction tasks: a flanker task and a mental rotation task. To control for speed‐accuracy effects, speed and accuracy instructions were balanced in a between subjects design. For both tasks ICA and dipole analysis revealed one component (Ne‐IC) explaining most of the variance for the difference between correct and erroneous trials. The Ne‐IC showed virtually the same features as the raw postresponse ERP, being larger for erroneous compared to correct trials and for the flanker than for the rotation task. In addition, it peaked earlier for corrected than for uncorrected errors. The results favor the hypothesis that Ne and Nc reflect the same process, which is modulated by response correctness and type of task. On the basis of the literature and the present results, we assume that this process induces online response control, which is much stronger in error than correct trials and with direct rather than indirect stimulus response mapping. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.
Keywords: ICA, EEG, errors, error processing, executive functions, response monitoring
INTRODUCTION
The efficiency in monitoring action and adapting to erroneous operations is a unique human ability. Already Rabbit [ 1966] showed that participants in reaction time tasks immediately notice their erroneous reaction and initiate adaptive strategies such as corrective movements, decrease of response time in subsequent trials (“post‐error slowing”), and the reduction of error probability in subsequent trials. From these strategies, an adaptive system for the control and monitoring of (re‐)actions was inferred. The first evidence for a neural correlate of such a system came from EEG studies. Errors in simple reaction choice task (“slips”) provoke a typical event‐related potential (ERP): the “error negativity” [Ne, Falkenstein et al., 1990] or “error‐related negativity” [ERN, Gehring et al., 1993]. The maximum negative deflection of the Ne occurs about 60 ms following an erroneous response at medial fronto‐central electrode positions (FCz). It is possible that the Ne is not constituted by a unitary source but rather reflects a compound of several CNS processes. This is supported by the observation that the major sources of the Ne are located in the anterior cingulate (ACC) and/or the supplemental motor cortex (SMA) [Dehaene et al., 1994; Ullsperger and von Cramon, 2001; Vidal et al., 2000]. Furthermore, in studies utilizing intracranial recordings [Brazdil et al., 2002] or fMRT [O'Connell et al., 2007] additional sources of the Ne could be described. However, beside its physiological origins, there exist several hypotheses with respect to its functional significance.
The “mismatch hypothesis” [Falkenstein et al., 1990, 1991, 2000; Gehring et al., 1993; Scheffers et al., 1996] assumed that the neural representations of the initiated and demanded reaction are compared. As a consequence, a mismatch of both representations provokes a Ne. Holroyd and Coles [ 2002] proposed an extension of this hypothesis assuming a general Ne activation if the outcome of an event is worse than expected. In this model, the signal initiates remedial actions, i.e. measures are taken to control and avoid errors. Another theory, the “conflict hypothesis” [Botvinick et al., 2001; Carter et al., 1998; van Veen and Carter, 2002] assumes that the Ne results from a conflict of representations of responses that overlap in time.
However, there exists some agreement between the different positions, that the essential functional relevance of the Ne may be the initiation of control following or during an erroneous action [Ridderinkhof et al., 2004]. This control obviously affects posterror trials [Debener et al., 2005; Rabbitt, 1966], which stresses the role of the Ne for online response control. It is not entirely clear whether the amplitude or latency of the Ne reflect a correlate of such a control. The data of Gehring et al. [ 1993] and Debener et al. [ 2005] suggest that the Ne‐amplitude corresponds to a certain degree with the strength of control in subsequent reactions. However, Hajcak et al. [ 2003] did not find such relation for the Ne but for the error positivity (Pe), which is an error specific potential with a parietal maximum. As to online control, Gehring et al. [ 1993] showed an inverse relationship between the force of the actual erroneous key press and the amplitude of the Ne. More recently, Masaki and Segalowitz [ 2004] found an earlier and smaller Ne in subliminal compared to full errors. This was supported by the findings of Carbonnell and Falkenstein [ 2006] who found the Ne to start and peak earlier for partial than full errors, whereas the amplitude was the same for both. Taken together these findings indicate relevance at least of the Ne‐latency for actual, i.e. online, control: in conditions with partial errors (possibly inhibited errors), the Ne occurs very early. A certain methodological problem in those studies is that the Ne was measured in the averages, which may induce variance due to different latency jitter in the different conditions. To bypass this problem the statistical comparisons of amplitude measures are not based on comparing peaks of averages but rather averages of single‐trials peaks.
In this study, we want to address the control issue by focusing on error correction. More specifically, we want to assess Ne differences between corrected (more control) and uncorrected errors (less control), using single‐trial analysis to avoid the aforementioned problems. Assuming online control the Ne should be larger and/or occur earlier for corrected than for uncorrected errors.
The issue of the functional relevance of the Ne is complicated by the fact that also following correct responses a negativity occurs: the “correct response negativity” (CRN) or Nc [Ford, 1998; Vidal et al., 2000; Yordanova et al., 2004]. It is unclear whether Ne and Nc are reflections of distinct processes or rather the same process which is larger in erroneous responses [Vidal et al., 2000]. Bartholow et al. [ 2005] showed that the Nc is larger following unexpected stimuli. Thus, they relate the Nc to strategic control. Since the Ne reacted in a similar manner as the Nc to a violation of expectation, the Bartholow et al. data support the idea of a common process.
The results of Band and Kok [ 2000] as well as Falkenstein [ 2004] indicate that the Ne‐amplitude is smaller and its latency longer in more difficult tasks. In contrast, the Nc was constant across conditions. Thus, in very difficult tasks, Ne and Nc were more similar in amplitude and latency than in easy tasks. This could be interpreted in two ways: the Nc occurs in correct trials as well as in erroneous trials, while the Ne is only elicited in error trials. Thus, the Nc is included in the Ne during erroneous trials and occurs isolated (without Ne) in correct trials. The Nc has constant amplitude irrespective of task difficulty, while the Ne is attenuated in the more difficult tasks. An alternate interpretation is that the process reflected in Ne and Nc is simply larger in erroneous trials (Ne) than in error trials (Nc) [Vidal et al., 2000] and that this enlargement is being attenuated in a more difficult task.
These two models should be tested by the present study. For this purpose, independent component analysis (ICA, Comon, 1994] was conducted to decompose the Ne in possible independent components. ICA is an approach for the solution of the blind source separation (BSS) problem [Comon, 1994]. The general model of ICA is that the observed signals x are constituted by linearly mixed (A) sources s (x = As). These are unknown and mutually statistically independent. Because mixture and sources are unknown, the inverse of the mixing matrix W has to be estimated blindly. This leads to a solution u = Wx, where u are the estimated sources. The estimation of W is based on minimizing a cost function that enforces statistical independence.
ICA is, like PCA, a method for decorrelating data, but whereas PCA uses only second order statistics and assumes the underlying sources to be orthogonal, ICA uses higher order statistics. Concerning the EEG, it is assumed that the recorded signal is a linear mixture of unknown sources within the brain [Makeig et al., 1996, 2004a]. Because the sources and therefore the mixture are unknown, they need to be estimated. The basic assumption of ICA, that the sources are statistically independent while the mixture is not, is neuroanatomically and neurophysiologically plausible, because cortical (and other) areas are spatially distinct and generate a specific activation, but correlate in their flow of information [Makeig et al., 2004a].
In this study, temporal ICA was conducted to disentangle the latent components constituting the signal mixture denoted as Ne/Nc. For this purpose, the error‐specific IC‐component was extracted from the error minus correct ERPs and its variation with response correctness and type of task was compared with the variation of the raw postresponse ERP. Hence, the hypotheses of this study can be shaped straightforward: The two‐component hypothesis would predict an error‐specific component showing no, or at least decreased activity in the postresponse ERPs of the correct trial ERPs, whereas another correct‐response specific component would show increased activation in the postresponse ERPs of the correct trials ERPs or the same activation in error and correct trials. On the other hand, the one‐component hypothesis would assume that it is still present in correct trials, simply showing smaller amplitude. The more recent literature [Debener et al., 2005] reported only one component in a flanker task showing the typical time course of activation, topography, source and error dependent variation of the Ne. However, those studies solely used the flanker task, which is very easy and might constitute a special case because errors are induced by the flankers that are mapped directly to the incorrect response. Hence, in our study, we used the flanker task and an additional task with more indirect S‐R relation, namely a mental rotation task. One possible confound is that the flanker task may induce a speed strategy, whereas the rotation task may induce an accuracy strategy. Hence, possible task effects may be rather strategy effects. To control for this, we varied speed‐accuracy trade‐off in both tasks. This was achieved with separate groups of subjects (accuracy‐instructed vs. speed‐instructed).
A final issue addressed in this study is the whether Ne or Nc are only response‐related components or are also elicited by the stimuli. Already Coles et al. [ 2001] mentioned the possibility of a stimulus‐related part in the Ne. This influence could be particularly strong in tasks with direct S‐R‐relation such as the flanker task, which is very frequently used in Ne research. This problem was addressed in this study by introducing the second task with very indirect S‐R mapping, and by analyzing single trials and sorting them by RT. For this purposes, ERP‐images and analysis of intertrial coherence as implemented in EEGLAB [Delorme and Makeig, 2004; Jung et al., 2000; Makeig et al., 2004a, b, 1999] were utilized.
RESULTS
Behavioral Data
Neither error rate or reaction time did differ significantly between the speed and the accuracy instructed group (error rate: F(1,18) = 1.74, P = 0.20, λ = 0.91; reaction time: F(1,18) = 3.627, P = 0.07, λ = 0.83). Significantly fewer errors were committed in the flanker task (13.87%) than in the rotation task (17.67%) (F(1,18) = 4.53, P = 0.04, λ = 0.79), even though the effect was not very large as indicated by Wilk's λ = 0.79. The reaction times (RTs) were significantly shorter for the flanker task (246 ms) than for the rotation task (464 ms) (Fig. 1) F(1,18) = 79.27, P < 0.001, λ = 0.185). In general, RTs were shorter for incorrect than for correct responses (Fig. 1, F(1,18) = 48.93, P < 0.001, λ = 0.269). Moreover, there was a significant interaction of task and response (Fig. 1, F(1,18) = 26.29, P < 0.001, λ = 0.406). Multiple comparisons by means of t‐tests (one sided) revealed that for the flanker task the RTs were faster for incorrect (246 ms) than for correct responses (318 ms; Fig. 1; t(19) = −19.58, P < 0.001, d = 3.31). This was not the case for the rotation task (464 vs. 473 ms; Fig. 1, t(19) = −0.78, P = 1, d = 0.91). Further, RTs were longer for incorrect responses in the rotation task than in the flanker task (Fig. 1, t(19) = 8.30, P < 0.001, d = 2.32). This was also true for the correct responses, being longer in the rotation task (Fig. 1, t(19) = 8.57, P < 0.001, d = 1.91).
Figure 1.
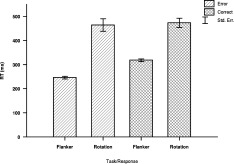
Mean response times of the different tasks and response types. Note the absence of a difference between correct and erroneous responses for the rotation task. The means were collapsed across groups, since there was no significant group effect.
EEG Data and ICA
Independent component analysis revealed, in line with the one component model, for every participant one component explaining most of the variance in the critical time window of the Ne (Supp. Info. Fig. 2a,b). This was true for both flanker task and rotation task. In the critical Ne time window, this component accounted for about 80.75% of variance in the flanker task, and for 64.36% in the rotation task. Dipole modeling revealed comparable source locations for the average component topographies of both tasks, although ICA was conducted for both tasks separately (Fig. 2a,b).
Figure 2.
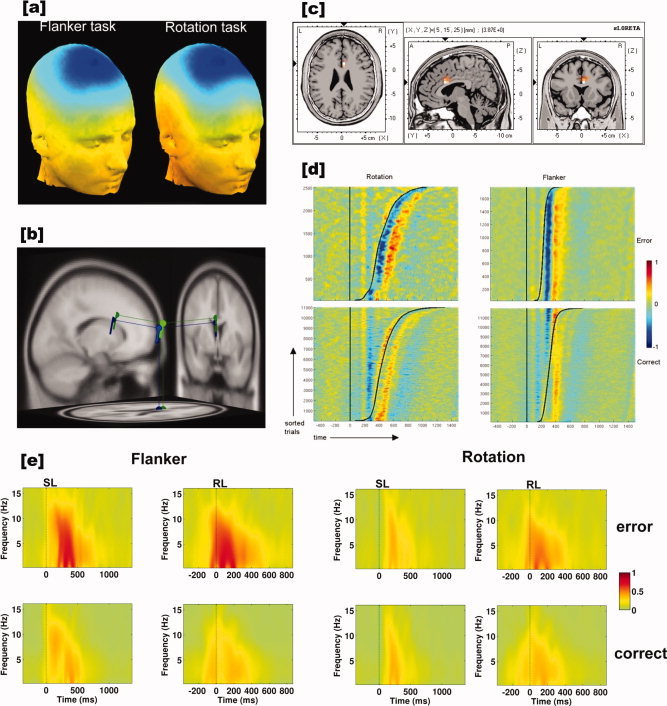
(a) Grand average topographic maps of the derived Ne‐IC for both tasks. (b) Dipole solutions (DIPFIT) for both topographies (Flanker task: Talairach coordinates (Tal (x, y, z)) = −2, 15, 15; residual variance (r.v.) = 2.97%; rotation task: Tal(x, y, z) = −2, 10, 21; r.v. = 6.37%) (flanker = green; rotation = blue). Note that ICA was conducted for both tasks separately, but yielding comparable results. (c) sLORETA solution for the Ne‐IC topographies of flanker and rotation. The generator for both topographies was located in the anterior cingulate (Tal(x, y, z) = 5, 16, 22). The sLORETA estimations of all participants' topographies were projected on an averaged normalized brain (MNI template). (d) Stimulus locked ERP‐images for each task and response (error, correct) collapsed across both groups. The solid vertical line at time point zero indicates the stimulus. The right hand sinusoid line indicates the response. Trials were sorted with respect to the response time, i.e. from shortest to longest. All data were standardized from the range 0–1 for plotting. (e) Stimulus (SL) and response‐locked (RL) intertrial coherence (ITC) of the Ne‐IC projected to FCz for both tasks (flanker, rotation) and response types (error, correct). Nonsignificant values are masked by green color. Note that for the rotation task ITC was consistent for SL correct and erroneous responses. This was not the case for the flanker task.
The dipole position as well as the topography of this component was consistent with those estimated for the Ne in previous studies, i.e. showing a fronto‐central topography and a position that fit well in the anterior cingulate (Flanker task: Talairach coordinates (Tal(x, y, z) = −2, 15, 15; residual variance (r.v.) = 2.97%; rotation task: Tal (x, y, z) = −2, 10, 21; r.v. = 6.37%, Fig. 2b).
To estimate which source explains the variation between flanker and rotation task Ne‐IC, sLORETA estimations of flanker and rotation Ne‐IC‐topographies were conducted (see Methods section). sLORETA located the source of the topographies close to the ones derived from the DIPFIT analysis (Anterior cingulate, Brodman area 33, Tal(x, y, z) = 5, 16, 22; t > 4.3, P < 0.05, Fig. 2c).
No other components showed consistent activation across subjects for the difference signals (correct, error) across subjects.
The component (called Ne‐IC) was projected back to the scalp for each participant; the resulting EEG consisted only of the component that was assumed to reflect the Ne/ERN activity. For this the analysis of the Ne‐IC, parameterized at FCz (by means of detecting and averaging the single‐trials ERPs) revealed a significant main effect of task (F(1,18) = 27.601, P < 0.001, λ = 0.395), response (F(1,18) = 119.891, P < 0.001, λ = 0.131), and a significant interaction of task and response (F(1,18) = 37.726, P < 0.001, λ = 0.323). Multiple comparisons by means of t‐tests (one sided) revealed for the flanker task that the mean amplitude of the Ne‐IC was more negative for incorrect than for correct responses (t(19) = −11.19, P < 0.001, d = 2.5). The same was true for the rotation task (t(19) = −5.73, P < 0.001, d = 1.29).
The smaller effect sizes (d) indicate that the correctness effect is much smaller for the rotation task than for the flanker task. The Ne‐IC amplitude for incorrect responses was significantly less negative in the rotation task than in the flanker task (t(19) = 5.82, P < 0.001, d = 1.29), whereas the Ne‐IC for correct trials showed no task difference (t(19) = 1.29, P = 0.21, d = 0.21). Figure 3 provides the corresponding response‐locked grand averages for the Ne‐IC projected back to FCz.
Figure 3.
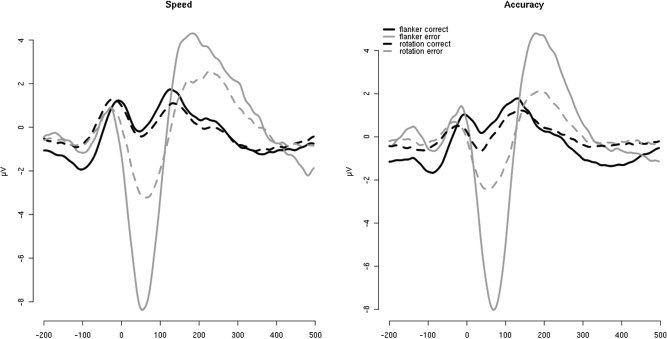
Response‐locked (t = 0 ms) grand averages of the Ne‐IC projected back to FCz for both groups. Solid lines: flanker task; dashed lines: rotation task; grey: errors; black: correct.
Comparing the backprojected Ne‐IC to the standard Grand Averages reveals a comparable pattern, which supports the assumption that the derived component indeed constitutes the ERPs denoted as Ne/Nc (Supp. Info. Fig. 1).
In addition, trials in which responses were corrected were compared with trials with uncorrected responses. For the flanker task the Ne‐IC amplitude did not differ significantly between corrected and uncorrected errors (t = 1.09, P = 0.86, d = 0.24), but its latency was significantly shorter for corrected than for uncorrected (Fig. 4; mean difference: 22.6 ms; t(19) = −6.3957, P < 0.001, d = 1.41). For the rotation task, too few errors were corrected to provide the opportunity for statistical analyses.
Figure 4.
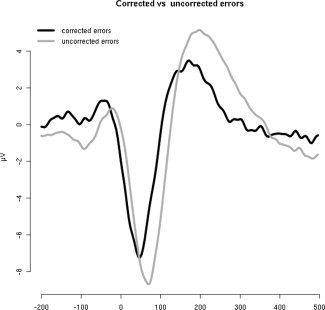
Response‐locked (t = 0 ms) grand averages of the Ne‐IC projected back to FCz for corrected and uncorrected errors in the flanker task.
Since in the statistics for the flanker task, incompatible and compatible trials are pooled a second MANOVA for repeated measures with the factor response (error incompatible, correct incompatible, correct compatible) and the between factor group (speed, accuracy intruction) was conducted to exclude that the amplitude variation is due to compatibility and not due to errors. Here only errors after incompatible stimuli were taken into account because there were too few errors after compatible stimuli. The results show a significant effect of the factor response (F(2,17) = 76.56, P > 0.001, λ = 0.1). Multiple comparisons (one‐sided t‐tests) of the response factor levels showed that the amplitude of the Ne‐IC was significantly more negative for incompatible errors than for incompatible correct responses (t(19) = −9.16, P < 0.001, d = 2.05). The same was true for the difference between incompatible errors and compatible correct responses (t(19) = −10.97, P < 0.001, d = 4.45). The difference between correct compatible and correct incompatible was not significant (t(19) = −0.77, P = 0.45, d = 0.18).
The ERP‐images indicate that the observed Ne‐IC consistently followed the incorrect response. This was true for both, flanker and rotation task, respectively (Fig. 2d). Interestingly, a remarkable stimulus‐locked activity of the Ne‐IC that was observable. This was very small and hardly visible in the rotation task, but well visible in the flanker task.
Figure 2e illustrates the higher response locking of the flanker task compared to the rotation task. The figure (function tftopo() in EEGLAB) shows stimulus‐ and response‐locked intertrial coherence images of both tasks and response types for the Ne‐IC backprojected to FCz. Only time‐points and frequencies are highlighted that were significant (P < 0.01) for all participants following bootstrap testing as implemented in EEGLAB (nonsignificant values are plotted in green, i.e. zero; see legend).
Further, it supports the notion from the ERP‐images that for errors in the rotation task there is no stimulus‐locked error‐related activity, while there is such activity for the flanker task.
Analysis of intertrial coherence of response‐locked data (flanker error, flanker correct, rotation error, rotation correct) by means of a Friedman rank‐test revealed a significant effect (χ2(3) = 34.98, P < 0.001). Post‐hoc comparisons by means of exact Wilcoxon signed rank tests of the four conditions (flanker error, rotation error, flanker correct, rotation correct) revealed a higher response locking for flanker error than for flanker correct (V = 208, P < 0.001); a higher response locking for rotation error than for rotation correct (V = 174, P = 0.004), and a higher response locking for flanker error than for rotation error (V = 206, P < 0.001). The correct responses did not differ significantly (V = 75, P = 0.277).
To exclude that the difference between both tasks is due to speed‐accuracy trade‐off, correlations between mean reaction times and mean backprojected Ne‐NC amplitudes were calculated for each task and response type (error, correct), revealing that there was no significant correlation except for correct responses in the flanker task (r = 0.5, t(18) = 2.46, P = 0.02).
DISCUSSION
This study aimed to test the hypothesis that Ne and Nc might reflect the same neural process. The decomposition of the EEG data revealed for each task (rotation, flanker) one independent component accounting for erroneous and correct response related EEG activity. This result is in line with previous results of Vidal et al. [ 2000] and Debener et al. [ 2005]. In line with Debener et al. [ 2005], ICA revealed only one component accounting for the major portion of variance in the critical postresponse time window of the Ne/Nc. Thus, in the further analysis, this component was projected back to the scalp and further analyzed with respect to the initially formulated hypotheses (Ne‐IC). As predicted by the hypothesis of Falkenstein [ 2004], the amplitude of the Ne‐IC was significantly smaller in the difficult task (i.e. task with weaker stimulus‐response mapping, rotation task) than in the flanker task. In addition, the amplitude of the Ne‐IC was significantly larger in incorrect trials than in correct trials. The amplitude of the Ne‐IC did not vary between correct responses of both tasks. Source analysis by means of sLORETA revealed that the components extracted independently from both tasks could be located at almost the same position in the anterior cingulate (ACC). Both components showed the similar pattern with respect to topography and reaction to correct and incorrect responses. The strong response locking as revealed by means of ERP‐images supports this view. Thus, our data support the one‐component hypothesis, i.e. that Ne and Nc reflect the same process. The ERP‐images also indicate that the difference in amplitude between flanker and rotation task is not due to a jitter of the Ne‐IC. In addition, the method used for estimating the average Ne‐IC response prevents such a jittering artifact, as the single‐trial amplitudes were computed and subsequently averaged.
Interestingly, the two instruction groups (speed, accuracy emphasis) did not differ with respect to Ne‐IC amplitude. This is a quite important result as the task was adaptively programmed (i.e. increasing the deadline if too many errors occurred and decreasing the deadline if too few errors occurred), and participants were forced to produce comparable error rates and response times, irrespective of the instruction. Hence, any differences between both groups would be only due to instruction. However, there were differences in neither the Ne‐IC amplitude nor latency for the different instructions nor a significant interaction of instruction and task. Thus, the difference in amplitude between flanker and rotation task is not due to the possibility that in both tasks the participants apply different strategies (e.g. speed with the flanker task and accuracy with the rotation task). Our results suggest that the frequently‐found amplitude effects on the Ne in the literature due to speed vs. accuracy instructions [Gehring et al., 1993] or time pressure manipulations [Falkenstein et al., 1990] are not reflecting true variation of the Ne at the single trials level. Rather they are probably due to differences in error rate, namely fewer errors in accuracy/low time pressure conditions. A lower number of error epochs should lead to less smearing and hence causes larger amplitudes of the average Ne. Hence, further Ne studies should try either to equalize Ne amplitudes across conditions or use single trial measures.
It could be argued that the difference between rotation task and flanker is due to speed accuracy trade‐off (SAT). However, the response times did not differ significantly between correct and erroneous responses (see Fig. 1) for the rotation task. Anyhow, when having a look at the ERP‐images it becomes clear that the activity of this component does not vary with response time within this task, but between correct and erroneous responses. In the flanker task the response times for correct and incorrect responses do differ, but the pattern in the ERP‐images is comparable to the rotation task. Hence, we conclude that RT difference between incorrect and correct responses is not the crucial factors that influence the difference of the Ne‐IC.
Another point is that for the difference signals (error, correct) only one component showed consistent activity across subjects (for the critical post response time window from 0:100 ms). This supports the hypothesis of Vidal [ 2000] that Ne and Nc are likely generated by the same neural process. Indeed, in the ERP‐images of both tasks clearly a slight activation of the Ne‐IC is visible in correct responses.
Most interestingly, there is also considerable stimulus‐locked negative activity of the Ne‐IC in correct trials. For the flanker task, this activity occurs at the same time‐point as within the erroneous responses. This is because those responses are much faster. In addition, the variability of RTs is considerable slow in the flanker task, compared to the rotation task. Hence, with the flanker task it is not clear whether this negative activation is stimulus or rather response related. Hence, for further investigation, it appears advisable, always to show single‐trial activity, as this fact is camouflaged by the classical ERP methodology. ERPs only roughly allow a decision about stimulus or response relation by comparing stimulus and response related averages. If the potential is larger for the stimulus‐related average, one could conclude that the potential is stimulus‐related. However, even though this appears plausible it can only be proved by single trial analysis.
For the rotation task the picture becomes quite clearer. Here the response locking of the component that was assumed to explain the Ne‐activity was seen much clearer than in the flanker task. Indeed, the response and stimulus locked intertrial coherence differed substantially not only between the flanker and rotation task. The analysis also showed that the error‐related activity in the rotation task differentiated between stimulus and response locked data. In the rotation task, the Ne‐IC showed less intertrial coherence in the stimulus‐locked segments of erroneous responses compared to response‐locked segments of erroneous responses (Fig. 2e). This was not so clear in the flanker task. Here, error‐related activity was observable in the response‐locked data, but also in the stimulus‐locked data. In sum, the mean activity of that Ne‐IC was much lower in the rotation task than in the flanker task.
In summary, the results indicate that for both, correct and incorrect responses, the same process is active, as reflected in the Ne‐IC. This process is not only sensitive for errors, but also to task type (i.e. stimulus response mapping), and possibly to task difficulty. But what could be the functional significance of such a process?
It is clear that both tasks are completely different. The flanker task induces a very strong stimulus response mapping [Wascher et al., 1999; Willemssen et al., 2004] and the response, irrespective of being correct or not, is highly automated, as the mapping (arrowheads towards the response site) is obvious for the participants. Hence, the response times are much faster than in the rotation task. In the latter, the stimulus responses mapping is not so strong, as it has to be learned just prior beginning of the task. However, there still occurs activity related to the error response, which is nevertheless quite smaller than in the flanker task. However, is this error related “Ne‐IC” activity really error specific or rather some kind of conflict? In that case, one would predict that the activity is larger in trials in which the response was corrected, hence producing strong overlap of response activations and hence conflict. However, Carbonnell and Falkenstein [ 2006] showed that there is no such a relation: the Ne did not differ between partial and full errors and hence degrees of conflict. Instead, their results indicated that the Ne occurred earlier for partial than for full errors. This finding implicates rather some kind of control process than a process reflecting conflict. Indeed, in the present study the amplitude of the Ne‐IC did not differ between corrected and uncorrected errors in the flanker task, but it peaked significantly earlier for corrected than for uncorrected errors, which is a replication of Fiehler et al. [ 2005] who showed that the Ne amplitude did not differ, but the latency between corrected and uncorrected errors. In sum the present data add further evidence to the assumption that the Ne reflects or induces online response control, and that the latency, rather than the amplitude of the response locked Ne, is the critical factor for the effectiveness of this control. This process is strongly attenuated in correct trials and in difficult tasks.
Surprisingly, and what was not expected, a remarkable stimulus locking of the derived Ne‐IC occurred in correct trials for both tasks. This is surprising, since ICA should separate the signals into temporal independent components. Hence, we expected the derived Ne‐IC to be strictly response locked. Here it might be argued that simply the decomposition failed. However, this is rather improbable, since, as can be seen in the ERP‐images: the stimulus locked activity is observable across all subjects. Furthermore, it appears at least for the rotation task as if the stimulus locked activity is much stronger in trials in which the reaction time for correct response was shorter, compared to trials with a longer reaction time. Thus, further studies should give more attention to the stimulus locked part of the observed process. What would be the function of such process? The results of the present study indicate that it might be that the variation of the Ne‐amplitude is not error specific. From the viewpoint of “control” it could be argued, that in erroneous trials it is required to initiate the required response. In correct trials, this control is much smaller and ends earlier since the subject has already arrived at the desired goal state, i.e. a correctly panned and executed response.
METHODS
Participants
A sample of 20 healthy young subjects participated (11 women). Subjects were aged between 21 and 27 year (mean = 23.8; sd = 1.9) and gave written informed consent prior to participation. Subjects received 10 euro/h payment for participation.
General Procedure and Experimental Design
Participants were seated in an ergonomic seat in front of a 19″‐CRT monitor (100 Hz). Responses were given by a button press of the left or right thumb. The experiment consisted of two tasks each consisting of eight blocks (one training block). Each block consisted of 80 trials. Following each block, a break of 20 s was provided. After half of the experimental blocks, a break of 120 s was provided.
The experiment consisted of a mixed 2 (group) × 2 (task) design with the between subjects factor group (accuracy vs. speed instruction) and the within subjects factor task (flanker vs. rotation). The design was fully balanced with respect to group, sequence of tasks, and response side for mirrored/non‐mirrored letters.
Tasks
The first task was a modified flanker task [Kopp et al., 1996]. In the center of the screen, an arrowhead indicated the button that had to be pressed. Hence, the stimulus‐response mapping was very direct in the flanker task. This arrowhead was accompanied by two distracting arrowheads below and above appearing 100 ms before target occurrence, which is known to induce maximal distraction [Wascher et al., 1999; Willemssen et al., 2004]. These flankers could be congruent (pointing to the same direction) or incongruent (opposite direction). The occurrence of congruent and incongruent flankers was equiprobable.
The second task was a mental rotation task modified for ERP measurement to yield a comparable time line and workflow for the participants during conduction of the experiment. One of two letters (F,R) was presented to the participants. This letter was either rotated, mirrored across the main axis or both. Subjects had to indicate with a left or right button press of the corresponding thumb if the letter was mirrored or not. The letters were rotated by 0°, 45°, 135°, 225°, or 315°. The 20 possible stimuli (5 × 2 × 2) were presented in random order. Thus, the rotation task was not only much more difficult than the flanker task; it also differs with respect to the degree of stimulus‐response mapping, which was quite indirect in the rotation task.
In both tasks the subjects received postresponse feedback indicating whether they responded fast enough or too fast/too slow. The feedback consisted of two pictograms. If the participants responded fast enough a yellow pictogram of a smiling face (“smiley”) appeared in the center of the screen. A red angry looking pictogram appeared if they responded too fast or too slow. The deadline for the feedback was adapted block wise. If the error rate in one block (80 trials) was below 8%, the deadline was decreased adding one standard deviation to the mean RT in the previous block. If the error rate was above 12%, the deadline was increased by adding four standard deviations to the mean RT of the previous block.
EEG‐Recording and Preprocessing
EEG was recorded unipolar from 63‐electrodes (FPz, FP1, FP2, AFz, AF7, AF3, AF4, AF8, Fz, F7, F3, F4, F8, FCz, FT7, FC5, FC3, FC1, FC2, FC4, FC6, FT8, T7, C5, C3, Cz, C1, C2, C4, C6, T8, TP7, TP8, CPz, CP5, CP3, CP1, CP2, CP4, CP6, Pz, P7, P3, P1, P2, P4, P8, POz, PO9, PO7, PO3, PO4, PO8, PO10, Oz, O1, O2, M1, M2) with a sampling rate of 500 Hz. The EOG was recorded from the outer canthi and from above and below the right eye (SO2, IO2, LO1, LO2). Data were re‐referenced off‐line relative to average reference. Initially, data were manually cleaned from artifacts. Data was filtered off‐line using a nonlinear FIR filter (high‐pass filter: 0.5 Hz, low‐pass filter: 25 Hz).
Independent Component Analysis
Independent component analysis (ICA) was conducted with the unsegmented raw data with extended infomax and implemented natural gradient [Amari, 1998; Bell and Sejnowski, 1995; Delorme and Makeig, 2004; Lee et al., 1999]. The algorithm converged for all data sets within 500 training steps. Following this, artifact correction was conducted using the derived independent components, i.e. by removing sporadically occurring artifactual activity in the continuous independent component activations. Subsequently, a second ICA was conducted with the pruned data set. ICA was only conducted with data sets exceeding an error rate of 10% and a minimum training data set length of 6 × 642 data points (all data set fulfilled these thresholds). Again, the algorithm converged for all data sets within 500 training steps. The next analysis step was a dipole analysis to model the derived components by a spherical 3D model. All components that could not be located within the cortex, as well as artifactual components (eye movements, blinks, muscle artifact) were removed, i.e. the data were cleaned by backprojection of the remaining components to the scalp [Jung et al., 2000]. Subsequently, stimulus‐(SL) and response‐locked (RL) segments were extracted (SL = −500:1,500 ms; RL = −500:1,500). For detecting the component accounting for the Ne activity being specific for error trials, the mutual variance between each component and the Ne in the corresponding time window was calculated. This was done by estimating the percent of variance the components accounted for in the difference wave between correct and error trials in the critical time window of Ne occurrence (EEGLAB function difftopo()). For the resulting components dipole analysis was conducted. For the further analysis, the component explaining most variance in the Ne time window, showing a comparable topography and having corresponding dipole localization was projected back to the scalp, and single‐trial analysis (see below) was conducted. To model the neural source of the remaining components, the grand average IC‐topography was analyzed by utilization of the DIPIFIT plug‐in in EEGLAB. This plug‐in can be used to model neural sources of independent component scalp topographies by means of source localization by fitting an equivalent current dipole model using a nonlinear optimization technique [Scherg, 1990] and a four‐shell spherical model [Kavanagh et al., 1978]. In addition, sLORETA estimations of the source of variation between flanker and rotation ICs were conducted. sLORETA can be used to estimate the source generating the variance between two experimental conditions. LORETA has recently been used to estimate the origins of independent component scalp maps. [Marco‐Pallares et al., 2005]. sLORETA is an improved version of LORETA. The main difference is that sources are estimated based on standardized current density allowing a more precise source localization than the previous LORETA‐method [Pascual‐Marqui, 2002]. sLORETA was performed with the scalp maps of the Ne‐ICs of both tasks to find the generators of these maps. This was done by comparison of the voxel‐based sLORETA‐images (6,239 voxels at a spatial resolution of 5 mm; MNI template) of the Ne‐IC topography in the flanker task [Pascual‐Marqui, 2002] and the Ne‐IC topography of the rotation task. Statistical quantification was conducted by using the sLORETA‐built‐in voxelwise randomization tests (5,000 permutations) based on statistical non‐parametric mapping (SnPM), corrected for multiple comparisons [for details see Nichols and Holmes, 2002]. The voxels with significant differences (P < 0.05) were located in specific brain regions.
Single‐Trial Analysis
For quantification of the Ne‐amplitude, the average single‐trial amplitude of the Ne‐IC was computed. The single‐trial peaks were quantified by the difference between the most positive peak in the time‐window −80:0 ms before response onset and the most negative deflection in the time‐window 0:150 ms. Subsequently, the average single‐trial amplitude for every subject and condition was calculated. For linking behavioral data to the single‐trial peaks, the RTs of the corresponding trials were collected. As with solely analyzing response locked averages it cannot be assured that the collected peaks are response specific and not stimulus driven, ERP‐images [Jung et al., 2001; Makeig et al., 1996] were generated to evaluate the Ne‐IC activation on a single trial level. For these ERP‐images, the single trials of all subjects were normalized and sorted by reaction time.
In addition, intertrial coherence [ITC, e.g. Delorme and Makeig, 2004] was calculated in the frequency range from 0.5 to 16 Hz for each participant, task and response type. ITC was calculated with stimulus and response locked single‐trial data. ITC significance levels (P < 0.01) were assessed for each subject using surrogate data by randomly shuffling the single‐trial spectral estimates from different latency windows during the baseline period (−500:0 ms). For generation of the time‐frequency figures (Fig. 2e), the EEGLAB tftopo() function was used [Delorme and Makeig, 2004]. It applies a threshold derived by simple statistics on the number of subjects for which the spectral decomposition is significant at a given time/frequency point. If not enough subjects show a significant change at the specified point, it is considered nonsignificant in the group average. In this study, we defined the threshold in such a way that for each specified point each participant should show a significant effect, which is statistically a quite conservative approach.
Statistical Analysis
Error rates were analyzed by a repeated measures MANOVA with the within subjects factor task (flanker, rotation) and the between subjects factor group (speed instruction, accuracy instruction).
The reaction times (RTs) were analyzed by means of repeated measures MANOVA (Wilks test statistic) with the within subject factors task (flanker, rotation) and response (error, correct) and the between subjects factor group (speed instruction, accuracy instruction). Subsequently, multiple comparisons (t‐tests, P‐values Bonferroni adjusted) were conducted. The significance level was set to 0.05.
The average Ne‐IC single‐trial amplitudes were also analyzed by means of repeated measures MANOVA (Wilks test statistic) with the within subject factors task (flanker, rotation) and response (error, correct) and the between subjects factor group (speed instruction, accuracy instruction). The flanker task was analyzed also separately by repeated measures MANOVA with the within subjects factor response (error incompatible, correct compatible, correct incompatible) and the between subjects factor group (S, A). Here, also multiple comparisons were conducted analogously to the RT data. Effect sizes are reported by means of Wilks λ (MANOVA) and Cohen's d [Cohen, 1988]. For all statistical analyses, GNU R was used (R Core Development Team, 2008). For analyses of the EEG and ICA data EEGLAB [Delorme and Makeig, 2004] and Matlab© were used.
In addition, the mean ITC in the for the Ne relevant 4 Hz range [e.g. Cavanagh et al., 2009; Luu et al., 2004; Trujillo and Allen, 2007] of the response‐related data (flanker error, rotation error, flanker correct, rotation correct) was analyzed by means of a nonparametric Friedman‐test and post‐hoc exact Wilcoxon signed‐rank tests (only Bonferroni adjusted P‐values are reported) since Shapiro–Wilks tests revealed a nongaussian distribution of these data.
Supporting information
Additional Supporting Information may be found in the online version of this article.
Supportinf Information.
Supportinf Information.
Acknowledgements
We thank Ludger Blanke, Ines Bommert, Christiane Westedt and Manon Wicking for their invaluable personnel and technical support. We also thank Christian Beste, Stephan Getzmann for fruitful discussions and an anonymous reviewer for the very constructive comments.
References
- Amari SI ( 1998): Natural gradient works efficiently in learning. Neural Comput 10: 251–276. [Google Scholar]
- Band GP,Kok A ( 2000): Age effects on response monitoring in a mental‐rotation task. Biol Psychol 51: 201–221. [DOI] [PubMed] [Google Scholar]
- Bartholow BD,Pearson MA,Dickter CL,Sher KJ,Fabiani M, Gratton G ( 2005): Strategic control and medial frontal negativity: Beyond errors and response conflict. Psychophysiology 42: 33–42. [DOI] [PubMed] [Google Scholar]
- Bell AJ,Sejnowski TJ ( 1995): An Information‐maximization approach to blind separation and blind deconvolution. Neural Comput 7: 1129–1159. [DOI] [PubMed] [Google Scholar]
- Botvinick MM, Braver TS, Barch DM, Carter CS, Cohen JD ( 2001): Conflict monitoring and cognitive control. Psychol Rev 108: 624–652. [DOI] [PubMed] [Google Scholar]
- Brazdil M, Roman R, Falkenstein M, Daniel P, Jurk P, Rektor I ( 2002): Error processing––Evidence from intracerebral ERP recordings. Exp Brain Res 46: 460–466. [DOI] [PubMed] [Google Scholar]
- Carbonnell L, Falkenstein M ( 2006): Does the error negativity reflect the degree of response conflict? Brain Res 1095: 124–130. [DOI] [PubMed] [Google Scholar]
- Carter CS, Braver TS, Barch DM, Botvinick MM, Noll D, Cohen JD ( 1998): Anterior cingulate cortex, error detection, and the online monitoring of performance. Science 280: 747–749. [DOI] [PubMed] [Google Scholar]
- Cavanagh JF, Cohen MX, Allen JJ ( 2009): Prelude to and resolution of an error: EEG phase synchrony reveals cognitive control dynamics during action monitoring. J Neurosci 29: 98–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen J ( 1988): Statistical Power Analysis for the Behavioral Sciences, 2nd ed Hillsdale, NJ: Lawrence Erlbaum. [Google Scholar]
- Coles MG, Scheffers MK, Holroyd CB ( 2001): Why is there an ERN/Ne on correct trials? Response representations, stimulus‐related components, and the theory of error processing. Biol Psychol 56: 173–189. [DOI] [PubMed] [Google Scholar]
- Comon P ( 1994): Independent component analysis––A new concept? Signal Process 36: 287–314. [Google Scholar]
- Debener S, Ullsperger M, Siegel M, Fiehler K, von Cramon DY, Engel AK ( 2005): Trial‐by‐trial coupling of concurrent electroencephalogram and functional magnetic resonance imaging identifies the dynamics of performance monitoring. J Neurosci 25: 11730–11737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Posner MI, Tucker DM ( 1994): Localization of a neural system for error detection and compensation. Psychol Sci 5: 303–305. [Google Scholar]
- Delorme A, Makeig S ( 2004): EEGLAB: An open source toolbox for analysis of single‐trial EEG dynamics including independent component analysis. J Neurosci Methods 134: 9–21. [DOI] [PubMed] [Google Scholar]
- Falkenstein M ( 2004): ERP correlates of erroneous performance In: Ullsperger M, Falkenstein M, editors. Errors, Conflicts, and the Brain. Current Opinions on Performance Monitoring. Leipzig: Max‐Planck‐Institute for Human Cognitive and Brain Sciences; pp 5–14. [Google Scholar]
- Falkenstein M,Hohnsbein J,Hoormann J,Blanke L ( 1990): Effects of errors in choice reaction tasks on the {ERP} under focused and divided attention In: Brunia CHM, Gaillard AWK, Kok A, editors. Psychophysiological Brain Research. Tilburg: Tilburg University Press; pp 192–195. [Google Scholar]
- Falkenstein M,Hohnsbein J,Hoormann J,Blanke L ( 1991): Effects of crossmodal divided attention on late ERP components. II. Error processing in choice reaction tasks. Electroencephalogr Clin Neurophysiol 78: 447–455. [DOI] [PubMed] [Google Scholar]
- Falkenstein M, Hoormann J, Christ S, Hohnsbein J ( 2000): ERP components on reaction errors and their functional significance: A tutorial. Biol Psychol 51: 87–107. [DOI] [PubMed] [Google Scholar]
- Fiehler K, Ullsperger M, von Cramon DY ( 2005): Electrophysiological correlates of error correction. Psychophysiology 42: 72–82. [DOI] [PubMed] [Google Scholar]
- Ford JM ( 1998): Schizophrenia: The broken P300 and beyond. Psychophysiolology 36: 667–682. [PubMed] [Google Scholar]
- Gehring WJ, Goss G, Michael GHC, Meyer DE, Donchin E ( 1993): A neural system for error detection and compensation. Psychol Sci 4: 385–390. [Google Scholar]
- Hajcak G, McDonald N, Simons RF ( 2003): To err is autonomic: Error‐related brain potentials, ANS activity, and post‐error compensatory behavior. Psychophysiology 40: 895–903. [DOI] [PubMed] [Google Scholar]
- Holroyd CB, Coles MGH ( 2002): The neural basis of human error processing: reinforcement learning, dopamine, and the error‐related negativity. Psychol Rev 109: 679–709. [DOI] [PubMed] [Google Scholar]
- Jung TP, Makeig S, Humphries C, Lee TW, McKeown MJ, Iragui V, Sejnowski TJ ( 2000): Removing electroencephalographic artifacts by blind source separation. Psychophysiology 37: 163–178. [PubMed] [Google Scholar]
- Jung TP, Makeig S, Westerfield W, Townsend J, Courchesne E, Sejnowski TJ ( 2001): Analysis and visualization of single‐trial event‐related potentials. Hum Brain Mapp 14: 166–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kavanagh RN, Darcey TM, Lehmann D, Fender DH ( 1978): Evaluation of methods for three‐dimensional localization of electrical sources in the human brain. IEEE Trans Biomed Eng 25: 421–429. [DOI] [PubMed] [Google Scholar]
- Kopp B, Rist F, Mattler U ( 1996): N200 in the flanker task as a neurobehavioral tool for investigating executive control. Psychophysiology 33: 282–294. [DOI] [PubMed] [Google Scholar]
- Lee TW,Girolami M,Sejnowski TJ ( 1999): Independent component analysis using an extended infomax algorithm for mixed subgaussian and supergaussian sources. Neural Comput 11: 417–441. [DOI] [PubMed] [Google Scholar]
- Luu P, Tucker DM, Makeig S ( 2004): Frontal midline theta and the error‐related negativity: Neurophysiological mechanisms of action regulation. Clin Neurophysiol 115: 1821–1835. [DOI] [PubMed] [Google Scholar]
- Makeig S, Bell AJ, Jung TP, Sejnowski T ( 1996): Independent component analysis of electroencephalographic data In: Touretzky DS, Mozer MC, Hasselmo ME, editors. Advances in Neural Information Processing Systems 8. Cambridge, MA: MIT Press; pp 145–151. [Google Scholar]
- Makeig S, Debener S, Onton J, Delorme A ( 2004a): Mining event‐related brain dynamics. Trends Cogn Sci 8: 204–210. [DOI] [PubMed] [Google Scholar]
- Makeig S, Delorme A, Westerfield M, Jung TP, Townsend J, Courchesne E, Sejnowski TJ ( 2004b): Electroencephalographic brain dynamics following manually responded visual targets. PLoS Biol 2: 747–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makeig S, Westerfield M, Townsend J, Jung TP, Courchesne E, Sejnowski TJ ( 1999): Functionally independent components of early event‐related potentials in a visual spatial attention task. Philos Trans R Soc Lond B Biol Sci 354: 1135–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marco‐Pallares J, Grau C, Ruffini G ( 2005): Combined ICA‐LORETA analysis of mismatch negativity. Neuroimage 25: 471–477. [DOI] [PubMed] [Google Scholar]
- Masaki H, Segalowitz SJ ( 2004): Error negativity: A test of the response conflict versus error detection hypothesis In: Ullsperger M, Falkenstein M, editors. Errors, Conflicts, and the Brain. Current Opinions on Performance Monitoring. Leipzig: Max‐Planck‐Institute for Human Cognitive and Brain Sciences; pp 76–84. [Google Scholar]
- Nichols TE, Holmes AP ( 2002): Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Mapp 15: 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Connell RG, Dockree PM, Bellgrove MA, Kelly SP, Hester R, Garavan H, Robertson IH, Foxe JJ ( 2007): The role of cingulate cortex in the detection of errors with and without awareness: A high‐density electrical mapping study. Eur J Neurosci 25: 2571–2579. [DOI] [PubMed] [Google Scholar]
- Pascual‐Marqui RD ( 2002): Standardized low‐resolution brain electromagnetic tomography (sLORETA): Technical details. Methods Find Exp Clin Pharmacol 24( Suppl D): 5–12. [PubMed] [Google Scholar]
- Rabbitt PM ( 1966): Errors and error correction in choice reaction tasks. J Exp Psychol 71: 264–272. [DOI] [PubMed] [Google Scholar]
- Ridderinkhof KR, Ullsperger M, Crone EA, Nieuwenhuis S ( 2004): The role of the medial frontal cortex in cognitive control. Science 306: 443–447. [DOI] [PubMed] [Google Scholar]
- Scheffers MK, Coles MG, Bernstein P, Gehring WJ, Donchin E ( 1996): Event‐related brain potentials and error‐related processing: An analysis of incorrect responses to go and no‐go stimuli. Psychophysiology 33: 42–53. [DOI] [PubMed] [Google Scholar]
- Scherg M ( 1990): Fundamentals of dipole source potential analysis In: Grandori F, Hoke M, Romani GL, editor. Auditory Evoked Magnetic Fields and Electric Potentials. Basel: Karger; pp 40–69. [Google Scholar]
- Team RDC ( 2008): R: A Language and Environment for Statistical Computing Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Trujillo LT, Allen JJB ( 2007): Theta EEG dynamics of the error‐related negativity. Clin Neurophysiol 118: 645–668. [DOI] [PubMed] [Google Scholar]
- Ullsperger M, von Cramon DY ( 2001): Subprocesses of performance monitoring: A dissociation of error processing and response competition revealed by event‐related fMRI and ERPs. Neuroimage 14: 1387–1401. [DOI] [PubMed] [Google Scholar]
- van Veen V, Carter CS ( 2002): The anterior cingulate as a conflict monitor: fMRI and ERP studies. Physiol Behav 77: 477–482. [DOI] [PubMed] [Google Scholar]
- Vidal F, Hasbroucq T, Grapperon J, Bonnet M ( 2000): Is the ‘error negativity’ specific to errors? Biol Psychol 51: 109–128. [DOI] [PubMed] [Google Scholar]
- Wascher E, Reinhard M, Wauschkuhn B, Verleger R ( 1999): Spatial S‐R compatibility with centrally presented stimuli. An event‐related asymmetry study on dimensional overlap. J Cogn Neurosci 11: 214–229. [DOI] [PubMed] [Google Scholar]
- Willemssen R, Hoormann J, Hohnsbein J, Falkenstein M ( 2004): Central and parietal event‐related lateralizations in a flanker task. Psychophysiology 41: 762–771. [DOI] [PubMed] [Google Scholar]
- Yordanova J, Falkenstein M, Hohnsbein J, Kolev V ( 2004): Parallel systems of error processing in the brain. Neuroimage 22: 590–602. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found in the online version of this article.
Supportinf Information.
Supportinf Information.


