Abstract
The acquisition of functional magnetic resonance imaging (fMRI) data in a finite subset of k‐space produces ring‐artifacts and ‘side lobes’ that distort the image. In this article, we explore the consequences of this problem for functional imaging studies, which can be considerable, and propose a solution. The truncation of k‐space is mathematically equivalent to convolving the underlying “true” image with a sinc function whose width is inversely related to the amount of truncation. Spatial smoothing with a large enough kernel can eliminate these artifacts, but at a cost in image resolution. However, too little spatial smoothing leaves the ringing artifacts and side lobes caused by k‐space truncation intact, leading to a potential decrease in signal‐to‐noise ratio and statistical power. Thus, to make use of the high‐resolution afforded by MRI without introducing artifacts, new smoothing filters are needed that are optimized to correct k‐space truncation‐related artifacts. We develop a prolate spheroidal wave function (PSWF) filter designed to eliminate truncation artifacts and compare its performance to the standard Gaussian filter in simulations and analysis of fMRI data on a visual‐motor task. The PSWF filter effectively corrected truncation artifacts and resulted in more sensitive detection of visual‐motor activity in expected brain regions, demonstrating its efficacy. Hum Brain Mapp 2008. © 2007 Wiley‐Liss, Inc.
Keywords: fMRI, spatial smoothing, prolate spheroidal wave function, Gaussian smoothing, preprocessing, spatial filtering
INTRODUCTION
In functional magnetic resonance imaging (fMRI) studies it is common practice to spatially smooth the acquired data prior to performing statistical analysis. Spatial smoothing involves blurring the functional MRI images by convolving the image data with a filter kernel, most frequently a Gaussian, though other types of kernels (e.g., sinc kernel) may also be used. Gaussian smoothing is implemented in major software packages such as SPM (Statistical Parametric Mapping, Wellcome Institute of Cognitive Neurology, University College London), AFNI (Analysis of Functional Imaging Data), and FSL (FMRIB software library, Oxford). It is used primarily to minimize the errors in group analysis introduced by the spatial normalization of brains into a common space and to make data conform to the assumptions of Gaussian random field theory if it is used for correction for multiple comparisons (Worsley and Friston, 1995). In addition, if the spatial extent of a region of interest (ROI) is larger than the spatial resolution, smoothing may reduce random noise in individual voxels and increase the signal‐to‐noise ratio (SNR) within the ROI (Rosenfeld and Kak, 1982; Smith, 2003). Although it is advantageous to smooth data for these reasons, there are also obvious costs in spatial resolution. With larger sample sizes, higher field strengths, and other advances in imaging technology, many groups may wish to take advantage of the high potential spatial resolution of fMRI data and minimize the amount of smoothing.
However, there is a cost to not smoothing images that is perhaps under‐appreciated. The cost comes from the fact that data are acquired in a finite portion of k‐space, which is often quite limited in functional (T2*) acquisition schemes. To obtain a “perfect” reconstruction of an image, an infinite number of k‐space measurements need to be made. The restriction of sampling to a finite space introduces blurring in the image: this truncation is mathematically equivalent to convolving the image with a sinc function whose width is inversely related to the amount of k‐space that is sampled. The result is ringing artifacts and side lobes ‐ aliased portions of the image that extend beyond the actual location of the imaged object ‐ that distort the images (Fig. 1B). Such artifacts, if significantly large, may at best reduce signal to noise ratio, and at worst result in mis‐localization of functional activation.
Figure 1.
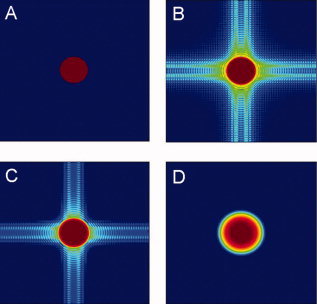
(A) A circular region of radius 22.5 mm is placed in an image with FOV 240 mm and theoretical k‐space measurements are calculated corresponding to a 64 × 64 region of k‐space. (B) Image reconstruction with no smoothing. The ringing is due to the fact that k‐space is truncated. (C) The image in (B) is smoothed using a Gaussian filter with 4 mm FWHM. The ringing artifacts are reduced but not completely eliminated. (D) The image in (B) is smoothed using a Gaussian filter with 12 mm FWHM. The ringing artifacts are eliminated, at the cost of reduced image resolution. The images are plotted on the log‐scale to better illuminate the ringing artifacts. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Spatial smoothing of images (e.g., with a Gaussian filter) can ameliorate these problems. The process of spatial smoothing is equivalent to applying a low‐pass filter to the sampled k‐space data. It has the effect of altering the spatial resolution in the image, as it reduces the intensity of high‐frequency points in k‐space, as well as changing the image's resulting point‐spread function. If the frequencies sampled in the images are higher than the filter cutoff, the high frequency information (i.e., fine spatial resolution) will be lost, though the side lobes will be eliminated (Fig. 1D). Alternatively, if the frequencies sampled are lower than those in the filter, direct application of the filter will not be able to completely eliminate the side lobes. In this case, k‐space is insufficiently sampled to support the applied filter and significant truncation artifacts will remain (Fig. 1C). The effective smoothing applied to the images will therefore be wider than intended. Thus, when image data are rather coarsely sampled (e.g. 64 × 64 3.75 mm voxels in a 240 mm field of view) special care needs to be taken to minimize truncation artifacts. In this article we show that in certain situations a Gaussian filter will not allow for control for these serious effects and should not be used when applying a narrow filter (e.g., with FWHM <8 mm) to a low resolution (e.g. 64 × 64) image. We show in a series of simulations that failure to take proper care of these issues will lead to a decrease in SNR and to decreased power in the resulting statistical tests.
In principal, one can make a distinction between two separate, but related, preprocessing steps. The first is the need to correct artifacts because of the reconstruction of finite k‐space data, and the second is smoothing as a means of increasing signal‐to‐noise and validating certain statistical techniques. While, most smoothing kernels are designed primarily to deal with the latter issue, they can if properly designed also be used to handle the former. One method that is well‐suited to controlling truncation artifacts is the 0th order prolate spheroidal wave function (PSWF) (Landau and Pollak, 1961, 1962; Slepian and Pollak, 1961). The PSWF is the function, with compact support on a fixed subset of k‐space, which maximizes the signal over a certain predefined subset of image‐space. Computationally, this function is the largest eigenfunction of the finite, or truncated, Fourier transform. It should be noted that discrete prolate spheroidal sequences (Slepian and Pollak, 1961) have previously appeared in the fMRI literature as part of the multitaper technique for temporal smoothing (Mitra and Pesaran, 1999; Mitra et al., 1997). The attractive features of the PSWF spatial smoothing filter are discussed in this article. Simulations show that the power to detect activation is significantly increased when using the PSWF filter instead of a Gaussian filter if the FWHM is below 8 mm. Further data from a visual task is used to illustrate its efficiency when applied to fMRI data.
In this work we will focus on comparing the PSWF filter with its Gaussian counterpart. However, it is important to note that a number of other studies have been concerned with finding alternatives to smoothing with a fixed Gaussian filter. For example, statistical analysis frameworks using Gaussians of varying width (Poline and Mazoyer, 1994; Worsley et al., 1996) and rotations (Shafie et al., 2003) have been proposed. As an alternative to using a Gaussian kernel, a number of articles have suggested the use of wavelets (see Van De Ville et al., 2006 for an excellent overview of the literature). In addition, data‐dependent smoothing methods have also been suggested. One promising example is the use of anisotropic diffusion (Kim et al., 2005). It should be noted that while the approach we are suggesting is data‐independent, as are both the Gaussian and wavelet techniques, it does depend on the acquisition parameters.
METHODS
Theory
Spatial smoothing
Spatial smoothing involves blurring the functional MRI images by applying a moving average filter to the images. When smoothing an image, each voxel is effectively transformed into the weighted sum over a ROI, which consists of the voxels lying under the kernel of the filter. The size of the kernel is determined by the full width at half maximum (FWHM), which measures the width of the kernel at 50% of its peak value. Hence, voxels that lie within the range defined by the FWHM are weighted higher than voxels lying outside of this range.
To carry out spatial smoothing in MRI, a smoothing matrix, representing the filter, is constructed which has the same size as the image. The image matrix is convolved with the smoothing matrix by first Fourier transforming both the image and the smoothing matrix, and then calculating the inverse Fourier transform of the product of these two matrices. The process of convolving the image using a smoothing kernel can be written as
| (1) |
where K(x) is the smoothing matrix, K̂(k) its Fourier transform, F̂(k) is the experimental sampling function in k‐space and F(x) is its corresponding inverse Fourier transform (the image). Here F̃(x) represents the value of the smoothed data at the coordinate point, x, of the image.
Typically when performing spatial smoothing in fMRI one uses a Gaussian kernel, though other choices are also possible. However, because of the popularity of the Gaussian we will concentrate on studying its properties in this particular article. It can be expressed on the form:
| (2) |
Convolving the image using the Gaussian kernel is equivalent to multiplying the k‐space data by the Fourier transform of the kernel function, which in turn can be written as:
| (3) |
Studying the Fourier transform of the Gaussian in Eq. (3), it is clear that it also follows a Gaussian distribution, in this case with a standard deviation equal to (2πσ)−1.
The width of the smoothing kernel is determined by the amount of spatial smoothing required and is written in terms of the FWHM. It is important to note that the relationship between the FWHM and the standard deviation of the Gaussian can be written as
| (4) |
Figure 2A (first and second row‐right column) shows an example of K Φ(x) and K̂ Φ(k) in one‐dimension. By studying the shape of K̂ Φ(k) it is clear that application of this filter devalues points in the outer regions of k‐space and is therefore equivalent to low‐pass filtering.
Figure 2.
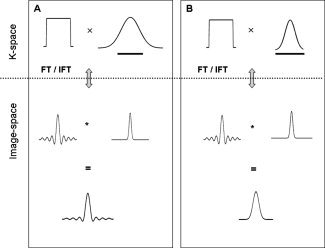
(A) A boxcar function (top left) is multiplied with a Gaussian kernel (top right). The line under the Gaussian shows the frequency extent of the boxcar compared to the Gaussian. After performing the inverse Fourier transform on the product, the result is equivalent by the Fourier Convolution Theorem, to convolving the point spread function (center left) with a Gaussian kernel (center right). The results of this convolution are shown in the bottom row. (B) A boxcar function (top left) is multiplied with a kernel (top right) designed to have the same frequency extent as the boxcar. After performing the inverse Fourier transform on the product, the result is equivalent to convolving the point spread function (center left) with the inverse Fourier transform of the kernel (center right). The results of this convolution are shown in the bottom row. The filter effectively controls for the ringing artifacts.
A well known fact about the Gaussian distribution states that 99.7% of its mass is contained in a region lying within three standard deviations of its mean. Because of the symmetric nature of the Gaussian, this region will make up a circular shape in two‐dimensions (spherical in three‐dimensions). Hence, 99.7% of the mass of K̂ Φ(k) will lie within a circular region with radius 3(2πσ)−1. Using this property, we can define an alternative measure for the extent of a filter. Let the width of the kernel in k‐space be defined as W, if 99.7% of the kernels mass lies in the range [−0.5W,0.5W]. Though the support of the Gaussian is infinite, the width of K̂ Φ(k) is related to the FWHM by Eq. (4) and can be expressed as
| (5) |
Similarly, we can define the width of the filter, K Φ(x), in image‐space as T, if 99.7% of the kernels mass in image‐space lies in the range [−0.5T,0.5T]. Hence, the width can be expressed using Eq. (4) as
| (6) |
Effective smoothing
As aforementioned, there is an additional source of blurring inherent in the reconstruction of MR images. This blurring is due to the fact that sampling is performed over a finite subset of k‐space. To obtain a “perfect” reconstruction of the underlying image one would need to sample an infinitely large region of k‐space. Unfortunately, this is not possible and k‐space is by necessity truncated. This truncation results in a ringing artifact in the image which is due to the under‐sampling of high spatial frequency components of k‐space (Fig. 1B). By truncating k‐space we are performing an operation that is mathematically equivalent to convolving the underlying “true” image with a sinc function, whose width is inversely related to the amount of truncation. It should be noted that throughout this article we are assuming that we are dealing with images that have been reconstructed using the inverse discrete Fourier transform (IDFT). Other reconstruction algorithms (e.g., SENSE and GRAPPA based reconstruction) give rise to other types of artifacts than those described earlier. However, since the bandwidth issues are comparable for all reconstruction techniques, the ringing artifacts are expected to be similar. For this reason, and the fact that most practitioners still work directly with images reconstructed using the IDFT, we concentrate on artifacts related to the IDFT in this work.
If one were to apply a filter with 4 mm FWHM directly to a 64 × 64 image, the resulting smoothed image would not possess the exact amount of smoothness that would be expected, as the applied filter is too narrow to completely eliminate the side‐lobes of the sinc function that arise because of truncation (Figs. 1C and 2A). It is important to realize that directly applying the filter to the image‐space data is equivalent, by the Fourier convolution theorem, to applying a truncated (in k‐space) version of the filter to the k‐space data. In the continuation we will refer to effective smoothing as the blurring in the image because of the combination of the applied filter and the truncation effects. The effective smoothing kernel will thus be the convolution of the applied filter and the sinc function that arises because of finite sampling (Fig. 2‐last row).
We measured the effects of ringing when applying a Gaussian filter, with varying FWHM (3–12 mm), directly to an image. If no truncation effects were present we would expect 99.7% of the mass to lie within ±3σ (or ±1.274 FWHM) of the center of the effective smoothing kernel, that is, within the width of the kernel. It is clear from Figure 3A that the proportion of the effective smoothing kernel that lies in this range is greatly affected for filters with FWHM less than 8 mm. Further, according to Figure 3B, the FWHM of the effective smoothing kernel deviates from the applied FWHM. It is clear that for narrow filters (FWHM <8 mm) this deviation becomes rather significant. For example, when the FOV is equal to 240 mm, a Gaussian filter with FWHM of 4 mm applied directly in image‐space will have an effective FWHM of 5.35 mm when the effects of finite sampling are included. In addition over 25% of its mass will lie outside of its intended width. It would clearly be beneficial to design a filter that is able to reduce the effects of truncation artifacts in the image. In the next section we discuss a filter that provides optimal control over truncation artifacts.
Figure 3.
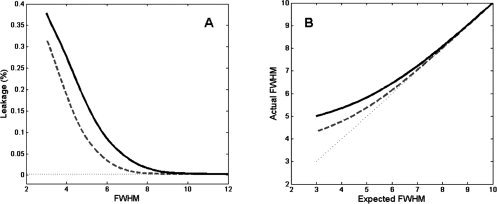
(A) The proportion of the effective Gaussian smoothing kernel that lies further than ±3σ (or ± 1.274 FWHM) from the center of the filter when N = 64 and the FOV is equal to 200 and 240 mm (dashed and bold line respectively). (B) The actual and expected FWHM plotted for a Gaussian filter for the case when N = 64 and the FOV is equal to 200 and 240 mm (dashed and bold line respectively). For comparison purposes the dotted line shows where the actual and expected FWHM coincide.
The prolate spheroidal wave function filter
The PSWF filter is the function, with compact support on a fixed set of k‐space, which maximizes the signal over a certain predefined subset of image‐space. To find this function, we begin by setting up the problem formulation. As k‐space consists of a sequence of discrete measurements during MRI data acquisition, it should therefore be chosen to be a discrete space. On the other hand, image‐space, denoted by Ω in this article, can be chosen to be either a discrete space consisting of a collection of the image voxels (e.g., the N × N voxels in an image) or as a continuous space. We discuss the latter below. Next, consider a convex ROI, denoted B, in image‐space and the k‐space sampling region, A (e.g., the collection of measured points on a 64 × 64 grid – see Fig. 4A,B). The objective is to find the filter function g(k), that satisfies the following two criteria:
-
1
It takes the value 0 for points outside of A.
-
2Its inverse Fourier transform, G(x), has maximal signal concentration in B, that is, the ratio
is maximized over all possible functions for which the first criterion holds.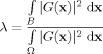
(7)
Figure 4.
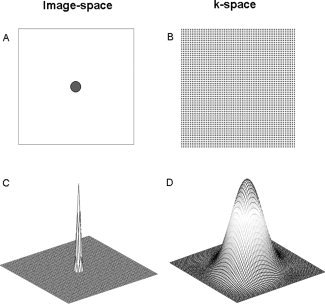
A circular region B in image‐space (top left) and a k‐space subset A (top right). The PSWF filter g(k) (bottom right) and its inverse Fourier transform G(x) (bottom left) corresponding to the choice of A and B. Note the minimal ringing present in the image‐space filter.
These conditions ensure that g(k) is the function with compact support on A, whose inverse Fourier transform has the least amount of signal leakage outside of the region B. Thus, it is the function with optimal control over ringing artifacts outside of B. Note that λ takes values between 0 and 1 and can be used to calculate the amount of signal leakage that the filter gives rise to outside of the predetermined ROI B.
As an additional constraint, the denominator of the ratio in Eq. (7) is set equal to one. This simplifies the problem to finding the function, g(k), with norm equal to one, whose inverse Fourier transform maximizes,
| (8) |
Using Parseval's identity, the problem can be written in matrix form as
| (9) |
under the constraint
| (10) |
Let us define K̂ B to be the Fourier transform of the indicator function of the region B, which can be written:
| (11) |
Then it can be shown (Lindquist, 2003; Lindquist et al., 2006; Yang et al., 2002; Shepp and Zhang, 2000) that the kernel, K̂ B, is given by,
| (12) |
for k,k′ ∈ A. A more detailed derivation of these results can be found in the Appendix. For simple regions B (e.g., circles, squares, and ellipses) there exist analytical expressions for K̂ B, which allow for easy computation of the kernel defined in Eq. (12).
The kernel K̂ B is positive definite which implies that all of its eigenvalues λk, k = 0,…a − 1, are non‐negative, where a denotes the number of points sampled in k‐space (e.g., a = N 2). In fact,
| (13) |
The eigenfunction, g 0, associated with the largest eigenvalue, λ0, is termed the 0‐order solution, and provides the solution to the problem stated in Eq. (7). In addition, λ0 is equal to the fraction of the total signal intensity in B calculated according to Eq. (7) and provides a quantitative measure of the signal leakage that the eigenvector gives rise to. A value of λ0 close to 1 indicates little signal leakage, while the leakage increases as λ0 decreases. The set of eigenfunctions g 0, g 1, … g a−1 have some interesting properties. As we will always choose A to be symmetrical about the center of k‐space (k = 0), the set of eigenvectors can always be taken to be real and orthogonal on B. In addition, the index i not only ranks the eigenvalues, but also specifies the number of zeros the function g i has within the region B (Percival and Walden, 1993). The function g 0 will therefore be positive over the whole region B, a property it shares with the Gaussian kernel.
By applying the filter g(k) directly to the k‐space data and thereafter taking the inverse Fourier transform of the filtered k‐space data, the resulting image will represent the true image convolved with the function G(x). Therefore the PSWF can be used as a filter to spatially smooth fMRI data. The amount of smoothing applied will depend upon the size of the region B. In our discussion of the PSWF filter it will often make more sense to talk about the filters width instead of the traditional FWHM used for the Gaussian. As long as λ ≥ 0.997, the width of the PSWF is bounded by the diameter of the region B, as this condition ensures that less than 0.3% of the signal lies outside of B. The PSWF filter has the important property that any other choice of filter will give rise to a greater amount of signal leakage outside of the spatial coverage region. Hence, the PSWF filter is chosen to minimize the amount of signal leakage, and thereby ringing, outside of the region B. This property leads us to believe that it has excellent potential as a spatial smoothing filter in fMRI.
In practice, one can construct a smoothing kernel by taking the IDFT of g(k) and reconstructing it onto a matrix with the same dimensions as the image. Smoothing can thereafter be performed in an analogous manner as for Gaussian, which is described algebraically in Eq. (1). In our implementation, A is chosen to correspond to the sampled region of k‐space (Fig. 4B) and B is chosen to be a circular region with diameter 1.274 FWHM (equal to 6σ) to ensure a kernel with similar width as a Gaussian filter of a given FWHM. Figure 4C,D show examples of G(x) and g(k) corresponding to the regions A and B. The PSWF filter shares many of the same qualities as the Gaussian filter. However, it is completely concentrated on a sub‐region, A, of k‐space, while the Fourier transform of the Gaussian kernel has infinite support. If one wishes to obtain a filter that more exactly mimics the properties of the Gaussian, A can be chosen as a circular region with diameter equal to the minimum of N and W, where N denotes the image dimensions and W the width of the Gaussian one seeks to mimic. This criteria ensures that the PSWF filter will have equivalent width in the frequency domain as the Gaussian whenever possible (W > N for filters with FWHM < 8 mm), and will therefore give rise to filters with similar properties in image‐space. It should be noted that the idea of matching the equivalent FWHM of a function is not new, and has been done before for different wavelet functions (Fadili and Bullmore, 2004; Van De Ville et al., 2003). Figure 5 shows the effective FWHM and leakage for a PSWF constructed in this manner, when N = 64 and FOV = 200 mm. Also included are similar plots for the Gaussian filter, which is equivalent to those shown in Figure 3. It is clear that the PSWF filter gives rise to filters that have equivalent properties to the Gaussian for FWHM > 8 mm. In addition, for narrow filters, it is clear that the PSWF filter gives improved control over the amount of leakage outside of the width of the filter. The price one pays for this is a slight increase in the effective FWHM of the filter. For comparison purposes we show in Figure 6 two examples of the combined effects of truncation and smoothing when using PSWF and Gaussian kernels. The left panel shows the results for a narrow filter (4 mm FWHM), while the right panel shows the results for a wide filter (12 mm FWHM). While the effective smoothing kernels are roughly equivalent for the wide filter, the narrow PSWF filter shows better control of ringing artifacts and slightly widened FWHM compared to its Gaussian counterpart. This is consistent with the results shown in Figure 5.
Figure 5.

(A) The proportion of the PSWF kernel (bold) and the Gaussian kernel (dashed) that lies further than ±3σ (or (1.274 FWHM) from the center of the filter when N = 64 and the FOV is equal to 200 mm. (B) The actual and expected FWHM plotted for the PSWF and Gaussian filter for the case when N = 64 and the FOV is equal to 200 mm (bold and dashed line respectively). For comparison purposes the dotted line shows where the actual and expected FWHM coincide.
Figure 6.
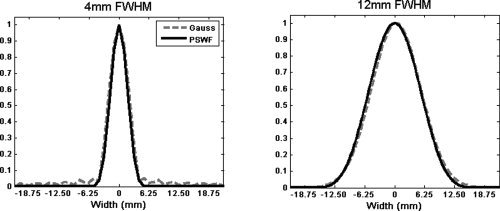
The effective smoothing kernel obtained using the PSWF (bold) and the Gaussian (dashed) with 4 mm (left) and 12 mm (right) FWHM (N = 64, FOV = 200 mm). While the filters are roughly equivalent for the wider FWHM, the narrow PSWF filter shows better control of ringing artifacts and slightly widened FWHM compared to its Gaussian counterpart.
Simulation Studies
Simulation 1
To more closely study the issues involved with truncation artifacts we performed a simulation study, in which a circular region of radius 22.5 mm was placed in the center of a blank image with FOV 240 mm (Fig. 1A). Using the simple geometry of the image, theoretical k‐space measurements were calculated corresponding to a 64 × 64 region of k‐space. The image was then reconstructed using the inverse fast Fourier transform (IFFT) (Fig. 1B) and Gaussian smoothing with 4 and 12 mm FWHM was applied to the resulting images. In addition, a PSWF filter with the same width as the Gaussian with 4 mm FWHM was applied to the data.
Simulation 2
(Part A) The image described in the previous simulation (Fig. 1A) was recreated 160 times. In 80 of the images the intensity for voxels within the circle was set to 1.0. These images were denoted as OFF images. In the remaining 80 images the intensity was set to 1.05. These are denoted as ON images. The images were thereafter ordered according to the paradigm of 4 repetitions of 20 OFF/20 ON images and Gaussian noise was added to the data with a standard deviation corresponding to a Cohen's d of 0.25 (Cohen, 1988). Theoretical k‐space measurements were calculated corresponding to a 64 × 64 region of k‐space and the images were reconstructed at this resolution using the IFFT. The resulting data was smoothed using both PSWF and Gaussian filters with FWHM equal to 4, 8, and 12 mm. The resulting data was analyzed using the standard GLM approach. This procedure was repeated 1,000 times and the statistical power to detect activation was calculated for each filter type and width. (Part B) The procedure outlined in part A was repeated using a more realistic activation pattern (Fig. 8B). Using a gray matter mask a region of activity was created. The resulting data was interpolated to 10 times its size (640 × 640) and the fast Fourier transform was used to calculate k‐space data. The central 64 × 64 region was used to mimic the effects of finite k‐space sampling. Using this data set the same experimental paradigm as described in (A), with 4 repetitions of 20 OFF/20 ON images, was created. The data was analyzed in an analogous manner as described in part A.
Figure 8.
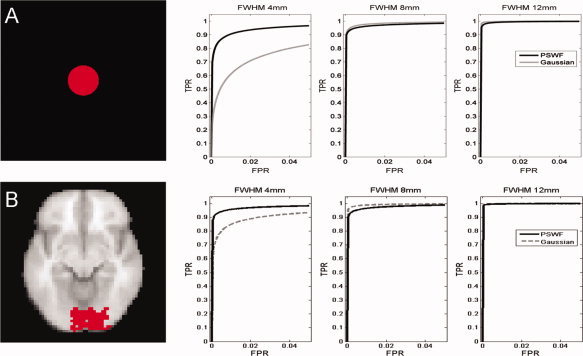
(A) The simulated activation pattern and ROC curves for Simulation 2A obtained using Gaussian (dashed) and PSWF (bold) filters with 3 different FWHM (4, 8, and 12 mm). For narrow filters (e.g., 4 mm) using a Gaussian filter will lead to a significant decrease in statistical power compared to the PSWF. (B) The same results for Simulation 2B. Analogous results hold in this situation.
Experiment
Nine students at the University of Michigan were recruited and paid $50 for participation in the study. All human participant procedures were conducted in accordance with Institutional Review Board guidelines. The experimental data consisted of a visual paradigm conducted on the nine subjects. It consisted of a blocked alternation of 11 s of full‐field contrast‐reversing checkerboards (16 Hz) with 30 s of open‐eye fixation baseline. Blocks of unilateral contrast‐reversing checkerboards were presented on an in‐scanner LCD screen (IFIS, Psychology Software Tools). Spiral‐out gradient echo images were collected on a GE 3T fMRI scanner (Noll et al., 1995). Seven oblique slices were collected through visual and motor cortex, 3.12 × 3.12 × 5 mm voxels, TR = 0.5 s, TE = 25 ms, flip angle = 90, FOV = 20 cm, 410 images. Data from all images were corrected for slice‐acquisition timing differences using 4‐point sinc interpolation (Oppenheim et al. 1999) and corrected for head movement using six‐parameter affine registration (Woods et al., 1998) prior to analysis.
For each subject Gaussian filters with FWHM of 4, 8, and 12 mm were applied to the slice of the data, which contained the largest signal over the visual cortex (slice No. 3). Thereafter, three PSWF filters, with equivalent width were applied to the same data set, giving a total of six series of smoothed images for each subject. Next a standard GLM analysis was performed on each of the 54 data sets (six series of smoothed images for each of the nine subjects). The data was thresholded and the number of active voxels in the visual cortex was counted for each series and a matched‐pairs sign‐test was performed for each level of smoothness. The test was designed to determine whether there is a significant difference in the number of active voxels between the two filter types across subjects.
RESULTS
Simulation Studies
Simulation 1
The simulated k‐space data was reconstructed using the IFFT (Fig. 1B) and Gaussian smoothing with 4 and 12 mm FWHM was applied to the resulting images (Fig. 7A,B). It is apparent that significant ringing artifacts exist in the reconstructed nonsmoothed image. It is also clear that the filter with 4 mm FWHM was able to minimize, but not completely eliminate, these artifacts. The filter with 12 mm FWHM successfully eliminated these artifacts, at the price of decreased spatial resolution. Next, we applied a PSWF filter with the same width as the Gaussian with 4 mm FWHM and applied this to the same data set (Fig. 7C). It is clear that the PSWF was able to effectively control the ringing artifacts, while still maintaining a similar spatial resolution as the 4 mm Gaussian. Figure 7D shows a cross‐section through the center of each image to better illustrate the ringing effects apparent in the various images. In particular note the smooth behavior of the PSWF compared to the 4 mm Gaussian.
Figure 7.
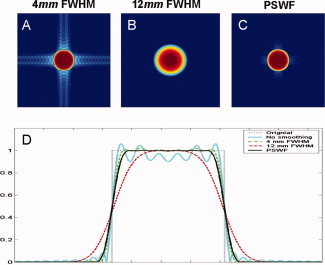
The image in Figure 1B is smoothed using a Gaussian filter with FWHM equal to (A) 4 mm and (B) 12 mm, as well as with a PSWF with width equivalent to a 4 mm Gaussian (C). The images (A–C) are plotted on the log‐scale to better illuminate the ringing artifacts. (D) A cross‐section through the center of each image (A–C, along with Fig. 1A,B) illustrates the ringing effects apparent in each case. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Simulation 2
The functional simulation studies described in the Methods section were repeated 1,000 times for each filter type and width. The resulting data was analyzed using a standard GLM approach and false positive rates and power were assessed. Figure 8 shows receiver operating characteristic (ROC) curves for the Gaussian (dashed) and PSWF (bold) filters corresponding to each of the three different FWHM (4, 8, and 12 mm) and both simulation types (A and B). For both simulations there is minimal difference in power between the two filter types for wider filters (e.g., 8 and 12 mm), while for narrow filters (e.g., 4 mm) using a Gaussian filter will lead to a significant decrease in statistical power compared to the PSWF.
Experimental Results
Table I shows the number of significant voxels (P‐value <0.005, uncorrected) in the visual cortex for each subject, obtained using both filter types for each of the three different degrees of smoothing. The P‐values in the last row show the results of a sign test for matched pairs. The null hypothesis of no difference in the number of active voxels is rejected (P‐value <0.05) for both 4 and 8 mm smoothing. The increase in the number of active voxels for the data smoothed using the PSWF voxel is due to the increased SNR in the data, as a result of minimizing the signal leakage, and is consistent with the theoretical results. Figure 9 show the results for five randomly chosen subjects for each of the 3 degrees of smoothing. It is clear that there is an increased number of active voxels in the PSWF‐smoothed data for narrow (≤8 mm) kernels. Finally, Figure 10 shows the difference in the number of significant voxels between the two smoothing methods as a function of the chosen threshold. It is clear that for the case when the FWHM is 4 mm, there is a significant increase in the number of active voxels when using the PSWF filter, which is consistent with the increase in power shown in Figure 8.
Table I.
The total number of significant voxels (P‐value <0.005) found in the visual cortex for data smoothed using both PSWF and Gaussian kernels for three different levels of smoothing (4, 8, and 12 mm)
| Subject | 4 mm | 8 mm | 12 mm | |||
|---|---|---|---|---|---|---|
| PSWF | Gauss | PSWF | Gauss | PSWF | Gauss | |
| 1 | 44 | 35 | 54 | 49 | 43 | 45 |
| 2 | 15 | 12 | 26 | 21 | 26 | 25 |
| 3 | 60 | 48 | 66 | 62 | 70 | 73 |
| 4 | 62 | 50 | 76 | 65 | 63 | 63 |
| 5 | 33 | 28 | 58 | 44 | 59 | 65 |
| 6 | 29 | 22 | 41 | 35 | 36 | 38 |
| 7 | 21 | 19 | 22 | 23 | 20 | 19 |
| 8 | 69 | 60 | 82 | 74 | 88 | 89 |
| 9 | 28 | 28 | 29 | 28 | 23 | 16 |
| P‐value | 0.0078 | 0.0391 | 0.7266 | |||
The results are shown for each of the nine subjects included in the experiment. The last row show P‐values from a sign test for matched pairs, which tests whether there is a significant difference in the number of active voxels between the two smoothing methods. The null hypothesis of no difference is rejected for both 4 and 8 mm smoothing at the 5% level of significance.
Figure 9.
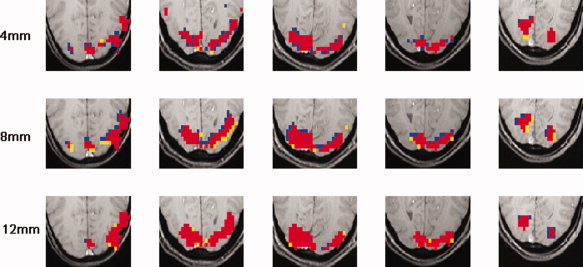
Statistical parametric maps, obtained from 5 randomly chosen subjects, showing voxels with significant activation (P‐value <0.005) for each of the three different degrees of smoothing. Red represents voxels that are significant for both data that was smoothed using the PSWF and the Gaussian filter. Blue indicates voxels that were significant for the PSWF data only and yellow voxels that were significant for the Gaussian data only.
Figure 10.
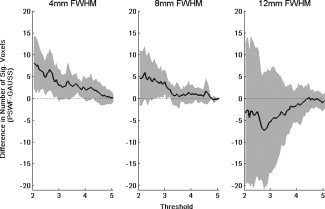
The difference in the number of significant voxels obtained using the PSWF and Gaussian kernel for a variety of thresholds (t* = 2, … 5 corresponding to P‐values ranging from 0.025 to 0) using filters with FWHM 4, 8, and 12 mm. It is clear that there is a significant increase in the number of active voxels in the 4 mm case when using the PSWF filter that is attributable to the increase in power shown in Figure 8.
DISCUSSION
In this article we have discussed two potential sources of blurring in fMRI data. The first is due to the algorithm used to reconstruct the image from finite k‐space data and is generally considered an unwanted artifact of image reconstruction. The second is due to the voluntary application of a smoothing kernel ‐ typically used to increase SNR. The sinc function shown in Figure 2 is the smoothing (spatial response function) that arises when reconstruction is performed using the IDFT. It is important to note that other reconstruction algorithms will ultimately give rise to other spatial response functions and may therefore be more or less effective in dealing with issues such as Gibbs ringing. For example, data obtained using parallel imaging techniques, do not reconstruct the image using the inverse DFT. In these situations the spatial response function is much more complicated than the sinc assumed in this article. While the results of this article can not be readily generalized to all reconstruction techniques, we have ultimately decided to focus on the artifacts that arise from using the DFT to reconstruct the images, as this is the type of data most practitioners will likely have to work with. In addition, as each reconstruction technique is faced with the same bandwidth problems the ringing artifacts should ultimately take a similar form. However, it should be noted that the PSWF methodology outlined in this article have been generalized to k‐space data that is sampled on noncartesian k‐space (Lindquist et al., 2006). Hence, this would in principal allow for reconstruction and smoothing of data obtained in any manner using the PSWF methodology.
In this work we have illustrated that when applying a narrow Gaussian filter (e.g. 4 mm FWHM) to low‐resolution data (e.g., 64 × 64), an insufficient number of measurements are made in k‐space to support the applied filter. Hence the smoothed images will contain more blurring than originally intended and the effective smoothing will be greater than the nominally applied smoothing. The truncation artifacts can be effectively controlled by applying a tapered filter function directly to the k‐space data. There are a number of ways of tapering the filter function. For example one can apply a Hamming filter to the truncated Gaussian, thereby eliminating its steep edges. However, in this work we introduce another tapered filter function, based on the theory of the PSWF, which can be used to control the amount of ringing in the resulting smoothed images. The PSWF has similar properties to the Gaussian, with the added benefit that it provides optimal control over truncation artifacts. The PSWF filter has an additional benefit that has not previously been discussed. Throughout this article we have defined the spatial coverage region of our filter, given by B, to be a circular region in order to obtain an isotropic filter comparable to a Gaussian. However, it is important to note that there is nothing in the theory of the PSWF that limits us to constructing isotropic filters, as B can be chosen to take other shapes as well. For example, we may want to choose B to be an oval or some other “blob‐like” shape and a filter with spatial coverage corresponding to this region can be constructed using the PSWF methodology (Lindquist et al., 2006; Yang et al., 2002).
In principal, the amount of smoothing applied is determined by the expected extent of activation. By the matched filter theorem, optimal filtering is provided by using a filter with the same spatial extent as the activation. Of course this region is never known exactly, making it difficult to determine the optimal amount of smoothing in practice. However, it is reasonable to assume that the activation pattern takes place in a coherent “blob” in the brain and it would be difficult to argue that the pattern would be rippled in the manner that would be present after the application of a narrow Gaussian filter. We therefore feel that the PSWF is more in the spirit of the matched filter theorem than the Gaussian. However, with the introduction of high‐field scanners and state‐of‐the‐art MR imaging techniques, the “problematic” spatial resolutions under discussion in this work (e.g., 64 × 64 matrix 3.75 mm resolution) may eventually become obsolete. In these situations the advantages of the PSWF filter over the Gaussian are less clear. On the other hand, in these situations the rational for smoothing at all is questionable.
It should be noted that the Convolution theorem (illustrated in Fig. 2) only holds when the filter is applied directly to the complex image‐space data and most researchers instead work with magnitude images. However, since the PSWF filter is positive and real‐valued in our implementation (like the Gaussian), it does not matter whether we apply the filter to the complex image‐space data or to the positive magnitude images. The results will be equivalent regardless and the Convolution theorem is still valid. The implementation of the filter is straightforward and Matlab code is available from the authors (http://www.stat.columbia.edu/~martin/Software.html). There is a one‐time cost in calculating the filter corresponding to a specific width, FOV and matrix size. This calculation involves calculating the largest eigenfunction of an a × a matrix. However, if we want an n‐dimensional smoothing kernel we can approximate them as the separable product of n one‐dimensional 0‐order PSWFs. This significantly simplifies calculation with minimal loss of efficiency.
Simulation studies showed an increase in power compared to Gaussian smoothing with a small FWHM (<8 mm). In addition, the experimental data presented in this article clearly showed the benefits of using a PSWF filter. In general, we feel that the increase in power shown in both simulations, in conjunction with the increased number of activated voxels in the experimental data, together make a strong case for the PSWF methods superiority when narrow kernels (<8 mm) are required for smoothing fMRI data. These results are consistent with the theory, which states that for narrow filters the PSWF has superior concentration properties compared to the Gaussian. By applying the PSWF filter we are able to increase the signal‐to‐noise by maintaining control over truncation effects.
While SNR is one important issue relating to spatial smoothing, also important are the statistical issues of inter‐subject variability and statistical validity. When using a tapered filter such as the PSWF these issues can only be positively impacted, as a reduction of the ringing effects can only be good for the subsequent statistical analysis, as it allows for construction of a kernel that better matches the extent of activation. Finally, we feel that it is reasonable to assume that the PSWF filter is interchangeable to the Gaussian in the sense that both can be used to provide the appropriate amount of smoothness needed to make the assumptions of the random field theory valid. In determining the appropriate filter width required for valid inference, we suggest using the same rule‐of‐thumb typically used for a Gaussian kernel (e.g., 2–3 voxels).
CONCLUSION
In this work a new spatial smoothing filter for fMRI is introduced. The filter is based on the use of PSWFs and provides optimal control of truncation artifacts present in MR images. The PSWF filter has the important property that any other choice of filter will give rise to a greater amount of signal leakage outside of the width of the filter. This property leads us to believe that it has excellent potential as a spatial smoothing filter in fMRI. Simulation studies showed a significant increase in power compared to the traditionally used Gaussian filter when smoothing with narrow filters (e.g., FWHM < 8 mm). Experimental data from a visual paradigm showed when smoothing with narrow filters the PSWF filter gave rise to a significant rise in the number of active voxels in the visual cortex compared to data smoothed with a comparable Gaussian filter. This rise is attributable to an increase in SNR.
For a given A and B, the prolate spheroidal wave function, g(k), is obtained by finding the function whose inverse Fourier transform maximizes the ratio in Eq. (7). With the proper normalization of G(x) we can assume that
| (A1) |
The problem then becomes finding the solution to the following equation, subject to the above constraint on G(x):
| (A2) |
We can rewrite the integral on the right hand side of Eq. (A2) as follows:
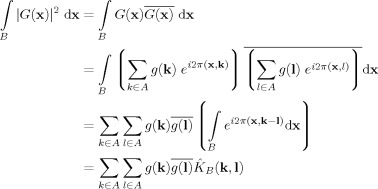 |
(A3) |
where
| (A4) |
Combining Eqs. (A2) and (A3), the problem now becomes solving the equation
| (A5) |
or, alternatively,
| (A6) |
where K̂ B is an a × a matrix with elements given by K̂ B(k,l) for k,l ∈ A. It is well known that the solution to this problem is the largest eigenfunction of the matrix K̂ B. This gives us the 0‐order prolate spheroidal wave function filter. One can construct a smoothing kernel by taking the IDFT of g(k) and reconstructing it onto a matrix with the same dimensions as the image. Smoothing can thereafter be performed in an analogous manner as for Gaussian, which is described algebraically in Eq. (1).
REFERENCES
- Cohen J ( 1988): Statistical Power Analysis for the Behavioral Sciences, 2nd ed., Hillsdale, NJ: Erlbaum. [Google Scholar]
- Fadili MJ,Bullmore ET ( 2004): A comparative evaluation of wavelet‐based methods for hypothesis testing of brain activation maps. NeuroImage 23: 1112–1128. [DOI] [PubMed] [Google Scholar]
- Kim HY,Giacomantone J,Cho ZH ( 2005): Robust anisotropic diffusion to produce enhanced statistical parametric map from noisy fMRI. Comput Vis Image Underst 99: 435–452. [Google Scholar]
- Landau HJ,Pollak HO ( 1961): Prolate spheroidal wave functions, fourier analysis and uncertainty, II. Bell Syst Tech J 40: 65–84. [Google Scholar]
- Landau HJ,Pollak HO ( 1962): Prolate spheroidal wave functions, fourier analysis and uncertainty, III. Bell SystTech J, 41: 1295–1336. [Google Scholar]
- Lindquist MA ( 2003): Optimal data acquisition in fMRI using prolate spheroidal wave functions. Int J Imag Syst Technol 13: 126–132. [Google Scholar]
- Lindquist MA,Zhang C‐H,Glover G,Shepp L,Yang QA ( 2006): Generalization of the two dimensional prolate spheroidal wave function method for non‐rectilinear MRI data acquisition methods. IEEE Trans Image Process 15: 2792–2804. [DOI] [PubMed] [Google Scholar]
- Mitra PP,Pesaran B ( 1999): Analysis of dynamic brain imaging data. Biophys J 76: 691–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra PP,Ogawa S,Hu X,Ugurbil K ( 1997): The nature of spatiotemporal changes in cerebral hemodynamics as manifested in functional magnetic resonance imaging. Magn Reson Med 37: 511–518. [DOI] [PubMed] [Google Scholar]
- Noll DC,Cohen JD,Meyer CH,Schneider W ( 1995): Spiral K‐space MR imaging of cortical activation. J Magn Reson Imaging 5: 49–56. [DOI] [PubMed] [Google Scholar]
- Oppenheim AV,Schafer RW,Buck JR ( 1999). Discrete‐Time Signal Processing, 2nd ed. Upper Saddle River, NJ: Prentice Hall. [Google Scholar]
- Percival DB,Walden A ( 1993): Spectral Analysis for Physical Applications. Cambridge, UK: Cambridge University Press. [Google Scholar]
- Poline JB,Mazoyer B ( 1994): Analysis of individual brain activation maps using hierarchical description and multiscale detection. IEEE Trans Med Imag 4: 702–710. [DOI] [PubMed] [Google Scholar]
- Rosenfeld A,Kak AC ( 1982): Digital Picture Processing, Vol. 2, Orlando, Florida: Academic Press. [Google Scholar]
- Shafie K,Sigal B,Siegmund D,Worsley K ( 2003): Rotation space random fields with an application to fMRI data. Ann Stat 31: 1732–1771. [Google Scholar]
- Shepp L,Zhang CH ( 2000): Fast functional magnetic resonance imaging via prolate wavelets. Appl Comput Harmonic Anal 9: 99–119. [Google Scholar]
- Slepian D,Pollak HO ( 1961): Prolate spheroidal wave functions, fourier analysis and uncertainty, I. Bell Syst Tech J 40: 43–64. [Google Scholar]
- Smith SM ( 2003): Preparing fMRI data for statistical analysis In: Jezzard P,Matthews PM,Smith SM, editors. Functional MRI: An Introduction to Methods. Oxford, UK: Oxford University Press. [Google Scholar]
- Van De Ville D,Blu T,Unser M ( 2003): Wavelets Versus Resels in the Context of fMRI: Establishing the Link with SPM. In the Proceedings of the SPIE Conference on Mathematical Imaging: Wavelet Applications in Signal and Image Processing X, San Diego, CA, 5207: 417–425.
- Van De Ville D,Blu T,Unser M ( 2006): Surfing the brain‐an overview of wavelet‐based techniques for fMRI data analysis. IEEE Eng Med Biol Mag 25: 65–78. [DOI] [PubMed] [Google Scholar]
- Woods RP,Grafton ST,Holmes CJ,Cherry SR,Mazziotta JC ( 1998): Automated image registration. I. General methods and intrasubject, intramodality validation. J Comput Assist Tomogr 22: 139–152. [DOI] [PubMed] [Google Scholar]
- Worsley K,Marrett S,Neelin P,Evans A ( 1996): Searching scale space for activation in PET images. Hum Brain Mapp 4: 74–90. [DOI] [PubMed] [Google Scholar]
- Worsley KJ,Friston KJ ( 1995): Analysis of fMRI time‐series revisited—Again. Neuroimage 2: 173–197. [DOI] [PubMed] [Google Scholar]
- Yang QX,Lindquist MA,Shepp L,Zhang CH,Wang J,Smith MB ( 2002): Two dimensional prolate spheroidal wave functions for MRI. J Magn Reson 158: 43–51. [DOI] [PubMed] [Google Scholar]


