Abstract
Objective:
To determine the functional connectivity of different EEG bands at the “baseline” situation (rest) and during mathematical thinking in children and young adults to study the maturation effect on brain networks at rest and during a cognitive task.
Methods:
Twenty children (8–12 years) and twenty students (21–26 years) were studied. The synchronization likelihood was used to evaluate the interregional synchronization of different EEG frequency bands in children and adults, at rest and during math. Then, graphs were constructed and characterized in terms of local structure (clustering coefficient) and overall integration (path length) and the “optimal” organization of the connectivity i.e., the small world network (SWN).
Results:
The main findings were: (i) Enhanced synchronization for theta band during math more prominent in adults. (ii) Decrease of the optimal SWN organization of the alpha2 band during math. (iii) The beta and especially gamma bands showed lower synchronization and signs of lower SWN organization in both situations in adults.
Conclusion:
There are interesting findings related to the two age groups and the two situations. The theta band showed higher synchronization during math in adults as a result of higher capacity of the working memory in this age group. The alpha2 band showed some SWN disorganization during math, a process analog to the known desynchronization. In adults, a dramatic reduction of the connections in gray matter occurs. Although this maturation process is probably related to higher efficiency, reduced connectivity is expressed by lower synchronization and lower mean values of the graph parameters in adults. Hum Brain Mapp 2009. © 2007 Wiley‐Liss, Inc.
Keywords: graph theory, small‐world networks, synchronization, functional connectivity, brain maturation, mathematical thinking
INTRODUCTION
Oscillatory phenomena corresponding to the electroencephalographic (EEG) frequency bands play a major role in functional communication in the brain at rest and during different integrative functions. Functional interactions between different brain regions may be studied by estimating statistical interdependencies between EEG signals recorded over different brain regions, a concept referred to as “functional connectivity.” The connectivity at rest and during various tasks is expressed differently by the distinct frequency bands [Bąsar et al, 2001; Bruns and Eckhorn, 2004; Dumermuth et al., 1971; Palva et al., 2005; Röhm et al., 2001; Sauseng et al., 2002; Varela et al., 2001]. Most studies have been performed in adults. Several studies have shown the influence of maturation on the immature EEG signals of childhood [Clarke et al., 2001; Dustman et al., 1999]. This raises the question whether general patterns can be detected in the way functional brain networks mature.
Connectivity at rest and during cognitive tasks has been studied using several methods [Ioannides, 2007; Sporns et al., 2000; Stam et al., 2007]. Recently, tools from graph theory have been used in several studies to investigate the general properties of the spatial structure of anatomical as well as functional networks as studied with EEG, MEG and fMRI [Achard et al., 2006; Basset and Bullmore, 2006; He et al., 2007; Humphries, 2006; Stam and Reijneveld, 2007; Stam et al., 2007]. The connectedness of the neuronal assemblies is usually assessed with two characteristic measures of the representations of the networks (graphs). The first measure is the clustering coefficient (C), a measure of “transitivity,” which indicates the connectedness of the nodes neighbors (if A connects to B and C, what is the chance that B and C will be connected as well). The second measure is the path length (L), which is an indicator of the overall connectedness (integration) of the graph. With these measures the topological organization of the neural networks involved in the generation of the EEG signals in various frequency bands and their interrelations can be studied. Further computation of these measures and comparison with random networks can provide information about a property called “small‐world” network organization, referring to the near‐optimal networks, which are intermediate between ordered and random networks. They correspond to graphs with many local connections and a few random distance connections. They are characterized by a high clustering coefficient (like ordered networks) and a short path length (like random networks). An optimal SWN organization has been found in anatomical, functional neuroimaging and electrophysiological studies to occur in healthy individuals [He et al., 2007; Sporns et al., 2000; for review see: Stam and Reijneveld, 2007]. In contrast, brain pathology changes network structure, generally in the direction of more “random” networks [Micheloyannis et al., 2006; Stam et al., 2007].
In the present study we address the following two questions: (i) does normal ageing influence network structure? (ii) is the ageing effect on network structure influenced by task demands? For this study we evaluated the synchronization and organization of the neuronal networks using the synchronization likelihood (SL) i.e., a linear and nonlinear estimation of the synchronization of the neuronal networks separately for each frequency band and then constructed graphs to evaluate their properties, in particular C and L. This was done at rest and during a difficult mathematical task in a group of children and in another group of young adults. Since there is evidence that SWN organization is a cost‐effective information processing system established during the evolution [Basset and Bullmore, 2006], we wanted to study the influence of maturation and the changes during a cognitive task in children and adults.
MATERIALS AND METHODS
Twenty children aged 8–12 years and twenty students of the medical faculty in Crete, aged 21–26 years were evaluated. The children had no medical history. Intellectual and school‐achievement abilities and behavior were normal. They were tested using four subscales of the Greek version of the WISC‐III test, the auditory association and reception subscales of the Greek version of the Illinois test of psycholinguistic abilities, the ZAREKI test for calculation abilities and the Greek version of the child behavior checklist. The students had no pathological history and no learning difficulties as shown by good degrees in the previous 2 years of their study in the university. The EEG recording was performed, while the individuals were comfortably seated in a declined chair in a dimly illuminated and sound attenuated room. The EEG was recorded from 30 electrodes according to the international 10/20 system: FP2, F4, FC4, C4, CP4, P4, O2, F8, FT8, T4, TP8, PO8, Fz, FCz, Cz, CPz, Pz, Oz, FP1, F3, FC3, C3, CP3, P3, O1, F7, FT7, T3, TP7, PO7, and A1 + A2 as reference. First they fixed on a small star on the screen of a PC. Then followed the second part of the EEG recording while they performed a difficult calculation, while looking on the numbers they calculated presented on the PC screen. The calculations presented intended to produce, apart from specific activations, simultaneously widespread cortical activation as known to occur in difficult mathematical calculations [Micheloyannis et al., 2005]. Many similar calculations as those used in the study were given and tested in students and children of the same age span prior to the study. They succeeded about 80% of these tests. The calculations were two‐digit multiplications for students, a difficult task, and two‐digit subtractions for children since, after their curriculum, this was a difficult mathematics, while the two‐digit multiplications were impossible for the children.
The EEGs were recorded using “CONTACT Precision Instruments amplifiers” and with the help of a “DATAQ AD Converter.” From the EEG recorded during these calculations, we selected off line from the screen of a PC one artifact free epoch of 8 s (4,096 samples with a sample frequency of 500 Hz) from each subject and for each condition. The pieces corresponding to the mathematics were pieces during successful calculations. We computed the SL using the DIGEEGXP software developed by one of the authors (Cornelis J. Stam). The parameter settings for this computation were as described by Montez et al. [ 2006]. A brief description is given in the Appendix A. The SL is a measure of statistical independencies between a time series and one or more other time series within a dynamical system sensitive to linear and nonlinear independencies. It has been used in normal and pathological studies and it takes in account the linear as well as the nonlinear properties of the EEG signals [Montez et al., 2006; Ponten et al., 2007; Stam, 2005; Stam et al., 2007]. Using a zero phase pass‐band filer, we defined the EEG bands, using the classic EEG bands as employed in many EEG studies. From the EEG filtered in theta (4–8 Hz), alpha1 (8–10 Hz), alpha2 (10–13 Hz), beta (13–30 Hz), and gamma (30–45 Hz) bands we calculated the mean values of the SL as an index of the average synchronization. We did not analyze delta and higher gamma bands because of contamination of artifacts (eye movement or muscle activity) in these bands and because the information extracted from the analyzed bands is proper for the proposed cognitive evaluations. Each 30 × 30 synchronization matrix of size 30 i.e., the number of channels, was converted into a binary (unweighted) graph using a threshold so that SL values higher than the threshold indicate the existing edges [see Stam and Reijneveld, 2007; Stam et al., 2007 and Appendix B]. Since the structure of the graph is generally biased by the number of existing edges, statistical measures should be calculated on graphs of equal degree K. Therefore, threshold T was chosen such for each analyzed epoch that all the produced graphs had a fixed mean degree (K = 5), which is the average number of edges per node of the graph (see and Appendix B). The choice for K = 5 was identical to a previous study on similar experiment, in which C and L were calculated as a function of K and subsequent t‐tests between the two groups revealed significant differences of L in a neighborhood around K = 5 [Micheloyannis et al., 2006; Montez et al., 2006]. Then, we computed their characteristic parameters C (clustering coefficient) and L (path length) as well as the other graph theoretical parameters (for explanations, see Appendix B). The values of C and L were compared with the corresponding values of ensembles of twenty random graphs (C‐s, L‐s) using the ratios λ = L/L‐s and γ = C/C‐s. Subsequently, a summary measure of “small‐worldness” can be defined by the ratio S = γ/λ, which will be greater than 1 for small‐world networks [Humphries et al., 2006; Stam and Reijneveld, 2007; Stam et al., 2007]. For statistics we used SPSS 14.0 for windows and we performed a repeated measures ANOVA for each frequency band and for the mean SL values averaged over all electrode pairs, C, L, C/C‐s, L/L‐s, and S taking the two situations (rest, math) as within subjects' factors for the two groups (children or students as between subject factors). Since values of SL are bounded (P ref < SL < 1), departure from normality should be carefully considered. A test for normality is not useful for samples of this size leaving us with the option of data transformation. Therefore, we repeated the statistical analysis after transforming the data using the logit transform: y = log (x/(1 − x)). There was no alteration on the significance of the hypothesis testing results compared with the ones using the raw data. For the gamma band we repeated the analysis with two cases excluded. These two individuals were outliers showing great differences in their values i.e., high values explained as the result of muscle artifacts.
RESULTS
Figure 1 shows the mean values of SL and Figure 2 the mean values of S of the different bands, the two groups, the rest situation and the math task. Table I shows the mean C and L values and Table II the mean values of S and the corresponding values of C/C‐s and L/L‐s.
Figure 1.
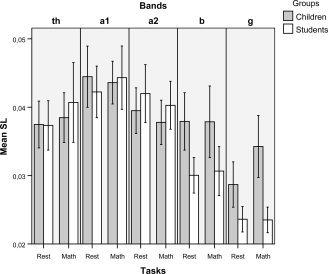
Presented are the mean SL values in children and adults of the different frequency bands during rest and the cognitive task (math); error bars = 95% of the CI. Significant differences are: (1) Increase of theta band during math in students [Rest values 0.0373 (SD = 0.0072); Math values 0.0407 (SD = 0.0117) i.e., 8.35% higher, P = 0.029]. (2) Increase of gamma band during math in comparison with rest in children [Rest values 0.0289 (SD = 0.0068); Math values 0.0378 (SD = 0.0035) i.e., 23.54% higher, P = 0.010]. (3) At rest the values of beta band were higher in children [Children 0.0379 (SD = 0.0089); Students 0.0300 (SD = 0.0052) i.e., 20.84% higher, P = 0.002]. (4) At rest the values of gamma band were higher in children [Children 0.0289 (SD = 0.0068); Students 0.0237 (SD = 0.0035) i.e., 17.99% higher in children, P = 0.010]. (5) During math, the values of beta band were higher in children [Children 0.0379 (SD = 0.0112); Students 0.0307 (SD = 0.0072) i.e., 18.99% higher in children, P = 0.025]. (6) During math, the values of gamma band were higher in children [Children 0.0378 (SD = 0.0184); Students 0.0262 (SD = 0.0117) i.e., 30.68% higher in children, P < 0.001].
Figure 2.
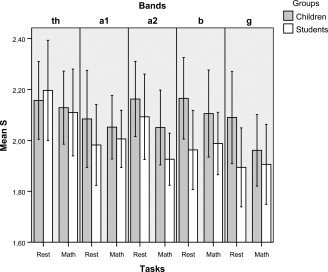
The bars present the mean values of S (the small world index) during the rest situation and the cognitive task (math) in children and adults for all the frequency bands studied (error bars = 95% of the CI). Significant higher are the values of S at rest for the beta band in children in relation to the students [9.37% higher, P = 0.025].
Table I.
The C and L values at rest and during math in both groups
| Bands | Children rest C: mean ± SD | Children math C: mean ± SD | Children rest L: mean ± SD | Children math L: mean ± SD | Students rest C: mean ± SD | Students math C: mean ± SD | Students rest L: mean ± SD | Students math L: mean ± SD |
|---|---|---|---|---|---|---|---|---|
| Theta | 0.3760 ± 0.0663 | 0.3768 ± 0.0673 | 2.3450 ± 0.1346 | 2.3708 ± 0.238 | 0.3690 ± 0.0727 | 0.3696 ± 0.0574 | 2.3074 ± 0.1169 | 2.3722 ± 0.2027 |
| Alpha1 | 0.3706 ± 0.0687 | 0.3669 ± 0.0486 | 2.4134 ± 0.3157 | 2.4277 ± 0.2293 | 0.3465 ± 0.0635 | 0.3608 ± 0.0426 | 2.3544 ± 0.1825 | 2.4088 ± 0.1991 |
| Alpha2 | 0.3788 ± 0.0691 | 0.3537 ± 0.0571 | 2.4348 ± 0.3763 | 2.3363 ± 0.1812 | 0.3611 ± 0.0511 | 0.3421 ± 0.0488 | 2.3712 ± 0.2374 | 2.3897 ± 0.2176 |
| Beta | 0.3887a ± 0.0574 | 0.3808 ± 0.0669 | 2.4342 ± 0.2847 | 2.4685 ± 0.2910 | 0.3448a ± 0.0582 | 0.3646 ± 0.0537 | 2.3998 ± 0.1760 | 2.4874 ± 0.2189 |
| Gamma | 0.3796b ± 0.0666 | 0.3946c ± 0.0598 | 2.4774d ± 0.2418 | 2.7441d ± 0.4787 | 0.3288b ± 0.0494 | 0.3443c ± 0.0572 | 2.4200 ± 0.1924 | 2.4873 ± 0.2978 |
The beta values of C in children at rest were 11.29% higher in relation to those of students: P = 0.025.
The gamma band values of C in children at rest were 13.38% higher in relation to those of students: P = 0.017.
The C values of children during math were 12.75% higher in relation to those of the students: P = 0.017.
The L values of children at rest were 10.76% higher in relation to those during math : P = 0.001.
Table II.
The graph parameters at rest and during math in both groups: the “raw” data of C p/<C p−r and L p/<L p−r and the S values
| Bands | Children rest: C p/C p−s (mean ± SD) | Children math: C p/C p−s (mean ± SD) | Children rest: L p/L p−s (Mean ± SD) | Children math: L p/L p−s (mean ± SD) | Children rest: S (mean ± SD) | Children math: S (mean ± SD) |
|---|---|---|---|---|---|---|
| Theta | 2.5880 ± 0.4582 | 2.5869 ± 0.4778 | 1.1970 ± 0.0679 | 1.2133 ± 0.1240 | 2.1571 ± 0.3262 | 2.1286 ± 0.3066 |
| Alpha1 | 2.5588 ± 0.4776 | 2.5411 ± 0.3586 | 1.2362 ± 0.1605 | 1.2421 ± 0.1200 | 2.0844 ± 0.4073 | 2.0521 ± 0.2673 |
| Alpha2 | 2.6832 ± 0.4740 | 2.4387 ± 0.3829 | 1.2454 ± 0.1919 | 1.1911 ± 0.0942 | 2.1628 ± 0.3155 | 2.0506 ± 0.3143 |
| Beta | 2.6897 ± 0.4519 | 2.6502 ± 0.5285 | 1.2472 ± 0.1474 | 1.2622 ± 0.1509 | 2.1654a ± 0.3418 | 2.1055 ± 0.3650 |
| Gamma | 2.6060 ± 0.4669 | 2.7584 ± 0.4095 | 1.2632 ± 0.1231 | 2.0723 ± 0.3748 | 2.0005 ± 0.3343 | |
| Bands | Students rest: Cp/Cp−s (mean ± SD) | Students math: Cp/Cp−s (mean ± SD) | Students rest: Lp/Lp−s (mean ± SD) | Students math: Lp/Lp−s (mean ± SD) | Students rest: S (mean ± SD) | Students math: S (mean ± SD) |
| Theta | 2.5999 ± 0.5612 | 2.5481 ± 0.4200 | 1.1800 ± 0.0616 | 1.2117 ± 0.1033 | 2.1962 ± 0.3962 | 2.1097 ± 0.3428 |
| Alpha1 | 2.3967 ± 0.4904 | 2.4711 ± 0.3268 | 1.2041 ± 0.1217 | 1.2320 ± 0.1017 | 1.9821 ± 0.3191 | 2.0061 ± 0.22578 |
| Alpha2 | 2.5251 ± 0.4147 | 2.3559 ± 0.3360 | 1.2120 ± 0.1217 | 1.2120 ± 0.1100 | 2.0927 ± 0.3377 | 1.9262 ± 0.2061 |
| Beta | 2.4095 ± 0.4177 | 2.5193 ± 0.3285 | 1.2280 ± 0.0889 | 1.2704 ± 0.1106 | 1.9627a ± 0.3126 | 1.9877 ± 0.2466 |
| Gamma | 2.3235 ± 0.3669 | 2.4017 ± 0.4745 | 1.2342 ± 0.0994 | 1.2691 ± 0.1533 | 1.8878 ± 0.2940 | 1.8930 ± 0.3015 |
Beta band in children has 9.36% higher values of S during rest in comparison with the corresponding values of students: P = 0.025.
The main findings are the increased SL values of theta and gamma band during math. Additionally, the SL values were higher in children compared with adults for both the higher bands and both conditions. The graph parameters for alpha2, beta, and gamma bands are indicative of a degree of change of the organization towards more random networks in adults. Additionally, graph parameters of alpha2 band show a decline of SWN organization during math. Beta and especially gamma band also show a similar decline during math. In detail:
-
1
Theta band: For SL there was a significant main task effect: The SL for math was higher than the SL at rest; (P = 0.039; F [1.36] = 4.582) and for students the SL values were higher for math in relation to rest (P = 0.029) as resulted from the pair wise comparisons. The graph parameters C, L, and S showed no differences.
-
2
Alpha1 band: No differences were found in any of the measures.
-
3
Alpha2 band: The C values showed a significant main task effect: The values during math were lower in comparison with the values at rest (P = 0.023; F [1.36] = 5.660). The values of S showed a significant decline during math: The main task effect was significant; (P = 0.029; F [1.36] = 5.175) with lower values during math.
-
4
Beta band: The SL values showed a significant main group effect i.e., higher values for children than for students (P = 0.006; F [1.36] = 8.534). The SL values for children were higher at rest as well as during the math task in comparison with the values of the students: For rest (P = 0.002; F [1.36] = 10.629) and for the math task (P = 0.025; F [1.36] = 5.447). For C, the values at rest were lower in adults in comparison with the children (P = 0.025; F [1.36] = 5.465).
-
5
Gamma band: For SL there was a significant main group effect (P < 0.001; F [1.34] = 17.379) as well as a significant task by group interaction (P = 0.011; F [1.34] = 7.229). At rest, the children showed higher values in relation to the students (P = 0.010; F [1.34] = 7.394). Additionally, during math, the children showed higher values in relation to the students (P = 0.000; F [1.34] = 19.450). The children showed higher values during math in relation to rest (P = 0.010; F[1.34] = 14.772).
The C values showed a significant main group effect: The values for adults were lower in comparison with those of children (P = 0.010; F [1.34] = 7.527). Additionally, the pair wise comparison showed lower values in adults in comparison with the children at rest (P = 0.017; F [1.34] = 6.348) as well as during math (P = 0.017; F [1.34] = 6.289). The L showed a significant main task effect with higher values during math in relation to the rest (P = 0.010; F [1.34] = 7.395), a significant task by group interaction (P = 0.022; F [1.34] = 5.768) and a main group effect: The children showed higher values in relation to the students (P = 0.037; F [1.34] = 4.693). The pair wise comparison showed higher values for children in relation to the students during the math task (P = 0.017; F [1.34] = 6.328). In children the values of L were higher during math in comparison with the rest situation (P = 0.001).
DISCUSSION
In this study, we used an estimate of linear and nonlinear synchronization and then graph theoretical tools to interpret the neural networks of EEG bands of children and young adults at rest and during a cognitive task i.e., a difficult mathematical calculation. We found differences in network organization of all but the alpha1 band related to age, condition and bands. In detail:
Synchronization as Expressed by the SL
The increase of the synchronization of theta band during the math task as shown by the main task effect is explained by the increase in WM function during math [Canolty et al., 2006; Humphries et al., 2006; Schack et al., 2002; Stam et al., 2002]. The more prominent enhancement of theta band synchronization during WM in adults could be explained as the result of the differences in the WM capacity. There was no WM overload since performance on most of the math tasks were successful as shown by the clinical data and the difficulty of the math tasks was adjusted to the age and education. WM capacity increases especially from childhood to adolescent, which expands up to the end of the second decade of the life [Blakemore and Choudnhury, 2006; Klingberg, 2006; Luna, 2004; Whitford et al., 2007]. WM, like other cognitive functions, depend on distinct specialized areas of the cortex, which communicate via neural connectivity across specialized brain regions [Paus, 2005; Röhm et al., 2001; Stam et al., 2002]. Gray and white matter maturation during puberty is characterized by reduction of neuronal connections such that infrequently used connections are eliminated, a process called “pruning” [Kuhn, 2006; Paus, 2005]. An expression of this dramatic reduction in the number of cortical synapses (about 40%) is the reduction of the EEG power at rest. In the white matter, myelinization is enhanced to improve the efficiency of the neuronal connections. Thus, more selective and stronger neuronal connections during activations are the result of the maturation [Kuhn, 2006]. This organization due to maturation may explain the enhanced theta synchronization of the students during WM as the result of the math task in comparison with the values of the rest situation.
The alpha frequency band was separately evaluated in lower and higher frequencies since there are different frequency effects [Klimesch, 1999; Laufs et al., 2006; Stam et al., 1999]. Many studies have found differing patterns of reactivity when the alpha frequency is divided in the lower and higher frequencies [Fink et al., 2005; Klimesch, 1999]. There are some studies showing similar reactivity patterns of both frequencies in the alpha range in contrast to other studies where they have found distinct patterns and there is evidence that in simple tasks, there is a similarity in the reactions and more difficult tasks show different reactions and some kind of functional specialization of the lower and upper frequencies [Fink et al., 2005]. In the present study the SL values for both alpha bands showed no differences between the two groups or the tasks.
The higher synchronization of the higher “cognitive” [Bruns and Eckhorn, 2004; Haenschel et al., 2000; Hermann et al., 2004; Kaiser and Lutzenberger, 2005] bands in childhood at rest and during the cognitive task is interesting and has not been previously described. The maturation of the cortex accompanied by synaptic elimination could explain this difference of SL in the range of the higher frequency bands. These frequencies express short or local connectivity in the cortex, independent of the fact that they can be activated simultaneously with lower frequencies. Thus, the SL with its sensitivity to linear and nonlinear connectivity shows the interesting finding that the synchronization in these bands is higher in children at rest. Additionally, the children react with higher synchronization during math as expressed by the gamma band eventually because of the richer connections in this age. The adults have reduced connections and react more efficient with less synchronization needed. This synchronization mainly involves regions co activated by connections related to slower bands, “mature” in this age.
Graph Parameters
The alpha2 frequency band showed interesting findings. The lower C and S values of the alpha2 band during math in both groups are indicative of lower local clustering with lower SWN organization of the alpha2 band during the difficult math task, which produces more widespread cortical activation [Micheloyannis et al., 2005]. This reorganization during math towards the randomization (lower S) and less local (low C) organization during the difficult math task is interesting although difficult to explain. As known from the desynchronization of this frequency band during this cortical reactivity seen in EEG signals, a simultaneous increase of blood oxygen level is seen in functional magnetic resonance imaging indicative of an increase in cortical activity [Laufs et al., 2006]. This means that (visual and attentional) activated cortical areas show more tide regional functions in relation to rest. These changes during math occurring in some places in cortex could result in lowering of the measured C since the measured C is the mean value. Lowering of the mean value of C has as result lowering of S values as well.
The higher, beta and gamma frequency bands, express mainly short and local connections enhanced during activations. The children show enhanced interregional synchronization in the baseline situation as well as during the cognitive task. Graph parameters show differences in rest and during math between children and adults. These findings are more prominent in the gamma band. The optimal SWN organization, which is the evolutionary goal is evident in children and differs in some degree in adults in both situations for the higher frequencies, especially for the gamma band. In children, a vast majority of short cortical connections are the anatomical substrate for the beta and gamma bands responsible for the SWN organization of the default situation with higher synchronization and local clustering values. Thus, the changes of the higher frequency bands towards less SWN organization occur in adults where an enormous reduction of the short connections has changed the anatomical substrate. Although these changes intent higher efficiency, our measurements show differences of the parameters, which we can explain as the result of the reduction of the number of connections between the nodes resulting in lower local clustering and SWN organization.
Conclusion
The above mentioned findings using a synchronization measure and graph theoretical methods, are related (i) to the organization of the neuronal networks of the different EEG frequency bands at rest i.e., at the so called “baseline” or the “default mode” [Morcom and Fletcher, 2006] in children and adults and (ii) to the changes of these bands during a cognitive process known to produce increased WM and widespread cortical reaction. During childhood, the cortical connections are denser, while they are reduced in the students. However, in adults the overall loss of synapses may be counterbalanced by enhancement of special connections. Thus, during maturation, fine changes of the local and distant interconnections occur [Kuhn, 2006] and the baseline shows anatomical differences in the two age groups influencing the organization of the “default mode” in children and adults. During a function such as a cognitive task, the changed patterns of connections due to maturation are expressed by differences in neuronal connectivity organizations.
During the cognitive task, theta band show enhanced synchronization more prominent for adults (WM, which has higher capacity in adults) and alpha2 band show a decline of the “optimal” SWN organization, an interesting finding indicative of some disorganization, which could be related to the known desynchronization. Concerning the higher frequencies, they show differences in the “baseline” between children and adults. The synchronization shows lower values at rest in adults and the graph parameters show organization towards the random networks in adults. Gamma band shows less SWN organization in adults at rest and during math in comparison with the corresponding values of children whereas beta band shows such a difference only at rest. The SWN organization developed for better performance is more obvious in children. The anatomical changes occurring during maturation intent also to more efficient differentiation.
Using scalp electrodes as nodes to construct the graphs, theta and alpha bands give more precise results since they have higher power and are the expression of distant connections. In contrast, higher frequencies have lower power and express connections in short distances. These factors result in difficulties for precise interpretation of the high frequency bands using graphs constructed from the scalp electrodes. Nevertheless, the less SWN organization of the higher bands can be explained as the result of anatomical changes. In children there exist high connectivity and more SWN organization, in adults reduced connectivity at rest and reduced but more efficient connectivity during the cognitive process. The above findings add new knowledge concerning the organization of the different EEG bands at the baseline in children and adults as well as their reactivity during the cognitive activation.
Acknowledgements
This research was performed with support by the BIOPATTERN EU program.
APPENDIX A.
Calculation of the Synchronization Likelihood
The SL [Montez et al., 2006; Ponten et al., 2007; Stam, 2005; Stam et al., 2007] is a measure of the generalized synchronization between two dynamical systems X and Y. Generalized synchronization exists between X and Y of the state of the response system is a function of the driver system: Y = F(X). The first step in the computation of the SL is to convert the time series xi and yi recorded from X and Y as a series of state space vectors using the method of time delay embedding [Stam and Reijneveld, 2007]: (1)
| (1) |
where L is the time lag, and m is the embedding dimension. From a time series of N samples, N − mL vectors can be reconstructed. State space vectors Yi are reconstructed in the same way.
SL is defined as the conditional likelihood that the distance between Yi and Yj will be smaller than a cut‐off distance ry given that the distance between Xi and Xj is smaller than a cut‐off distance rx. In the case of maximal synchronization this likelihood is 1; in the case of independent systems, it is a small, but nonzero, number, namely P ref. This small number is the likelihood that two randomly chosen vectors Y (or X) will be closer than the cut‐off distance r. In practice, the cut‐off distance is chosen such that the likelihood of random vectors being close is fixed at P ref, which is chosen the same for X and for Y. To understand how P ref is used to fix rx and ry we first consider the correlation integral: (2)
| (2) |
Here the correlation integral C(r) is the likelihood that two randomly chosen vectors X will be closer than r. The vertical bars represent the Euclidean distance between the vectors. N is the number of vectors, w is the Theiler correction for autocorrelation [Theiler, 1986] and θ is the Heaviside function:
Now, rx is chosen such that C(rx) = P ref and ry is chosen such that C(ry) = P ref. The SL between X and Y can now be formally defined as:
| (3) |
SL is a symmetric measure of the strength of synchronization between X and Y (SLXY = SLYX). In Equation (3) the averaging is done over all i and j; by doing the averaging only over j, SL can be computed as a function of time i. From (3) it can be seen that in the case of complete synchronization SL = 1; in the case of complete independence SL = P ref. In the case of intermediate levels of synchronization P ref < SL <1.
In the present study the following parameters were used: P ref was set at 0.01, for the state space embedding a time lag of 10 samples, an embedding dimension of 10 and a Theiler correction of 0.1 [Montez et al., 2006; Ponten et al., 2007].
APPENDIX B.
Explanation of the Graph Parameters Calculation
A threshold was applied on the synchronization matrix to derive unweighted (binary) graphs [see also Montez et al., 2006; Stam and Reijneveld, 2007; Stam et al., 2007]. According to this, elements of the synchronization matrix exceeding a certain threshold T designate an existing connection between the corresponding pair of nodes (i.e. channels). The clustering coefficient C and the characteristic path length L were subsequently used to characterize the local and global structure of the calculated graphs.
The clustering coefficient Ci of a vertex i with degree ki is defined as the ratio of the number of existing edges (ei) between neighbours of i, and the maximum possible number of edges between neighbours of i.
The clustering coefficient C of the graph is the average over all vertices Ci
The path length di,j between two vertices i and j is the minimal number of edges that have to be travelled to go from i to j. The characteristic path length L of a graph is the mean of the path lengths between all possible pairs of vertices.
To avoid the problem of the disconnected graphs we used an alternative approach based on the global efficiency E [Latora and Marchiori, 2001] where L is calculated as the reciprocal of the average of the reciprocals.
It should be noted that the actual procedure involved conversion of the synchronization matrix to a graph for each subject first and finally averaging over subjects the individual values of C and L for a given T. Selection of the threshold T was done on the basis of obtaining a fixed degree, in which this study was set to K = 5. The comparison of C and L between the groups using a common value of K assures that any differences represent changes in graph organization.
The values of C and L were also compared with the corresponding values of “equivalent” random graphs generated according to a procedure that preserves the degree distribution [Sporns and Zwi, 2004]. For each subject, twenty random graphs were generated for K = 5 and the average values of clustering index C‐s and path length L‐s were compared with the ones of the real EEG data.
For a small‐world network the expected ratio λ = L/L‐s is ∼1, while the ratio γ = C/C‐s is greater than 1. To summarize these two ratios, we calculated the scalar measure S = γ/λ, which will be greater than 1 for small‐world networks, that is, networks of greater than random clustering and near random path length.
REFERENCES
- Achard S,Salvador R,Whitcher B,Suckling J,Bullmore Ed ( 2006): A resilient, low‐frequency, small‐world human brain functional network with highly connected association cortical hubs. J Neuroscience 26: 63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bąsar E,Bąsar‐Eroglu C,Karakąs S,Schürmann M ( 2001): Gamma, alpha, delta, and theta oscillations govern cognitive processes. Int J Psychophysiol 39: 241–248. [DOI] [PubMed] [Google Scholar]
- Basset DS,Bullmore Ed ( 2006): Small‐world networks. Neuroscientist 12: 512–523. [DOI] [PubMed] [Google Scholar]
- Blakemore S‐J,Choudnhury S ( 2006): Development of the adolescent brain: Implications for executive function and social cognition. J Child Psychol Psychiatry 47: 296–312. [DOI] [PubMed] [Google Scholar]
- Bruns A,Eckhorn R ( 2004): Task related coupling from high‐ to low‐frequency signals among visual cortical areas in human subdural recordings. Int J Psychophysiol 51: 97–116. [DOI] [PubMed] [Google Scholar]
- Canolty RT,Edwards E,Dalal SS,Soltani M,Nagarajan SS,Kirsch HE,Berger MS,Barbaro NM,Knight RT ( 2006): High gamma power is phase‐locked to theta oscillations in human neocortex. Science 313: 1626–1628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke AR,Barry RJ,McCarthy R,Selikowitz M ( 2001): Age and sex effects in the EEG: Development of the normal child. Clin Neurophysiol 112: 806–814. [DOI] [PubMed] [Google Scholar]
- Dumermuth G,Huber PJ,Kleiner B,Gasser T ( 1971): Analysis of interrelations between frequency bands of EEG by means of bispectrum‐preliminary study. Electroencephalogr Clin Neurophysiol 31: 137–148. [DOI] [PubMed] [Google Scholar]
- Dustman RE,Shearer DE,Emmerson RV ( 1999): Life‐span changes in EEG spectral amplitude, amplitude variability and mean frequency. Clin Neurophysiol 110: 1399–1409. [DOI] [PubMed] [Google Scholar]
- Fink A,Brabner RH,Neuper C,Neubauer AC ( 2005): EEG alpha band dissociation with increasing task demands. Cogn Brain Res 24: 252–259. [DOI] [PubMed] [Google Scholar]
- Haenschel C,Baldeweg T,Croft RJ,Whittington M,Gruzelier J ( 2000): Gamma and beta frequency oscillations in response to novel auditory stimuli: A comparison of human electroencephalogram (EEG) data with in vitro models. Proc Natl Acad Sci USA 97: 7645–7650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermann CS,Munk MHJ,Engel AK ( 2004): Cognitive functions of gamma activity: Memory match and utilization. Trends Cogn Sci 8: 347–355. [DOI] [PubMed] [Google Scholar]
- Humphries MD,Gurney K,Prescott TJ ( 2006): The brainstem reticular formation is a small‐world, not scale‐free network. Proc Biol Sci 273: 503–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannides AA ( 2007): Dynamic functional connectivity. Curr Opin Neurobiol 17: 1–10. [DOI] [PubMed] [Google Scholar]
- Kaiser J,Lutzenberger W ( 2005): Human gamma‐band activity: A window to cognitive processing. NeuroReport 16: 207–211. [DOI] [PubMed] [Google Scholar]
- Klimesch W ( 1999): EEG alpha and theta oscillations reflect cognitive and memory performance: A review and analysis. Brain Res Rev 29: 169–195. [DOI] [PubMed] [Google Scholar]
- Klingberg T ( 2006): Development of a superior frontal‐intraparietal network for visuo‐spatial working memory. Neuropsychologia 44: 2171–2177. [DOI] [PubMed] [Google Scholar]
- Kuhn D ( 2006): Do cognitive changes accompany developments in the adolescent brain? Perspect Psychol Sci 1: 59–67. [DOI] [PubMed] [Google Scholar]
- Latora V,Marchiori M ( 2001): Efficient behaviour of small‐world networks. Phys Rev Lett 87: 198701. [DOI] [PubMed] [Google Scholar]
- Laufs H,Holt JL,Elfont R,Krams M,Paul JS,Krakow K,Kleinschmidt A ( 2006): Where the BOLD signals goes when alpha EEG leaves. NeuroImage 31: 1408–1418. [DOI] [PubMed] [Google Scholar]
- Luna B,Garver KE,Urban TA,Lazar NA,Sweeney JA ( 2004): Maturation of cognitive processes from late childhood to adulthood. Child Dev 75: 1357–1372. [DOI] [PubMed] [Google Scholar]
- Micheloyannis S,Sakkalis V,Vourkas M,Stam CJ,Simos PG ( 2005): Neural networks involved in mathematical thinking: Evidence from linear and non‐linear analysis of electroencephalographic activity. Neurosci Lett 373: 212–217. [DOI] [PubMed] [Google Scholar]
- Micheloyannis S,Pachou E,Stam CJ,Breakspear M,Bitsios P,Vourkas M,Erimaki S,Zervakis M ( 2006): Small‐world networks and disturbed functional connectivity in schizophrenia. Schizophr Res 87: 60–66. [DOI] [PubMed] [Google Scholar]
- Morcom AM,Fletcher PC ( 2007): Does the brain has baseline? Why we should be resisting a rest. NeuroImage 37: 1073–1082. [DOI] [PubMed] [Google Scholar]
- Montez T,Linkenkaer‐Hansen K,van Dijk BW,Stam CJ ( 2006): Synchronization likelihood with explicit time‐frequency prions. Neuroimage 33: 1117–1125. [DOI] [PubMed] [Google Scholar]
- Palva JM,Palva S,Kaila K ( 2005): Phase synchrony among neuronal oscillations in the human cortex. J Neurosci 25: 3962–3972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paus T ( 2005): Mapping brain maturation and cognitive development during adolescence. Trends Cogn Sci 9: 60–68. [DOI] [PubMed] [Google Scholar]
- Ponten SC,Bartolomei F,Stam CJ ( 2007): Small‐world networks and epilepsy: Graph theoretical analysis of intracerebrally recorded menial temporal lobe seizures. Clin Neurophysiol 118: 918–927. [DOI] [PubMed] [Google Scholar]
- Röhm D,Klimesch W,Haider H,Doppelmayr M ( 2001): The role of theta and alpha oscillations for language comprehension in the human electroencephalogram. Neurosci Lett 310: 137–140. [DOI] [PubMed] [Google Scholar]
- Sauseng P,Klimesch W,Gruber W,Doppelmayr M,Stadler W,Schabus M ( 2002): The interplay between theta and alpha oscillations in the human electroencephalogram reflects the transfer of information between memory systems. Neurosci Lett 324: 121–124. [DOI] [PubMed] [Google Scholar]
- Schack B,Vath N,Petsche H,Geissler H‐G,Moeller E ( 2002): Phase coupling of theta‐gamma EEG rhythms during short‐term memory processing. Int J Psychophysiol 44: 143–163. [DOI] [PubMed] [Google Scholar]
- Sporns O,Zwi JD ( 2004): The small‐world of the cerebral cortex. Neuroinformatics 2: 145–162. [DOI] [PubMed] [Google Scholar]
- Sporns O,Tononi G,Edelman GE ( 2000): Connectivity and complexity: The relationship between neuroanatomy and brain dynamics. Neural Netw 13: 909–922. [DOI] [PubMed] [Google Scholar]
- Stam CJ ( 2005): Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin Neurophysiol 116: 2266–2301. [DOI] [PubMed] [Google Scholar]
- Stam CJ,Reijneveld JC. ( 2007): Graph theoretical analysis of complex networks in the brain. Nonlinear Biomed Phys 1:3. doi: 10.1186/1753‐4631‐1‐3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam CJ,Pijn JPM,Suffczynski P,Lopes da Silva FH ( 1999): Dynamics of the human alpha rhythm: Evidence for non‐linearity? Clin Neurophysiol 110: 1801–1813. [DOI] [PubMed] [Google Scholar]
- Stam CJ,van Cappellen van Walsum AM,Micheloyannis S ( 2002): Variability of EEG synchronization during a working memory task in healthy subjects. Int J Psychophysiol 46: 53–66. [DOI] [PubMed] [Google Scholar]
- Stam CJ,Jones BF,Nolte G,Breakspear M,Scheltens Ph ( 2007): Small‐world networks and functional connectivity in Alzheimer's disease. Cereb Cortex 17: 92–99. [DOI] [PubMed] [Google Scholar]
- Theiler ( 1986): Spurious dimensions from correlation algorithms applied to limited time series data. Phys Rev A 34: 2427–2432. [DOI] [PubMed] [Google Scholar]
- Varela F,Lachaux J‐P,Rodriguez E,Martinerie J ( 2001): The brainweb: Phase synchronization and large‐scale integration. Nat Rev Neurosci 2: 229–239. [DOI] [PubMed] [Google Scholar]
- Whitford TJ,Rennie CJ,Grieve SM,Clark CR,Gordon E,Williams LM ( 2007): Brain maturation in adolescence: Concurrent changes in neuroanatomy and neurophysiology. Hum Brain Mapp 28: 228–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y,Chen ZJ,Evans AC ( 2007): Small‐world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex 17: 2409–2419. doi:10.1093/cercor/bhl 149. [DOI] [PubMed] [Google Scholar]


