Hand sensory–motor cortical network assessed by functional source separation

Abstract

The functional source separation procedure (FSS) was applied to identify the activities of the primary sensorimotor areas (SM1) devoted to hand control. FSS adds a functional constraint to the cost function of the basic independent component analysis, and obtains source activity all along different processing states. Magnetoencephalographic signals from the left SM1 were recorded in 14 healthy subjects during a simple sensorimotor paradigm—galvanic right median nerve stimuli intermingled with submaximal isometric thumb opposition. Two functional sources related to the sensory flow in the primary cortex were extracted requiring maximal responsiveness to the nerve stimulation at around 20 and 30 ms (S1a, S1b). Maximal cortico‐muscular coherence was required for the extraction of the motor source (M1). Sources were multiplied by the Euclidean norm of their corresponding weight vectors, allowing amplitude comparisons among sources in a fixed position. In all subjects, S1a, S1b, M1 were successfully obtained, positioned consistently with the SM1 organization, and behaved as physiologically expected during the movement and processing of the sensory stimuli. The M1 source reacted to the nerve stimulation with higher intensity at latencies around 30 ms than around 20 ms. The FSS method was demonstrated to be able to obtain the dynamics of different primary cortical network activities, two devoted mainly to sensory inflow, and the other to the motor control of the contralateral hand. It was possible to observe each source both during pure sensory processing and during motor tasks. In all conditions, a direct comparison of source intensities can be achieved. Hum Brain Mapp, 2008. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

In a preceding paper [Barbati et al., 2006], a novel source‐extraction method from magnetoencephalographic extra‐cephalic signals was introduced. This new procedure, named functional source separation (FSS), adds a functional reactivity constraint to a basic independent component analysis (ICA) algorithm, and optimizes a cost function where a task‐related constraint is added to the kurtosis maximization of the standard ICA model, to bias the extraction towards the cerebral source of interest. A single source, corresponding to the global maximum of the cost function, is extracted at each time. In Barbati et al. [2006], two cortical sources describing the thumb and the little finger were obtained, and an adequate description of the highly interconnected and temporally overlapping primary hand cortical network was achieved. Taking into account the optimization procedure used in the algorithm, FSS is a flexible instrument having the possibility to include different functional constraints.

In the present work, we move from the description of different hand district sensory representation to study the cortical sources devoted to the hand motor control. It is far from necessary to underline the importance of assessing the motor component of the hand central representation. It is well known the difficulty in realizing the experimental setting to record the activity sustaining the voluntary motor performance, as it requires many repetitions of extremely abrupt and precise movements, which is a situation especially hard when patients are involved. In the last years, the coupling of cortical and muscular rhythmic oscillations has been introduced to characterize the cortical control of voluntary movement, which requires much simpler patient compliance and lower motor control abilities. In fact, systematic cortico‐muscular coherence characteristics, assessed by simple isometric contraction periods, were shown to be related to the patterns of motor output and sensory input, not only in healthy subjects [Brown et al., 1998; Brown and Marsden, 2001; Conway et al., 1995; Gross et al., 2000; Kristeva‐Feige et al., 2002], but also in patients suffering from a wide spectrum of movement disorders [Brown et al., 1999; Kristeva et al., 2004; Timmermann et al., 2003; Volkmann et al., 1996].

Magnetoencephalography (MEG), which provided the first noninvasive demonstration of oscillatory cortex–muscle coupling [Conway et al., 1995; Volkmann et al., 1996], is a noninvasive technique, which detects at the cranial surface magnetic fields generated by postsynaptic currents associated with synchronous neuronal firing in the brain at rest or in response to an external stimulus [for review, see Del Gratta et al., 2001]. Because of their physical properties, MEG signals are not influenced by extra‐cerebral intervening tissues, and do not need any reference electrodes; therefore, they allow accurate localization of the brain sources of the stimulus‐related activities, with high accuracy in the sensorimotor areas devoted to hand control [Hari et al., 1984; Pizzella et al., 1999; Tecchio et al., 1997; Wikstrom et al., 1997; Zappasodi et al., 2006].

On this basis, in the present paper the new source‐extraction procedure was applied with different functional constraints to extract three sources in SM1. The first constraint required source maximal cortico‐muscular coherence. The other two were related to the response to the nerve stimulation. To identify the neural cortical network describing the well, known marker of the stimulus arrival in the primary sensory cortex (M20), generated by excitatory postsynaptic potentials impinging on pyramidal neurons within Broadman area (BA) 3b, one of these two constraints required the maximal responsiveness at around 20 ms [Allison et al., 1991; Hari and Kaukoranta, 1985; Tecchio et al., 1997]. The other one required the maximal responsiveness at around 30 ms (M30 component). In this way, the network reflecting intra‐cortical connectivity was taken into account. It is in fact the sum of the inhibitory postsynaptic potentials of the intra‐cortical structures impinging on pyramidal neurons within BA 3b, and of the excitatory postsynaptic potentials impinging on pyramidal neurons within the primary motor area [BA 4, Huang et al., 2000; Kawamura et al., 1996; Tecchio et al., 1997, 2005; Wikstrom et al., 1996]. The final aim was to achieve cortical source activities describing both sensory and motor cortical networks devoted to the contralateral hand control. To validate the three FSS source extraction, three criteria of “goodness” were used, that is, reactivity properties of each source during movement (isometric low‐force contraction) and galvanic median nerve stimulation, source position, residual task‐related signal present in the original data not explained by the extracted source.

MATERIALS AND METHODS

Fourteen healthy and drug‐free volunteers (9 males, 5 females, mean age 41 ± 15, age range 24–66 years) were enrolled. All subjects were right‐handed, with an average Edinburgh Manuality test [Oldfield, 1971] of 83 ± 16. The approval of the local Ethical Committee and subject informed consents were obtained.

Experimental Procedures

A tone beep indicated to the subjects to alternate periods of relax and isometric contraction of the right Opponens Pollicis (OP, median nerve‐supplied) in pressing a water sphygmomanometer (Fig. 1). Before starting the experiment, each subject adjusted the isometric contraction at a level of around 20–35% of the maximal OP contraction. All along the experiment, the level of contraction was controlled by visual feedback on the water sphygmomanometer. A train of electric pulses lasting 10 s was delivered on the median nerve at wrist (interstimulus interval 631 ms, intensity at 300%‐sensory threshold) while the subject was at rest. In this way, data related to three different conditions were collected (Fig. 1), i. e., rest with open eyes (Relax), median nerve stimulation (Sensory), voluntary isometric contraction (Motor). This procedure lasted 10 min.

Figure 1.

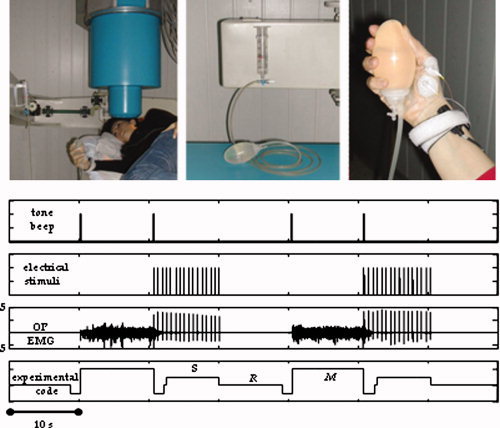
(Top) From left: Subject position during recordings from Rolandic area contralateral to the moved/stimulated hand. Nonmagnetic device, i.e., a water sphygmomanometer, to control the level of contraction. Particular of the thumb position during OP contraction, with electrodes recording the EMG signal as well as the median nerve stimulation at wrist. (Bottom) From the top: Trigger indicating a tone beep for starting/stopping the isometric contraction. Trigger indicating sensory stimuli to the median nerve at wrist. EMG signal, where relax and contraction periods are clearly noticeable, as well as the sensory stimulus artifact. Off line‐generated signal code differentiating the three experimental conditions as follows: Relax (R), Sensory (S), Motor (M). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Recordings

MEG measurements were performed using a 28‐channel system operating in a magnetically shielded room (Vacuumschmelze GMBH), the active channels being regularly distributed on a spherical surface (13.5 cm of curvature radius) covering a total area of about 180 cm². Cerebral activity from left rolandic areas, contralateral to the contracted or stimulated hand, was recorded via a single position, by centring the recording apparatus on the C3 position of the 10–20 international electroencephalographic (EEG) system. Ag–AgCl cup electrodes served for recording electrooculogram and electrocardiogram in order to control for eye blinking or cardiac interferences. The electromyographic (EMG) activity of the right OP was acquired by electrode pairs in a collodium montage, with the active electrode placed on the skin over the belly of the muscle, and the reference electrode on the tendon at a distance of 2.5 cm.

Data were sampled at 1,000 Hz (presampling analogical filter 0.48–256 Hz), and collected for off‐line processing

Data Analysis

Functional source separation

The FSS procedure introduced by Barbati et al. [2006] was applied after saturated‐trial exclusion. This procedure provides the extracted‐source activity during the different experimental conditions, with the same recording time resolution.

The procedure starts from a basic ICA model (fastICA, [Hyvarinen et al., 2001], in which the set of MEG signals X are assumed to be obtained as a linear combination (through an unknown mixing matrix A) of statistically independent non‐Gaussian sources S (at most one Gaussian):

(1)

Sources S are estimated (up to arbitrary scaling and permutation) by independent components Y as:

(2)

where the unmixing matrix W is estimated along with the ICs Y. In the FSS procedure, additional information to bias the decomposition algorithm towards solutions that satisfy physiological assumptions are explicitly used by the contrast function:

(3)

where J is kurtosis generally used in fastICA, λ is a parameter to weigh the two parts of the contrast function (Appendix 1), and R _FS accounts for the prior information we used to extract single sources. Different R _FS are used for different source extractions, starting each time from the original MEG data matrix; this means that the extracted sources (FS) are not required to be orthogonal.

Accordingly, with the sensorimotor network under investigation, in the present work the three ad‐hoc functional constraints R _FS below were introduced.

We decided to identify in the primary cortex two functional sources related to the sensory flow induced by median nerve stimulation. The first one, named S1a, describes the activity related to the well‐known marker of the stimulus arrival in the primary sensory cortex [Allison et al., 1991; Hari and Kaukoranta, 1985; Tecchio et al., 1997]. This is known to be mainly generated by excitatory postsynaptic potentials impinging on BA 3a pyramidal cells. As it is maximally recruited at around 20 ms from the stimuli at wrist, the functional constraint taking into account the “reactivity” to the stimuli was defined as:

(4)

with the evoked activity EA computed by averaging source (FS = S1a) signal epochs triggered on the median nerve stimulus at wrist (t = 0); t ₂₀ is the time point with the maximum magnetic‐field value on the maximal original MEG channel around 20 ms (searched in the [16–24] ms window) after the stimulus arrival; Δ₁ t ₂₀(Δ₂ t ₂₀) = time point corresponding to a field amplitude of 50% of the maximal value, by definition in t ₂₀, before (after) t ₂₀; the baseline (no response) was computed in the time interval from 10 to 15 ms. As only one component is extracted at each time, it is possible to avoid the amplitude indeterminacy inherent to the general ICA method. Once the source that optimizes the contrast function F has been obtained, the estimated solution is multiplied by the Euclidean norm of its weight vector a _S1a (a _S1a such as a _S1a = a _S1a â_S1a, with |â_S1a| = 1), allowing amplitude comparisons among sources in a fixed position.

We considered a second cerebral source named S1b, i.e., the source maximally activated at around 30 ms from nerve stimulation, in the sensory areas. This one is mainly generated by BA 3b inhibitory and BA 4 excitatory networks [Huang et al., 2000; Kawamura et al., 1996; Tecchio et al., 2005; Wikstrom et al., 1996]. The functional constraint was defined as:

(5)

EA was computed as in Eq. (4) with FS = S1b; t ₃₀ corresponded to the maximum magnetic‐field value on the maximal channel around 30 ms (searched in the [26–36] ms window) after the stimulus arrival; Δ₁ t ₃₀ and Δ₂ t ₃₀ were as in Eq. (4), with t ₃₀ instead of t ₂₀; the baseline was defined as in Eq. (4). Again, the estimated solution was multiplied by the Euclidean norm of its weight vector a _S1b (a _S1b such as a _S1b = a _S1b â_S1b, with |â_S1b| = 1).

To identify the source in the primary motor area (named M1), the coupling of cortical and muscular rhythmic oscillations in the beta band was taken into account. In fact, it has been demonstrated that the component of the synchronized cortical activity, coupled to synchronous rhythmic motor‐unit firing, assessed by surface EMG, within this band, characterizes aspects of cortical control on voluntary movement [Conway et al., 1995; Gross et al., 2000; Kilner et al., 2000; Tecchio et al., 2006], and is generated in the primary motor cortex [Brown et al., 1998; Brown, 2000; Gerloff et al., 2006]. The corresponding functional constraint was:

(6)

where Coh is a function of frequency ω, obtained for each ω as the amplitude of the cross‐spectrum between the source (FS = M1) signal and the rectified EMG, normalized by the root mean square of the power spectral densities of these two signals; the Bartlett procedure with a frequency resolution of 1.95 Hz (average of time segments lasting 512 ms, Hamming window, no overlap) was followed; Δ₁ω_max(Δ₂ω_max) = frequency point corresponding to a coherence amplitude of 50% of the maximal value between [13.5–33] Hz, called ω_max, before (after) ω_max.

As for S1a and S1b, M1 was obtained by multiplying it by the Euclidean norm of its weight vector a _M1 (a _M1 such as a _M1 = a _M1â_M1, with |â_M1 = 1).

For the cortico‐muscular coherence, the 95% confidence limit was estimated according to Halliday et al. [1995], by 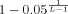, where L is the number of averages (about 200, resulting in a limit of 0.015).

Extracted source evaluation

Behaviour

Functional extracted source activation properties were studied during the different experimental conditions. The indexes below were used to estimate the activation of each source (S1a, S1b, and M1), both during galvanic stimulation of the contralateral median nerve, and during the voluntary contraction. In particular, each source reactivity to the nerve stimulation was evaluated around 20 ms as:

(7)

where R _S1a, Δ₂ t ₂₀, and Δ₁ t ₂₀ are defined as in Eq. (4), and FS = S1a, S1b, M1.

For each source the reactivity to the nerve stimulation around 30 ms was also considered

(8)

where R _S1b, Δ₂ t ₃₀, and Δ₁ t ₃₀ are defined as in Eq. (5) and FS = S1a, S1b, M1.

The source behaviour during movement was estimated by

(9)

where R _M1, Δ₂ω_max, and Δ₁ω_max are defined as in Eq. (6) and FS = S1a, S1b, M1.

Position

The extracted sources representing primary sensory and motor areas (S1a, S1b, and M1) were separately retro‐projected so as to obtain their field distribution, by:

(10)

with: FS = S1a, S1b, M1.

A moving equivalent current dipole (ECD) model inside a homogeneous sphere was used. ECD coordinates were expressed in a right‐handed Cartesian coordinate system defined on the basis of three anatomical landmarks (the x y‐plane passing through the two preauricolar points and the nasion, the x‐axis passing through the two preauricolar points directed rightward, the y‐axis orthogonal to x‐axis passing through the midpoint between the two preauricolar points. The positive z‐axis was positioned consequently, PAN coordinates). Only sources with a goodness‐of‐fit exceeding 90% were accepted. It is to be noted that the field distribution obtained by retro‐projecting only one component is time‐invariant up to a scale factor; consequently, the subtending current distribution shape (ECD position, in our case) is time‐independent. For the M1 source, a more complex nature of the neural recruitment sustaining a simple voluntary isometric contraction is indicated in previous literature [Dum and Strick, 2005; Grafton et al., 1991; Graziano et al., 2002; Indovina and Sanes, 2001; Poliakov and Schieber, 1999; Sanes et al., 1995]. For this reason, a multi‐dipolar model was used, and the number of dipoles for each subject was obtained by maximizing the goodness of fit.

Discrepancy

To check for the level of residual response to the nerve stimulation after source S1a extraction, we defined a “discrepancy response” index as follows:

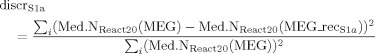(11)

where Med.N_React20(MEG) and Med.N_React20(MEG_rec_S1a) are the reactivity indexes as defined in Eq. (7) computed on MEG original data and on reconstructed MEG data with the S1a source; the index i runs upon the four channels of minimal and maximal amplitude at M20 latency. In fact, these channels well represent the dipolar field distribution at this peak latency [Tecchio et al., 2005]. Similarly, we obtained the discrepancy of S1b source by:

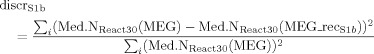(12)

To check for the level of residual cortico‐muscular coherence after M1 source extraction, the following index was estimated:

(13)

where Coh is calculated as indicated in Eq. (6) by substituting the source M1 signal, with the signal difference between MEG original data and M1 retro‐projection on the sensor channels.

Statistical analysis

General linear models (GLM) for repeated measures were estimated to test for differences in source reactivity and source localization across subjects. To compare source reactivities, the dependent variable was the 3‐dimensional reactivity vector (Med.N_React20, Med.N_React30,Mov_Coh), and the within‐subject independent variable was the three‐level factor Source (S1a, S1b, M1). The same model was applied for the source positions, with the dependent variable being the 3‐dimensional dipole coordinate vectors (x, y, z), in the case of single dipoles, and the barycentre coordinates, in the case of the multi‐dipole model and the within‐subject factor was Source (S1a, S1b, M1).

For discrepancy, index percentile values were provided

RESULTS

As detailed in the Appendix, in all subjects the three sources were estimated with λ = 1,000.

In all 14 subjects, the three functional sources S1a, S1b, and M1 were successfully obtained. The M1 source showed higher cortico‐muscular coherence than the original MEG channels in all subjects. In fact, the maximal peak of M1‐EMG coherence was higher than the maximal MEG‐EMG coherence (computed on the channel with maximal coherence, Fig. 2), with mean values of 0.08 ± 0.06 for the retro‐projected M1, and of 0.04 ± 0.03 for the original data (paired t‐test P < 0.0001). In particular, in all subjects the coherence of the M1 source with the rectified EMG was above the confidence limit (one sample t test vs. 0.015, P = 0.019) occurring at a mean frequency of 22 ± 5 Hz.

Figure 2.

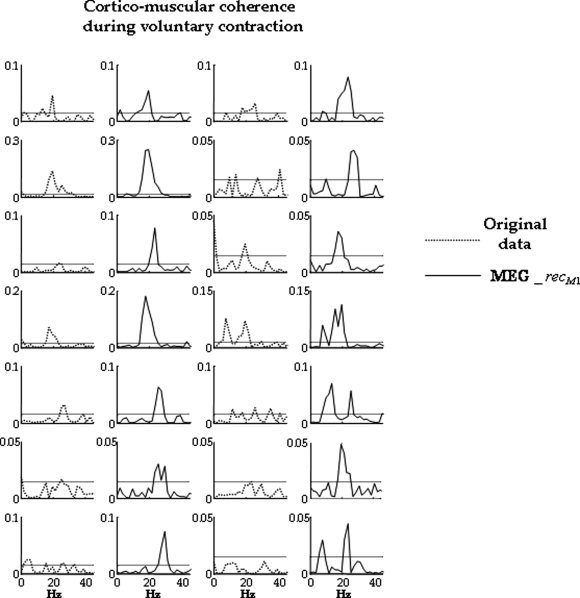
In each subject, comparison between maximal channel cortico‐muscular coherence (original data, dotted line, columns 1 and 3) and the coherence which has been calculated between rectified EMG and signal obtained by retro‐projecting only the M1 source (MEG_rec_M1, solid line, columns 2 and 4). Horizontal line indicates the confidence limit (see Materials and Methods section, 0.015). In all cases, it is evident that cortico‐muscular coherence is higher for the M1 retro‐projected signal than for the original channels.

The three extracted functional sources reacted differently during galvanic median nerve stimulation and isometric contraction (Source effect [F(6,8) = 8.398, P = 0.004, Figs. 3 and 4]). In particular, S1a reacted maximally at latencies around 20 ms following contralateral median nerve stimulation, compared to S1b and M1 (within subject contrasts Med.N_React20 (S1a) − Med.N_React20 (S1b) P = 0.007; Med. N_React20(S1a) − Med.N_React20(M1) P < 0.0001, Fig. 3). S1b reacted maximally at latencies around 30 ms (within‐subject contrasts Med.N_React30 (S1b) − Med.N_React30 (S1a) P < 0.0001; Med.N_React30 (S1b) − Med.N_React30 (M1) P < 0.0001, Fig. 3). M1 showed maximal cortico‐muscular coherence during isometric contraction (within‐subject contrasts Mov_Coh (M1) − Mov_Coh (S1a) P = 0.005; Mov_Coh (M1) − Mov_Coh (S1b) P = 0.001, Fig. 4).

Figure 3.

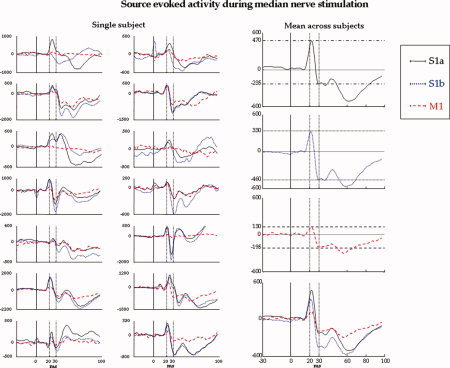
Single subject: For each subject, superimposition of S1a (solid line), S1b (dotted line), and M1 (dashed line) sources averaged by centring on the median nerve stimulation (t = 0, vertical solid line) in the time window [−30, 100] ms. For reference, 20 and 30 ms are indicated (vertical dotted lines). Mean across subjects: The three source signals averaged on nerve stimuli are reported separately, as well as the superimposed ones (bottom). It clearly results that the S1a source reacts maximally at around 20 ms, S1b at around 30 ms, and M1 less than S1a and S1b, but with higher reaction at 30 ms than at 20 ms. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 4.

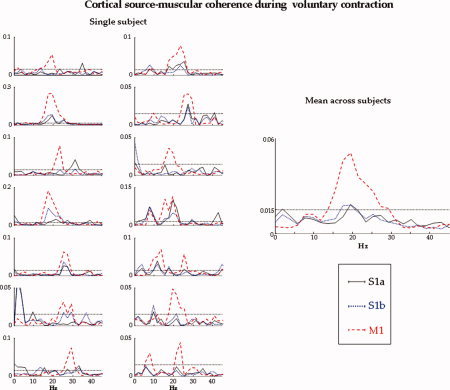
Single subject: Superimposition of the coherences of the S1a (solid line), S1b (dotted line), and M1 (dashed line) sources with the rectified EMG in the frequency interval [0, 45] Hz, for each subject. The horizontal line indicates the confidence limit. Mean across subjects: For S1a, S1b, and M1, source‐muscular coherence averaged across subjects. M1 displays an evidently greater coherence than S1a and S1b. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The same properties during the movement are to be noted for the extracted sources processing the sensory stimulation. In fact, the S1a and S1b sources showed not different cortico‐muscular coherence levels during isometric contraction (Mov_Coh (S1a) − Mov_Coh (S1b) P = 0.539, Fig. 4). In particular, neither S1a nor S1b showed coherence with the rectified EMG above the confidence limit (one sample t test vs. 0.015, P > 0.200).

The relationship among the reactivity to the nerve stimulus of the three sources showed an interesting property, that is, the responsiveness at around 30 ms of S1b was similar to the sum of the responsiveness of S1a and M1 (intraclass correlation coefficient (ICC) of Med.N_React30 (S1b) vs. Med.N_React30 (S1a) + Med.N_React30 (M1), ICC = 0.91, 95% CI: 0.74–0.97).

The M1 source reacted to median nerve stimulation with higher intensity at latencies around 30 ms than around 20 ms (Med.N_React30 (M1) > Med.N_React20 (M1), paired t‐test P = 0.018, Fig. 3).

While in all cases the single dipole explained more than 90% for S1a and S1b, for M1 such model failed in 13/14 cases. In these subjects, the multi‐dipole model was used. The S1a position was more lateral and inferior with respect to M1 (P = 0.073 for x coordinate, 0.040 for z). S1b was in between in both these directions (P = 0.076 and 0.090 respectively, Table I and Fig. 5).

Table I.

Mean across subjects 6± SD of localization results using MEG_rec_S1a, MEG_rec_S1b and MEG_rec_M1 in the individual space (PAN coordinates) and the average across subjects after normalization of individual data in the MNI space (MNI coordinates)

	x	y	z
PAN Coordinates
S1a	−40 ± 8	9 ± 6	95 ± 11
S1b	−38 ± 13	10 ± 17	97 ± 4
M1	−32 ± 12	7 ± 6	100 ± 16
MNI coordinates
S1a	−42 ± 4	−15 ± 7	57 ± 3	BA 3b
S1b	−43 ± 4	−10 ± 8	55 ± 3	BA 3a
M1	−38 ± 3	−4 ± 7	58 ± 5	BA 4

Mean across subjects ± SD of localization results using MEG_rec_S1a, MEG_rec_S1b and MEG_rec_M1 in the individual space (PAN coordinates) and the average across subjects after normalization of individual data in the MNI space (MNI coordinates). The coordinates (mm) refer to a single dipole or to the barycentre of the multi‐dipole model when required. For subject having individual MRI, the normalization procedure was performed using Statistical Parametric Mapping (SPM2, < http://www.fil.ion.ucl.ac.uk/spm/spm2.html>) under MatLab7.0. In the subjects lacking MRI data, MNI coordinates were automatically obtained by sofTaxic Navigator System (E.M.S. Italy, http://www.emsmedical.net), exploiting the warping of the MNI MRI (152‐T1) template on the basis of a set of 40 digitized scalp points including 4 anatomical landmarks (Nasion, Inion, left and right preauricular points) from the subject [Rossi et al., 2001, 2006]. In the last column labeling of the mean positions on the basis of the MNI atlas is provided.

Figure 5.

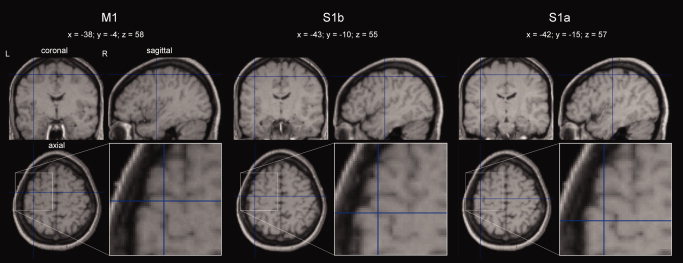
Mean positions across subjects of the three M1, S1b, and S1a FSs, after normalization of individual data in the MNI space (for the procedure, see the legend of Table I). The magnification of the source position in the axial view is shown in the corresponding inset, where the topographical relationship with ω‐shaped Rolandic sulcus tract is clearly identifiable. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The inter‐quartile ranges of the discrepancy indices (Fig. 6), i.e., the values including the central 50% of the distribution, were 0.3–3.6% for S1a, 0.1–0.8% for S1b, and 0.8–1.4% for M1. Median values were respectively 1.4, 0.3, and 1.2%.

Figure 6.

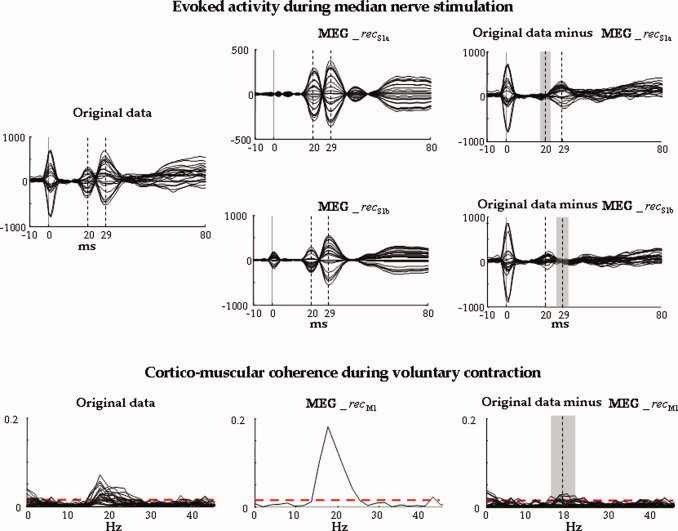
Evoked activity during median nerve stimulation in one representative subject. All parietal channels' superimposition averaged on median nerve stimuli, in the time window [−10, 80] ms, t = 0 the stimulus arrival being at wrist (vertical solid line). The time points corresponding to M20 and M30 components are indicated (vertical dashed lines). Left: Original data. Centre: Retro‐projected data with only the S1a source (top, MEG_rec_S1a) and with only the S1b source (bottom, MEG_rec_S1b). Right: Original data minus MEG_rec_S1a (top) and original data minus MEG_rec_S1b (bottom). The grey area indicates the time interval (Δ₂ t ₂₀ + Δ₁ t ₂₀ + 1 up, Δ₂ t ₃₀ + Δ₁ t ₃₀ + 1, bottom) where the discrepancy indices (discr_S1a up, discr_S1b, bottom) are calculated. Note that both S1a and S1b well explain the generated field at their respective latencies. Cortico‐muscular coherence during voluntary contraction. Superimposition of all channels' coherences with the rectified EMG in the frequency window [0, 45] Hz. The confidence limit is indicated (0.015, horizontal dashed line). Left: Original MEG channels. Centre: Retro‐projected channels with only M1 (MEG_rec_M1). All channels display the same coherence with the EMG signal; this is because all the channels obtained by retro‐projecting only one FS display the same time evolution, unless a multiplicative factor and the coherence are independent from the signals amplitude. Right: Original MEG data minus MEG_rec_M1 channels. The grey area indicates the frequency interval (Δ₂ω_max + Δ₁ω_max + 1) where the discrepancy index (discr_M1) is calculated. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

DISCUSSION

FS Properties

In all subjects, different sources were obtained, describing the cortical networks devoted to the contralateral, mainly sensory hand control, and to the contralateral, mainly motor hand control. The residual signal present in the original task‐related data not explained by the introduced source was below 3% in all cases. The three sources were obtained all along different experimental conditions by exploiting a key FSS feature. The identified sources displayed satisfactory reactivity properties during movement and during galvanic median nerve stimulation. In all subjects, S1a reacted maximally at around 20 ms, and S1b maximally at around 30 ms; moreover, S1a almost completely described the filed distribution at around 20 ms, and S1b at around 30 ms, in all subjects. The source M1, extracted to describe the primary motor pyramidal neuron group activity, showed maximal cortico‐muscular coherence, was positioned consistently in the primary motor area and reacted more to galvanic median nerve stimulation at around 30 ms than at 20 ms. This last property sustains a contribution from precentral neuronal pools in originating M30 component [BA4, Huang et al., 2000; Kawamura et al., 1996; Tecchio et al., 1997, 2005]. The present FSS algorithm extracts, in the motor cortex, those neuronal pool activities displaying strong synchrony with cycle‐triggered averages of EMG activity [Baker et al., 1997; Murthy and Fetz, 1992]. In animal models [Donoghue et al., 1998; Sanes and Donoghue, 1993], the relationship between the motor cortex neuronal discharge and the appearance of oscillations synchronous with the muscular activity indicated that these latter reflect a global process active in conjunction with motor planning or preparatory functions, while the motor action details are encoded in the neuronal firing rate. In conclusion, M1 describes a neural activity more related to oscillations which synchronize to the muscular activity than to neuronal firing rate fine‐tuning.

The relationship concerning the responsiveness of the three sources to nerve stimuli in correspondence with the M30 component, i.e., S1b responsiveness similar to the sum of the S1a and M1 responsiveness, was in strict accordance with the hypothesis about M30 generators. In fact, converging evidence supports the contribution given by two components, i.e., the inhibitory structures impinging on BA 3b pyramidal neurons [Tecchio et al., 1997, 2005; Wikstrom et al., 1996], and the excitation of BA 4 pyramidal neurons [Huang et al., 2000; Kawamura et al., 1996; Tecchio et al., 1997, 2005]. The same BA 3b pyramidal neurons generate M20 through the effect of excitatory projections and their activity is described by S1a; BA 4 pyramidal neuron groups are represented in M1.

Absolute Amplitude of FS

All the amplitude comparisons were performed onto the source amplitude directly, without needing to reconstruct the retro‐projected magnetic field with the specific component—requirement induced by the amplitude indeterminacy inherent to the general ICA method. As FSS extracts only one component at each time from the same complete solution space, it was possible to multiply the extracted component by the Euclidean norm of its weight vector. In this way, also all the amplitude information are contained in the FS source. This allows a direct and unequivocal estimate of the source amplitude for between‐subject comparisons of both the same and different sources in a single subject. In fact, the other ways to assess the source amplitude require the component retro‐projection. Once the magnetic field distribution in time has been obtained, there is the need to either identify the source position by a suitable inverse method—necessarily affected by approximation problems—or choose some channels to represent the source amplitude, which depends on the relative source‐to‐sensor position.

Motor Cerebral Source

The M1 identified source poses the basis to study the dynamics of a motor cortex compound in different experimental conditions, via a very simple motor task already used to assess the association of systematic cortico‐muscular coherence alterations with specific traits of movement disorders in patients [Brown et al., 1999; Kristeva et al., 2004; Timmermann et al., 2003; Volkmann et al., 1996]. With respect to the classical MEG/EEG‐EMG analysis, the present FSS application provides a cerebral motor source time behaviour.

While in all cases the single dipole succeeded in explaining the field distribution generated by S1a and S1b, for the M1 source a multi‐dipole model provided the required goodness of fit. This completely agrees with robust and mutually coherent findings in animal models and humans, which show different finger and wrist movements activating a wide expanse of the precentral gyrus, with representations overlapping each other at multiple sites [Dum and Strick, 2005; Grafton et al., 1991; Graziano et al., 2002; Indovina and Sanes, 2001; Poliakov and Schieber, 1999; Sanes et al., 1995].

Considerations About the Paradigm

Our aim was to obtain a tool to study the activity of the region dedicated to hand control, focusing onto the primary sensory and motor cortices via a suitable and repeatable paradigm. To select the primary sensory cortical excitability, the M20 and M30 components of the brain responses to nerve stimuli were focused, and the cortico‐muscular coherence was exploited to identify the primary motor cortex [Brown et al., 1998; Gerloff et al., 2006]. As our intent was to achieve a potentially useful description both in research and in clinical practice, e.g., in diseases affecting the hand motor control, like stroke and Parkinson's Disease or hand dystonia, the paradigm was set up requiring a motor task as simple and common as possible (and therefore most suitable in patients with upper limb impairments), as well as involving an easy accessible muscle characterized by a high‐quality EMG signal. Moreover, to make the paradigm suitable and repeatable, the median nerve stimulation at wrist was used, as it evokes a robust and stable response also in patients. A relative high‐frequency nerve stimulation (around 2 Hz) was adopted to reduce the recording time. Also, in the case that the stimulus of the mixed nerve does evoke the thumb twitch, the S1a and S1b source activities are minimally affected by proprioceptive inflow. In fact, at the latency of M20, this is not yet arrived to central areas. In principle, the S1b source, subtending the M30 component and including a contribution from BA 4, could be modulated by proprioception. As the M30 peak latency has been demonstrated to be independent from the stimulus intensity, and in particular to remain unchanged with the intensity increasing from below to above the motor threshold [Lin et al., 2005], proprioception is not expected to prevail in the M30 component.

In conclusion, a FSS application was proposed, achieving a satisfactory solution to the very demanding problem of identifying cortical sources devoted to the hand motor central representation. Moreover, the FSS solution was modified in order to avoid the amplitude indeterminacy inherent to the general ICA method, so making possible the direct comparison of source amplitudes without the need to reconstruct the retro‐projected signal.

Contrast Function Settings

In this appendix, we specify how the values of the parameter λ in Eq. (3) was determined in the present application. It has to be noted that we did not use the constrained optimization procedure adopted in Barbati et al. [2006], which also included the fixation of the parameter k measuring the required minimum response. Instead, a multi‐objective optimization scheme was adopted, considering together kurtosis and functional constraints to reach the optimum configuration. Such a choice was made in consideration of the very different nature of the constraints we used (in particular, R _M1 w.r.t. R _S1a and R _S1b), and in view of simplifying the automatization of the algorithm.

The parameter λ was selected by means of the following procedure: an initial grid was fixed with nine different λ‐values (λ = 0, 0.01, 0.1, 0.5, 1, 10, 100, 500, 1,000) plus a last condition with λ = 1 but only activating the functional constraint in Eq. (3), i.e., removing the J‐part of the contrast function (case named as “Only Constraint”, OC). For each subject, the three sources (S1a, S1b, M1) were extracted, keeping trace of the computational times, for each case of the grid. The indices R _S1a, R _S1b, and R _M1 were evaluated for their corresponding sources. λ was chosen to both minimize computational times and maximize R _S1a, R _S1b, and R _M1 indices. Starting from the case λ ≥ 100, the maximum value of the three indices was reliably reached for all the subjects and the three sources (Fig. A1, top). Moreover, looking at computational time distribution (Fig. A1, bottom), the λ value minimizing the computational effort for the three sources was λ = 1,000. The computational time was estimated for a computer with 3.2 GHz CPU and 1.0 GB RAM, on the data matrix of 28 rows × 240,000 time points.

Figure A1.

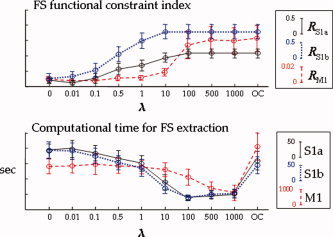
Mean and standard errors across subjects for the tested λ‐values of the R_S1a (solid line), R_S1b (dotted line), and R_M1 (dashed line) indices (top), and of the computational times for the three source extractions (bottom)r. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]