An evaluation of spatial thresholding techniques in fMRI analysis

Abstract

Many fMRI experiments have a common objective of identifying active voxels in a neuroimaging dataset. This is done in single subject experiments, for example, by performing individual voxel‐wise tests of the null hypothesis that the observed time course is not significantly related to an assigned reference function. A voxel activation map is then constructed by applying a thresholding rule to the resulting statistics (e.g., t‐statistics). Typically the task‐related activation is expected to occur in clusters of voxels rather than in isolated single voxels. A variety of spatial thresholding techniques have been proposed to reflect this belief, including smoothing the raw t‐statistics, cluster size inference, and spatial mixture modeling. We study two aspects of these spatial thresholding procedures applied to single subject fMRI analysis through simulation. First, we examine the performance of these procedures in terms of sensitivity to detect voxel activation, using receiver operating characteristic curves. Second, we consider the accuracy of these spatial thresholding procedures in estimation of the size of the activation region, both in terms of bias and variance. The findings indicate that smoothing has the highest sensitivity to modest magnitude signals, but tend to overestimate the size of the activation region. Spatial mixture models estimate the size of a spatially distributed activation region well, but may be less sensitive to modest magnitude signals, indicating that additional research into more sensitive spatial mixture models is needed. Finally, the methods are illustrated with a real bilateral finger‐tapping fMRI experiment. Hum Brain Mapp, 2008. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

Many fMRI experiments have a common objective of identifying active voxels in a neuroimaging dataset. This is done in single subject experiments for example by performing individual voxel‐wise tests of the null hypothesis that the observed time course is not significantly related to an assigned reference function [Bandettini et al., 1993; Cox et al., 1995]. A voxel activation map is then constructed by applying a thresholding rule to the resulting t‐statistics.

Typically, the task‐related activation is expected to occur in clusters of voxels rather than in isolated single voxels. A variety of spatial thresholding techniques have been proposed to reflect this belief, including smoothing either the raw data or the summary t‐statistics for each voxel, cluster size inference, and spatial mixture modeling. Although smoothing is commonly done on the raw data before fitting a linear model and obtaining a summary t‐statistic, it can also be applied in the opposite order, first fitting a linear model to obtain a t‐statistic for each voxel, and then smoothing the t‐statistics. Skudlarski et al. [1999] reported that the order of smoothing has only a slight effect on power. We consider only smoothing of the t‐statistics in this article for simplicity, so that all of the techniques described can be applied to the summary statistical parametric map (SPM) containing the t‐statistics. Smoothing is typically done using a Gaussian kernel function, and then a standard thresholding procedure can be applied to the smoothed t‐statistics. Alternatively, cluster size inference may be performed on the smoothed t‐statistics, in which clusters or sets of neighboring voxels with t‐statistics above a predetermined threshold u are determined. In this case, the null hypothesis being tested is whether the cluster is occurring due to chance alone against the alternative hypothesis that the cluster is due to some true spatial activation. Statistical inference is performed on the cluster sizes (number of voxels in the clusters) using either random field theory [Friston et al., 1994; Worsley et al., 1996] or permutation‐based inference [Hayasaka and Nichols, 2003]. Mixture models were proposed for the independent activation case by Everitt and Bullmore [1999], and were extended by Hartvig and Jensen [2000] to account for spatial clustering of activation.

Although a number of techniques have been proposed, there is limited information about which procedures are more useful or under what situations one should prefer one method over another. The focus of this article is to compare these methods in detail and in different ways than have been studied previously. Skudlarski et al. [1999] present an analysis using receiver operating characteristics (ROC) curves, in which they consider several different spatial clustering techniques, including smoothing and cluster size inference. However, they did not consider spatial mixture models in their study. Nichols and Hayasaka [2003] compared multiplicity adjustments for smoothed data using random field theory with adjustments using permutation resampling to assess control of the familywise error (FWE) rate, but they did not consider performance in terms of power to identify activated regions. Marchini and Presanis [2004] compared smoothing with either FWE or false discovery rate (FDR) adjustment versus spatial mixture models in terms of power. However, they only applied the spatial mixture models to data after it was smoothed. We feel that spatial mixture models are a potential alternative to smoothing, and in contrast to Marchini and Presanis [2004], we compare the performance of smoothing and cluster inference in applying spatial mixture models to raw or unsmoothed data. Additionally, Marchini and Presanis [2004] compare the power of the procedures applied at different inherent Type I error rates (FWE = 0.05, FDR = 0.05), while we align the error rates using ROC curves, ensuring that power differences are because of the spatial method used, and not differences in the Type I error rate.

A further objective of researchers may be to investigate whether the size of the activation region (the set of voxels identified as active) is changing within a subject under different conditions. For example, among people who have suffered a stroke, one might be interested in whether the size of the region of activation for a particular task is getting bigger over time as a measure of whether they are recovering from the stroke. Spatial mixture models in particular hold a lot of promise for this objective because of their parametrization in terms of voxels being active or not, which naturally defines a region of activation. There is very little published about how accurate any of these various spatial thresholding procedures are in terms of estimation of the size of the activation region, and how much uncertainty there is in this estimate. Geliazkova and Logan [2005] study the accuracy of estimation of spatial mixture models using different parametrizations including neighborhood size and spatial structure, and provide recommendations on practical use. To consider the problem of modeling the size of activation, it is important to first understand just how well these spatial thresholding procedures estimate the size of activation.

The purpose of this paper is to study two aspects of these spatial thresholding procedures applied to single subject fMRI analysis through simulation and in experimental data. First, we examine the performance of these procedures in terms of sensitivity to detect voxel activation, using ROC curves. Second, we consider the accuracy of these spatial thresholding procedures in estimation of the size of the activation region, in terms of both bias and variance. We examine these operating characteristics both as the size or shape of the region changes, and as the magnitude of the activation changes.

The organization of the paper is as follows. In the Materials and Methods section we first review smoothing, clustering, and spatial mixture model methods. We also describe the simulation study of the properties of the spatial thresholding procedures, and discuss the application of the procedures to a real dataset. In the Results and Discussion section we present and discuss the results of the simulation study in three parts. The first part compares ROC curves, the second part covers estimation of the size of the region of activation, while the third part examines robustness of the results to the shape of the activation region. We also illustrate the application of the methods to the real dataset. Finally, conclusions are given in the last section.

MATERIALS AND METHODS

Statistical Parametric Maps

In the following, we assume that the investigator has already performed an analysis to obtain a statistical parametric map (SPM), which is a matrix of test statistics corresponding to the null hypothesis of no task related activation. These could come, for example, from a series of univariate regression analyses at each voxel, where the independent variables include a linear drift term and a variable reflecting the task such as a “boxcar” predictor or other hemodynamic response function.

Under the null hypothesis, these test statistics typically have a t _ν distribution, where ν is large, so that it can be well approximated by a normal distribution.

Smoothing

Smoothing may be done on the matrix of t‐ or z‐ statistics using a Gaussian kernel with a prespecified full width half maximum (FWHM). For single‐subject fMRI data typically modest smoothing is performed, such as with a two voxel FWHM kernel. The smoothed data then can be thresholded using any of a number of standard multiplicity adjustments. These include an unadjusted analysis, which controls the per comparison error rate at prespecified level α; the Bonferroni procedure, which controls the FWE rate at level α; and the Benjamini–Hochberg (BH) procedure [Benjamini and Hochberg, 1995], which controls the FDR at level α. More refined procedures to control the FWE are available through the “unified” approach to adjusting the P‐value [Worsley et al., 1996, 2004], and permutation resampling may also be used to adjust the P‐values and control a desired error rate [Holmes et al., 1996; Nichols and Holmes, 2001]. However, because of the modest smoothing used for single‐subject fMRI, the Bonferroni and BH procedures work well, and we will restrict our attention to these [Logan and Rowe, 2004].

It is important to note that the presence of a true task‐related signal located at some voxels in the image can distort the control of the respective error rates when the data are smoothed. The FWE is controlled at a prespecified level α by the thresholding procedures discussed earlier under the overall null hypothesis or when none of the voxels are truly active. However, when there is a task‐related signal present, the smoothing of the signal may alter the mean of some voxels which were considered before smoothing to be null or nonactive voxels. The resulting nonzero means thereby inflates the FWE if we calibrate it based on the activation status or mean activation of each voxel prior to smoothing. This means that smoothing followed by an adjustment to control the FWE offers only weak control of the FWE, as opposed to strong control where the FWE is controlled over all nonactive voxels even when some voxels are active. This dispersion of the activation signal also affects control of the FDR in a similar fashion. Also, this inflation of the FWE in the presence of task‐related activation can occur even when smoothing is performed on raw data before analysis. In this case, spatial smoothing of a nonactive voxel's raw time series adjacent to an active voxel can affect the shape of the time‐series so that it is more likely to reject the null hypothesis of no activation.

Cluster Size Inference

Inference on smoothed data can also be performed using cluster size inference. Inference on Gaussian SPM's using random field approximations are discussed in Friston et al. [1994] and Worsley et al. [1996]. Inference on t‐ SPM's using random field approximations are developed in Cao [1999] and Cao and Worsley [2001]. Forman et al. [1995] introduced thresholding based on cluster size using a simulated distribution of the cluster size under the null hypothesis, an approach which is implemented in AFNI [Cox, 1996]. Hayasaka and Nichols [2003] present a nice review of cluster inference, and compare random field approximations with cluster inference using permutation testing.

Briefly, a cluster is a set of neighboring voxels whose t‐statistics are above some predetermined threshold u. The null hypothesis which we are testing is whether the cluster is occurring due to chance alone against the alternative that the cluster is due to some true spatial activation. Let S be the size of the cluster, or the number of contiguous voxels with t_i > u. The null distribution of S is unknown, but we can use random field (RF) theory to approximate this distribution. Then inference on a cluster with size s is based on a multiplicity adjusted P‐value representing the probability of at least one cluster of size s or larger occurring in an image with no activation. Alternatively, a critical value S _α can be obtained which corresponds to an adjusted cluster error rate of α. Various random field theory approximations are implemented in fmristat and SPM2 [see Hayasaka and Nichols, 2003 for details].

Spatial Mixture Models

In 1999, Everitt and Bullmore proposed an alternative approach for detecting activated voxels in the human brain under a cognitive task. They fitted a finite mixture distribution to the observed distribution of the test statistic. The mixture distribution has two components, one of which accounts for the activated voxels and the other of which represents the nonactivated voxels. They also estimated the proportion of voxels which are activated, denoted p, and the parameter that characterizes the activation distribution δ using maximum likelihood methods. Hartvig and Jensen [2000] extended this mixture model to allow for association between neighboring voxels in terms of activation status. This association mimics the clustering of activation typically seen in fMRI data. The interpretation of the results is similar to a Bayesian analysis. A prior distribution (e.g., a distribution not informed by the data) for the activation status indicator variables is updated, given the observed test statistic data. This results in posterior distributions (informed by or given the data) for the activation status variables, also called posterior probabilities of activation. These posterior probabilities of activation are expressed for each voxel in terms of the estimated model parameters. They can be thresholded (e.g., taking 0.5 as a threshold) to identify which of the voxels are activated and which are not. Note that while the interpretation is similar to a Bayesian analysis, the Hartvig and Jensen approach is not a fully Bayesian method; only point estimates of the model parameters are used to compute the posterior probabilities of activation, rather than posterior distributions of the model parameters. We give a brief description of the details later.

Let A_i be the indicator for voxel i being activated. The distribution of the observed t‐statistic in each voxel depends on the indicator A_i; here we take 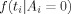to be a standard normal distribution N(0,1), while 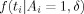is assumed to be a nonstandard normal distribution N(δ,1). Hartvig and Jensen [2000] consider prior models for activation indicator variables in a neighborhood around voxel i, denoted A _N(i), which reflect the tendency of voxels to be active in clusters. They use this model to determine the posterior probability of activation for voxel i given the observed t‐statistics in the neighborhood, 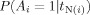. Three models are presented for the joint prior distribution of A _N(i), denoted P(A _N(i)). Model 1 has only one parameter such that

where l is the number of voxels in the neighborhood. This essentially reduces neighborhood activation information to just the presence or absence of active voxels in the neighborhood. Model 2 uses the number of active voxels in the neighborhood, such that

This model can be parameterized through the marginal probability P of a voxel being activated as 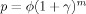, where ϕ is a measure of association between neighboring voxels. Model 3 requires four parameters and was not recommended by Hartvig and Jensen [2000]. Geliazkova and Logan [2005] studied the performance of Models 1 and 2 for four or eight neighbor regions, and concluded that Hartvig and Jensen's Model 2 with eight neighbors performed the best. Therefore, we will limit our simulation study to Model 2 with eight neighbors. Under Model 2, the posterior probabilities of activation for a particular voxel given the values t _N(i) in the neighborhood is given by

where

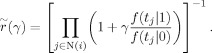Parameters of the model are estimated by maximizing a pseudo‐likelihood function, which is used because the spatial structure in the likelihood function makes it too difficult to maximize. In this case, the pseudo‐likelihood is constructed as the product of the neighborhood likelihoods for each voxel as if they were independent, ignoring the spatial structure. Under certain conditions, the maximum pseudo‐likelihood estimates can be shown to be consistent estimates of the model parameters. Once the model parameters are estimated, posterior probabilities of activation can be computed using the closed‐form expressions above. Implementation of the previous procedure takes about 10–15 s to implement on a single‐slice 64 by 64 image, using a SunBlade 100 with a 500 MHz CPU.

FMRI Simulation Study

Part I: ROC curves

The first part of the simulation study compares the characteristics of these spatial thresholding procedures in terms of their sensitivity to voxel activation. We use ROC curves to display the results. ROC curves are a plot of the sensitivity (on the y‐axis) versus 1 minus the specificity (on the x‐axis), plotted over a range of test statistic thresholds. Each threshold determines a (x,y) point on the curve. Here sensitivity is the probability of identifying an active voxel as active because it is over the threshold, while 1 minus the specificity is the false positive rate, or the probability of incorrectly identifying an inactive voxel as active because it is above the threshold. ROC curves range from (0,0) to (1,1), and ideally we want the curve to be as close to the upper left quadrant (1,0) as possible. ROC analysis has been used in several previous studies to validate approaches in fMRI [Constable et al., 1995; Lange et al., 1999; Lukic et al., 2002; Sorenson and Wang, 1996; Xiong et al., 1996].

In each case, data is generated to simulate a t‐statistic SPM where the true regions of activation (ROAs) are known. A 64 by 64 image slice is selected for analysis within which two square ROAs are designated to have activation. For this slice, simulated fMRI t‐statistics (assuming large d.f.) outside the ROAs are generated from a N(0,1) distribution, while inside the ROAs they are generated from a N(δ,1). Here δ can be interpreted as the mean of the standardized t‐statistics for activated voxels. We use δ = 1.5 and ROAs varying from 3 by 3 to 7 by 7. Figure 1a illustrates sample 7 by 7 ROAs as considered in the first two parts of the simulation study, while Figure 1b illustrates the ROAs considered in the third part of the simulation study. To estimate the (x,y) point on the ROC curve, first a fixed threshold in terms of the test statistic is set. Then using that threshold value, the sensitivity and (1‐Specificity) is computed for each image. These are then averaged across 500 simulated images to generate the (x,y) point. This is repeated for a range of thresholds to generate a curve. This is similar to the approach used in Lange et al. [1999]. A total of 500 simulations for each scenario are used in all simulations.

Figure 1.

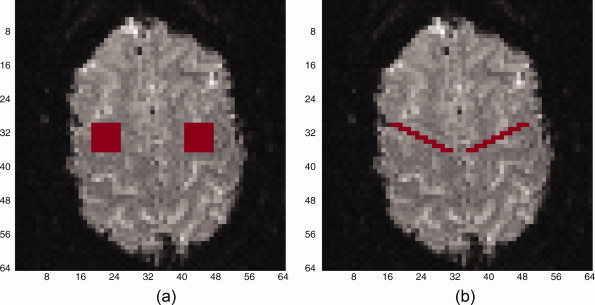
Regions of activation (ROA) for simulation studies. (a) Parts I and II. (b) Part III.

The smoothing is performed using a 2 voxel FWHM Gaussian kernel, and thresholded over a range of smoothed t‐statistics. Cluster size inference follows smoothing with a 2 voxel FWHM kernel, and is performed using three different magnitude thresholds of u = (2.0, 2.5, or 3.0) and thresholded over a range of cluster sizes. Because the cluster sizes are discrete, the ROC curves tend to have sharp jumps at points where the cluster size threshold changes. The spatial mixture model is done using a neighborhood of eight neighbors, and is thresholded over a range of posterior probabilities of activation.

Part II: Estimation of the size of the ROA

In this simulation study, we measure the bias and the variance of the estimate of the size of the activation region for each procedure. The size of the activation region is the number of truly active voxels across both ROAs, while the estimated size is the number of voxels who are declared active by one of the thresholding procedures. The true number of active voxels ranges from 18 for 3 by 3 regions to 98 for 7 by 7 regions. Two scenarios are considered; in the first we study the bias and variance of each procedure as the size of the activation regions get larger, and in the second we compare the bias and variance as the magnitude of activation changes. The data generation model is as in Part I. In the first scenario, we vary the dimensions of the square ROAs from 3 by 3 to 5 by 5 to 7 by 7, with δ = 2.25. In the second scenario, we use two 7 by 7 square ROAs while varying δ from 1.5 to 3.0 in increments of 0.5.

Each of the procedures discussed earlier is studied under a variety of thresholding techniques. The smoothing is performed using a 2 voxel FWHM Gaussian kernel, combined with one of two P‐value thresholding techniques (BH procedure and Bonferroni procedure) at respective error rates of 5%. Cluster size inference follows smoothing with a 2 voxel FWHM kernel, and is performed using a magnitude threshold of u = (2.0, 2.5, 3.0) with critical cluster size determined according to a cluster error rate of 5%. Spatial mixture Model 2 is done using a neighborhood of eight neighbors, and is thresholded at a 0.5 posterior probability of activation.

Part III: Effect of the shape of the ROA

In this section, we examined the effect of the shape of the ROA on the findings in the previous simulation studies. The previous two sections used square ROAs, which are very smooth, with a small ratio of edge to interior voxels, and these may be conducive to smoothing as a spatial technique. Here we study a more jagged shape of the ROA with more edges relative to interior voxel points. An illustration of this shape is given in Figure 1b. As before, we have two ROAs, and the total number of truly active voxels is 42 (21 in each ROA).

Real Data Example

A bilateral finger‐tapping experiment was performed to illustrate the spatial thresholding procedures investigated earlier. To generate the functional data, bilateral finger tapping was performed in a block design with eight epochs of 16 s off and 16 s on, followed by 20 s off. Scanning was performed using a GE 3T scanner in which 15 axial slices of size 96 × 96 were acquired. A mask was applied so that only the interior 64 × 64 image is used. Each voxel has dimensions 2 mm cubic voxels, with TE = 48 ms. Observations were taken every TR = 2,000 ms so that there are 138 in each voxel. Data from a single axial slice through the motor cortex were selected for analysis. A multiple regression model was fit to the data with an intercept, a time trend, and a reference function. The first 6 s were omitted to remove warm‐up effects, and the reference function was a boxcar shape, shifted by 6 s to match the hemodynamic response. Temporal AR(1) autocorrelation was checked, found to be minimal, and so was not adjusted for. Each of the methods discussed were applied to the dataset.

RESULTS AND DISCUSSION

Simulation Study Part I: ROC Curves

The ROC curves for 3 by 3 ROAs are given in Figure 2. In general, the smoothed z‐statistics perform best, except when specificity is high, where cluster inference with low u performs better. The spatial mixture model does not perform as well as cluster inference with a low (1‐Specificity) or false positive rate, while it may perform better than the cluster inference for larger false positive rates. The spatial mixture model seems to consistently have lower sensitivity for fixed false positive rate than smoothing. However, it is important to note that one technique is not uniformly better than all others; the relative performance depends in many cases on the level of specificity desired. Also, this comparison does not take into consideration how a threshold should be chosen, and its impact on the sensitivity and specificity. ROC curves were also generated for 7 by 7 ROAs (not shown). The sensitivity was generally higher for 7 by 7 ROAs than for 3 by 3 ROAs. This is likely because the ROAs are larger, resulting in a more spatially distributed signal which is easier to detect with a spatial thresholding procedure. Otherwise, the relative performance of the methods was similar, except that the difference between the spatial mixture models and the other statistics was not as pronounced.

Figure 2.

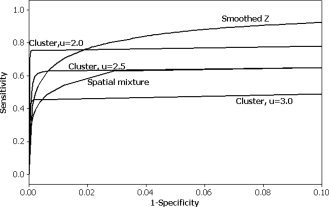
ROC curves for 3 by 3 square ROAs. Sensitivity refers to the true positive rate while 1‐Specificity refers to the false positive rate.

Simulation Study Part II: Estimation of Size of ROA

Figure 3 contains the bias (a,b) and SD (c,d) estimates of each procedure. In Figure 3a, the bias is plotted against the width of the square ROA. In Figure 3b, the bias is plotted against the magnitude of activation, δ. Note that the cluster size techniques tend to overestimate the size of the ROA, as does the smoothed data analysis with the BH threshold. This can be seen for δ = 2.25 in Figure 3a and as δ gets larger in Figure 3b, where the bias continues to increase as δ gets larger. This is likely due to the smoothing, which tends to overdistribute the true signal beyond its original boundary. In Figure 3b, the Bonferroni procedure applied to the smoothed data is too conservative and underestimates the size of the ROA except when δ is very large. The spatial mixture model performs well and is not very sensitive to either the width of the ROA or δ. t also has a bias that appears to converge to 0 as δ increases, in contrast to the methods based on the smoothed data.

Figure 3.

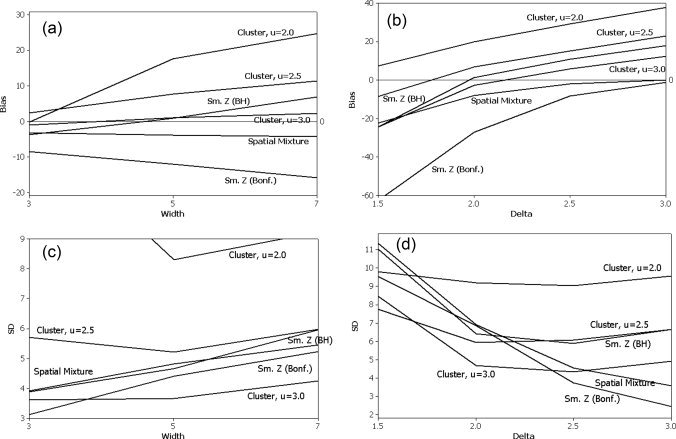
Bias (in number of voxels) and standard deviation (SD) of ROA size estimate as a function of width of the two square ROAs or the mean of the activated voxels. There are two ROAs so the total number of truly active voxels in the bias calculation is twice the number of voxels in each square ROA. (a) Bias as a function of the width of the two square ROAs, with activation mean δ = 2.25. (b) Bias as a function of the mean of the activated voxels, δ, using two 7 by 7 square ROAs. (c) SD as a function of the width of the two square ROAs, with activation mean δ = 2.25. (d) SD as a function of the mean of the activated voxels, δ, using two 7 by 7 square ROAs.

In Figure 3c, the SD is plotted against the width of the square ROA, while in Figure 3d the SD is plotted against the magnitude of activation. In Figure 3c, the SD of the size estimate tends to increase slightly as the width of the ROA increases, except for the cluster size procedure with u = 2.0. This exception is likely due to the additional variability from smoothing and using a low cluster threshold. As a function of δ in Figure 3d, the SD for the methods based on smoothing with a BH thresholding procedure or the cluster size methods decrease initially, plateau between 2 and 2.5, and increase slightly thereafter. This late increase also may be an artifact of the smoothing increasing the variability of the estimated ROA. The spatial mixture model and Bonferroni procedure have a SD that decreases steadily with increasing δ in Figure 3d.

In terms of MSE (Bias + Variance, not shown), when δ = 2.25 and the dimensions of the square ROAs are varied, the cluster size threshold with u = 3.0 performs the best, followed closely by the spatial mixture model and the BH procedure applied to the smoothed data. However, the latter procedure tends to perform slightly worse when the ROA is very large, possibly due to the impact of the signal‐dispersing effect of smoothing on the bias. When δ is varied using a 7 by 7 square ROA, the cluster size thresholds with u = 2.0, 2.5 perform the best for small δ = 1.5, while the Bonferroni procedure applied to the smoothed data performs very poorly. For modest δ between 2.0 and 2.5, several of the procedures including cluster size threshold with u = 2.5, 3.0, spatial mixture model, and smoothed t‐statistics with BH procedure perform comparably. For large δ = 3.0, the bias term dominates and the spatial mixture model and Bonferroni adjusted smoothed t‐ statistics perform the best. Overall, the spatial mixture model performs well across a wide range of δ, except when the signal is very small.

Simulation Part III: Effect of Shape of ROA

For brevity, we only show the ROC curve and the plot of the bias of the size estimate against δ in Figure 4. In general, the results are consistent with what we found for the square ROAs. In Figure 4a the smoothed t‐statistics generally perform the best in terms of sensitivity as a function of (1‐Specificity), except when the false positive rate is very small, in which case cluster size thresholding with small u performs the best. The spatial mixture model does not perform as well as smoothing in terms of the ROC curves. In Figure 4b, the cluster size techniques and the smoothed data analysis with a BH threshold tend to overestimate the size of the ROA as δ gets large. The spatial mixture model, in contrast, has a bias which decreases as δ increases. Smoothing with a Bonferroni threshold is generally too conservative and underestimates the size of the ROA.

Figure 4.

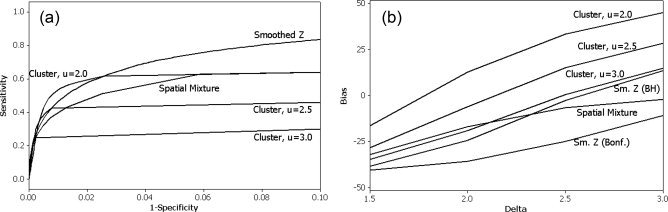
Operating characteristics when the two ROAs have a more jagged shape as in Figure 1b. (a) ROC curve. (b) Bias of ROA size estimate across both ROAs plotted against the mean of the activated voxels, δ.

Real Data Example

The image of t‐statistics is shown in Figure 5a, followed by the same image after applying a variety of thresholding procedures. All subsequent thresholding procedures are based on one‐sided testing to simplify the illustration. The t‐statistics are thresholded at a one‐sided unadjusted error rate of 5% (t = 1.645) in Figure 5b. Figure 5c shows the raw t‐statistics thresholded using the BH procedure with a 5% FDR. Figure 5d shows the posterior probabilities of activation from the spatial mixture model, thresholded at 0.5. Note the change in the colorbar for Figure 5d because the posterior probabilities have a restricted scale between 0 and 1. Figure 5e,f show the t‐statistics, smoothed with a 2 voxel FWHM Gaussian kernel and thresholded using the Bonferroni (5% FWE) and BH (5% FDR) procedures, respectively. Note that here a 2 voxel FWHM Gaussian kernel smoother corresponds to a 4 mm FWHM smoother, given the voxel dimensions of 2 mm. Figure 5g–i show the smoothed t‐statistic images, thresholded using a cluster size error rate of 5% with u = 2.0, 2.5, 3.0, respectively. The cluster size threshold with u = 2.0 shows the most activation, while the cluster size threshold with u = 3.0 shows the least activation. All cluster size threshold procedures eliminate the noise in Figure 5f from isolated voxels appearing above the threshold. Note that the smoothing or cluster size thresholding methods tend to overdisperse the signal beyond where it appears to be likely from the raw t‐image, although the Bonferroni procedure (Fig. 5e) shows the least overdispersion. The spatial mixture model captures the spatially distributed signal nicely, while still eliminating much of the noise present in Figure 5b.

Figure 5.

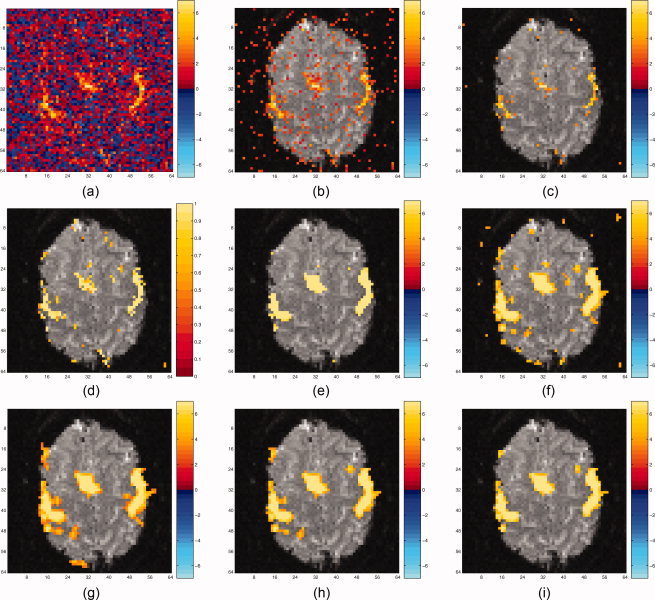
Various thresholding procedures applied to real dataset. (a) shows the unthresholded raw t‐statistics, (b) and (c) show two thresholding procedures applied to the raw t‐statistics (b, fixed threshold of 1.645; c, BH procedure), (d) shows the posterior probabilities from the spatial mixture model thresholded at 0.5, (e) and (f) show two thresholding procedures applied to the t‐statistics smoothed with a 2 voxel FWHM Gaussian kernel (e, Bonferroni with smoothing; f, BH with smoothing), while (g)‐(i) show several cluster size thresholding procedures with var ying u and cluster error rate of 5%, applied to the smoothed t‐statis‐tics. (g) Cluster size threshold, u = 2.0; (h) Cluster size thresh‐old, u = 2.5; (i) Cluster size threshold, u = 3.0.

CONCLUSIONS

We have investigated the operating characteristics of a number of spatial thresholding methods. When investigators are interested in identifying a spatially distributed signal in an exploratory context, it is important to have high signal to noise ratio. Our ROC simulation study simply illustrates the tradeoff between signal and noise in terms of the sensitivity versus the false positive rate. In terms of raw sensitivity to activation for a fixed false positive rate, the spatial thresholding procedure does not perform as well as methods which incorporate smoothing. This is probably to be expected, as information may be lost when applying the spatial model to the binary categorization of voxels (active vs. inactive) instead of the raw continuous t‐statistics. It performs worse when the size of the ROA is smaller; possibly the loss of information is greater. When comparing cluster size inference with univariate thresholding of the smoothed t‐statistics, there is no uniformly better procedure across false positive rates. For very small false positive rates as is often used in practice, cluster size inference may work better than univariate thresholding of the smoothed t‐statistics when the signal is spatially distributed. Furthermore, cluster size inference with smaller u values (t‐statistic thresholds) appears to work better than larger u values, especially for smaller ROAs. Possibly some of this advantage is attributed to a smoother distribution of cluster sizes, although the accuracy of the random field theory may be an issue here in application [Hayasaka and Nichols, 2003]. Overall, either univariate thresholding of smoothed t‐statistics or cluster size thresholding with u = 2.0 are recommended for having high sensitivity to detect voxel activation.

While sensitivity to activation in an exploratory context is a common and important goal, sometimes it is important to accurately identify the location of a ROA. In this setting, smoothing tends to overdisperse the signal beyond its original boundary, making accurate delineation of the activation region difficult. This is particularly problematic when the magnitude of the activation is large, thereby increasing the likelihood that nonactive voxels adjacent to active voxels will be declared active due to smoothing. Several authors have attempted to mitigate the overdispersion of the signal inherent in Gaussian kernel smoothing. Recent work in techniques such as bilateral spatial filtering [Walker et al., 2006] which combine smoothing with an edge stopping function may reduce this problem. However, such techniques may make the statistical analysis and threshold selection difficult. Beckmann and Smith [2004] perform hypothesis testing using independent components analysis, arguing that because the inferential steps are not based on Gaussian RF theory, they can use nonlinear smoothing to reduce the bleeding of spatial activation into neighboring nonactive areas. Other authors have used Bayesian modeling with spatial prior distributions in order to spatially smooth regression coefficients. Gossl et al. [2001] and Woolrich et al. [2004a, b] used Bayesian models with Markov random field or continuous autoregressive (CAR) priors to detect activation, while Penny et al. [2005] use a Laplacian spatial prior. Inference in such Bayesian models is based on marginal posterior probabilities that the regression coefficient for a particular voxel is at least of a prespecified magnitude. Such smoothing of the regression parameters may still have the problem of overdispersion of the voxel activation, and thresholding is somewhat subjective in terms of specification of the magnitude of interest. A couple of authors have proposed Bayesian spatial mixture models analogous to the spatial mixture model of Hartvig and Jensen studied here. Holmes and Ford [1993] demonstrated the use of discrete Markov random fields for determining activation, implemented using Gibbs sampling. Smith et al. [2003] use a Bayesian spatial mixture model with an Ising prior on the vector of activation indicators, and proposed a fast algorithm for estimating the posterior probabilities of activation. Woolrich et al. [2005] approximate the indicator variables in the discrete mixture model likelihood with a set of continuous random variables, and then place a spatial CAR prior on a transformation of these continuous variables. Lukic et al. [2004] model the activation as a mixture of nonactive voxels and a series of circular activation patterns, where the number of circular activations is estimated via reversible jump Markov chain Monte Carlo techniques. Descombes et al. [1998] propose a spatio‐temporal analysis using discrete Markov random fields with edge‐preserving potentials. However, their model requires prespecification of a large number of spatial parameters to determine the potentials, and the resulting thresholding method is likely sensitive to these values.

In general, the potential advantage of the spatial mixture model formulation is that it incorporates shrinkage towards zero for voxels which are likely inactive, directly accounting for the multiplicity problem. Also, they have better edge‐preserving characteristics, since the spatial model is applied to the binary activation indicators, rather than the raw parameters or test statistics. Overall, if the focus is on accurate identification of the location of a ROA, spatial mixture modeling may be preferred to smoothing, especially if the magnitude of activation is expected to be large. However, as we have shown with the Hartvig and Jensen approach, spatial mixture models can be less sensitive to modest magnitude signals than smoothing the data, and generally work better for larger magnitude, more dispersed signals. This trend is likely to hold for Bayesian spatial mixture models as well. The use of edge‐preserving techniques holds promise, but further understanding of the effect of these methods on the thresholding error rates is needed.