Mapping reliability in multicenter MRI: Voxel‐based morphometry and cortical thickness

Abstract

Multicenter structural MRI studies can have greater statistical power than single‐center studies. However, across‐center differences in contrast sensitivity, spatial uniformity, etc., may lead to tissue classification or image registration differences that could reduce or wholly offset the enhanced statistical power of multicenter data. Prior work has validated volumetric multicenter MRI, but robust methods for assessing reliability and power of multisite analyses with voxel‐based morphometry (VBM) and cortical thickness measurement (CORT) are not yet available. We developed quantitative methods to investigate the reproducibility of VBM and CORT to detect group differences and estimate heritability when MRI scans from different scanners running different acquisition protocols in a multicenter setup are included. The method produces brain maps displaying information such as lowest detectable effect size (or heritability) and effective number of subjects in the multicenter study. We applied the method to a five‐site multicenter calibration study using scanners from four different manufacturers, running different acquisition protocols. The reliability maps showed an overall good comparability between the sites, providing a reasonable gain in sensitivity in most parts of the brain. In large parts of the cerebrum and cortex scan pooling improved heritability estimates, with “effective‐N” values upto the theoretical maximum. For some areas, “optimal‐pool” maps indicated that leaving out a site would give better results. The reliability maps also reveal which brain regions are in any case difficult to measure reliably (e.g., around the thalamus). These tools will facilitate the design and analysis of multisite VBM and CORT studies for detecting group differences and estimating heritability. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.

INTRODUCTION

Investigating the genetic and neural bases of complexly determined psychiatric disorders requires large subject numbers. In particular, twin studies investigating genetic and environmental influences in such disorders often require more twins than are available in the local area, necessitating multicenter studies. As in any measurement process, one must consider that MR scanner and acquisition parameter settings can influence quantitative MRI estimates. Put simply, combining poorly compatible data from different MR scanners at different centers might reduce or even wholly offset any gain in power for detecting group differences. Heritability estimates are even more crucially dependent on measurement reliability, as they rely on correlations within twin pairs. Ideally, MR acquisition protocols should be optimized in advance by scanning calibration subjects before starting multicenter data acquisition (see, e.g., Van Haren et al. 2003 for a three‐center optimization, and Clark et al., 2006, for a single‐center/two‐protocol optimization). However, this is not always feasable, it may be impossible to optimize a common protocol at a certain site due to scanner or organizational restrictions, while the decision to combine multicenter data is often taken after all the data has been collected using different site‐specific protocols. In all cases, it is necessary to establish the comparability of the resulting brain measures from the different scanners and protocols. Several reliability studies have been reported for volumetric data (e.g., (Clark et al., 2006; Reig et al. 2009; Schnack et al. 2004). We (Schnack et al. 2004) tested the reliability of total brain, cerebral gray (GM) and white matter (WM), cerebellar, and lateral and third ventricular volumes in six subjects from five different scanners and protocols. The image processing pipeline algorithm was optimized by tuning two calibration factors that separated GM, WM, and cerebrospinal fluid (CSF). We concluded that we were able to obtain comparable between‐site volumetric results for most brain structures and across most sites. However, volumetric comparability does not imply that voxel by voxel tissue classification is reliable (Clark et al., 2006), as differences in contrast sensitivity, spatial uniformity, voxel size, etc. may lead to tissue classification or image registration differences. This spatial comparability between tissue segments from different sites becomes important when a multicenter study is to combine local tissue distributions using techniques such as voxel‐based morphometry (VBM; For an overview of VBM methodology, see Ashburner and Friston, 2000), tensor‐based morphometry (TBM; for a reliability study on longitudinal TBM data, see Leow et al. 2006) and cortical thickness measurements (CORT). Given the importance of this issue very few methodological approaches have been described to establish the reliability of multicenter VBM. Ewers et al., (2006) calculated voxelwise coefficients of variance from a single subject scanned on 10 scanners. Pardoe et al., (2008) carried out a multicenter study on childhood absence epilepsy, comparing single‐site results and determining between‐site differences, while Stonnington et al. (2008) analyzed multicenter Alzheimer's disease data to explore whether site‐effects were significant. While the last two studies focused on mapping inter‐site differences, we set out to map inter‐site comparability to show the gain in power, partly comparable with Tardif et al.'s approach (2009) in sensitivity analysis of 3 T imaging protocols. Considering cortical thickness, only two studies (Han et al., 2006; Wonderlick et al., 2009) have mapped measurement variability (intra‐class correlation coefficients) for different scan acquisitions. Wonderlick et al. calculated global minimum detectable thickness changes, but not for multicenter data. Han et al. calculated the minimum number of subjects required to detect a certain effect in a multicenter setting, but for an average value of measurement error. In this article, we report a method to calculate the combined power of scans from different sites and produce maps displaying this power on a voxel‐by‐voxel or vertex‐by‐vertex basis throughout the cerebrum.

There are important differences between testing volumetric comparability and voxel/vertex‐wise comparability. Firstly, even if the tissue classification method has tunable parameters, allowing optimization, this process cannot be used for each separate voxel or vertex, as it would undermine segmentation consistency. One has to use an “as is” method, or one that has been calibrated on the volumes, or, more generally, on the overall segmentation agreement. Secondly, volumetric reliability leads to a convenient table of reliability measures for each volume (see, e.g., Schnack et al. 2004), indicating which sites can reliably be combined to study a certain volume or interest. For VBM and CORT, the large number of voxels, usually in the order of 10⁵, makes such an approach impossible and even undesirable: One should not choose sites on a voxel by voxel (or vertex by vertex) basis.

A reliability study for multicenter VBM or CORT should produce clear measures that provide (a) reliability maps that visualize brain regions of good and bad agreement, and (b) a few usable quantitative measures to inform how good or bad these are. This information would identify (1) the favorable pool of sites for studying a certain brain region of interest, or (2), for a chosen pool, to determine in which brain areas data from different sites can be fruitfully combined and in which not, or (3), when establishing a multicenter study, estimate the regional gain in sensitivity when pooling data from the different candidate sites. (Note that we use “pooling” in the sense of “combining” data; not in the sense of “collapsing of factor levels when combining data” in which it is often used in multicenter trials (e.g., Schwemer, 2000).)

In this article, we report a method to establish multicenter VBM/CORT reliability and derive a number of reliability indicators. The method can be used to map the reliability of multicenter studies setup to detect voxel/vertex‐wise group differences or heritabilities. The method utilizes a (voxel/vertex‐wise) intraclass correlation coefficient (ICC)‐like measure derived from a calibration study of subjects scanned at each of the participating sites. As a demonstration we apply the method to the same data set in which the earlier volumetric reliabilities were tested. Brain maps displaying regional ICC, lowest detectable effect size, lowest detectable heritability, and effective‐N are reported. These maps estimate the multicenter gain and the added sensitivity per contributing site, given its reliability and number of subjects. As a rule of thumb, the contribution of a site to the effective‐N of a multicenter pool is of the order of the number of subjects from the site times the reliability (squared, for a heritability study).

METHODS

We will consider the cases of a multicenter VBM or CORT study for voxel/vertex‐wise investigation of effects of (psychiatric) diseases (i.e., group differences), or heritability of brain tissue (twin study) where the object is to combine MRI data from k scanners (sites), where each site j (j = 1, .., k) contributes n _j patients and n _j healthy subjects (or n _j monozygotic and n _j dizygotic twin pairs, in case of a heritability study). The total number of subjects (or twin pairs) is 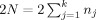. First, we derive a voxel/vertex‐wise reliability measure for each site, R _j, that can be used to calculate the voxel/vertex‐wise gain in sensitivity when pooling the data. Secondly, we will determine these reliability measures R _j experimentally from a multicenter calibration study and apply these values to produce brain maps showing the possible gain in sensitivity for all voxels/vertices.

We assume that measured VBM tissue “density” is related to some true, but unknown, tissue presence in each voxel. Similarly, MRI derived cortical thickness (CORT) is a direct estimation of the (unknown) true cortical thickness at each vertex. These relationships are modeled for each voxel/vertex as follows:

(1)

In this equation, x _ij is the measured density/thickness for subject i at site j; v _i is the true density/thickness for this subject; c _j is the systematic offset of this scanner, and b _j is the sensitivity or multiplication factor of this scanner (ideally, c _j ≈ 0, and b _j ≈ 1); e _ij is the (random) measurement error, i.e., noise. We assume that v _i is normally distributed around a mean μ with variance σ${}_{\mathit{\text{v}}}^{\text{2}}$, and that e _ij is normally distributed around zero with variance σ${}_{\mathit{\text{j}}}^{\text{2}}$. We allow this variance to be site‐specific, as noise can differ between scanners. Note that although we refer to c _j and b _j as scanner properties, they are in fact properties of the interaction between scan acquisition and the applied image processing algorithms. Since we use a fixed image processing pipeline in this work, we simply call these parameters scanner properties. We shall now derive reliability measures for both a group effect (disease) study and a twin (heritability) study.

Group Effect Study

One could either pool the raw data from the different sites and perform statistics on the pooled data, or first calculate standardized residuals using each site's mean and standard deviation, and pool these. We follow the second approach, as it does not suffer from possible offset effects between the sites and possible differences in variance, the latter complicating a sound statistical analysis. If one tries to detect a group difference in density of size Δv, measuring 2n _j subjects at site j, the test statistic z _j can be shown to be (see Appendix A for the derivation of this and following formulas):

(2)

with

(3)

Here Δv/σ_v = d is Cohen's (theoretical) effect size, and R _j is an intraclass correlation‐like coefficient of reliability, ranging from 0 to 1. The extension with respect to the standard intraclass correlation coefficient (ICC; see, e.g., Shrout and Fleiss, 1979) is the inclusion of the factor b _j and a site‐specific noise σ_j: The reliability becomes specific for each site and is a function of the ratio between its sensitivity factor b _j and its noise σ_j (if one sets b _j to 1, and assumes the same noise for all sites, R _j = ICC). Just like a standard ICC, R _j is a measure of the relative amount of true between‐subject variation with respect to the total variation of the measurement. A value close to 1 means that only a small amount of irrelevant variance (noise) is added to the between‐subjects variance, which is a desirable feature of any measurement. From Eq. (2) it is seen that increasing the number of subjects participating in the study increases the test statistic, but that it becomes lower for lower values of R _j: A group difference is less easily detected at sites that have more noise in their measurements. For a multicenter study pooling data that have been standardized per site (see Appendix A), the test statistic of the pool becomes:

(4)

with

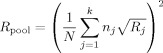(5)

Equations (2) or (4) can be used to calculate the study's lowest detectable effect size d _lim for chosen α‐ and β‐levels (α, the chance of false positives; β, the chance of false negatives, or 1 minus the power), by solving the requirement of a significant finding: |z| > |z _αβ|, where z _αβ is the limiting z‐value (standard normal deviate) for chosen α and β. Equating z _j or z _pool to z _αβ, we find:

(6)

In this equation, R _j or R _pool can be inserted for R, to calculate d _lim for a single site or a pool, respectively. The difference between the d _lim values for the single site and the pool tells us the gain in detection limit when sites are pooled. We define the effective number of subjects in a study as the number of subjects at one perfect site (R _j = 1) in a single‐site study that gives the same lowest detectable effect size as the current study (either a single site or a multicenter study). From Eqs. (2) and (4) it is seen that:

(7)

where N is the total number of subjects included and R is the reliability coefficient of the site or the pool, according to Eq. (3) or (5). The effective‐N can be used as a more tangible quantity to interpret differences in detection power between sites and pools.

Heritability Study with Twin Pairs

In a twin study, monozygotic (MZ) and dizygotic (DZ) twin‐pairs are measured to calculate a quantity's heritability: the fraction of the quantity's variance explained by genetic factors.

The heritability can be estimated by:

(8)

with r _MZ and r _DZ the within twin‐pair correlations of MZ and DZ twin‐pairs, respectively (Falconer and Mackay, 1996). The reliability of measuring within‐pair correlations is thus important. We assume that the members of a twin‐pair are measured at the same site. Using Eqs. (1) and (3), we find (see Appendix A):

(9)

The measured heritability is thus the true heritability lowered by the reliability factor.

For a measured heritability to be significant, it has to be “large enough” compared to its standard error, depending on the chosen levels of significance (α and β). Statistics on correlation coefficients is usually done after applying Fisher's z‐transform, because this produces normally distributed measured correlation coefficients: z = F(r) = (1/2) ln((1+r)/(1‐r)), leading to the statistic Y to test significance of h ²:

(10)

where z _MZ = F(r _MZ) and z _DZ = F(r _DZ). To calculate the lowest detectable heritability (ignoring possible shared environmental factors), we set Y equal to the limiting value z _αβ, for given α and β, and solve for h ². For a single site, an analytical expression can be obtained, but for a pool, where we use a weighted average of z‐transformed correlations, it should be done numerically (which is what we did in all calculations in this work). However, approximate formulas for lowest detectable h ² and effective‐N can be given (see Appendix A):

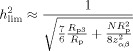(11)

and

(12)

for large enough N. Here R _p is the weighted average of the per‐site reliabilities:

Comparing this result with the effective‐N for group comparisons [Eq. (7)], one sees that the reliability factor R appears squared in the case of twin studies: Carrying out a (multicenter) twin study reliably demands reliability factors R _j that are higher than those necessary for group comparison studies. As a rule of thumb, the contribution of a site's data to N _eff of a multicenter pool is of the order of n _j × R _j for a group study and n _j × R ${}_{\mathit{\text{j}}}^{\text{2}}$ for a heritability study.

Quantities such as R _j, h ${}_{\text{lim}}^{\text{2}}$, and N _eff allow us to visualize voxel‐wise multicenter reliability in a way that is easily appreciated: What do we gain by pooling data? These metrics can also be used to create masks within which VBM or CORT analyses can reliably be carried out. Another way to use them is by comparing the lowest detectable effect size maps between different pools in order to determine the best pool for a VBM/CORT analysis in a certain region of interest.

What remains is the estimation of the R _js. This can be done by a calibration study in which a number of subjects is scanned at all participating sites, as we shall show in the next section.

Calibration: Determination of R _j from v _i, c _j, b _j, σ${}_{\mathit{\text{j}}}^{\text{2}}$, and σ_v

In a calibration study, a number (n _c) of subjects is scanned at all (k) participating sites, providing us, after post‐processing, with measured “density” or cortical thickness values x _ij (i = 1,..,n _c; j = 1,..,k).

We have to estimate the true subject values v _i from the measured data x _ij to be able to estimate the scanner parameters c _j, b _j, σ${}_{\mathit{\text{j}}}^{\text{2}}$ and subject variance σ${}_{\mathit{\text{v}}}^{\text{2}}$ needed to calculate R _j using Eq. (3). It is of course impossible to determine “the” truth; we only can determine “a” truth, estimated from the measured data by the k scanners. Different “truths” can thus be derived from different pools of sites.

In an iterative procedure, the scanner parameters c _j, b _j, σ${}_{\mathit{\text{j}}}^{\text{2}}$ and the “true” subject variance σ${}_{\mathit{\text{v}}}^{\text{2}}$ can be determined for each voxel or vertex. For the first iteration, “true” subject values v _i are estimated as the (unweighted) averages of the measured subject values x _ij. In each iteration (new), estimates of the scanner parameters c _j (offset), b _j (slope) are found by linearly regressing the measured subject values for scanner j (x _ij) on the current estimated “true” subject values v _i. The residual variances estimate σ${}_{\mathit{\text{j}}}^{\text{2}}$. New “true” subject values are determined by a weighted average of the measured values from all sites: 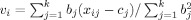. This process is iterated until convergence, i.e., changes in the estimated value of σ_v become smaller than some small specified value ε. After calculating the R _js [Eqs. (3) and (5)], the quantities d _lim [Eq. (6)], h ${}_{\text{lim}}^{\text{2}}$ [Eq. (10) (or A14, solving Y = z _αβ numerically)], and N _eff [for group studies, Eq. (7); for twin studies, solving Eq. (A14) numerically] can be calculated for the individual sites and for the pool.

For very small calibration sets, the number of measurements is too small to estimate v_i, c_j, b _j reliably. In those cases, one has to assume b _j = 1 for all j, and the iterative procedure reduces to calculating the site offsets c _j as the average subject value for site j minus the average subject value over all sites. The “true” subject values are the measured values averaged over the sites.

Uncertainty of Calibration Procedure

To get an impression of the uncertainty in the h ${}_{\text{lim}}^{\text{2}}$ values as determined from calibration data, we carried out simulations to test the goodness of the iterative fit procedure as well as the influence of calibration set size and number of sites. Multicenter calibrations with k = 2, 3, 4, 5, 6, and 8 participating sites were simulated, with calibration set sizes of n _c = 3, 4, 5, 6, 7, 8, 9, 10, 20, and 100 subjects. For each combination of n _c and k, 10,000 simulations were performed. In each simulation, n _c “density” values (v _i) were randomly drawn from a normal distribution with standard deviation σ_v. The value of σ_v itself was also randomly drawn: From the STAR VBM data (see Application section) we observed that the square root of σ_v was normally distributed with mean 0.28 and standard deviation 0.06. The parameters of the k scanners were also randomly drawn using values taken from the experimental data: c _j ∼ 0 ± 0.25; b _j ∼ 1 ± 0.30; √σ_j ∼ 0.20 ± 0.06. The true “density” values were converted into “measured” “density” values [Eq. (1)]. These were used to calculate h ${}_{\text{lim}}^{\text{2}}$, using the iterative procedure described earlier, and compared with the simulated value of h ${}_{\text{lim}}^{\text{2}}$, leading to an uncertainty in the determination of h ${}_{\text{lim}}^{\text{2}}$ as a function of calibration set size and number of sites. The total number of subjects in the simulated multicenter studies was kept constant, i.e., N = k × n _j = 160, which is about the N of the STAR study (see Application section).

RECIPE

This section summarizes the method and provides guidelines for a multicenter study and its calibration.

Inventory

Make an inventory of participating sites, and determine for each of the k sites: n _j—the numbers of subjects per group (healthy/patient) or twin pairs per group (MZ/DZ). The total number is N = n ₁ + .. + n _k. (If the n _j differs per group, use the average of the two values. One should try to avoid too unbalanced distributions of subjects, e.g., sites contributing an n _j much smaller or larger than N/k, or sites contributing only patients and no control subjects.)

Statistics

Choose level(s) of statistical significance z _αβ for the multicenter study, according to α, β, and optional method for controlling false positives in multiple comparions. Calculate the best attainable lowest detectable effect sizes (d _lim, h ${}_{\text{lim}}^{\text{2}}$), that is, if all sites would be perfect (all R _j = 1), using Eq. (6) (with R = 1) and Eq. (A13) (with n _j = N). If one thinks these ideal values are already too poor to justify the effort of a multicenter study, one can stop here (or try to include more subjects and/or sites).

Calibration Subjects

Determine how many calibration subjects (n _c) are needed. The number depends on the number of sites, but at least about five subjects are needed. For a multicenter study involving only two sites a few more should be included, while for studies with six or more sites four would suffice, depending on how precise one wants the estimates of lowest detectable effect sizes to be (Fig. 1 can serve as a guide for twin studies.) Be aware of the possible drop‐out of scans (or subjects)—A spare subject may be of use! The subjects should be representative of the study samples, e.g., the calibration set should include men and women if the samples contain men and women, and in an age range comparable to the ages in the samples. In general, the more calibration subjects the better, but costs and practical issues also play a role here.

Figure 1.

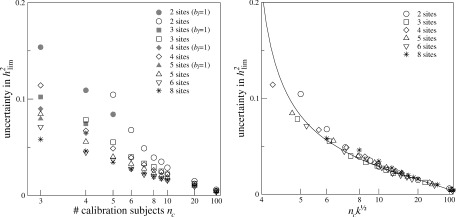
Left: Uncertainty in the determination of h ${}_{\text{lim}}^{\text{2}}$ (pool), as a function of the number of calibration subjects n _c, for k‐site multicenter studies (k = 2, 3, 4, 5, 6, 8) with n _j MZ and DZ twin pairs per site, around h ${}_{\text{lim}}^{\text{2}}$ = 0.51. We kept 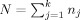= 160 for all values of k. The uncertainty was determined in a simulation experiment as the mean absolute difference between the experimentally determined values and the true, i.e., simulated, values of h ${}_{\text{lim}}^{\text{2}}$. The gray‐area symbols represent uncertainties in h ${}_{\text{lim}}^{\text{2}}$ for which b _j = 1 was set; they are only displayed if the uncertainty was smaller than those obtained with free b _j (for the same n _c; same symbol shape). Right: scaled uncertainties of h ${}_{\text{lim}}^{\text{2}}$. The uncertainties turn out to follow the same curve (drawn line) after scaling of n _c and k: Uncertainty ≈ 0.098(n _c√k − 3.69)^−2/3.

Calibration Scans

Scan all calibration subjects at all sites, using the same acquisition protocols that are (or, have been) used for the individual studies. This assumes that the hardware/software of the scanners have not changed (a lot) as the data for the studies were collected. One should try to scan the calibration subjects at all sites within a short period of time. Process the MRI calibration data using the same algorithms as for the processing of the study data, resulting in VBM densities or cortical thicknesses ready for statistical analyses. [Optionally, one could first perform scan protocol optimization rounds, in which scan parameters are tuned at each site in order to produce as comparable protocols (and scans) as possible. This is beyond the scope of this work, and if all study scans have already been acquired, such an approach is not even possible.]

Reliabilities

For each voxel/vertex, calculate R _j and h ${}_{\text{lim}}^{\text{2}}$, etc. (see aforementioned Section “Calibration”). Examine each site's contribution [Eqs. (7) and (12)] to N _eff: if a site's contribution is too low, one could decide to omit this site from the multicenter study (or from the analyses in certain brain areas, see Fig. 8). If the quantities are satisfactory one can continue with the multicenter study (i.e., image processing, statistical analyses); if they are not, one could either try to improve the study by including more sites or subjects, or decide to stop.

Figure 8.

Transverse slice of the model brain showing the best combinations of sites for each voxel, for a multicenter twin study. Each color represents one of the five possible combinations of sites: all four sites, and four combinations leaving out one site at the time.

APPLICATION TO A MULTICENTER MRI SET

Study

The Schizophrenia Twin and Relatives (STAR) consortium investigates the relationship between schizophrenia, brain morphology and genetic risk in twins and relatives. MRI brain scans were acquired at five research sites: University Medical Center Utrecht, Institute of Psychiatry, London, Universitätskliniek Heidelberg, University of Jena, and University of Helsinki. All subjects (mean (SD) age, 34 ± 10.6 year; 50% female) had already been scanned before the multicenter project started, so no pre‐scan acquisition optimization was possible. We have reported the between‐sites volumetric reliability before (Schnack et al. 2004). We now report the between‐sites voxel‐ and vertexwise reliabilities for the four 1.5 Tesla scanners (Utrecht, London, Jena, Heidelberg), while in a post‐hoc analysis the comparability of the 1.0 Tesla scanner (Helsinki) with respect to the other scanners is investigated.

Subjects for Calibration

For the between‐sites reliability, estimates of Utrecht (U0), London (L), Heidelberg (H) and Jena (J), six healthy volunteers (c1‐c6), two males, four females, aged between 20 and 35 years (mean (SD) 28 ± 3.5 year), were scanned at each site over an 8 month period. Five of these subjects (c1‐c5) were rescanned twice in Utrecht (U1 and U2), between 15 and 18 months after the first scan. Over the same period, four (c1–c4) were scanned in Helsinki (F). All volunteers gave written informed consent to participate in the calibration study. The study was approved by the medical ethics committee for research in humans (METC) of the University Medical Centre Utrecht, and was carried out according to the directives of the “Declaration of Helsinki” (amended Edinburgh, 2000).

MRI Acquisition and Processing

MR images from Utrecht were obtained on two 1.5 Tesla Philips Gyroscan NT scanners Release 5 (Best, Netherlands). For volumetric analysis, a three‐dimensional T1‐weighted coronal spoiled gradient echo scan (3D‐FFE) of the whole head was acquired. The same protocols were used for sets U0, U1, and U2.

MR images from London were obtained on a 1.5 Tesla General Electric Signa System scanner (Milwaukee, WI). For volumetric analysis, a three‐dimensional T1‐weighted coronal SPGR scan of the whole head was acquired.

MR images from Heidelberg were obtained on a 1.5 Tesla Picker (Marconi) Edge scanner. For volumetric analysis, a three‐dimensional T1‐weighted sagittal 3D‐FLASH scan of the whole head was acquired.

MR images from Jena were obtained on a 1.5 Tesla Philips ACS II scanner (Best, Netherlands). For volumetric analysis, a three‐dimensional T1‐weighted sagittal 3D‐FFE scan of the whole head was acquired.

MR images from Helsinki were obtained on a 1.0 Tesla Siemens Magnetom Impact scanner (Erlangen, Germany). For volumetric analysis, a three‐dimensional T1‐weighted sagittal MPRAGE scan of the whole head was acquired.

A summary of the scanners and acquisition protocols at each site is given in Table I.

Table I.

Summary of the scanners and calibration scans at the five research sites

Site	Code	Scanner manufacturer and type	Acquisition protocol voxel size (mm) (# slices)	TE (ms)	TR (ms)	Flip angle	Subjects scanned
Utrecht, base scan	U0	Philips NT 1.5 T	3D‐FFE coronal	4.6	30	30°	c1‐c6
repeated 1	U1		1×1×1.2 (180)				c1‐c5
repeated 2	U2						c1‐c5
London	L	GE Signa 1.5 T	3D‐SPGR coronal	5	35	35°	c1‐c6
			0.781×0.781×1.5 (124)
Heidelberg	H	Picker Edge 1.5 T	3D‐FLASH sagittal	3	30	30°	c1‐c6
			1×1×1.5 (128)
Jena	J	Philips ACS II 1.5 T	3D‐FFE sagittal	5	13	25°	c1‐c6
			1×1×1 (256)
Helsinki	F	Siemens Magnetom Impact 1.0 T	MPRAGE sagittal	4.4	11.4	12°	c1‐c4
			1×1×1.2 (128)

Image processing of the brain scans from the healthy volunteers was done using the image processing pipeline developed in the neuroimaging computer network of the Department of Psychiatry in Utrecht. The T1‐weighted images were first put into Talairach orientation (no scaling) (Talairach and Tournoux, 1988). For the sagittal scans (Heidelberg and Helsinki), a resampling to isotropic (1 × 1 × 1 mm³) voxels was included in this step. The N3 algorithm was used to correct the images for scanner RF‐field nonuniformity (Sled et al., 1998). All further operations were performed on the nonuniformity corrected images. Total brain segmentation was performed automatically (Schnack et al. 2001, 2004), checked visually and manually corrected if necessary. Separation of gray and white matter of the cerebrum was fully automatic (Schnack et al. 2001, 2004).

To prepare the gray and white matter segments for VBM analysis, they were first blurred using a three‐dimensional Gaussian kernel (full‐width half‐maximum (FWHM) = 8 mm), in order to gain statistical power. The voxel values of these blurred gray and white matter segments reflect the local presence, or concentration, of gray or white matter, respectively, and these images will be referred to as “density maps.” To compare brain tissue at the same anatomical location between all subjects and sites, the gray and white matter segments were transformed into a standardized coordinate system using a two step process. First, the T1‐weighted images were linearly transformed to a model brain (Hulshoff Pol et al. 2001). In this linear step, a joint entropy mutual information metric was optimized (Maes et al. 1997). In the second step, nonlinear (elastic) transformations were calculated to register the linearly transformed images to the model brain up to a scale of 4 mm (FWHM), thus removing global shape differences between the brains, but retaining local differences. For this step, the program ANIMAL (Collins et al., 1995) was used. The gray and white matter density maps were now transformed to the model space by applying the concatenated linear and nonlinear transformations. As the density maps have been blurred to an effective resolution of 8 mm, it is not necessary to carry out statistical tests at the 1‐mm level. Therefore, to decrease the number of statistical tests to be carried out, the maps were resampled to voxels of size 2 × 2 × 2.4 mm³, i.e., doubling the original voxel sizes.

For cortical thickness measurements, we used a custom implementation of the CLASP algorithm (Kim et al., 2005; Lyttelton et al., 2007) which starts from the gray and white matter segments created by our own algorithm. A surface consisting of 81,920 polygons and 40,962 vertices was fitted to the white matter/gray matter interface of each subject's left and right hemisphere, which was then expanded out to fit the gray matter/cerebrospinal fluid interface, thereby creating the outer cortical surface. Cortical thickness was estimated vertex‐wise by taking the distance between corresponding vertices on the two surfaces. The thickness values were smoothed across the surface using a 20 mm (FWHM) surface‐based blurring kernel (Chung and Taylor, 2004) to improve statistical power. The surfaces of each subject were registered to an average surface created from 152 subjects (ICBM; Lyttelton et al., 2007), allowing comparison of cortical thickness locally between subjects.

In regular VBM and CORT studies, the next step is to carry out voxel‐wise and vertex‐wise statistical analyses on these images. Here the images are used to calculate the voxel/vertex‐wise reliability for each site (R _j), and the pooled data (R _pool), and from these, metrics such as lowest detectable effect size and N _eff, for given statistical threshold levels and numbers of subjects per site. We set α = 0.001 and 1‐β = 0.80, giving z _αβ = 3.939 for the one‐sided test for heritabilities, and z _αβ = 4.132 for the two‐sided test for group differences. We chose n _j = 40 for all sites, which is about the average n _j of the k = 4 STAR study data sets. This value reflects a multicenter study with attainable and comparable numbers of subjects from each site.

Our main calibration was carried out for the four 1.5 Tesla scanners Utrecht (U0), Jena, London, Heidelberg. The data set from Helsinki was not included in the main calibration because of the lower magnetic field strength (1 Tesla). Moreover, only four subjects were scanned at this site and the data were collected considerably later at this site. All three effects could impair this site's comparability, making an influence of this site's data on the “truth” less desirable. See Appendix B for a post‐hoc analysis including this site.

RESULTS

Simulations

The effect of the calibration study sample size on the uncertainty in the determination of h ${}_{\text{lim}}^{\text{2}}$, as determined from the simulations, is shown in Figure 1, for different numbers of sites. The error in the determined h ${}_{\text{lim}}^{\text{2}}$ is in general small; only for very small calibration sets it increases rapidly. Including one or two more calibration subjects to the sample quite improves the certainty, but this effect becomes smaller for sample sizes beyond 7. The uncertainties can be described by one formula, empirically found to depend on n _c√k: uncertainty ∼ 0.098(n _c√k − 3.69)^−2/3 (Fig. 1, right).

Multicenter MRI Data

Figures 2, 3, 4, 5, 6, 7, 8 and Table II show the multicenter reliability results determined from the calibration data from Utrecht (U0), Jena (J), London (L), and Heidelberg (H). As the aim of this work was to derive useful reliability measures for VBM and CORT, we use the application to the STAR data set to present several examples of ways to map local reliability, rather than an exhaustive description of the reliability of this set.

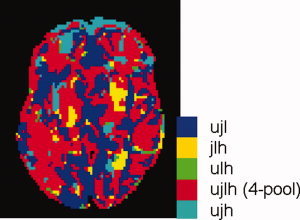
Figure 2.

Transverse slices of the model brain showing the lowest detectable effect size h ${}_{\text{lim}}^{\text{2}}$ for the single sites (from top downward, U0, J, L, H), and the 4‐site multicenter pool (bottom, P) (left column; see Fig. 6 for this slice's anatomy). Distributions of voxelwise lowest detectable heritabilities for the whole cerebrum (second column). View of the left hemisphere of the cerebrum with vertexwise lowest detectable effect sizes (d _lim) (third column). Distributions of vertexwise lowest detectable effect sizes for the whole cerebral cortex (right column). Calculations were done with z _αβ = 3.939 (twin; one‐sided) and 4.132 (group; two‐sided), and n _j = 40 for all sites.

Figure 3.

Top row: Transverse slice of the brain showing gain in lowest detectable heritability h ${}_{\text{lim}}^{\text{2}}$ (twin study) of the 4‐pool versus the average single site (left), and gain in lowest detectable effect size d _lim (group study, right). Negative values reflect a gain in sensitivity when pooling data from the four sites. Bottom row: Lateral view of left cerebral hemisphere showing gain in lowest detectable h ${}_{\text{lim}}^{\text{2}}$ (left) and gain in lowest detectable effect size d _lim (right).

Figure 4.

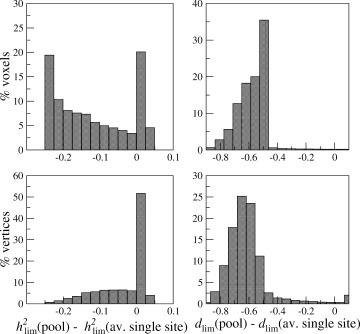
Distribution of gain in lowest detectable heritability h ${}_{\text{lim}}^{\text{2}}$ (twin study): h ${}_{\text{lim}}^{\text{2}}$ (pool)—h ${}_{\text{lim}}^{\text{2}}$ (average single site) and lowest detectable effect size d _lim (group study): d _lim(pool)—d _lim(average single site). Negative values reflect a gain in sensitivity when pooling data from the four sites.

Figure 5.

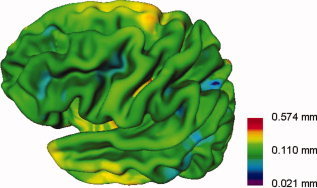
View of the left cerebral cortex showing lowest detectable thickness differences between two groups (patients and control subjects) for the multicenter 4‐pool. A logarithmic color scale is used.

Figure 6.

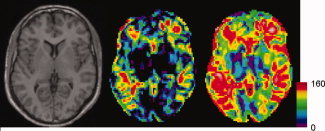
Transverse slices of the model brain (left) showing the multicenter N _effs for a twin study (middle) and a disease effect (group) study (right).

Figure 7.

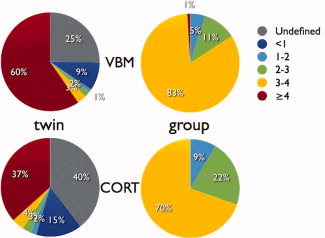
Pie charts displaying the distribution of gain factors N _eff(pool)/N _eff (single site) (% voxels or vertices), for VBM (top row) and CORT (bottom row); twin (left column) and group (right column) studies. Gain factors are calculated voxel‐/vertexwise with respect to the average of the single sites. Undefined: all single site N _effs were zero (gray). Note that for heritability (twin) studies gain factors larger than 4 are possible. For group studies, this percentage refers to a gain factor of exactly 4 (red).

Table II.

Mean (SD) effective‐N over all voxels (VBM)/ vertices (CORT) for group (d _lim) and twin studies (h ${}_{\text{lim}}^{\text{2}}$) for the four sites and the 4‐pool

Site	VBM		CORT
	Twin	Group	Twin	Group
Utrecht	8.8 (12.4)	28.2 (11.7)	3.7 (8.6)	23.5 (12.2)
Jena	10.4 (13.3)	29.3 (11.2)	2.9 (7.8)	22.1 (12.1)
London	8.4 (12.5)	27.5 (11.9)	2.5 (7.1)	20.7 (12.4)
Heidelberg	7.2 (12.4)	25.3 (12.7)	2.6 (8.2)	17.2 (13.1)
4‐pool	54.0 (45.6)	104.1 (38.5)	16.1 (23.2)	73.4 (32.6)

Upper limits are 40 and 160, respectively.

Figure 2 (left column) shows a slice of the model brain with voxel‐wise lowest detectable heritabilities for each of the four sites and the 4‐site pool. It is clear that in most voxels the lowest detectable heritability is lower for the pool than for the sites individually, thus in most voxels pooling increases power. The lowest possible h ${}_{\text{lim}}^{\text{2}}$ at a single site is 0.874 and for the pool 0.652 [found from Eq. (A13), inserting R = 1, z _αβ = 3.939, and N = 40 for a single site, and N = Σ n _j = 160, for a pool]. Note that this does not mean that one could not encounter significant heritabilities below these values in such twin studies: The above values regard true heritabilities: The measured heritability is the true heritability lowered by R _j [Eq. (9)]. The third column displays the left hemisphere with vertex‐wise lowest detectable effect sizes. The lowest possible d _lim for a single site is 0.924 and for the pool 0.462 [found from Eq. (A3/A5), inserting R = 1, z _αβ = 4.132, and N = 40 for the single sites and N = Σ n _j = 160 for the pool]. The second and fourth columns show the distributions of lowest detectable heritabilities and effect sizes, for VBM and CORT, respectively. The spatial distribution over the cortex and in a slice of the brain of the gain in lowest detectable effect size and heritability is shown in Figure 3 for the 4‐site multicenter pool versus the average of the single sites. Histograms of these gains are shown in Figure 4. The peak of the d _lim gain lies between −0.50 and −0.65 [four “good” sites with R _j = 0.8 would give a gain of −0.52 according to Eq. (A3/A5)]. In 0.4% of the voxels and 2.3% of the vertices, there is a (very) small loss in power (increases in d _lim up to 0.1) when pooling. These vertices are visible as pink/red spots in Figure 3 (right column). According to Eq. (A13), the maximum gain in h ${}_{\text{lim}}^{\text{2}}$ attainable with four comparable sites would be −0.254 (R _j = 0.764), a value that is reached for 20% of the voxels (upper left figure).

Figure 5 presents the conversion from lowest detectable effect size to lowest detectable thickness difference between groups on a vertex by vertex basis at the statistical thresholds and pooled subject numbers specified.

Table II gives the mean values of effective‐N for the single sites and the pool while the spatial distributions of multicenter N _effs for a VBM twin study and a group (disease effect) study are presented in Figure 6. The values in the group map are higher than in the heritability map, reflecting the greater reliability needed for twin studies [cf Eqs. (7) and (12); see also Table II]. In some areas, the maximum attainable effective‐N is reached, i.e., N _eff = N = Σ n _j = 160. In Figure 7, the distributions of gain factors N _eff(pool)/N _eff (single site) are presented. VBM gain factors are on average higher than CORT gain factors. Multicenter pooling leads to higher gain factors for twin studies than for group studies. This is due to the fact that N _eff increases disproportinately with the number of twin pairs [see Eq. (A17)], so that even gain factors larger than 4 are possible.

Figure 8 presents a map of best‐pool‐compositions, identifying which combination of sites gives the highest effective‐N (or lowest detectable effect size), the majority of voxels benefiting most from the complete four site pool.

DISCUSSION

We developed a method to investigate the feasability of voxel‐based morphometry (VBM) and cortical thickness measurements (CORT) from multi scanner, multi site data collected using different acquisition sequences. The method produces maps of lowest detectable effect size and effective number of subjects. A recipe section summarizes the method and provides guidelines for a multicenter study and its calibration. We applied the method in a multicenter calibration study with six healthy volunteers scanned at five research sites with scanners from four different manufacturers, each running different acquisition protocols. The resulting reliability maps showed good comparability between the four sites, showing a reasonable gain in sensitivity in most parts of the brain. In some areas, e.g., around the thalamus, scan pooling from different sites was less fruitful and in some of these areas, leaving out one of the sites gave better results. The reliability maps also reveal which brain regions are in any case difficult to measure reliably: if pooling leads to unreliable data for a certain voxel/vertex, due to strong disagreement between the sites, then one can probably not trust results from some individual sites or even any individual sites.

Our method of estimating lowest detectable effect size shares features with Suckling's power calculation for multicenter fMRI (Suckling et al., 2008). Apart from the fact that we allow different sites to have different “sensitivity” factors b _j, an important difference is that Suckling et al. calculate the power of detecting an assumed effect size, whereas we calculate the lowest detectable effect size, for given power. We suggest that our method offers a statistical advantage. Instead of assuming an effect size for all voxels, the (true) subject variation and noise are estimated voxel‐wise, producing lowest detectable effect size estimates voxel by voxel. This allows us to produce maps from which one can immediately see what heritabilities and disease effects could be detected in which brain regions, for any selected power.

Han et al. (2006) calculated cortical thickness measurement variability maps for different acquistion protocols, but did not convert this information to “power maps,” while Wonderlick et al. (2009) went one step further and reported CORT ICC maps for different acquisition sequences. Both these studies and our own (Fig. 2, bottom/right) suggest that cortical thickness estimates in the orbito‐temporal lobe will be the most unreliable. Imaging artefacts are often present in this region, probably due to the close vicinity of the base of the skull. The patchy way in which the reliability varies over the cortex is also seen in these two studies; the reason is unknown, but may be partly due to difficult separation of cortex from dura at some locations (Han et al., 2006).

Clark et al. (2006), investigating scanner/post‐processing combinations with optimal segmentation quality, concluded that due to partial voluming effects the thalamic region was susceptible to voxelwise segmentation errors, consistent with our results. Stonnington et al. (2008) reached similar conclusions in a study of Alzheimer's disease, but they set out to detect significant scanner effects, as was done by Pardoe et al. (2008). In our opinion, the key issues is not merely whether a possible scanner effect is significant or not, as a (just) nonsignificant scanner effect could add a substantial variance, thereby reducing power. Therefore, we calculated lowest detectable effect size maps; regions where a scanner performs substantially worse than others can be found from either the site's R _j map, or the “best‐combination” map (see Fig. 8).

Ewers et al. (2006) calculated voxel‐wise coefficients of variation (COV) of voxel intensities from different scanners. This measure differs from VBM “density,” and does not deal with the effect of segmentation. The COV map showed very high COVs (up to 59%) at the brain edges, possibly secondary to sampling grid and registration mismatch effects, that could also play a role in our low‐reliability regions at the edges of the brain.

Although not a multicenter study, Tardiff et al. (2009) investigated the sensitivity of VBM at 3 T for several imaging protocols, and produced F‐maps representing the ratio of biological tissue variance and measurement variance, which can be transformed into an ICC comparable to our R _j. The variations in reliability take place on a scale very similar to what we see in our maps (cf their Fig. 8 with our Fig. 2, bottom/left).

We were able to compare the reliability of VBM and CORT. Table II highlights that the average effective‐N of VBM is higher than the effective‐N of CORT for all sites. This is presumably because the cortical thickness is only a few multiples of the voxel dimensions (∼2–4 × 1 mm). The measurement is, therefore, sensitive to the actual sampling, and it is highly dependant on the segmentation and surface fitting: a tiny shift in tissue classification or surface fit could have considerable effects on the measured thickness. These effects can only partly be compensated by surface smoothing (FWHM = 20 mm in our case). VBM, on the other hand, measures the presence, i.e., relative amount, of a tissue in a neighborhood roughly twice the size of the blurring kernel (2 × 8 mm = 16 mm in our case; beyond this distance the value of the blurring kernel becomes small; see also Ashburner and Friston 2000), for which the loss of sub‐voxel geometric information is less crucial; also, classification errors due to noise cancel out more easily. (Note that CORT is sometimes preferred to VBM, because it produces more accurate, in the sense of better defined measures, namely, the local thickness of the cortex, rather than the more indicative “presence of tissue” by VBM. This property is disconnected from reliability.)

The translation of reliability to effective‐N also allows us to compare reliability between diagnostic group studies and heritability studies. In Table II, we see that the twin study reliability is always lower than the group study reliability, [Eqs. (7) and (12)], as heritability measurements crucially depend on correlations between the members of a twin pair and thus reproducible measures. As a rule of thumb, the site contribution to the effective‐N in a multicenter pool is of the order of the product of the individual site's N and the site's reliability (squared, for a heritability study). If a site's contribution is small compared to the other sites', one might conclude that the effort of adding this site to the study is not adequately rewarded by the small gain in power.

The uncertainty of the reliability estimates is a possible methodological limitation. The “true” subject values and scanner responses were determined from a limited number of healthy volunteers. The more calibration subjects that are included, the more trustworthy the reliability estimates, but at the cost of time, money, and effort. Accuracy roughly drops reciprocally with the number of calibration subjects, as was found from calibration runs on simulated subject and scanner parameters (see Fig. 1). Reasonable accuracy can be achieved from relatively small numbers, but one should not include too few calibration subjects, for if one has to exclude one or more scans from a small calibration set, one might run into trouble. On the other hand, while a small calibration set might introduce noise to the R _j values, one can still get a good impression of the expected pooling reliability. Another point of concern is how well the calibration subjects represent the study cohort. Of course, here again, the more the better applies. In the power calculations, it is further assumed that patient and control variance are the same which is not necessarily the case. Both these issues can be addressed by estimating the true subject variations from the single‐site study subjects, though this might result in noisy values in cases of low sensitivity (b _j).

Lowest detectable effect size and effective‐N were derived for relatively simple analyses, group differences and heritability calculations by comparing correlations. Nevertheless, we believe that the reliability results obtained from these calculations reflect the reliabilities for more complex analyses, as the limiting factors (contrast and measurement repeatability) remain the same.

The amount of work involved in a validation/calibration procedure such as the one we carried out is large. A group of healthy volunteers need to be scanned at all participating sites within a certain amount of time. However, this seems to be the only way to obtain quantitative information on comparability between sites. For a (qualitative) impression of the comparability, each site's study sample's variance could be calculated voxel/vertex‐wise. Differences in variance could point to a reduced comparability, but since each site's sample consists of different subjects, true sample differences could also lead to such differences. The possibility of reliability determination without a calibration set remains to be investigated.

This multicenter calibration study is limited to scans acquired using local protocols. In the quest for reproducibility, Tofts (1998) suggested the sequences themselves should be similar, an objective we could not retrospectively achieve. However, our results suggest that such pooling is beneficial. Looking for acquisition parameters that influence comparability, we see from the “best pool” maps (see Fig. 8) that if a 3‐pool study is more powerful than the 4‐pool, it is most often (76% of these voxels) the Heidelberg scan that should be left out. From the picture and an analysis per sagittal slice (not shown) it is seen that most of the leave‐Heidelberg‐out voxels lay around the mid‐sagittal plane. The reason is potentially related to the relatively large voxel size (1.5 mm) perpendicular to this plane, resulting in less reliable segmentation in this region. Note that in our volumetric reliability study (Schnack et al., 2004) third ventricular volume, a flat structure lying in the midsagittal plane, from the Heidelberg scan was again incomparable (low ICC) to the other centers. The London voxel length is also 1.5 mm, but oriented coronally while the London voxel volume is also much smaller. Summing up, it appears that the highest reliability is obtained by scanning smaller, “not too” anisotropic voxels, and avoiding long voxels perpendicular to large thin planar structures such as the midsagittal space between the two hemispheres.

In conclusion, we have derived a few quantities showing the reliability of multicenter VBM/CORT in a way that is easily appreciated in terms of gain in detection limit and power. These measures can be obtained from a calibration study. In an application of this approach, we have shown that multicenter VBM data can be tested on reliability and expected gain obtained from pooling the data. For most locations in the brain, the VBM densities were in good agreement with each other, allowing for pooling of the data from all sites. For locations showing strong disagreement, the reliability maps show if a pool of different composition might give sufficient agreement.

APPENDIX A.

(Derivation of the formulas in the Methods section.)

We start from Eq. (1), and, by definition, our test statistic is,

(A1)

with 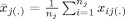, the mean values per group (pat and con) at site j. We assume that a site contributes equal numbers of patients and controls, n _j. The squared pooled standard error is 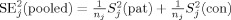, with S ² the variances per group. Our null‐hypothesis is that patients and controls follow the same distribution, so that, using Eq. (1), SE² _j(pooled) estimates 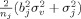. Since the expection of 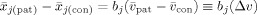, with Δv the true group (disease) effect, we obtain:

(A2)

with 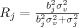and Δv/σ_v = d is Cohen's (theoretical) effect size [Method's Eqs. (2) and (3)]. R _j is an intraclass correlation‐like coefficient of reliability, ranging from 0 to 1. An observed group effect is considered significant if the test statistic z _j exceeds the critical value z _α (for a two‐sided test at, e.g., α = 0.05, z _α = 1.96). To determine the lowest possible effect size to be measured significantly, we set z _j equal to z _αβ, where z _αβ = z _α + z _β, with z _β the z‐value for power 1‐β (for a power of, e.g., 0.80, z _β = 0.842, so that z _αβ = 2.802). The lowest effect size to be measured significantly is thus [Eq. (6)]:

(A3)

For a multicenter study, we pool the measured data divided by their site's standard deviation, y _ij = x _ij/S _j, so that we pool data with standard deviation 1:

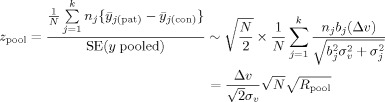(A4)

with 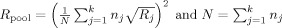[Eqs. (4) and (5)]. We can calculate the lowest detectable effect size again by setting z _pool equal to z _αβ and find [Eq. (6)]:

(A5)

The investigation of genetic and environmental influences on a quantity v is usually done in an ACE model, by splitting the quantity's value in three contributions:

(A6)

with a the (additive) genetic, c the common environmental, and u the unique environmental contributions (Neale and Cardon, 1992). For the variance this means:

(A7)

In a twin study, the covariance between monozygotic (MZ) co‐twins is σ${}_{\mathit{\text{a}}}^{\text{2}}$ + σ${}_{\mathit{\text{c}}}^{\text{2}}$, since MZ twins share 100% of their genes and, by definition, their shared environment. For dizygotic (DZ) twins, sharing on average 50% of their genes, the covariance is 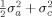. The heritability is defined as the fraction of variance explained by genes, i.e.:

(A8)

The heritability can be calculated in the simplest way from the MZ and DZ (intraclass) correlations [Method's Eq. (8)]:

(A9)

However, we do not measure v, but x, and the measured MZ correlation at site j becomes:

(A10)

Applying the same correction to the DZ correlation, using Eq. (A7), we obtain [Eq. (9)]:

(A11)

Thus, the experimental heritability h ${}_{\text{o}}^{\text{2}}$ is lowered by a factor R _j. The significance of this experimental heritability could be tested by comparing its value to its standard error, but it is better to first transform the correlation coefficients with Fisher's z‐transform: z = F(r) = (1/2) ln((1 + r)/(1 − r)) = atanh(r), because the z‐values follow a normal distribution with standard error SE(z) = 1/√(n − 3). This leads to the test statistic (we assume the numbers of MZ and DZ pairs, n _j, are the same within each site, and we omit the −3, for large n _j [Eq. (10)]):

(A12)

In the right‐hand side of (A12), we can set the common environmental contribution to zero, allowing us to calculate the lowest detectable heritability, by equating Y _j to z _αβ (z _αβ = z _α+ z _β with z _α = 1.645 for a one‐sided test of r _MZ > r _DZ at α = 0.05):

(A13)

We see that the lowest detectable true heritability is proportional to 1/R, where the lowest detectable group difference was proportional to 1/√R. If the right hand side of (A13) is larger than 1, h ${}_{\text{lim}}^{\text{2}}$ = 1. For a multicenter study, we can directly pool the z _js, 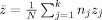, and 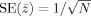, leading to:

(A14)

Y _pool = z _αβ should be solved numerically to determine the lowest detectable heritability for the multicenter study, but we can also derive an approximate solution. Expanding Eq. (A14) in a Taylor series in terms of R_jh ²,

(A15)

Equating the left‐hand side to 1, squaring both sides, and solving for 1/h ⁴, leads to:

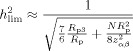(A16)

to first order in R _p3/R _p [Eq. 11 of the Methods section]. Here R _p is the weighted average of the per‐site reliabilities: 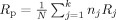and 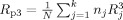. To obtain the corresponding N _eff, i.e., the number of subjects needed in a single site study to give the same h ${}_{\text{lim}}^{\text{2}}$, we use Eq. (A12), inserting the approximate h ${}_{\text{lim}}^{\text{2}}$ from Eq. (A16), and solve Y _j = z _αβ for n _j (= N _eff), keeping only the zeroth order term:

(A17)

for large N [Eq. (12)]. The first term is independent of N and negative in the range of R values for which the approximation is valid: N _eff increases disproportionately with increasing N.

APPENDIX B.

(Post‐hoc analysis, including Helsinki calibration data)

We compared the Helsinki data with the Utrecht data acquired at the same time (U1 and U2), and, when found comparable enough, entered the Helsinki data in the calibration, leaving the “truth” as determined in the main calibration from the other four sites. In this way, we could still get an idea about the reliability of the Helsinki site.

From the voxel‐wise ICCs for all possible two‐site combinations (data not shown) we observed: (1) ICC estimations between sites from {U0, J, L, H} were highly comparable for the subject sets c1‐c6, c1‐c5, c1‐c4; (2) Replacing U0 by U1 or U2 lead to very comparable ICC estimations (sets c1‐c6 and c1‐c5); (3) ICCs between U0 and U1, U0 and U2, and U1 and U2 were all very good (>0.85). From point (1), we concluded that the c1‐c4 calibration set, although only four subjects, could be used to estimate reliability. From points (2) and (3), we concluded that the calibration data obtained 7–10 months later (U1, U2, and F) were sufficiently comparable to the data collected earlier (U0, J, L, H). Following this line of thought, we judged that it was permissable to include data from Helsinki (H), by comparing the measured values with the values obtained from their regression on the “true” subject values as determined from the main calibration. Note that the reliability values for Helsinki might be an underestimate, as there might be (small) brain changes with respect to the earlier scans, and, more importantly, the Helsinki data were not used in the determination of the “truth” (as described earlier). We found that the distributions of the lowest detectable effect sizes for Helsinki were comparable to those of Heidelberg (see Fig. 2). Adding Helsinki's data to the pool of the other four sites results in an additive average gain in lowest detectable effect size d _lim for CORT of −0.07 (with respect to the 4‐pool's average gain of −0.61, cf Fig. 4).