Activated region fitting: A robust high‐power method for fMRI analysis using parameterized regions of activation

Abstract

An important issue in the analysis of fMRI is how to account for the spatial smoothness of activated regions. In this article a method is proposed to accomplish this by modeling activated regions with Gaussian shapes. Hypothesis tests on the location, spatial extent, and amplitude of these regions are performed instead of hypothesis tests of individual voxels. This increases power and eases interpretation. Simulation studies show robust hypothesis tests under misspecification of the shape model, and increased power over standard techniques especially at low signal‐to‐noise ratios. An application to real single‐subject data also indicates that the method has increased power over standard methods. Hum Brain Mapp 2009. © 2009 Wiley‐Liss, Inc.

INTRODUCTION

The main purpose of fMRI analysis is to determine which brain regions are activated. This question is answered by looking for groups of significantly activated voxels but not by looking for single voxel activity. At the basis of this train of thought is the assumption that activation (i.e. the BOLD response) measured by fMRI has a spatial extent of several millimeters and that the activation pattern is smooth [Hartvig,2002]. This assumption is often incorporated by assuming positive spatial correlations between voxels, either positive correlations between fMRI noise or positive correlations between fMRI signals. Methods that incorporate fMRI noise correlations are, for example, Monte Carlo multiple testing corrections [Forman et al.,1995], permutation test frameworks [Hayasaka and Nichols,2004], preprocessing smoothing kernels [Friman et al.,2003], and random field theory [Poline et al.,1997; Worsley et al.,1996]. Methods that incorporate signal correlations are clustering approaches [Neumann et al.,2006; Thirion et al.,2006], spatiotemporal analyses [Bowman,2005; Kiebel et al.,2000], mixture models with spatial constraints [Hartvig and Jensen,2000; Woolrich et al.,2005], and priors in a Bayesian framework [Flandin and Penny,2007; Penny and Friston,2003].

Another way to incorporate positive spatial correlations of fMRI signals is to explicitly use the assumptions of an underlying smooth process to model the spatial activation pattern. By assuming that each active brain region can be approximated by a generic spatial model of activation, one can model activity in an entire fMRI image [Hartvig,2002; Lukic et al.2004,2007; Tzikas et al.,2004]. The successfulness of this type of method depends on the shape model used. A model too simple leads to severe misspecification and biased inference. A model too complex may describe the shape of activation well but may hinder interpretation, because of modeling noise and containing too many parameters.

Aiming for a sensible, easy to interpret way to analyze the spatial pattern of fMRI data we propose an alternative method of fMRI analysis, termed “activated region fitting” (ARF). At the heart lies the assumption that a region of brain activation can be approximated by a Gaussian‐shaped function and that a number of these Gaussian functions can be used to describe the activation pattern in an fMRI image. The Gaussian function was chosen as it is relatively simple—it uses six parameters which are easy to interpret—and still has good flexibility in terms of different shapes. The optimal number of Gaussians is determined by fitting increasingly complex models (i.e. more Gaussian functions) to the data until a parsimonious description of the data is given. Hypothesis tests are then performed on the parameters of the Gaussian functions, allowing for hypotheses of location, spatial extent, and amplitude.

Analyzing fMRI data with ARF has several advantages. First, an objective measure is available for the location, spatial extent, and amplitude of each area of activation. Second, these locations, spatial extents, and amplitudes may serve as input for a functional connectivity analysis. Third, an entire image is described with relatively few parameters, thereby increasing power and reducing the multiple testing problem. Fourth, ARF corrects for model misspecification, allowing for robust hypothesis tests. Fifth, as the method of ARF is performed on the output of a standard GLM analysis (unthresholded), it is easy to add to the standard analysis steps and computational load is relatively low.

The outline of the article is as follows. First, the technical details of ARF will be explained. Details on the spatial model, parameter and variance estimation, model fit, and hypothesis testing will be given. Thereafter, details on the simulation studies are given, performed to assess bias, variance estimation under misspecification, and power. Then an application to real data is given, followed by the discussion in which the findings are summarized, and in which possible limitations and extensions are highlighted.

METHOD

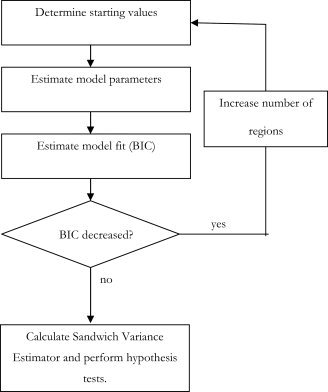
ARF works by fitting a spatial model of activation to an entire image of signal change. This image is either a 2D slice or a flattened 3D map. The spatial model is one, or a sum of two or more bivariate Gaussian‐shaped regions. Each region is described by two parameters to model the location of activation, three parameters to model the extent of activation, and one parameter to model the amplitude of activation. The spatial model is fitted to the data using generalized least squares (GLS). The number of regions that best describe the data is decided by using the Bayesian information criterion (BIC). Once a decision is made on the number of regions, robust hypothesis tests are performed on the parameters of the regions. The following sections will explain the ARF method in detail.

Input

ARF works on the estimated scaling parameters and associated variances of a standard GLM analysis (note that t‐values can also be used, with their variances set to 1). ARF requires multiple independent measurements of the condition of interest. This requires multiple measurements from different runs of the experiment. In a block design the multiple measurements can be derived from multiple blocks of the same condition. In an event‐related design the data of several runs of the experiment can be used. A GLM analysis is performed on these multiple measurements, and the resulting unthresholded values are then used as trials in the ARF analysis. The number of trials in the present study was set to either 5 or 15, but other values can be chosen as well. The actual ARF estimation is performed on the average over these trials. The individual trials are used to obtain robust hypothesis tests.

Let b _k be a (N × 1) vector, with N indicating the number of voxels, containing the scaling parameters from the GLM analysis of trial k. Let σ${}_{\mathit{\text{k}}}^{\text{2}}$ be a (N × 1) vector containing the squared standard errors of b _k. The average over K trials is then:

(1)

Assuming independent variances σ${}_{\mathit{\text{k}}}^{\text{2}}$ over k = 1, …, K trials, the variance of b is calculated as follows [Parzen,1960]:

(2)

with w being a (N × 1) vector of variances.

Spatial Model

The main assumption in the ARF procedure is the spatial model used to describe the data. This shape model must be anatomically sensible, relatively simple, and interpretable. For these reasons a slight adaptation of a bivariate Gaussian distribution function was chosen. A graphical representation of a region is given in Figure 1.

Figure 1.

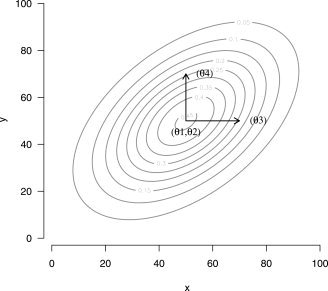
Isocontours of an activated region. θ₁ and θ₂ define the center of the region; θ₃, θ₄, and θ₅ (not shown) define the spatial extent of the region; θ₆ (not shown) defines the amplitude of the region.

The parameters θ₁ and θ₂ define the location of the center of a region, θ₃, θ₄, and θ₅ define the spatial extent of a region, and θ₆ defines its amplitude. The model for voxel n, for j = 1, …, J regions is

(3)

The location of voxel n is contained in a (2 × 1) vector x _n = (x _n,y _n)′. The parameters defining the center of the activated region j are contained in a (2 × 1) vector k _j = (θ_1j, θ_2j)′. Finally, 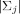denotes the determinant of matrix Σ_j, defined as

Estimation

Recall that b was the (N × 1) vector containing the average scaling parameter values. Now let the diagonal of a (N × N) weight matrix W (with 0s on the off‐diagonal) be w. To estimate the parameters of the model, GLS estimation is adopted:

(4)

In the above equation f(X, θ) is a (N × 1) vector containing the model predictions using Eq. (3) for all voxels within X. The sums‐of‐squares function is minimized using a Newton‐type algorithm [Schnabel et al.,1983]. Boundaries of the parameter space are checked after convergence to avoid convergence to local minima near the boundaries. In addition, the algorithm is restarted several times with different starting values in order to avoid local minima.

ARF adopts a sequential fitting paradigm where the procedure starts to model the data with one region and increases the number of regions until the model fit criterion is reached (cf. next section). The model fit criterion is calculated after convergence of the model. At each level in the sequence all parameters are estimated, no parameters are held fixed between levels. A concise outline of the algorithm steps can be found in Appendix C.

Model Selection

ARF chooses the number of regions that is needed to obtain a good but parsimonious description of the data. This necessitates a goodness of fit measure which takes both goodness of fit and the number of parameters into account. It is especially convenient to keep the number of regions low to obtain high power, and therefore the BIC is used [Schwarz,1978]. Ignoring constants the BIC equals:

(5)

In the above equation p indicates the number of parameters (which is six times the number of regions J). The BIC is corrected for the number of parameters used in the model, which allows ARF to find a model with a good trade‐off between the fit of the model and the number of parameters used in the model, given the number of voxels in the analysis [Waldorp et al.,2005b]. The current implementation is to start with the simplest model (one region), check the BIC, increase the number of regions by one, check the BIC, increase with one region, etc., until the BIC starts to increase. Then the model that had the minimum BIC value is chosen.

Variance Estimation

Since the underlying spatial process in fMRI is unknown, every spatial model has some degree of misspecification. This can lead to incorrect estimates of variances of the estimated region parameters and consequently to unreliable hypothesis tests of the parameters [White,1980]. Misspecification in our case can either refer to the fact that a Gaussian‐shaped function only gives an approximation to an active region, or to the fact that the number of regions incorporated in the model is incorrect.

Usually with GLS the variance–covariance matrix of the parameters is calculated using the observed Hessian matrix containing the second‐order partial derivatives of the model with respect to the parameters. Let 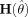be a (p × p) matrix, such that each element (r = 1, …, p; s = 1, …, p):

(6)

[Seber and Wild,1989]. The variance–covariance matrix 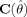is then calculated by:

(7)

Equations (6) and (7) assume that the model is correctly specified [Waldorp et al.,2005a; White,1980], an assumption that is not tenable in the situation of ARF. To correct for this misspecification the variances of the parameter estimates are calculated using the sandwich estimate [Waldorp et al.,2005a; White,1980]. Let 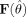be the (N × p) matrix of first‐order derivatives of the model with respect to the parameters. Let 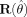be a (N × N) matrix of the outerproduct of the residuals:

(8)

Note that each element in 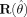has to be divided by the number of trials once more to scale it to the averaged data. The sandwich estimate is then as follows:

(9)

Note in addition that when the model is correctly specified in both the mean and variance, the function reverts to the standard expression for the covariance matrix of parameters estimates [cf. Seber and Wild,1989 , paragraph 12.2.4], as the matrix 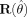containing the residuals, goes to W and the residuals in 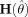tend to zero. For spatially uncorrelated data the diagonal of 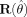can be used.

Hypothesis Testing

ARF allows hypothesis tests on the parameters of each activated region, or on functions of these parameters. Hypothesis tests on the location, spatial extent, and amplitude of the regions can be performed, individually and as an omnibus test. All tests are calculated by a Wald statistic [Seber and Wild,1989] and are calculated for each activated region j. That is, the hypothesis tests are calculated per region. The test statistic equals:

(10)

In the above equation C _j denotes the (6 × 6) variance–covariance matrix of the parameter estimates of a region j. 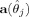is a (4 × 1) column vector which consists of four null‐hypotheses, namely, (1) the x‐coordinate of the center of region j equals a hypothesized x‐coordinate c ₁, (2) the y‐coordinate of the center of region j equals a hypothesized y‐coordinate c ₂, (3) the spatial extent of region j is 0, and (4) the amplitude of region j is 0. Note that the extent of a region can be defined by the determinant of matrix Σ from Eq. (3), where this determinant is given by the usual expression for a 2 × 2 matrix 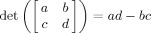[Schott,1997]. So 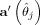is defined as follows:

(11)

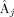is defined as a (4 × 6) matrix containing the partial derivatives of 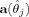to the θ_j‐parameters:

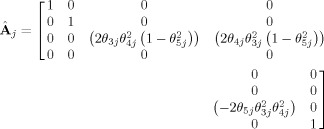(11)

The test‐statistic in Eq. (10) under H ₀ is asymptotically F distributed with N and (N − p) degrees of freedom [Seber and Wild,1989; for misspecified models, see White,1982], with p indicating the number of parameters.

The Wald statistic is based on the estimated variances of parameter estimates, and these variances are only estimated adequately in asymptotic circumstances, in our case, if the number of voxels is very large and/or if the signal‐to‐noise ratio (SNR) is high [cf. Seber and Wild,1989]. In nonasymptotic cases the variances might be underestimated thus giving rise to tests that are too liberal [see, for example, Fears,1996; Seber and Wild,1989]. Therefore we determined in simulations whether the variances are estimated adequately. If so, then the asymptotic approximation is adequate and the test results can be trusted.

Starting Values

Starting values might be calculated by searching for maxima in the input map. The x and y location of a maximum are used as the starting values for θ_1j and θ_2j. At this location the starting values for θ_3j and θ_4j are calculated by finding at what distance from this maximum the input values are half this maximum. The starting values of θ_5j and θ_6j are manually set. To overcome problems with convergence to local minima, the procedure can be run several times with different starting values.

Simulations

To check the ARF procedure several simulation studies were performed. First, the procedure was checked for producing unbiased parameter estimates, i.e. it was determined if the simulation parameters were correctly recovered by the procedure. Second, the variance estimates of the parameters were checked to be adequate and robust against model misspecification in different SNR conditions. Finally, the procedure was tested for its detection power in different SNR conditions.

For the simulation studies, maps with 18 × 18 voxels were created. The signals were either the correct model, a misspecified model in shape, or a misspecified model in the number of regions. Different SNRs were created by adjusting the amount of noise added to the signals. The chosen SNR values were calculated over the image map and were set at 1, 2, 5, and 10 [Smith and Nichols, 2009], with SNR 1 and 2 indicating low SNRs and 5 and 10 indicating high SNRs. In Appendix A the setting of SNRs is explained in more detail. The number of trials was set to either 5 or 15, but the SNR of the averaged data was held constant between these two trial conditions. To get an adequate measure of parameter recovery, variance estimates, and detection power, each condition was run 1,000 times.

Correct model

The correct spatial model used the Gaussian model as specified in Eq. (3). For the simulations the following parameters were used, θ = (9,9,2,3,0.1,100)′, creating a slightly rotated elliptical activation area. The simulations were used to check correct parameter recovery, to check the variance estimates, and to perform power analyses.

Incorrect shape model

The shape model in this case was a pyramidal shape, with a base of 7 × 5 voxels, placed in the center of the map. The data were not smoothed, thus creating a misspecified shape. This model was used to check the variance estimates and to perform power analyses.

Incorrect number of regions

The shape model in this case was the sum of two Gaussian regions placed next to each other in the map using the following parameters: θ₁ = (8,8,1,2−0.3,50)′, θ₂ = (10,10,1,3,0.3,70)′. The ARF procedure was set to fit only one region, therefore creating a model misspecified in the number of regions. This model was used to check the variance estimates and to perform power analyses.

Standard thresholding

To compare ARF with standard voxel‐wise threshold methods, Bonferroni, false discovery rate (FDR) [Genovese et al.,2002; Nichols and Hayasaka,2003], and the cluster‐size threshold corrections [Forman et al.,1995] were chosen. For FDR the q parameter was set to 0.05 and the C parameter was set to 1, which are common values in fMRI studies [Genovese et al.,2002]. The cluster‐size threshold was determined using the Bonferroni corrected P‐value and a cluster size of 3 contiguous voxels.

RESULTS

Parameter Recovery

Bias in parameter estimates was calculated for each parameter at different SNR values. The bias was divided by its standard error to obtain standardized bias.

As can be seen in Figure 2, the bias is approximately zero. The parameters are recovered successfully with high accuracy even in low SNR conditions.

Figure 2.

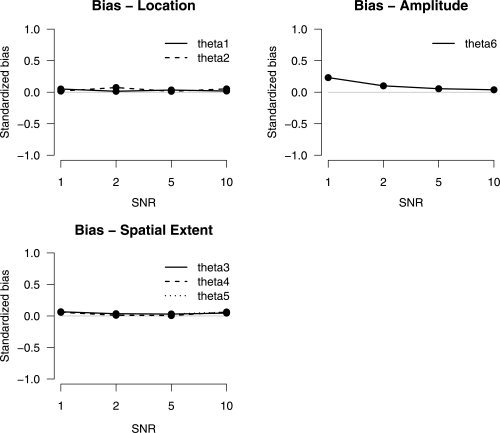
Standardized bias for location, spatial extent, and amplitude parameters as a function of signal‐to‐noise ratio.

Variance Estimation

To evaluate the ARF procedure in producing correct variance estimates, the correct model, the pyramidal model and the “incorrect number of regions model” (double model) were used to create data that were subsequently analyzed with a model with one Gaussian shape. The variance estimation was performed using Eq. (9) with a diagonal matrix and differing numbers of trials (5 and 15). The sandwich estimations were furthermore contrasted with standard variance estimation based on the standard Hessian matrix using Eq. (7). It is expected that the sandwich estimates will outperform the standard estimates.

To promote conciseness, only the results for the location and amplitude parameters will be reported. For these parameters the mean estimated variances over the 1,000 simulations were divided by the variance of the parameter estimates over the 1,000 simulations. This ratio should be close to 1. Ratios higher than 1 indicate too large estimated variances and thus conservativeness of the ARF procedure; whereas ratios lower than 1 would indicate liberal testing.

Figure 3 shows the variance ratios for the three different models. As can be seen the sandwich estimates perform better than the standard Hessian estimates in all situations. For the correct model, the sandwich estimates are to be preferred in low SNR conditions and are equal to the Hessian estimates for the higher SNR conditions. For the incorrect models, the sandwich estimates are in all SNR conditions more adequate than the Hessian estimates. It can also be seen that the number of trials used for the sandwich estimation does not have a profound effect on the ratios, thus indicating that only five trials are sufficient. Note that the estimates of the standard Hessian for misspecified models are too small for low SNR and too large for high SNR. As can be seen by comparing the estimates for the pyramidal and double model (both incorrect), the type of misspecification determines the performance of the standard Hessian. Note in addition that the sandwich estimates do not underestimate the actual variances; in fact, there is a slight tendency to over estimate variances. Therefore, the resulting tests will be slightly conservative.

Figure 3.

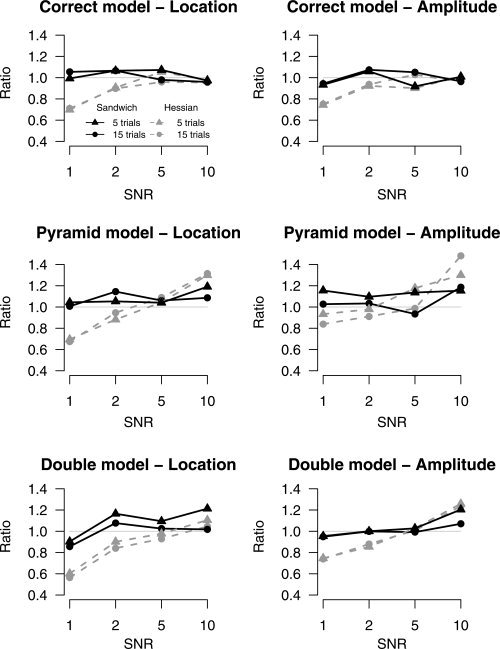
Variance ratios for location and amplitude parameters of the different shape models (correct, pyramidal, and double) as a function of signal‐to‐noise ratio.

Power Analysis

The ARF method was contrasted with the standard methods of Bonferroni, FDR [Nichols and Hayasaka,2003], and the cluster size threshold (CST) method of Forman et al. [1995]. The power for the methods was calculated as follows: for ARF if the Wald test of the amplitude parameter 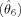was significant (P < 0.05) the region was classified as active. For Bonferroni and FDR, two methods are adopted. In the first method if a minimum of 1 significant voxel was below the threshold it was classified as active. For the second method if a minimum of 3, not necessarily adjacent, significant voxels were below the threshold it was classified as active. For the CST method the Bonferroni threshold was used with a cluster size of 3 voxels to obtain the CST. If 3 adjacent voxels were below this threshold it was classified as active. Included was a so‐called SNR = 0 condition, to determine whether the test would not detect a signal in more than 5% of the simulations, when in fact there is no signal present (i.e. the false‐positive rate). The proportion correct discoveries (for all methods) refer to the proportion of cases where a signal was detected irrespective of its location.

As can be seen in Figure 4a–c, the ARF method clearly has an advantage when SNR is low (1 or 2), detecting around 60–95%, respectively, irrespective of the number of trials used and irrespective of the kind of misspecification. For the higher SNRs (5 and 10) the power of the ARF method goes up to 100% together with Bonferroni, FDR, and the cluster size method. Note in addition that the ARF method does not yield too liberal results, since its false‐positive rate is about 5%.

Figure 4.

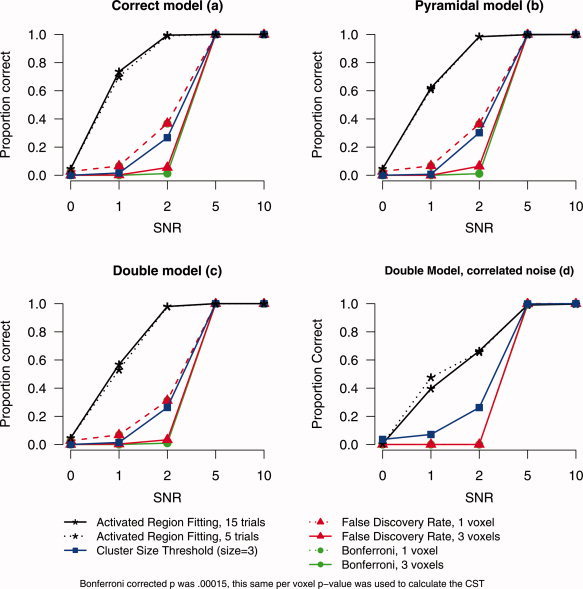
Proportion correct discoveries (power) for activated region fitting, Cluster size threshold, false discovery rate, and Bonferroni as a function of signal‐to‐noise ratio for three shape models [correct (a), pyramidal (b), and double (c)]. (a–c) The uncorrelated noise data. (d) The correlated noise data with the double model. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

For the standard methods the difference between the 1 voxel criterion and the 3 voxel criterion is also clear. Power is increased for the 1 when compared with the 3‐voxel criterion, but it is still below ARF performance. For the cluster size method there is a power advantage over Bonferroni (3 voxel) and FDR (3 voxel). But for Bonferroni (1 voxel) and FDR (1 voxel) the results were comparable to CST.

As an aside in order to check whether ARF is sensitive to correlated noise, power simulations were run for the double model with noise convolved with a FWHM filter of 2 voxels (see Appendix A). All other simulation parameters remained the same as before. The most interesting condition in this case is the SNR = 0 condition. The percentage of false positives should again be 5% or lower. Figure 4d shows the false‐positive rate (SNR = 0) and the power (SNR = 1, 2, 5, 10) of the ARF method and the standard techniques. The percentage of false positives for the ARF method with five trials was 1% and with 15 trials 0.6%.

Real Data Example

ARF was tested on a real dataset of a verbal feedback experiment [Christoffels et al.,2007]. For a single subject an inflated brain was created for the left hemisphere. For four runs the unthresholded t‐values (df = 133), including negative values, were exported as four trials analyzed by ARF. The images consisted of 126 × 74 voxels and were averaged over trials, creating the average map to estimate the ARF regions. The distribution of the averaged t‐values had a minimum of −4.22, a mean of 0.12, and a maximum of 4.28. The first quartile was −0.64 and the third quartile was 0.98. This created a highly peaked and small tailed distribution. The input image is shown in Figure 5.

Figure 5.

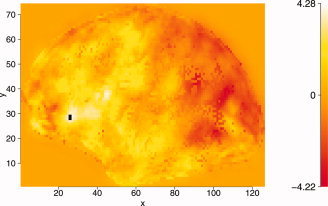
Average activation (t‐values) of the left hemisphere from four runs of the experiment (unthresholded). Active voxels (based on FDR correction) are marked black. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Standard thresholding with a FDR correction yielded only 2 significant voxels (mainly because the small tails of the distribution), and both CST (with Bonferroni threshold and a cluster size of 3 voxels) and Bonferroni showed no significant voxels. The significant FDR voxels are marked in black in Figure 5. For the ARF procedure a sequential fitting of 18 regions was performed to select the correct model. The program was run in R [R Development Core Team,2007] and took 37.5 min for the final solution on a 2.21‐GHz AMD Opteron. The ARF algorithms are available as a free R package and can be downloaded from (http://home.medewerker.uva.nl/w.d.weeda1/). The BIC indicated that a model with 13 regions showed the best fit, as can be seen in Figure 6. The variances of the region parameters were derived from the sandwich estimates. Details of the estimates and test are shown in Tables BI and BII (Appendix B). The final solution is displayed in Figure 7.

Figure 6.

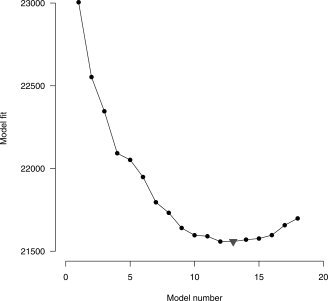
BIC values for 18 sequential models. The triangle indicates the best fitting model (13 regions). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 7.

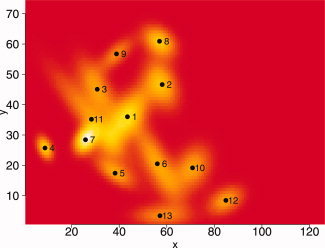
Activated region fitting solution with 13 active regions. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The ARF solution clearly yields more significant active regions than the standard thresholded image, again showing increased power over standard techniques. Note that these results were obtained for a single subject. It may also be clear that with 4 [location (2), spatial extent (1) and amplitude (1)] × 13 = 52 parameters of interest, the ARF solution gives a very concise description of the 126 × 74 = 9,324 voxels.

DISCUSSION

The method of ARF uses the observation that fMRI activation consists of spatially smooth clusters: it describes an entire fMRI image with a multitude of Gaussian‐shaped regions. In the simulations and in a real experiment it was shown that ARF is robust against model misspecification and has increased detection power over standard thresholding techniques. Although ARF has increased power, it was also shown that ARF does yield tests that are slightly conservative. This indicates that the regions detected by ARF can be considered as being active regions, but there may still be other active regions that remain undetected.

Three extensions of ARF might be considered. First, ARF works on 2D slices or flattened 3D images. The method may be extended to 3D. This requires however one additional parameter to define location, and three additional parameters to define the spatial extent of each activated region. This increases computational complexity and might reduce the power of the technique. This added to the fact that fMRI results are nearly always presented in 2D, suggesting that the 2D or flattened 3D analysis might suffice.

Second, in our simulations we have assumed that the temporal noise is uncorrelated. Of course this is an unrealistic assumption, but in real applications an appropriate temporal correlation model can be incorporated in the GLM that serves as input for the ARF procedure. Third, although we showed in simulations that ARF does not detect any spurious clusters introduced by correlated noise, the performance of ARF in such situations should be studied further.

The idea of using specific shape models is not entirely new to fMRI analysis. One of the most well‐known implementations comes from Hartvig [2002], who also uses a Gaussian shape model to describe regions of fMRI images. The main difference between the Stochastic Geometry Model of Hartvig and ARF is that the former is a spatio‐temporal approach in a Bayesian framework, while ARF uses temporal and spatial information in distinct models. Therefore, ARF might be more applicable in practice, because standard analysis packages can be used to pre‐process and analyze the temporal structure, after which ARF is invoked to model the spatial structure.

Lukic et al. [2007] also used an explicit shape model to describe fMRI data very similar to the ARF method. Both methods fit a multitude of spatial functions to activation data and use the parameters to test hypotheses. The major difference between the methods is that ARF uses a Gaussian shape with parameter estimates of location, spatial extent, and amplitude, whereas in the method of Lukic et al. a blurred pillbox shape or a Gaussian shape with a fixed width was used. In this sense ARF has more flexibility in shapes of activation. Another advantage of ARF is that it produces robust hypothesis tests under misspecification of the shape model.

In sum, it is important to account for the spatial smoothness of activated regions, since it improves the detection power. ARF accounts for spatial smoothness by parameterizing activated regions by Gaussian shapes. Since this only gives an approximation to reality, the tests on region parameters are designed to be robust against model specification. Simulation studies and a real data example have shown that ARF is a robust high‐power method for fMRI analysis.

APPENDIX A: NOISE SIMULATIONS

For the simulation studies, data with different SNRs were created by adjusting the amount of noise added to the signals. The white noise added to the signal was normally distributed with zero mean and standard deviation 1/SNR × max (β) [Krueger and Glover,2001], where β denotes the true noiseless signal and where the maximum is taken over the voxels. It is shown in the work of Wink and Roerdink [2006] that noise is approximately normally distributed. It is assumed that the noise is both spatially and temporally uncorrelated, which are of course only crude approximations to reality but which suffice for the present purposes. The chosen SNR values are based on typical SNRs found in fMRI experiments (see, for example, Smith and Nichols, 2009).

To assess the false positives and power under correlated noise conditions, the same procedure was used except that ϵ_n was convolved with a FWHM filter of 2 voxels before the signal was added. This created a condition where the spatial extent of the noise is relatively high compared with the spatial extent of the signal.

Procedure

Let n = 1, …, N denote voxels, t = 1, …, T time points in a time series, and SNR be a chosen SNR. Let β_n be a vector of length T containing the real signal at voxel n which is constant over all time points T. Then, for each voxel n:

• aCreate a vector ϵ_n of length T with for each element a sample from ;
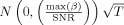• bThe real time series at voxel n is then given by β_n + ϵ_n;
• c b _n is then given by the mean of β_n + ϵ_n;
• dThe standard error of b _n is given by the standard error of β_n + ϵ_n;
• eThe t‐value with (T − 1) degrees of freedom is then given by b _n/se(b _n).

APPENDIX B: REAL DATA TABLES

Table BI.

Estimates and standard errors for location and amplitude parameters

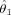
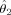
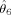
Region		se		se		se
1	43.44	0.39	36.03	0.21	596.52	18.70
2	58.04	0.17	46.64	0.22	353.65	10.73
3	30.73	0.72	45.10	0.32	385.04	24.96
4	8.77	0.11	25.73	0.18	104.88	7.65
5	38.28	0.42	17.39	0.34	159.96	18.81
6	56.05	0.25	20.49	0.56	513.31	22.55
7	25.81	0.20	28.46	0.21	228.69	16.58
8	56.95	0.34	60.90	0.22	256.50	15.18
9	38.87	1.01	56.74	0.69	137.79	7.36
10	70.86	0.18	19.15	0.20	348.48	11.98
11	28.30	0.66	35.21	0.77	560.73	36.48
12	84.87	0.46	8.43	0.27	205.88	19.62
13	57.12	0.72	3.39	0.18	205.70	27.39

Table BII.

Wald statistic P values for spatial extent and amplitude

Region	Spatial extent	Amplitude
1	0.0000*	0.0000*
2	0.0000*	0.0000*
3	0.0000*	0.0000*
4	0.0000*	0.0000*
5	0.0014*	0.0000*
6	0.0000*	0.0000*
7	0.0000*	0.0000*
8	0.0000*	0.0000*
9	0.0000*	0.0000*
10	0.0000*	0.0000*
11	0.0000*	0.0000*
12	0.0000*	0.0000*
13	0.0000*	0.0000*

^*Significant with P < 0.0038 (Bonferroni corrected).

APPENDIX C: ALGORITHM OVERVIEW