Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2008 Apr 25;29(7):802–809. doi: 10.1002/hbm.20579

Dynamical consequences of lesions in cortical networks

Christopher J Honey 1, Olaf Sporns 1,✉
PMCID: PMC6870962  PMID: 18438885

Abstract

To understand the effects of a cortical lesion it is necessary to consider not only the loss of local neural function, but also the lesion‐induced changes in the larger network of endogenous oscillatory interactions in the brain. To investigate how network embedding influences a region's functional role, and the consequences of its being damaged, we implement two models of oscillatory cortical interactions, both of which inherit their coupling architecture from the available anatomical connection data for macaque cerebral cortex. In the first model, node dynamics are governed by Kuramoto phase oscillator equations, and we investigate the sequence in which areas entrain one another in the transition to global synchrony. In the second model, node dynamics are governed by a more realistic neural mass model, and we assess long‐run inter‐regional interactions using a measure of directed information flow. Highly connected parietal and frontal areas are found to synchronize most rapidly, more so than equally highly connected visual and somatosensory areas, and this difference can be explained in terms of the network's clustered architecture. For both models, lesion effects extend beyond the immediate neighbors of the lesioned site, and the amplitude and dispersal of nonlocal effects are again influenced by cluster patterns in the network. Although the consequences of in vivo lesions will always depend on circuitry local to the damaged site, we conclude that lesions of parietal regions (especially areas 5 and 7a) and frontal regions (especially areas 46 and FEF) have the greatest potential to disrupt the integrative aspects of neocortical function. Hum Brain Mapp, 2008. © 2008 Wiley‐Liss, Inc.

Keywords: connectivity, neuroanatomy, lesion, graph theory, network, robustness, Kuramoto model

INTRODUCTION

Observations of the functional consequences of cerebral lesions continue to be invaluable to the project of human brain mapping [Finger, 1994; Moses and Stiles, 2002]. Structural damage can produce behavioral deficits not only through the disruption of neural circuits local to the lesion site, but also by disrupting information flow along larger‐scale pathways or by unbalancing competitive inter‐regional interactions [Jackson, 1884; Sprague, 1966; Lomber and Payne, 1996; Young et al., 2000]. In this article we aim to characterize these nonlocal effects of local lesions. Our method is to implement simplified models of macaque cerebral cortical dynamics and then to track the consequences of the removal of individual brain regions from the models.

Previously [Sporns et al., 2007] we examined the effects of regional lesions on the anatomical connection structure of cat and macaque cortices. Lesions of highly connected and central nodes (i.e. “hub” nodes) within these anatomical networks were found to have the largest effects on network structure. Since macaque cortex can naturally be decomposed into just two clusters (see Fig. 1A) we were also able, following Bassett et al. [ 2006], to separately analyze the lesions of two distinct types of hubs, where hub type is determined in relation to the cluster structure of the network. Hubs of the first type (“provincial” hubs) are defined by their tendency to link nodes within a single network cluster, while hubs of the second type (“connector” hubs) tend to link nodes in different clusters. We found that lesioning provincial hubs (such as Area V4) produced the largest decreases in the small world index of the cortical network, whereas lesioning connector hubs (such as Area 46 and the FEF) produced the largest increases in the small world index. The small world index [Humphries, 2006] characterizes the balance between local and global connectivity in a network. The fact that lesions of highly connected nodes can have such contrary effects on this connection balance reinforces the idea that lesion effects depend on the global network embedding.

Figure 1.

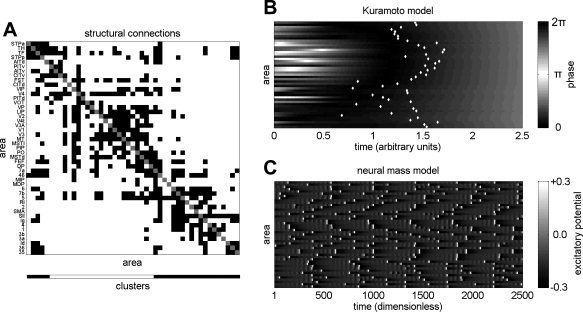
Figure 1

Open in a new tab

(A) Interregional connection data for the macaque monkey. A black square in the i‐th row and j‐th column indicates the presence of a confirmed directed anatomical link from area i to area j, while a white square indicates the absence of a confirmed connection. Cluster membership is indicated at the bottom of the plot, with clusters derived using the spectral community detection algorithm as described in [Sporns et al., 2007]. (B) A single example run of the Kuramoto model as it evolves towards a globally synchronous state. Columns correspond to time points (arbitrary units) and rows correspond to areas (nodes) shown in the same ordering as for the connection matrix in panel A. The gray scale represents the phase (in radians) of each oscillator at a point in time. The time, STi, at which each node synchronizes, is marked with a white dot. (C) A single example of the neural mass dynamics, illustrating the process of intermittent synchronization. Columns correspond to time points (dimensionless) and rows correspond to areas shown in the same ordering as for the connection matrix. The gray scale represents the mean excitatory membrane potential (dimensionless) of a region at a given time.

In an attempt to move beyond these purely structural analyses, and to make contact with explicitly functional questions, we now extend our investigation by implementing two simple oscillator models of cortico‐cortical interaction. The models have identical coupling structure (derived from macaque anatomical data, Fig. 1A) but they employ different node dynamics. In the first model, the network nodes follow classical phase oscillator equations [Kuramoto, 1975], while in the second they are governed by neural mass equations [Breakspear et al., 2003; Honey et al., 2007]. This investigation forms a part of a more general program [e.g. Arenas et al., 2006; Timme, 2006; Zhao et al., 2005] aiming to characterize the relationship between the static properties (e.g. coupling topology) and the dynamic properties (e.g. synchrony, stability) of systems of coupled oscillators. Since isolated oscillators exhibit a wide range of behaviors and since coupling architectures (especially when asymmetric) can influence global dynamics unpredictably [Timme, 2006], an entirely general description of this structure‐function relationship is unlikely to be forthcoming.

Rapid dissolution and restoration of synchrony is a hallmark of processes such as selective attention and motor planning [Engel et al., 2001; Varela et al., 2001] and cognitive and motor integrative pathologies are associated with abnormal patterns of synchrony [Schnitzler and Gross, 2005; Spencer et al., 2003]. Our first investigation, using the abstract Kuramoto phase oscillator model, is therefore aimed at understanding how rapidly, and in which regional order, the cortical network will synchronize from a randomly perturbed initial state. The Kuramoto model we implement will always evolve towards a globally synchronized state, i.e. a state in which the phases of all interacting regions are equal. Following [Arenas et al., 2006], we repeatedly perturb the system away from its stable synchronized state and then observe the sequence in which brain regions entrain one another as the system progresses towards synchrony from different unstable positions (Fig. 1B illustrates a single stabilization). We then repeat this analysis after lesioning individual brain regions from the network, and study the differences in the pattern of mutual entrainment. Our dependent measure is the stabilization time, STi, which approximates the time taken for an individual network element to phase‐lock with its neighbors on a single run. Changes in the relationships between the STi (aggregated across many different perturbations) provide a theoretical snapshot of a typical entrainment sequence.

In our second investigation we examine a neural mass model that does not globally synchronize, but does exhibit transient inter‐regional phase‐locking (Lachaux et al., 1999; Fig. 1C). Here, the aim is to characterize the effect of lesions on the patterns of inter‐regional influence (i.e. the effective connectivity) that manifest over 16 min of millisecond‐scale dynamics. These patterns of influence are quantified using the transfer entropy [Schreiber, 2000], which is an information‐theoretic metric of the directed influence of one variable over another. Transfer Entropy (TE) is an asymmetric measure, and can thus discriminate the influence of region A on region B from the influence of B on A. This model and metric have previously been successful in relating the clustered architecture of the macaque anatomical network to resting state functional connectivity in the same animal [Honey et al. 2007]. By repeating these earlier analyses on lesioned networks we now hope to predict lesion‐induced changes in macaque resting state functional connectivity.

We hypothesize that lesions of hub nodes will have the largest magnitude effects on both the pairwise interaction strengths (TEij) and node stabilization times (STi), a result that would be consistent with earlier results obtained from a spreading activation model [Young et al., 2000]. We further hypothesize that lesions of provincial hubs will selectively decrease the strength of intra‐cluster interactions while lesions of connector hubs will have more widespread effects including the weakening of functional interactions across clusters.

METHODS

Connection Data

The macaque cortical connectivity matrix (Fig. 1A) was generated following the parcellation scheme of [Felleman and Van Essen, 1991]. Data were manually collated in the CoCoMac database from published tracing studies according to standard procedures and were then algorithmically transformed into the Felleman and Van Essen map using coordinate‐independent mapping [Kötter, 2004; Stephan et al., 2001]. Following resolution of redundant and inconsistent results a binary connection matrix with N = 47 regional nodes and K = 505 inter‐regional connections was generated. Further details on connection data and graph theoretic terminology are available in [Honey et al., 2007].

Kuramoto Model

Each node in this classic noiseless oscillator model is described by a single phase variable φi. Nodes oscillate at an intrinsic frequency ωi and shift attractively towards the mean phase of their neighbors. If we denote by ki the number of edges incoming to the i‐th node, we can define the normalized adjacency matrix A(i,j) of the cortical graph G, such that A(i,j) is equal to J/ki if there is an arc from node j to node i, and 0 otherwise. The row sums of the matrix A are thus all equal to the coupling constant J, which was set to 10. The first‐order nonlinear differential equation governing the i‐th phase oscillator is then:

equation image

We emphasize that, since ωi was fixed at unity, this model always evolves towards a globally synchronized state (Fig. 1B). Under each lesion condition, the model was simulated 1,000 times for 10 time units, with the initial phases of each oscillator drawn uniformly at random from the range [0‐2π]. The coupled differential equations were numerically integrated using a standard 4th‐order Runge‐Kutta method as implemented in MATLAB R2007a.

Neural Mass Model

The neural mass equations, based on [Morris and Lecar, 1981] and [Larter et al., 1999] and studied in detail in [Breakspear et al., 2003], model the behavior of local ensembles of neurons. The state of each neural mass is represented by three variables: the first is the mean membrane potential of pyramidal cells (show as a function of time in Fig. 1C); the second represents the mean membrane potential of inhibitory interneurons; the third and final variable represents the average number of “open” potassium ion channels. The mean cell membrane potential of the pyramidal cells is governed by the conductance of sodium, potassium and calcium ions through both voltage‐ and ligand‐gated membrane channels. The firing of these cell populations feeds back onto the ensemble through synaptic coupling to open ligand‐gated channels and raise or lower the membrane potential accordingly. Inhibitory and excitatory interactions are modeled within the individual neural masses, which behave, in the current parameter regime, as chaotic oscillators. Connections between masses (i.e. the inter‐regional connections) are excitatory. The model is described in much greater detail in [Breakspear et al., 2003] and parameters for the present study were unchanged from [Honey et al., 2007].

Stabilization Time

The stabilization time, STi, which we employ here to characterize the transition to synchrony in the Kuramoto dynamics, is defined as the smallest time t such that the absolute angular acceleration falls below a threshold value ε = 0.02 and remains below it for at least 5 time units, i.e. 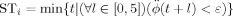Inline graphic. Since the time to stabilization exhibits more variance across trials (and across lesions) than the relative ordering of stabilization times, we also assess lesion effects by examining the differences in patterns of stabilization rank, with lower ranks assigned to the most rapidly stabilizing nodes and highest ranks to the nodes that stabilize most slowly on a given trial.

Transfer Entropy

Transfer Entropy is an information theoretic measure introduced by Schreiber [ 2000], which measures the amount by which conditioning on the present value of one variable reduces the entropy rate of another. Given time‐series x(t) and y(t) for two brain regions, we first resample the data on all variables to follow a normal distribution with zero mean and unit variance. Resampling is performed in the following way: given M raw data values x 1, x 2, …, xM, we generate M random samples r 1, r 2, … rM, from a standard normal distribution. We then replace the smallest raw data value with the smallest randomly sampled value, the second‐smallest raw data value with the second‐smallest randomly sampled value, and so on until all raw data values are replaced. This results in a set of M resampled data values which are distributed according to a standard normal distribution.

We then partition the range of the resampled x(t) and y(t) into 32 regions (or states) and assign each variable's value at each point in time to an individual partition. This process produces discrete random variables X n and Y n which track the state of our neural masses across time, and we can now apply information theoretic measures to these state variables in order to quantify the predictive relationship between them. The entropy rate of the process x(t) is the average amount of uncertainty about the future state of x(t), conditional on its current state. 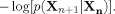The entropy rate, h X, can be written as the expectation of Inline graphic The “y‐conditional entropy rate” of x(t) is the average amount of uncertainty about the future state of x(t), conditional on its current state and on the current state of y(t). 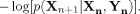This quantity, h X|Y, can be written as the expectation of Inline graphic Transfer entropy is then defined as the difference between h X and h X|Y. In other words, transfer entropy measures the extent to which our uncertainty about the future state of x(t) is reduced by knowledge of the present state of y(t), given that we already knew the present state of x(t). Transfer entropy is written

equation image

a quantity which we calculated directly from data histograms. Transfer Entropy is bounded below by zero and above by the entropy rate, h X, of the target process X. TE values were averaged across 10 long runs of the model for each lesion condition, with each 16‐min run comprising 4 nonoverlapping segments of 4 min (240,000 time steps, each interpreted as being of 1 ms duration). In order to compensate for sampling error, we subtracted from all TE values a “baseline TE.” The baseline TE was calculated by taking the mean value of TE evaluated between all time series pairs, but with one time‐series shifted by 5,000 time steps. This baseline subtraction had negligible effect on the pattern of results we report here.

RESULTS

The Kuramoto Model

We are interested to understand how network structure affects the sequence in which brain regions synchronize from a random initial state. Node degree is a simple but diagnostic estimator of the structural importance of a node within a network. It is not obvious a priori whether high degree nodes should stabilize most slowly (since they receive a large number of competing influences on their state) or whether they should stabilize most quickly (since high‐degree nodes average their inputs and then widely broadcast this average, possibly providing an anchor for rapid local synchronization). We find, as illustrated in Figure 2A, that node degree and the median rank‐order of stabilization are robustly anticorrelated (Spearman's ρ = −0.66, P < 10−6), i.e. high‐degree nodes stabilize earlier and low‐degree nodes stabilize later. It is also clear from Figure 2A that there is an exception to this pattern: area V4, which has the second highest degree of all nodes, stabilizes more slowly than half the nodes in the network. This functional distinction may be a result of the fact that V4 is the only high‐degree node that clearly classifies as a provincial hub [Sporns et al., 2007]; all other high‐degree nodes are connectors.

Figure 2.

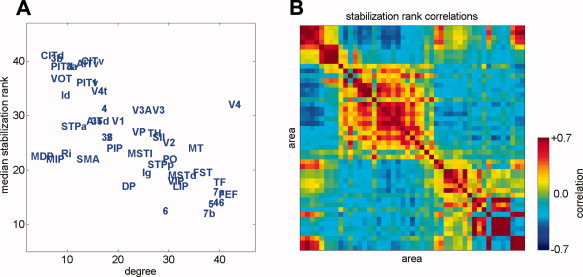
Figure 2

Open in a new tab

(A) Scatterplot of median stabilization rank against degree (sum of in‐ and out‐degrees). (B) A map of the correlations in stabilization rank across runs, with areas arranged in the same ordering as in Figure 1A. Warmer values indicate that a region pair will have correlated stabilization ranks; cooler values indicate that regions will have anti‐correlated stabilization ranks. There is significant agreement of these stabilization rank correlations with either TE patterns or BOLD cross‐correlations obtained from a previous model of macaque cortex [Honey et al., 2007].

The median rank‐order of stabilization times inform us whether a particular node will synchronize earlier or later than others, but it does not inform us about the inter‐node influences that are felt within runs. To assess inter‐node influences, we assigned a stabilization rank to every node on every run and calculated rank correlation coefficients between all pairs of nodes across all runs (Fig. 2B). Consistent with previous results [ Honey et al., 2007; Zemanova et al., 2006; Zhou et al., 2006] the patterns of functional influence tend to recapitulate the structural connection patterns: the stabilization ranks of regions are correlated within clusters and anticorrelated across clusters. This suggests that the two major structural clusters (visuo‐temporal and somatomotor) stabilize locally and then engage in a competitive interaction (via the connector hubs) to determine the globally synchronous phase, with the losing cluster experiencing a later destabilization.

Having assessed the functional consequences of network structure in intact networks, we now move on to examine the effects of lesions. To assess the effect of regional lesions on the Kuramoto dynamics, we calculate the difference in median stabilization ranks (Fig. 3A) and in median stabilization times (Fig. 3B) resulting from each lesion. We find that lesions within a cluster tend to delay the stabilization of nodes within that cluster and to speed the stabilization of those outside the cluster. Area 5, a posterior parietal region believed to be involved in visual, somatosensory and motor integration [Breveglieri et al., 2007], has the largest impact on both rank and time; its removal drastically slows somatosensory and speeds visuo‐temporal synchronization (Fig. 3A,B).

Figure 3.

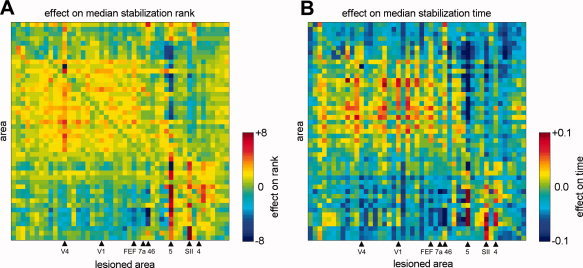
Figure 3

Open in a new tab

Effects on the median stabilization rank (A) and on the median stabilization time (B) produced by the lesioning of individual brain regions. Each column shows the pattern of differences in stabilization time (A) and rank (B) resulting from the lesion of a single area, with rows and columns arranged in the same ordering as Figure 1A. Individual cell colors correspond to the difference in rank or time between the lesioned and unlesioned networks. Brain areas indicated at the bottom are further analyzed in Figure 4.

Neural Mass Model

As in our previous work with a neural mass model [Honey et al., 2007] we found that patterns of functional connectivity in intact networks roughly recapitulated the underlying structural connection map. Because of the computational demands of the neural mass model, we were unable to examine the consequences of lesioning all nodes, and so we restricted our attention to 8 network regions: 4 connector hubs (areas 7a, FEF, 46, and 5) located in the frontal and parietal lobes, 2 provincial hubs (V4 and SII) and two primary sensory and motor areas (V1 and area 4).

For each lesioned area we calculate the difference of all Transfer Entropy (TE) values between the lesioned and unlesioned dynamics (Fig. 4A). Most lesion‐induced increases or decreases in pairwise TE were found to be less than 10% of the original TE value for that pair, while some exceeded 25%. Although our sample of lesioned nodes is small the average magnitude of TE reductions produced by lesions of high‐degree nodes appears to be larger than those produced by lesions of low degree nodes. We also observed a difference between connector hubs (areas 7a, FEF, 46, and 5) and provincial hubs (areas V4 and SII): Lesions of provincial hubs have larger cluster‐local effects while lesions of connector hubs exhibit a more distributed pattern.

Figure 4.

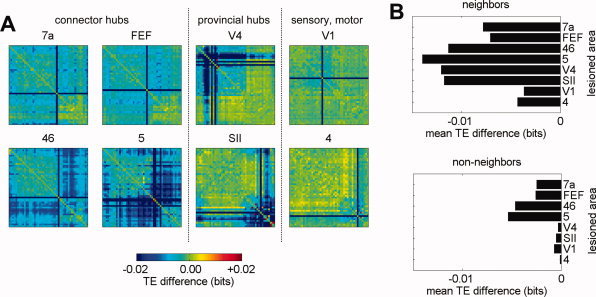
Figure 4

Open in a new tab

For the 8 areas analyzed, we show the distribution of lesion‐induced effects on TE, displayed as the difference in the interaction strength maps between the lesioned and unlesioned case (A). Lesions predominantly result in decreased TE, with a decrease of 0.02 bits corresponding to approximately 25% of baseline. Panel (B) shows the sizes of the average TE effects for links between neighbors (left) and links between non‐neighbors (right) of the lesioned node. Disconnected nodes were excluded from this analysis.

Lesion‐induced changes in TE extend well beyond the immediate neighbors of (i.e. the recipients of direct connections from) the lesioned node. To quantify this statement, we compared probability histograms of the lesion‐induced TE difference on (a) edges between neighbors of the lesioned node and (b) edges between non‐neighbors of the lesioned node. We found, as shown in Figure 4B, that the average effect for both neighbors and non‐neighbors of the lesioned node is a decrease in functional connectivity. Although the effects on TE between neighbors of the lesioned area are larger than the effects on TE between non‐neighbors of the lesioned area (two‐sided Wilcoxon Rank sum tests, P < 10−10 for all lesions) the distributions of effect sizes nevertheless exhibit substantial overlap (data not shown). Lesions of connector hubs resulted in greater nonlocal TE effects than lesions of provincial nubs, and lesions of primary visual or primary motor cortex had the smallest effects overall.

The pattern of results we report based on TE are very similar to those obtained when using mutual information (MI) as the dependent measure (data not shown, methods as in [Honey et al., 2007]).

DISCUSSION

Using two different dynamical cortical models we have investigated the relationship between inter‐regional influences and inter‐regional coupling structure. We further examine how cortical lesion consequences change as a function of the network embedding of the lesioned region. As expected, lesions of high‐degree nodes produced the largest and most widespread effects on cortico‐cortical interactions in both models we tested. However, the clustering (or community) architecture of the cortex was found to be a significant factor in predicting lesion effects, since the removal of cluster‐central nodes tended to produce effects confined to the cluster, even for high‐degree nodes such as area V4.

Within the context of the abstract Kuramoto oscillator model we found that connector hubs, which are located mostly in parietal and frontal regions of the brain, were the first to (re)stabilize their phase from a random phase perturbation or initialization. This is consistent with their posited roles as the facilitators of synchrony between distal regions of cortex [Corbetta and Shulman, 2002; Engel et al., 2001].

Within the context of the neural mass model, we observed, once again, that lesion‐induced TE changes were influenced by the cluster structure of the network. Removing provincial hubs had stronger effects within the hub's own cluster while the removal of connector hubs produced more widely and evenly spread effects. We emphasize, however, that despite these differences, and consistent with the findings of [Young et al., 2000], substantial nonlocal influence was observed for all lesions.

The most significant discrepancy between the simple models we explore here and real neural circuits is that such circuits can endogenously generate oscillations within a single or a few frequency bands, each of which may act as an independent channel of communication and coordination [see e.g. Buszáki and Draguhn, 2004; Börgers et al., 2005]. Future models should take account of these preferred oscillatory frequencies, their potential for signal gating, and their dependence on levels of exogenous driving. Another limitation of the present study is that the anatomical data for macaque are incomplete, especially in the absence of all thalamic and many frontal neocortical regions. Whole‐brain diffusion spectrum imaging in humans [Hagmann et al., 2007; Wedeen et al., 2005] is already providing the necessary connection data for us to extend the present investigation to the human brain.

Despite the fact that our two models show broadly similar patterns of results, they also show some important differences. In particular, we note that the lesion‐induced changes in functional connections in the Kuramoto model (Fig. 2B) do not correspond on an edge‐by‐edge basis to the lesion‐induced changes observed in the neural mass model (data not shown). This is an indication that inference from coupling structure to functional properties may not always be possible, since the relation between the two does depend on details of the node dynamics.

Our function of interest here is the ongoing process of inter‐regional information integration, and the relevant dynamical feature is the tendency to synchronize. Inter‐regional integration is crucial not only for the performance of demanding psychological tasks, but for almost all cognitive function, and so it is unsurprising that integrative disorders such as Alzheimer's disease and schizophrenia are accompanied by changes in functional connectivity that are present even in the resting state [Bluhm et al., 2007; Rombouts et al., 2005].

The present data suggest that connector hubs will most rapidly synchronize following an external perturbation and that lesions of these regions have the most widespread effects. We therefore suggest that parietal lesions (especially of areas 5 and 7a) and frontal lesions (especially of areas 46 and FEF) are most likely to disrupt the system‐wide integrative processes that require rapid de‐ and resynchronization of endogenous brain oscillatory networks.

Acknowledgements

OS and CH were supported by the J.S. McDonnell Foundation.

REFERENCES

  1. Arenas A,Díaz‐Gilera A,Pérez‐Vicente CJ ( 2006): Synchronization reveals topological scales in complex networks. Phys Rev Lett 96: 114102. [DOI] [PubMed] [Google Scholar]
  2. Bassett DS,Meyer‐Lindenbergh A,Achard S,Duke T,Bullmore E ( 2006): Adaptive reconfiguration of fractal small‐world human brain functional networks. PNAS 103: 19518–19523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bluhm RL,Miller J,Lanius RA,Osuch EA,Boksman K ( 2007): Spontaneous low‐frequency fluctuations in the BOLD signal in schizophrenic patients: Anomalies in the default network. Schizophrenia Bull 33: 1004–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Börgers C,Epstein S,Kopell NJ ( 2005): Background gamma rhythmicity and attention in cortical local circuits: A computational study. PNAS 102: 7002–7007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Breakspear M,Terry J,Friston K ( 2003): Modulation of excitatory synaptic coupling facilitates synchronization and complex dynamics in a nonlinear model of neuronal dynamics. Network Comp Neural Syst 14: 703–732. [PubMed] [Google Scholar]
  6. Breveglieri R,Galletti C,Monaco S,Fattori P ( 2007): Visual, somatosensory and bimodal activities in the macaque parietal area PEc. Cerebral Cortex Adv Access, published on November 2, 2007, doi 10.1093/cercor/bhm127. [DOI] [PubMed] [Google Scholar]
  7. Buszáki G,Draguhn A ( 2004): Neuronal oscillations in cortical networks. Science 304: 1926–1929. [DOI] [PubMed] [Google Scholar]
  8. Corbetta M,Shulman GL ( 2002): Control of goal‐directed and stimulus‐driven attention in the brain. Nat Rev Neurosci 3: 201–215. [DOI] [PubMed] [Google Scholar]
  9. Engel AK,Fries P,Singer W ( 2001): Dynamic predictions: Oscillations and synchrony in top‐down Processing. Nat Rev Neurosci 2: 704–716. [DOI] [PubMed] [Google Scholar]
  10. Felleman DJ,Van Essen DC ( 1991): Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex 1: 1–47. [DOI] [PubMed] [Google Scholar]
  11. Finger S ( 1994): Origins of neuroscience: A history of explorations into brain function. New York: Oxford University Press; pp 32–62. [Google Scholar]
  12. Hagmann P,Kurant M,Gigandet X,Thiran P,Wedeen VJ,Meuli R,Thiran J‐P. ( 2007): Mapping human whole‐brain structural networks with diffusion MRI. PLoS ONE 2: e597. doi: 10.1371/journal.pone.0000597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Honey CJ,Kötter R,Breakspear M,Sporns O ( 2007): Network structure of cerebral cortex shapes functional connectivity on multiple time scales. PNAS 104: 10240–10245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Humphries MD,Gurney K,Prescott TJ ( 2006): The brainstem reticular formation is a small‐world, not scale‐free, network. Proc Roy Soc B Biol Sci 273: 503–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kötter R ( 2004): Online retrieval, processing, and visualization of primate connectivity data from the CoCoMac database. Neuroinformatics 2: 127–144. [DOI] [PubMed] [Google Scholar]
  16. Jackson JH ( 1884): Evolution and dissolution of the nervous system. Croonian lectures In: Taylor J,Editor.The Selected Writings of John Hughlings Jackson, Vol 2 London: Hodder and Stoughton; pp 45–75. [Google Scholar]
  17. Kuramoto Y ( 1975): International Symposium on Mathematical Problems in Theoretical Physics In: Araki H,Editor. Lecture Notes in Physics No. 30. New York: Springer; pp 420–422. [Google Scholar]
  18. Lachaux J‐P,Rodriguez E,Martinerie J,Varela FJ ( 1999): Measuring phase synchrony in brain signals. Hum Brain Mapping 8: 194–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Larter R,Speelman B,Worth RM ( 1999): A coupled ordinary differential equation lattice model for the simulation of epileptic seizures. Chaos 9: 795–804. [DOI] [PubMed] [Google Scholar]
  20. Lomber SG,Payne BR ( 1996): Removal of 2 halves restores the whole: Reversal of visual hemineglect during bilateral cortical or collicular inactivation in the cat. Vis Neurosci 13: 1143–1156. [DOI] [PubMed] [Google Scholar]
  21. Morris C,Lecar H ( 1981): Voltage oscillations in the barnacle giant muscle fiber. Biophys J 35: 193–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Moses P,Stiles J ( 2002): The lesion methodology: Contrasting views from adult and child Studies. Dev Psychobiol 40: 266–277. [DOI] [PubMed] [Google Scholar]
  23. Rombouts SARB,Barkhof F,Goekoop R,Stam CJ,Scheltens P ( 2005): Altered resting state networks in mild cognitive impairment and mild Alzheimer's disease: An fMRI study. Human Brain Mapping 26: 231–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schreiber T ( 2000): Measuring information transfer. Phys Rev Lett 85: 461–464. [DOI] [PubMed] [Google Scholar]
  25. Schnitzler A,Gross J ( 2005): Normal and pathological oscillatory communication in the Brain. Nat Rev Neurosci 6: 285–296. [DOI] [PubMed] [Google Scholar]
  26. Spencer KM,Nestor PG,Niznikiewicz MA,Salisbury DF,Shenton ME,McCarley RW ( 2003): Abnormal neural synchrony in schizophrenia. J Neurosci 23: 7407–7411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Sporns O,Honey CJ,Kötter R ( 2007): Identification and classification of hubs in brain networks. PLoS ONE 2: e1049. doi: 10.1371/journal.pone.0001049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Sprague JM ( 1966): Interaction of cortex and superior colliculus in mediation of visually guided behavior in the cat. Science 153: 1544–1547. [DOI] [PubMed] [Google Scholar]
  29. Stephan KE,Kamper L,Bozkurt A,Burns GA,Young MP,Kötter R ( 2001): Advanced database methodology for the collation of the connectivity data on the macaque brain (CoCoMac). Philos Trans R Soc Lond B Biol Sci 356: 1159–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Timme M ( 2006): Does dynamics reflect topology in directed networks? Europhys Lett 76: 367–373. [Google Scholar]
  31. Varela F,Lachaux J‐P,Rodriguez E,Martinerie J ( 2001): The brainweb: Phase synchronization and large‐scale integration. Nat Rev Neurosci 2: 229–239. [DOI] [PubMed] [Google Scholar]
  32. Wedeen VJ,Hagmann P,Tseng W‐YI,Reese TG,Weisskopf RM ( 2005): Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Res Med 54: 1377–1386. [DOI] [PubMed] [Google Scholar]
  33. Young PY,Hilgetag C‐C,Scannell JW ( 2000): On imputing function to structure from the behavioural effects of brain lesions. Philos Trans R Soc Lond B Biol Sci 355: 147–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zemanová L,Zhou C,Kurths J ( 2006): Structural and functional clusters of complex brain networks. Physica D 224: 202–212. [Google Scholar]
  35. Zhao M,Zhou T,Wang B‐H,Wang W‐X ( 2005): Enhanced synchronizability by structural perturbations. Phys Rev E 72: 057102. [DOI] [PubMed] [Google Scholar]
  36. Zhou C,Zemanová L,Zamora G,Hilgetag C‐C,Kurths J ( 2006): Hierarchical organization unveiled by functional connectivity in complex brain networks. Phys Rev Lett 97: 238103. [DOI] [PubMed] [Google Scholar]

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES