Sensitivity of beamformer source analysis to deficiencies in forward modeling

Abstract

Beamforming approaches have recently been developed for the field of electroencephalography (EEG) and magnetoencephalography (MEG) source analysis and opened up new applications within various fields of neuroscience. While the number of beamformer applications thus increases fast‐paced, fundamental methodological considerations, especially the dependence of beamformer performance on leadfield accuracy, is still quite unclear. In this article, we present a systematic study on the influence of improper volume conductor modeling on the source reconstruction performance of an EEG‐data based synthetic aperture magnetometry (SAM) beamforming approach. A finite element model of a human head is derived from multimodal MR images and serves as a realistic volume conductor model. By means of a theoretical analysis followed by a series of computer simulations insight is gained into beamformer performance with respect to reconstruction errors in peak location, peak amplitude, and peak width resulting from geometry and anisotropy volume conductor misspecifications, sensor noise, and insufficient sensor coverage. We conclude that depending on source position, sensor coverage, and accuracy of the volume conductor model, localization errors up to several centimeters must be expected. As we could show that the beamformer tries to find the best fitting leadfield (least squares) with respect to its scanning space, this result can be generalized to other localization methods. More specific, amplitude, and width of the beamformer peaks significantly depend on the interaction between noise and accuracy of the volume conductor model. The beamformer can strongly profit from a high signal‐to‐noise ratio, but this requires a sufficiently realistic volume conductor model. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.

INTRODUCTION

Inverse methods are used to reconstruct current sources in the human brain by means of electroencephalography (EEG) and/or magnetoencephalography (MEG) measurements. EEG and MEG measure potential differences on the scalp or magnetic fields outside the head induced by electrical brain activity, respectively. Among currently used functional imaging techniques MEG and EEG source reconstruction have an outstanding temporal resolution in the millisecond range [Baillet et al., 2001] and, therefore, have the potential not only to detect networks of neuronal assemblies but also to determine causality within these networks [Darvas et al., 2004]. The EEG and MEG inverse problem is underdetermined, i.e., the generators of measured fields cannot uniquely be reconstructed without further constraints [Hämäläinen et al., 1993; von Helmholtz, 1853]. This is the main reason why source analysis methods are often considered not to reach the spatial resolution of functional magnetic resonance imaging (fMRI) or positron emission tomography (PET). However in contrast to the latter methods, which detect neural activity indirectly by means of hemodynamic effects, EEG, and MEG benefit from the direct coupling between measured fields and neural activity.

MEG and especially EEG signals are sensitive to the conductivity profile of the head. Therefore, source reconstruction requires accurate modeling of head volume conductor properties within the embedded forward problem, i.e., within the procedure of simulating potentials and fields due to a known current dipole source in the brain. The source localization performance, therefore, depends on both the appropriateness of the chosen constraints through the selection of the inverse method as well as the quality of the volume conductor model within the forward problem.

In this article, we investigate the sensitivity of a beamformer inverse approach to head model misspecifications to gain a deeper insight into the interplay of beamforming and volume conductor modeling and, by means of the synergy, to present an overall improved beamformer source analysis strategy that can be used by others since the methods were implemented in the freely available open source toolbox SimBio [ 2009].

Although spatial filtering or beamforming approaches have been well‐known methods in the radar and sonar field for a longer time, they have only recently been introduced to the area of source analysis [Barnes et al., 2004; Brookes et al., 2004; Chau et al., 2004; Chen et al., 2006; Cheyne et al., 2006; Dalal et al., 2006; Gross et al., 2003; Hillebrand and Barnes, 2003; Huang et al., 2004; Robinson and Vrba, 1999; Sekihara et al., 2001; Singh et al., 2003; Spencer et al., 1992; van Veen et al., 1997]. Since then, the beamforming inverse approach has been successfully applied in a variety of neuroimaging studies or, even stronger, has opened up new source analysis application fields, e.g., Cheyne et al. [ 2006]; Cornwell et al. [ 2007]; Dziewas et al. [ 2003]; Furlong et al. [ 2004]; Garolera et al. [ 2007]; Gunji et al. [ 2007]; Herdman et al. [ 2003]; Teismann et al. [ 2009]. Beamforming, or spatial filtering, is a scanning method that tries to estimate the contribution of a given source location to the measured EEG or MEG signal by suppressing (filtering out) the contributions of other sources. The beamformer approach has interesting features. For instance, in contrast to the classical dipole fit method [Scherg and von Cramon, 1985], for a beamformer analysis, the number of sources does not have to be a known parameter in advance. More importantly, in contrast to most other source localization approaches, the beamformer does not rely on trial averaged data and can, therefore, be used to analyze the so‐called induced activity, i.e., brain activity with quite weak time or phase locking to a given stimulus. On the other hand, if trial averaging should be exploited, the event‐related extension of the beamformer approach can be used [Cheyne et al., 2006, 2007; Robinson, 2004]. Similarly, if the number of sources is a priori known, this information can be exploited by separating signal and noise subspace and constraining the beamformer to the signal space: Eigenspace beamformer [Sekihara et al., 2001, 2002b]. The most important drawback of the beamformer approach is its blindness to highly correlated sources [Sekihara et al., 2002a; van Veen et al., 1997]. Methods were developed to deal with this problem in specific situations [Brookes et al., 2007; Dalal et al., 2006; Herdman et al., 2003], but the basic problem remained.

In this article, we focus on synthetic aperture magnetometry (SAM) as introduced by Robinson and Vrba, [ 1999]. SAM is a so‐called scalar beamformer, which, in spite of the name, can also be applied to EEG data. Scalar beamformers give output signal‐to‐noise ratios superior to those of conventional vector beamformers [Sekihara et al., 2004] but need explicit information about the orientations of the possible sources. An integrated nonlinear estimation of source orientations is the distinctive feature of SAM [Vrba and Robinson, 2000]. Alternatively, the source orientations can be estimated from the head model (the sources are expected to be perpendicular to the cortical surface). The advantages and disadvantages of the latter approach are discussed in Hillebrand and Barnes [ 2003].

In this article, we focus on EEG, because it is well known that EEG source analysis is more sensitive to an appropriate modeling of the head conductivity profile than MEG [Cuffin, 1996; Hämäläinen and Sarvas, 1987; Hämäläinen et al., 1993; Huiskamp et al., 1999; Ramon et al., 2004; Roth et al., 1993; van den Broek et al., 1998; Wolters et al., 2006]. As beamformers are generally sensitive to errors in the volume conductor model [Sekihara et al., 2002b], this may explain why the majority of beamformer studies up to now have been based on MEG.

For a spherical model which typically approximates the head by three concentric spherical shells representing brain, skull, and scalp, quasi‐analytical solutions exist for the EEG forward problem [de Munck and Peters, 1993]. Although only a rough approximation to reality, this model is still often used, e.g., in situations where no individual structural image is available [Steinstraeter et al., 2009], for validating numerical codes for realistic head modeling or just because of its simplicity and computational speed. However, for realistic head modeling, numerical approximation methods are more and more frequently used such as the boundary element method (BEM) [Kybic et al., 2005], the finite difference method (FDM) [Hallez et al., 2005], the finite volume method (FVM) [Cook and Koles, 2006], or the finite element method (FEM). This article focuses on the FEM, which allows high accuracy in the numerical solution of elliptic partial differential equations since it is specifically tailored to the corresponding variational formulation and allows high flexibility in modeling the forward problem in geometrically complicated inhomogeneous and anisotropic head volume conductors [Bertrand et al., 1991; Buchner et al., 1997; Drechsler et al., 2009; Haueisen, 1996; Lew et al., 2009; Marin et al., 1998; Ramon et al., 2004; Schimpf et al., 2002; Vallaghe and Clerc, 2009; van den Broek et al., 1998; Wolters et al., 2006; Zhang et al., 2006]. The use of recently developed transfer matrix approaches [Gencer and Acar, 2004; Weinstein et al., 2000; Wolters et al., 2004] or reciprocity approaches [Hallez et al., 2005; Vallaghe et al., 2009] and advances in efficient FEM solver techniques for source analysis [Lew et al., 2009] drastically reduced the time complexity of the computations. Thus, the main disadvantage of FEM modeling has been eliminated.

Our study, therefore, focuses on examining the sensitivity of SAM with respect to two main aspects of volume conductor modeling using the FEM: realistic geometry approximation of the three head compartments (scalp, skull, and brain) and realistic modeling of the skull conductivity. As SAM reconstructs even punctiform sources as activation peaks with finite extensions and amplitudes depending on the local signal‐to‐noise ratio, in addition to the examination of localization error we also study the effect of improper volume conductor modeling on amplitude and width of the beamformer reconstruction. Consequently, our investigations give an insight into the behavior of EEG‐data–based SAM beamforming. To our knowledge, we present the first systematic study on the influence of improper volume conductor modeling to the source reconstruction performance of beamformers.

THEORY

FEM‐Based Forward Problem

In the considered low‐frequency band of EEG (frequencies below 1,000 Hz), the capacitive component of tissue impedance, the inductive effect, and the electromagnetic propagation effect can be neglected in the Maxwell equations of electrodynamics so that the relationship between bioelectric fields and the underlying current sources in the brain can be represented by the quasi‐static equation

(1)

with homogeneous Neumann boundary conditions at the head surface

(2)

and a reference electrode with given potential, i.e., ϕ(x _ref) = 0, where σ is the conductivity distribution, ϕ is the scalar electric potential, j ₀ is the primary (impressed) current, Ω the head domain, Γ its surface, and n the surface normal at Γ [Plonsey and Heppner, 1967; Sarvas, 1987]. The primary current is generally modeled by a mathematical dipole at position x ₀ with the moment M ₀, j ₀ = M ₀δ(x−x ₀) [Sarvas, 1987]. For a given primary current and conductivity distribution, the potential can be uniquely determined (see proof in Wolters et al. [ 2007]) for what is known as the bioelectric forward problem.

For the numerical approximation of Eqs. (1) and (2) in combination with the reference electrode, we use the FEM. Different FE approaches for modeling the source singularity are known from the literature: a subtraction approach [Bertrand et al., 1991; Drechsler et al., 2009; Wolters et al., 2007], a partial integration direct method [Weinstein et al., 2000], and a Venant direct method [Buchner et al., 1997]. On the basis of the performance comparisons of all three different methods in multilayer sphere models, we decided to use the Venant approach in the study at hand as this method yields suitable accuracy when using sufficiently regular meshes combined with high computational speed [Lew et al., 2009]. The potential is projected into the FE space, i.e., 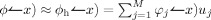, where φ_j are piecewise linear FE basis functions and M is the number of FE nodes. Standard variational and FE techniques for Eqs. (1) and (2) yield the linear system

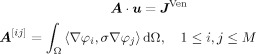where A is the stiffness matrix with dimension M × M, u the coefficient vector for ϕ_h (M × 1), J ^Ven the Venant approach right‐hand‐side vector (M × 1) [Buchner et al., 1997; Lew et al., 2009], and 〈·,·〉 the scalar product. A key feature of this study was to pursue solutions that achieve high computational efficiency, so that we combined the Venant approach with the FE transfer matrix method as described in detail in Wolters et al. [ 2004]. Note that J ^Ven has only T nonzero entries (with T being the number of neighbors of the closest FE node to the source) so that, when using the fast FE transfer matrix approach, each forward computation only amounts in 2 × N × T operations with N being the number of independent sensors.1

SAM

Scalar beamformers w = w(r,θ) like SAM estimate the contribution of a possible dipole source at location r and with orientation θ to the measured sensor data X(t) [Vrba and Robinson, 2001]:

The sensor data X(t) as well as the beamformer filter w are N × 1 matrices and s(t) is the scalar time course of a dipolar source (r,θ). The beamformer theory defines the source strength of a dipole (r,θ) with respect to a time window T as variance ρ² = var_T(s) across this time window [van Veen et al., 1997], which can be expressed by the data covariance C = cov_T(X) likewise calculated across T [van Veen et al., 1997; Vrba and Robinson, 2001]:

(3)

A perfect estimation of s(t) requires that the filter w removes all contributions of sources other than (r,θ) from X(t). Because of the limited degrees of freedom, N, this requirement can typically not be fulfilled in a global sense, i.e., for all possible X(t) [van Veen et al., 1997]. Instead, w is optimized with respect to the measured data (linearly constrained minimum variance (LCMV) beamformer [van Veen et al., 1997; Vrba and Robinson, 2001]):

(4)

Here l = l(r,θ) is the leadfield of the dipole at (r,θ), i.e., the sensor data generated by a dipole at (r,θ) with unit strength. The minimization process tries to remove all contributions of sources other than (r,θ) from the beamformer output and the condition w ^t l = 1 ensures that the source of interest is not removed. The solution to this minimization is given by [van Veen et al., 1997; Vrba and Robinson, 2001]

(5)

If sensor noise is modeled as spatially white, i.e., with covariance matrix Σ = σ² l (σ² variance of the noise, I unit matrix), the beamformer projected noise is [Vrba and Robinson, 2001]

(6)

Therefore, the projected noise (in contrast to the noise at sensor level) is inhomogeneously distributed across the brain and may be huge, much larger than the signal strength, if the norm of the leadfield is small (‖w‖ ∼ 1/‖l‖ because of w ^t l = 1). As shown by Sekihara et al. [ 2005], the projected noise introduces a localization bias leading to significant mislocalization, especially for leadfields with small norms. This can be avoided if the so called pseudo‐Z value instead of the original beamformer output is used [Vrba and Robinson, 2001]:

(7)

As ρ² includes the noise ρ${}_{\text{noise}}^{\text{2}}$ the pseudo‐Z value can be interpreted as 1 + SNR, with SNR the signal‐to‐noise ratio in source space between source strength and projected noise (not identical to SNR in sensor space, see later). Z ² does not have a localization bias [Sekihara et al., 2005].

As described so far, beamformer calculations depend on the location r and the orientation θ of a possible source. While r is typically specified by the user (list of scan location), θ has to be derived from r. The scalar beamformer SAM [Robinson and Vrba, 1999] estimates source orientations on the basis of measured EEG or MEG data by maximizing the pseudo‐Z output across all possible orientations θ [Cheyne et al., 2007]:

This can be translated in an Eigenvalue problem [Sekihara et al., 2004], which can efficiently be solved.

If h ₀ is the leadfield of a simulated dipole at position r ₀ and orientation θ₀ the data covariance matrix is given by [Sekihara et al., 2004]

(8)

Here, ρ${}_{\text{0}}^{\text{2}}$ is the variance of the source and σ² is the sensor noise variance (spatially white noise). In this case, the pseudo‐Z output for (r,θ) with the model dependent leadfield l = l _model(r,θ) can be calculated (see Appendix A) to

(9)

with v = sin(∡(h ₀,l)) (v, instead of v ², as argument to Z ² eases the comparison with simulation results in certain cases, see later) and .

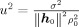The parameter u ² introduces the sensor noise into the calculation of Z² and has the characteristic of a noise‐to‐signal ratio. 1/u ² is sometimes called input signal‐to‐noise ratio [Sekihara et al., 2004, 2005]; however, it is not the SNR conventionally used in MEG/EEG measurements. If we define the measurement SNR ξ² according to Sekihara et al. [ 2002a] as the ratio between mean signal variance (at sensor level) and mean noise variance (both across sensors and time points) we find,

1/u ² is, therefore, N times larger than the conventionally measured SNR.

v = sin(∡(h ₀,l)) describes the deviation between the leadfield of the source, h ₀, and the leadfield for the scan grid location and dipole orientation for which Z ² is calculated, l. The role of v in Z ² can be interpreted in two ways. First, v ↦ Z ² describes the decay of the pseudo‐Z value with increasing distance to the source. The actual shape of a SAM peak in a source reconstruction, in particular the peak width, also depends on the local relation between v and the distance to the peak maximum Δr. As v can also be expressed by the leadfield correlation between h ₀ and l, 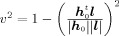, we could apply the approximation proposed by Gross et al. [ 2003]2 resulting in v ≈ Δr/a with a scaling factor a depending on the position of the peak maximum. Following this approximation, we based our theoretical considerations on v, instead of v ², to ease the comparison with our distance‐based simulation results.

In a second interpretation, Z ²(v _peak, u ²) gives the peak amplitude of a source reconstruction at v = v _peak. For an exact volume conductor model, v _peak is 0 and Z ² solely depends on the noise parameter u ²: Z ² = 1 + 1/u ². For an inexact model, v _peak = 0 can (typically) not be reached and v _peak, therefore, reflects the local effect of deviation from the exact volume conductor. Figure 1a shows the influence of the noise on the peak amplitude for different local modeling errors v_peak. In contrast to the exact model (v _peak = 0, cyan curve), whose curve strictly monotonically decreases with increasing noise parameter u ², for inexact models Z ² shows a local maximum at u ² = v _peak, i.e., the peak amplitude first increases with increasing noise level.

Figure 1.

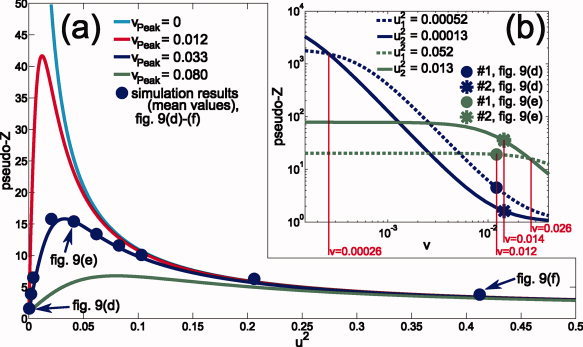
Theoretical pseudo‐Z curves: (a) u ² ↦ Z ² for local modeling errors v _peak found for the simulations presented in Figures 9 and 10 [exact model (v _peak = 0) and simplified model at minimum (0.012), mean (0.033), and maximum (0.080) of v _peak]. The blue disks show simulation results (means across all sources, cf. Fig. 9) for different noise levels (including the noise levels presented in Fig. 9): σ² = 2, 10, 20, 100, 200, 300, 400, 500, 1000, 2000 × 10⁻¹⁵ V². (b) v ↦ Z ² (logarithmic scales) for the sources #1 (disk) and #2 (asterisk) of the simulations highlighted in Figure 9d, blue curves, and Figure 9e, green curves. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 1b, in more detail discussed in the Results section, shows the course of the pseudo‐Z values in dependence on v for four different u ². Curves with noise parameters u ${}_{\text{1}}^{\text{2}}$ and u ${}_{\text{2}}^{\text{2}}$ intersect at v _inters = u ₁ u ₂. With increasing noise level σ², u ${}_{\text{1}}^{\text{2}}$, and u ${}_{\text{2}}^{\text{2}}$ and therefore also v _inters increase ( 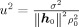). The intersection point, therefore, moves to higher v if the overall noise level increases.

From Eq. (9), an equation for the peak width [full width half maximum (FWHM)] can be derived (see Appendix B)

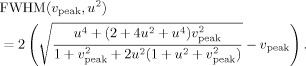(10)

Figure 2 shows u ² ↦ FWHM for four different values of v _peak found in our simulations (see Fig. 10). The figure is discussed in greater detail in the Results section.

Figure 2.

Theoretical FWHM curves in dependence of the noise parameter u ² for four different local modeling errors v _peak found for the simulations presented in Figure 10: v _peak = 0 (blue curve) for the exact model; v _peak = 0.014 (green curve), v _peak = 0.040 (red curve), and v _peak = 0.041 (cyan curve) for the example sources #2, #3, and #4 reconstructed by using the simplified model (cf. Fig. 10). (b) and (c) show magnifications of the curves in (a): The ranges of u ² values shown in (a), (b), and (c) result from the simulations shown in Figure 10f, e, and d, respectively. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

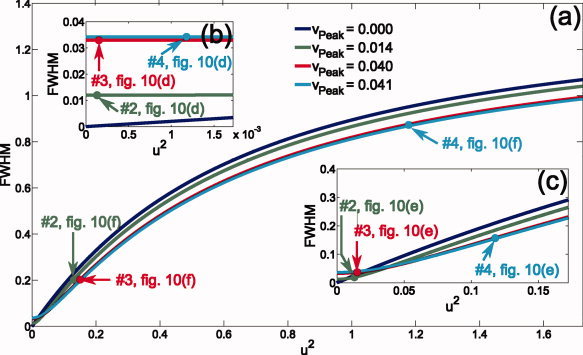
Figure 10.

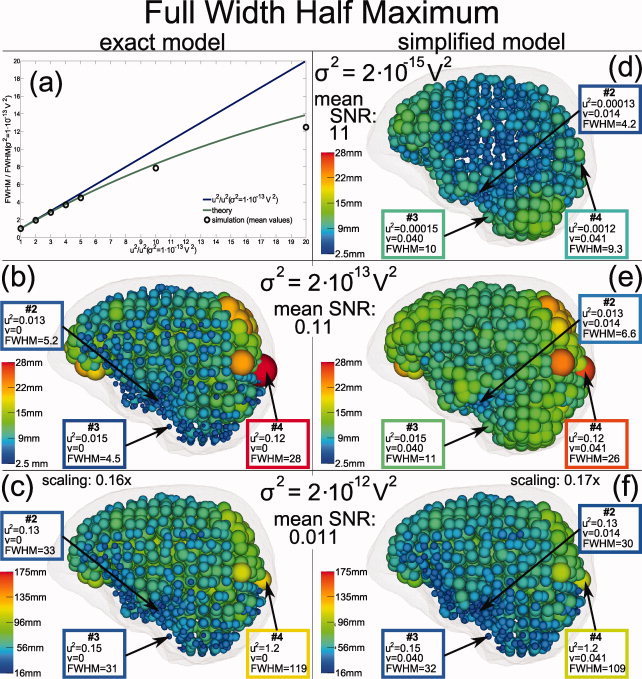
Distribution of the beamformer (SAM) peak widths for the same simulations as in Figure 9. Sphere radii correspond to FWHM peak widths—please note different scaling in bottom row. Results for three sample sources, labeled #2 (cf. Fig. 9), #3, and #4, are emphasized. Figure 2 compares these values with the theory. In Figure 10a mean FWHM values simulated with the exact model for different noise levels (black circles) are compared to the theoretical function (green curve). To allow a comparison of distance based simulation results and the leadfield deviation based theory, relative FWHM values (dimensionless) based on the noise level σ² = 1 × 10⁻¹³ V² are shown (see text). The blue curve illustrates a linear approximation of the theoretical function. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Equation (10) describes the peak width in terms of the leadfield deviation v. To allow quantitative comparisons with our simulation results, for the exact model, v _peak = 0, we also used a relative peak width

based on a given reference noise parameter u ${}_{\text{ref}}^{\text{2}}$. For high SNR (u ², u ${}_{\text{ref}}^{\text{2}}$ ≪ 1), FWHM_rel becomes linear (in terms of u ²/u ${}_{\text{rel}}^{\text{2}}$):

MATERIALS AND METHODS

MRI‐Based FE Head Model

Our simulations were based on a realistic three compartment (skin, skull, brain) head model derived from bimodal T1‐ and proton density‐ (PD‐) MR image datasets as described in detail in Wolters et al. [ 2006]. By means of the bimodal T1‐, PD‐MRI datasets, special attention was paid to a correct segmentation of the poorly conducting skull compartment because source analysis is especially sensitive to a correct modeling of this highly resistive layer [Cuffin, 1996; Hämäläinen and Sarvas, 1987; Huiskamp et al., 1999; Ramon et al., 2004; Roth et al., 1993]. We used three different FE‐based volume conductor models that only differ in their electric properties (see next section) but that all share the same geometry represented by an FE mesh with 147,287 nodes and 892,115 tetrahedral elements.

Volume Conductor Models

FE models

Rush and Driscoll [ 1968] reported that the human skull can be considered as an anisotropic conductor, because they measured a low conductivity in the radial and a much higher conductivity in the tangential direction. As a first approximation of the radial conductivity, the three different skull compartments inner compacta, spongiosa, and outer compacta can be estimated as a series connection of a high, a low, and a high resistor: Ω_Σ = Ω_IC + Ω_Sp + Ω_OC. The tangential conductivity can be approximated as a parallel connection of the same three resistors, 1/Ω_Σ = 1/Ω_IC + 1/Ω_Sp + 1/Ω_OC, thus resulting in a higher value for the tangential compared with the radial direction [Fuchs et al., 2007; Rush and Driscoll, 1968]. The importance of skull conductivity anisotropy modeling has already been pointed out by Marin et al. [ 1998] and van den Broek et al. [ 1998], who reported significant localization errors of simulated EEG generators in case of inadequate modeling. Besides geometrical aspects, our main goal of this study was to investigate the effects of anisotropic skull conductivity on beamformer source localization performance: Generators were thus simulated within FE models realizing different anisotropic approaches for the skull conductivity (forward models) and were reconstructed on the basis of an isotropic FE model (inverse model). The estimated conductivity for skin and brain compartment, 0.33 S/m, respectively, was identical for all models, only the radial and tangential skull conductivities differed.

Starting from an isotropic skull conductivity of 0.0042 S/m [Buchner et al., 1997; Cuffin, 1996; Huiskamp et al., 1999] two different 1:10 (according to [de Munck, 1988; Marin et al., 1998; Peters and de Munck, 1991; Rush and Driscoll, 1968; van den Broek et al., 1998]) realizations of skull anisotropy were derived: one using a volume constraint, leading to a decreased radial, μ_rad = 0.000905 S/m, and an increased tangential skull conductivity, μ_tang = 0.00905 S/m, following Wolters et al. [ 2006], and one where the radial was kept constant, μ_rad = 0.0042 S/m, while the tangential was increased by a factor of 10, μ_tang = 0.042 S/m (see, e.g., Marin et al. [ 1998]).

Spherical head model

Geometrical aspects were studied by comparing our realistically shaped three‐compartment isotropic FE model with a three‐layer isotropic sphere model (skin, skull, brain). The center and the outer radius of the sphere model were obtained by fitting the model to 71 electrodes of an international 10‐10 electrode configuration constructed on the outer skin surface of the segmented MRI (see later). This led to an outer radius (outer surface of the skin) of 89.66 mm. For the outer surface of the skull a radius of 83.33 mm and for the inner skull surface a radius of 74.89 mm was chosen. A homogeneous skull thickness of 8.44 mm was, thus, used for the spherical volume conductor. We assigned the same conductivity values as in the case of the isotropic FE model (0.33 S/m for skin and brain, 0.0042 S/m for the skull).

Sensor Configurations

Two different sensor configurations were used for the simulations. First, a realistic sensor configuration based on the international 10‐10 electrode configuration was constructed on the segmented outer skin surface. The left side of Figure 3 shows the positions of the 71 electrodes relative to the segmented brain surface (volume rendering). To study the influence of insufficient sensor coverage, a second sensor configuration enclosing the complete head was also used (full coverage configuration, right side of Fig. 3). The construction based on the spherical head model distributed 258 sensors uniformly over the outer sphere layer. As EEG simulations require the contact of the sensors to the modeled skin surface, the actual sensor configuration depends on the volume conductor model. The predefined sensor positions were projected on the outer skin surface as represented in the respective model. In Figure 3, both the sensor configurations are shown with respect to the FE models.

Figure 3.

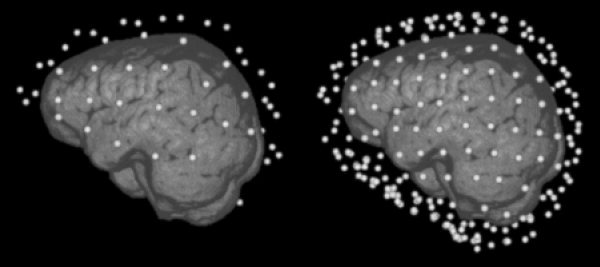
The two sensor configurations used in this study: A realistic sensor cap with 71 electrodes based on the international 10‐10 system and a synthetic sensor configuration with 258 sensors covering the complete head.

Simulation of the Reference Sources

The segmentation of the brain as described in Wolters et al. [ 2006] was used to position a large number of sources uniformly distributed across the grey matter. The procedure resulted in 1,574 remaining source locations that were used for the generation of reference forward data and later visualization purposes.

Dipole orientations were selected so that the leadfield differences between source simulation and source reconstruction were maximized: For each dipole location r and for each pair of volume conductor models the 3 × N leadfields H _sim(r) for the simulation and H _rec(r) for the reconstruction were computed. For the difference between these leadfields, H _sim(r) − H _rec(r), a singular value decomposition (SVD) was performed. The dipole orientation was chosen to have the direction of the Eigenvector to the largest eigenvalue of this SVD. In this direction, the L ² norm of the potential difference between simulation and reconstruction model is maximized. Choosing this dipole orientation, we expect to find a localization error which is close to the maximum localization error for a dipole at that position.

For the strength of the sources a variance of 50 nAm² was selected, realized by a 40 Hz sinus wave with 10 nAm amplitude (sampling frequency 1,200 Hz).

SAM Reconstruction

As described in the theory section, a SAM source reconstruction requires the construction of SAM filters for a predefined grid covering the part of the brain where sources can be assumed. Based on the constructed beamformer filters pseudo‐Z values are calculated for each grid point resulting in a three‐dimensional map of activations. In this framework, the reconstructed source location was defined as the maximum pseudo‐Z value across the grid.

As the individual filter constructions are mutually independent the choice of the scan grid does not influence the reconstruction result as long as the grid covers all possible sources. Mislocalized sources may be found far away from their correct position; therefore a scan grid with 2 mm isotropic resolution covering the complete segmented head was used in this study.

As shown in the theory section, the width of the SAM peak significantly depends on the noise level. For low noise, the resulting SAM peak is nearly fully located at the position of the source. Small differences to the leadfield used in the simulation (small difference in location due to the choice of the scan grid or differences due to different volume conductor models) may lead to SAM results close to the level of the background noise. For this reason, SAM reconstructions may benefit from higher noise levels as a significant peak width exceeding the grid distance is needed if the source leadfield is not exactly represented at scan grid nodes [Hillebrand et al., 2005]. Here, spatial white noise (σ² is constant across sensors) with three different noise levels σ${}_{\text{high SNR}}^{\text{2}}$ = 2 × 10⁻¹⁵ V², σ${}_{\text{medium SNR}}^{\text{2}}$ = 2 × 10⁻¹⁴ V², and σ${}_{\text{low SNR}}^{\text{2}}$ = 2 × 10⁻¹³ V² was applied (σ² as the variance of the noise at sensor level). The actual signal‐to‐noise level ξ² is proportional to the square of the leadfield norm of the source (see Theory section). ξ², therefore, varies with the source position, reflecting real measurements as deeper neural sources show lower SNRs.

To abstract from localization errors caused by inaccurate covariance estimations due to finite time windows [Brookes et al., 2008], noise has not been added to the sensor data but directly to the covariance matrix analyzed by the beamformer: C = C _{simulated source} + σ² I.

Visualization of Geometrical Aspects of the Volume Conductor Models

To visualize the differences between the outer skin surfaces of the FE and the sphere models, the distance between each boundary node of the FE mesh and the outer surface of the spherical head model was calculated. Using the software package SCIRun [ 2009], this result was visualized in the left column of Figure 4.

Figure 4.

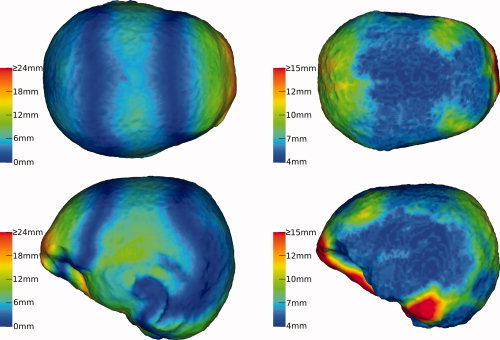
Geometrical properties of the FE models: The left column illustrates the local deviation between the FE outer skin surface and its approximation by the spherical head model. The right column visualizes the local thickness of the skull. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In the same way, the local skull thickness was visualized in the right column of Figure 4. For each node at the outer skull surface (intersection between skin and skull tetrahedrons of the FE mesh), the distance to the closest node at the inner skull surface (shared by skull and brain tetrahedrons) was calculated.

To compare localization results with these geometrical maps, localization errors were also projected to skin and skull surface: For each node of the respective surface the distance d to the closest simulated dipole was calculated. The distance weighted mean across the localization errors found for the dipoles not exceeding a distance of d + 5 mm from this node was then used as its value. These surface maps of reconstruction errors for superficial sources are again visualized with SCIRun [ 2009] (the right side of Fig. 5 shows an example).

Figure 5.

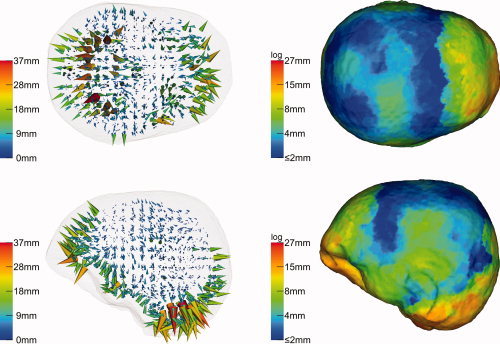
Beamformer (SAM) reconstruction inaccuracies as mere consequence of geometrical modeling imprecision if based on realistic sensor coverage (10‐10 system): An isotropically conducting FE model has been used for the forward solution while the inverse reconstruction was based on an isotropically conducting spherical head model. The left column illustrates the reconstruction results for each simulated dipole as three‐dimensional field of displacement vectors (cones). The right column visualizes the superficial reconstruction errors as projection to the outer skin surface. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

FWHM

Especially for larger peak widths, the shape of a SAM peak is not necessarily isotropic. To characterize the peak width by a scalar value, we defined the FWHM by the volume of the three‐dimensional peak. As pseudo‐Z values (Z ²) have a theoretical minimum of 1, the calculation of the peak width was based on Z ² − 1. All 2 × 2 × 2 mm³ grid voxels with a value for Z ² − 1 not smaller than the half of the maximum of this quantity were marked. The FWHM of the peak was now defined as the diameter of an equivalent sphere with the same volume as the set of marked voxels.

Software Implementation and Computing Platform

The SAM beamformer approach was implemented in the freely available open source SimBio software environment [SimBio, 2009] and can thus be used by others. The SimBio code contains a variety of EEG and MEG inverse source reconstruction algorithms which can be combined with multilayer‐sphere, boundary element or FE forward approaches. The most simulations and evaluations ran on a Linux‐Workstation with an Intel Core 2 Duo E6600 processor (2.4 Ghz) and a main memory of 4 GB. On this platform, the calculation of the leadfields for the whole‐head scanning grid (2 × 2 × 2 mm³ resolution, 368,015 scan locations) takes less than 22 min for the realistic sensor configuration (71 sensors) and less than 38 min for the full coverage sensor configuration (258 sensors).

RESULTS

Results are presented in three main sections: First, the influence of geometrical volume conductor modeling errors on the localization performance of SAM is studied. The second section reports the effects of skull anisotropy on SAM localization. The third section deals with noise and its influence on amplitude and width of the SAM peaks. As the actual level of spatially white sensor noise turned out to be irrelevant for the localization errors, this issue is also moved to the last section.

In addition to these main sections, we start by reporting some important geometrical aspects of the used models.

Deviation from Spherical Shape and Skull Thickness

Two important geometrical properties of the FE model are visualized in Figure 4 using color codes assigned to different surfaces of the FE mesh: The local difference between the outer skin surfaces of the spherical and the FE head model was assigned to the skin surface of the FE model (left column) and the outer surface of the FE skull compartment was colorized according to the course of the skull thickness derived from the FE mesh (right column). Differences from 0 to 33 mm (left column) and local thicknesses of the skull between 4 and 26 mm (right column) were found.

Geometry Effect

The effect of improper‐modeled geometry was examined by simulating individual dipoles in a realistically shaped isotropic FE forward model and, for the inverse reconstruction, performing SAM on the basis of the spherical head model. Figure 5 shows the result for the realistic sensor configuration of 71 electrodes based on the 10‐10 system. In the left column of this figure, each cone visualizes the result for one of the 1,574 simulations. The basis of a cone represents the position of the simulated dipole in the forward model, whereas its vertex points to the location reconstructed by SAM. The distances between simulated and reconstructed positions are additionally color coded. The cone representation is less appropriate to visualize the course of smaller reconstruction errors. Therefore a second illustration of the mislocalization of superficial dipoles is presented in the right column of the figure. Here, the lengths of the displacement cones were projected to the skin surface of the FE model (see Materials and Methods section).

Reconstruction errors of up to 37 mm were found (left column). The largest errors could be observed in prefrontal and occipital areas, especially at the cerebellum, and in temporal areas. In the right column, due to inherent smoothing of the projection procedure, the influence of outliers was reduced and a maximum displacement value of 27 mm appeared. A possible reasoning for the outliers is that dipole locations and orientations were chosen in such a way that they could not project their two poles to the measurement sensors so that their reconstruction was especially error‐prone to changes in the underlying volume conductor model. A comparison with Figure 4 reveals that the SAM reconstruction errors are mainly a function of the deviations from spherical shape and especially from realistic skull thickness. In areas, where the spherical “skull compartment” is thinner than the realistic one, the cones point outside (in occipital and most prefrontal areas), whereas they point inside where it is thicker (prefrontal areas at the eye‐sockets and temporal areas).

The influence of the full coverage sensor configuration is demonstrated in Figure 6. Apart from the used sensor configuration, the investigation was identical to that shown in Figure 5. The maximal reconstruction error (left column), now achieved in the prefrontal area, is with 32 mm just slightly smaller compared to the 10‐10 system coverage. However, the area at the cerebellum benefits much from the better sensor coverage.

Figure 6.

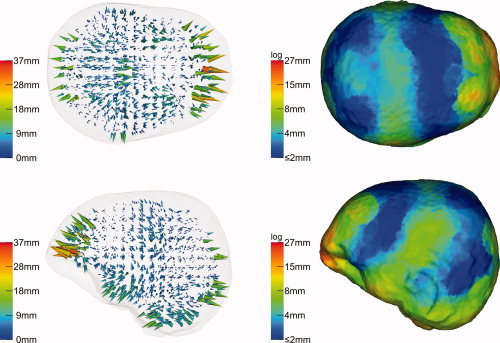
Beamformer (SAM) reconstruction inaccuracies due to geometrical errors if based on a synthetic full coverage sensor configuration—otherwise identical to simulation shown in Figure 5. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Anisotropy Effect

The effect of skull conductivity anisotropy modeling was examined by simulating individual dipoles in both anisotropic FE forward models (see Materials and Methods section) and, for the inverse reconstruction, performing SAM on the basis of the isotropic FE volume conductor. In the first scenario, radial and tangential skull conductivities were first calculated with respect to the volume constraint. As results for the realistic 71 sensor cap were almost identical with the full coverage configuration, only the later results are shown in Figure 7. The projection of the SAM reconstruction errors (right column) was based on the outer skull surface. Reconstruction errors up to 20 mm were found, increasing with decreasing source depths (left column) and with decreasing distance to areas with larger skull thickness (compare right column to the right column of Fig. 4). The projection (right column) shows the same maximum, 20 mm, which indicates that outliers were less relevant as in the previous simulation. SAM reconstructed the location of the dipoles consistently too deep (left column): Nearly all deviation cones point in quasi‐radial direction, i.e., inwards.

Figure 7.

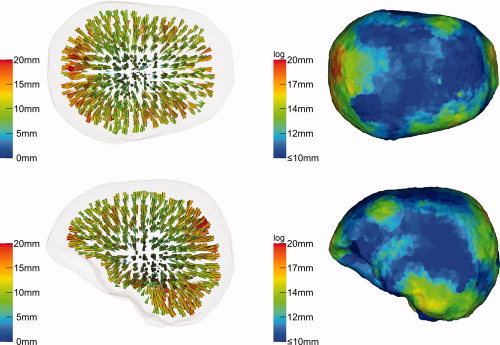
Beamformer (SAM) reconstruction inaccuracies due to skull anisotropy: Volume constraint. Forward model: 1:10 anisotropic FEM with volume constraint (skull conductivity: μ_rad = 0.000905 S/m, μ_tang = 0.00905 S/m). Inverse model: Isotropic FEM (skull conductivity of 0.0042 S/m). Sensor configuration: Full coverage (258 sensors). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In the second scenario, skull anisotropy was modeled by means of a 10 times increased tangential skull conductivity, while the conductivity in radial direction through the skull was kept identical to that of the isotropic model. Figure 8 visualizes the reconstruction results for the realistic cap with 71 electrodes. Even if a maximum reconstruction error of 22 mm was found, this relatively large value is mainly based on a few outliers at the cerebellum where the sensor coverage is rather poor (left column). In general, errors are much smaller than with the volume constraint simulations above. The projection result (right column), typically less sensitive to outliers, only shows a maximum of 14 mm in the area with poor sensor coverage at the cerebellum and errors between 3 and 9 mm in temporal, prefrontal, and occipital areas. The consistence with the map of local skull thicknesses is again obvious (compare right column to the right column of Fig. 4). In the case of full sensor coverage, while most errors remained nearly identical to the 71 electrode case, errors at the cerebellum and in temporal areas could still be significantly reduced to maximally 8 mm.

Figure 8.

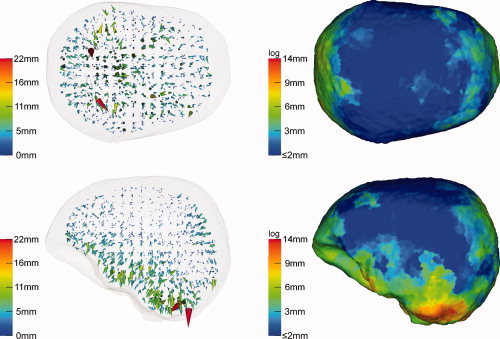
Beamformer (SAM) reconstruction inaccuracies due to skull anisotropy: Increased tangential conductivity. Forward model: 1:10 anisotropic FEM (μ_rad = 0.0042 S/m, μ_tang = 0.042 S/m). Inverse model: isotropic FEM (skull conductivity of 0.0042 S/m). Sensor configuration: realistic 10‐10 sensor system. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Peak Width and Amplitude

The simulations presented in the previous sections were performed for different noise levels σ² ranging from 2 × 10⁻¹⁵ to 2 × 10⁻¹² V². Localization results were identical for all noise levels which is consistent with the theory. With increasing noise level (increasing u ²), the pseudo‐Z peaks get broader and the peak amplitudes decrease (see e.g., Fig. 1b), nevertheless the pseudo‐Z curves are strictly monotonic and the best fitting leadfield throughout the SAM grid, i.e., the smallest v, can therefore uniquely be identified by searching for the highest pseudo‐Z value, independent of the noise level. Because of our simulation conditions—single source and ideal noise—the peak position therefore solely depends on the volume conductor model and the selected SAM grid (which is idealized here in the sense that the true source location is included). In contrast, the widths and amplitudes of the peaks turned out to significantly depend on the noise level.

In Figure 9, SAM peak amplitudes are visualized for three noise levels, σ² = 2 × 10⁻¹⁵, 2 × 10⁻¹³, and 2 × 10⁻¹² V² and for two volume conductor models. On the left side, the SAM calculations were based on the “exact” volume conductor model, i.e., the same anisotropic FE model (1:10 skull anisotropy with volume constrain) as used for the simulation of the sources; on the right side these sources were reconstructed by using the associated isotropic FE model (see Materials and Methods section) as a “simplified” volume conductor model. All calculations were based on the full coverage sensor configuration. The reconstructions using the exact volume conductor model led to a perfect localization of the sources whereas the simplified model introduced localization errors up to 20 mm (cf. Fig. 7).

Figure 9.

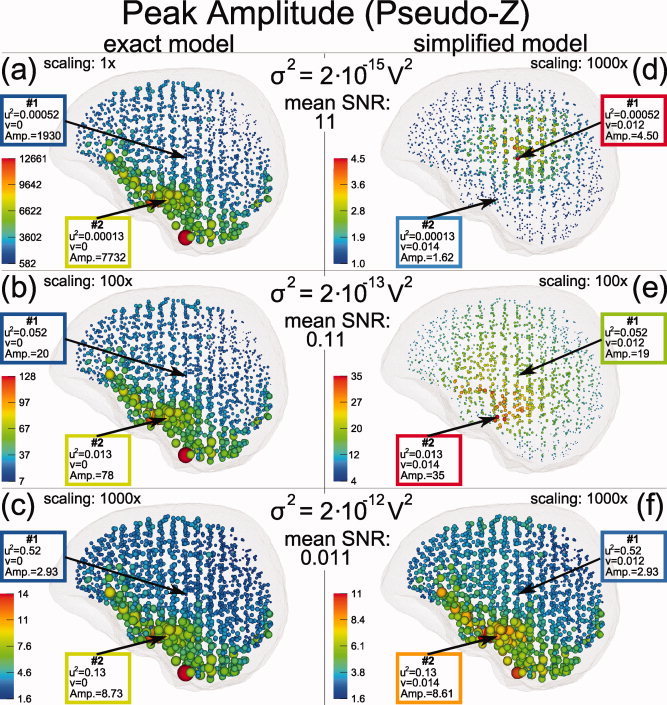
Distribution of beamformer (SAM) peak amplitudes in dependence of noise level and modeling errors. Peak amplitudes are illustrated by sphere radii—note the different scalings. Sources were simulated within the FE model with 1:10 skull anisotropy (volume constraint). The left side illustrated SAM reconstruction results if the inverse modeling was based on this exact volume conductor model. On the right side, the beamformer reconstruction was based on a simplified volume conductor model: the associated isotropic FE model. From the top to the bottom row increasing noise levels were selected. Results for two sample sources, labeled #1 and #2, are emphasized, for which connected theoretical curves are presented in Figure 1. All calculations were based on the full coverage sensor configuration. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In Figure 9, the reconstruction results are visualized by spheres located at the positions of the simulated sources. Peak amplitudes are color coded and linearly mapped to the sphere radii though with different scaling factors as indicated in the figure.

The reconstructed peak amplitudes strongly differed across the six simulation conditions. For the exact model, left column of Figure 9, the spatial distribution of the peak amplitudes were noise independent, only the overall scaling had to be increased with increasing noise level: (1×, 100×, 1000×) compared to (1, 100, 1000) × 10⁻¹⁵ V² . This is consistent with the theory predicting a peak amplitude of 1 + 1/u ², which solely depends on the local SNR and approximates to 1/u ² in the case of high SNR (low u ²). The high peak amplitudes found at the bottom of the brain correspond to the increased sensor coverage of our somewhat artificial full coverage sensor configuration.

For the reconstruction based on the simplified model, right column of Figure 9, the distribution of the peak amplitudes were not monotonically decreasing with increasing noise level, but largest peak amplitudes were found for the medium noise level (Fig. 9e). Again, this is consistent with the theory as shown in Figure 1a. Here the theoretical curve (blue) for v_peak = 0.033, the mean local modeling error found for the simulations based on the simplified volume conductor, is presented together with the mean peak amplitudes found for simulations with different noise levels in the range from 2 × 10⁻¹⁵ to 2 × 10⁻¹² V² (blue disks).

Also in contrast to the exact model, the peak amplitude topography varied strongly with the noise level. In Figure 9d the largest peak amplitudes were found at deeper brain structures, i.e., at positions with typically low SNR: E.g., for the source marked as #1 in Figure 9d the input SNR 1/u ² was found about four times smaller than the SNR value found for source #2, even so the peak amplitude for #1 was much larger than for source #2. In contrast, for the higher noise level in Figure 9e the order of the peak amplitudes for #1 and #2 is reversed. This is consistent with the theory as shown in Figure 1b. The figure shows four different pseudo‐Z curves connected with the four different values of u ² found for source #1 and #2 in 9(d) and (e). The blue curves belong to Figure 9d, the green curves to Figure 9e. For both colors the disc represents source #1, the asterisk source #2. As seen in the figure the sequence of the amplitude of the two sources depends on their position relative to the intersection v _inters of the associated curves. Only if the sources are located before the intersection the sequence of their amplitudes follows the sequence of the local SNRs 1/u ² connected to them. As shown in the theory section v _inters increases with increasing noise level σ². Therefore, with increasing noise level more and more sources are located before v _inters. This can be observed in Figure 9d–f, where the zone of higher amplitudes moves from the low SNR area in the middle of the brain to areas of higher SNR also found for the exact model (Fig. 9a–c). This also means: With increasing noise level the difference between the exact and the simplified model becomes smaller (see also Fig. 1a for the convergence of the pseudo‐Z curves with increasing u ²).

Figure 10 visualizes the peak widths for the same simulations as in Figure 9. As described in the Materials and Methods section the FWHM values of the peaks were defined as diameters of equivalent spheres (identical volumes). The spheres shown in the Figure 10b–f are these equivalent FWHM spheres positioned at the correct source locations.3

The theoretical curves connected to the results of Figure 10 are found in Figure 2. The main part of the figure, (a), corresponds to the values of u ² found for σ² = 2 × 10⁻¹² V² (u ² = 0.079–1.7), whereas the magnifications (b) and (c) correspond to the noise levels σ² = 2 × 10⁻¹⁵ V² (u ² = 0.000079–0.0017) and σ² = 2 × 10⁻¹³ V² (u ² = 0.0079–0.17), respectively. In blue, the theoretical curve for the exact model (v _peak = 0) is shown; the three remaining curves are calculated for the local modeling errors, v _peak, found for the three example sources marked as #2, #3, and #4 in the Figure 10d–f.

For σ² = 2 × 10⁻¹⁵ V², the theory predicts larger peak widths for the simplified than for the exact model (Fig. 2b). This is consistent with our simulation results: For the exact model (not shown in Fig. 10) we found the same peak width of 2.5 mm for each source, whereas for the simplified model FWHM values up to 15.3 mm were found (Fig. 10d). The lower resolution limit was 2.5 mm. Each SAM peak consists of at least one voxel and 2.5 is the equivalent FWHM value of a single voxel.

For the exact model and higher SNR, the theory predicts a linear increase of the peak width with increasing u ² (Fig. 2b,c). Figure 10a compares the theoretical relative FWHM curve FWHM_rel(u ²/u ${}_{\text{ref}}^{\text{2}}$) (see theory section), the green curve in the figure, with simulation results (mean relative peak width as function of mean noise parameters) found for different noise levels in the range σ² = 1 × 10⁻¹³ to 2 × 10⁻¹² V², the black circles in the figure. A linear approximation, FWHM_rel ≈ u ²/u ${}_{\text{ref}}^{\text{2}}$ is shown as blue line. Here, u ${}_{\text{ref}}^{\text{2}}$ is the mean value of u ² found for the simulation at σ² = 1 × 10⁻¹³ V². For lower noise levels a good accordance to the theory were found. For higher noise levels and, therefore, larger peak widths, our results showed larger deviations.

For the simplified model, the peak width topography was more complex: For low noise levels, according to Figure 2b, the peak width should nearly solely depend on the local modeling error v _peak. This is consistent with our simulation results (Fig. 10d): Although u ² for source #4 was about eight times larger than for #2 and #3 the found FWHM values reflect the v _peak differences: #2 < #3 ≈ #4. In addition, the simulation result for σ² = 2 × 10⁻¹⁴ V² (not shown in Fig. 10) was nearly identical to that presented in Figure 10d; this also demonstrates the independence of the FWHM values from the local SNR for low noise levels.

In contrast, the distribution of the FWHM values found for σ² = 2 × 10⁻¹³ V² (Fig. 10e) were significantly different. Although the peak widths for #2 and #3 had only moderately changed the peak width for #4 was now nearly three times larger compared to the result shown in Figure 10d. This is, at least qualitatively, predicted by the theoretical curves in Figure 2c: While #2 and #3 are still in the range dominated by v _peak, for #4 the local noise‐to‐signal ratio u ² becomes dominant. The spatial distribution of the peak widths at σ² = 2 × 10⁻¹³ V² is influenced by both the local modeling error v _peak as well as the local noise‐to‐signal ratio u ².

As predicted by Figure 2a, the distribution of the peak widths found at σ² = 2 × 10⁻¹² V² were dominated by the local noise‐to‐signal ratio: In Figure 10f, the peak widths found for #2 and #3 were similar whereas the FWHM value for #4 was about 3.5 times larger. In addition, the spatial topography of the peak widths was now similar to that found for the exact model which solely depends on the local SNR.

In contrast to the low noise case (Fig. 2b), for higher noise levels Figure 2a predicts higher peak width for the exact than for the simplified model. This prediction was fulfilled for 91% of the simulated sources (Fig. 10c,f).

DISCUSSION AND CONCLUSIONS

To our knowledge, this is the first systematic study on the influence of improper volume conductor modeling to the source reconstruction performance of a beamformer. All implementations were performed in the freely available open source toolbox SimBio [ 2009] and can thus be used by others.

In a first study, we focused our interest on the localization performance of the EEG SAM beamformer when using a geometrically simplified head model. The reference data were generated in the isotropic three‐layer FE head model and inverse SAM beamforming was carried out in the corresponding three‐layer sphere head model. For a realistic EEG sensor configuration, localization errors of up to 37 mm, mainly in frontal, frontotemporal, and occipital areas were found. SAM localization errors were shown to be a function of the deviation from spherical shape and especially from realistic skull thickness. Our results for the SAM beamformer using FE‐computed reference leadfields correspond well to former studies, where the importance of modeling the realistic head compartment geometry was pointed out in boundary element method (BEM)‐based MEG forward problem examinations [Hämäläinen and Sarvas, 1987] and in BEM‐based EEG dipole fit inverse approaches [Cuffin, 1996; Huiskamp et al., 1999; Roth et al., 1993].

In a second study, the influence of skull conductivity anisotropy on SAM localization performance was studied. Although for the generation of the reference data, the FE model with an anisotropic skull conductivity was used; the SAM reconstruction was based on the FE model with the corresponding isotropic skull compartment. For the transmission between isotropic and anisotropic tensors two different approaches were used: A volume constraint [Wolters et al., 2006] approach effectively leading to a reduction in radial conductivity and an approach proposed by Marin et al. [ 1998], which keeps the radial conductivity value identical to the isotropic one.

For a volume constraint anisotropy ratio of 1:10, SAM localization errors of up to 20 mm were found, increasing with decreasing source depths and with decreasing distance to areas with larger skull thickness. Sources were consistently localized too deep, i.e., the visualized deviation cones all pointed in quasi‐radial direction away from the inner skull surface. When keeping the radial conductivity constant and increasing the tangential conductivity by a factor of 10 [Marin et al., 1998], besides larger errors of up to 22 mm in the area of the cerebellum with poor sensor coverage, SAM localization errors were only between 3 and 9 mm in temporal, frontal, and occipital areas, again consistent with the map of local skull thicknesses. In the area of the central sulcus, localization errors were even below 3 mm, a result, which is in agreement with the global sensitivity analysis of Vallaghe and Clerc [ 2009], who showed that for a single fixed dipole at the posterior wall of the central sulcus the effect of skull conductivity mainly comes from its radial component. Because the skull anisotropy ratio might rather be 1:3 instead of 1:10 as claimed by Fuchs et al. [ 2007], we also run examinations with a 1:3 anisotropy ratio and found errors of mainly between 1 and 5 mm (some outliers of up to 10 mm mainly in areas with poorer sensor coverage). This result, however, has to be interpreted with caution, in scenarios with multiple sources, errors might be much larger.

By using the exact volume conductor model, at any noise level the sources could perfectly be reconstructed. If the reconstruction was based on an inaccurate volume conductor model the beamformer found the location connected with the smallest deviation v to the true leadfield of the source. As shown in Appendix C, this is equivalent to an ideal dipole fit solution for noiseless single source data. In the scope of our simulations the beamformer therefore directly reflects the errors in the forward model and our localization results can be generalized to other inverse methods. In contrast to a single source dipole fit, a beamformer reconstruction is more challenging as the number of sources is not known in advance. In fact, for each scan location r connected with a leadfield different from that of the true source, the beamformer effectively faces a two sources problem: The constraint in Eq. (4) forces the beamformer to expect a source at r (independent of the data) and the true source is a disturbance source which has to suppressed. Because of the noise, this suppression only partly succeeded for scan locations with leadfields similar to that of the true source resulting in a peak width increasing with increasing noise level. We used spatial white noise in this study. This leads to a homogeneous projection of the noise to the source space and explains why the peak locations stayed stable even for high noise levels and small peak amplitudes. For more complicated noise structures, e.g., brain noise, the localization errors will increase especially for small peak amplitudes.

For a SAM reconstruction based on an exact volume conductor model (v _peak ≡ 0), the peak amplitude of the pseudo‐Z value Z ²(0;u ²) = 1 + 1/u ² decreases monotonically with decreasing SNR. As the pseudo‐Z value is designed as an SNR value at source level this is not surprising but must be taken into account if peak values from different brain regions should be compared: Although the strength of all simulated sources were identical the peak amplitudes strongly varied across the brain with a complicated inhomogeneous distribution depending on volume conductor and sensor coverage. For the exact volume conductor model we found the topography of the peak amplitudes stable for a wide range of noise levels (for high SNR, the noise level simply acts as a global scaling factor).

In the case of significant volume conductor modeling error however, the distribution of the peak amplitude is much more complicated and unpredictable. In contrast to the exact model, for high SNR the peak amplitude first increases with increasing noise level up to a maximum found for an SNR depending on the modeling error: u ² = v _peak. Although counterintuitive this may be useful as the peak amplitude for high SNR and significant modeling error is relatively close to the level of the background noise; unimportant in our simulations but meaningful if the level of background noise increases due to brain noise and non‐ideal sensor noise. Unfortunately, the topography of the peak amplitude is not stable across noise levels. In fact, the relation of SNR and peak amplitude may even be reversed: For low noise we found the highest peaks in a region with low local SNR. A comparison of the pseudo‐Z peaks from different brain regions based on the expected ratio of the leadfield strengths will fail in such cases. On the other hand, for noise levels much higher than the modeling error (related by u ² = v _peak) the topography of the peak amplitude converges to the topography found for the exact model (at the same noise level). A realistic volume conductor model is, therefore, particularly important if the noise level is low. Thus, in contrast to traditional inverse modeling approaches, the success of any efforts for optimizing beamformer resolution by SNR increase (optimization of paradigm, stimulation, data acquisition, measuring more subjects, etc.) depend on an adequate goodness of volume conductor modeling. On the other hand, for less exact volume conductor models the noise level can be increased by regularization (see e.g., Brookes et al. [ 2008] and Robinson and Vrba [ 1999]), a technique already introduced in Robinson and Vrba [ 1999] but up to now rarely used for the analysis of real data. In any case if a peak increases with increasing regularization value, the noise level will typically be too low.

In comparison to peak amplitudes, the analysis of the peak width is more complicated as for this case also the local decay of the leadfield deviation Δv = v(Δr) with increasing distance Δr from the peak maximum r _peak has to be considered. Nevertheless, for the exact model the predicted relative peak widths FWHM(0; u ²)/FWHM(0; u ${}_{\text{ref}}^{\text{2}}$), which do not explicitly consider the local course of Δv(Δr), explained our simulation results surprisingly well. This supports the approximation Δv(Δr) ≈ Δr/a(r _peak) supposed by Gross et al. [ 2003].

Consistent with other authors (e.g., Vrba and Robinson [ 2000] for pseudo‐Z and Barnes and Hillebrand [ 2003]; Barnes et al. [ 2004]; Gross et al. [ 2003]; Hillebrand and Barnes [ 2003] for source power), we found an increasing peak width with decreasing SNR. For the exact model, the topography of the FWHM distribution was relatively stable across different noise levels and for higher SNR again the noise level simply acts as a scaling factor:

In the case of significant modeling error, the dependency of the peak width from the noise level is more complex. For high SNR, the peak widths were dominated by the local modeling error v _peak, increasing peak width with increasing v _peak; whereas, for low SNR, the distribution of the FWHM values was dominated by the local SNR: increasing peak width with increasing u ². For intermediate SNR the peak widths were significantly influenced by both the local volume conductor modeling error as well as the local SNR. In analogy to the peak amplitude, with increasing noise level the distribution of the peak width converges to the result found for the exact model.

In this study, we focused on EEG, but our results are mostly transferable to MEG beamformers. The beamformer theory is mainly identical for EEG and MEG beamformers, but as it is well known that EEG source analysis is more sensitive to errors in the modeling of the head conductivity profile than MEG, we expect smaller localization errors in the case of MEG beamformers. On the other hand, whole‐head MEG scanners typically have a significant larger number of sensors, N, as EEG sensor caps. For a given SNR at sensor level ξ², the input SNR 1/u ², relevant for the beamformer performance, scales with the number of sensors: 1/u ² = Nξ². The described instabilities for inexact volume conductor models and high input SNR are therefore especially relevant for MEG beamformers. Thus, EEG as well as MEG beamformers significantly profit from realistic volume conductor models. As shown here, the FEM is very flexible in constructing such high realistic volume conductor models. Furthermore, the calculation of the forward solution for a beamformer scanning grid with 2 × 2 × 2 mm³ resolution covering the whole head (368,015 nodes) took less than half an hour, unproblematic for most applications.

The presented study is based on the simulation of single sources and spatial white noise. Hence, the influence of volume conductor deficiencies to the beamformer performance could widely be abstracted from factors known to degrade the performance even in the case of perfect volume conductors (up to now typically discussed in spherical head models): more than one source in close proximity, the effect of small integration windows, brain noise, etc.. Further investigations are needed to study the detailed interaction between these performance relevant factors and the quality of the volume conductor beyond the global effects shown in this study. Especially the detailed investigation of the influence of brain noise may be important as its inherent non‐white structure will influence beamformers in a more complicated way as spatial white noise. In addition, the actual noise structure is strongly influenced by the volume conductor.

In summary, our study gave insight into the dependence of the beamformer peak localization, peak amplitude, and peak width on leadfield accuracy, source position, sensor noise and sensor coverage. It can be concluded that realistic head modeling of both tissue geometry and conductivity significantly improve the performance of beamformer approaches and its importance increases with increasing signal to noise levels (SNR). The success of efforts for optimizing beamformer resolution by SNR increase significantly depend on the accuracy of volume conductor modeling.

APPENDIX A.

By combining Eqs. (3), (5), (6), and (7), the pseudo‐Z value at a position with leadfield l can be expressed as [Sekihara et al., 2004]

The data covariance matrix C can be separated into source covariance matrix C _src and noise covariance matrix σ² I:

As C _src is symmetric, a rotation of the coordinate system U (special orthogonal matrix, UU ^t = U ^t U = I, det U = 1) exists for that C _src becomes diagonal:

For C this leads to

In the coordinate system defined by U the data covariance matrix is diagonal and can easily be inverted. In the case of a single source, i.e., C _src = ρ${}_{\text{0}}^{\text{2}}$ h ₀ h ${}_{\text{0}}^{\text{t}}$, D _src can be expressed as

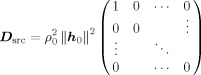and therefore,

with 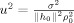. As the pseudo‐Z value is independent of the coordinate system, Z ² can be calculated in the rotated system by substituting C ⁻ⁿ with D ⁻ⁿ and l with its rotated counterpart 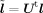. With these substitutions Z ² can be simplified to Eq. (9). Note that the angle between the leadfield vectors is invariant with respect to the coordinate transformation U: .

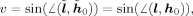
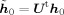APPENDIX B.

A pseudo‐Z scan peaks for that position with leadfield l _peak for which the deviation to the source leadfield h ₀, v _peak = sin(∡(l _peak,h ₀)), is minimal. With increasing distance to the optimal position v _peak, v increases and Z ² decreases. We define the peak radius Δv _peak as the difference between v _peak, and the leadfield deviation for which Z² − 1 (note that Z² ≥ 1 for all v) has fallen to the half of its maximum:

For u ² > 0 the above equation can be solved by means of

The FWHM value in Eq. (10) is defined as 2Δv _peak.

APPENDIX C.

A dipole fit typically minimizes the sum of squared differences between measured data X ₀ = h ₀ s(t ₀) (h ₀ leadfield and s wave form of the source) and fitted data 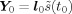(l ₀ leadfield and wave form of the reconstruction):

For any Y ₀ the above minimization requires (with 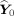unit vector along Y ₀). Searching for 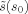and l ₀ can therefore be performed separately:

The above maximization is equivalent with minimizing . The beamformer maximizes Z ²(v,u ²), but this is equivalent with minimizing v because Z ² is strictly monotonically decreasing (and u ² does not depend on l).