Decrease in early right alpha band phase synchronization and late gamma band oscillations in processing syntax in music

Abstract

The present study investigated the neural correlates associated with the processing of music‐syntactical irregularities as compared with regular syntactic structures in music. Previous studies reported an early (∼200 ms) right anterior negative component (ERAN) by traditional event‐related‐potential analysis during music‐syntactical irregularities, yet little is known about the underlying oscillatory and synchronization properties of brain responses which are supposed to play a crucial role in general cognition including music perception. First we showed that the ERAN was primarily represented by low frequency (<8 Hz) brain oscillations. Further, we found that music‐syntactical irregularities as compared with music‐syntactical regularities, were associated with (i) an early decrease in the alpha band (9–10 Hz) phase synchronization between right fronto‐central and left temporal brain regions, and (ii) a late (∼500 ms) decrease in gamma band (38–50 Hz) oscillations over fronto‐central brain regions. These results indicate a weaker degree of long‐range integration when the musical expectancy is violated. In summary, our results reveal neural mechanisms of music‐syntactic processing that operate at different levels of cortical integration, ranging from early decrease in long‐range alpha phase synchronization to late local gamma oscillations. Hum Brain Mapp 2009. © 2008 Wiley‐Liss, Inc.

INTRODUCTION

Music processing is a complex set of perceptive and cognitive operations, which in turn are temporally integrated and linked to previous experiences recruiting extensive memory systems by which emotions emerge. Consequently, the investigation of the neurocognition of music has been increasingly important for the understanding of human cognition and its underlying brain mechanisms [Koelsch and Siebel,2005]. The present study focused on syntactic processing in music perception. Music involves perceptually discrete elements (e.g. tones, intervals, and chords) organized into sequences which are hierarchically structured according to syntactic regularities [Patel,2003; Tillmann et al.,2000]. In the context of major‐minor tonal music, regularities consist of the arrangement of chord functions within harmonic progressions [Krumhansl and Toiviainen,2001; Schönberg,1969]. The computation of structural relations between these elements, for instance between a chord function and a preceding harmonic context, is part of the analysis of musical structure. The integration of both regular and irregular events into a larger meaningful musical context is required for the emergence of meaning based on the processing of musical structure [Krumhansl,1997; Meyer,1956].

A multitude of studies have focused on syntax violations in the language domain [Eckstein and Friederici,2006; Friederici et al.,1996; Friederici,2001,2002; Gunter et al.,1999; Hahne and Friederici,1999; Palolahti et al.,2005], reporting a robust event‐related‐potential (ERP) component, the early (100–350 ms) left anterior negativity (ELAN), which is taken to reflect initial syntactic structure building. These studies have shown that the neural generators of the ELAN lie in the left inferior frontal cortex (inferior BA 44), an area which is also involved in the processing of syntactic information in music [Maess et al.,2001]. A study of speech perception reported an early negativity, which was elicited bilaterally in response to combined prosodic‐syntactic violations [Eckstein and Friederici,2006]. This result indicated that additional right hemispheric resources were recruited for the initial structure building processes [Eckstein and Friederici,2006]. On the other hand, syntax violations in mathematical expressions (e.g. equations) were recently investigated in an ERP paradigm [Martin‐Loeches et al.,2006], which reported parieto‐occipital negativities instead of frontal negativities, leading to a conclusion of less overlap between the syntactic processing of language and mathematics than previously thought [Dehaene and Cohen,1995].

Most of the electrophysiological studies on musical syntax also adopted the classical ERP paradigm [Koelsch et al.,2000; Koelsch et al.,2002a,b; Patel et al.,1998]. Using chord sequences with final chords that were either harmonic syntactically regular or irregular, it has been shown that music‐syntactical violations elicit an early right anterior negative (ERAN) component; this component is maximal at 200 ms after the onset of irregular chords and is strongest over right frontal electrode regions [Koelsch et al.,2000; Koelsch et al.,2002b]. The ERAN can be elicited in absence of directed attention [Koelsch et al.,2002a] in both musicians and nonmusicians [Koelsch et al.,2000; Loui et al.,2005], indicating an inherent human ability to acquire knowledge about musical syntax through everyday listening experiences [Tillmann et al.,2000]. Using magnetoencephalogram, it was found that the mERAN (magnetic‐ERAN) was generated predominantly in the inferior fronto‐lateral cortex [Maess et al.,2001]. However, using fMRI, it was found that posterior temporal regions (Heschl's gyrus, superior temporal sulcus, planum temporale), in addition to the frontal areas, were also activated during music‐syntactic processing [Koelsch et al.,2002c].

Although these studies offer invaluable information about the neural correlates of music‐syntactic irregularities, they suffer from two primary limitations. First, electrophysiological studies relied heavily on the averaging techniques which do not adequately represent aspects of brain activity that we expect to be relevant for music cognition, such as the information about the underlying oscillatory dynamics. These dynamics are increasingly believed to provide insights into neuronal substrates of perceptual and cognitive processes [Basar et al.,2001; Kahana,2006; Rizzuto et al.,2003; Singer,1999; Tallon‐Baudry and Bertrand,1999; Ward,2003]. Second, neuroimaging studies suggest that irregularities in musical syntax are processed by multiple brain areas, yet it is not clear whether these regions operate in isolation or interact with each other. This latter information is supposed to be crucial since there is extensive evidence that any cognitive task demands not only simultaneous co‐activation of various brain regions but also functional interaction between these regions [Bressler and Kelso,2001; Bressler,1995; Brovelli et al.,2004; Engel and Singer,2001; Engel et al.,2001; Friston,2001]. This dynamic interaction is considered to be best characterized by transient phase relationships between the oscillatory activities of underlying neuronal populations, termed as phase synchronization, at the frequency of interest [Lachaux et al.,1999; Tass et al.,1998; Varela et al.,2001].

Therefore, in this study we aimed to address these limitations by investigating the oscillation and synchronization content of the electrical brain responses recorded from human subjects during listening to chord sequences ending in regular or irregular chords.

MATERIALS AND METHODS

Stimuli

The stimuli of our experiment consisted of two chord sequences, both with five chords and a pause (half‐note). Chord sequences were composed according to the classical rules of harmony (voice leading was performed in a counterpoint‐like fashion, without parallel fifths or octaves). The presentation time for each of the first four chords was 600 ms, and for the final chord was 1200 ms. The first four chords were identical for both types of sequences: tonic, subdominant, supertonic, dominant. The final of the fifth chords was either a tonic (regular) or a supertonic (irregular) chord. In major‐minor tonal music, one particular example of a music‐syntactic regularity is the end of a harmonic progression, which is usually characterized by a dominant‐tonic progression. Thus, the final supertonic chord in our experiment represents a music‐structural irregularity. Note that, psychoacoustically, supertonics do not represent physical oddballs, at least not with respect to pitch commonality or roughness. Moreover, the pitches of the supertonics correlated higher with the pitches in the preceding harmonic context than those of the tonic chords (calculated according to the echoic memory based model [Martens et al.,2005]; see also Koelsch et al. [2007] for detailed correlations of local context (pitch image of the current chord) with global context (echoic memory representation as established by previously heard chords).

We presented 1,350 sequences, half of them ending on a tonic, and the other half ending on a supertonic (see Fig. 1). That is, each sequence type (A/B) was assigned equal probability. Both sequences were presented in each of the twelve major keys and randomly in a tonal key different from the key of the preceding sequence (see Fig. 1C). Additionally, they were randomly intermixed. All chords had the same decay of loudness and were played with a piano‐sound (General Midi sound No. 2) under computerized control on a synthesizer (ROLAND JV 8010; Roland Corporation, Hamamatsu, Japan). See Koelsch and Jentschke, [2008] for more details.

Figure 1.

Examples of musical stimuli. Top row: chord sequences (in D‐major), ending either on a tonic chord (regular, A), or on a supertonic (irregular, B). (C) In the experiment, sequences from all twelve major keys were presented in pseudo‐random order. Each sequence was presented in a tonal key that differed from the key of the preceding sequence; regular and irregular sequence endings occurred equiprobably (P = 0.5).

Another 120 chord sequences (half of them ending on a tonic, and half of them ending on a supertonic) were played with an instrumental timbre other than piano (e.g., trumpet, organ, and violin). Participants were informed a priori about these chords played by a deviant instrument and that their task was to detect them, but these deviant chords were not analyzed. This task was used to focus the participants on the timbre, in order to avoid directed attention to the musical syntax. Participants were not explicitly informed of the occurrence of music‐syntactic irregularities.

Participants

Twenty right‐handed participants (11 females, age range 20–30 years, mean 24.5 years) participated in this study. Eleven of them were nonmusicians, who had never attended a music lesson, and nine of them were amateur musicians, who had learned to play an instrument or sung in a choir for 2–10 years (mean 5.4 years). All participants reported normal hearing. Each experimental session lasted approximately 2 hours. During the session the participants were watching a silent movie with subtitles and performing the timbre change detection task at the same time. The inclusion of a subtitled movie served two purposes: (i) it made the daunting task of listening for 120 min to detect the deviant stimuli feasible, and (ii) it reduced the amount of directed attention to the music syntactically regular or irregular chords, thereby reducing the effect of attentional modulation of the brain responses associated with processing the syntax in music.

EEG Recording and Pre‐Processing

Multivariate EEG signals were recorded from 40 electrodes placed over the scalp according to the extended 10–20 system referenced to the left mastoid. Additionally, electrooculogram was recorded to monitor blinks and eye movements. We used the EEGLAB Matlab Toolbox [Delorme and Makeig,2004] for visualization and filtering purposes. After rejecting segments of data with artefacts like blinks, eye movements and muscle artefacts as determined by visual inspection, we applied a high‐pass filter at 0.5 Hz to remove linear trends and a notch filter at 50 Hz (49–51 Hz) to eliminate power‐line noise. The filtering option in EEGLAB used the MatLab routine filter (zero‐phase forward and reverse digital filtering). The sampling rate was 250 Hz. The data epochs representing single experimental trials time locked to the onset of the last chord were extracted from −500 ms to 1,000 ms, resulting in approximately n = 600 epochs per condition and participant.

Data Analysis

We performed the following three types of analysis: (i) standard averaging technique to analyze ERP components, wavelet based time‐frequency representations (TFR) to analyze (ii) the spectral power of the oscillatory contents and (iii) the spatiotemporal dynamics of the phase synchronization. This last analysis was done by means of bivariate synchronization and synchronization cluster analysis (SCA).

Neural phase synchrony refers to the phenomenon in which neurons coding for a common representation synchronize their oscillatory firing activity within a restricted frequency band [Trujillo et al.,2005; Varela et al.,2001]. The analysis of the spectral power of the oscillatory activity focuses on the local synchrony of neuronal populations (synchrony within neighboring cortical areas), whereas the phase synchronization analysis refers to the phase coupling between neuronal assemblies, which lie either within the same hemisphere or at different hemispheres. This large‐scale integration is believed to be required for the manifestation of a complete cognitive structure [Varela et al.,2001]. Thus, the two approaches provide complementary information about the underlying neuronal processing [Le Van Quyen and Bragin,2007].

Time‐frequency analysis

We studied the oscillatory brain responses by means of wavelet based TFR analysis [Tallon‐Baudry et al.,1997]. We chose a complex Morlet wavelet with a Gaussian shape both in time and in frequency [Mallat,1999]:

(1)

The convolution of translated (t′) and rescaled (s) versions of this wavelet with a signal x(t) gives the wavelet transform for each scale and time instant,

(2)

with

(3)

In the time domain, the wavelet spreads around t = t′ with a standard deviation σ_t = s/2, and in the frequency domain its centre frequency is f = η/2πs with a standard deviation σ_f = 1/2πs [Allefeld,2004]. The value η defines the constant relation between the centre frequency and the bandwidth η = f/σ_f, and therefore is characteristic of the wavelet family in use; η determines the temporal resolution (σ_t = η/4πf) and frequency‐resolution (σ_f = f/η) which is always within the limit imposed by the uncertainty principle σ_fσ_t = 1/4π [Mallat,1999]. For the analysis of the fast cognitive processes, the temporal‐resolution is critical to detect possible functional states occurring close in time [Schack et al.,1999; Trujillo et al.,2005]. We chose η = 7 (η > 5 is needed for the convergence of the convolution integral in numerical calculations [Grossman et al.,1989]), which provides a good compromise between high frequency resolution at low frequencies and high time resolution at high frequencies (for example, σ_t = 55 ms and σ_f = 1.4 Hz at 10 Hz; σ_t = 11 ms and σ_f = 7 Hz at 50 Hz). The frequency domain was sampled from 2 to 60 Hz with a 1 Hz interval between frequencies.

To study changes in the spectral content of the oscillatory activity, we used the wavelet energy, which was computed as the squared norm of the complex wavelet transform:

(4)

We distinguished between two types of oscillatory brain responses: (i) evoked response or response phased‐locked to the stimulus onset, and (ii) induced response or response not phased‐locked to the stimulus onset [Galambos,1992]. The former response was estimated by applying the wavelet transform to the averaged ERP profile, thus keeping the phase‐locked information across epochs. The joint response (evoked + induced) was obtained by applying the wavelet transform to each trial followed by averaging. Thus, the induced activity was computed by subtracting the evoked response from the joint response. Although this technique is valid to distinguish evoked from induced responses, in the case of extensive latence variability in the onset of the ERP, the phase‐locked activity could be underestimated. A more detailed study of the evoked and induced responses in our paradigm should take that into account.

For both types of responses, the mean TFR energy μ_base(f) of the pre‐stimulus period (between −300 and −100 ms) was subtracted. The wavelet energy was further normalized by the standard deviation σ_base(f) of the baseline period as follows:

(5)

Our investigation of the TFR energy emphasized high frequency oscillations (>30 Hz) due to the relevance of the fast gamma oscillations for both the binding of temporal (and spatial) information necessary to build a coherent perception [Tallon‐Baudry et al.,1997] and the integration of bottom‐up and top‐down processes [Engel and Singer,2001; Herrmann et al.,2004a; Pulvermuller et al.,1997; Varela et al.,2001].

A post‐hoc analysis of the TFR energy in the delta and theta band was performed due to the fact that the dominant frequencies of the EEG signal which contributed to the generation of the ERAN component were below 8 Hz. Here the non‐normalized form of the wavelet energy Eq. (4) was used to compare explicitly for each condition the poststimulus with the prestimulus TFR, because of the possible influence of the prestimulus brain state on the event‐related brain responses [Doppelmayr et al.,1998].

Phase synchrony analysis

The wavelet transform Eq. (2) can be expressed explicitly in terms of frequency and time by using the relationship between the frequency f and the scale s = η/2πf, and from this complex‐valued signal the corresponding frequency‐specific instantaneous phase can be calculated as follows:

(6)

For each trial we computed the complex phases ϕ_ik(t,f) of the channel i at an epoch k and used them for the subsequent synchronization analysis. It has been widely reported in the literature [Hurtado et al.,2004; Lachaux et al.,1999; Pereda et al.,2005; Rodriguez et al.,1999; Tass et al.,1998] that the assessment of phase synchronization between neurophysiological signals is better understood in a statistical sense. One of the approaches taking this into account is use of the concept of directional statistics [Mardia,1972] in bivariate phase synchronization.

The strength of the phase synchronization between two electrodes i and j, at time t and with centre frequency f, is:

(7)

where n is the number of epochs. This index is nearly 0 when there is no phase relationship between the considered electrode pair across the epochs, and approaches 1 for strong phase synchronization. In the context of directional statistics, this reflects whether the distribution of the relative phase between two electrodes is spread or concentrated on the unit circle, respectively.

In the case of large number of recording electrodes a measure of global synchronization strength can be computed, from the pair‐wise synchronization matrix, 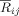, for each time point t and centre frequency f:

(8)

But this measure conceals the spatial distribution of the synchronization, an issue of fundamental importance in cognitive neuroimaging where one has to look for possible short‐ or long‐range phase synchronization between different cortical areas. Recently a new method was proposed that can provide information about both the global synchronization strength and the topographical details of the synchronization in event‐related brain‐responses: the SCA [Allefeld and Kurths,2004], which has been applied to visual attention and language processing experiments [Allefeld,2004; Allefeld et al.,2005].

The underlying idea is to model the array of electrodes as individual oscillators that take part in different strength c _i in a single synchronized cluster C. This individual cluster characterizes, in each epoch k, the dynamics of the array as a whole through the cluster phase Φ_k, which is the result of a circular weighted mean of the oscillator phases,

(9)

where the participation indices c _i are calculated as a (monotonously increasing) function 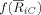of the phase locking between each individual oscillator and the cluster,

(10)

The basic premises that are relevant to this approach are that the dynamics of the phase differences can be decoupled by introducing a mean field, i.e. that the assumption of a single synchronized cluster holds, and that its stochastic part is independent for each of them. Taking this into account, the population values ρ_ij of the empirical estimate of bivariate synchronization 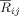can be factorized as ρ_iC ρ_jC and a self‐consistent solution of this set of equations can be found. The SCA algorithm provides a maximum likelihood estimation of the ρ_iC, representing the phase synchronization index between the oscillator i and the cluster, .

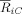By computing the index 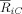, we could detect subpopulations of electrodes that adjust differently to the global rhythm and obtain a topographical picture of the synchronization and its temporal dynamics. As a measure of the global synchronization strength we used the cluster mean,

(11)

It is important to mention that the SCA assumes phase differences distributed around zero, whereas the bivariate synchronization analysis can detect a more general case of phase differences bounded by a constant value different from zero. Consequently, the index 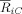would not detect a delay in the phase synchronization between electrodes and cluster. However, a combined use of the SCA and the bivariate synchronization analysis could clarify this issue. If both approaches deliver converging results, we could assume that the distribution of phase differences is around zero, but if the data of the bivariate synchronization analysis show different results, they could be due to a constant (non‐zero) phase different between electrodes.

With the SCA we explored low (< 15 Hz) and high (15–50 Hz) frequency bands, but the SCA delivered weak effects in the beta (15–30 Hz) and gamma (30–50 Hz) bands which, consequently, were left out from this study.

In a number of studies synchronization in EEG signals has been investigated using classical magnitude‐squared coherence function [Schack et al.,1999; Srinivasan et al.,1998; von Stein and Sarnthein,2000; von Stein et al.,2000], which is equivalent to a correlation coefficient in the frequency domain, as a linear measure of bivariate synchronization. Magnitude‐squared‐coherence mixes both phase and amplitude correlation [Womelsdorf et al.,2007], and there exists no clear‐cut way to extract the phase synchronization information from the coherence function [Lachaux et al.,1999]. Further, Tass et al. [1998] pointed out that synchronization of two oscillators is not equivalent to the linear correlation of two signals that is measured by coherence. For instance, if the oscillators are chaotic and their amplitudes are varying without any temporal correlation yet their phases are coupled, coherence would be very low and it would not be possible to detect synchronization of their phases. Since phase synchronization requires an adjustment of phases but not of amplitudes, it is a more general approach to address the study of synchronization between EEG signals.

Reference Analysis

The use of a common reference for coherence and phase synchronization analysis has been criticized in recent years based on the argument that the common reference introduces spurious correlations uniformly distributed over the scalp [Fein et al.,1988; Guevara et al.,2005; Nunez et al.,1997; Schiff,2005]. Instead, the use of surface Laplacians has been encouraged because they are essentially reference‐free and additionally reduce the volume conduction effect [Nunez,1995; Pernier et al.,1988; Perrin et al.,1987,1989; Schiff,2005]. Nevertheless, Nunez et al. [1997,1999] demonstrated that although surface Laplacian methods remove most of the distortions caused by the common reference electrode and volume conduction, common reference methods, like average reference and digitally linked mastoids, produce reasonably reliable results for long‐range coherence. Moreover, the surface Laplacian acts as a spatial band‐pass filter of scalp potential, thus emphasizing the locally synchronized sources and deemphasizing the long‐range synchronized sources. Furthermore, it is less accurate near the edges of the electrode array due to a lack of neighboring electrodes [Nunez et al.,1997; Srinivasan et al.,1998]. However, it provides a more precise representation of the underlying source synchronization, as it is a rather good estimate of the local dura potential. Therefore, this reference scheme is preferred when studying the topography of the synchronization. In any study of (phase) synchronization, all of these issues should be taken into consideration in order to avoid the systematic rejection of any particular scheme of reference: both common reference and surface Laplacian supply useful information, but that has to be interpreted within the limitations of each approach. An interesting new approach to the problem of volume conduction and active reference is the use of the phase lag index, a novel measure of phase synchronization, which has been recently shown to be less affected by the influences of common sources and active reference electrodes [Stam et al.,2007].

In this study, we used both average reference (as common reference) and Laplacian methods. Both recommend high density EEG (≥48 electrodes) to perform optimally. We had 40 EEG electrodes, montage which is not ideal but still useful. We chose the spherical spline Laplacian [Perrin et al.,1989], assigning idealized positions on the unit sphere to the electrodes. We selected spline of order m = 4 after Perrin et al. [1989].

Statistics

Statistical analysis for the ERP components and the TFR based oscillation and phase synchronization indices was performed with the use of a non‐parametric pair‐wise permutation test [Good,1994]. It was necessary to use a non‐parametric test because the distributions cannot be assumed to be Gaussian. Also, the permutation test provides exact significance levels even for small sample sizes and small differences between conditions. For all indices, with the exception of the delta and the theta band TFR energy, the test statistic was the difference between the two sample means: irregular (supertonic) chords minus regular (tonic) chords. In the case of the delta and theta spectral power we first analyzed each condition separately. This analysis was done by comparing statistically the maximum peak of the non‐normalized TFR energy Eq. (4) within a time window from 0 to 300 ms poststimulus with the mean value of the TFR energy averaged between 300 and 100 ms prior to the stimulus onset. Next we compared the difference between conditions, using as test statistic the difference between the two sample means (normalized expression, Eq. (5)).

Additionally, we tested whether the induced gamma spectral power for each separated condition was significantly different of the pre‐stimulus levels. In this case, the test statistic was the difference between the sample mean after stimulation and the mean pre‐stimulus value.

In all cases, the permutation tests were computed by taking the first and second half of 5,000 random permutations of the joint sample and calculating replications of the test statistics. The p‐values were then obtained as the frequencies that the replications had larger absolute values than the experimental difference. When multiple permutation tests are performed, the Bonferroni correction of the p‐values gives usually exceedingly conservative results when applied to EEG signals, due to the violation of the assumption of independent tests. Consequently, we complemented the permutation test with a step‐down approach [Good,2005; Troendle,1995]. This step‐down method explicitly takes into account the correlations between the tests and, as a consequence, the final p‐values do not need to be corrected further. Therefore, when several tests were computed via this stepwise algorithm the threshold values used were the standard 0.05 and 0.01 significance levels.

To study the spatiotemporal progression of ERP components, electrodes were grouped into six regions of interest (ROIs): LA (left anterior: FP1, F9, AF7, F7, F3), LC (left central: FT7, FC3, T7, C3, TP7, CP5, CP3), LP (Left posterior: P7, P3, P9, PO7, O1), RA (right anterior: FP2, AF8, F10, F4, F8), RC (right central: FC4, FT8, C4, T8, CP4, CP6, TP8), RP (right posterior: P4, P8, PO8, P10, O2). These same six ROIs were used in the analysis of the spectral power distributions of evoked and total theta oscillatory activities.

To search for significant differences between conditions, and between each condition separately and the pre‐stimulus level, in terms of the gamma band spectral power, we evaluated a permutation test for each of the 20 frequencies in the range of 30–50 Hz. To study the topographical differences in the phase synchronization indices obtained after computing the surface Laplacian, electrodes were grouped into eight ROIs. Some of the groups of electrodes were the same as those used in the ERP analysis (LA, LP, RA, RP), but the electrodes of central regions were separated into central ROIs and temporal ROIs: RC (Right central: FC4, C4, CP4, CP6), RT (Right temporal: FT8, T8, TP8), LC (left central: FC3, C3, CP5, CP3) and LT (Left temporal: FT7, T7, TP7).

RESULTS

ERP Analysis

ERPs were derived by averaging the raw trials for each subject and condition after re‐referencing to the mean potential of the mastoids and performing a baseline correction between 500 and 0 ms prior to the onset of the final chord. The grand‐averaged ERP waveforms for the regular tonic and irregular supertonic chords show that the irregular chords elicited a clear ERAN compared with the regular chords (see Fig. 2). The ERAN component peaked around 200 ms and was widely distributed over the scalp with slightly higher amplitudes at right anterior electrodes than at their left counterparts. Figure 3A depicts the 6 ROIs, whereas in Figure 3B the statistically significant (P < 0.01) differences between the two chord types for the 6 ROIs are plotted. This representation offers a picture of the spatiotemporal progression of the ERAN, indicating clusters of scalp areas showing significant differences in the waveforms. The earliest effect was found at right anterior electrode regions, mainly at the right fronto‐central region with a temporal spread of 160–220 ms. This effect then manifested in central and posterior electrode regions bilaterally.

Figure 2.

ERP analysis. Grand average of the ERPs obtained for the following: processing of regular chords (represented by black lines), processing of irregular chords (blue), and the difference profiles (blue‐black, red). The response to the irregular chords is less positive than the response to the regular chords, leading to a negative component known as the ERAN.

Figure 3.

(A) Head positions of the electrodes and 6 ROIs used for the ERP and spectral power analysis. (B) Latency periods of statistically significant (P < 0.01) differences between the grand averages of the ERPs of the irregular and the regular conditions, calculated with respect to a pair‐wise non‐parametric permutation test (over subjects). The p‐values are presented for different areas of electrodes: LA (left anterior), LC (left central), LP (left posterior), RA (right anterior), RC (right central) and RP (right posterior). The most pronounced significance values were obtained in RA and RC electrodes, followed by the RP electrodes.

Since the ERAN component almost disappeared when the ERPs were recomputed after filtering the raw signal with 8 Hz low‐pass (figure not shown), we concluded that this component was mainly constituted of brain oscillations with frequencies lower than 8 Hz.

Spectral Power Analysis

Theta band responses

Since the ERAN disappeared with 8 Hz low‐pass filtering, we further tested whether this ERP component was manifested as a decrease in the evoked or total (evoked + induced) slow oscillations. Around the latency of the ERAN, we investigated whether the changes in the evoked and total spectral power distributions relative to prestimulus levels were more specifically localized in the delta (< 4 Hz) or in the theta (4–7 Hz) frequency bands. For this purpose we used the average reference scheme. The time courses of the total and evoked TFR energy for the delta and theta bands are presented in Figure 4 at the right electrodes F4 and FT8. A poststimulus increase in these measurements can be observed for both regular and irregular chords (Fig. 4A–H), with higher increases for the regular condition.

Figure 4.

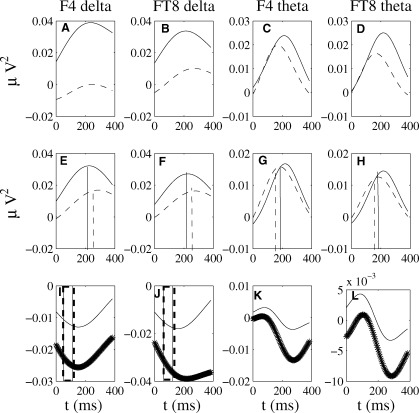
Time course of the spectral power distribution of total and evoked delta and theta oscillatory activity (non‐normalized expression, Eq. (4) at the right‐hemisphere electrodes F4 and FT8 with average reference scheme. (A–D) Total oscillatory activity in the delta band (A,B) and theta band (C,D) for the irregular (dashed lines) and regular (solid lines) conditions showing clear larger values for the regular condition. (E–H) Same for the evoked oscillatory activity. Significant differences (P < 0.01) between the maximum poststimulus peak and mean baseline level are indicated at the average latency for regular chords (vertical solid lines) and irregular chords (vertical dashed lines). (I–L) Difference (irregular minus regular) total (dotted lines) and evoked (solid lines) oscillatory activity indicated in standard deviations from the 100–300 prestimulus baseline Eq. (5). Irregular chords exhibit less spectral power as compared with regular chords, both in the phase‐locked and in the total oscillations. The vertical lines represent regions of significance (P < 0.05) for the comparison conditions in the delta band phase‐locked and total spectral power.

Curves in Figure 4A–H exhibit local maxima in the spectral power relative to baseline levels in all cases considered, with more dramatic changes in the regular condition. These results indicate that the processing of regular chords elicits increases in phase‐locked but also non‐phase locked oscillatory activity in delta and theta frequency bands, increases which are weaker when processing irregular chords.

The difference (irregular minus regular) curves confirm the lower spectral power for irregular chords relative to regular chords, difference which is more pronounced in the total spectral power (Fig. 4I–L, dotted curves).

For statistical analyses, total and evoked theta and delta activities, for each condition separately, were first averaged across the electrodes of the 6 ROIs (see Statistics in Materials & Methods). Next, the maximum values between 100 and 300 ms poststimulus of the indices were compared for each condition separately (via permutation test) with the mean baseline level between 300 and 100 ms prior to the stimulus onset at each ROI (Fig. A–H). Finally, we tested for differences between conditions for the evoked and total theta and delta activities at each ROI, by comparing in the time window 100–300 ms the normalized spectral power Eq. (5) of irregular and regular chords.

The permutation test did not reveal significant (P > 0.05) changes at any of the ROIs in response to stimulation in the total spectral power elicited by the regular or irregular chords. However, significant (P < 0.01) increases in the delta and theta evoked spectral power were found. More specifically, the theta evoked spectral power differed from baseline levels in all 6 ROIs for processing both regular and irregular chords. The mean latency across ROIs of this effect was 203 ms, for the regular chords, and 189 ms, for the irregular chords. Similar increases relative to baseline levels in the delta evoked spectral power were found to be significant (P < 0.01) at anterior and central electrode regions, bilaterally, with a mean latency across ROIs of 237 ms for music‐syntactically regular chords and 260 ms for music‐syntactically irregular chords. Interestingly, the peaks in the delta evoked spectral power were delayed relative to the peaks in the theta evoked spectral power.

The difference (supertonic minus tonic) total spectral power was not significant (P > 0.05) in the theta frequency range, but in the delta band (P < 0.01) at RA and RC electrode regions with a latency period of 100–150 ms. Significant differences in the spectral power of phase‐locked theta activity were obtained between 100 ms and 160 ms at left‐ and right‐anterior (P < 0.05) brain areas.

As indicated in this section, the poststimulus changes were due to a smaller spectral power for irregular relative to regular chords.

Gamma band responses

The TFR analysis was extended to investigate the spectral power distribution of evoked and induced oscillatory activities in the high frequency range (30–50 Hz). The early processing of irregular and regular chords elicited similar bursts of gamma oscillations (50–100 ms, 30–37 Hz, figure not shown) but no statistically significant differences between the two conditions were found. The difference TFR, irregular‐regular, is plotted in Figure 5 for both common reference (A) and Laplacian algorithm (B). Only one significant zone of reduced spectral power was found, which was similar for both reference schemes: a decrease between 40 and 50 Hz in the time span of 510–560 ms for the common reference, and a broader decrease between 38 and 50 Hz and with a latent period of 500–550 ms for the Laplacian scheme. This decrease was due to both an increase (from the baseline) in the induced gamma spectral power during regular chord processing and a decrease (from the corresponding baseline) in the induced gamma spectral power during irregular chord processing (see Fig. 6). Only the increase relative to pre‐stimulus levels in the regular condition was significant (P < 0.01), indicating that for the processing of irregular chords late changes in induced oscillatory activity were absent.

Figure 5.

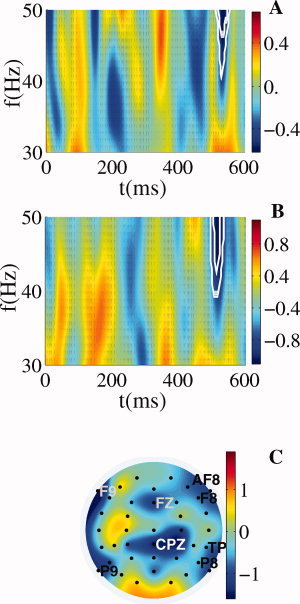
Late gamma activity. Difference between conditions of the global spectral power averaged across trials in the band 30–50 Hz for common reference (A) and spline Laplacian (B). The white contours denote regions where the difference between the two conditions is significant at 0.01 and 0.05 levels according to the permutation test over subjects. (C) Topographical map of the 38–50 Hz spectral power averaged in the time window 500–550 ms for spline Laplacian. The decrease in induced gamma activity is maximal at frontal electrodes (FZ, AF8, F8, and F9) and at parietal electrodes (CPZ, TP8, P8, and P9).

Figure 6.

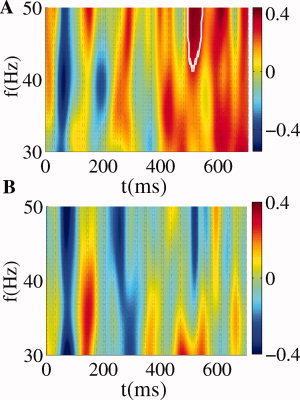
Late gamma activity. Induced spectral power in the 30–50 Hz band for spline Laplacian computed for the music‐syntactically regular (A) and irregular (B) chords. The change relative to pre‐stimulus levels in the time window between −100 ms and −300 ms was significant (P < 0.01) only in the regular condition.

The topography of the decrease in the spectral power of the induced oscillatory activity averaged over the frequency range 38–50 Hz and the time window 500–550 ms is illustrated in Figure 5C. In this plot the TFR energy obtained after applying the surface Laplacian was averaged across trials and the difference (irregular minus regular chord) was presented. Peaks of reduced spectral power emerged at the frontal electrodes FZ, AF8, F8, and F9 as well as at the centro‐parietal CPz, temporo‐parietal electrode TP8 and parietal electrodes P8 and P9.

Phase Synchrony Analysis

Synchronization cluster analysis

After re‐referencing the data using common reference, for each frequency <15 Hz and time instant, the cluster mean was computed as an index of spatial global synchronization strength as indicated by the SCA approach (see Materials and Methods for details). The difference values are shown in Figure 7A. The main effect is that irregular chords, as compared with regular chords, were associated with a robust decrease in the degree of global phase synchrony in the lower alpha band with the frequency span of 8–10 Hz and the time span of 175–250 ms. The analyses were repeated after Laplacian, and the result was very similar to that based on common reference (see Fig. 7B).

Figure 7.

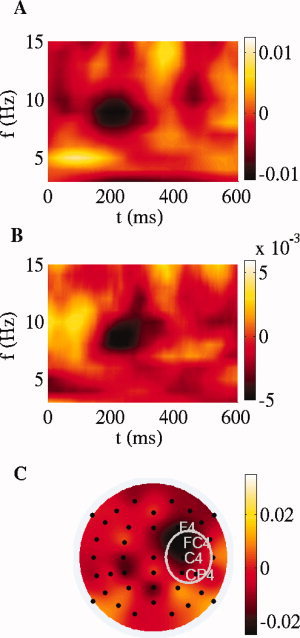
SCA. Time‐frequency plot of the difference between supertonic condition and regular condition for the cluster strength, in the frequency range <15 Hz, (A) using the mean of the mastoids behind the ears as reference and (B) after spherical spline Laplacian. (C) Topographical distribution of the difference between conditions of the synchronization strength between each electrode and cluster, obtained for 8 ROIs by averaging the 8–9 Hz index between 185 and 210 ms. A ROI‐wise paired permutation test over subjects in each ROI was computed to detect the statistical differences between supertonic and tonic condition. The permutation test yielded significant differences (P < 0.01) at right central electrodes, the ROI which is indicated by the white ellipse.

To obtain the topography of this decrease in phase synchronization effect, we averaged the 8–9 Hz index 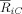of the electrode i over the time window 175–250 ms for each condition separately and analyzed the difference (irregular minus regular chords, Fig. 7C). For both conditions separately, the main synchronized structure was localized mainly at the left temporal region but also at the electrode FC4 (not shown). It is important to note that the synchronized cluster denotes which electrodes are more dynamically coupled between them in a time‐frequency window, information which is not necessarily related to the local spectral power at the electrodes. The 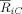measure in each separate condition ranged from 0.2, for EEG channels weakly synchronized to the cluster, to 0.8 for the electrodes FT7, T7 and TP7.

The between‐conditions difference in the phase synchronization topography showed a strong localization of the decrease in synchronization at fronto‐central right electrodes (F4, FC4, C4) with a maximal decrease at the FC4 electrode (Fig. 7C). According to the permutation test across participants computed at the 8 ROIs (see Materials & Methods), significant differences (P < 0.01) were found at right central electrodes (see marked white ellipse in Fig. 7C).

Next we studied the temporal dynamics of the strength of alpha band phase synchronization both when comparing the two conditions (Fig. 8A) and for each condition separately (Fig. 8B–D). For the electrode FC4, the irregular chord exhibited a steep decrease in phase synchronization relative to the regular chord. This effect began almost immediately after stimulus presentation, reaching a maximum between 175 and 210 ms (Fig. 8B). Differences between two conditions were also evident for electrodes C4 and F4 (Fig. 8C,D), but the earlier sharp decrease was not found.

Figure 8.

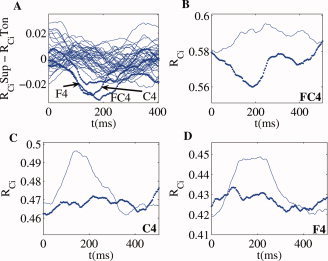
Temporal profiles of cluster synchronization. (A) Temporal evolution of the difference (supertonic vs. tonic) indices of synchronization strength between cluster and oscillator, computed for all electrodes. Additionally, the temporal profile of 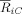for the supertonic (dotted) and tonic condition (line) is depicted for electrodes FC4 (B), C4 (C) and F4 (D). Contrary to the channels C4 and F4, the electrode FC4 elicits a steep decrease in the synchronization index for the irregular final chord.

Bivariate synchronization analysis

To study changes in the phase coupling during the processing of music‐syntactical irregularities, we used the pair‐wise synchronization index 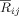Eq. (6). Following the robust decrease in alpha band phase synchronization at right fronto‐central regions (as found by the SCA method), we investigated whether this effect was due to a decrease in either short‐range synchronization between adjacent electrodes or a long‐range synchronization between the right fronto‐central electrodes and other distant electrodes. Consequently, for the same time and frequency windows, where the reported reduction of phase synchronization was maximal, we computed the mean pair‐wise synchronization index between the electrode FC4 and each of the other EEG channels. Similarly, the phase synchrony indices between electrode C4 and each of the other EEG channels were calculated. FC4 and C4 were selected because the difference (ST minus T) index 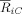was maximal at these 2 electrodes (see Fig. 8). Additionally, we investigated the index 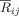for the pairs FC4‐F4, C4‐F4 and FC4‐C4. Thus, we could test whether these EEG channels constitute a cluster themselves. Significant outcomes of the permutation tests for the differences in the pair‐wise synchronization index between conditions in this time‐frequency range are depicted in Figure 9, and show a reduction of long‐range interaction between electrode FC4 and each of the left temporo‐parietal electrodes T7, TP7, P7. Similar tests on time ranges earlier than 175 ms or later then 300 ms produced no statistically significant differences between the two conditions.

Figure 9.

Bivariate synchronization analysis. Differences between conditions of the pair‐wise synchronization index in the frequency band 8–9 Hz and time window 185–250 ms. Differences between electrode FC4 and the rest of electrodes significant at the level P < 0.01, according to a permutation test over subjects, are plotted by a dashed line. The test yielded three significant effects, namely a decrease in synchronization between channel FC4 and each of the left temporo‐parietal electrodes T7, TP7 and P7.

We did not find a significant difference between conditions for the short‐range phase coupling of the pairs FC4‐F4, C4‐F4 or FC4‐C4. However, interestingly, the index 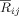for these pairs did show maximum values for each of the conditions separately (Fig. 10A,B), indicating that the three electrodes constituted a synchronized cluster for processing both the supertonic and tonic chords.

Figure 10.

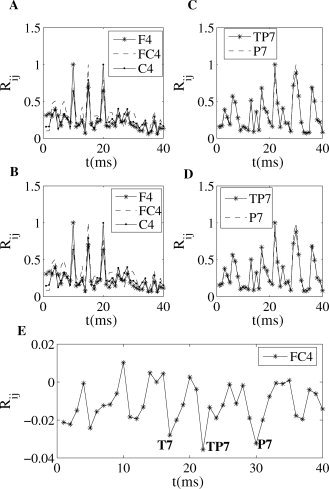
Bivariate synchronization analysis. (A,B) Pair‐wise synchronization index versus channel number (1–40) for electrodes F4 (No. 10), FC4 (No. 15) and C4 (No. 20) averaged in the frequency band 8–9 Hz and time window 185–250 ms, presented during processing regular (A) and irregular (B) chords. Note that the index R _ii (phase coupling of en electrode with itself) is always 1. (C,D) Same but for electrodes TP7 (No. 22) and P7 (No. 30). Maximum values appear at these same channels, No. 22 and No. 30. (E) Difference (supertonic minus tonic) of the bivariate synchronization index for electrode FC4 (No. 15), showing decreases in the phase synchronization with electrode positions T7, TP7, and P7 (No. 17, 22, 30).

Additionally, Figure 10 depicts for each condition the phase coupling for channels TP7 and P7, separately, with the rest of the electrodes. We can observe the higher values at electrode numbers No. 22 (TP7) and No. 30 (P7), which indicates a stronger phase synchronization between these electrodes for processing both harmonical regularities and irregularities. The aforementioned difference between conditions for the bivariate index of the EEG channel FC4 is illustrated in Figure 10E.

DISCUSSION

Neapolitan vs. Supertonic Chords

Most of the earlier studies using similar chord sequence paradigms presented Neapolitan chords as music‐structural irregularities [Koelsch et al.,2000; Koelsch et al.,2002a,b; Maess et al.,2001]. Although these chords elicited very large ERAN amplitudes, the following two problems arise: (a) The Neapolitan chords have fewer pitches in common with the directly preceding chord than the final (regular) tonic chords have, thus creating a larger degree of ‘sensory dissonance’. Therefore, it is difficult to dissociate the processing of sensory dissonance from the processing of musical syntax. (b) Neapolitan chords also represent Frequency deviants: Whereas the preceding chords were presented in the same tonal key, the Neapolitan chords introduced notes that did not occur in the preceding chords (in contrast to the notes of the regular tonic chords). Thus, the processing of frequency deviance (neurally represented by a frequency MMN component) and the processing of musical syntax could have overlapped. For this reason, it is crucially important to minimize the acoustic differences between music‐syntactically irregular and regular chords by taking into account various acoustical features. Consequently, we used supertonics as irregular chords, which are in‐key chord functions, and have even higher pitch correlations with the preceding harmonic context than those of the regular/tonic chords. So, in short, the reported findings mainly reflect components of the brain responses which are specifically associated with processing syntax in music, because components due to acoustical differences were minimized.

ERP Analysis: Anterior Frontal Negativity

We reconfirmed the result of previous studies [Koelsch et al.,2000; Koelsch et al.,2002a,c], that processing of music‐syntactically irregular chords relative to regular chords elicited an early right anterior negativity (ERAN). This negativity was statistically significant in the time window from 160 to 220 ms and represented predominantly by frequencies below 8 Hz. The ERAN was more significant when the difference mean amplitude values were averaged over the ROIs at right fronto‐central regions, but also clearly present in the left hemisphere. The ERAN component was assumed to reflect neural activity related to the processing of a harmonic expectancy violation [Koelsch et al.,2002a,2005a; Tillmann et al.,2006]. Like earlier studies, the present data showed that the ERAN can be elicited under task‐irrelevant conditions and also in nonmusicians, supporting the notion that listeners familiar with Western tonal music normally possess an implicit knowledge of music‐syntactic regularities, even when not formally trained.

Spectral Power Analysis: Low Frequency Response

We investigated whether this ERAN component was mainly generated by a decrease in the spectral content of slow (<8 Hz) evoked oscillations, total power, or both. Evoked oscillations have a fixed phase latency across trials relative to the stimulus onset, whereas total oscillatory activity refers to oscillations both phase‐locked and non‐phase‐locked to the stimulus onset. Our results demonstrated that the delta and theta total spectral power increases were concurrent with a phase‐alignment in the delta and theta band, respectively, after the final chord onset, and these effects were weaker in irregular than in regular chords. However, only the changes in the evoked spectral power were significant. Fronto‐central regions bilaterally were involved in significant poststimulus changes in delta frequency phase‐locked oscillations, while all scalp areas selected exhibited poststimulus changes in the spectral power of theta band evoked oscillations. These findings support the arguments against a strict lateralization of music processing to the right hemisphere [Koelsch et al., 2002], and rather show that neural resources for syntactic processes are shared between the two hemispheres, in which inferior frontal regions play a major role [Tillmann et al.,2006]. The poststimulus increases in the theta phase‐locked oscillations had a latency similar to that of the ERAN component (∼190 to 200 ms), whereas the effect in the delta band was delayed, indicating that the different poststimulus bursts of oscillations could be complementary but not identical. When studying differences between conditions, the delta band revealed an effect for both phase‐locked and total spectral power at fronto‐central regions bilaterally.

Several EEG studies have reported two mechanisms that contribute to the generation of ERPs: a phase‐resetting of the ongoing oscillatory activity and a neuronal response added to the ongoing oscillations [Basar,1980; Brandt et al.,1991; Lopes da Silva,1999; Makeig et al.,2002]. We consider that each model separately can only account for ERPs occurring in simple paradigms, involving basic sensory stimulus configurations, whereas for complex paradigms, such as in music processing, a contribution of both additive power and phase‐resetting of oscillations is to be expected [Mazaheri and Jensen,2006; Min et al.,2007]. Thus, our results can be interpreted within the framework of the current debate as an indication that both amplitude and phase‐locking vary in response to stimulation [Herrmann et al.,2004b].

A previous study using oscillatory analysis in language comprehension paradigms has reported that grammatical violations lead to a higher degree of stimulus‐evoked activity in the lower theta band than the grammatical conditions [Roehm et al.,2004]. This study claimed that an irresolvable conflict in language processing produces a reorganization in the sense of phase resetting. Rather, our results would indicate that it is the regular in‐key chord, which may reorganize more coherently the spontaneous distribution of phase in the EEG and simultaneously elicit higher increases in the amplitude of the oscillations. Further investigations comparing specifically syntax processing in music and language should address this issue.

Spectral Power Analysis: High Frequency Gamma Response

Early evoked gamma activity did not differ between the conditions, yet significant differences were found in the induced gamma oscillations at a later stage of processing (around 500–550 ms). The lack of significant differences in the initial processing stage was possibly due to the fact that both regular (tonic) and irregular (supertonic) chords were correct musical objects themselves that would provide a similar outcome after the initial acoustical feature extraction and binding processes. In major keys, the supertonic is the in‐key chord built on the second scale tone, which implies that this chord function cannot be detected as irregular by the occurrence of out‐of‐key tones. Only after the integration of the initial processes of feature extraction with the working memory representing the previous musical context, the differences between the final chords would be apparent and the subsequent stage of harmonic integration would differ. This is nicely reflected by the differences in the induced gamma activity appearing at a later stage of processing, due to a significant increase in the gamma spectral power during regular chord processing and the absence of a similar increase in the gamma spectral power during irregular chord processing. Therefore, our results suggest that induced gamma responses reflect the integration of bottom‐up and top‐down processes, within the framework of the match‐and‐utilization model (MUM) of Herrmann et al. [2004a]. According to the MUM, the comparison of stimulus related information with the memory contents produces a “match” or “mismatch” output, reflected in the early gamma band responses. This output can then be used for coordinating behavioral performance, for redirecting attention or for storage in memory. These “utilization” processes modulate the late gamma response. Similarly, in our context, after the processing of stimulus‐related information and building up of a musical context, the comparison of these processes with long‐term memory contents (such as abstract representations of music‐syntactic regularities, possibly implemented at the right inferior frontal cortex) would lead to the different induced gamma activity. Consequently, these data also suggest that the harmonic integration requires the consolidation of bottom‐up and top‐down processes. We propose that the successful consolidation of these processes was manifested in the increase of induced gamma oscillations for the processing of regular chords. The irregular supertonic chords did not match so well with the harmonic long‐term memory and, consequently, the gamma spectral power decreased. Our interpretation is further supported by Lentz et al. [2007], who recently demonstrated that matches of auditory patterns which are stored as representations in long‐term memory are reflected in increased induced γ‐band oscillations.

It is noteworthy to mention that the latency of this gamma effect (500–550 ms) is strongly reminiscent of the latency of the N5, an ERP which follows the ERAN in very similar paradigms [Koelsch et al.,2000,2002a; Koelsch,2005]. The N5 has been taken to reflect processes of harmonic integration: the final irregular chords are more difficult to integrate into the preceding harmonic context, and this increased processing demand may be reflected in the increased amplitude of the N5, similar to the N400 elicited by semantically incongruous words (Koelsch et al., 2000). This observation is coherent with the decrease of γ‐band activity for the irregular chords relative to the regular chords in our study.

The spline Laplacian localized the induced gamma activity at the frontal (Fz, AF8, F8, and F9) and parietal (CPZ, TP8, P7, and P9) brain regions. This demonstrated the predominance of the prefrontal cortex in processing of musical syntax including the integration of final chord with the preceding harmonic context. The present data also showed an important role of temporo‐parietal regions, which is consistent with previous data of activations in the supratemporal cortex (anterior and superior STG) reported in both fMRI and EEG studies [Koelsch and Friederici,2003; Koelsch et al.,2002c,2003,2005b]. Previous studies implicated the parietal lobe in harmonic processing [Beisteiner et al.,1999] and in auditory working memory [Platel et al.,1997]. Here, we propose that the gamma oscillations that mediate the integration of top‐down and bottom‐up processes at later stages are elicited in regions responsible for auditory working memory and long‐term memory processing. This proposal is also consistent with previous reports of activations in response to music‐syntactic irregularities in both inferior parietal regions and regions along the inferior frontal sulcus, both of which are known to play a role in auditory working memory [Janata et al.,2002; Koelsch et al.,2005b]. Notwithstanding, fMRI activations and changes in γ‐band activity do not always correlate positively, because an increase in regional cerebral blood flow detected by fMRI could concur with a decrease in the γ‐band activity. The former would be linked to an increased neural activity, but the latter would indicate that the local neural population is less synchronized.

Finally, there has been some debate on the possible relationship between the ERAN and the mismatch negativity (MMN). The MMN is a negative ERP component, which is elicited by deviant auditory stimuli in an otherwise repetitive auditory environment [Naatanen,1992]. Both MMN and ERAN can be elicited in the absence of attention [Koelsch et al.,2001], while their amplitudes can be influenced by attentional demands [Loui et al.,2005; Woldorff et al.,1998]. These findings were based on traditional ERP averaging techniques which ignore the oscillatory content of the underlying neural response. Several studies have shown early oscillatory components of the MMN in the gamma band, particularly a decrease of stimulus‐locked or evoked gamma activity onset [Fell et al.,1997], and a transient decrease in the induced gamma response [Bertrand et al.,1998]. In contrast to the MMN, oscillatory activity in the gamma band associated to the ERAN has not been reported previously. Here, the gamma band effect occurring at later processing stages (around 500–550 ms), presumably reflects primarily harmonic integration (i.e., top‐down, rather than bottom‐up processing). Thus, our data also reflect that the processing of irregular chord functions involves implicit knowledge about the complex regularities of major‐minor tonal music [Koelsch et al.,2001], whereas MMN mainly involves processing related to sensory aspects of acoustic information (different assumptions might apply for abstract‐feature MMNs [Paavilainen et al.,2001]).

Decrease in Long‐Range Alpha Band Phase Synchronization

The global decrease in phase synchronization in the lower alpha band (8–10 Hz) evoked by the syntactically irregular chords (relative to the regular chords) 185–250 ms was primarily represented by the neural sources in right fronto‐central and frontal electrode regions (FC4, C4 and F4). This decrease appeared to be due to a reduction of the phase coupling between these electrodes and other scalp regions. Using a bivariate synchronization index, we found that the phase locking between electrode FC4 and left temporo‐parietal regions was significantly reduced during the similar time‐frequency window. This characterized the decrease in the alpha band synchronization as a spatial long‐range effect. Interestingly, the right fronto‐central electrodes, where the reduction of phase synchronization was maximal, also elicited the strongest significant decrease in the spectral power of the local delta oscillations and the larger amplitude of the ERAN. In a related study on musical expectancy [Janata and Petsche,1993], EEG parameters, such as amplitude and magnitude‐squared‐coherence in various frequency bands, change over right frontal regions for varying degrees of violations of musical expectancy.

The relevance of long‐range alpha synchronization in paradigms of complex multiple integration has been recently reported [von Stein and Sarnthein,2000; von Stein et al.,2000] based on the functional measure of coherence or synchrony. More specifically, in the first of the mentioned studies, perception of stimuli with varying behavioral significance was shown not to be only driven by “bottom‐up” processes but also to be modified by internal constraints such as expectancy or behavioral aim. The neural correlates of the internal constraints were interaeral synchronization in the alpha (and theta) band. The hypothesized role of the alpha band in providing top‐down control was explained as follows: alpha activity is present in the “idling” brain states (such as the activity in the visual cortex while closing the eyes). These brain states may thus reflect states without bottom‐up input, and as such, the alpha rhythm may be an extreme case of top‐down processing, which is modulated by purely internal mental activity (e.g. imaginary, thinking or planning) or by the degree of expectancy [Chatila et al.,1992]. The authors showed that top‐down alpha and theta band cortical interactions are integrated with bottom‐up γ band activity during the successful processing of stimuli that are associated with behavioral relevance. This view of the alpha band is compatible with our results, showing that after the initial processing of the musical stimuli, the violation of the harmonic expectations was reflected in the top‐down mechanism. Notice that the role of interaeral phase coupling in the alpha band does not require lack of bottom‐up processes, rather it may be just a second stage of processing, once the bottom‐up interactions have taken place and the internal constraints dominate the modulation of the brain responses.

Further increases in between‐regions coherences in the alpha band have been found in studies on mental imagery and mental performance of music [Petsche et al.,1997] and have also been claimed to be critically important for maintaining spontaneous functioning of the healthy brain [Bhattacharya,2001]. These findings support the role of the alpha band in providing top‐down control, by mediating the integration from multiple cortical areas which are activated during the task.

Our results indicate that the violation of musical expectancy was reflected in the electrical brain responses as a decrease in long‐range alpha phase coupling due to top‐down processing. The integration of the multiple cortical areas responsible for the early processing stages (such as the left temporo‐parietal brain regions) with higher areas (mainly the inferior frontal gyrus), where the relation between a chord function and the previous context is presumably established, was weaker for the supertonic chord relative to the regular chord because it deviates from the stored harmonic expectations.

Similar evidence for the interplay between right auditory and prefrontal cortex has been described for an MMN paradigm [Doeller et al.,2003]. Several studies support that many aspects of melodic processing rely on both superior temporal and frontal cortices. More specifically, functional imaging studies indicate that areas of the auditory cortex within the right superior temporal gyrus are involved in the processing of pitch and timbre [Zatorre,1988; Zatorre and Samson,1991], and that working memory for pitch entails interaction between temporal and frontal cortices [Zatorre et al.,1994]. Hyde et al. [2006] found, in the brains of individuals with amusia (tone deafness), white matter changes in the right IFG area (BA 47) as correlates of a musical pitch processing, which was interpreted as an anomalous connectivity between frontal and auditory cortical areas. A PET study [Blood et al.,1999] reported positive correlations of activity in orbitofrontal and bilateral frontopolar cortex with increasing dissonance, and the predominance of inferior frontal areas has been further demonstrated in an fMRI study investigating musical syntax processing where activation of this region increased for strong musical expectancy violations [Tillmann et al.,2003], but also for more subtle harmonic irregularities [Tillmann et al.,2006]. A recent extensive review of musical disorders provides further evidence for the interaction of frontal and temporal brain regions [Stewart et al.,2006]. More specifically, the left posterior planum temporale has been reported to be involved in the processing and primary storage of various complex sound patterns [Griffiths and Warren,2002] and to play a role in bridging the external auditory information with further judgment [Saito et al.,2006].

Overall the phase synchronization analysis provided the first evidence for a role of the integration between the right inferior frontal cortex and left temporo‐parietal regions in processing structural relations in music. Once the early stages of acoustic feature extraction and auditory sensory memory are completed, this information together with the auditory Gestalts and analysis of intervals would have to be implemented in the working memory. Here, we suggest that the decoupling between left temporo‐parietal and right anterior regions for the harmonically incorrect chords reflected the mismatch between the working memory contents, which could lie in the left temporo‐parietal regions, and the long‐term memory contents (abstract model of harmonic regularities), perhaps stored in the prefrontal cortex. Nevertheless, future experiments should further elucidate the generality of this mechanism in syntactic processing of music.

In summary, the interesting outcome of our study was that different neural processes, which were distributed across the brain, complemented each other in order to perceive the harmonic structure of music. Different scales of cortical integration, ranging from local delta, theta and gamma oscillations, to long‐range alpha phase synchronization, were here demonstrated to mediate the processing of syntax in music and, as a result of their interplay, to contribute to the emergence of a “unified cognitive moment” [Varela et al.,2001].