Abstract
We investigate the effect of the magnetic field generated by neural activity on the magnitude and phase of the MRI signal in terms of a phenomenological parameter with the dimensions of length; it involves the product of the strength and duration of these currents. We obtain an analytic approximation to the MRI signal when the neuromagnetically induced phase is small inside the MRI voxel. The phase shift is the average of the MRI phase over the voxel, and therefore first order in that phase; and the reduction in the signal magnitude is one half the square of the standard deviation of the MRI phase, which is second order. The analytic approximation is compared with numerical simulations. For weak currents the agreement is excellent, and the magnitude change is generally much smaller than the phase shift. Using MEG data as a weak constraint on the current strength we find that for a net dipole moment of 10 nAm, a typical value for an evoked response, the reduction in the magnitude of the MRI signal is two parts in 105, and the maximum value of the overall phase shift is 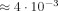 , obtained when the MRI voxel is displaced 2/3 the size of the neuronal activity. We also show signal changes over a large range of values of the net dipole moment. We compare these results with others in the literature. Our model overestimates the effect on the MRI signal. Hum Brain Mapp 2009. © 2007 Wiley‐Liss, Inc.
, obtained when the MRI voxel is displaced 2/3 the size of the neuronal activity. We also show signal changes over a large range of values of the net dipole moment. We compare these results with others in the literature. Our model overestimates the effect on the MRI signal. Hum Brain Mapp 2009. © 2007 Wiley‐Liss, Inc.
Keywords: MRI, MEG, neuronal magnetic field, modeling
INTRODUCTION
Currents flowing in neurons produce local magnetic fields that alter the precession frequency of protons in the neighborhood. On one side of a dendritic compartment containing current the neuromagnetic field will add to the strength of the external applied field, and on the other side it will subtract from that strength. The transverse components of the magnetic moments of protons on the two sides will, therefore, get out of phase, i.e., they will point in slightly different directions. Since the net transverse magnetic moment μ+ inside an MRI voxel involves the volume integral of the transverse magnetization, neuronal activity is expected to modify both the magnitude and phase of μ+, and consequently that of the MRI signal.
It would be very exciting if it were possible to actually detect the neuronal magnetic field directly using MRI, because that would provide reliable position information based on the electrical activity of neural populations instead of secondary metabolic or hemodynamic effects exploited by conventional fMRI techniques. Because MRI provides a 3D tomographic measure, the ill‐posed inverse problems associated with surface based physiological techniques such as electro‐ and magnetoencephalography (EEG and MEG) would no longer be a factor.
In principle, MRI‐based techniques might probe the dynamics of neural function directly, and emerging techniques for fast MRI based on detector arrays underscore this possibility [Lin et al., 2006; Pruessmann et al., 1999; Sodickson and Manning, 1997]. Alternatively, reliable location information from neural current MRI might be coupled with accurate timing information obtained from EEG or MEG [Dale et al., 2000; George et al., 2001; George et al., 1995] to transcend the limitations of each technique in isolation.
Experimental investigations of the possibility of direct detection of neural currents by phase mapping techniques have been reported [Bodurka et al., 1999; Bodurka and Bandettini, 2002]. Kamei et al. [ 1999] claimed the first human detection of magnitude changes due to neuronal activity, but reproducibility of these results remains to be demonstrated. Xiong et al. [ 2003] also claimed the detection of magnitude changes due to dephasing produced by neural currents has been achieved. A later study, however, says that the sensitivity of MRI to detect evoked responses is well below that of BOLD‐based functional MRI [Chu et al., 2004]. Bandettini et al. [ 2005] has presented a thorough examination of this question and the relevant experiments. Probably the most compelling evidence to date comes from a snail ganglia study [Park et al., 2006], and a study using rat‐brain cultures [Petridou et al., 2006].
The size of the putative effect depends on the strength of the currents flowing in the dendrites and also on the geometric arrangement of the currents as well as their relation to the location of the MRI voxel. Although dendrites look like long thin cylinders, for a first attempt at obtaining an analytic approximation and also for our numerical simulations we shall use a simpler mathematical model and approximate these cylindrical currents as spheres with the same radius, r 0, and the same total moment; we call these “spherical dipoles”. It can be shown that this approximation overestimates the size of the effect on the MRI signal; it will also be shown below that it greatly overestimates the importance of diffusion.
If the current density is uniform on the inside of a spherical dipole there is a simple analytic formula for the magnetic field, which increases in magnitude linearly from zero at the center of the sphere to a maximum value on the surface [see The Neuromagnetic Field]. Far from conductivity barriers the magnetic field outside of a spherical dipole falls off as 1/r 2, and consequently so does the additional phase acquired by the magnetic moments. But the phase is a dimensionless quantity, hence a parameter, L, having the dimensions of length naturally arises, which sets the scale of the 1/r 2 falloff.
THEORY
Basic Equations
We write the magnetic field at any position in the brain as the sum of the external field,
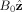 , and B′, the field due to electric current flowing in neurons, and assume B′ is much smaller than B
0. Neglecting relaxation the Bloch‐Torrey equation [Torrey, 1956] determines the evolution of the magnetization,
, and B′, the field due to electric current flowing in neurons, and assume B′ is much smaller than B
0. Neglecting relaxation the Bloch‐Torrey equation [Torrey, 1956] determines the evolution of the magnetization,
| (1) |
We shall neglect the diffusion term initially and later estimate its effect. Without that term M precesses about the direction of the total field B with angular frequency
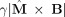 .
.
Calling M 0 the magnetization due to just the external field, and assuming that initially it is in the x − y plane, it evolves according to
| (2) |
With
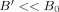 a component of B′ in the z direction will modify the precession frequency to first order, whereas a component transverse to z will have only a second order effect; it also tilts the plane of the precession slightly. [The situation could be very different in low field MRI [McDermott et al., 2004; Matlachov et al., 2004; Matlachov et al., 2007] if the strength of the neuromagnetic field near a dendrite is more nearly comparable with that of the measuring field.] Neglecting a transverse component of B′, the evolution of M
+ is given by
a component of B′ in the z direction will modify the precession frequency to first order, whereas a component transverse to z will have only a second order effect; it also tilts the plane of the precession slightly. [The situation could be very different in low field MRI [McDermott et al., 2004; Matlachov et al., 2004; Matlachov et al., 2007] if the strength of the neuromagnetic field near a dendrite is more nearly comparable with that of the measuring field.] Neglecting a transverse component of B′, the evolution of M
+ is given by
| (3) |
where the additional phase due to neuronal activity is given by
| (4) |
γ, the gyromagnetic moment of a proton, has the value 2.67 × 108/Ts. Hence a magnetic field of strength 10 nT acting for 100 ms would produce a phase shift of only 0.2 radians.
The experimental MRI signal is proportional to the net transverse magnetic moment in the volume V of a voxel,
| (5) |
and making use of Eq. (3), the ratio of this moment to its value in the absence of the neuromagnetic field becomes
| (6) |
where
| (7) |
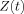 represents the modification of the MRI signal due to neuronal activity. Since Φ occurs in the exponent, Z depends nonlinearly on the strength of the neuronal magnetic field. If either B
0 or the unperturbed magnetization M
0+ varies in strength over the size of the MRI voxel then in place of the simple average of
represents the modification of the MRI signal due to neuronal activity. Since Φ occurs in the exponent, Z depends nonlinearly on the strength of the neuronal magnetic field. If either B
0 or the unperturbed magnetization M
0+ varies in strength over the size of the MRI voxel then in place of the simple average of 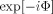 shown in Eq. (7)
shown in Eq. (7)
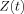 becomes the weighted average, weighted by the magnetization
becomes the weighted average, weighted by the magnetization  . In particular, B
0 may contain a spatial gradient,
. In particular, B
0 may contain a spatial gradient, 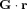 .
.
In principle, both the magnitude and phase of Z can be measured. The change in the phase of the MRI signal due to neuronal activity is given by
| (8) |
and the fractional change in the magnitude of the signal is
| (9) |
Note that a phase having little spatial variation would produce a net phase shift, χ, that might be detected with phase imaging techniques [Bodurka et al., 1999; Bodurka and Bandettini, 2002], but contributes little to δ. The large spatial variation close to dendritic currents can make a larger contribution.
These remarks can be verified explicitly in the important case that Φ, the neuromagnetically induced phase, is small over the volume of the MRI voxel. Using the small angle approximation for
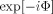 gives
gives
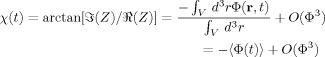 |
(10) |
where
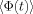 is the average of
is the average of 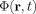 over the voxel.
over the voxel.
To find the approximate expression for
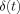 start with
start with 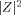 obtained from Eq. (7) as
obtained from Eq. (7) as
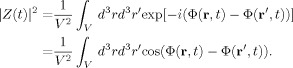 |
(11) |
Now expand the cosine and keep terms up to second order in Φ. This leads to
| (12) |
where σ2 is the square of the standard deviation of
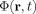 over the voxel. Taking the square root of this equation finally yields
over the voxel. Taking the square root of this equation finally yields
| (13) |
Eq. (13) for δ, the fractional reduction in the magnitude of the MRI signal, confirms the expectation above that it is a measure of the variation in the phase over the voxel. This fact seems to have been recognized, but the quantitative result in Eq. (13) appears to be new.
Note that χ, the change in phase of the MRI signal, is linear in the strength of the neuronal currents; δ, on the other hand, is quadratic in the current strength. This complicates the interpretation of MRI data. Observation of a phase shift accompanied by little or no magnitude change does not necessarily mean that the phase Φ had little spatial variation; it could have resulted from the currents being too weak to affect the magnitude.
The Neuromagnetic Field
Now comes the critical task of estimating the magnetic field created by neuronal activity as a function of position and time. Although a cylindrical approximation to dendritic currents is probably more realistic, two geometric parameters would be needed: the length and radius of the cylinder. For the purpose of the present first look at the problem we shall approximate these currents by assuming that they are distributed with uniform density throughout a spherical volume, and call them “spherical dipoles” needing just one geometric parameter, the radius r 0; just as with point dipoles they are described by a net dipole moment p i located at position r i, the center of the sphere. The greater variation of the phase Φ near a spherical dipole than near a cylindrical dipole with the same total moment means that our approximation overestimates the size of δ, the change in magnitude of the MRI signal.
To show this quantitatively we have compared the magnitude of δ from a single cylindrical dipole with that of a spherical dipole, having the same radius of 1 μm and the same dipole moment, and acting for the same duration. For a cylinder of length 10 μm δ is ∼2/3 as large as for a sphere; and for a cylinder of length 100 μm δ is ∼1/8 as large as for a sphere.
Comparing single dipoles is not the whole story, of course. Placement of cylinders in an MRI voxel is restricted by the length of the cylinder. But for dendrites of length 100 microns in a voxel of dimensions 2 mm or more the geometric constraint would appear to be minor. Furthermore, with the number of dipoles and the voxel size used in the present article the cylinders would occupy only 5% of the voxel volume.
To see if there is more interference between the contributions of different dipoles to δ with cylinders rather than spheres would require a full‐scale calculation with many cylinders, which is beyond the scope of the present article. Since the interference between different spherical sources is not very great we conjecture that the final result for the signal magnitude would be approximately as described above for single dipoles: with cylindrical dipoles of length 100 μm we would expect δ to be significantly smaller than its value with spherical dipoles, only on the order of 10% of the latter. For the rest of this article we will approximate the dendritic currents by spherical dipoles.
If the current density is uniform inside the sphere the exact solution for the neuromagnetic field due to the primary current is
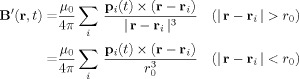 |
(14) |
and the corresponding contribution to the phase Φ is
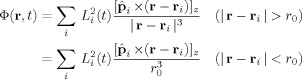 |
(15) |
where
| (16) |
From Eqs. (14) and (15) it is seen that for distances from a dipole that are less than r
0, B′ and Φ increase linearly with distance; but beyond r
0 they fall off as 1/r
2, and
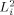 sets the scale of the falloff of the phase. The maximum value of Φ occurs at the surface of the dendritic current, where it becomes
sets the scale of the falloff of the phase. The maximum value of Φ occurs at the surface of the dendritic current, where it becomes 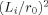 . The size of this ratio is a critical parameter. If
. The size of this ratio is a critical parameter. If 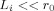 the phase is small everywhere; if
the phase is small everywhere; if 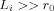 , Φ remains sizeable well outside the dendritic current.
, Φ remains sizeable well outside the dendritic current.
The summation in these equations runs over all dendritic currents that are active during the time of an MRI run. (In writing Eq. (16) we have assumed the direction of each dipole moment remains constant during the time t; if this is not the case, for example if the moment reverses direction, then
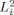 is defined as the magnitude of the vector obtained from the right hand side of Eq. (16) by replacing
is defined as the magnitude of the vector obtained from the right hand side of Eq. (16) by replacing 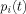 by
by 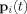 .) The return current contribution to B′ is much smaller than the primary current contribution in the neighborhood of the source, provided one is not near a conductivity barrier. This is shown analytically [Heller, 2004] and numerical studies confirm this result [Konn et al., 2003].
.) The return current contribution to B′ is much smaller than the primary current contribution in the neighborhood of the source, provided one is not near a conductivity barrier. This is shown analytically [Heller, 2004] and numerical studies confirm this result [Konn et al., 2003].
Using the value
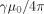 = 26.7 m/As for a proton shows that a dipole moment of 0.1 pAm acting for 100 ms would make L = 0.52 μm, which is comparable with r
0. Such a moment would result, for example, from a current of 1 nA acting over a distance of 100 μm.
= 26.7 m/As for a proton shows that a dipole moment of 0.1 pAm acting for 100 ms would make L = 0.52 μm, which is comparable with r
0. Such a moment would result, for example, from a current of 1 nA acting over a distance of 100 μm.
EVALUATION OF Z
It is useful to obtain an approximate analytic formula for Z in a limiting case to serve as a check on the numerical procedures used for the simulations in The Model.
A Single Current Source
For a single spherical dipole located at the center of the voxel the summation in Eq. (15) reduces to a single term; and taking the origin of the coordinates to be at the position of the dipole and the direction of the dipole moment
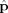 to be along the y axis, the phase can be written
to be along the y axis, the phase can be written
| (17) |
where ˜r is r or r
0 according as r is greater than or less than r
0. With this expression for Φ Eq. (7) for
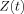 becomes
becomes
| (18) |
In Appendix this integral is evaluated approximately using spherical polar coordinates centered at the dipole. An important point is that the voxel size is on the order of millimeters, whereas we expect L and r 0 to be on the order of microns. Consequently the phase is very small in most of the volume, so it is convenient to subtract and add unity to the integrand.
It is shown in Appendix that for this example of a single current source centered in the MRI voxel, and with L and r 0 much smaller than the size of the voxel
| (19) |
and
| (20) |
where
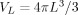 is the volume inside a sphere of radius L and
is the volume inside a sphere of radius L and
| (21) |
The functions f and g are defined in the Appendix and refer, respectively, to the portions of the integration in Eq. (18) for r < r
0 and r > r
0. A plot of the function
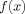 is shown in Figure 1;
is shown in Figure 1; 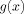 is shown in Figure 2, and
is shown in Figure 2, and 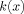 in Figure 3. Examination of Figure 3 shows that δ is well behaved in the limit r
0 → 0. It turns out that the contribution to δ from the inside never exceeds 20% of that from the outside, for any value of the ratio L/r
0. Eqs. (19) and (20) for χ and δ do not require the assumption that the magnitude of the phase Φ is small; but if it is then it is straightforward to show that they are consistent with Eqs. (10) and (13), respectively.
in Figure 3. Examination of Figure 3 shows that δ is well behaved in the limit r
0 → 0. It turns out that the contribution to δ from the inside never exceeds 20% of that from the outside, for any value of the ratio L/r
0. Eqs. (19) and (20) for χ and δ do not require the assumption that the magnitude of the phase Φ is small; but if it is then it is straightforward to show that they are consistent with Eqs. (10) and (13), respectively.
Figure 1.
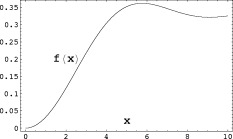
The contribution to the magnitude of the MRI signal coming from inside a single spherical dipole, Eq. (A6), is proportional to the function
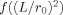 , where
, where 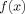 is defined in Eq. (A7).
is defined in Eq. (A7).
Figure 2.
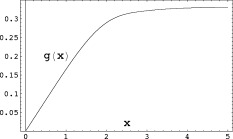
The contribution to the magnitude of the MRI signal coming from outside a single spherical dipole, Eq. (A4), is proportional to the function
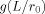 , where
, where 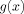 is defined in Eq. (A5).
is defined in Eq. (A5).
Figure 3.

The complete contribution to the magnitude of the MRI signal from a single spherical dipole is proportional to the function
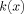 defined in Eq. (A9).
defined in Eq. (A9).
Interference
It was mentioned above that for the important case of small phases δ is quadratic in the strength of the currents. Consequently δ due to a set of sources is not simply the sum of its values from those sources treated separately. From Eqs. (7) and (15) it is seen that the contributions to
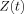 are largest at positions r that are within a distance of order max(L,r
0) from an active dendrite. One might expect, therefore, that for sufficiently large average separation of these dendrites, S, when Φ is inserted in Eq. (7) for the change in the MRI signal, the integral would approximately decompose into a sum over disjoint regions surrounding each current, with very little contribution coming from the portion of the voxel volume between these regions, i.e.,
are largest at positions r that are within a distance of order max(L,r
0) from an active dendrite. One might expect, therefore, that for sufficiently large average separation of these dendrites, S, when Φ is inserted in Eq. (7) for the change in the MRI signal, the integral would approximately decompose into a sum over disjoint regions surrounding each current, with very little contribution coming from the portion of the voxel volume between these regions, i.e., 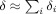 . The shortcoming of this reasoning is due to the very slow falloff of the magnetic field. Since
. The shortcoming of this reasoning is due to the very slow falloff of the magnetic field. Since 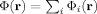 , from Eq. (13) the interference term can be written as
, from Eq. (13) the interference term can be written as
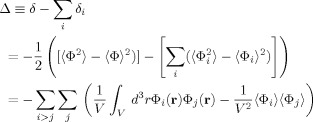 |
(22) |
For two spherical sources that are not too close to a boundary of the voxel the ratio Δ/δ can be shown to be O[max(L,r 0)/S], which falls off only as the inverse first power of the separation. Of course each source has several nearest neighbors and many more next nearest neighbors, etc., so it is difficult to make an a priori estimate of the importance of interference in a problem with many sources. In Varying the parameters the magnitude of the interference in our model will be shown.
THE MODEL
In this section we describe a simplified geometric model of dendritic structure that incorporates the main features of the electrical activity, and permits a simultaneous description of the MEG signal and the MRI signal. The model neurons each contain an apical dendrite and a set of dendrites transverse to it. The apical dendrites, because of their geometric order approximately normal to the cortical surface, are thought to be the source of the MEG signal; and the experimental magnitude of that signal provides an estimate of the strength of the net dipole moment of the simultaneously active neurons, typically around 10 nAm for an evoked response [Hämäläinen et al., 1993]. The transverse dendrites lack geometric order and have a minimal effect on the distant MEG signal; but all the dendritic currents orthogonal to the externally applied field contribute to the MRI signal.
We neglect the contribution of action potentials to the MRI signal. Although the strength of each of the two oppositely oriented dipoles composing the action potential is about 0.1 pAm [Hämäläinen et al., 1993], which is comparable with the strength we assume in our model of the dendritic currents, the time course of only about 1 ms means that the length L from Eq. (16) will be small.
Simulations
Finding the contribution to the MRI signal from a voxel containing N ≈ 106 sources constitutes a daunting yet well posed challenge. We have developed a numerical simulation that yields an estimate for the change in the magnitude and phase of the signal. This simulation approximates dendritic microscale current sources as spherical dipoles; as mentioned above, for the same current dipole moment, a sphere produces a larger effect than a cylinder. We use a multilevel approach which is similar to the Barnes‐Hut algorithm [Barnes and Hut, 1986]. Our simulation can accommodate accurate neuronal geometries containing a billion sources or more either placed randomly in the voxel or placed according to geometry file formats such as the Southampton format [Cannon et al., 1998; Duke‐Southhampton Archive, 2005]. We use this simulation to estimate Z for various combinations of S and L and for realistic sizes of active cortex.
Direct computation of
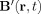 at a set of J field points r
j from this volume of cortex would result in a computational complexity of O(NJ). Brute force numerical evaluation of the integral in Eq. (7) would require field sampling be at least on the order of min{L,r
0}, leading to J ≈ 1010. Therefore, finding Z for an active cortical region of area 10 mm2 and thickness 2 mm would require roughly 1016 computations.
at a set of J field points r
j from this volume of cortex would result in a computational complexity of O(NJ). Brute force numerical evaluation of the integral in Eq. (7) would require field sampling be at least on the order of min{L,r
0}, leading to J ≈ 1010. Therefore, finding Z for an active cortical region of area 10 mm2 and thickness 2 mm would require roughly 1016 computations.
Two techniques greatly reduce the computational complexity required. Multilevel approximations based on a modified Barnes‐Hut treecode algorithm [Barnes and Hut, 1986] and Monte Carlo integration [Hammersley, 1960; Press et al., 1992]. Our multilevel algorithm divides the source filled region into successively smaller cubical regions which are, at each level, approximated by aggregated spherical dipole sources. Instead of each source interacting with each field point exactly, a distance criterion is established beyond which the Mth level's sources are aggregated into a single source. For spherical dipoles, this corresponds to replacing all of the sources in a given sector of the Mth level into a single dipole with effective moment p
eff equal to the vector sum of the moments of the constituent dipoles. If there is very little correlation between the positions and dipole moments of the sources in a given group, the fractional error due to this approximation is
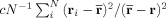 , where c is a constant of order unity. The sum runs over all the dipoles in that group, and
, where c is a constant of order unity. The sum runs over all the dipoles in that group, and  is their unweighted center of mass. As expected, the farther a given group is from r the larger it can be. The contribution of this group to the phase at position r is obtained from the first line of Eqs. (15) and (16) with r
i replaced by
is their unweighted center of mass. As expected, the farther a given group is from r the larger it can be. The contribution of this group to the phase at position r is obtained from the first line of Eqs. (15) and (16) with r
i replaced by  and Li replaced by
and Li replaced by 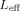 , which is computed from
, which is computed from 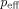 .
.
After initial setup time, this technique reduces computation to O(J log N). For a more complete treatment of our algorithms and error criterion, see [Barrowes et al., in press(a)]. We find at most a 1.5 % error introduced by the multilevel algorithm based on the simulation parameters we have chosen.
Magnitude and Phase of the MRI Signal
Choice of parameters
To estimate the expected size of δ, the fractional change in the magnitude of the MRI signal due to neuronal activity, we use the model of apical and transverse dendrites described above, with parameters partially constrained by MEG data. The external magnetic field is taken to be in the z‐direction, and we assign a moment of 0.1 pAm to each of 105 apical dipoles pointing in the y‐direction, making an effective dipole moment of 10 nAm; as mentioned above this is a typical value found in MEG evoked response experiments [Hämäläinen et al, 1993]. In addition, we have chosen 30 times as many transverse dipoles pointing in random directions in the x − z plane, each with the same value of the dipole moment. [The number 30 is a crude estimate taken from pictures of some stained neurons. It will be seen that the difference between choosing 30 transverse dendrites and choosing none at all changes our result for δ by at most a factor of 2.] All dipoles were assigned a radius r 0 = 1.0 μm.
All dipoles are at randomly chosen positions in a volume of dimensions
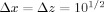 mm, and Δy = 2 mm. This makes S, the mean spacing of the dipoles, 18.6 μm. For the transverse dipoles only those with a dipole component along the x‐axis contribute to the z‐component of the magnetic field. When this is taken into account it effectively reduces by half the number of the transverse currents.
mm, and Δy = 2 mm. This makes S, the mean spacing of the dipoles, 18.6 μm. For the transverse dipoles only those with a dipole component along the x‐axis contribute to the z‐component of the magnetic field. When this is taken into account it effectively reduces by half the number of the transverse currents.
The MRI voxel is assigned the same dimensions, and we consider two cases. In the first the voxel is centered on the active region. For this case χ, the net phase shift of the MRI signal, should be zero because the additional magnetic field due to neuronal activity is symmetric around the active region. In the second case the voxel is displaced in the x‐direction such that it contains only a fraction of the active cortical volume.
In addition to the strength of the dipole moments, which along with their geometry determine the strength of the magnetic field at each position, it is necessary to assign a duration to their activity in order to estmate the phase
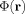 . Considerable variation is found in the latencies and durations of the effective dipole moments obtained from analysis of MEG evoked response experiments, from 5 ms in a short latency median nerve response to stimulation [Jun et al., 2006] to a range from 10 to 100 ms in a visual stimulus experiment [Aine et al., 2000].
. Considerable variation is found in the latencies and durations of the effective dipole moments obtained from analysis of MEG evoked response experiments, from 5 ms in a short latency median nerve response to stimulation [Jun et al., 2006] to a range from 10 to 100 ms in a visual stimulus experiment [Aine et al., 2000].
At a more fundamental level the duration of postsynaptic potentials measured electrophysiologically typically varies from 5–20 ms. Of course most cells can fire multiple times in 100 ms, either as a burst elicited by a unitary stimulus or as a cosequence of continuous stimulation. As a practical matter the time that neuromagnetic fields can interact with an evolving spin population is generally limited by the echo time. A 100 ms is a typical upper limit for TE and we have chosen 100 ms for our simulations; reducing it will lead to a smaller effect on the MRI signal.
With all sources assigned a dipole moment of 0.1 pAm and a duration of 100 ms, the common value of L from Eq. (16) is 0.52 μm. With the dipole radius r 0 = 1.0 μm the phase Φ is everywhere small so we expect Eq. (10) for χ, the overall phase shift, and (13) for δ should be accurate. As χ is first order in the magnetic field produced by the neuronal currents it receives no mean contribution from the transverse dendrites in our model because those currents point in random directions. The magnitude change δ, on the other hand, being second order in the magnetic field receives contributions from all the dendritic currents.
Figure 4 shows the convergence of the Monte Carlo integration of Eq. (7) for the first case (centered voxel), as follows. N = 20,000 values of Φ are sampled at random inside the voxel, and the average value of exp[−iΦ] is regarded as an approximation to Z in Eq. (7); each square represents the value of
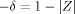 for that run. This process is repeated 39 times and the circles represent the cumulative average of −δ. The result of this calculation is
for that run. This process is repeated 39 times and the circles represent the cumulative average of −δ. The result of this calculation is 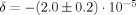 . Equation (13) predicts
. Equation (13) predicts 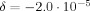 , which is in excellent agreement with the simulation. This was obtained by directly evaluating the standard deviation of all 780,000 randomly chosen values of Φ. Equation (10) predicts χ = 0.0033°, which is also in excellent agreement with the simulation (not shown), but not statistically different from zero.
, which is in excellent agreement with the simulation. This was obtained by directly evaluating the standard deviation of all 780,000 randomly chosen values of Φ. Equation (10) predicts χ = 0.0033°, which is also in excellent agreement with the simulation (not shown), but not statistically different from zero.
Figure 4.
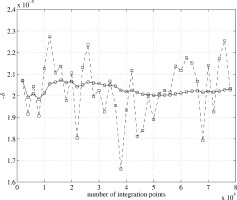
Convergence of the Monte Carlo integration for −δ, the fractional reduction in the magnitude of the MRI signal, for the case that the MRI voxel is coincident with the neuronal activity. Each square is obtained by averaging
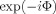 over 20,000 randomly chosen positions as an approximation to Z in Eq. (7), and then evaluating
over 20,000 randomly chosen positions as an approximation to Z in Eq. (7), and then evaluating 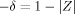 . This process is repeated 39 times, and the circles represent the cumulative average of −δ.
. This process is repeated 39 times, and the circles represent the cumulative average of −δ.
For the second case (offset voxel) Eqs. (10) and (13) are again in excellent agreement with the simulations. As expected δ has a diminished magnitude since only a fraction of the currents are inside the voxel; and χ increases to a maximum value of
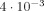 when the voxel is displaced ∼2/3 the size of the active region.
when the voxel is displaced ∼2/3 the size of the active region.
Varying the parameters
Although we have argued in favor of the set of parameters chosen above, in Figure 5 we show δ over a large range of values of the parameter L from 0 to 2.6 μm, keeping the number of active neurons in the voxel at 105. With the same duration as above, namely 100 ms, the largest value of the individual dipole moment would be 2.5 pAm, and hence the net apical dipole moment would be 250 nAm. This would produce a very large MEG signal; and from Figure 5 δ would be almost 1%.
Figure 5.
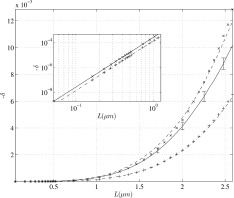
The reduction in the magnitude of the MRI signal as a function of the parameter L defined in Eq. (16). The solid curve with error bars is the result of the simulation with 100,000 neurons each having one apical dendrite and 30 transverse dendrites. The activity is located in a volume of 20 mm3 which is coincident with the MRI voxel. The (x) symbols represent the approximation to −δ given in Eq. (13); it is very accurate for L < 1.5 μm. The (
 ) symbols are obtained from the simulation with just apical dendrites, and the (+) symbols represent Eq. (13) for that case. The (‐‐‐) symbols represent the addition of the simulation results for apical dendrites acting alone with that for the transverse dendrites acting alone; the difference between (‐‐‐) and the solid curve is the result of interference. The inset shows that
) symbols are obtained from the simulation with just apical dendrites, and the (+) symbols represent Eq. (13) for that case. The (‐‐‐) symbols represent the addition of the simulation results for apical dendrites acting alone with that for the transverse dendrites acting alone; the difference between (‐‐‐) and the solid curve is the result of interference. The inset shows that 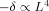 for small L.
for small L.
An unpublished observation has been mentioned [Hagberg et al., 2006] of a 400 nAm dipole moment during epilectic activity. On Figure 5 it is seen that above L = 1.5 δ behaves approximately like L to the power 3, which translates into dipole moment to the power 3/2. We expect, therefore, δ at 400 nAm to be approximately two times its value at 250 nAm, namely 2%. Since the overall phase shift is linear in the dipole moment over this range, we expect it to attain a value of ∼9°. [See Figure 6.] at the end of the paragraph.
Figure 6.
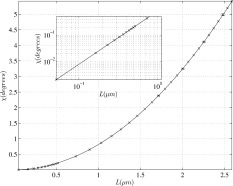
The overall phase shift χ as a function of L when the activity is displaced 2/3 the length of the MRI voxel. The solid curve with very small error bars is the result of the simulation with all dendrites active, and the (x) symbols represent the approximation given in Eq. (10). The inset shows that
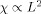 for small L.
for small L.
From the insert on Figure 5 it is seen that for small values of L,
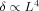 , as expected from Eq. (13). Also shown on Figure 5 is the approximation to δ given by Eq. (13); it is very accurate for L < 1.5 μm.
, as expected from Eq. (13). Also shown on Figure 5 is the approximation to δ given by Eq. (13); it is very accurate for L < 1.5 μm.
The importance of interference can be seen on Figure 5 by comparing the curve with apical and transverse dendrites active together, with the sum of the delta values when they act separately. For our chosen value of L = 0.52 μm interference reduces δ by 14%; but for the largest L‐value shown, it is reduced by 46%.
Another illustration of the effect of interference is obtained from the apical dendrites alone by putting half the dipole moments in the +y‐direction and half in the −y‐direction, which might be due, for example, to excitatory vs. inhibitory postsynaptic potentials. This reduces δ from
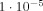 to
to 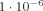 .
.
Figure 6 shows the variation of the overall phase shift χ as a function of the parameter L, when the active cortical region is displaced with respect to the voxel by 2/3 the length of the voxel, which is the approximate separation at which χ has the maximum value. Also shown on Figure 6 is the approximation to χ given by Eq. (10); it is very accurate over the entire range of L‐values shown.
Effect of Diffusion
To estimate the importance of the diffusion term in Eq. (1) we take the example of a single spherical dipole with radius r 0 and moment p pointing in the y‐direction, as in Introduction. Including a spatial gradient in the external field, the complete z‐component of the field becomes
| (23) |
where, as before, r̃ is r or r 0 according as r is greater than or less than r 0, and
| (24) |
Inside the dipole where r̃ is constant the term
 is a linear gradient, and for such a magnetic field there is an analytic solution of Eq. (1) [Abragam, 1961] and somewhat more generally [Stejskal and Tanner, 1964], which clearly exhibits the effect of diffusion. Although this solution is only valid inside the dipole we expect it provides a fair approximation to the effect of diffusion. The result for the magnetization is
is a linear gradient, and for such a magnetic field there is an analytic solution of Eq. (1) [Abragam, 1961] and somewhat more generally [Stejskal and Tanner, 1964], which clearly exhibits the effect of diffusion. Although this solution is only valid inside the dipole we expect it provides a fair approximation to the effect of diffusion. The result for the magnetization is
| (25) |
with
| (26) |
To estimate the final exponential in Eq. (25) we use the following parameters. For the diffusion coefficient of water we take the value
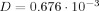 mm2/s obtained in occipital cortex [Darquié et al, 2001]. For a typical applied gradient G we take 0.1 T/m, and for the dipole moment p and the radius r
0 the same values used above, 0.1 pAm and 1μm. G and p are taken to be constant over the time interval t = 100 ms. With these parameters the gradient of the neuronal field has the value
mm2/s obtained in occipital cortex [Darquié et al, 2001]. For a typical applied gradient G we take 0.1 T/m, and for the dipole moment p and the radius r
0 the same values used above, 0.1 pAm and 1μm. G and p are taken to be constant over the time interval t = 100 ms. With these parameters the gradient of the neuronal field has the value 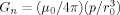 = 0.01 T/m, which is 10% of the applied gradient.
= 0.01 T/m, which is 10% of the applied gradient.
Two cases have to be considered depending upon whether the gradient of the applied field G is in the x‐ direction or perpendicular to it. In the latter case K
2 contains no interference between the applied gradient and the neuronal gradient; and since the applied gradient contributes to the diffusion effect both with and without neuronal current, its effect cancels out in the ratio of the magnetization with neuronal current to that without. With the parameters above the effect of diffusion associated specifically with the neuronal current is to reduce the magnitude of the magnetization by the factor
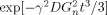 = 0.20.
= 0.20.
As mentioned at the beginning of the article the approximation using spherical dipoles rather than cylindrical dipoles overestimates the magnitude of the neuronal magnetic field and its gradient. Indeed, a cylindrical dipole of length 100 μm having the same moment and radius would produce a gradient of only
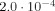 T/m, a factor of 50 less than G
n above. In the absence of interference with the applied gradient this would make the diffusion effect negligible; but interference with an applied gradient of 0.1 T/m would reduce the magnitude of the signal by a factor of 2.
T/m, a factor of 50 less than G
n above. In the absence of interference with the applied gradient this would make the diffusion effect negligible; but interference with an applied gradient of 0.1 T/m would reduce the magnitude of the signal by a factor of 2.
DISCUSSION
We have employed a very simple model of neuronal currents and the magnetic fields they produce to estimate the size of the modification of the MRI signal due to dephasing of the proton magnetic moments. This information is contained in the quantity
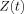 defined in Eq. (7). Although we have assumed the strength of the measurement field B
0 is large compared to that of the neuromagnetic field, Z does not have any explicit dependence on B
0.
defined in Eq. (7). Although we have assumed the strength of the measurement field B
0 is large compared to that of the neuromagnetic field, Z does not have any explicit dependence on B
0.
Our analysis has focused on the overall size of the expected effects, but it is also useful to consider the geometric distribution of the response. In phase mapping the signals will vary approximately linearly across the active region, with peaks of opposite polarity flanking the region. Magnitude changes due to dephasing would be relatively constant across the region. Phase mapping would be expected to produce a rather distinctive signature of neural currents, while dephasing techniques would give rise to spatial distributions similar to those associated with the positive or negative BOLD signals.
The main approximation we have made is to take an estimate of the current dipole moment of a dendrite, current times length, and assign that same moment to a sphere of the same radius. The magnetic field near a point (or sphere) varies more rapidly than that near a line (or cylinder) of the same moment; Eq. (13) shows, therefore, that this approximation overestimates the size of δ, the change in the magnitude of the MRI signal. Similarly, we expect it to overestimate the size of χ, the overall phase shift. We have also shown that it considerably overestimates the importance of diffusion, which probably has only a small effect.
In Eq. (16) we have defined an important length parameter, L, which sets the scale of the falloff of the phase of the transverse magnetization with distance from the current source; L 2 is proportional to the time integral of the dipole moment of the source. A moment of 0.1 pAm acting for 100 ms makes L = 0.52 μm. Such a moment would arise, for example, from a current of 1 nA over a distance of 100 μm.
In the physically important case that the neuromagnetically induced phase
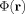 of the transverse magnetization is small the overall phase shift χ of the MRI signal is just the average of Φ over the voxel; and δ is (minus) 1/2 the square of the standard deviation of Φ. This shows that for small values of the phase δ is second order in the product of the current strength and its duration, and hence fourth order in L. Experimental observation of a phase shift in the absence of a significant magnitude change does not, therefore, guarantee that Φ has little spatial variation; it could just be that the currents are too weak to affect δ.
of the transverse magnetization is small the overall phase shift χ of the MRI signal is just the average of Φ over the voxel; and δ is (minus) 1/2 the square of the standard deviation of Φ. This shows that for small values of the phase δ is second order in the product of the current strength and its duration, and hence fourth order in L. Experimental observation of a phase shift in the absence of a significant magnitude change does not, therefore, guarantee that Φ has little spatial variation; it could just be that the currents are too weak to affect δ.
We performed simulations involving 105 active neurons in a voxel volume of 20 mm3, and considered three separate cases: 1 apical dendrite per neuron; 30 dendrites per neuron transverse to the apical direction; and apical and transverse dendrites simultaneously active. All dipoles were assigned a radius of 1.0 μm, and the same value of L. Graphs of the signal magnitude change δ and the overall phase shift χ are presented over a wide range of values of L.
The dominant uncertainty in this model is the product of the estimated current dipole strength in individual dendrites and the duration of the activity, as summarized in the parameter L. Agreement with MEG measurements is a necessary requirement, but is not a sufficient one because MEG measurements at a distance primarily reflect the net dipole moment from neuronal currents. While this may be all that is needed for phase mapping techniques, phase dispersion or signal magnitude depends critically on the local fine structure of the neural magnetic field, which is not directly measured by any existing technique.
Choosing the individual dipole moments to be 0.1 pAm makes the net dipole moment of the 105 apical dendrites equal to 10 nAm, which is a typical value in MEG evoked response experiments. For the duration of the dipole moments we have chosen 100 ms, which is at the upper end of the range seen in MEG evoked response experiments, and is also a typical upper limit for echo time. This combination makes L = 0.52μm. For the case that the MRI voxel is coincident with the cortical activity χ is expected to be zero by symmetry, and the simulation does indeed produce an extremely small overall phase shift. For that same case with the currents active in a volume of 20 mm3, the simulation gives a value
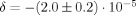 . (See Fig. 5) The analytic approximation given in Eq. (13) is relevant here and gives
. (See Fig. 5) The analytic approximation given in Eq. (13) is relevant here and gives 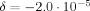 , in excellent agreement with the simulation. With the voxel partially displaced from the cortical activity δ diminishes further and χ approaches a maximum value of
, in excellent agreement with the simulation. With the voxel partially displaced from the cortical activity δ diminishes further and χ approaches a maximum value of 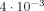 .
.
Other Models and Estimates
A magnetic field of 100 fT at a distance of 2–4 cm outside the head, which is a typical value in an evoked response experiment, was scaled by the inverse square of the distance to a position within 1–2 mm of the effective dipole moment to obtain an estimate for the magnetic field of ≈ 0.1 nT [Bodurka and Bandettini, 2002]. In an experiment with a wire carrying current in a water filled container they were able to detect 40 ms duration current induced field changes as small as 0.2 nT. This represents a phase change of
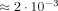 , but does not shed any light on the expected size of the magnitude change.
, but does not shed any light on the expected size of the magnitude change.
In other modeling work [Konn et al., 2003] a set of point dipoles was uniformly placed on a three‐dimensional lattice of spacing 0.1 mm, with each carrying an equal fraction of the net dipole moment; these play a similar role to the apical dendrites of the present paper. From their experimental work using an extended dipole in a phantom [Konn et al., 2003] they say that a magnetic field change of ≈ 0.1 nT could be detected, and this leads to a similar estimate for a detectable phase change [Bodurka and Bandettini, 2002]. They also say that the expected value of the magnitude change is very small.
Another modeling article [Xue et al., 2006] reports a value for the modification of the MRI signal that is about three orders of magnitude larger than our result. Here we summarize the different assumptions made in that article. Their currents [Xue et al., 2006] are taken to be parallel cylinders of radius 0.25 μm and length 1 mm uniformly distributed on a two‐dimensional grid inside a region of dimensions 3 × 3 × 3 mm3 [We have argued that for the same dipole moment spherical sources produce a larger effect on the MRI signal than cylindrical sources.] For the results cited in the Tables [Xue et al., 2006] the current was taken to be 5 nA, making the dipole moment of each source 5 pAm. This is 50 times larger than the value assumed in the present article and as mentioned above would, if all other features were the same (they are not), lead to an increase in δ by a factor 502. This could account for the three orders of magnitude difference in our results: they find [Xue et al., 2006] a 2% reduction in the magnitude of the MRI signal whereas we obtain
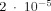 . They also find phase changes as large as 10°.
. They also find phase changes as large as 10°.
With 100,000 simultaneously active parallel currents, as assumed for the values in their Tables [Xue et al., 2006; Xiong, 2006, private communication] the net dipole moment, which is seen at a distance by MEG, is 500 nAm. This is also 50 times larger than the value in the present article, and would produce a very strong magnetic field at a distance of 2–4 cm.
Working in a very low measuring magnetic field strength of a few microtesla the Los Alamos group [Volegov, 2006, private communication] says that in a tightly controlled environment a change in the magnitude of the MRI signal of
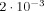 could be detected. This is two orders of magnitude larger than the estimate of the expected value in the present article. However, planned enhancement of the pulsed field strength employed for spin polarization would improve the signal‐to‐noise ratio achieved in the measurements, and could provide at least one order of magnitude improvement.
could be detected. This is two orders of magnitude larger than the estimate of the expected value in the present article. However, planned enhancement of the pulsed field strength employed for spin polarization would improve the signal‐to‐noise ratio achieved in the measurements, and could provide at least one order of magnitude improvement.
Improved estimates of the effect described in this article could be made using a more realistic model of dendritic currents, including their magnitude and geometric arrangement, and possibly including action potentials. Elsewhere we describe computational tools to facilitate such advances [Barrowes et al, in press (b)]. The study of the neuronal modification of the signal as measured in microtesla fields would also be very interesting, especially including the actual time dependence of the current [Kraus et al., 2007a; in press (b)]. Ultra low field MRI measurements would greatly reduce the effects of magnetic susceptibility due, for example, to circulation, respiration and the BOLD effect, thus reducing major sources of physiological noise. Ultra low field MRI also facilitates direct (instead of heterodyned) detection of the NMR signal, which could allow more sensitive and stable measurements of phase and phase dispersion.
CONCLUSION
Using a very simple model of dendritic geometry we have explored the dependence of the phase shift and magnitude of the MRI signal on a length parameter L whose square is proportional to the product of dipole moment and duration, over a large range of values. For values of L up to ≈ 1.5 μm,
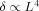 ; and for 1.5 μm < L < 2.6 μm the power is closer to 3. The phase shift is proportional to the second power of L.
; and for 1.5 μm < L < 2.6 μm the power is closer to 3. The phase shift is proportional to the second power of L.
In our numerical simulations we approximate the dendritic currents as spheres, rather than more realistic cylinders. We discuss the advantages of this procedure, and offer our conjecture that for cylinders of length 100 μm or less the geometric restriction on placement of the cylinders in the MRI voxel is not a serious issue. The significant difference is that for the same dipole moment and duration spherical dipoles overestimate the size of the modification of the MRI signal as compared with cylindrical dipoles.
For a net dipole moment of 10 nAm, which is a typical value in evoked response experiments, requiring agreement with MEG data in a very simple manner picks out an approximate value of L = 0.52 μm. This is obtained, for example, from 100,000 apical dendrites with individual dipole moments of 0.1 pAm acting for 100 ms, and leads to an expected reduction in δ, the magnitude of the MRI signal, of
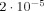 ; it also produces a maximum phase shift of
; it also produces a maximum phase shift of 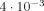 , obtained when the MRI voxel is partially displaced with respect to the neuronal activity. These numerical results are in excellent agreement with an analytic approximation, and with our expectation that δ is generally much smaller than the phase shift.
, obtained when the MRI voxel is partially displaced with respect to the neuronal activity. These numerical results are in excellent agreement with an analytic approximation, and with our expectation that δ is generally much smaller than the phase shift.
On Figures 5 and 6 we show results for signal magnitude and phase shift change up to L = 2.6 μm; in the model described above this would correspond to a very large net dipole moment of 250 nAm. We also extrapolate even further to 400 nAm, where the reduction in δ is ∼2%.
Acknowledgements
We thank Peter Volegov for many informative talks and suggestions regarding the manuscript. We also thank Charles.C. Wood, David Schmidt, Garrett Kenyon, Douglas Ranken, Yoshio Okada, Christof Koch, and Carl Gold for valuable discussions and correspondence. Correspondence with Jinhu Xiong concerning reference [30] is gratefully acknowledged.
A Single Dipole
In this Appendix we work out the steps leading from Eq. (18)– (20) for a single dipole located at the center of the voxel. To evaluate
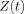 in Eq. (18) we introduce spherical polar coordinates (r, θ, ϕ) with the origin at the dipole and the polar axis along the x direction, hence x = rμ with
in Eq. (18) we introduce spherical polar coordinates (r, θ, ϕ) with the origin at the dipole and the polar axis along the x direction, hence x = rμ with 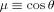 . Note that there is a largest sphere centered at the origin that is contained entirely inside the voxel, of dimension D. For all r < D the angular integrations in Eq. (18) are complete, leading to
. Note that there is a largest sphere centered at the origin that is contained entirely inside the voxel, of dimension D. For all r < D the angular integrations in Eq. (18) are complete, leading to
| (A1) |
As explained in the text, for r < r 0, the radius of the dendrite, r̃ = r 0; and for r > r 0, r̃ = r. We also leave the upper limit of integration, Λ, arbitrary and will examine how Z depends on it; the only requirement on Λ is that it be less than D. The remainder, ε, results from the portion of the voxel volume, V′, that is outside the sphere of radius Λ.
Since L and r 0 are of order microns and the voxel dimensions are millimeters, the phase is small over most of the volume, so it is convenient to add and subtract unity from the integrand. Furthermore, the imaginary part of the integral is an odd function of μ and hence vanishes. This leads to
| (A2) |
From Eq. (A1) the imaginary part of ε can be bounded by
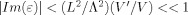 , which means that
, which means that 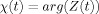 , which is the net phase shift, is negligible for the case being considered here. The real part of ε is
, which is the net phase shift, is negligible for the case being considered here. The real part of ε is 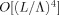 , and, as shown below, represents a fractional error of O(L/D) compared to the integral term in Eq. (A2). We verify below that the integral term itself is small compared to unity, hence
, and, as shown below, represents a fractional error of O(L/D) compared to the integral term in Eq. (A2). We verify below that the integral term itself is small compared to unity, hence
| (A3) |
After carrying out the integration over μ, the portion of the integration for
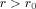 , called
, called 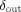 , can be obtained by a change of variable to
, can be obtained by a change of variable to 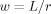 , and leads to
, and leads to
| (A4) |
where
| (A5) |
Note that approximate convergence is achieved if the second term in the brackets in Eq. (A4) is negligible compared to the first. Since Λ may not exceed D, a dimension of the voxel, examination of Figure 2 for
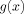 shows that the fractional error resulting from the neglect of that term is
shows that the fractional error resulting from the neglect of that term is 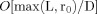 .
.
The portion of the integration for
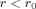 , called
, called 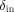 , can similarly be evaluated and leads to
, can similarly be evaluated and leads to
| (A6) |
where
| (A7) |
and j 1 is the spherical Bessel function.
Summing Eqs. (A4) and (A6) leads to
| (A8) |
where
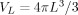 is the volume inside a sphere of radius L and
is the volume inside a sphere of radius L and
| (A9) |
The functions f,g, and k are plotted in Figures 1, 2, and 3. In writing Eq. (A9) we have made use of the assumption
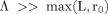 so that the second term in the brackets in Eq. (A4) can be neglected. The ratio of the two terms in Eq. (A9) represents the relative contributions to
so that the second term in the brackets in Eq. (A4) can be neglected. The ratio of the two terms in Eq. (A9) represents the relative contributions to 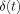 coming from inside and outside the dipole. Comparison of Eqs. (A4) and (A6) shows that the contribution to
coming from inside and outside the dipole. Comparison of Eqs. (A4) and (A6) shows that the contribution to 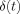 from inside the dipole never exceeds 20% of that from outside, the maximum being achieved for small
from inside the dipole never exceeds 20% of that from outside, the maximum being achieved for small 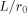 .
.
REFERENCES
- Abragam A ( 1961): The Principles of Nuclear Magnetism. Oxford: Oxford University Press. [Google Scholar]
- Aine C,Huang M,Stephen J,Christner R ( 2000): Multistart algorithms for MEG empirical data analysis reliably characterize locations and time courses of multiple sources. NeuroImage 12: 159–172. [DOI] [PubMed] [Google Scholar]
- Bandettini PA,Petridou N,Bodurka J ( 2005): Direct detection of neuronal activity with MRI: Fantasy, possibility, or reality? Appl Magn Reson 28: 1–24. [Google Scholar]
- Barnes J,Hut P ( 1986): A hierarchical O(NlogN) force‐calculation algorithm. Nature 324: 446–449. [Google Scholar]
- Barrowes BE,George JS,Heller L (a): Estimating the contribution to MRI signals due to neuronal activity using a multilevel approach,(in press).
- Barrowes BE,Teeter C,George JS (b): On modeling the magnetic field produced by active neurons with complex morphologies, (in press).
- Bodurka J,Jesmanowicz A,Hyde JS,Xu H,Estowski L,Li S‐J( 1999): Current‐induced magnetic resonance phase imaging. J Magn Reson 137: 265–271. [DOI] [PubMed] [Google Scholar]
- Bodurka J,Bandettini PA ( 2002): Toward direct mapping of neuronal activity: MRI detection of ultraweak, transient magnetic field changes. Magn Reson Med 47: 1052–1058. [DOI] [PubMed] [Google Scholar]
- Cannon RC,Turner DA,Pyapali GK,Wheal HV ( 1998): An on‐line archive of reconstructed hippocampal neurons. J Neurosci Methods 84: 49–54. [DOI] [PubMed] [Google Scholar]
- Chu R,de Zwart JA,van Gelderen P,Fukunaga M,Kellman P,Holroyd T,Duyn JH ( 2004): Hunting for neuronal currents: Absence of rapid MRI signal changes during visual‐evoked response. NeuroImage 23: 1059–1067. [DOI] [PubMed] [Google Scholar]
- Dale AM,Liu AK,Buckner BR,Belliveau JW,Lewine JD,Halgren E ( 2000): Dynamic statistical parametric mapping: Combining fMRI and MEG for high resolution imaging of cortical activity. Neuron 26: 55–67. [DOI] [PubMed] [Google Scholar]
- Darquié A,Poline J‐B,Poupon C,Saint‐Jalmes H,Le Bihan D ( 2001): Transient decrease in water diffusion observed in human occipital cortex during visual stimulation. Proc Natl Acad Science USA 98: 9391–9395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duke‐Southampton archive of neuronal morphology format ( 2005): Available at: http://ux.koki.hu/gulyas/ca1cells/dsaformat.htm
- George JS,Schmidt DM,Rector DM,Wood CC ( 2001): Dynamic functional neuroimaging integrating multiple modalities In: Jezzard, Matthewand Smith, editors. Functional MRI: An Introduction to Methods. Oxford: Oxford University Press; pp 352–383. [Google Scholar]
- George JS,Aine CJ,Mosher JC,Ranken DM,Schlitt HA,Wood CC,Lewine JD,Sanders JA,Belliveau JW ( 1995): Mapping function in the human brain with MEG anatomical MRI and functional MRI. J Clin Neurophysiol 12: 406–431. [DOI] [PubMed] [Google Scholar]
- Hagberg GE,Bianciardi M,Maraviglia B ( 2006): Challenges for detection of neuronal currents by MRI. Magn Reson Imaging 24: 483–493. [DOI] [PubMed] [Google Scholar]
- Hämäläinen M,Hari R,Ilmoneimi R,Knuutila J,Lounäsmää OV ( 1993): Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Revs Mod Phys 65: 413–497. [Google Scholar]
- Hammersley JH ( 1960): Related problems 3. Monte‐Carlo methods for solving multivariable problems. Ann NY Acad Sci 86: 844–874. [Google Scholar]
- Heller L ( 2004): The magnetic field inside special conducting geometries due to internal current. IEEE Trans Biomed Eng 51: 1310–1318. [DOI] [PubMed] [Google Scholar]
- Jun SC,George JS,Plis SM,Ranken DM,Schmidt DM,Wood CC ( 2006): Improving source detection and separation in a spatiotemporal Bayesian inference dipole analysis. Phys Med Biol 51: 2395–2414. [DOI] [PubMed] [Google Scholar]
- Kamei H,Iramina K,Yoshikawa K,Ueno S ( 1999): Neuronal current distribution imaging using magnetic resonance. IEEE Trans Magn 35: 4109–4111. [Google Scholar]
- Konn D,Gowland P,Bowtell R ( 2003): MRI detection of weak magnetic fields due to an extended current dipole in a conducting sphere: A model for direct detection of neuronal currents in the brain. Magn Reson Med 50: 40–49. [DOI] [PubMed] [Google Scholar]
- Kraus RH Jr,Espy MA,Volegov PL,Matlachov AN,Mosher JC,Urbaitis AV,Zotev VS( 2007a): Toward SQUID‐based direct measurement of neural currents by nuclear magnetic resonance. IEEE Trans Appl Superconduct 17: 854–857. [Google Scholar]
- Kraus RH Jr,Volegov P,Matlachov A( b): Toward direct neural current imaging by resonant mechanisms at ultra‐low field, (in press). [DOI] [PubMed]
- Lin FH,Wald LL,Alhfors SP,Hämäläinen MS,Kwong KK,Belliveau JW 2006: Dynamic magnetic resonance inverse imaging of human brain function. Magn Reson Med 56: 787–802 [DOI] [PubMed] [Google Scholar]
- Matlachov A,Volegov PL,Espy MA,George JS,Kraus RH Jr ( 2004): SQUID‐detected NMR in microtesla magnetic fields. JMag Reson 170: 1–7. [DOI] [PubMed] [Google Scholar]
- Matlachov AN,Volegov PL,Zotev VS,Espy MA,Mosher JC, Kraus, RH Jr ( 2007): Using ultra‐low field nuclear magnetic resonance for direct neural current measurements. International Congress Series Volume 1300, supplement, 582–585. [Google Scholar]
- McDermott R,Kelso N,Lee S‐K,Mößle M,Mück M,Myers W,ten Haken B,Seton HC,Trabesinger AH,Pines A,Clarke J ( 2004): SQUID‐detected magnetic resonance imaging in microtesla magnetic fields. J Low Temp Phys 135: 793–821. [Google Scholar]
- Park TS,Lee SY,Park J‐H,Cho MH,Soo YL ( 2006): Observation of the fast response of a magnetic resonance signal to neuronal activity: A snail ganglia study. Physiol Meas 27: 181–190. [DOI] [PubMed] [Google Scholar]
- Petridou N,Plenz D,Silva AC,Loew M,Bodurka J,Bandettini PA ( 2006): Direct magnetic resonance detection of neuronal electrical activity. PNAS 103: 16015–16020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH,Flannery BP,Teukolsky SA,Vetterling WT ( 1992): Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed Cambridge (UK) and New York: Cambridge University Press. [Google Scholar]
- Pruessmann KP,Weiger M,Scheidegger MB,Boesiger P ( 1999): SENSE: Sensitivity encoding for fast MRI. Magn Res Med 42: 952–962. [PubMed] [Google Scholar]
- Sodickson DK,Manning WJ ( 1997): Simultaneous acquisition of spatial harmonics (SMASH): Fast imaging with radiofrequency coil arrays. Magn Reson Med 38: 591–603. [DOI] [PubMed] [Google Scholar]
- Stejskal EO,Tanner JE ( 1964): Spin diffusion measurements: Spin echos in the presence of a time‐dependent field gradient. J Chem Phys 42: 288–292. [Google Scholar]
- Torrey HC ( 1956): Bloch equations with diffusion terms. Phys Rev 104: 563–565. [Google Scholar]
- Xiong J,Fox PY,Gao JH ( 2003): Directly mapping magnetic field effects of neuronal activity by Magnetic Resonance Imaging. Hum Brain Mapp 20: 41–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue Y,Gao J‐H,Xiong J ( 2006): Direct MRI detection of neuronal magnetic fields in the brain: Theoretical modeling. NeuroImage 31: 550–559. [DOI] [PubMed] [Google Scholar]


