Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2007 Mar 29;29(2):142–156. doi: 10.1002/hbm.20379

Modeling low‐frequency fluctuation and hemodynamic response timecourse in event‐related fMRI

Kendrick N Kay 1, Stephen V David 2,5, Ryan J Prenger 3, Kathleen A Hansen 1,6, Jack L Gallant 1,4,✉
PMCID: PMC6871156  PMID: 17394212

Abstract

Functional magnetic resonance imaging (fMRI) suffers from many problems that make signal estimation difficult. These include variation in the hemodynamic response across voxels and low signal‐to‐noise ratio (SNR). We evaluate several analysis techniques that address these problems for event‐related fMRI. (1) Many fMRI analyses assume a canonical hemodynamic response function, but this assumption may lead to inaccurate data models. By adopting the finite impulse response model, we show that voxel‐specific hemodynamic response functions can be estimated directly from the data. (2) There is a large amount of low‐frequency noise fluctuation (LFF) in blood oxygenation level dependent (BOLD) time‐series data. To compensate for this problem, we use polynomials as regressors for LFF. We show that this technique substantially improves SNR and is more accurate than high‐pass filtering of the data. (3) Model overfitting is a problem for the finite impulse response model because of the low SNR of the BOLD response. To reduce overfitting, we estimate a hemodynamic response timecourse for each voxel and incorporate the constraint of time‐event separability, the constraint that hemodynamic responses across event types are identical up to a scale factor. We show that this technique substantially improves the accuracy of hemodynamic response estimates and can be computed efficiently. For the analysis techniques we present, we evaluate improvement in modeling accuracy via 10‐fold cross‐validation. Hum Brain Mapp, 2008. © 2007 Wiley‐Liss, Inc.

Keywords: hemodynamic response function, low‐frequency noise, model evaluation, cross‐validation, reverse correlation

INTRODUCTION

Event‐related functional magnetic resonance imaging (fMRI) experimental designs offer several important advantages over block designs: more efficient estimates of the timing and shape of the hemodynamic response (HDR), increased flexibility in experimental design and analysis, and reduction of anticipation and adaptation effects [Josephs and Henson, 1999; Zarahn et al., 1997a]. However, event‐related fMRI has reduced statistical power for detecting signal activations [Liu, 2004]. In addition, event‐related fMRI increases the complexity of the data and the assumptions underlying the data analysis (e.g. temporal linearity of the BOLD response). It is therefore critical to maximize precision and accuracy in the analysis of event‐related fMRI data.

In this study we address three problems in the analysis of event‐related fMRI data. Many of the specific techniques we present have been published previously. The goal of the present study is to evaluate rigorously and systematically the value of these techniques, applied in concert, on empirical data. We emphasize cross‐validation predictive performance as an objective metric for quantifying model accuracy. (This is in contrast to such metrics as reproducibility and statistical significance, which are important but not directly related to model accuracy.) We also emphasize single voxel modeling, which is likely to become increasingly important as the spatial resolution and signal‐to‐noise ratio (SNR) of fMRI improve.

One problem in event‐related fMRI analysis is variation in the HDR across voxels [Aguirre et al., 1998; Handwerker et al., 2004; Miezin et al., 2000; Neumann et al., 2003; Saad et al., 2001]. Although the assumption of a canonical HDR function (HRF) is common in fMRI analyses, this assumption may lead to incorrect data inferences [Burock and Dale, 2000; Handwerker et al., 2004]. We avoid the assumption of an a priori HRF by adopting the framework of the finite impulse response (FIR) model [Dale, 1999]. Under the FIR model, a HDR is estimated for each voxel to each event type, and there is no constraint on the shape of the responses.

A second problem is the large amount of low‐frequency noise fluctuation (LFF) in blood oxygenation level dependent (BOLD) time‐series data [Aguirre et al., 1997; Purdon and Weisskoff, 1998; Zarahn et al., 1997b]. LFF has been attributed to scanner and physiological noise [Smith et al., 1999; Zarahn et al., 1997b]. We compensate for LFF by using polynomials [Liu et al., 2001] as regressors for the baseline signal level, i.e. the signal level associated with the absence of the stimulus. We show that this technique improves the SNR and is more accurate than high‐pass filtering of the time‐series data. Moreover, we show that polynomials can produce more accurate results than Fourier basis functions.

A third problem is model overfitting. Overfitting tends to occur when a model has a large number of parameters relative to the amount of available data. To reduce overfitting by the FIR model, we incorporate the constraint of time‐event separability. This is the constraint that HDR estimates across event types are identical up to a scale factor, and is reasonable for many experimental paradigms. In a related study, Hinrichs et al. [2000] confirmed increased estimation efficiency under the time‐event separable model. We extend their results by demonstrating a simple, fast method for fitting the time‐event separable model and by confirming improved cross‐validation predictive performance.

We evaluate the proposed analysis techniques on empirical data. These data were obtained from occipital cortex during brief presentations of a checkerboard pattern at different locations in the visual field. Data from this experiment are especially useful for methodological development, because the stimulus is tightly controlled, the SNR is robust, and the data are richly structured. In addition, the sheer number of activated voxels makes it easy to discern population effects. To maximize precision, we analyze the data at the single voxel level, with no spatial smoothing or spatial averaging. We also summarize results from data involving other stimulus designs.

MATERIALS AND METHODS

Stimulus

The stimulus design was similar to that of a previous study from our laboratory [Hansen et al., 2004]. The stimulus consisted of a 7.5‐Hz contrast‐reversing checkerboard pattern presented within 12 wedges of 30° polar angle width (Fig. 1). The pattern had a radial spatial frequency of 12 cycles per revolution and was scaled with eccentricity. At any given time, the pattern was presented within each wedge at 0% (OFF) or 99% (ON) Michelson contrast. The presentation timing was controlled by an m‐sequence of level 2, order 8, and length 28 − 1 = 255. The m‐sequence was cyclically shifted by 21 elements to produce the ON–OFF pattern for each wedge. The bin duration of the m‐sequence was 4 s, and the total stimulus duration was 255 trials × 4 s = 17 min. For each wedge, there was a total of 128 ON states and 127 OFF states. The minimum, maximum, and mean stimulus onset asynchrony for a given wedge was 4 s, 32 s, and 8 s, respectively.

Figure 1.

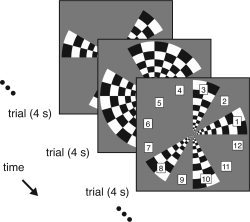
Figure 1

Open in a new tab

Schematic of visual stimulus. The stimulus consisted of a 7.5‐Hz contrast‐reversing checkerboard pattern presented within 12 wedges in the visual field. A cyclically shifted binary m‐sequence controlled the presentation timing for each wedge. Each trial lasted 4 s, and there were 255 consecutive trials. For data analysis we define 12 event types, one event type per wedge.

The use of an m‐sequence minimizes correlations between wedges and enables efficient estimation of HDRs [Buracas and Boynton, 2002; Liu, 2004]. m‐Sequences have been used in other fMRI studies [de Zwart et al., 2005; Hansen et al., 2004; Kellman et al., 2003]. Code for m‐sequence generation was provided by T. Liu (http://fmriserver.ucsd.edu/ttliu/mttfmri_toolbox.html).

The stimulus was displayed by an Epson PowerLite 7700p LCD projector (Epson America, Long Beach, CA) fitted with a custom zoom lens (Buhl Optical, Rochester, NY). The image was focused onto a semitranslucent backprojection screen (Aeroview 100 material, Stewart Filmscreen, Torrance, CA). The subject viewed the screen via a first‐surface mirror. The viewing distance was 38 cm, and the stimulus subtended 20° × 20° of visual angle. An occluding device prevented the subject from seeing the unreflected image of the screen. During stimulus presentation, the subject performed a change detection task at a central fixation dot (the mean interval between changes was 2 s). An optical button response box (Current Designs, Philadelphia, PA) recorded subject responses.

The projector operated at a resolution of 1,024 × 768 at 60 Hz. Luminance output was measured using a Minolta LS‐110 photometer (Konica Minolta Photo Imaging, Mahwah, NJ), and the luminance response was linearized via a lookup table. The mean luminance of the stimulus was ∼550 cd/m2. The stimulus was time‐locked to the projector refresh rate and synchronized to scanner data acquisition. A Macintosh PowerBook G4 computer (Apple Computer, Cupertino, CA) controlled stimulus presentation and logged button responses, using software written in MATLAB 5.2.1 (The Mathworks, Natick, MA) and Psychophysics Toolbox 2.53 [Brainard, 1997; Pelli, 1997].

Data Collection

The experimental protocol was approved by the UC Berkeley Committee for the Protection of Human Subjects. MRI data were collected at the Brain Imaging Center at UC Berkeley using a 4 T INOVA MR scanner (Varian, Palo Alto, CA) with a whole‐body gradient set capable of 35 mT/m with a rise time of 300 μs (Tesla Engineering, Sussex, UK). A curvilinear quadrature transmit/receive surface coil (Midwest RF, LLC, Hartland, WI) was positioned over the occipital pole for enhanced MR SNR. Head motion was minimized with foam padding. Manual shimming of the magnetic field was used to improve image quality and reduce image distortion.

Coronal slices covering occipital cortex were selected: 16 slices, slice thickness 1.8 mm, slice gap 0.2 mm, field‐of‐view 128 × 128 mm2, matrix size 64 × 64, and nominal resolution 2 × 2 × 2 mm3. For BOLD data, a T2*‐weighted, single‐shot, slice‐interleaved, gradient‐echo echo planar imaging (EPI) sequence was used: TR 1 s, TE 0.028 s, flip angle 20°. An initial dummy period was included to allow magnetization to reach steady‐state.

During stimulus presentation, the first eight trials were repeated after the end of the 255‐trial sequence. BOLD data were collected up through the last trial, and data collected during the initial 8 s × 4 s = 32 s were ignored [Kellman et al., 2003]. This strategy avoids potential attentional artifacts at the beginning and end of stimulus presentation, compensates for the delay in the HDR, and allows complete sampling of the m‐sequence.

Data Preprocessing

A nonlinear phase correction was applied to the image data to reduce Nyquist ghosts and image distortion. Differences in slice acquisition times were corrected via sinc interpolation. To compensate for slow changes in head position, SPM99 motion correction was performed with the following modification: motion parameter estimates were low‐pass filtered at 1/20 Hz to remove high‐frequency modulations caused by signal activations [Freire and Mangin, 2001]. No additional spatial or temporal filtering was applied.

FIR Model

Our analysis approach is based on the FIR model for event‐related fMRI [Dale, 1999]. Our earlier reverse correlation approach [Hansen et al., 2004] is a special case of the FIR model, applicable when stimulus events are uncorrelated.

In the FIR model, the BOLD signal is assumed to be a linear, time‐invariant system with respect to the stimulus. A HDR is estimated for each stimulus event type using a set of shifted delta functions as regressors. No assumption on the shape of HDRs is made. Additional regressors are used to model the baseline signal level, i.e. the signal level associated with the absence of the stimulus. The model characterizes two types of effects in the data: stimulus effects consist of the transient HDRs to stimulus events, and nuisance effects consist of the persistent baseline signal level that may vary over time.

Let e be the number of event types, l be the number of time points in one HDR, m be the number of nuisance terms, and t be the number of time‐series data points. The time‐series data are modeled as y=Xh+Sb+n, where y is the data (t × 1), X is the stimulus matrix (t × el), h is the concatenation of the HDR associated with each event type (el × 1), S is the nuisance matrix (t × m), b is a set of nuisance parameters (m × 1), and n is a noise term (t × 1). The stimulus matrix is the concatenation of the stimulus convolution matrix for each event type. The stimulus convolution matrix for a given event type consists of shifted versions of a binary sequence, where ones indicate event occurrences (Fig. 2). Stimulus effects are given by Xh, and nuisance effects are given by Sb.

Figure 2.

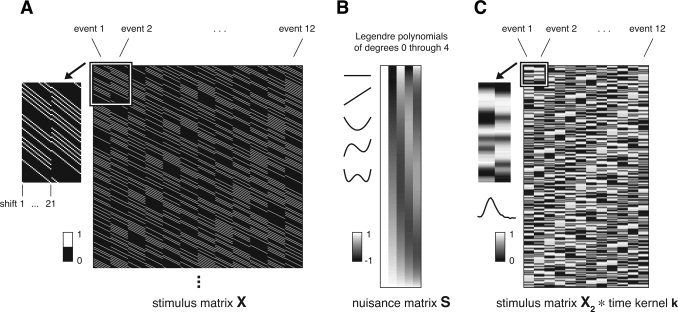
Figure 2

Open in a new tab

Schematic of data models. (A) Stimulus matrix X (FIR model). The matrix dimensions are 1,020 time points × 252 parameters. The matrix is the concatenation of the stimulus convolution matrix for each of the 12 event types. The stimulus convolution matrix for a given event type consists of shifted versions of a binary sequence, where ones indicate event occurrences. There are 21 shifts, one shift for each time point in the HDR estimate. The inset (upper‐left) depicts an enlarged view of the parameters for the first two event types. (B) Nuisance matrix S (polynomial version). The matrix dimensions are 1,020 time points × 5 parameters. The matrix consists of Legendre polynomials of degrees 0 through 4. The inset (upper‐left) depicts the polynomials in a line format. (C) Convolution of stimulus matrix X 2 and time kernel k (time‐event separable model). The matrix dimensions are 1,020 time points × 12 parameters. Stimulus matrix X 2 (1,020 × 12) consists of one parameter for each of the 12 event types. The parameter for a given event type is a binary sequence, where ones indicate event occurrences. Time kernel k (21 × 1) is a voxel‐specific response timecourse estimated from the data. The inset (upper‐left) depicts an enlarged view of the parameters for the first two event types. The inset (left) depicts the time kernel in a line format.

For our data, there are a total of 1,020 time‐series data points (t = 1,020). We define 12 event types, one event type per wedge (e = 12). We treat the ON state (99% contrast) of a wedge at the beginning of a trial as an event occurrence. We estimate a HDR of duration 20 s for each event type (l = 21). The baseline signal level is the signal level associated with viewing the fixation dot against the gray background.

Modeling LFF

We evaluate several versions of the FIR model. These versions differ in how they compensate for LFF.

In the simple version of the FIR model, LFF is ignored and nuisance matrix S consists of only a constant term. This constant term characterizes the baseline signal level as a DC offset in the time‐series data. HDR estimates obtained under this version of the FIR model will be poor if the magnitude of LFF is large. This is because LFF adds noise to the time‐series data.

One strategy for compensating for LFF is to include in nuisance matrix S regressors that model the timecourse of LFF. This strategy enables the modeled baseline signal level to vary over time. Fourier basis functions are commonly used as regressors; in this case, the nuisance matrix consists of a constant term and a set of sine and cosine functions. A different choice of regressors is a set of polynomials of increasing degree (Fig. 2). We use Legendre polynomials [Liu et al., 2001] which are pairwise orthogonal. Equivalent model fits can be obtained with other sets of polynomials (e.g., 1, t, t 2, etc.) that span the same subspace as Legendre polynomials.

Another strategy for compensating for LFF is to detrend the time‐series data as a preprocessing step [Kruggel et al., 1999; Marchini and Ripley, 2000; Skudlarski et al., 1999; Tanabe et al., 2002]. We use a high‐pass filtering technique: we first remove a linear trend to avoid wrap‐around effects and then high‐pass filter the data. On the filtered data, we fit the simple version of the FIR model in which nuisance matrix S consists of a constant term.

Time‐Event Separable Model

The FIR model uses a large number of parameters to characterize stimulus effects. In our case, there are (e = 12) × (l = 21) = 252 parameters in stimulus matrix X and only 1,020 data points. Given the limited amount of data available in a typical fMRI experiment, the FIR model risks overfitting the data.

To reduce the number of model parameters, we incorporate the constraint of time‐event separability. This is the condition that HDR estimates across event types are identical up to a scale factor. (More loosely, time‐event separability is the condition that the shape of the HDR is the same for any event type.) Under the time‐event separable model, stimulus effects are characterized by a single response timecourse—the time kernel—and an amplitude value for each event type. The HDR to an event type is the product of the time kernel and the amplitude value associated with the event type.

The time‐series data are modeled as y=(X 2 *k)h 2+Sb+n, where X 2 is the stimulus matrix (t × e), k is the time kernel (l × 1), * represents convolution, h 2 is a set of event amplitudes (e × 1), and S, h, and n are as in the FIR model. The stimulus matrix consists of one parameter for each event type. The parameter for a given event type is a binary sequence, where ones indicate event occurrences (Fig. 2). Stimulus effects are given by (X 2 *k)h 2, and nuisance effects are given by Sb.

For our data, the time‐event separable model uses (l = 21) + (e = 12) = 33 parameters to characterize stimulus effects. This is much fewer than the 252 parameters used in the FIR model.

Model Fitting

We fit the FIR model by obtaining the ordinary least‐squares estimate 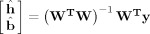Inline graphic where W=[X S]. This produces ĥ, a set of HDR estimates, and b̂, a set of nuisance parameter estimates.

We fit the time‐event separable model using two different methods. In the first method (SEPNL), we use an iterative fitting approach [Hinrichs et al., 2000]. We estimate the time kernel, event amplitudes, and nuisance parameters using nonlinear least‐squares optimization (MATLAB Optimization Toolbox, Levenberg‐Marquardt method). This method determines all model parameters simultaneously, minimizing the squared error between the model fit and the data. A disadvantage of the iterative fitting method is that it is computationally intensive—the method may be impractical given that thousands of voxels are analyzed in a typical fMRI experiment. Also, the fitting method may converge to a local minimum of the error function.

In the second method for fitting the time‐event separable model (SEPSVD), we estimate the time kernel before the other model parameters. This approach avoids iterative computation but may not produce an optimal model fit (in the least‐squares sense). The method proceeds as follows. We obtain HDR estimates ĥ from the FIR model. We reshape ĥ into a matrix with rows corresponding to event types and columns corresponding to time points (e × l). We perform singular value decomposition on this matrix to obtain the singular vector associated with the largest singular value. This vector is the l‐dimensional vector along which variance in ĥ is maximized; this is the time kernel estimate k̂. (Another way to conceptualize k̂ is as the l‐dimensional vector that best reconstructs ĥ in the least‐squares sense.) Using k̂, we obtain the ordinary least‐squares estimate 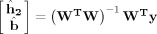Inline graphic where W = [(X2 * k̂)S]. This produces ĥ 2, a set of event amplitude estimates, and b̂, a set of nuisance parameter estimates. Note that the time kernel estimate is based on the FIR model fit. Thus, overfitting by the FIR model has some effect on the time kernel estimate. In practice, however, the SEPSVD method performs quite well (see Results).

To obtain standard errors on the parameter estimates of a model, we use a nonparametric jackknife procedure [Efron and Tibshirani, 1993]. We randomly divide the time‐series data points into 10 subsets and fit the model 10 times, each time with a different subset excluded. (To exclude data points, we delete rows of y and the corresponding rows of X, S, and X 2 *k.) Standard errors are calculated from the distributions of parameter estimates across the 10 model fits.

To quantify the amplitude of a HDR, we sum over a time window corresponding to the peak of the positive BOLD response [de Zwart et al., 2005]. (For our data, we use the time window of 3–7 s based on inspection of HDR estimates across voxels and event types (Fig. 3).) We quantify the SNR of an event type as the absolute value of the HDR amplitude divided by the standard error of the HDR amplitude. (The standard error is calculated via a jackknife procedure; see earlier.) We quantify the SNR of a voxel as the maximum SNR achieved over all event types. We calculate percent BOLD change relative to the DC parameter estimate (i.e. the parameter estimate for the constant term included in the nuisance matrix).

Figure 3.

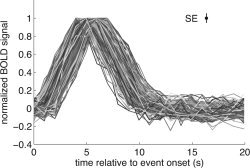
Figure 3

Open in a new tab

Inspection of HDR estimates across voxels and event types. Using the POLY model (FIR model combined with polynomials), we obtained for each voxel an estimate of the HDR to each of the 12 event types. The figure depicts positive HDR estimates with a SNR of at least 30 (n = 216 from 212 unique voxels). The x‐axis indicates time relative to event onset; the y‐axis indicates the BOLD signal. For display purposes, each HDR estimate is normalized by dividing by its maximum value. The inset indicates the median standard error for the depicted data points. The robustness of the shapes of the timecourses indicates the high SNR in the data, despite the small voxel size (2 mm) and the moderate amount of data (17 min).

In one instance we use an alternative SNR metric, which we denote by SNRalt. This metric is useful for comparing the SNR of different models. For a given voxel, we calculate the maximum absolute HDR amplitude (MAX) obtained under any of the models. We then quantify the SNRalt for each model as MAX divided by the median standard error on HDR amplitudes across events. This metric prevents variability in HDR amplitude estimates from influencing SNR values.

Note that the SNR metrics described earlier are similar to the conventional t‐statistic. Thus, one can interpret changes in SNR in terms of statistical significance and effect size. For example, suppose we wish to detect a signal change whose magnitude is four times the magnitude of the noise, given a fixed amount of data. At an α value of 0.001 and 9 degrees of freedom (10 jackknifes were taken), the power to detect such a change is 0.23. With a 50% increase in SNR, the power to detect such a change increases to 0.87.

To quantify the magnitude of LFF, we calculate the median absolute deviation (relative to the mean) of the time points of the estimated nuisance effects. We convert the raw BOLD units to standard deviation units, where one standard deviation unit equals the standard deviation of the time‐series data with the nuisance effects subtracted. We define the resulting quantity as the LFF magnitude index. Intuitively, this index quantifies the typical deviation of the baseline signal level over the course of the time‐ series. For example, a value of 0.4 indicates that, on average, the baseline signal level is 0.4 standard deviation units away from the mean baseline signal level.

Model Evaluation

We quantify the fit accuracy of a model as the coefficient of multiple determination (R 2) between the data and the model fit to the data. This value is the amount of variance in the data explained by the model fit.

When comparing models, an improvement in fit accuracy could reflect improvement in model accuracy, but could also reflect model overfitting. To measure the accuracy of a model while controlling for overfitting, we use a nonparametric n‐fold cross‐validation procedure where n = 10. We randomly divide the time‐series data points into 10 subsets. We exclude one subset and fit the model on the remaining data points. (To exclude data points, we delete rows of y and the corresponding rows of X, S, and X 2 * k.) We use the obtained model parameter estimates to predict the data in the excluded subset. The process is repeated 10 times, such that each subset is excluded once. We thereby obtain a prediction for each data point. We quantify the prediction accuracy of a model as the coefficient of multiple determination (R 2) between the data and the model prediction of the data. This value is the amount of variance in the data explained by the model prediction. The prediction accuracy of a model is how well the model generalizes to new data, i.e. data not used in the fitting of the model.

LFF often dominate the variance in the time‐series data. In these cases, the coefficient of multiple determination is artificially high (e.g., ≫ 0.9) and reflects primarily how well LFF is modeled. To obtain a prediction accuracy metric that reflects strictly how well stimulus effects are modeled, we perform the following procedure. We subtract the predicted nuisance effects from both the original data and the model prediction. We then calculate the coefficient of multiple determination between the adjusted data and adjusted prediction. We define the resulting value as the LFF‐adjusted prediction accuracy. (Because the predicted nuisance effects are only estimates and not the true nuisance effects, the metric is potentially biased. However, we observe the same trends in model performance with either prediction accuracy metric.)

In the present context, the coefficient of multiple determination (R 2) directly quantifies how well a given model explains the observed data. Reporting R 2 values is not common in the literature [one exception is Razavi et al., 2003]. When comparing models with respect to R 2 values, a difference of 1–2% can be considered a small effect, a difference of 5% can be considered a moderate effect, and a difference of 10% can be considered a large effect.

Additional Data Sets

We also collected data sets using different subjects, imaging parameters, and stimulus designs. From the perspective of the present study, there is no specific motivation for the particular characteristics of these other data sets. The purpose of these additional data sets is to show that results are not specific to a particular experiment.

Data set 1 is the primary data set described earlier, and involved subject KH (an author). Data set 2 involved subject KK (an author), a volume coil, a two‐shot EPI sequence (TR 1 s per shot), and a 3 × 3 × 3 mm3 voxel size. The stimulus was the same as in data set 1.

Data set 3 involved subject TN and a 2 × 2 × 2.5 mm3 voxel size. The stimulus consisted of achromatic sinusoidal gratings of eight different orientations. One trial consisted of the presentation of a grating for 1 s followed by 3 s of a gray background. The eight orientations were repeated 15 times each, and the presentation order was randomly chosen. The stimulus alternated between 16‐s periods during which a gray background was presented and 80 s periods during which trials were presented. The stimulus duration was 9.9 min. For data analysis we used eight event types, one event type for each grating orientation.

Data set 4 involved subject TN and a 2 × 2 × 2.5 mm3 voxel size. The stimulus consisted of 12 grayscale natural photos. One trial consisted of the presentation of a photo for 1 s followed by 3 s of a gray background. Each photo was repeated 13 times; the presentation order was controlled by an m‐sequence of level 13, order 2, and length 132 − 1 = 168. The stimulus duration was 11.2 min. For data analysis we used 12 event types, one event type for each distinct photo.

RESULTS

We collected data using multiple subjects, imaging parameters, and stimulus designs. Our analysis results were largely consistent across data sets. In this section we present in‐depth results for a single data set (Figs. 1, 2, 3, 4, 5, 6, 7, 8), indicate which results were variable in other data sets, and summarize results for all data sets (Fig. 9).

Figure 4.

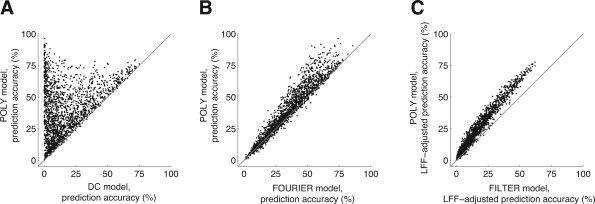
Figure 4

Open in a new tab

Modeling LFF with polynomials maximizes prediction accuracy. In these graphs we compare different strategies for LFF compensation (Table I). For each graph, we selected voxels with a minimum SNR of 10 under either of the models being compared. Each point in a graph represents prediction accuracy for a single voxel. (A) DC vs. POLY. The x‐ and y‐axes indicate prediction accuracy under the DC and POLY models, respectively. There was a large increase in accuracy under the POLY model compared to the DC model (n = 1904; median increase 14.8%; P < 0.001). This indicates that ignoring LFF resulted in model fits with poor generalizability, and that a substantial amount of LFF exists in the time‐series data. Some voxels exhibited very large increases in prediction accuracy; in these cases, the contribution of LFF to variance in the time‐series data is much larger than the contribution of stimulus effects. (B) FOURIER vs. POLY. The x‐ and y‐axes indicate the prediction accuracy under the FOURIER and POLY models, respectively. There was a small increase in accuracy under the POLY model compared to the FOURIER model (n = 1,971; median increase 2.3%; P < 0.001). This indicates polynomials more accurately characterized LFF compared to Fourier basis functions in this data set. (C) FILTER vs. POLY. The x‐ and y‐axes indicate the LFF‐adjusted prediction accuracy under the FILTER and POLY models, respectively. There was a large increase in accuracy under the POLY model compared to the FILTER model (n = 1,880; median increase 6.5%; P < 0.001). This indicates that stimulus effects were better characterized when polynomials were used to model LFF compared to when the time‐series data were high‐pass filtered to remove LFF.

Figure 5.

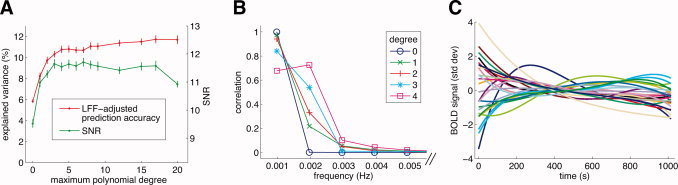
Figure 5

Open in a new tab

Characteristics of LFF. (A) The effect of the maximum polynomial degree on model performance. We manipulated the maximum degree of the polynomials included in the POLY model (x‐axis) and evaluated the effect on LFF‐adjusted prediction accuracy (y‐axis; red line) and SNR (y‐axis; green line). For this graph we selected voxels with a minimum SNR of 10 under any of the model variants (n = 2,890). Dots indicate the median across voxels, and error bars indicate ±1 SE (bootstrap procedure). With increasing polynomial degree, both LFF‐adjusted prediction accuracy and SNR dramatically increased. (B) Spectral content of Legendre polynomials of degrees 0 through 4. The polynomials extend over the course of the time‐series data (17 min). We calculated the discrete Fourier transform of each polynomial after applying a Hanning window to avoid edge artifacts and subtracting the mean value. The correlation (y‐axis) between the time‐series data and the Fourier component at each frequency (x‐axis) is plotted. For display purposes the zero‐frequency point is omitted. Note that the polynomials consist predominantly of very low frequencies (0–0.004 Hz). (C) Example timecourses of LFF. For 25 voxels we plot nuisance effects as determined under the POLY model. These voxels were randomly selected from voxels with a minimum SNR of 10 (n = 1,730). The x‐axis indicates time; the y‐axis indicates standard deviation units (see Methods). For display purposes, the mean of each timecourse is removed.

Figure 6.

Figure 6

Open in a new tab

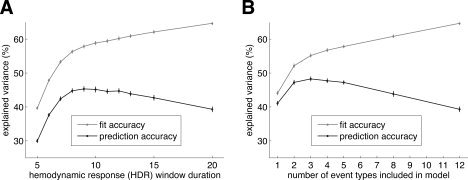
Overfitting by the FIR model. We manipulated two characteristics of the POLY model (Table I) and evaluated the effect on fit accuracy (gray line) and prediction accuracy (black line). For these graphs we selected voxels with a minimum SNR of 10 under the POLY model (n = 1,730). Dots indicate the median across voxels, and error bars indicate ±1 SE (bootstrap procedure). (A) The effect of HDR window duration on fit accuracy and prediction accuracy. The x‐axis indicates the HDR window duration used in the model; the y‐axis indicates explained variance. Prediction accuracy was maximized at a duration of 9 s. This indicates that, on average, estimating HDRs beyond 9 s resulted in overfitting and reduced model generalizability. (B) The effect of the number of event types on fit accuracy and prediction accuracy. Based on SNR estimates obtained under the POLY model, we refit the model including only the top event types with respect to SNR. (Because different voxels respond to different event types, the included event types varied on a voxel‐by‐voxel basis.) The x‐axis indicates the number of event types; the y‐axis indicates explained variance. Prediction accuracy was maximized at three event types. This indicates that, on average, estimating more than three event types resulted in overfitting and reduced model generalizability. This result is explained by the fact that voxels in visual cortex are often highly selective for spatial position, in such a way that stimuli positioned at nonpreferred locations produce no discernable activation.

Figure 7.

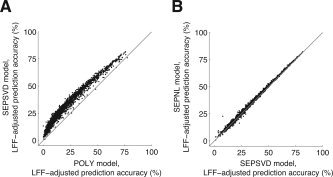
Figure 7

Open in a new tab

Time‐event separability reduces overfitting and increases prediction accuracy. In these graphs we compare the FIR model to the time‐event separable model (Table I). Each point in a graph represents prediction accuracy for a single voxel. (A) POLY vs. SEPSVD. The x‐ and y‐axes indicate the LFF‐adjusted prediction accuracy under the POLY and SEPSVD models, respectively. The graph depicts voxels with a minimum SNR of 10 under either data model (n = 1,884). There was a large increase in accuracy under the SEPSVD model compared to the POLY model (median increase 9.9%; P < 0.001). This indicates that voxel responses were largely time‐event separable, and that time‐event separability improved the accuracy of HDR estimates. (B) SEPSVD vs. SEPNL. The x‐ and y‐axes indicate the LFF‐adjusted prediction accuracy under the SEPSVD and SEPNL models, respectively. The graph depicts voxels with a minimum SNR of 10 under the POLY model (n = 1,730). There was a tiny increase in accuracy under the SEPNL model compared to the SEPSVD model (median increase 0.5%; P < 0.001). This indicates that the singular value decomposition fitting method compared favorably against the iterative fitting method in this data set.

Figure 8.

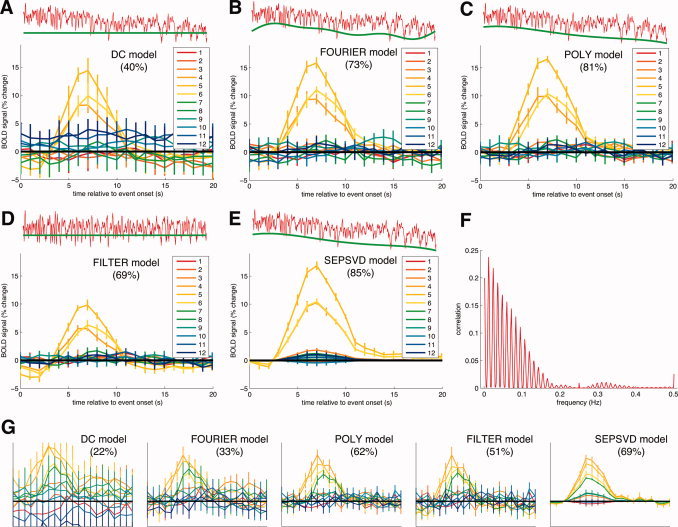
Figure 8

Open in a new tab

Comparison of data models for two typical voxels in occipital cortex. Panels A–F depict one voxel, and panel G depicts a second voxel. In panels A–E and G, the main axes show HDR estimates for the 12 event types. The x‐axis indicates time relative to event onset; the y‐axis indicates percent BOLD change. A thick black horizontal line indicates zero percent BOLD change. Error bars indicate ±1 SE (jackknife procedure). Indicated in parentheses is the LFF‐adjusted prediction accuracy, which is calculated via 10‐fold cross‐validation. The inset axes above the main axes depict the time‐series data (red line) and nuisance effects (green line). (A) DC model. This model ignores LFF and uses only a constant term to characterize the baseline signal level. Under this model, HDR estimates were very noisy and prediction accuracy was poor. (B) FOURIER model. This model uses a constant term and Fourier basis functions with 1, 2, and 3 cycles to model LFF. Compared to the DC model, HDR estimates were less noisy and prediction accuracy was better. Note that the nuisance effects poorly track the time‐series data at the beginning and end of the time‐series. (C) POLY model. This model uses polynomials of degrees 0 through 4 to model LFF. Compared to the FOURIER model, HDR estimates were slightly less noisy and prediction accuracy was better. Notice the nuisance effects track the time‐series data well. The LFF magnitude index is 0.87. (D) FILTER model. This model high‐pass filters the time‐series data at 1/60 Hz to remove LFF as a preprocessing step. The filtered data are shown in red in the inset (above). HDR estimates were considerably different from those obtained under other data models. (E) SEPSVD model. This model incorporates the constraint of time‐event separability and uses polynomials of degrees 0 through 4 to model LFF. Time‐event separability is the condition that HDR estimates across event types are identical up to a scale factor. Prediction accuracy was highest under the SEPSVD model. The LFF magnitude index is 0.86. (F) Spectral content of stimulus effects. We obtained the estimated timecourse of stimulus effects under the SEPSVD model. We calculated the discrete Fourier transform of this timecourse after subtracting the mean value. The correlation (y‐axis) between the time‐series data and the Fourier component at each frequency (x‐axis) is plotted. For display purposes the zero‐frequency point is omitted. Note that the power is distributed over a wide range of frequencies. (G) Comparison of data models for a second voxel. The format is identical to that of panels A–E, except that the y‐axis ranges from −3 to 7. Again, the SEPSVD model had the highest prediction accuracy.

Figure 9.

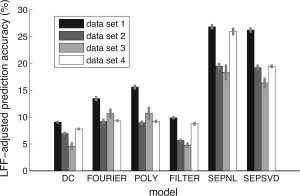
Figure 9

Open in a new tab

Summary of data model performance. This graph summarizes results from four data sets involving different subjects, imaging parameters, and stimulus designs: the primary data set (illustrated in Figs. 1, 2, 3, 4, 5, 6, 7, 8) and three additional data sets. For each data set, we selected voxels (n = 2,223, 699, 236, 825, respectively) passing a minimum SNR threshold (= 10, 10, 7, 10, respectively) under any of the models that do not involve iterative fitting (this excludes the SEPNL model). (The SNR threshold is lowered for data set 3 due to low signal in that data set.) The x‐axis indicates the data models we evaluated; and the y‐axis indicates the LFF‐adjusted prediction accuracy. The height of each bar indicates the median across voxels, and the bar shading indicates the data set. Error bars indicate ±1 SE (bootstrap procedure). The same basic trend in performance was observed across the four data sets: the SEPNL and SEPSVD models were the most accurate, the FOURIER and POLY models were moderately accurate, and the DC and FILTER models were the least accurate.

Basic Data Inspection

We conducted an event‐related fMRI experiment involving brief (4 s) presentations of a checkerboard pattern within 12 wedges in the visual field (Fig. 1). Our analysis approach is based on the FIR model for event‐related fMRI [Dale, 1999]. We define 12 event types, one event type per wedge. For each voxel, a HDR to each of the 12 event types is estimated using a set of shifted delta functions. No assumption on the shape of HDRs is made. Additional regressors are used to model the time‐varying baseline signal level (Fig. 2).

We obtained strong BOLD activations in occipital cortex. Figure 3 depicts positive HDR estimates obtained under the POLY model (Table I) with a SNR of at least 30. (This strict criterion selects only those estimates that are nearly noise‐free.) The robustness of the shapes of the timecourses confirms the high SNR in the data, despite the small voxel size (2 mm) and the moderate amount of data (17 min). The high SNR is due to the high magnetic field (4 T), the use of a surface coil, the use of an experienced fMRI subject, the m‐sequence experimental design, and the high‐contrast visual stimulus.

Table I.

Summary of data models

Model Stimulus effects Nuisance effects
DC Finite impulse response Constant term
FOURIER Finite impulse response Constant term, sine and cosine functions with 1, 2, and 3 cycles
POLY Finite impulse response Polynomials of degrees 0 through 4
FILTER Finite impulse response Constant term, after removing a linear trend and high‐pass filtering at 1/60 Hz
SEPNL Time‐event separable, iterative fitting method Polynomials of degrees 0 through 4
SEPSVD Time‐event separable, singular value decomposition fitting method Polynomials of degrees 0 through 4
Open in a new tab

This table lists how each model characterizes stimulus effects (i.e. hemodynamic responses to stimulus events) and how each model compensates for nuisance effects (i.e. the baseline signal level).

Compensation for LFF

We evaluated several strategies for compensating for LFF in the time‐series data. (1) The DC model ignores LFF and uses only a constant term to model DC offset. (2) The FOURIER model uses a constant term and Fourier basis functions with 1, 2, and 3 cycles to model LFF. (3) The POLY model uses Legendre polynomials of degrees 0 through 4 to model LFF. (The spectral content of these polynomials approximately match those of the Fourier basis functions.) (4) The FILTER model removes a linear trend and high‐pass filters the time‐series data at 1/60 Hz as a preprocessing step.

Panel A of Figure 4 shows that the POLY model greatly increased prediction accuracy compared to the DC model (median increase 14.8%; P < 0.001). This indicates ignoring LFF resulted in model fits with poor generalizability. This also indicates that a substantial amount of LFF exists in the time‐series data.

Panel B of Figure 4 shows that the POLY model somewhat increased prediction accuracy compared to the FOURIER model (median increase 2.3%; P < 0.001). This indicates that polynomials more accurately characterized LFF compared to Fourier basis functions. However, in other data sets, the POLY and FOURIER models had comparable performance (Fig. 9).

Panel C of Figure 4 shows the POLY model substantially increased LFF‐adjusted prediction accuracy compared to the FILTER model (median increase 6.5%; P < 0.001). The use of the LFF‐adjusted prediction accuracy metric (see Methods) ensures that increased accuracy under the POLY model is not simply due to the modeling of LFF. The result indicates that stimulus effects were better characterized when polynomials were used to model LFF compared to when the time‐series data were high‐pass filtered to remove LFF. (We also evaluated the FILTER model using a frequency cutoff of 1/500 Hz; compared to this model, the POLY model still provided a median increase of 2.8% LFF‐adjusted prediction accuracy.)

Characteristics of LFF

We investigated in more detail the timecourses of LFF. Panel A of Figure 5 illustrates the effect of manipulating the maximum degree of the polynomials included in the POLY model. Dramatic increases in LFF‐adjusted prediction accuracy were obtained by increasing the maximum degree from 0 (median accuracy 5.8%) to 4 (median accuracy 10.8%). Polynomials with degree greater than 4 only marginally increased accuracy; moreover, these increases were inconsistent across voxels (data not shown). Panel A also illustrates the effect of maximum polynomial degree on the SNR. Substantial increases in SNR were obtained by increasing the maximum degree from 0 (median SNR 9.4) to 3 (median SNR 11.6), beyond which SNR did not increase appreciably.

Panel B of Figure 5 depicts the spectral content of Legendre polynomials of degrees 0 through 4. These polynomials consist predominantly of very low frequencies (0–0.004 Hz). With each additional polynomial degree, higher frequencies in the time‐series data can be modeled. Panel C of Figure 5 illustrates several example LFF timecourses. Note that the shape and magnitude of LFF vary across voxels.

We quantified the magnitude of LFF with the LFF magnitude index. The index quantifies the typical deviation of the baseline signal level over the time‐series data, and is in standard deviation units (see Methods). The 25th and 75th percentiles of the index are 0.18 and 0.57, respectively. (These percentiles were calculated for voxels with a minimum SNR of 10 under the POLY model.) This indicates that noise due to LFF accounts for a substantial fraction of the variation in the time‐series data.

Overfitting by the FIR Model

Overfitting tends to occur when a model has a large number of parameters relative to the amount of available data. Two lines of evidence show that the FIR model suffers from overfitting.

The specific HDR window used in the FIR model substantially affected the quality of model fits. Panel A of Figure 6 shows that fit accuracy monotonically increased with window duration. This reflects the fact that, with a longer window duration, additional model parameters are available to fit the data. However, prediction accuracy did not monotonically increase, but was maximized at a duration of 9 s. This indicates that on average, estimating HDRs beyond 9 s resulted in overfitting and reduced model generalizability. This result is consistent with the observation that HDRs have mostly died off by 9 s after event onset (see Fig. 3).

The number of event types included in the FIR model also substantially affected the quality of model fits. We evaluated variants of the model in which only the top event types with respect to SNR are included. (The top event types were determined on a voxel‐by‐voxel basis.) Panel B of Figure 6 indicates that fit accuracy monotonically increased with number of event types. This reflects the fact that, with more event types, additional model parameters are available to fit the data. However, prediction accuracy did not monotonically increase, but was maximized at three event types. This indicates that on average estimating more than three event types resulted in overfitting and reduced model generalizability. This result is explained by the fact that voxels in visual cortex are often highly selective for spatial position, in such a way that stimuli positioned at nonpreferred locations produce no discernable activation.

Time‐Event Separability

To reduce overfitting by the FIR model, we incorporated the constraint of time‐event separability. Under the time‐event separable model, stimulus effects are characterized by a single response timecourse—the time kernel—and an amplitude value for each event type (Fig. 2). This reduces the number of model parameters that need to be estimated. We evaluated two methods for fitting the time‐event separable model, SEPNL and SEPSVD (see Methods).

Panel A of Figure 7 shows that the SEPSVD model greatly increased LFF‐adjusted prediction accuracy compared to the POLY model (median increase 9.9%; P < 0.001). This indicates that voxel responses were largely time‐event separable, and that time‐event separability improved the accuracy of HDR estimates. Panel B of Figure 7 shows that the SEPNL model slightly increased LFF‐adjusted prediction accuracy compared to the SEPSVD model (median increase 0.5%; P < 0.001). This indicates that the two fitting methods produced very similar results. However, in one of the other data sets, the SEPNL model performed substantially better than the SEPSVD model (Fig. 9).

The incorporation of time‐event separability also increased the SNR. We selected voxels with a minimum SNR of 10 under either the POLY or SEPSVD model. Of these voxels, the median SNRalt for the POLY model was 14.3, while the median SNRalt for the SEPSVD model was 15.5. This increase was statistically significant (P < 0.001).

Example Voxels

We have presented population results thus far, but it is also useful to inspect results for individual voxels. Panels A–E of Figure 8 show model parameter estimates for a typical voxel. Notice the DC model produced very noisy HDR estimates; the FILTER model produced HDR estimates considerably different from those produced by other models; and the SEPSVD model produced the most accurate HDR estimates. Panel F of Figure 8 depicts the spectral content of stimulus effects for the voxel. Notice power is distributed over a wide range of frequencies. Panel G of Figure 8 shows model parameter estimates for another typical voxel. Again, the SEPSVD model produced the most accurate HDR estimates.

Model Performance Summary

Figure 9 summarizes the LFF‐adjusted prediction accuracy of the data models we evaluated, and includes results from additional data sets. Across four data sets, the same basic trend in accuracy was observed: the SEPNL and SEPSVD models were the most accurate, the FOURIER and POLY models were moderately accurate, and the DC and FILTER models were the least accurate.

There were two interesting anomalies. First, whereas the POLY model outperformed the FOURIER model for data set 1 (see also Fig. 4), the two models had similar performance in other data sets. The only difference between the two models is the choice of regressors for LFF. The variable results across data sets suggest that LFF characteristics are dependent on the subject, imaging parameters, and/or stimulus design.

Second, whereas in data sets 1–3, the SEPNL and SEPSVD models had similar performance, in data set 4, the SEPNL model substantially increased accuracy compared to the SEPSVD model (median increase across voxels 5.4%; P < 0.001). The reason for the large but inconsistent increase in accuracy under the SEPNL model is an issue for further investigation. We speculate that the variable results may be due to strong temporal nonlinearities in data set 4.

DISCUSSION

Linearity Assumptions

The FIR and time‐event separable models assume that the BOLD response is a linear, time‐invariant system with respect to the stimulus. However, violations of time‐invariance have been widely documented [Boynton et al., 1996; Buxton et al., 2004; Dale and Buckner, 1997; Friston et al., 2000b; Glover, 1999; Huettel and McCarthy, 2001; Logothetis, 2003; Miezin et al., 2000; Wager et al., 2005]. In general, the response to an event closely preceded by another event has a greater delay and lower amplitude than expected. This temporal nonlinearity may be neural in origin (e.g. adaptation) and/or related to the coupling between neural activity and the BOLD response [Bandettini et al., 2002; Birn et al., 2001; Boynton and Finney, 2003; Huettel et al., 2004; Janz et al., 2001; Ogawa et al., 2000].

We dampened the impact of temporal nonlinearities in our experimental design by the use of a 4‐s bin duration. This is because deviations from linearity are large only at short‐stimulus durations [Birn et al., 2001; Boynton et al., 1996; Pfeuffer et al., 2003; Vazquez and Noll, 1998]. Whereas the response to a moderate‐length stimulus (4 s) well predicts the response to a longer stimulus (8 s), the response to a short stimulus (1 s) poorly predicts the response to a longer stimulus (2 s). It may be possible to devise models to account for temporal nonlinearities when they exist [Friston et al., 2000b; Wager et al., 2005].

Our experimental design involves simultaneous presentation of different event types (i.e. multiple wedges in the visual field at any given time). The primary purpose of simultaneous presentation is to increase the number of event repetitions and thereby increase the SNR. Note that both the FIR and time‐event separable models assume that the BOLD response is additive across events: that is, the response to events presented simultaneously is equal to the sum of the responses to the events presented in isolation. The validity of this assumption depends on the experimental paradigm [Hansen et al., 2004]. However, the analysis techniques we present are not specific to experimental designs using simultaneous event presentation.

Low‐Frequency Fluctuation

We found that using polynomials to model LFF resulted in more accurate HDR estimates than those obtained with other strategies. We used an event‐related experimental design, and our study complements studies that investigated LFF for block designs [LaConte et al., 2003; Razavi et al., 2003].

The poor performance of high‐pass filtering is explained by the fact that stimulus effects in our data exist at low frequencies. High‐pass filtering removes LFF but also removes a portion of the stimulus effects [Kruggel et al., 1999; Ollinger et al., 2001; Skudlarski et al., 1999; Smith et al., 1999]. Moreover, the removal of stimulus effects induces bias in HDR estimates (Fig. 8). Detrending techniques (of which high‐pass filtering is one instance) are appropriate only when stimulus effects can be assumed to be absent at low frequencies (e.g. a periodic ON–OFF block experimental design).

Using regressors to model LFF is not equivalent to removing these regressors from the time‐series data before fitting the data model [Liu et al., 2001]. The latter is effectively a detrending technique. As such, it neglects potential correlation between stimulus effects and the regressors that are removed. Detrending may also increase autocorrelation in the noise component of the time‐series data, and thereby decrease the validity of a model that assumes uncorrelated noise [Razavi et al., 2003]. It is necessary to fit both stimulus effects and nuisance effects simultaneously in order to estimate the individual contributions of these two effects at low frequencies.

We found that a set of polynomials of degrees 0 through 4 modeled LFF well. Most of the spectral power in these polynomials is between 0 and 0.004 Hz (for a 17‐min data set). Because the 1‐Hz data sampling rate is sufficient for characterizing the respiratory cycle (∼0.25 Hz), it is unlikely that LFF reflects respiration‐related noise. However, the 1‐Hz data sampling rate is insufficient for characterizing the cardiac cycle (∼1 Hz), and so aliasing of cardiac‐related signals could be contributing to LFF. Measurement of the cardiac cycle during data acquisition could perhaps be used to improve modeling of the time‐series data. However, there is some evidence that LFF is dominated by nonphysiological factors such as scanner instability [Smith et al., 1999].

Including polynomials of higher degree increased prediction accuracy, but only marginally and inconsistently. This indicates that the magnitude of LFF at higher frequencies was relatively small, and that including additional polynomials risked overfitting. Tailoring the number of polynomials on a voxel‐by‐voxel basis is a possible strategy.

In our data, the baseline signal level is generally not the same at the beginning and at the end of the time‐series data. This is one reason that Fourier basis functions, which are periodic, did not model LFF as well as polynomials in data set 1. However, the characteristics of LFF may be specific to the experimental setup [Aguirre et al., 1997; Purdon and Weisskoff, 1998; Zarahn et al., 1997b]. It is therefore necessary to evaluate different models for LFF on a case‐by‐case basis (Fig. 9).

A different way to approach the problem of LFF is to focus on the autocorrelation in the noise in BOLD time‐series data [for reviews, see Bullmore et al., 2001; Friston et al., 2000a]. Prewhitening strategies have been proposed for obtaining estimates under the general linear model that have less variance than ordinary least‐squares estimates [Bullmore et al., 1996; Burock and Dale, 2000; Friman et al., 2004; Locascio et al., 1997; Marchini and Ripley, 2000; Purdon and Weisskoff, 1998; Woolrich et al., 2001; Worsley et al., 2002]. The addition of prewhitening to the use of regressors for LFF may result in further improvements in SNR and prediction accuracy.

Time Kernel Estimation

The time kernel for a voxel can be viewed as a voxel‐specific HRF. The technique of time kernel estimation occupies a middle ground between assuming a canonical HRF and making no assumption about the shape of HDRs (FIR model). In the first case, the shape of the HDR is assumed to be known, and the only free model parameters are the amplitude for each event type. Overfitting is unlikely because there are few model parameters, but model accuracy is suboptimal because of variation in HDR shape across voxels. In the second case, a separate HDR is estimated for each event type, resulting in many free model parameters. Variation in HDR shape can be accounted for, but model accuracy is suboptimal because of overfitting. By estimating a time kernel, we greatly reduce the number of free model parameters, but still make no assumption about the shape of the HDR across voxels.

Increased prediction accuracy under the time‐event separable model is contingent on the degree to which voxel responses are in fact time‐event separable. The large increase in prediction accuracy in our data indicates that voxel responses were largely time‐event separable, but does not necessarily imply complete separability. Time‐event separability likely holds in many experimental paradigms. Because the BOLD response temporally blurs underlying neural activity, we expect time‐event separability to hold whenever the timescale of neural activity is roughly the same across event types.

In some experimental paradigms, we may expect aspects of the HDR timecourse (e.g. onset, width) to vary across event types. For example, we might expect the delay of the neural activity in a voxel to be dependent on the level of difficulty of a cognitive task. In such a case, we would expect the onset of the HDR timecourse to vary across easy and hard instances of the task. The assumption of time‐event separability would be inappropriate for such experimental paradigms.

Overfitting and Regularization

The FIR model substantially overfitted our data, producing HDR estimates that had suboptimal prediction accuracy. Overfitting is a substantial problem for event‐related fMRI because of the low SNR of the BOLD response and the large number of parameters necessary to accommodate variations in the shape of the HDR.

Overfitting by the FIR model can be reduced by tailoring the HDR window or by modeling only a subset of the event types. However, the optimal HDR window and subset of event types for a given voxel may not generalize to other voxels. Searching for the optimal parameters on a voxel‐by‐voxel basis is computationally impractical.

A practical solution to overfitting by the FIR model is to incorporate the constraint of time‐event separability. This constraint greatly reduces the number of model parameters—in our case, the number of model parameters is reduced from 252 to 33. Note that the time‐event separable model does not have any additional descriptive power compared to the FIR model: any set of HDRs that can be characterized by the time‐event separable model can also be characterized by the FIR model. Thus, we can view time‐event separability as a means of regularizing the FIR model. (Regularization refers to techniques that attempt to improve prediction accuracy by introducing a specific bias to model parameter estimates.)

Other regularization techniques are possible and are not mutually exclusive to time‐event separability. They include fitting a parametric function, such as a γ function, to HDR estimates [Boynton et al., 1996; Cohen, 1997; Glover, 1999]; incorporating temporal basis set restrictions or other priors into the FIR model [Burock and Dale, 2000; Dale, 1999; Goutte et al., 2000]; and incorporating constraints on the spatial pattern of signal activations [Katanoda et al., 2002; Kiebel et al., 2000; Kruggel et al., 1999; Purdon et al., 2001]. If these techniques are used, it is important to verify that they improve prediction accuracy.

Acknowledgements

We thank B. Inglis for extensive MRI assistance; R. Redfern for equipment design and construction; M. Banks, K. Schreiber, and S. Watt for stimulus presentation advice; B. Pasley, M. Silver, and T. Liu for helpful discussions; J. Ollinger for image reconstruction software; and K. Gustavsen, B. Inglis, A. Rokem, and anonymous reviewers for comments on the manuscript. K. Kay was supported by the National Defense Science and Engineering Graduate Fellowship.

REFERENCES

  1. Aguirre GK, Zarahn E, D'Esposito M( 1997): Empirical analyses of BOLD fMRI statistics. II. Spatially smoothed data collected under null‐hypothesis and experimental conditions. Neuroimage 5: 199–212. [DOI] [PubMed] [Google Scholar]
  2. Aguirre GK, Zarahn E, D'Esposito M( 1998): The variability of human, BOLD hemodynamic responses. Neuroimage 8: 360–369. [DOI] [PubMed] [Google Scholar]
  3. Bandettini PA, Birn RM, Kelley D, Saad Z ( 2002): Dynamic nonlinearities in BOLD contrast: Neuronal or hemodynamic? Int Congr Ser 1235: 73–95. [Google Scholar]
  4. Birn RM, Saad ZS, Bandettini PA( 2001): Spatial heterogeneity of the nonlinear dynamics in the FMRI BOLD response. Neuroimage 14: 817–826. [DOI] [PubMed] [Google Scholar]
  5. Boynton GM, Finney EM( 2003): Orientation‐specific adaptation in human visual cortex. J Neurosci 23: 8781–8787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Boynton GM, Engel SA, Glover GH, Heeger DJ( 1996): Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci 16: 4207–4221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brainard DH( 1997): The psychophysics toolbox. Spat Vis 10: 433–436. [PubMed] [Google Scholar]
  8. Bullmore E, Brammer M, Williams SC, Rabe‐Hesketh S, Janot N, David A, Mellers J, Howard R, Sham P( 1996): Statistical methods of estimation and inference for functional MR image analysis. Magn Reson Med 35: 261–277. [DOI] [PubMed] [Google Scholar]
  9. Bullmore E, Long C, Suckling J, Fadili J, Calvert G, Zelaya F, Carpenter TA, Brammer M( 2001): Colored noise and computational inference in neurophysiological (fMRI) time series analysis: Resampling methods in time and wavelet domains. Hum Brain Mapp 12: 61–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Buracas GT, Boynton GM ( 2002): Efficient design of event‐related fMRI experiments using M‐sequences. Neuroimage 16(3, Part 1): 801–813. [DOI] [PubMed] [Google Scholar]
  11. Burock MA, Dale AM( 2000): Estimation and detection of event‐related fMRI signals with temporally correlated noise: A statistically efficient and unbiased approach. Hum Brain Mapp 11: 249–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Buxton RB, Uludag K, Dubowitz DJ, Liu TT ( 2004): Modeling the hemodynamic response to brain activation. Neuroimage 23( Suppl 1): S220–S233. [DOI] [PubMed] [Google Scholar]
  13. Cohen MS( 1997): Parametric analysis of fMRI data using linear systems methods. Neuroimage 6: 93–103. [DOI] [PubMed] [Google Scholar]
  14. Dale AM( 1999): Optimal experimental design for event‐related fMRI. Hum Brain Mapp 8: 109–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dale AM, Buckner RL( 1997): Selective averaging of rapidly presented individual trials using fMRI. Hum Brain Mapp 5: 329–340. [DOI] [PubMed] [Google Scholar]
  16. de Zwart JA, Silva AC, van Gelderen P, Kellman P, Fukunaga M, Chu R, Koretsky AP, Frank JA, Duyn JH( 2005): Temporal dynamics of the BOLD fMRI impulse response. Neuroimage 24: 667–677. [DOI] [PubMed] [Google Scholar]
  17. Efron B, Tibshirani R ( 1993): An Introduction to the Bootstrap Vol. 16 New York: Chapman & Hall; 436pp. [Google Scholar]
  18. Freire L, Mangin JF( 2001): Motion correction algorithms may create spurious brain activations in the absence of subject motion. Neuroimage 14: 709–722. [DOI] [PubMed] [Google Scholar]
  19. Friman O, Borga M, Lundberg P, Knutsson H( 2004): Detection and detrending in fMRI data analysis. Neuroimage 22: 645–655. [DOI] [PubMed] [Google Scholar]
  20. Friston KJ, Josephs O, Zarahn E, Holmes AP, Rouquette S, Poline J( 2000a): To smooth or not to smooth? Bias and efficiency in fMRI time‐series analysis. Neuroimage 12: 196–208. [DOI] [PubMed] [Google Scholar]
  21. Friston KJ, Mechelli A, Turner R, Price CJ( 2000b): Nonlinear responses in fMRI: The balloon model, volterra kernels, and other hemodynamics. Neuroimage 12: 466–477. [DOI] [PubMed] [Google Scholar]
  22. Glover GH( 1999): Deconvolution of impulse response in event‐related BOLD fMRI. Neuroimage 9: 416–429. [DOI] [PubMed] [Google Scholar]
  23. Goutte C, Nielsen FA, Hansen LK( 2000): Modeling the haemodynamic response in fMRI using smooth FIR filters. IEEE Trans Med Imaging 19: 1188–1201. [DOI] [PubMed] [Google Scholar]
  24. Handwerker DA, Ollinger JM, D'Esposito M( 2004): Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage 21: 1639–1651. [DOI] [PubMed] [Google Scholar]
  25. Hansen KA, David SV, Gallant JL( 2004): Parametric reverse correlation reveals spatial linearity of retinotopic human V1 BOLD response. Neuroimage 23: 233–241. [DOI] [PubMed] [Google Scholar]
  26. Hinrichs H, Scholz M, Tempelmann C, Woldorff MG, Dale AM, Heinze HJ( 2000): Deconvolution of event‐related fMRI responses in fast‐rate experimental designs: Tracking amplitude variations. J Cogn Neurosci 12( Suppl 2): 76–89. [DOI] [PubMed] [Google Scholar]
  27. Huettel SA, McCarthy G( 2001): Regional differences in the refractory period of the hemodynamic response: An event‐related fMRI study. Neuroimage 14: 967–976. [DOI] [PubMed] [Google Scholar]
  28. Huettel SA, Obembe OO, Song AW, Woldorff MG( 2004): The BOLD fMRI refractory effect is specific to stimulus attributes: Evidence from a visual motion paradigm. Neuroimage 23: 402–408. [DOI] [PubMed] [Google Scholar]
  29. Janz C, Heinrich SP, Kornmayer J, Bach M, Hennig J( 2001): Coupling of neural activity and BOLD fMRI response: New insights by combination of fMRI and VEP experiments in transition from single events to continuous stimulation. Magn Reson Med 46: 482–486. [DOI] [PubMed] [Google Scholar]
  30. Josephs O, Henson RN( 1999): Event‐related functional magnetic resonance imaging: Modelling, inference and optimization. Philos Trans R Soc Lond B Biol Sci 354: 1215–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Katanoda K, Matsuda Y, Sugishita M( 2002): A spatio‐temporal regression model for the analysis of functional MRI data. Neuroimage 17: 1415–1428. [DOI] [PubMed] [Google Scholar]
  32. Kellman P, Gelderen P, de Zwart JA, Duyn JH( 2003): Method for functional MRI mapping of nonlinear response. Neuroimage 19: 190–199. [DOI] [PubMed] [Google Scholar]
  33. Kiebel SJ, Goebel R, Friston KJ ( 2000): Anatomically informed basis functions. Neuroimage 11(6, Part 1): 656–667. [DOI] [PubMed] [Google Scholar]
  34. Kruggel F, von Cramon DY, Descombes X( 1999): Comparison of filtering methods for fMRI datasets. Neuroimage 10: 530–543. [DOI] [PubMed] [Google Scholar]
  35. LaConte S, Anderson J, Muley S, Ashe J, Frutiger S, Rehm K, Hansen LK, Yacoub E, Hu X, Rottenberg D, Strother S( 2003): The evaluation of preprocessing choices in single‐subject BOLD fMRI using NPAIRS performance metrics. Neuroimage 18: 10–27. [DOI] [PubMed] [Google Scholar]
  36. Liu TT( 2004): Efficiency, power, and entropy in event‐related fMRI with multiple trial types. II. Design of experiments. Neuroimage 21: 401–413. [DOI] [PubMed] [Google Scholar]
  37. Liu TT, Frank LR, Wong EC, Buxton RB( 2001): Detection power, estimation efficiency, and predictability in event‐related fMRI. Neuroimage 13: 759–773. [DOI] [PubMed] [Google Scholar]
  38. Locascio JL, Jennings PJ, Moore CI, Corkin S ( 1997): Time series analysis in the time domain and resampling methods for studies of functional magnetic resonance brain imaging. Hum Brain Mapp 5: 168–193. [DOI] [PubMed] [Google Scholar]
  39. Logothetis NK( 2003): The underpinnings of the BOLD functional magnetic resonance imaging signal. J Neurosci 23: 3963–3971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Marchini JL, Ripley BD( 2000): A new statistical approach to detecting significant activation in functional MRI. Neuroimage 12: 366–380. [DOI] [PubMed] [Google Scholar]
  41. Miezin FM, Maccotta L, Ollinger JM, Petersen SE, Buckner RL ( 2000): Characterizing the hemodynamic response: Effects of presentation rate, sampling procedure, and the possibility of ordering brain activity based on relative timing. Neuroimage 11(6, Part 1): 735–759. [DOI] [PubMed] [Google Scholar]
  42. Neumann J, Lohmann G, Zysset S, von Cramon DY( 2003): Within‐subject variability of BOLD response dynamics. Neuroimage 19: 784–796. [DOI] [PubMed] [Google Scholar]
  43. Ogawa S, Lee TM, Stepnoski R, Chen W, Zhu XH, Ugurbil K( 2000): An approach to probe some neural systems interaction by functional MRI at neural time scale down to milliseconds. Proc Natl Acad Sci USA 97: 11026–11031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Ollinger JM, Corbetta M, Shulman GL( 2001): Separating processes within a trial in event‐related functional MRI. Neuroimage 13: 218–229. [DOI] [PubMed] [Google Scholar]
  45. Pelli DG( 1997): The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spat Vis 10: 437–442. [PubMed] [Google Scholar]
  46. Pfeuffer J, McCullough JC, Van de Moortele PF, Ugurbil K, Hu X( 2003): Spatial dependence of the nonlinear BOLD response at short stimulus duration. Neuroimage 18: 990–1000. [DOI] [PubMed] [Google Scholar]
  47. Purdon PL, Weisskoff RM( 1998): Effect of temporal autocorrelation due to physiological noise and stimulus paradigm on voxel‐level false‐positive rates in fMRI. Hum Brain Mapp 6: 239–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Purdon PL, Solo V, Weisskoff RM, Brown EN( 2001): Locally regularized spatiotemporal modeling and model comparison for functional MRI. Neuroimage 14: 912–923. [DOI] [PubMed] [Google Scholar]
  49. Razavi M, Grabowski TJ, Vispoel WP, Monahan P, Mehta S, Eaton B, Bolinger L( 2003): Model assessment and model building in fMRI. Hum Brain Mapp 20: 227–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Saad ZS, Ropella KM, Cox RW, DeYoe EA( 2001): Analysis and use of FMRI response delays. Hum Brain Mapp 13: 74–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Skudlarski P, Constable RT, Gore JC( 1999): ROC analysis of statistical methods used in functional MRI: Individual subjects. Neuroimage 9: 311–329. [DOI] [PubMed] [Google Scholar]
  52. Smith AM, Lewis BK, Ruttimann UE, Ye FQ, Sinnwell TM, Yang Y, Duyn JH, Frank JA( 1999): Investigation of low frequency drift in fMRI signal. Neuroimage 9: 526–533. [DOI] [PubMed] [Google Scholar]
  53. Tanabe J, Miller D, Tregellas J, Freedman R, Meyer FG( 2002): Comparison of detrending methods for optimal fMRI preprocessing. Neuroimage 15: 902–907. [DOI] [PubMed] [Google Scholar]
  54. Vazquez AL, Noll DC( 1998): Nonlinear aspects of the BOLD response in functional MRI. Neuroimage 7: 108–118. [DOI] [PubMed] [Google Scholar]
  55. Wager TD, Vazquez A, Hernandez L, Noll DC( 2005): Accounting for nonlinear BOLD effects in fMRI: Parameter estimates and a model for prediction in rapid event‐related studies. Neuroimage 25: 206–218. [DOI] [PubMed] [Google Scholar]
  56. Woolrich MW, Ripley BD, Brady M, Smith SM( 2001): Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage 14: 1370–1386. [DOI] [PubMed] [Google Scholar]
  57. Worsley KJ, Liao CH, Aston J, Petre V, Duncan GH, Morales F, Evans AC( 2002): A general statistical analysis for fMRI data. Neuroimage 15: 1–15. [DOI] [PubMed] [Google Scholar]
  58. Zarahn E, Aguirre G, D'Esposito M( 1997a): A trial‐based experimental design for fMRI. Neuroimage 6: 122–138. [DOI] [PubMed] [Google Scholar]
  59. Zarahn E, Aguirre GK, D'Esposito M( 1997b): Empirical analyses of BOLD fMRI statistics. I. Spatially unsmoothed data collected under null‐hypothesis conditions. Neuroimage 5: 179–197. [DOI] [PubMed] [Google Scholar]

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES