Assessment of the increase in variability when combining volumetric data from different scanners

Abstract

In multicenter MRI studies, pooling of volumetric data requires a prior evaluation of compatibility between the different machines used. We tested the compatibility of five different scanners (2 General Electric Signa, 2 Siemens Symphony, and a Philips Gyroscan) at five different sites by repeating the scans of five volunteers at each of the sites. Using a semiautomatic method based on the Talairach atlas, and SPM algorithms for tissue segmentation (multimodal T1 and T2, or T1‐only), we obtained volume measurements of the main brain lobes (frontal, parietal, occipital, temporal) and for each tissue type. Our results suggest that pooling of multisite data adds small error for whole brain measurements, intersite coefficient of variation (CV) ranging from 1.8 to 5.2%, respectively, for GM and CSF. However, in the occipital lobe, intersite CV can be as high as 11.7% for WM and 17.3% for CSF. Compared with the intersite, intrasite CV values were always much lower. Whenever possible, T1 and T2 tissue segmentation methods should be used because they yield more consistent volume measurements between sites than T1‐only, especially when some of the scans were obtained with different sequence parameters and pixel size from those of the other sites. Our study shows that highest compatibility among scanners would be obtained using equipments of the same manufacturer and also image acquisition parameters as similar as possible. After validation, data from a specific ROI or scanner showing values markedly different from the other sites might be excluded from the analysis. Hum Brain Mapp, 2009. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

The study of structural changes associated with psychiatric and neurological disorders often requires measurements to be made repeatedly over long periods of time, frequently on large samples of individuals [Evans, 2002]. Low prevalence of some diseases sometimes makes it impossible to collect appropriate sample sizes from a single institution, leading to an increasing need to use MRI data from multiple sites to achieve larger sample sizes. Nowadays, longitudinal studies are particularly prone to the problem of combining data from different scanners because of the frequent updates in medical equipment. While this frequent renewal favors the use of newer exploration techniques in research, it makes it very likely that scanner facilities will not be the same at baseline and at follow‐up. Consequently, there is increasing interest in the assessment of the reproducibility and compatibility between MRI machines.

The bias introduced by combining data obtained at different clinical sites and thus under different technical conditions is largely unknown. Some of the possible sources of error involved in the analysis of multisite data are different acquisition parameters, uneven technical capabilities of MRI systems from different manufacturers, and the intersite differences among segmentation protocols for the quantitative analysis of images [Tofts, 1998].

Few studies have investigated the repeatability of multicenter analysis. One way of circumventing discordance in the measurements obtained at different sites is the optimization and calibration of the quantitative analysis to increase the congruence of the data obtained from each site. The rationale for such a calibration process is to explore combinations of parameters that yield the maximum correspondence in the segmentation and quantification of image data [Schnack et al., 2004; van Haren et al., 2003]. However, the search for congruent multicenter measurements may produce the unwanted effect of spreading inaccurate measurements obtained from the reference scanner [Tofts, 1998]. Thus, multisite calibration involves a trade‐off between intersite reproducibility and accuracy (closeness to the truth, lack of systematic error). Despite the potential gain in compatibility among scanners, a suboptimal result of the segmentation process for one site might increase the overall error of volume quantification.

When choosing the most suitable method for tissue segmentation, it is of great interest to assess the compatibility of the data in a multisite setting. A recent study [Styner et al., 2002] explored intersite and intrasite variability to test whether manual or automatic segmentation methods were more repeatable. The study recommended the use of multimodal data for tissue segmentation and automated rather than manual methods, concluding that the variability of tissue volumes was always larger between sites than within sites [Styner et al., 2002]. The material used in Styner's study consisted of MRI acquisitions from a single subject, repeated on one scanner to estimate intrasite variability, and also in four other centers to evaluate intersite variation. However, using a single subject may lead to underestimation of intersite differences because of the enormous variability of the human brain, i.e., we may overlook the effect of overall brain size or shape differences, and maybe constrain segmentation algorithms to provide an optimal result for a particular brain [Tofts, 1998].

An estimation of the intersite variability of volumetric measurements is warranted in multicenter studies, and should be made not only for total brain volumes but also for the ROI measurements of gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) used in morphometric research. On the other hand, multicenter studies do not necessarily have to follow a previously accepted scanning protocol, and it is possible that the decision to combine data is made after the data has been collected. Thus, a study of multicenter variability including sites with the same or different manufacturers, and running the same or different acquisition parameters will provide valuable information about the sources and magnitude of error of pooling data from various sites.

Our goal was to estimate the differences between volumetric MRI measurements obtained from different scanners and to evaluate the effect of pooling data in a joint multicenter analysis. Estimation of overall variability across sites was made using data from five subjects scanned at five different sites. To be representative of a typical clinical study of brain volumetry, regional data were obtained for the main brain lobes and tissue types. This paper is motivated by the possibility of undertaking a multicenter project incorporating some of the institutions that participated in this study.

SUBJECTS AND METHODS

Design

The study is based on data from five volunteers scanned once at five different scanners. The whole data set was collected within one‐year and the average time between scans per subject was 1.5 months. Five different scanning facilities were included in the study, two Siemens Symphony, two General Electric Signa, and a Philips ACS Gyroscan (Table I). Data were collected from each site and processed at one site. A geometric phantom was also scanned to discard potential geometric distortions. The study was approved by the Ethics Committee of the coordinating institution.

Table I.

Summary of scanner characteristics and acquisition parameters at each site

Site	Scanner	Acquisition data
			Voxel size (mm3)	FOV	Matrix	Pixel band width	TR (ms)	TE (ms)	Inversion time (ms)	Flip angle (°)
PHILIPS	Philips Gyroscan ACS 1.5 T	T1	1.0 × 1.0 × 1.5	256 × 256	256 × 256	NA	15.3	4.6	0	30
		T2	1.0 × 1.0 × 3.5	256 × 256	256 × 256	NA	5,809	120	—	90
GE_1	GE Genesis Signa 1.5 T	T1	0.98 × 0.98 × 1.5	250 × 250	256 × 256	122	10.9	4.6	300	20
		T2	0.98 × 0.98 × 3.5	250 × 250	256 × 256	122	5,800	126	—	90
GE_2	GE Genesis Signa 1.5 T	T1	0.98 × 0.98 × 1.5	250 × 250	256 × 256	122	12.1	5.2	300	20
		T2	0.98 × 0.98 × 3.5	250 × 250	256 × 256	122	5,800	126	—	90
SIEMENS_1	Siemens Symphony 1.5 T	T1	1.0 × 1.0 × 1.5	256 × 256	256 × 256	230	1,810	2.39	1,100	20
		T2	1.0 × 1.0 × 3.5	256 × 180	256 × 180	120	5,800	120	—	150
SIEMENS_2	Siemens Symphony 1.5 T	T1	0.98 × 0.98 × 2.0	256 × 250	256 × 256	130	2,020	5.04	1,100	15
		T2	1.0 × 1.0 × 3.5	256 × 192	256 × 192	100	5,800	116	—	150

All scans were obtained in axial orientation, using a 3D gradient echo acquisition technique for T1 weighted images, and spin‐echo sequence in the T2 weighted images, using the quadrate head coil. Neither parallel imaging (SENSE, iPAT, ASSET) sequences nor multichannel coils were used in any of the sites. By default, GE scanners have the gradient linearity correction filter activated, and thus scans from GE sites were acquired with this parameter.

Subjects

Five healthy volunteers, two females (mean age = 40.2 years; SD = 5.9; range = 31–45 years), were enrolled in the study. All subjects were aware of the study purpose and nature and agreed to participate by signing a written informed consent.

MRI Acquisition Protocol

Two MRI sequences were acquired for each subject, a T1‐weighted 3D gradient echo and a T2‐weighted Turbo‐Spin Echo. All scans were obtained in axial orientation and using the quadrate head coil. Neither parallel imaging (SENSE, iPAT, ASSET) sequences nor multichannel coils were used in any of the sites. By default, GE scanners have the gradient linearity correction filter activated, and thus, scans from GE sites were acquired with this parameter. Full details about the acquisition parameters for each site are provided in Table I.

Scans were not performed with identical sequence parameters at each site because of the differences between the manufacturers and the acquisition software. Even in the case of scanners of the same model (GE and Siemens), the standard protocols for each radiology department differed because of local preferences, and the acquisition parameters were not identical. Although this difference reduces the overall reproducibility of the whole segmentation protocol, our interest was to take advantage of the ongoing longitudinal studies initiated at each site, as long as the contrast and resolution of the images were reasonably similar. On the other hand, having a nonunique combination of parameters allows evaluation of the effect of differences in sequence parameters on the similarity of volumetric data. Image similarity between scanners in terms of contrast and resolution was fairly good, as visually assessed, and in terms of contrast‐to‐noise ratio. Contrast‐to‐noise ratio was computed as the difference in mean pixel intensity values between GM and WM divided by the pooled standard deviation of GM and WM pixels in the whole brain (Fig. 1, Table I). Because our calculation of contrast‐to‐noise ratio requires segmented images, we show two sets values, one for multimodal, and one for T1‐only data (Table II). High values of this ratio indicate high contrast and better image resolution in terms of gray levels.

Figure 1.

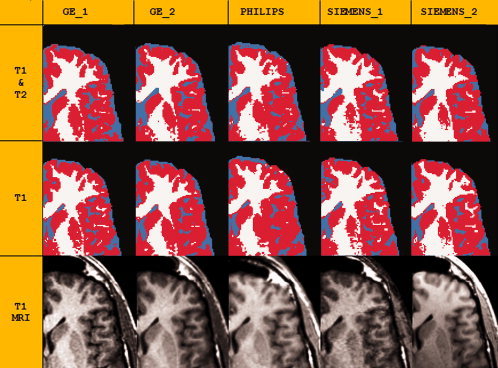
Zoomed section of an axial view of the same subject scanned at five different centers, to illustrate qualitative differences of MRI and of tissue segmentation. Top: Results of tissue segmentation, using T1‐only or T1 and T2 data; tissue types are color coded: GM = red; WM = white; CSF = cyan. Bottom: MR scans. Scans were all registered to the image obtained with the Philips scanner. Note that the segmentation of WM and GM tissue seems more accurate in multimodal segmentation because the cortex distribution along the sulci and gyri looks more realistic, whereas the higher volumes of CSF obtained using T1 and T2 segmentation seem to arise from an exaggeration of sulcal spaces.

Table II.

Volume data (Mean, SD) for contrast‐to‐noise ratios (CNR), intracranial volume (ICV), and whole brain GM, WM, and CSF measured at each site for the sample of five subjects and using two tissue segmentation methods (see Methods)

	GE_1		GE_2		PHILIPS		SIEMENS_1		SIEMENS_2		Intersite CV	% Diff max–min	Effect size max–min	ICC
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
ICV (cc)	1,422	113	1,448	118	1,443	97.7	1,469	90.6	1,479	102	1.9	3.9	0.3 (0.2)a	0.991
T1 and T2 Segm.
CNRi	2.01	0.09	1.91	0.08	1.80	0.08	1.66	0.07	0.68	0.09
GM (cc)	719.2	80.4	728.5	63.7	727.5	56.7	737.4	46.3	762.4	70.6	3.0	5.8	0.4 (0.1)	0.979
WM (cc)	413.0	36.7	413.9	48.5	434.6	41.0	453.5	52.8	425.8	35.1	4.7	9.3	0.7 (0.1)	0.980
CSF (cc)	290.1	24.6	305.8	41.8	281.6	20.7	278.1	20.5	291.3	23.0	5.6	9.5	0.7 (0.4)	0.900
GM (%)	50.5	2.2	50.3	1.8	50.4	1.0	50.2	0.6	51.5	1.5	1.8	2.6	1.0 (0.1)	0.899
WM (%)	29.1	1.9	28.5	1.6	30.1	1.1	30.8	1.8	28.8	0.6	4.6	7.8	1.2 (0.3)	0.777
CSF (%)	20.5	1.8	21.2	2.6	19.6	1.7	19.0	2.1	19.8	2.1	5.2	10.9	0.8 (0.3)	0.956
T1 Segm.
CNRi	2.17	0.12	2.08	0.08	2.03	0.04	2.04	0.09	1.08	0.16
GM (cc)	784.9	79.5	807.4	67.4	777.7	64.0	779.5	59.0	747.3	55.2	3.3	7.7	0.8 (0.3)	0.984
WM (cc)	400.0	36.7	399.5	44.0	431.0	41.1	439.1	53.4	481.8	50.2	8.2	18.7	1.5 (0.1)	0.981
CSF (cc)	233.6	16.6	240.3	29.8	232.4	24.1	250.0	22.9	250.3	23.1	6.4	7.4	0.6 (0.3)	0.836
GM (%)	55.3	1.7	55.8	1.1	54.3	1.1	52.9	1.0	50.5	0.7	4.1	10.0	5.1 (0.3)	0.821
WM (%)	28.2	1.7	27.6	1.2	29.5	1.1	30.0	1.8	32.5	1.6	7.2	16.3	3.1 (0.4)	0.803
CSF (%)	16.5	1.4	16.6	2.0	16.2	2.1	17.1	2.5	17.0	1.9	5.2	5.4	0.3 (0.1)	0.940

Intersite CV: average of within subject coefficients of variation between scanners: % Diff max–min: percentage difference between maximum and minimum values among scanners; Effect size max–min: Cohen's effect size coefficient measuring the magnitude of the differences between the maximum and minimum values among scanners; ICC: intraclass correlation coefficient.

^aValues in parentheses are Cohen's effect size coefficient of the differences between GE_1 and GE_2 only.

Geometric Phantom

A simple phantom was built using a series of glass capillaries set along the three axis (length, width, height) and immersed in water (full details under request). T1 images of the geometric phantom were acquired at each site with the same parameters used for the brain MRI (Table I). Our main interest was to verify that there was no geometrical bias between the scanners rather than evaluating the intrinsic accuracy of the MRI systems. Twelve linear distances along the major axes (width, length, height) were measured on each phantom image (ranging from 60 to 170 mm). The intersite geometric error was measured for each of the 12 distances as the average root mean square (RMS) error between scanners. By obtaining intersite RMS values for each distance (phantom dimensions), we were able to assess the possible existence of a directional bias because of a higher distortion in a specific direction in space.

Segmentation and ROI Definition

MRI images were processed using locally developed software incorporating a variety of image processing and quantification tools [Desco et al., 2001]. The intracranial volume (ICV) mask was obtained from the T2‐weighted image by using manually supervised region growing tools. The resulting mask was registered to the T1‐weighted image and edited when necessary. To obtain volume measurements of the main brain lobes, we used a method for semiautomated segmentation of the brain based on the Talairach proportional grid system [Andreasen et al., 1996; Kates et al., 1999]. Basically, a two‐step procedure was followed [Desco et al., 2001]. First, an initial segmentation of cerebral tissues into GM, WM, and CSF was obtained using Statistical Parametric Mapping (SPM) routines (see later). Second, the Talairach grid was built on the edited brain MRI by manually selecting the position of the anterior and posterior commissures (AC, PC) and a third point in the mid‐sagittal plane. The coordinates of these points serve to calculate the transformation (rigid rotation) required to comply with the Talairach orientation: the plane of the AC‐PC as the axial horizontal plane, and the interhemispheric plane as the vertical axis [Talairach and Tournoux, 1988]. Then, our application automatically finds the outer brain limits in Talairach orientation, and 3D grids are built for each brain. The Talairach grid obtained in this way represents a piecewise linear transformation and a tessellation of the brain into a 3D grid of 1,056 cells representing homologous brain regions across subjects [Talairach and Tournoux, 1988]. The ROI measurements were obtained by superimposing the 3D tissue masks corresponding to GM, WM, and CSF onto each subject's Talairach reference grid, where the regions of interest were defined as sets of Talairach grid cells [Andreasen et al., 1996; Kates et al., 1999]. Volume for each tissue type was measured on this MRI by summing up the data from the Talairach grid cells associated with each ROI [Desco et al., 2001]. The validity of the Talairach‐based procedure as an automated segmentation and quantification tool suitable for volumetric studies has already been proven [Andreasen et al., 1996; Kates et al., 1999] and has also been used in other multicenter studies [Patwardhan et al., 2001]. In our implementation, all manual procedures were performed by a single operator blind to the origin of each scan, thus avoiding any potential interrater variability.

Regions of Interest

The analysis included total volumes of GM, WM, and CSF, as well as ROIs comprising the frontal, parietal, temporal, and occipital lobes, defined using the boundaries for the Talairach method described elsewhere [Andreasen et al., 1996; Kates et al., 1999]. To simplify the analysis, all the ROIs were measured bilaterally, adding right and left values. ICV was measured by adding total GM, WM, and CSF volumes, including the cerebellum.

Tissue Segmentation

Segmentation of cerebral tissues was obtained by means of an automated method included in the SPM program [Ashburner and Friston, 1997, 2000]. The method performs a cluster analysis on the likelihood of each MRI voxel being one of four tissue types—GM, WM, CSF, and “other tissues”—using a modified mixture model and a priori information. This a priori information is provided as anatomical templates that represent an “average” brain and offer information on the spatial distribution of the different brain tissues. Two different tissue segmentation procedures were tested, with the aim of obtaining maximum compatibility among scanners: single‐modality (T1) and multimodal (T1 and T2) segmentation. For multimodal segmentation, T2 images were coregistered and resliced to the T1 images. This registration was made by using mutual information methods [Collignon et al., 1995] and trilinear interpolation, which are available in our software tool for medical image processing [Desco et al., 2001].

The SPM algorithm for tissue segmentation includes a method to eliminate the effect of radiofrequency field inhomogeneities [Ashburner and Friston, 2000]. This method for bias field inhomogeneity correction has proven to be very robust [Gispert et al., 2004b] and it was used in both protocols single‐modality (T1) and multimodal (T1 and T2). Volume masks resulting from tissue segmentation were combined with the skull‐stripped ICV masks obtained using the T2 scan and later registered to the T1 image. Finally, the ICV masks containing the three tissue maps were checked for inconsistencies and manually corrected whenever necessary (i.e., isolated pixels classified as GM but located off from the sulcal CSF were excluded from the intracranial mask) by an experienced radiologist blind to the origin of each scan.

Measurement of Intersite Variability

We used the coefficient of variation (CV) as a measurement of intersite repeatability of ROI volumes [Styner et al., 2002] under the assumption that, for each subject, low CV between scanners would imply high similarity of volume measurements obtained at each scanner. Thus, average of the five CV from each subject would serve as an indicator of overall dispersion and similarity in volume measurements between scanners. The CV is computed by dividing the standard deviation by the mean, which, in our case, required the estimation of the pooled standard deviation and the grand mean of the five subjects measured in the five scanners. This was done by calculating the average intrasubject variance for the five subjects (between scanners) and dividing the square root of this by the overall grand mean volume of the five subjects in all scanners. The average within‐subject variance for our five subjects in the five scanners equals the mean square of the residual term in a one‐way ANOVA, using the scanner as the main factor [Bland and Altman, 1996].

Measurement of Intrasite Variability

Unfortunately, it was not possible to obtain repeated scans within sites. To partially overcome this limitation, we used data from another investigation on the impact of various sources of error on volumetric measurements, which included a larger (n = 12) sample of images [Gispert, 2003; Gispert et al., 2004a, 2005]. The data were obtained from subjects other than those used for the multicenter study, but the scanner was the same Philips Gyroscan ACS and the ROI and tissue segmentation and quantification procedures were the same as for the multicenter study. Two intrasite sources of error were measured in this set of 12 images (four subjects): image data acquisition (subject positioning in the scanner), and manual intervention during the segmentation method [Gispert, 2003; Gispert et al., 2004a, 2005]. Image data acquisition error (subject positioning in the scanner) was estimated by obtaining three repeated scans of four subjects in the scanner. To assess manual intervention error, five scans within the sample of 12 images were selected and the whole segmentation procedure was repeated by the same radiologist. Manual procedures included the selection of the anterior and posterior commissures, and the supervision of automated algorithms (tissue segmentation) and processing tools (ICV mask from the T2‐weighted image using region growing tools). This manipulation was performed by a single radiologist blind to the origin of the images. In both intrasite sources of error, volume data were obtained for each set of images and overall CV for each ROI was calculated using the same procedure as for the intersite data (see earlier). Concerning the SPM tissue segmentation algorithm, repeatability values in terms of variability due to repeats relative to variability among scans (ICC) ranged from 95 to 99% for total volumes of GM and WM, and from 89 to 99% in CSF [Agartz et al., 2001; Chard et al., 2002; Gispert et al., 2004a, 2005].

Statistical Analysis

The analysis of differences between sites for each volume variable was made by a one‐way ANOVA model using site as the between‐group factor. A repeated measures ANOVA model might also have been appropriate, considering scanner as the repeated‐measures factor. However, in our study, a simple ANOVA yields the same results as the repeated model because of the lack of covariance structure (no expected pattern of correlations among repeated measures) in our repeated factor (scanner) [Littell et al., 1998]. Whenever the ANOVA indicated that significant differences were present, a post‐hoc test (Sidak) was performed, to identify the two extreme pair of sites showing significant differences. To assess the magnitude of the differences between maximum and minimum values, we calculated the effect‐size using Cohen's D coefficient (difference between maximum and minimum values divided by the pooled standard deviation), adjusted for sample size (Hedge's g). Calculation of effect size for volumetric measurements provided a benchmark for intersite differences that could be compared with patient–control differences reported in the literature. Repeatability between scanners was also estimated by the intraclass correlation coefficient (ICC) using the Shrout and Fleiss formulae [Shrout, 1998] and considering our five scanners as the whole population of machines. This statistic has been used in other multicenter studies, and in our case provides a ratio of between scanner variation relative to within scanner (subjects).

Because our study focused on assessing interscanner variability, it was important to have the least possible intersubject variation (within scanner). To minimize this variation due to differences in brain size (up to 8.2% in GE_2, Table II), we adjusted volume measurements in such a way that ROI data were expressed as ratios to total ROI volume (GM + WM + CSF in each lobe), whereas whole brain GM, WM, and CSF measures were divided by ICV. To have a better appraisal of the changes in absolute volumes in cc, the results for global GM, WM and CSF measures are given both in absolute volumes and as ratios (Table II). In neurodegenerative processes, normalization of data as a percentage of the corresponding total ROI volume, instead of whole brain (ICV), is expected to be more informative about localized volumetric changes than absolute data [Cannon et al., 1998]. Statistics were performed using SAS 9.1 (SAS Institute, Durham, NC).

RESULTS

Geometric Distortion

Linear measurements obtained from the five phantom images showed high similarity between scanners, suggesting that intersite bias due to geometric distortions was unnoticeable. Mean RMS difference between distances measured in phantom images from the five scanners was 0.64 mm, i.e., below the spatial resolution of the brain images acquired (voxel size of ∼1 × 1 × 1 mm³, Table I). Of the distances measured in the phantom, the maximum RMS among scanners was 1.3 mm, which represents 1.6% of the mean distance measured (80.2 mm). No particular distribution of intersite differences among the distances was observed, thus ruling out any directionality in the geometric distortion.

Differences Between T1‐Only and T1 and T2 Tissue Segmentation

Volume data obtained using multimodal (T1 and T2) tissue segmentation were more consistent across sites than those obtained using single‐modality (T1) MRI data. Values of intersite CV, percentage difference, and effect size between maximum and minimum values were higher for T1‐only segmentation than for T1 and T2 (Table II). Using T1‐only data, the two Siemens scanners showed a characteristic bias overestimating WM and underestimating GM, relative to the other scanners (Table II, Figs. 1 and 2). However, this bias was unnoticeable when using multimodal data. The main differentiation between the results obtained with each segmentation method was a reduction in GM and an increase in CSF in the multimodal data (Table II, Figs. 1 and 2).

Figure 2.

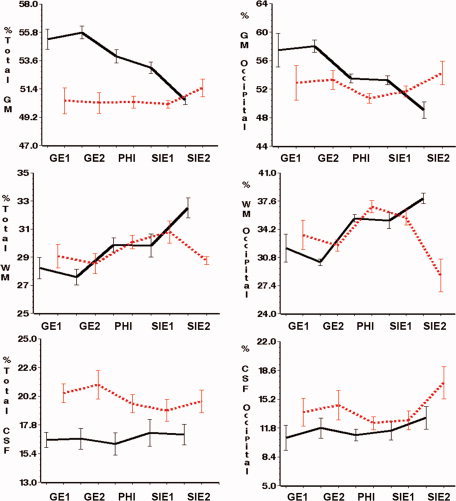
Plots showing the volumetric measurements obtained at each site using T1 and T2 (light, dashed line) and T1‐only (black, solid line) tissue segmentation (see Methods for details). Bars represent 1 SD around the mean. Lines join within site mean values. Left column: Whole‐brain volumes (data expressed as a percentage of intracranial volume). Right column: Tissue volumes of the occipital lobe (data expressed as a percentage of the total volume for the occipital lobe). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Effect sizes measured between maximum and minimum volumes of the five scanners also suggested higher compatibility between sites (lower effect size) when using T1 and T2 data (Table II). For whole brain GM (%), effect size was as much as five times higher using T1‐only (Table II). However, the values of effect size obtained from both segmentations are very similar when comparing data from the two GE sites, which used similar acquisition parameters; the range obtained being 0.1 to 0.4, instead of 0.3 to 5.1 for all five machines (Table II). Thus, results of the multimodal imaging may be equal to the T1‐only when the same scanner brand and nearly identical parameters are used. If we measure repeatability in terms of ICC, both single and multimodal segmentations show similar values, thus indicating overall good agreement between sites (Table II).

Contrast‐to‐noise ratios were similar among subjects and for most scanners except for the SIEMENS_2, which showed a 50% lower value than in the other sites (Table II). To asses the effect of contrast‐to‐noise ratios on the tissue segmentation results, values were plotted against GM/WM ratio, which is a structural parameter that remains fairly constant across subjects. This graph shows that using T1 and T2 data, contrast‐to‐noise has no effect on the segmentation, and the GM/WM ratio ranged from 1.5 to 1.9 across all subjects, regardless of their site of origin or contrast‐to‐noise value (Fig. 3). However, using the T1‐only data, low values of contrast‐to‐noise produce a bias on the segmentation; scans from the SIEMENS_2 show both the lowest GM/WM and contrast‐to‐noise ratios (Fig. 3).

Figure 3.

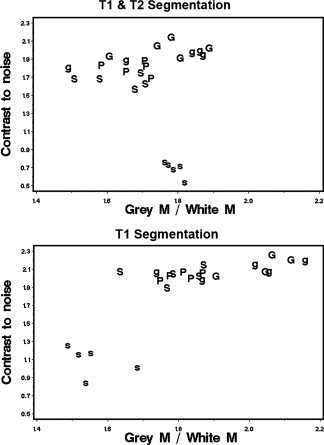
Scatter plots showing the relationship between contrast‐to‐noise ratio and GM/WM ratio for each subject scanned. Top data obtained using T1 and T2 segmentation. Bottom: Data obtained using T1 scans only. Data points are labeled with the scanner used. G: GE_1; g: GE_2; P: Philips; S: SIEMENS_1; s: SIEMENS_2. To facilitate the comparison between the two segmentation methods, the same scale was used in both plots.

The accuracy and quality of tissue segmentation results was assessed by examination of the tissue masks fused on top of T1 images, which revealed that the segmentation of WM and GM tissue seems more accurate in multimodal segmentation because the cortex distribution along with the sulci and gyri looks more realistic. This was observed in both the left and right hemispheres, suggesting that the bias field correction of the tissue segmentation method was successful (Fig. 1). On the other hand, the higher volumes of CSF obtained using T1 and T2 segmentation seem to arise from an exaggeration of sulcal spaces (Fig. 1).

In view of these results, it was reasonable to accept that multimodal segmentation is the most robust and suitable strategy for our multicenter data. Thus, to simplify the results for ROI measurements, intersite differences are only reported for T1 and T2 segmentation.

Intersite Differences

The ICV variability of our sample was rather high, with values ranging from 1,269.2 to 1,634.7 cc (overall grand mean = 1,451.0; SD = 97.7; n = 25). This variability reflects the mixture of gender and age within the sample of volunteers, and falling within the range observed in other samples of healthy individuals of similar age and gender composition [Molina et al., 2002, 2003]. For ICV, there was a maximum of 3.9% difference between scanners, whereas intersite CV was 1.9, lower than intrasite CV among subjects (range, 6.2–8.2%). Concerning tissue types, intersite CV of whole brain data was lowest in GM (1.8%) and highest in CSF volume (5.2%) (Table II).

Differences between scanners were higher for the regional tissue volumes of the four lobes than for the whole brain (Table III, Fig. 2). In the four ROIs examined, the lowest differences were in GM, and the highest were in CSF (Table III). Significant intersite differences were observed in the WM of the parietal and occipital lobes (ANOVA and Sidak post‐hoc) (Table III); in both variables, SIEMENS_2 shows the lowest values. Because of the high intersubject variability, no statistical significance was reached for mean CSF values between sites, despite the fact that both intersite CV and percentage difference between extreme values were highest for CSF volumes (Tables II and III).

Table III.

Volume data (Mean, SD) for each of the ROI measured at each site in the five subjects, and using T1 and T2 tissue segmentation

	GE_1		GE_2		PHILIPS		SIEMENS_1		SIEMENS_2		Intersite CV
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Frontal (cc)	308.5	24.1	311.6	25.1	301.9	21.5	322.7	25.3	326.6	22.9
GM (%)	42.0	2.1	41.5	1.9	42.5	1.8	41.5	1.0	42.9	1.7	2.2
WM (%)	32.8	1.9	32.8	2.5	33.5	2.5	35.2	2.7	32.9	2.1	5.4
CSF (%)	22.6	2.0	23.1	3.1	21.4	2.7	21.1	2.9	22.4	2.6	7.0
Temporal (cc)	236.9	21.9	241.4	23.7	240.7	20.3	240.4	15.6	239.9	21.4
GM (%)	60.8	1.7	58.7	1.5	59.8	0.8	60.3	1.0	59.8	1.5	2.0
WM (%)	24.6	0.9	25.9	1.0	26.7	1.0	25.9	1.8	26.9	2.0	4.9
CSF (%)	14.6	1.0	15.4	1.4	13.5	0.8	13.8	2.0	13.3	1.3	8.3
Parietal (cc)	271.7	20.4	274.6	21.4	271.6	13.9	280.8	17.6	287.6	20.0
GM (%)	38.5	3.9	39.0	2.3	37.7	1.3	38.5	1.5	40.3	2.1	4.3
WM (%)a	40.9	3.0	39.1	2.6	42.0	2.4	42.1	2.9	35.9	2.1	7.2
CSF (%)	19.2	3.0	20.5	3.7	18.9	2.0	18.1	2.6	22.6	2.6	10.1
Occipital (cc)	124.2	8.0	125.4	6.9	129.3	6.6	132.7	9.9	132.3	7.3
GM (%)	52.9	5.4	53.3	3.0	50.7	1.5	51.7	1.7	54.3	3.6	5.7
WM (%)a	33.5	3.9	32.2	1.5	36.9	1.6	35.6	2.0	28.6	4.4	11.7
CSF (%)	13.6	3.6	14.5	3.9	12.4	1.7	12.7	2.5	17.1	4.3	17.3

Intersite CV: average of within subject coefficients of variation between scanners (see Methods).

ROIs were measured bilaterally, adding right and left values.

^aROIs showing significant intersite differences in an ANOVA (P < 0.05). If the ANOVA was significant, the pair of extreme values showing significant differences is boldfaced (P < 0.05; Sidak test).

Increase of Variability Due to Pooling Multisite Data Relative to Intrasite Variation

For whole brain measurements, the overall pattern observed shows that mean intersite CV was lowest for GM, and highest for CSF data (Table II). The increase in variability of multicenter data for whole brain data and T1 and T2 segmentation was 3% and 1.8% in GM, respectively, for absolute volumes in cc or ratio volumes, whereas in CSF it was 5.6% and 5.2%, respectively, for absolute volumes in cc or ratios (Table II, Fig. 4). Using T1‐only segmentation, values of intersite CV were higher than using T1 and T2 data (Table II).

Figure 4.

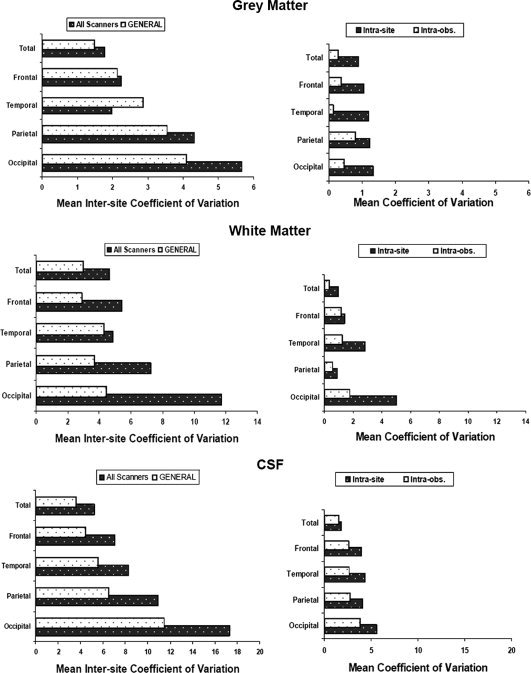
Estimation of the error in our volume measurements in whole‐brain and lobar data of GM, WM, and CSF due to different sources: intersite, intrascanner, and intrarater (see Methods for details). Left column: All scanners; bars show average of within subject coefficients of variation between scanners in the five sites. GENERAL; bars show the mean coefficient of variation of the five subjects in the GE‐1 and GE‐2 sites only. Right column: Intrasite; variability due to MRI acquisition (subject positioning in the scanner). Intraobs; variability due to manual intervention in the ROI segmentation method (see Methods). To facilitate comparisons, notice that for each tissue type, the range of values in the horizontal axis is the same for left and right columns.

The two factors of intrasite variability measured in this study showed much lower values (higher repeatability) than corresponding intersite values. The effect of manual intervention involved in our segmentation procedures was highest for CSF measurements (around 4%), whereas for GM and WM was less than 2% in all of the ROIs studied (Fig. 4). In all variables and tissue types, image acquisition, measured as subject positioning in the scanner, showed higher variability than manual intervention. Highest intersite CV (lowest repeatability) was observed in CSF variables, where manual intervention showed the highest values, close to those obtained by image acquisition. These values of intersite variability were roughly twice as much as our estimations of within‐site variability in GM, WM, and CSF (Fig. 4).

Considering brain subdivisions into ROI, the frontal and temporal lobes showed similar increase in variability (intersite CV) than whole brain measurements (Tables II and III), whereas in the parietal and occipital lobes, values of intersite CV were much higher than whole brain data. Regarding tissue types, we observed the same pattern as in the whole brain, the lowest intersite CV was obtained in GM tissue and the highest values in CSF (17.3 in the occipital lobe) (Table III, Fig. 4). On the other hand, the high variability obtained for CSF of the occipital lobe may partly be artificial and should be taken with caution because it reflects the small size of the occipital lobe itself (∼130 cc) and the amount of sulcal CSF within this region (∼17 cc). Thus, the intersite CV of 17.3% would represent only 3 cc, which is reasonable considering the precision of the whole procedure for volume quantification. Figure 4 suggests a common pattern of error among brain regions, in both inter‐ and intrasite values. In particular, CSF values show highest intra‐ and inter‐CV in the occipital lobe, and lowest in the frontal, which may suggest that partial volume effects play an important role in the variability observed in this region. In the most favorable scenario, if the intersite data are obtained by pooling scans from only two scanners of the same manufacturer and running the same acquisition parameters (i.e. the two GE scanners), the intersite CV is reduced considerably, specially in ROIs showing high intersite variation like the occipital lobe (Fig. 4).

DISCUSSION

In this study, we provide a new assessment of intersite variability by using a particular data set that encompasses most of the possible factors of variation that can occur in a multicenter study. The data were obtained from five sites including three scanner manufacturers that were running either similar or different acquisition protocols, and the subjects scanned were five volunteers different in sex and age. Although these factors increased the overall variability of the volume measurements obtained, on the other hand, they did make our data more representative of a variety of multicenter neuroimaging projects. In this regard, our study complements previous reports about the variability of multisite data [Patwardhan et al., 2001; Schnack et al., 2004; Styner et al., 2002; van Haren et al., 2003] by assessing the influence of acquisition factors that may not be always fully controlled in a multicenter setup. The method used for brain ROI segmentation and volume quantification allowed a comprehensive regional description of the impact of using multicenter data in psychiatric research.

Effect of Pooling Multicenter Data

In most of the variables measured, there was good agreement between machines in the mean volumes obtained for the five subjects, which supports the possibility of pooling data from different scanners, although bearing in mind that the error introduced is different depending on the particular volumetric variables included in the study. According to our data, the amount of variability added to volumetric data due to the multicenter setup is, on average, 4% for whole brain measurements (Intersite CV, % of GM, WM, CSF; Table II) and 7% for our 12 ROI variables (intersite CV; Table III), though it can reach as much as 17.3% for a specific ROI and tissue combination (CSF, occipital lobe; Table III). Our results suggest that, when multimodal segmentation is used, scanner‐dependent error is lower and follows a pattern that enables statistical analysis using models that incorporate the scanner as an additional source of variance, in the same way as head size, age, or sex. Using multimodal segmentation, our estimation of the effect size due to the multicenter factor ranged from 0.4 to 1.2, which appears to be acceptable for group comparison studies. For example, a review of biological effect sizes in schizophrenia shows that most volumetric studies report values higher than 2 [McCarley et al., 1999; Shenton et al., 2001]. Even though our results correspond to a heterogeneous mixture of subjects and scanners running different protocols, we were able to show that in the most favorable circumstances—similar scanner manufacturer and acquisition parameters—the average effect size was 0.2, which is low when compared with values from group comparison studies. Thus, it seems that, despite the fact that using multicenter data involves an additional source of error, there is still room to detect potential group differences, particularly if the multicenter setup includes machines from the same manufacturer running similar acquisition parameters.

Our estimation of intrasite variability due to the acquisition and manual intervention in the brain extraction and ROI segmentation was much lower than intersite variability. Intrasite repeatability followed the same pattern as the interscanner variability, the lowest CV being obtained for GM and the highest for CSF (Fig. 4). Error due to manual intervention was highest for CSF (4% max, Fig. 4) because of the difficulties in supervising the segmentation of sulcal CSF and the ICV mask. Thus, relative to intrasite repeatability, overall experiment‐wise error in our multicenter study is nearly twice the intrascanner value (Fig. 4) in most variables. Intrasite CV values reduce considerably when pooling scans from only two scanners of the same manufacturer and running the same acquisition parameters (i.e., the two GE scanners).

Concerning how the measurement of repeatability is made in multicenter studies, our data show that the ICC [Patwardhan et al., 2001; Schnack et al., 2004; Styner et al., 2002; van Haren et al., 2003] sometimes yields artificially high values in spite of poor agreement between sites. This bias is due to the nature of the ICC, which represents a ratio of interscanner variance relative to intrascanner variance (subjects), rather than providing absolute estimations of reproducibility. For instance, ICC values obtained for global GM and WM (%) were very similar in both segmentation data sets, despite the fact that the single‐modality segmentation showed much higher values (low agreement) in terms of effect size and percentage difference between maximum and minimum values (Table II). Thus, we believe that the CV used in this study provides a simple and direct measure of variation due to the scanner factor that can be easily compared with other data sets and variability factors (e.g., inter and intrasite).

The tissue segmentation algorithm used in our study [Ashburner and Friston, 1997] has been proved to be repeatable intrascanner [Agartz et al., 2001; Chard et al., 2002; Gispert, 2003; Gispert et al., 2004a]. Our study extends the robustness of SPM tissue segmentation to an interscanner factor, showing repeatability values of a similar magnitude to those obtained in similar multicenter studies [Schnack et al., 2004; Styner et al., 2002; Tofts, 1998; van Haren et al., 2003]. Our level of repeatability was achieved with a widely used ROI and tissue segmentation method that is freely available for clinical research, and without performing any precalibration process [Schnack et al., 2004; van Haren et al., 2003]. A calibration step, while maximizing overall repeatability, may eventually induce inaccuracies (closeness to the ground truth) in the volumetric measurements in the event of bias in a given machine, as might be the case in our study.

Our data suggest that using multimodal segmentation increases compatibility between machines of the same, or different, manufacturer. In our study, this gain in reproducibility seems to arise by eliminating the overestimation of WM observed in some scanners (Siemens) when using T1 segmentation only. This result complement previous reports made with a single subject and only two scanner manufacturers [Styner et al., 2002], now using data from a mixed sample of five subjects, and with a wider sample of scanners. Segmentation results using multimodal data were also more robust and independent of differences in contrast‐to‐noise ratios of scans from different sites (Fig. 3). However, although the recommendation to use T1 and T2 data is clear, our examination of the quality of both segmentations suggest that one should bear in mind that T1 and T2 segmentation may overestimate CSF volumes in our dataset (Fig. 1). Since this bias is likely to originate from the higher partial volume of our T2 images, increasing the scan resolution to the levels of the T1 image may help provide a more accurate CSF estimation. Not surprisingly, CSF data showed the lowest repeatability, because of the higher partial volume effect in T2 images, and also because of the manual steps involved in producing the ICV mask [Schnack et al., 2004; Styner et al., 2002].

Multimodal tissue segmentation is more likely to provide more robust results than using data from T1‐only. However, considering the values obtained for the two GE scanners, multimodal segmentation may perform as well as using T1‐only data if the same scanner brand and nearly identical parameters are utilized. Data from the two GE scanners combined, using T1 and T2 or T1‐only segmentation yielded similar results, as measured in terms of the effect size (Table II). This suggests that multimodal segmentation is more critical whenever the multicenter setup includes a variety of scanners running different acquisition parameters. We believe that this is a useful consideration because the higher demand of resources and complexity involved in multimodal segmentation might be prevented, if images from the same scanner model and acquisition parameters are available. Thus, in cases of similar scanner manufacturers and sequence parameters, the little increase in reproducibility gained should be weighed up against the potential loss of accuracy in the tissue segmentation (i.e., overestimation of CSF).

Our results show that it is important to study multicenter repeatability not only for whole brain data but also at the ROI level. In addition to tissue type, repeatability depends on the region. Intersite error (mean CV) was higher in the parietal and occipital lobes than in the frontal and temporal lobes (Table III, Fig. 4). In the occipital lobe, the increase in variability in CSF is related directly to the volume of CSF within this lobe of the brain. Because of the relatively little CSF within this region (∼17 cc), a small change in CSF produces a large percentage of change. At any rate, considering that lowest and highest intersite CV were observed respectively in the frontal and occipital lobe, which are also the largest and smallest ROIs, this pattern may suggest that differences in repeatability between ROI values could be related to the total size of the ROI. However, this rule does not hold for the parietal lobe, showing higher intersite CV values than the temporal lobe, despite the parietal is larger than the temporal (Table III, Fig. 4). Another relevant finding of our study, as a preliminary step to a clinical investigation, was the low reproducibility obtained for the WM and CSF volumes of the occipital lobe, suggesting that in a multicenter setup, this data should be excluded from comparative studies where the expected differences between groups are low (i.e., below 7–10%; which is the average error of WM and CSF variables; Table III).

Role of Acquisition Parameters and Scanner Manufacturer

Although we did not intend to measure or compare the accuracy of the machines studied, there were some signs of manufacturer‐dependent bias in the estimation of tissue volumes, particularly when using single‐modality tissue segmentation. According to our data, Siemens equipment, when compared with GE or Philips, tended to show higher values of WM (Table II). Overestimation of WM in Siemens scanners has also been reported in other studies [Schnack et al., 2004; van Haren et al., 2003]. However, this bias disappeared with multimodal segmentation (Table II). A distinguishable intensity inhomogeneity was observed in the images obtained at the two Siemens sites. This acquisition artifact, together with the differences in acquisition parameters in the two Siemens sites, might be one of the reasons for the bias observed in WM volumes, although all scans were equally corrected for bias field heterogeneity by the SPM tissue segmentation algorithm, which includes a robust correction method [Gispert et al., 2004b]. Bias field correction has been mentioned as one of the confounding factors for tissue segmentation methods; indeed, our data show that it has special relevance for multicenter studies [Evans, 2002; Tofts, 1998].

When planning a multicenter study, the question arises as to whether higher compatibility between sites would be obtained by emphasizing similarity of scanners or of acquisition parameters. In our study, volume measurements were more similar between the two GE sites (similar sequence parameters and pixel size) than between the two Siemens sites (different sequence parameters and pixel size). Our results indicate that volume measurements obtained with either one of the two SIEMENS are as close to the other SIEMENS than to any of the other scanner manufacturers. However, because sequence acquisition and the scanner factors are confounded in our data set, we cannot conclude that data similarity between SIEMENS scanners “per se” is necessarily poor. On the other hand, considering the higher similarity in the volumes obtained for the two GE scanners in which acquisition parameters were very close, we expect that using similar acquisition parameters should likewise improve the similarity between the two SIEMENS, though we cannot verify that, nor predict how significant that increase would be. Our study provides evidence that highest compatibility among scanners would be achieved by using equipments of the same manufacturer and image acquisition parameters as similar as possible, in particular when the same scanner is used. Thus, the same emphasis on running the scans with the same parameters should be made at all sites, whether they are using the same scanner manufacturer or not.

This was one of the limitations for our intersite comparison. Sequence parameters and pixel resolution were not the same in every site, thus the site factor was confounded with the sequence parameters. This circumstance limited somewhat the conclusions of the study and increased the overall variability of the sample, although it provided valuable data to estimate the impact of acquisition parameters. On the other hand, other multicenter studies have shown that images obtained not only from different scanner manufacturers, but also using different magnetic fields and orientation (axial, coronal, sagittal) can be somehow combined in a multicenter setup [Patwardhan et al., 2001; Schnack et al., 2004].

The small sample of subjects scanned is one of the main limitations of our study, although the total number of images was acceptable (n = 25). This difficulty is common in most of the multicenter studies performed. Some studies have been carried out with similar samples as in our study [Schnack et al., 2004], or with a similar sample size, but different subjects for each site [Patwardhan et al., 2001], or even including only a single subject scanned at the different sites [Styner et al., 2002]. Despite these differences in the subjects scanned, the results obtained in all of those studies, including ours, are reasonably concordant.

Another limitation of our study was the lack of repeated scans at each site to allow the assessment of intrasite variability with the same subjects used for intersite variability. We estimated the intrasite variability using data from another study on repeatability made with a larger sample of scans, the same protocol for ROI segmentation and volumetric quantification, and performed at one of the five sites (Philips site). Results obtained were of the same magnitude to those reported in other intrasite studies [Agartz et al., 2001]. Being aware that the values reported should be treated with caution, we believe that the overall results obtained with these data represent a reasonably appropriate and unbiased approximation to our intrasite variability, at least for the purpose of setting a reference of experiment‐wise error benchmark for comparison with intersite variation. Thus, our main conclusion that intrasite variation is always much lower than intersite seems fully reasonable and confirms previous findings [Schnack et al., 2004; Styner et al., 2002].

In the near future, we will probably be seeing clinical trials (e.g., neuroprotective drugs) in which regional brain volumes are the ancillary supportive variable. For these studies, MRI from different research sites will have to be pooled to obtain the required statistical power. In these scenarios, finding the most robust compromise between pooling data (increasing sample size) and minimizing the artificial variation added to the data could only be made after evaluating the compatibility among machines and taking into account the variables measured. On the other hand, we believe that the scanner effect should also be given careful consideration in a meta‐analysis of volumetric data, and in this respect our study may help in the estimation of the scanner effect when pooling results made at different sites.

In summary, bearing in mind the limitations of the study, our paper was intended to illustrate the effects and potential uses of combining data from different sites in a particular set up, rather than providing a model to follow in multicenter studies. Our results suggest that pooling our intersite data for whole brain measurements of GM, WM, and CSF adds only a reasonably small amount of variation (error) ranging from 1.8 to 5.2%, respectively. However, considering ROI variables like CSF volume of the occipital lobe, this error can reach 17.3%. Whenever possible, T1 and T2 tissue segmentation methods should be used because they yield more consistent volume measurements between sites than T1‐only segmentation, especially when scans are obtained with different sequence parameters and pixel sizes from those used at the other sites. Thus, in multicenter studies, tissue and ROI segmentation protocols should be validated to assess their intersite reproducibility. After this validation, we may choose to exclude data from a specific ROI (i.e., occipital lobe), or from scanners using acquisition parameters markedly different from those of other sites.