Mutual‐information‐based approach for neural connectivity during self‐paced finger lifting task

Abstract

Frequency‐dependent modulation between neuronal assemblies may provide insightful mechanisms of functional organization in the context of neural connectivity. We present a conjoined time‐frequency cross mutual information (TFCMI) method to explore the subtle brain neural connectivity by magnetoencephalography (MEG) during a self‐paced finger lifting task. Surface electromyogram (sEMG) was obtained from the extensor digitorum communis. Both within‐modality (MEG‐MEG) and between‐modality studies (sEMG‐MEG) were conducted. The TFCMI method measures both the linear and nonlinear dependencies of the temporal dynamics of signal power within a pre‐specified frequency band. Each single trial of MEG across channels and sEMG signals was transformed into time‐frequency domain with use of the Morlet wavelet to obtain better temporal spectral (power) information. As compared to coherence approach (linear dependency only) in broadband analysis, the TFCMI method demonstrated advantages in encompassing detection for the mesial frontocentral cortex and bilateral primary sensorimotor areas, clear demarcation of event‐ and non‐event‐related regions, and robustness for sEMG ‐ MEG between‐modality study, i.e., corticomuscular communication. We conclude that this novel TFCMI method promises a possibility to better unravel the intricate functional organizations of brain in the context of oscillation‐coded communication. Hum Brain Mapp, 2008. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

Several populations of human cortical neurons exhibit intrinsic properties of oscillation (∼10 and ∼20 Hz) in a resting state, predominantly in the vicinity of the primary sensorimotor and visual and auditory cortices, as recorded non‐invasively using electroencephalography (EEG) or magnetoencephalography (MEG) [Jasper and Penfield, 1949; Salmelin and Hari, 1994]. The power of oscillation can be modulated dynamically with respect to event occurrence, either decreasing or increasing, a phenomenon termed event‐related desynchronization (ERD) or synchronization (ERS) [Andrew and Pfurtscheller 1999]. In the context of movement, it has been suggested that the dynamics of ERD may reflect action planning and execution, while the dynamics of ERS may connote deactivation or inhibition of neural networks during the recovery phase [Lee et al., 2003b; Pfurtscheller et al., 1996]. According to principles of brain organization, the functional integration describes the global influence, which requires the interactions, such as functional connectivity, between large subsets in the nerve system to be coherent; these frequency‐dependent regulations make the brain a complex system [Friston, 1997; Tononi et al., 1994]. Several analysis methods have been developed to characterize neuronal couplings, including ERD/ERS quantifying small scale interactions, the coherence method measuring functional connectivity, and the cross mutual information (CMI) method estimating the statistic dependency between spatially separated areas or large scale interactions [Andrew and Pfurtscheller, 1999; David et al., 2004; Grosse et al., 2002].

Quantitative analysis of ERD and ERS around rolandic areas, typically segregated around 10 and 20 Hz, provides a means to understand the dynamics of neuronal populations and can be applied to address questions in physiology and pathophysiology of the human sensorimotor system [Aoki et al., 2001; Crone et al., 1998; Pfurtscheller et al., 1998]. For example, Magnani et al. [2002] evaluated mu ERD onset time in patients with idiopathic Parkinson's disease before and after l‐dopa treatment [Magnani et al., 2002]. They concluded that dispersible l‐dopa has acute positive effects to improve motor performance and advance the latency of cortical activation during motor programming. The basis of the ERD analysis employed, however, mainly rests on phenomenological description and does not provide insightful mechanisms in the context of functional connectivity.

The coherence method, an approach commonly used to study oscillatory activity, has been exploited to address functional coupling or interaction, information exchange, and temporal coordination between cortical regions [Gerloff et al., 1998; Leocani et al., 1997; Nagamine et al., 1996]. High coherence indicates potentially neuroanatomic or functional connections between cortical areas underlying the sensors, while decreased coherence may denote the disruption of functional couplings [Fein et al., 1988; Leocani and Comi, 1999]. For example, patients with Alzheimer's disease showed significant decrease of α‐activity coherence in temporo‐parieto‐occipital areas [Locatelli et al., 1998]. Patients with severe cognitive impairments display further decreases in coherence. In addition, the coherence method has been adopted to elucidate the oscillatory communication at around 20 Hz between somatomotor cortices and muscles in surface electromyogram‐magnetoencephalography (sEMG‐MEG) studies [Salenius et al., 1997]. In sEMG‐MEG coherence studies, it has been suggested that the transient synchronization of rhythmic activities between sensorimotor areas and muscles can be crucial for motor command [Kilner et al., 1999]. Timmermann et al. [2003] reported that abnormal synchronization at 4–6 Hz between the contralateral primary motor cortex and forearm muscles in Parkinsonian patients may contribute to resting tremors [Timmermann et al., 2003]. The investigation of functional connectivity promises the potential to assess functional derangement within or between modalities [Schnitzler et al., 2000].

The coherence method, however, can be problematic if the signals are contaminated by noise, or the oscillatory frequency band is not carefully defined [Andrew and Pfurtscheller, 1999; Nunez et al., 1997] despite the newly developed time‐domain [Jung et al., 2000; Lins et al., 1993; Vorobyov and Cichocki, 2002] or frequency‐domain approaches [Mima et al., 2000a; Whitton et al., 1978; Woestenburg et al., 1983]. Theoretically speaking, the coherence method mainly measures linear dependency and is insufficient for the study of complex and nonlinear brain dynamics [Lopes da Silva, 1991; Popivanov and Dushanova, 1999].

Mutual information (MI), which employs the entropy of high‐order statistics to estimate uncertainty, is a statistical measure of both linear and nonlinear dependencies between two time sequences [Shannon, 1948]. The cross mutual information (CMI) method in a time‐domain has been developed to quantify and assess the functional impairment of information transmission from one area to another in Alzheimer patients [Jeong et al., 2001]. David et al. [2004] used the neural mass model to evaluate the profiles of different dependency measurements in the analysis of functional connectivity [David et al., 2004]. They pointed out that the time‐domain CMI method is not reliable enough in broadband analysis, especially when the coupling between the modeled cortical areas is weak. Moreover, the CMI method only analyzes overall signal changes in time domain. The subtle temporal scenario of power changes within a defined frequency band is unfortunately lost; yet this information can be critical for the understanding of pathophysiology of disease condition.

The present study seeks to develop a conjoined time‐frequency analytical method for MEG‐MEG and sEMG‐MEG measurements based on mutual information [Shannon, 1948] for the investigation of functional connectivity. Each single trial of MEG across channels and sEMG signals was transformed into time‐frequency domain using the Morlet wavelet to obtain better temporal spectral (power) information [Grossmann and Morlet, 1984]. Time‐frequency maps were averaged across trials and the resulting maps were subsequently averaged over specific frequency bands to yield temporal profiles of power with improved signal‐to‐noise ratio (SNR). The averages of time series of power were used to compute the CMI across channels. Since MI is computed‐based on any two temporal power sequences within a task‐specific frequency band, the proposed method can be termed time‐frequency cross mutual information (TFCMI) method. This TFCMI method is then applied to within (MEG‐MEG) and between (sEMG‐MEG) modalities in a self‐paced finger lifting task and the results are discussed based on the simulation and the experimental data.

MATERIALS AND METHODS

Subjects and Task

Eight healthy, right‐handed subjects (24–32 years of age, gender balanced) were recruited for this study. All subjects gave written informed consent for the experiment with a protocol approved by the institutional review board. They sat comfortably in a magnetically shielded room with forearms relaxed. Subjects were asked to lift their right index fingers once every 8 s (35–40° extension angle) in a self‐pacing manner. The protocol in this study is the standard procedure for the Bereitschafts‐potential (BP; in EEG) or readiness field (RF; in MEG), as first reported by Kornhuber and Deecke [1965]. Subjects' left hands rested on a pillow in order to avoid contamination of movement‐related vibrations in the MEG measurements [Hari and Imada, 1999]. Movement onset was registered using an optical pad (4‐D Neuroimaging®, Helsinki, Finland). A trigger pulse was generated at the beginning of each movement taking the interdiction of the laser light from the optical pad as the index of movement onset (zero time). To prevent blinking, subjects were requested to keep their eyes fixed on a cross mark on the center of a back‐projection screen 1 m in front of them.

Data Acquisition and Preprocessing

MEG signals were continuously measured at a 1,000‐Hz sampling rate during task performance using a whole‐head, 204 planar gradiometers (Vectorview®, Neuromag, Helsinki, Finland). This planar type of gradiometer has the advantage of sensitivity of superficial sources, and is particularly suitable for the sensor level analyzing. The sEMG was simultaneously recorded at a 1,000‐Hz sampling rate from the extensor digitorum communis to verify movement. The total number of finger movements was about 100 for all subjects. Some of the data had been published to address the issue about cognitive demands on motor tasks [Wu et al., 2006]. All the sEMG data were rectified before subsequent calculation of TFCMI and coherence analysis. Bipolar horizontal and vertical electro‐oculograms (EOG) were obtained using electrodes placed at the bilateral outer canthi and the left eye respectively. At the beginning of each measurement, the positions of three anatomical landmarks (bilateral pre‐auricular points and nasion) were measured using a 3D magnetic digitizer (Isotrak 3s1002, Polhemus Navigation Science, Colchester, VT) to define a head coordinate system. Four head position indicators (HPIs) were subsequently defined and tracked by the MEG system to ensure no head movement during each measurement (maximal translation <1.5 cm). Individual MRI (T1‐weighted, 3D gradient‐echo pulse sequence, TR/TE/TI:88.1/4.12/650 (all ms), 128 × 128 × 128 matrix, FOV = 250 mm) were obtained with a 3.0‐T Bruker MedSpec S300 system (Bruker, Kalsrube, Germany).

MEG measurements of 204 channels were recorded continuously and termed as a Total Set. Among them, EOG‐free measurements (EOG <600 uV) were extracted as an Accepted Set (approximately at least 100 trials should be collected on‐line). All MEG measurements in the Total Set were used to evaluate the robustness of the TFCMI method against physiological noise.

Computation of Time‐Frequency Maps Using Morlet Wavelet Transformation

Each trial of MEG and sEMG raw data with 4,000 samples (from −2 to +2 s relative to the movement onset time) was processed using the Morlet wavelet transformation to generate the time‐frequency representation of signals (Fig. 1a,b). The time window was defined during this period based on the prominent spectral changes of movement‐related activities (Fig. 1d), which is in line with previous study of a self‐paced finger flexion task [Feige et al., 1996], where the 20‐Hz spectral power depress started at about −2.5 s and a power elevation in β frequency range started at about +0.5 s, with fading out at about +2 s. Let x _i,k(t) denote the data from the kth trial of ith channel at time instant t, its Morlet wavelet transformation is given by:

where W ${}_{\text{x}{}_{\text{i,k}}}$ (t, f) represents the energy density in frequency f of the kth trial of the ith channel at time instant t; 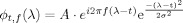are the Morlet wavelets; their time spread is defined by 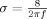; 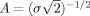is the normalization factor and 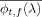are the complex conjugates of ϕ_{t, f} (λ).

Figure 1.

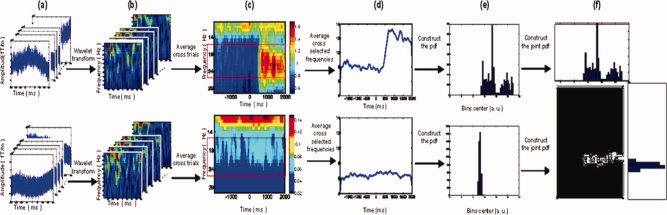
Schematic diagram of TFCMI computation. Raw MEG measurements from any two planar gradiometers of each trial (a) were processed using the Morlet wavelet transformation to obtain time‐frequency maps (b). Colors indicate power amplitude in an arbitrary unit (a.u.). The mean time‐frequency map (c) for each channel was created by averaging the individual time‐frequency maps across trials. The red rectangle represents the prespecified bandwidth in β band (16–25 Hz). The temporal curves of power changes for each channel (d) were created by averaging over the β band (or α band) in the mean time‐frequency map and were used to estimate the probability density function (e) and the joint probability density function (f).

Time‐frequency maps encompassing the α (8–13 Hz) and β (16–25 Hz) activities were created separately by averaging across trials within each subject (Fig. 1c). (Note that only two channels with β activity are shown on the map). They were displayed topographically with colors representing power (see Fig. 2). In the sEMG‐MEG study of corticomuscular coupling, only the time‐frequency map of the β activities underwent further analysis. Frequency components from 16 to 25 Hz were chosen, based on previous electromangentophysiological studies of weak and moderate tonic contractions [Baker et al., 1997; Conway et al., 1995; Halliday et al., 1998; Kilner et al., 1999; Mima and Hallett, 1999; Mima et al., 2000b; Salenius et al., 1997].

Figure 2.

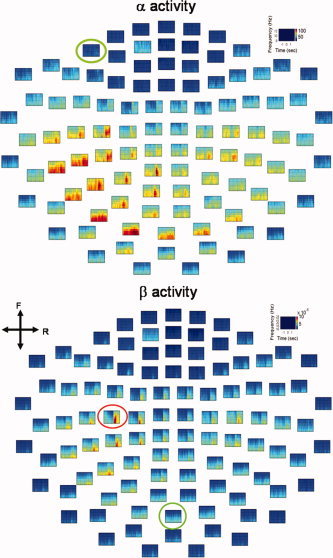
Mean time‐frequency maps of α and β oscillatory activities. The red circle indicates the channel‐of‐interest (COI) with the strongest β oscillatory activity (lower panel); the chosen COI was also used for analysis of α oscillation. Green circles denote arbitrary COIs (A‐COIs), irrelevant to the motor task. Both COI and A‐COIs were employed as reference channels in the subsequent analyses (see Figs. 4, 5). Color indicates power amplitude. The maps are shown in top view. F, front; R, right.

Detection of Neural Connectivity Using TFCMI

Power from two averaged time‐frequency maps was subsequently separately averaged over selected frequency bands to produce two temporal curves (Fig. 1d). Each curve represents 4,000 samples of a random variable, F _i,, at the ith MEG channel. These samples of F _i were used to construct the probability density function (pdf), p(F _i,b), (Fig. 1e) for the computation of entropy, H(F _i):

where the b = 1, 2,…,.64 was the index of sampling bins for the construction of approximated pdf. It is noteworthy that the estimation of pdf and joint pdf from the data histogram is crucial for the computation of mutual information. In order to estimate pdf and joint pdf stably, that is, neither underestimation nor overestimation [Fraser and Swinney, 1986], 64 bins were adopted for 4,000 samples as suggested by Jeong et al. [Jeong et al., 2001].

Entropy is the average amount of information reflecting the measure of uncertainty. Similarly, the joint probability density function (jpdf) between the ith and jth MEG channels can be computed as p(F _i,b, F _j,b) for the estimation of joint entropy, H(F _i, F _j) (Fig. 1f).

Then the TFCMI between two random variables F _i and F _j was calculated as follows:

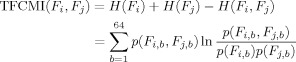The TFCMI value is used as an index of functional connectivity. Figure 1 shows the schematic diagram for TFCMI computation.

Determination of the COI

The channel located in the vicinity of the sensorimotor area exhibiting the most prominent β ERD was chosen as the channel of interest (COI) [Pfurtscheller and da Silva, 1999 for the details of β ERD computation; Andrew and Pfurtscheller, 1999; Pfurtscheller and Aranibar, 1979; Pfurtscheller and da Silva, 1999]. TFCMI and coherence were computed between the COI and any other channels. In addition, the COI was replaced by an arbitrary channel (A‐COI) unrelated to the motor task to investigate the specificity for regional detection. For the between‐modality study, that is, the sEMG‐MEG study, the sEMG was used as the COI.

Statistical Threshold

The 95% confidence limit of t‐distribution was used as a threshold to determine the regions of significant likelihood associated with the COI in TFCMI and coherence analysis, respectively. The confidence levels for TFCMI and coherence were computed in different ways fundamentally. For TFCMI method, value of TFCMI between the COI and any other channels was pre‐normalized with respect to the maximal value of TFCMI obtained at the COI. Normalized values were between 0 and 1 and were used to construct the t‐distribution. The degree of freedom is 1 since we have averaged across trials before TFCMI calculating. In other words, the TFCMI was computed from only one averaged power spectrum. The 95% confidence level was then set at mean +6.314 standard deviation (SD; df = 1, one tailed) to eliminate the bias due to large variation. The conventional coherence method (or magnitude squared coherence) [Zaveri et al., 1999] was also applied to the same data set based on the same COI by using an fast Fourier transform window of 512 points with 256 points overlapping, trial by trial. This allows no overlapping of each epoch signals and makes the spectral resolution (ΔF) of this coherence estimate to be 0.25 Hz, the inverse of the epoch length, 1/4 sec⁻¹ [Zaveri et al., 1999]. Before averaging across trials, an arc‐hyperbolic tangent transform are applied to the coherence values, as described by Rosenberg et al. [1989], so that the coherence values have a normal distribution [Rosenberg et al., 1989]. The significant threshold of 95% confidence limit was then given by mean +1.65SD (df = 100, one tailed) [Halliday et al., 1995]. For the purpose of presentation, coherence values between 0 and 1 were rescaled to the maximal coherence value. Only values of TFCMI and coherence above the significant thresholds were cataloged as significant interactions and were represented topographically as maps with colors indicating the relative coupling level above significance.

Visualization of TFCMI maps

To better visualize the resolved coupled areas of each subject, the TFCMI maps were superimposed on top of each individual cortical surface. The procedure was described in following steps. First, the positions of four HPIs were used to calculate the relative rotation and translation between the sensor coordinate system and the head coordinate system. This allowed the sensor array positions to be transformed into the head coordinate system. Second, three anatomical landmarks (bilateral pre‐auricular points and nasion) on individual MRI were identified and aligned with head coordinate. The sensor array positions were subsequently transformed into the MRI coordinate system. Third, the cortex was segmented from each individual MRI and reconstructed using ASA® (A.N.T. software BV, The Netherlands). Fourth, a sphere was fitted to the transformed sensor array positions using the least squares technique and rescaled to make the sensors abut to the reconstructed cortical surface. Finally, the TFCMI results in the form of contour maps were projected onto the transformed sensor arrays overlaid on top of cortical surface.

It should be noted that the correspondence between the position of the MEG gradiometers and the underlying sources cannot be precisely determined without a proper source analysis. Nevertheless, the MEG gradiometer is designed to detect the largest signal right above the current source and suppressing ambient noise, suggesting that the gradiometer with the maximum current flux may ascribe to currents mainly from the directly beneath cortical area and partly from several surrounding cortical regions. In this article, the word “regions,” referring to “regions directly beneath MEG sensors and possibly surrounding regions,” is used loosely henceforth for the purpose of simplicity. Though the minor contribution from surrounding regions was not taken into account in this study, it will be exploited on the source space in future work.

Simulation of Coupling Between Two Regions

Two simulations (Simulation, Neuromag® system software) were conducted to establish the face validation of the TFCMI method in terms of the detection efficacy. Simulation 1 examined the ability of TFCMI to reject false coupling caused by noise when there were no actual coupled sources. Simulation 2 attempted to clarify the detection efficacy of TFCMI with regards to low SNR under the circumstance that the neuromagnetic signals received by planar MEG from the bilateral SMAs can be drastically attenuated due to anatomical architecture [Joliot et al., 1998; Lang et al., 1991].

In Simulation 1, one oscillatory dipole (23 Hz) was placed in the left SM1 (SM1‐dipole) of a chosen subject to synthesize magnetic fields on the sensor array. Position and moment of the SM1‐dipole were taken from the equivalent current dipole (ECD) fit [Hamalainen et al., 1993] to the movement evoked field I (MEFI) of the specific subject (Fig. 3a). The time point of the fit was 14 ms post movement. In Simulation 2, an additional dipole (23 Hz) (SMA‐dipole) was placed at a mesial region in the vicinity of SMA and pointed anteriorly based on the literature [Erdler et al., 2000; Lang et al., 1991]. The anatomical seeding of the SMA‐dipole was adopted from the same subject's results in a parallel functional MRI (fMRI) experiment using similar task (repetitive index finger movement; T2*‐weighted gradient‐echo echo planar imaging sequence, TR/TE/flip angle = 2000/50 ms/90°, 64 × 64 × 20 matrix, FOV = 192 mm) (Fig. 3b). The distance between the SM1‐ and SMA‐dipole was 55.07 mm (Fig. 3c). The oscillating source of the SMA‐dipole preceded that of the SM1‐dipole by 600 msec (Fig. 3d) [Erdler et al., 2000; Lang et al., 1991]. It is noteworthy that this design aims to emulate the spatially distributed connections in low SNR circumstance, rather than to link this simulation to the underlying functional connections during movements. Accordingly, the strength of the SMA‐dipole activity used in Simulation 2 was manipulated with a range of 0.5 to 1 times of SM1 dipole to modulate SNR [Chen et al., 1991; Erdler et al., 2000; Joliot et al., 1998]. Random noise was added onto each sensor measurement. Both TFCMI and coherence analysis were performed on the synthetic data. Moreover, conventional ECDs were fitted on the synthetic data to estimate the locations of neural generators, which were used as comparisons to TFCMI results.

Figure 3.

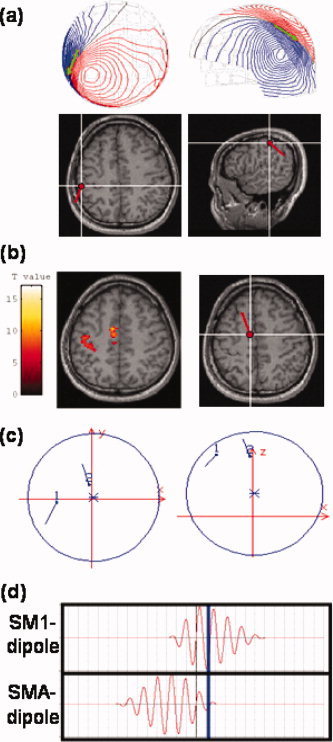
SM1‐ and SMA‐dipole allocation in simulation studies. (a) SM1‐dipole position and moment. The SM1‐dipole placement in the left SM1 was based on the equivalent current dipole (ECD) fit to movement evoked field I. Upper panel displays the isocontour maps of the recorded neuromagnetic signals and the dipole (in green). The SM1‐dipole was rendered onto the subject's own MRIs in axial view (lower panel; subject's right hemisphere to the right of the image). Anatomically, this SM1‐dipole was located slightly posterior to the contralateral central sulcus. (b) SMA‐dipole position and moment. The SMA‐dipole was seeded in the left SMA (right panel) close to the midline with coordinates adopted from a parallel fMRI experiment conducted by the same subject (left panel). (c) Spatial relationship between SM1‐ and SMA‐dipoles. Left, axial view; right, sagittal view. (d) Time courses of SM1‐dipole (upper panel) and SMA‐dipole (lower panel). In this simulation, the time course of the SMA‐dipole preceded that of SM1‐dipole by 600 m (Erdler et al., 2000; Lang et al., 1991). The blue line denotes the time‐point for the ECD fit in the subsequent analysis (see Fig. 7a).

RESULTS

Motor Task Performance

All subjects followed the instructions and performed the task well. The average number of trials in Accepted Sets among subjects was 98 epochs. Intervals between successive movements (intermovement interval, IMI) of Accepted Sets among subjects were between 7.968 and 15.162 seconds (mean, 13.124 s) and there was no feedback to cue subjects' movements. EOG ratio (the ratio of EOG sets to Total Sets) varied from 1.9% to 35.29%. Table I shows task performance and compositions of MEG test data for Accepted Set, IMI, EOG trials, Total Set and EOG ratio.

Table I.

Motor task performance and MEG test data

Subject index	Accepted set	IMI (mean ± SD; ms)	EOG Set	Total set	EOG ratio (%)
1	105	15,162 ± 6,969	27	132	20.45
2	93	14,571 ± 3,612	38	131	29.01
3	104	14,476 ± 3,774	41	145	28.27
4	91	13,867 ± 3,891	16	107	14.95
5	88	13,760 ± 7,589	48	136	35.29
6	103	14,302 ± 7,237	2	105	1.90
7	100	7,968 ± 1,573	8	108	7.40
8	98	14,968 ± 3,807	3	101	2.97
Average	98		22	120

IMI, inter‐movement interval; SD, standard deviation; EOG, electro‐oculogram.

Neural Correlates of Event‐Related α and β Oscillatory Activities: Within Modality

The resultant spatial distributions of neural connectivity for α and β activities, respectively, were represented by maps with colors representing the values, that is, the strengths of neural connectivity of α and β activities (Fig. 4a). TFCMI maps, both show strong connectivity within the contralateral sensorimotor region. The strengths of connectivity above threshold (95% confidence limit) can be alternatively displayed using colored lines, linking significant regions and the COI (Fig. 4b). Under the assumption that the gradiometer MEG sensors represent the major cortical oscillatory activity of underlying cortical tissues, contour maps projected on the reconstructed cortical surface reveal the regions coupled with the COI, including the mesial frontocentral cortex (termed the supplementary motor area, SMA, due to the anatomical correspondence; see simulation and discussion), bilateral primary sensorimotor areas (SM1), and contralateral premotor area (PM) (Fig. 4c). Table II lists neural correlates revealed by TFCMI and coherence methods. In MEG‐MEG studies, TFCMI results for all subjects (n = 8) show encompassing of bilateral SM1s, SMA, and contralateral PM in both α and β activities. The coherence results for β activity show encompassing of bilateral SM1s (n = 2), SMA (n = 3), and contralateral PM (n = 6) in some subjects. For α activity, contralateral SM1 was engaged in all subjects (n = 8). Two of the subjects had additional SMA encompassing, and four showed contralateral PM encompassing.

Figure 4.

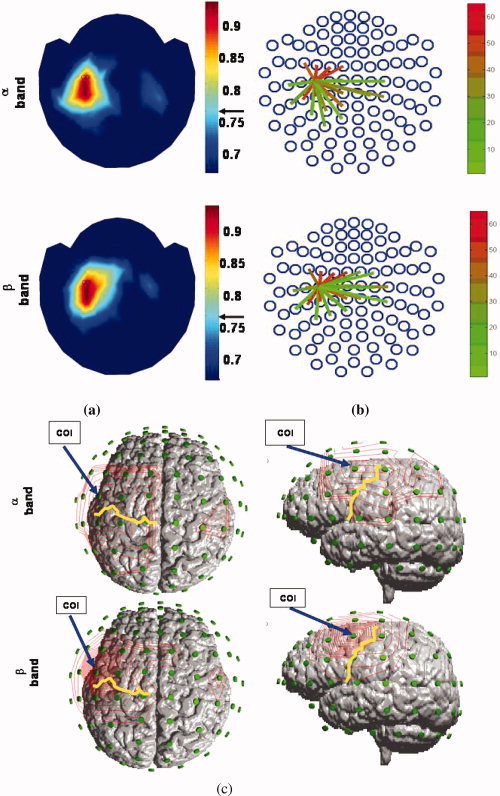
Event‐related α and β oscillatory activities networks (TFCMI). Individual data set. (a) Topographic maps of the spatial distribution of significant TFCMI values between COI and other MEG channels for α and β oscillatory activities. Color indicates the strength of connectivity. The arrows besides the color bar indicate the significant threshold. (b) An alternative display of the strengths of connectivity above the significant threshold. Regions of significant communications with the chosen COI were marked by links emanating from the COI. (c) TFCMI values in contour maps. The maps were projected onto the rescaled sensor array and the individual MRI to better the anatomical visualization of the coupled regions. Areas engaged included SMAs, bilateral SM1s, and contralateral PM. Yellow curves are the central sulcus; blue arrows indicate the location of COI. Left panel, view of top of the head; right panel, lateral view of the head from the left side.

Table II.

Neural correlates reflected in TFCMI and coherence methods

		MEG‐MEG study				sEMG‐MEG study
		cSM1	iSM1	SMA	PM	cSM1	iSM1	SMA	PM
TFCMI	α	8/8a	8/8	8/8	8/8
	β	8/8	8/8	8/8	8/8	8/8	8/8	7/8	8/8
Coherence	α	8/8		2/8	4/8
	β	8/8	2/8	3/8	6/8	8/8		2/8	4/8

^aThe results are given in a ratio of detection, which indicates the number of subjects against all eight subjects.

cSM1, contralateral primary sensorimotor area; iSM1, ipsilateral primary sensorimotor area; SMA, supplementary motor area; PM, premotor area; contralateral.

Impact of COI on TFCMI and Coherence Analysis

Figure 5 shows the COI‐specific results obtained from TFCMI method and coherence method. The TFCMI method resolved more neural connections than coherence method, such as ipsilateral SM1, when task‐related COI was chosen (Fig. 5, upper panel; Table II). When the task‐related COI was replaced by an A‐COI irrelevant to the motor task, the A‐COI TFCMI result demonstrated a highly focal encompassing centered at A‐COI area (exclusively within), while the A‐COI coherence result showed a rather dispersed neural connection with A‐COI, incongruent with the known anatomy (Fig. 5, lower panel).

Figure 5.

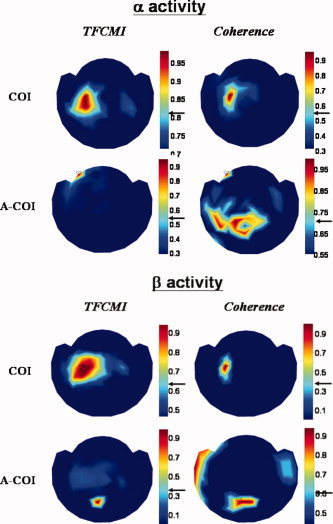
Influence of reference chosen on TFCMI and coherence analysis with respect to α and β activities. When the task‐related COI was properly chosen (upper panel), TFCMI results consistently showed more neural connections involving bilateral sensorimortor areas and the SMA for both α and β activities than coherence analysis. When the A‐COIs were chosen as reference (lower panel), the A‐COI TFCMI result demonstrated a highly focal encompassing centered at A‐COI area (connectivity exclusively to itself), while the A‐COI coherence result showed rather dispersed neural connections with A‐COI, incongruent with the known anatomy.

Between‐ and Within‐Modality Analysis: sEMG‐MEG and MEG‐MEG

Figure 6 gives analytical results for TFCMI and coherence around beta band (16–25 Hz) for between‐ and within‐modality signals, (sEMG‐MEG and MEG‐MEG studies) for subject 8. Simultaneous recording of sEMG for both right and left hands precluded mirror movement in the left hand (Fig. 6a). Both TFCMI and coherence results exhibited remarkable corticomuscular coupling over contralateral SM1 for all subjects (n = 8; Table II). The sEMG‐MEG maps resembled the MEG‐MEG maps, but there were subtle differences (Fig. 6b,c). The coupling between ipsilateral SM1 and sEMG was consistently resolved by the TFCMI method. Such coupling could not be detected by the coherence approach (Table II).

Figure 6.

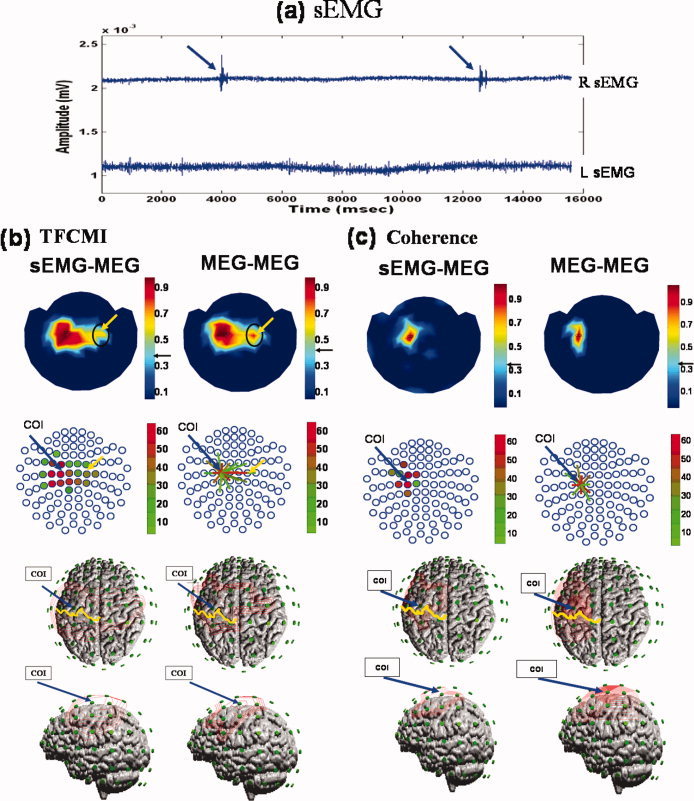
Ipsilateral SM1 in between‐ and within‐modality TFCMI studies. Individual data set. (a) Right (upper trace) and left (lower trace) hand sEMGs during right finger movement (blue arrows). The left sEMG precluded mirror movement of the left hand during the experiment. (b,c) Results of β activity from TFCMI and coherence, respectively, for between‐ (sEMG‐MEG; left panel) and within‐modality (MEG‐MEG; right panel) studies. The sEMG‐MEG maps (first row) exhibit prominent corticomuscular coupling at contralateral SM1 in both TFCMI and coherence analyses, and resemble MEG‐MEG maps. Yellow arrows indicate ipsilateral SM1 encompassing by TFCMI. No such coupling was detected using the coherence method. Second row presents couplings in an alternative manner, with blue circles representing MEG sensor sites. Blue arrows anchor the COI for MEG‐MEG analysis, which is also indicated in sEMG‐MEG maps only. Coupling strengths are coded in different colors either in the form of solid dots in the sEMG‐MEG maps or line links in the MEG‐MEG maps. The third (view of the top of the head) and fourth (left lateral view of the head) rows display the isocontour maps for a better appreciation of neuroanatomical correspondence. Yellow curves are the central sulci.

Simulation results

Figure 7 shows the simulation result when the SMA‐dipole strength is equal to that of the SM1‐dipole. The simulated output on SM1 sensor which exhibits the strongest power is shown in Figure 7a. Conventional ECDs, serving as a comparison to TFCMI, were fitted on the synthetic data to estimate the locations of neural generators. The time‐point for the ECD fit was chosen at maximal oscillatory amplitude (Fig. 7a; blue line) from which the corresponding simulated topographic pattern is displayed in Figure 7b. Spatial congruence of the simulated SM1‐dipole (red) and the estimated SM1‐dipole (blue) is displayed in Figure 7c. In Figure 7d, isocontour maps of the synthetic signals at the time point of max SMA‐dipole strength are shown in the right column. The synthetic signals from the channel over left SMA are shown in left upper panel, and the left middle and lower panels are the source activity from SM1‐dipole and SMA‐dipole, respectively. The goodness‐of‐fit (Gof) for the estimated left‐SM1 dipole was 97.2% for Simulation 1 (Table III). In Simulation 2, when both SMA dipole and SM1 dipole have the same strength, the Gof for SM1‐dipole and for SMA‐dipole were 96.2% and 42.3%, respectively. When the source strength of SMA dipole was half of SM1 dipole, the Gof of SM1 and SMA dipoles decreased to 88.6% and 40%, respectively (Table IV).

Figure 7.

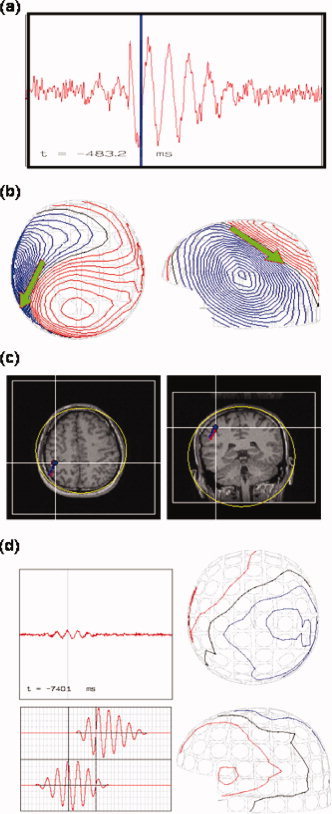
Poor detection of SMA‐dipole by simulation. (a) Synthetic signals from the channel over SM1 as produced by SM1‐ and SMA‐dipoles. (b) Isocontour maps of the synthetic signals and the ECD result of SM1‐dipole. The blue bar in (a) indicates snap time for the contour maps. (c) Spatial congruence of the simulated SM1‐dipole and the estimated SM1‐dipole. The estimated SM1‐dipole (in blue, with a very high goodness‐of‐fit, about 96%) almost coincides with the simulated (in red). (d) Isocontour maps of the synthetic signals at the time point of max SMA‐dipole strength (right column). The synthetic signals from the channel over left SMA are shown in left upper panel, and the left middle and lower panels are the source activity from SM1‐dipole and SMA‐dipole, respectively. The goodness‐of‐fit for the SMA‐dipole was 42.3% (Table IV). The poor Gof for the SMA‐dipole was in line with the consensus that the MEG dipole fit for SMA source can be ambiguous due to insufficient SNR.

Table III.

Simulated‐dipole parameters and ECD results for source estimation: Simulation 1

	Simulated‐dipole parameters			ECD results; SNR = 21.8 dB
Index		Location	Moment	Location	Moment	Distancea (mm)	Gof (%)
SM1‐dipole	x	−35.2	0.42	−35.3	0.43
	y	−7.2	0.80	−7.2	0.79	1.03	97.2b
	z	88.9	0.41	88.3	0.41

^aBetween the simulated and the estimated location.

^b85% Gof.

ECD, equivalent current dipole; SNR, signal‐to‐noise ratio in source space; Gof, goodness of fit.

Table IV.

Simulated‐dipole parameters and ECD results for source estimation: Simulation 2

Simulated‐dipole parameters				ECD results: SNR = 19.1 (dBSM1‐dipole strength:SMA‐dipole strength = 1:0.5)				ECD results: SNR = 21.8 (dBSM1‐dipole strength:SMA‐dipole strength = 1:1)
Index		Location	Moment	Location	Moment	Distancea (mm)	Gof (%)	Location	Moment	Distancea (mm)	Gof (%)
SM1‐dipole	x	−35.2	0.42	−36.8	0.2809			−34.3	0.42	1.15
	y	−7.8	0.80	−7.6	0.8827	4.87	88.6a	−7.2	0.79		96.2b
	z	88.9	0.41	84.3	0.3796			89.3	0.42
SMA‐dipole	x	−3.4	0.54					−1.0	0.68	10.71
	y	20.4	0.58				below 40	10.6	0.71		42.3
	z	87.9	0.60					91.5	0.14

^aBetween the simulated and the estimated location.

^b85% Gof.

ECD, equivalent current dipole; SNR, signal‐to‐noise ratio in source space; Gof, goodness of fit.

Both TFCMI and coherence analysis were performed on the synthetic data (see Fig. 8). In simulation 1 (SM1‐dipole only), both TFCMI and coherence maps showed a focal encompassing of SM1, that is, exclusive connectivity to itself only (Fig. 8; upper panel). In simulation 2 (SM1‐dipole and SMA‐dipole), the time courses of the two dipoles were coherent and had a significant transformed coherence value of 0.957 after averaging 100 simulation trials in source space since they are with similar temporal profile (Fig. 3d) and are stationary across trials. However, after forward modeling, only TFCMI resolved more spatially distributed connections in sensor space, anatomically encompassing the SM1 and SMA, respectively, where the two dipoles were seated whereas the coherence method cannot discern the coupling (coherence = 0.0023) and solely showed connectivity within SM1 (Fig. 8; lower panel).

Figure 8.

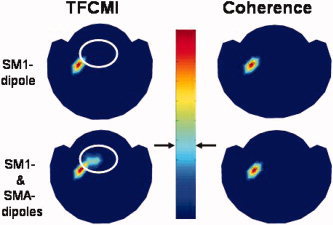
Detection specificity of TFCMI in low SNR data. Both TFCMI and the coherence method yielded one unambiguous focus in the first simulation (only SM1 dipole, upper panel). In the second simulation (SM1‐dipole and SMA‐dipole), only the TFCMI resolved more spatially distributed connections in low SNR data, anatomically encompassing the SM1 and SMA, respectively, where the two dipoles were seated (lower panel). The white circle in the lower panel highlights the difference between the TFCMI and coherence results which is the supposed SMA area. The white circle in the upper panel indicates the same SMA area only for comparison with the result in the lower panel.

In addition, we have computed the SNR (=10 log(signal power/noise power)) of the experimental data measured from the sensor above left SM1 for the comparison with the SNR in simulation. The segment of averaged data from −4 to −3.5 s was considered as the noise and that from −2 to +2 s was the signal of activity. The averaged SNR in averaged data from 8 subjects was 26.57 ± 2.9 dB. In Simulation 2, the minimum SNR for TFCMI method to detect the connection between SM1 and SMA (Table IV) is 21.8 dB, where the simulated signal was a composition generated from hypothetical SM1‐ and SMA‐dipoles with the same dipole strength. In summary, our simulations indicate that the TFCMI method has superior detection specificity compared to the coherence method in low SNR situation.

DISCUSSION

Detection Specificity in Low SNR Data: Computational Simulation

A question central to the discussion of TFCMI approach in the current study is whether TFCMI could detect and resolve spatially distributed connections in low SNR circumstance. In this study, two simulations were conducted to provide the face validation of the TFCMI method in this regard. As a result, the Simulation 1 (SM1 dipole only) shows a focal encompassing of SM1, that is, exclusive connectivity to itself only (Fig. 8; upper panel) and the Simulation 2 demonstrates that TFCMI can decipher spatially distributed connections in low SNR circumstance. It is noteworthy that, though the simulation results show that TFCMI method can resolve the spatially distributed connections in low SNR circumstance, we have not presented an exhaustive simulation to emulate the underlying functional connections during movements. Since the TFCMI method is a pair‐wise analysis and the TFCMI results from experimental data may be influenced by some distant but coupled sources fed into the COI and other channels, the interpretation of the TFCMI results should be restricted. Further validation is needed for the TFCMI method to process and represent on the source level instead of the sensor level. Nevertheless, the simulation results demonstrate that TFCMI was capable of discerning noise and showing the neural connectivity between distinct areas, in this case, between SM1 and SMA, with low SNR whereas both the ECD fit and the coherence method were not able to detect (Figs. 7, 8; Table IV).

Robustness of TFCMI Method

TFCMI analysis is resistant to reference selection and efficient in deciphering task‐related connections from the irrelevant ones. Proper selection of COI is critical for the study of functional coupling using the coherence method [Gerloff et al., 1998]. Such a prerequisite is also seen in Figure 5 when A‐COI was chosen as reference, despite which the coherence method is robust when the reference electrode is correct and the interaction is stationary across trials [David et al., 2004]. On the contrary, the A‐COI TFCMI result demonstrated a highly focal encompassing centering at the A‐COI area (exclusive connectivity to itself) which was validated by Simulation 1 (Fig. 8; upper panel) where the unconnected‐solitary source (chosen as COI) showed no factitious coupling. In addition, when sEMG was used as COI in the between‐modality study, the TFCMI showed neurophysiologically and neuoranatomically sEMG‐MEG topographies (Fig. 6b, Table II). Moreover, the TFCMI method in broadband analysis performs reliably compared with the conventional mutual information method whose sensitivity is less reliable in broadband and weak coupling signals [David et al., 2004]. Collectively, the data imply that TFCMI can better resolve task‐related connections.

Resolving Power Under Nonlinear Interactions

It is well known that the planning and execution of voluntary movement relies upon the integration of premotor and primary motor areas operating in conjunction with sensory and association areas, including SMA and cerebellum. The functional relevance between left and right SM1 in MEG‐MEG event‐related experiments as disclosed by the TFCMI is congruent with previous imaging studies showing bihemispheric engagement for motoric movement (Table II). [Gerloff et al., 1998; Hsieh et al., 2002; Joliot et al., 1998; Stippich et al., 1998]. The TFCMI also shows consistent engagement of ipsilateral SM1 in the sEMG‐MEG event‐related experiment (Table II; Fig. 6b). The inconsistent interhemispheric interaction in existing studies using the coherence or partial coherence approach has lead to a debate on bilateral involvement of SM1 for unilateral finger movement control [Andres et al., 1999; Andrew and Pfurtscheller, 1996, 1999; Gerloff et al., 1998; Manganotti et al., 1998; Mima et al., 2000a]. This inconsistency could also been seen in our coherence results (Table II). However, transcranial magnetic stimulation (TMS) studies have confirmed the role of ipsilateral SM1 in self‐paced finger movement tasks [Chen et al., 1997; Rau et al., 2003]. Studies on patients with motor disorders have shown a significant activation of ipsilateral SM1/corticospinal tract as compensatory mechanisms [Caramia et al., 2000; Cuadrado et al., 1999; Jones et al., 1989; Marshall et al., 2000; Ward and Cohen, 2004]. Our TFCMI analytical results are consistent with the known anatomy since 10% of corticospinal fibers have ipsilateral projections [for a review, see Kuypers, 1981] and the ipsilateral influence is integrated with the prevailing contralateral one (also evinced by the preponderant contralateral expression of TFCMI values) for the overall control of movement [de Oliveira, 2002]. Accordingly, it is plausible that the coupling between contra‐ and ipsi‐lateral SMI may be through a nonlinear or nonstationary interaction and could be better unraveled by TFCMI.

Fundamental Differences Between the TFCMI Method and Coherence Method

In this study, the functional connectivity during a self‐paced brisk finger movement task was studied. Such a discrete movement paradigm may mandate more cognitive processing than automatic movement paradigm within sub‐second inter‐movement interval [Lewis and Miall, 2003]. Moreover, the latency of maximal post‐movement β rebound exhibits trial‐to‐trial variability [Lee et al., 2003b]. These suggest that there is inherent nonstationarity in the neural processing. Under the assumption that neural processes are stationary across trials [Lachaux et al., 2002; Nunez et al., 1997], the coherence method measures the linear dependency between signals via normalized spectral covariances, that is, second‐order statistics. This second‐order method works well for Gaussianly distributed signals but may not for the non‐Gaussian ones, as shown in the upper panel of Fig. 1(e). The TFCMI method, on the contrary, utilizes the wavelet transform as the preprocessing procedure to bandpass the signals with better temporal resolution than Fourier transform such that the subtle temporal scenarios within pre‐specitifc frequency bands can be properly reserved. Then, based on the joint probability of coincidence occurrence of oscillatory signal power with more accurate temporal resolution, TFCMI computation is not limited to the linearity of spectral modulation across trials. In fact, the use of pdf and joint pdf takes the advantage of high‐order statistics to extract the nonlinear coupling that may not be correctly identified using the second‐order techniques. Therefore, the combination of wavelet and mutual information substantiate a significant contribution for nonlinear analysis and is a salient feature of the TFCMI method. Such fundamental differences make the TFCMI method more adaptive than coherence method in analyzing complex dynamic data.

The Limitations of and Prospects for the TFCMI Method

Since the cortical oscillatory activity acquired from a MEG sensor cannot be fully attributed to the underlying cortical region, the interpretation of TFCMI results is limited to the sensor space in current study. Further validation, such as simultaneous recording of EEG and fMRI, may serve as a complementary to the TFCMI method. Alternatively, the recording signals from MEG sensors can be the inversely mapped into the source space by using a spatial filter as developed in the dynamic imaging of coherent sources (DICS) method [Gross et al., 2001, 2002, 2003; Ishii et al., 2002]. This will allow the calculation of TFCMI on the source space and subsequently analyze the functional coupling within the brain. Another drawback of the TFCMI method is the low temporal resolution (4 s), since the estimation of probability density function and joint probability density function was based on the histograms of signal amplitudes over a 4‐s time window. Various lengths of time window will be used to assess the performance of TFCMI in the future work. Besides, the TFCMI method was not designed to unravel the propagation direction of the electrical activity among brain structures. Once the evident functional coupling on the sensor space was resolved using the TFCMI method, other approaches, such as the direct transfer function (DTF) method, phase synchronization, or the directional index can be employed for the quantification of coupling direction.

CONCLUSIONS

We present a novel method, TFCMI, for the exploration of the neural communication and interaction among distinct brain regions or regions of different neurophysiological modalities. When compared with the coherence approach (linear dependency only), the TFCMI method showed better specificity on dependency measurement in broadband analysis, clearer demarcation of event‐related regions from nonrelated, and more robustness for between‐modality study. Although TFCMI is not a stringently complete “data‐driven” approach, it can be considered as a “model‐free” approach [Lee et al., 2003a]: a priori knowledge of neuronal architecture at the anatomical level can be heuristic for the analytical penetration of functional organization. The TFCMI method promises a possibility to better unravel the intricate brain functional organizations in the context of oscillation‐coded communication. Further work is currently in progress to allow the TFCMI processing and representation on the source level instead of the sensor level.