Abstract
Although Electroencephalography (EEG) source localization is being widely used in adults, this promising technique has not yet been applied to newborns because of technical difficulties, such as lack of data concerning the newborn skull conductivity, thickness, and homogeneity. Using a new type of EEG headcap molded on each baby's head, we aimed to determine whether this technique could be adapted to neonates, and to evaluate the importance of these technical difficulties. We carried out EEG source reconstruction of the recordings of five neonates using dipole fit algorithm. We used four different head models for each neonate, obtained from individual MRI scans: normal skull thickness and conductivity of 0.0042 S/m; normal thickness and conductivity of 0.33 S/m; increased thickness and conductivity of 0.0042 S/m; and normal thickness and conductivity with a modeled bregma fontanel. Dipole locations were consistent with MRI and clinical data. The mean difference between the dipole locations in the 0.0042 and the 0.33 S/m skull layer models was 11.6 ± 2.5 mm, with an average 29.7% decrease in magnitude for the 0.33 S/m model but no significant changes for the dipoles orientation. Skull layer thickness had a large influence on magnitude, but no significant effect on position and orientation. The mean difference between the dipole locations induced by the modeled fontanel was 2.0 ± 2.1 mm, with an average 2.1% increase in magnitude. Our results show that EEG source localization is feasible in neonates. With further development, the technique may prove useful for neurological evaluation of neonates. Hum Brain Mapp, 2008. © 2007 Wiley‐Liss, Inc.
Keywords: EEG, source localization, neonates, premature infants, brain development
INTRODUCTION
Electroencephalography (EEG) source localization is a rapidly evolving technique of fundamental and clinical importance [for review, see Michel et al., 2004]. It estimates current dipoles in a volume conductor model of the head to model the intracerebral generators responsible for potentials observed on the scalp. It has been validated for the presurgical evaluation of adult patients suffering from refractory epilepsy [Boon et al., 1997; Krings et al., 1998; Merlet, 2001]. It allows the epileptogenic area to be located and comparisons to be made with clinical information, magnetic resonance imaging (MRI) anatomical data, and the results of metabolic imaging techniques.
As yet, there have been no reports of applying this technique to neonates, even though it could provide precious neurological information, especially in premature infants. EEG source localization has been considered not possible in newborns because of technical and anatomical constraints. The small head size of newborns means only low spatial resolution (eight electrodes) can be achieved using conventional EEG techniques. A high number of electrodes are necessary for accurate source localization, although most people have used 32–64 electrodes in adults [for review see Merlet, 2001 and Michel et al., 2004]. In adults, projection of the theoretical position of electrodes on the head model of in the 10–20 system [Wang and Gotman, 2001] can be used because standard head caps have fixed electrode positions. Such caps are not available for neonates and there is great variation in head geometry among neonates. Digitization of spatial positions of electrodes would be more efficient, but neonates in intensive care unit have to stay in their incubator and surrounding monitoring devices would disturb the digitizer. Inhomogeneity of the skull also limits the validity of source reconstruction. It has been demonstrated that holes in the adult skull lead to errors of about 10 mm [Bénar and Gotman, 2002; van Burik and Peters, 1999] and zones of higher conductivity to errors of about 20 mm [Ollikainen et al., 1999] in source localization. This is due to areas of high conductivity creating focal current leaks across the skull [Chauveau et al., 2004]. In neonates, the main structural inhomogeneities of the skull are the fontanels, especially the bregma anterior one. The fontanels cannot be considered as holes: they are thin, less ossified and more vascularized areas of the skull, and we have yet no clue on how it would affect EEG source localization.
Despite those difficulties, the adaptation of EEG source localization to neonates would provide a useful tool for newborn and preterm diagnosis and care. Physiological and pathological EEG features of the newborn have been extensively studied on raw EEG data [for review see Lamblin et al., 1999], but the spatial organization and maturation of cerebral generators of the EEG signal in neonates are still lacking. Source localization of physiological and pathological events in the premature and tern neonates would give a better understanding of the underlying neuronal networks and their evolution during the last weeks before term.
Here, we aim (1) to show the feasibility of this technique in neonates, to improve their neurological evaluation and to study more precisely the typical EEG features of that age, and (2) to give a preliminary quantitative estimation of the error due to uncertainties in skull layer conductivity and thickness and to the fontanel.
MATERIALS AND METHODS
A new acquisition probe for neonatal EEG with improved spatial resolution was developed, allowing spatial digitizing of electrode positions on the cap outside of the intensive care unit without moving the children from their beds. We used realistic individual head models obtained from individual MRI data for each child, combined with individual spatial positions of electrodes. We designed four head models for each patient, each with a different set of skull layer conductivity and thickness parameters, to understand better the effect of these parameters on source localization.
Patients
We analyzed the “high resolution” EEG recordings of five newborns. All had previously presented transients whose extent, nature or location were not clearly defined on routine recordings. Among them, two presented physiological activities, two presented pathological activities, and one presented both physiological and pathological activities. Frontal sharp transients (FST) were seen in three newborns (age = 34, 40, and 41 weeks GA). These are normal physiological activities occurring asynchronously in preterm newborns around the 33rd and 34th week of gestational age. They then become increasingly symmetrical between the 35th and the 41st weeks. Positive rolandic spikes (PRS) were seen in one newborn (age = 31 weeks GA). These are pathological activities that appear after periventricular leukomalacia (PVL) around the 28th week of gestational age, with or without intraventricular hemorrhage (IVH) and ventricular dilation (VD). Temporal spikes (TS) were seen in two newborns (age = 34 and 39 weeks GA). These are pathological activities occurring at all ages. [Lamblin et al., 1999]. Altogether, nine sets of data were studied (Table I, Fig. 1).
Table I.
Patients data (see Methods for abbreviations)
| Patient | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| E.F. | M.A. | A.L. | V.R. | J.R. | |||||
| Sex | M | F | M | M | M | ||||
| GA at birth (weeks) | 37 | 40 | 31 | 37 | 30 | ||||
| Age at the recording (days) | 21 | 10 | 20 | 17 | 9 | ||||
| GA at the recording (weeks) | 40 | 41 | 34 | 39 | 31 | ||||
| MRI | VD | IVH & VD | |||||||
| Number of electrodes | 32 | 32 | 25 | 19 | 19 | ||||
| EEG Events | Left FST | Right FST | Left FST | Right FST | Left FST | Right FST | Left TS | Left TS | PRS |
| Number of events | 13 | 28 | 23 | 21 | 22 | 20 | 21 | 18 | 27 |
Figure 1.
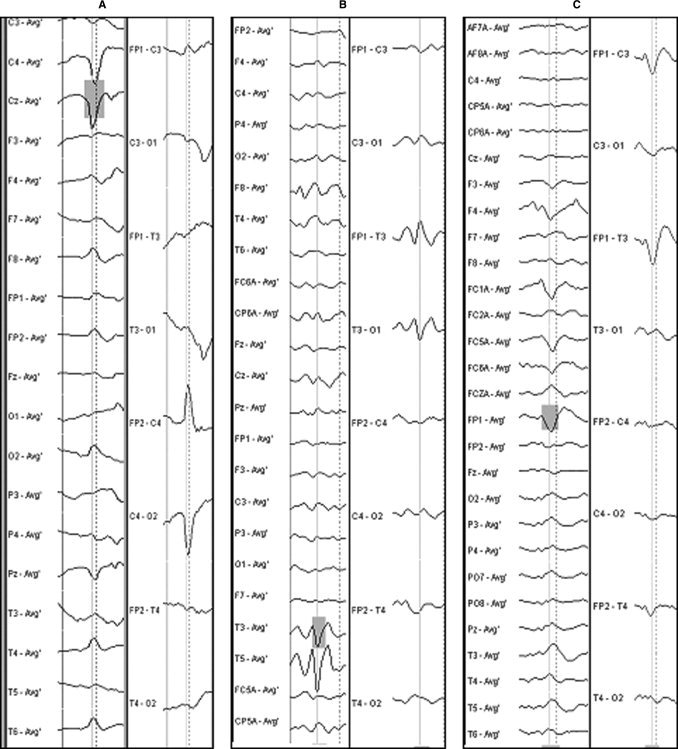
Example of EEG selections (vertical line) for (A) PRS, (B) Left TS, and (C) Left FST. The left columns show the montage used for analysis (mean reference), the right columns show the classical bipolar montage used for clinical interpretation.
The high resolution EEG technique was carried out as part of a research protocol, and informed consent was obtained from the parents of all subjects. The protocol was approved by the local ethics committee (CCPPRB C.H.U. Nord, Amiens, France) and conformed with the Declaration of Helsinki on human investigation.
Data Acquisition
A new type of EEG headcap (patented) was developed for this study. We molded silicon paste directly over each baby's head in the bed or incubator. This paste set in and took the shape of the subject's head in a few minutes. We marked the positions of the anatomical markers (nasion, right and left ear) and Cz position on the cap. The cap was removed from the head and classical newborn EEG Ag/AgCl electrodes (between 19 and 32 depending on the size of the head, see Table I) were manually embedded according to the International 10–20 System, with one of them placed at position AFz being used as a common ground. Normal EEG conductive paste was applied to the electrodes. After the scalp had been cleaned with a gentle abrasive gel, the cap was once again placed over the head respecting the position of anatomical markers previously defined, ready for connection and recording. The process lasted around 15 min, being equivalent to a traditional recording procedure.
Continuous EEG data was recorded using Deltamed amplifiers and Coherence3NT® software. Recordings were acquired at a sampling rate of 256 Hz, with a 0.1–100 Hz band pass filter. Electrode impedances were kept below 5 kΩ.
After recording, the cap was placed on a support outside of the intensive care unit, far from electronic devices that could disturb digitization. We used a 3 dimensional magnetic digitizer (Polhemus 3Space Fastrak®), and the ANT software EETrack® for 3D digitization of the spatial positions of the electrodes in relation to the anatomical markers.
For every child a 3D MRI scan of the head was taken at about the same time as the EEG and collected after independent clinical interpretation. T1‐weighted MRI data were acquired with a 1.5 T MRI scanner (GE Medical Systems). Slices were either coronal or axial (slice thickness = 1.4–2 mm, repetition time = 8.2–9.5 ms, echo time = 1.816–1.956 ms, inversion time = 500 ms, flip angle = 20°, matrix = 512 × 512 × 144 to 164, resolution = 0.47 × 0.47 × 1, 0.43 × 0.43 × 2.4 or 0.43 × 0.43 × 0.7 mm).
Data Processing
MRI segmentation
We constructed a realistic 3‐layer Boundary Element volume conductor model (BEM) of head from the 3D MRI data from each patient. The 3‐layer BEM consists in 3 concentric meshes modeling the air‐scalp interface (outer surface of the scalp layer), the scalp‐skull interface (outer surface of the skull layer), and the skull‐brain interface (outer surface of the brain layer). Each layer has a specific conductivity value. The different tissues were identified by segmentation using a combination of gray‐scale thresholding and a region growing algorithm plus three operators: opening, closing, dilation. Though neonates present low gray‐scale contrast between different tissues on MRI images, careful thresholding led to satisfying head modeling. For each child, we created four head models with four different sets of skull layer parameters. First, the conductivity of the brain, skull, and scalp layers were set to 0.33, 0.0042, and 0.33 S/m respectively, with a normal skull layer thickness according to the individual MRI. Then, we made a second model with a normal skull layer thickness and a conductivity of 0.33 S/m to determine the maximum error due to skull conductivity, as we assumed that a newborn skull conductivity would be between the standard adult value of 0.0042 S/m and the extreme value of cerebral conductivity (0.33 S/m) [Geddes and Baker, 1967; Gonçalves et al., 2003]. We created a third model by dilating the skull mesh during the MRI segmentation to the maximum possible without reaching the scalp mesh (to avoid numerical instabilities) and setting the skull conductivity to 0.0042 S/m conductivity to evaluate the maximum error due to the skull layer thickness. Finally, a fourth model (Fig. 2A) was obtained by adding a local diamond‐shaped (approximately 2 cm side length) thinning of the skull layer to the normal model (the maximum thinning possible without reaching the brain mesh). It created a structural inhomogeneity of the skull layer, which is the most realistic way to model the fontanel with a boundary elements model. We thus tried to determine the maximum errors that might occur due to the lack of data on newborn skull conductivity and thickness and to the fontanel. These four head models were called “normal”, “0.33”, “thick,” and “fontanel” respectively. We used a 0.14 mm mesh with an additional 0.1 mm scalp‐rendering for the scalp, and a 0.16 mm mesh for skull and brain. For the fontanel model, the scalp and skull layers mesh size was divided by eight in the region of the fontanel, to avoid numerical instabilities due to the proximity of the layers. We applied the isolated potential approach.
Figure 2.
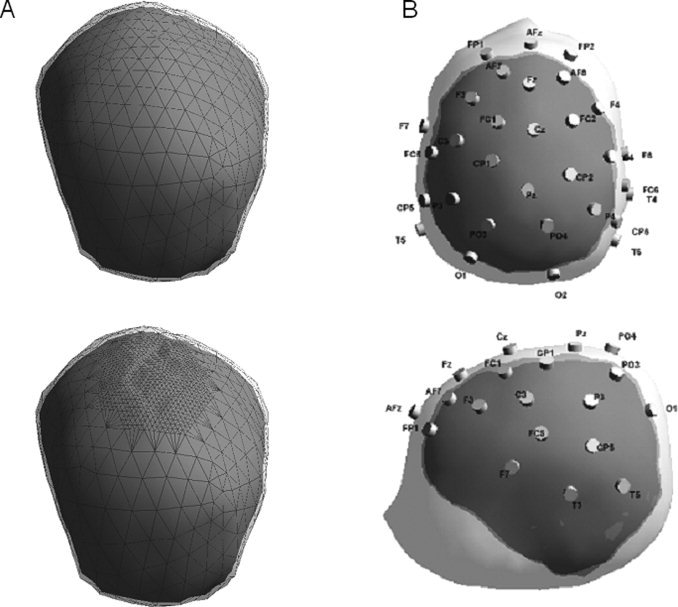
(A) Example of normal head model (up) and fontanel head model (down) (Patient A.L.). Only the skull (with mesh) and brain layers are visible. (B) Example of neonate realistic head model with scalp, skull and brain boundaries, and 32 digitized electrodes positions (Patient M.A.).
During the segmentation process, anatomical markers (nasion, right and left ear) were manually defined on the MRI images. These points were automatically included in the head models. The digitized positions of electrodes were then combined to the head models for each child, using the anatomical markers to match them (Fig. 2B).
EEG processing
EEG data were band‐pass filtered off‐line (0.5–1.6 Hz low cut‐off, 15–30 Hz high cut‐off), with an additional notch at 50 Hz. Average reference was used. We manually selected events of interest on the basis of the description by Lamblin et al. [1999] (Fig. 1). We applied the dipole fit algorithm in every case, on the whole time trace of the event. The dipole model is an equivalent dipole to a brain area of unknown size, but in this study events were assumed to be focal activities from only one source and not spread in large networks. Thus, for the dipole fit, single rotating dipoles were used and expected to give a location close to the cortex. The dipole fit using rotating dipoles gives in general stable and reliable source localization for the time interval of the event. The orientation and amplitude are given for the best fit latency. The source reconstruction solutions were projected onto the original 3D MRI images. For each set of data and for the four head models, we calculated the source localization using dipole fit on each selected event and then on the average of the events.
MRI segmentation, head modeling, and EEG source localization were processed using the ASA® software package (ANT Software, Enschede, The Netherlands) [Zanow and Knösche, 2004].
Data Analysis
The dipole dispersion was calculated as the mean distance of individual dipoles to the mean dipole localization. For the four head models a Student's t‐test for paired samples was applied to individual data (distance of every dipole to the mean localization).
After dispersion analysis, selected events were averaged. We used the resulting average events for the data analyses. The averaging trigger was the peak of selected events. The duration of an average event was the shortest duration among selected events.
All distances between dipole positions were calculated as the square root of the sum of squared differences between x, y, and z components for each position.
As our sample sizes were small, confidence intervals were calculated at 95% using the Student table.
An ANOVA test was applied to the dipole parameters for the averaged events in each head model. The tested parameters were position and orientation (moments at the best fit latency). Post‐hoc comparisons were performed using the Newman–Keuls test.
Magnitudes (at the best fit latency) were also calculated, but no statistical test was applied as they presented a large variance due to the different types of studied activities.
All statistical analyses were processed using STATISTICA® software.
RESULTS
Dispersion of Dipoles—Single Events
We first applied source localization for every selected event to evaluate the dispersion in the cluster of dipoles. The mean dispersion was 17.8 ± 4.0 mm in the normal head model, 13.5 ± 3.3 mm in the 0.33 head model, 17.5 ± 5.7 mm in the thick head model, and 20.0 ± 7.0 mm in the fontanel head model. We found a significant difference between the normal and 0.33 head models, between the thick and 0.33 head models and between the normal and fontanel head models (P < 0.05), but not between the normal and thick head models (P = 0.9). We considered that the dipole dispersion was small enough in all cases to guarantee that the event selection was homogeneous (Table II). Therefore, we kept the same filtering parameters and selected events to create the averaged events used for further analysis.
Table II.
Individual results (see Methods for abbreviations)
| Patient | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| E.F. | M.A. | A.L. | V.R. | J.R. | |||||
| EEG Events | Left FST | Right FST | Left FST | Right FST | Left FST | Right FST | Left TS | Left TS | PRS |
| Number of selected events | 13 | 28 | 23 | 21 | 22 | 20 | 21 | 18 | 27 |
| Dipoles dispersion in the normal head model (mm) | 13.2 | 18.5 | 10.6 | 20.7 | 22.8 | 26.0 | 19.9 | 10.9 | 18.0 |
| Dipoles dispersion in the 0.33 head model (mm) | 14.0 | 16.8 | 6.7 | 12.3 | 18.7 | 19.1 | 12.6 | 7.1 | 14.1 |
| Dipoles dispersion in the thick head model (mm) | 20.8 | 20.1 | 9.9 | 11.9 | 23.1 | 22.5 | 27.7 | 3.7 | 17.6 |
| Dipoles dispersion in the fontanel head model (mm) | 13.5 | 17.8 | 10.3 | 20.7 | 22.9 | 25.9 | 17.8 | 9.4 | 40.0 |
| Distance between solutions in the normal and 0.33 head models (mm) | 18.5 | 8.6 | 7.8 | 9.5 | 11.4 | 10.6 | 11.4 | 11.7 | 14.6 |
| Distance between solutions in the normal and thick head models (mm) | 2.8 | 4.0 | 4.6 | 6.5 | 8.0 | 3.0 | 8.1 | 15.3 | 1.2 |
| Distance between solutions in the normal and fontanel head models (mm) | 0.2 | 5.2 | 0.9 | 0.8 | 0.8 | 0.7 | 0.9 | 8.3 | 0.5 |
Position and Orientation of Dipoles—Averaged Events
Location in the brain
In the normal head models, the dipoles were found in the putative cerebral regions for all patients. None were found in cerebrospinal fluid or in the ventricles. However, the right FST of patient A.L. was on the border between cortex and ventricles, because of VD giving a very thin cortical layer in this patient. Both FST of patient MA were also a little too deep, at the border between gray and white matter.
Distance to the lesion border
For patient J.R., we hypothesized that the true location of the PRS should be on the lesion border. The dipole fit gave a location 5.5 mm above the nearest lesion border in the normal head model, and 0.9 mm below the nearest lesion border in the 0.33 head model (Fig. 3). An intermediary position between these two solutions would be the best match.
Figure 3.
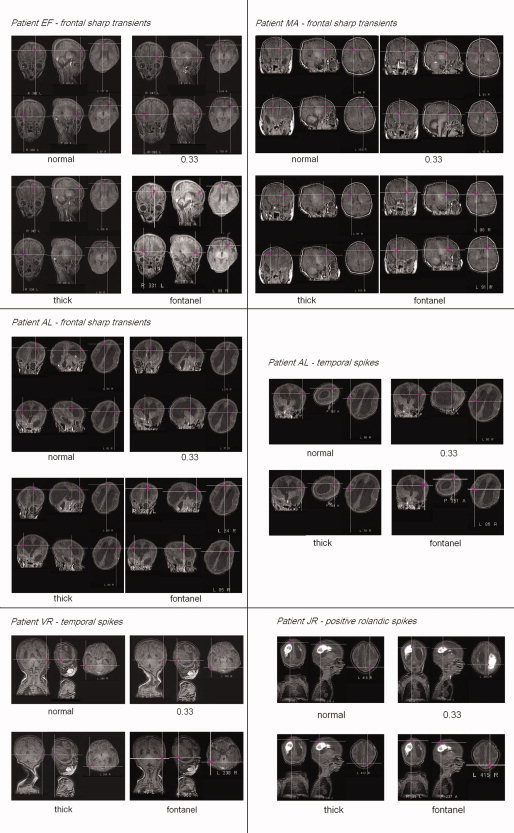
Dipole fit results on averaged events obtained with the four head models, projection to 3D MRI. From top to bottom and left to right : E.F.'s frontal sharp transients (left FST above, right FST below), M.A.'s frontal sharp transients, A.L.'s frontal sharp transients, A.L.'s temporal spikes, V.R.'s temporal spikes and J.R.'s positive rolandic spikes. Patient A.L.'s MRI is showing an important ventricular dilatation, patient J.R.'s a Periventricular Leucomalacia with ventricular dilatation.
Orientation
For FST, the dipole orientations pointed to symmetrical zones of the frontal cortex. For TS, they pointed to the temporal cortical zones, where it was suspected that abnormal EEG activities would be generated. For PRS, they were perpendicular to the nearest border of the lesion.
Influence of the Skull Conductivity, Thickness, and Fontanel—Averaged Events
Source localization was applied to averaged events in the four head models to evaluate the influence of uncertainties in skull conductivity and thickness. The mean distance of dipole locations was 11.6 ± 2.5 mm between the normal and 0.33 head models, 5.9 ± 3.2 mm between the normal and thick head models and 2.0 ± 2.1 mm between the normal and fontanel head models (Table II).
ANOVA confirmed the influence of the skull layer characteristics on the dipole positions. Using the Newman–Keuls post‐hoc test, we found a significant difference in dipole positions between the normal and 0.33 head models and between the thick and 0.33 head models (P < 0.05), but not between the normal and thick head models (P = 0.9), neither between the normal and fontanel head models (P > 0.9).
Using ANOVA, we detected no effect of the skull layer characteristics on dipole orientation (P > 0.5)
We found that magnitudes were on average 29.7% lower in the 0.33 head model than in the normal head model, 7.9% higher in the thick head model than in the normal head model, and 2.1% higher in the fontanel head model than in the normal head model.
DISCUSSION
Acquisition Probe
Our new headcap allows the spatial digitization of electrode positions on the scalp, without having to move children from their beds. This is the easiest way to minimize errors due to the variation of electrode positioning among subjects. A standard projection of the 10–20 system would probably be less reliable [Wang and Gotman, 2001] considering the large variation in head geometry among neonates. Therefore, for localization, we used a realistic individual head model obtained from MRI data from each child, with individual spatial localization of electrode positions. The cap can hold up to 32 standard electrodes, which is for neonates the equivalent of a dense sampling in adults. However, for bigger head sizes it is possible to embed the cap with as many electrodes as needed. This safe, flexible, and efficient acquisition technique should allow us to develop precise and reliable EEG source localization in neonates.
Dispersion of Dipoles—Single Events
For each group of selected events, we found a low dispersion of dipole locations, irrespective of the head model. The small dispersion of dipoles can be considered as a sign of homogeneity of selections and a good signal to noise ratio. However, this dispersion was significantly lower in the 0.33 head model and significantly higher in the fontanel head model than in the normal and thick models. In normal adults, the skull disperses the electrical signal very efficiently because of its higher resistivity, and dispersion on potentials induces dispersion of reconstructed sources. In the 0.33 model, the skull layer had the same conductivity as the scalp and the brain, and did not have this dispersing behavior: this model is completely homogeneous, and thus dipole dispersion is minimized. On the contrary, in the fontanel model the skull is dispersing and besides the fontanel borders are an important inhomogeneity in the skull layer probably inducing a supplementary dispersion. If the fontanel was modeled as a hole, reconstructed dipoles would tend to be concentrated around the current leakage. Here the fontanel was modeled as a thinning: a leakage may exist, but it seems that in this case the structural inhomogeneity of the skull surface induces instability of larger influence compared with the leakage. It is remarkable that one patient (J.R.) presented a much higher dispersion (40.0 mm) than other patients in the fontanel model. This patient's events (PRS) are the nearest of the modeled fontanel. The influence of the fontanel borders on dispersion may be higher on close dipoles. It is also possible that all the dipoles around the fontanel tend to explain equally well the data (all producing a field resembling a dipole in the fontanel because of current leakage), leading to a higher sensibility to noise. Finally, the dispersion could be the result of algorithm instabilities due to close layers, although we were careful to refine the mesh around the fontanel. These hypotheses should be checked in further studies.
Position and Orientation of Dipoles for Each Type of Activity—Averaged Events
Considering MRI anatomical data, the normal head model seemed the most accurate for localizations for all patients except J.R.
For the three subjects presenting FST, the locations and orientations of the left and right dipoles were almost symmetric, and were consistent with the MRI anatomical data for gray matter areas. In the normal head model, the locations of the dipoles were a little too deep, probably due to the low skull layer conductivity, and because the skull thickness at the frontal areas was high compared with the temporal and central areas. Orientation helps to define a more accurate cortical location.
For the two subjects presenting TS, the locations and orientations of the dipoles were consistent with the MRI anatomical data for gray matter areas and for temporal cortical zones, where it was suspected that abnormal EEG activities would be generated.
For patient J.R., who presented PRS, we hypothesized that the true location of the PRS should be on the lesion border. The borders of a lesion, especially when filled with blood, are frequently the source of abnormal activities and can evolve into epileptogenic zones [Boon et al., 1997]. In the normal head model, the dipole fit gave a PRS location 5.5 mm above the nearest lesion border and 0.9 mm below the nearest lesion border in the 0.33 head model. This is consistent with the true location of activities being somewhere between the locations given by these two head models. Moreover, the correct skull layer conductivity in this patient should be much closer to 0.33 S/m than to 0.0042 S/m, possibly due to the central location of the activity. Indeed, we primarily detected the PRS by electrodes located over the fontanel.
Influence of the Fontanel
The data from J.R. in normal and 0.33 head models suggests that the influence of the fontanel is comparable to that of holes [Bénar and Gotman, 2002] and zones of higher conductivity [Ollikainen et al., 1999] in the adult skull. That is, the nearer a dipole is situated to an inhomogeneity, the greater its influence on the reconstruction of the source. The effect of a hole in the skull can adequately be modeled by a region of higher conductivity in the skull layer, because a hole mainly consists of a current leakage. In the reconstruction of the dipole source, such a leakage produces a shift of the dipole in direction of the inhomogeneity. Hence, a hole mostly influences the nearest activities and the larger the difference between the skull and the hole conductivity, the larger effect.
We did not modeled the fontanel by a zone of higher conductivity in the skull, but by a zone of thinner resistive skull layer, yet the data from J.R. in fontanel head model seem to show the same kind of behavior: the averaged dipole has shifted toward the modeled fontanel. It is probably due to the same reason: the region where the skull is thinner is globally more conductive, and produced a current leakage. However this shift is very low, and globally we found a weak influence of the modeled fontanel in every patient.
In neonates, the skull is not completely ossified and is more vascularized than in adults. On the other hand, the fontanel is already beginning ossification. The skull is besides very thin. The error in EEG source localization is much lower than previously expected, and probably even lower for temporal or prefrontal activities as they are farther from the fontanel.
Influence of the Lesion
The influence of the lesion on the reliability of localization remains unresolved, although Vatta et al. have shown that a lesion located under the dipole, relative to the surface, has a negligible effect [Vatta et al., 2000]. The same is true for ventricles or brain cavities, both natural and after resection [Bénar and Gotman, 2002; He and Musha, 1989].
Influence of the Skull Conductivity and Thickness
The main source of uncertainty is the skull layer conductivity. Our results show that the change of skull layer conductivity affects the position and magnitude of the dipoles but not their orientation. The mean distance between dipole locations between the normal and 0.33 head models was 11.6 ± 2.5 mm. We assumed that the true result should be intermediate between the two if we had a more realistic value for the skull layer. This error is large if we consider the newborns head size. However, compared with the first EEG source localization results in adults [Homma et al., 1994; Krings et al., 1998, 1999, for review see Merlet, 2001] and to the technical difficulties in our study, the error is reasonable.
Only dipole magnitude seemed to be affected by the uncertainty in the skull layer thickness. This may be because the maximal thickness used in the thick head model was low compared with the thickness used in adult models, and is therefore not a large influence on results. Our results give the widest range or error that can be expected in the modeling of neonate heads from individual MRI data. Therefore, we assume that for individual realistic head models for neonates, the error on dipole parameters due to segmentation approximation on skull thickness are negligible. This is contrary to findings in adults [Chauveau et al., 2004].
CONCLUSION
In this study, we have attempted to determine whether it is possible, using an adapted EEG headcap, to adapt EEG source localization techniques to neonates, and to evaluate the importance of the technical difficulties specific to this population. We have overcome the principal difficulties specific to neonates, such as the EEG spatial resolution, the spatial electrode positions on the scalp and the skull layer parameters, and shown that EEG source localization is feasible in preterm and term neonates.
The results show that the maximum error in dipole positions due to the skull layer conductivity is probably less than previously thought. This may be due to the thinness of the newborn skull, which allows a good conduction of the EEG signal through the skull to the surface electrodes and reduces dipoles dispersion. This thinness, which was taken into account in our realistic head model, also probably reduces the influence of the skull layer conductivity and the influence of the fontanel on the dipole localization. The relative smoothness of the newborn cortex, especially in premature neonates may also help in reducing the error in dipole positions. Brain convolutions are not completely formed at that age, so the dipoles are mainly radial. Radial dipoles are less affected by skull effects (attenuation, dispersion, etc.), resulting in homogeneous dipole positions.
Finally, depth‐errors in dipole localization due to uncertainties in the skull conductivity and thickness are probably compensated by the adjustments made for magnitude, especially for thickness.
Further analysis should provide more quantitative information about the standard parameters to use. Although only focal activities were studied, this technique may prove useful for newborn and preterm medical diagnosis and care, especially in cases of epilepsy. It may also help in understanding pathological processes and evolution, and could be useful for maturational studies.
Acknowledgements
The authors thank Dr. Astrid Nehlig for revising the manuscript, and anonymous reviewers for critical reading and helpful comments on the manuscript. The excellent assistance of the Amiens North Hospital technicians Mrs. Laurence Legrand, Chantal Ponthieu, Armelle Zuba, and Mr. Philippe Forget is gratefully acknowledged.
REFERENCES
- Bénar C‐G, Gotman J ( 2002:) Modeling of post‐surgical brain and skull defects in the EEG inverse problem with the boundary element method. Clin Neurophysiol 113: 48–56. [DOI] [PubMed] [Google Scholar]
- Boon P, D'Havé M, Vandekerckhove T, Achten E, Adam C, Clémenceau S, Baulac M, Goosens L, Calliauw L, De Reuck J ( 1997:) Dipole modelling and intracranial EEG recording: Correlation between dipole and ictal onset zone. Acta Neurochir 139: 643–652. [DOI] [PubMed] [Google Scholar]
- Chauveau N, Franceries X, Doyon B, Rigaud B, Morucci JP, Celsis P ( 2004:) Effects of skull thickness, anisotropy, and inhomogeneity on forward EEG/ERP computations using a spherical three‐dimensional resistor mesh model. Hum Brain Mapp 21: 86–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geddes LA, Baker LE ( 1967:) The specific resistance of biological material—A compendium of data for the biomedical engineer and physiologist. Med Biol Eng 5: 271–293. [DOI] [PubMed] [Google Scholar]
- Gonçalves S, de Munck JC, Verbunt JPA, Bijma F, Heethar RM, Lopes da Silva F ( 2003:) In vivo measurement of the brain and skull resistivities using an EIT‐based method and realistic models for the head. IEEE Trans Biomed Eng 50: 754–767. [DOI] [PubMed] [Google Scholar]
- He B, Musha T ( 1989:) Effects of cavities on EEG dipole localization and their relations with electrode positions. Int J Biomed Comput 24: 269–282. [DOI] [PubMed] [Google Scholar]
- Homma S, Musha T, Nakajima Y, Okamoto Y, Blom S, Flink R, Hagbarth K‐E, Moström U ( 1994:) Location of electric current sources in the human brain estimated by the dipole tracing method of the scalp‐skull‐brain (SSB) headmodel. Electroencephal Clin Neurophysiol 91: 374–382. [DOI] [PubMed] [Google Scholar]
- Krings T, Chiappa KH, Cuffin BN, Buchbinder BR, Cosgrove GR ( 1998:) Accuracy of electroencephalographic dipole localization of epileptiform activities associated with focal brain lesions. Ann Neurol 44: 76–86. [DOI] [PubMed] [Google Scholar]
- Krings T, Chiappa KH, Cuffin BN, Cocchius JI, Connolly S, Cosgrove GR ( 1999:) Accuracy of EEG dipole source localization using implanted sources in the human brain. Clin Neurophysiol 110: 106–114. [DOI] [PubMed] [Google Scholar]
- Lamblin MD, André M, Challamel MJ, Curzi‐Dascalova L, D'Allest A‐M, De Giovanni E, Moussalli‐Salefranque F, Navelet Y, Plouin P, Radvanyi‐Bouvet MF, Samson‐Dollfus D, Vecchierini‐Blineau MF ( 1999:) Electroencéphalographie du nouveau‐né prématuré et à terme. Aspects maturatifs et glossaire. Neurophysiol Clin 29: 123–219. [DOI] [PubMed] [Google Scholar]
- Merlet I ( 2001:) Dipole modeling of interictal and ictal EEG and MEG paroxysms. Epileptic Disord 3 (special issue): 11–36. [PubMed] [Google Scholar]
- Michel CM, Murray MM, Lantz G, Gonzalez S, Spinelli L, Grave de Peralta R ( 2004:) EEG source imaging. Clin Neurophysiol 115: 2995–2222. [DOI] [PubMed] [Google Scholar]
- Ollikainen JO, Vauhkonen M, Karjalainen PA, Kaipio JP ( 1999:) Effects of local skull inhomogeneities on EEG source estimation. Med Eng Phys 21: 143–154. [DOI] [PubMed] [Google Scholar]
- van Burik MJ, Peters MJ ( 1999:) EEG and implanted sources in the brain. Arch Physiol Biochem 107: 367–375. [DOI] [PubMed] [Google Scholar]
- Vatta F, Bruno P, Inchingolo P ( 2000:) Accuracy of EEG dipole source localisation in presence of brain lesions. Biomed Sci Instrum 36: 403–408. [PubMed] [Google Scholar]
- Wang Y, Gotman J ( 2001:) The influence of electrode location errors on EEG dipole source localization with a realistic headmodel. Clin Neurophysiol 112: 1777–1780. [DOI] [PubMed] [Google Scholar]
- Zanow F, Knösche TR ( 2004:) ASA—Advanced source analysis of continuous and event‐related EEG/MEG signals. Brain Topogr 16: 287–290. [DOI] [PubMed] [Google Scholar]


