Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2009 Jun 8;30(12):4054–4069. doi: 10.1002/hbm.20829

Selectivity as well as sensitivity loss characterizes the cortical spatial frequency deficit in amblyopia

Robert F Hess 1,✉, Xingfeng Li 1, Behzad Mansouri 1, Benjamin Thompson 2, Bruce C Hansen 3
PMCID: PMC6871242  PMID: 19507159

Abstract

The processing deficit in amblyopia is not restricted to just high spatial frequencies but also involves low‐medium spatial frequency processing, for suprathreshold stimuli with a broad orientational bandwidth. This is the case in all three forms of amblyopia; strabismic, anisometropic, and deprivation. Here we use both a random block design and a phase‐encoded design to ascertain (1) the extent to which fMRI activation is reduced at low‐mid spatial frequencies in different visual areas, (2) how accurately spatial frequency is mapped across the amblyopic cortex. We report a loss of function to suprathreshold low‐medium spatial frequency stimuli that involves more than just area V1, suggesting a diffuse loss in spatial frequency processing in a number of different cortical areas. An analysis of the fidelity of the spatial frequency cortical map reveals that many voxels lose their spatial frequency preference when driven by the amblyopic eye, suggesting a broader tuning for spatial frequency for neurons driven by the amblyopic eye within this low‐mid spatial frequency range. Hum Brain Mapp, 2009. © 2009 Wiley‐Liss, Inc.

Keywords: amblyopia, cortex, fMRI, contrast sensitivity, spatial frequency mapping, spatial deficit, low spatial frequency, tuning

INTRODUCTION

The psychophysical picture of amblyopia provided by contrast sensitivity measurements implicates a selective loss for the processing of low contrast, high spatial frequency stimuli [Gstalder and Green, 1971; Hess and Howell, 1977; Levi and Harwerth, 1977]. However, this does not provide a complete description of the processing deficit because there is now ample evidence that the processing of suprathreshold stimuli of low‐mid spatial frequencies is also affected. This deficit for low‐mid spatial frequencies is apparent for global motion [Aaen‐Stockdale and Hess, 2008], for global form [Simmers et al., 2004], for positional accuracy [Hess and Holliday, 1992], for 2nd order global processing [Mansouri et al., 2005] and for shape discrimination [Hess et al., 1999].

Animal models of amblyopia provide further support that the deficit in amblyopia is not exclusively restricted to neurons tuned to high spatial frequencies. Crewther and Crewther [ 1990] only found a small difference in the average acuity of cells; the spatial performance of cells driven by the strabismic eye was very similar to that driven by the fellow fixing eye. Also a number of other studies have shown no difference in the spatial properties of cortical cells in strabismic cats and monkeys [Blakemore and Eggers, 1979; Blakemore and Vital‐Durand, 1992; Roelfsema et al., 1994]. Other studies have suggested that there may be subtle deficits. Both the optimum spatial frequency of some neurons within the central field driven by the strabismic eye, at least in severe cases, is displaced to lower spatial frequencies [Kiorpes and McKee, 1999; Kiorpes et al., 1998; Movshon et al., 1987] and the spatial tuning bandwidth may be broader when driven by the strabismic eye [Chino et al., 1983; Schmidt et al., 2004].

Human brain imaging also has the potential to address the question of the spatial frequency dependence of the cortical loss of function in amblyopia. Although fMRI studies conducted to date have all shown reduced cortical activation in response to amblyopic eye stimulation, there is still no consensus on how this deficit varies with the spatial frequency of stimulation [Algaze et al., 2002; Anderson et al., 1999; Barnes et al., 2001; Choi et al., 2001; Conner et al., 2007a, b; Demer, 1997; Demer et al., 1988; Goodyear et al., 2000; Imamura et al., 1997; Kabasakal et al., 1995; Li et al., 2007a, b; Muckli et al., 2006]. Recent studies [Barnes et al., 2001; Lee et al., 2001; Muckli et al., 2006] argue that responses to high spatial frequencies are not selectively reduced and that the deficit also involves the processing of low‐medium spatial frequencies.

Here we investigate the extent of the processing deficit in the low‐medium spatial frequency range, determine whether its spatial frequency dependence, its regional distribution and whether the cortical representation of spatial frequency for the amblyopic eye's input is disrupted. We use suprathreshold spatial frequency narrowband stimuli comprising two orientations (a sinusoidal checkerboard) as this represents a basic building block for the construction of more complex stimuli. Shape performance for similar suprathreshold, low‐medium spatial frequency stimuli, but with multiple orientations, has been shown to be abnormal in amblyopia [Hess et al., 1999]. Our selection of stimulus was designed to probe the early stages of this processing stream and to determine its spatial frequency dependence. We used a random block design to investigate the fMRI response to low‐medium spatial frequencies by comparing amplitude responses for different visual areas to assess the relative magnitude of the cortical response for fixing and fellow amblyopic eye stimulation within different retinotopically‐defined visual areas. In a separate but complementary, phase‐encoded design we measured phase responses to assess how spatial frequency selectivity is mapped across the cortex [Sasaki et al., 2001] for connections made by the amblyopic eye. We find deficits for the processing of suprathreshold, low‐mid spatial frequency checkerboard stimuli in all retinotopically‐mapped visual areas as well as a disruption to the cortical spatial frequency map that can be explained in terms of a less tuned response of individual neurons driven by the amblyopic eye.

METHODS

Subjects

Table I shows the clinical data for the 10 amblyopic subjects tested (average age 32.7 ± 4 years). Clinically, amblyopia in humans can be subdivided into pure strabismus without anisometropia, pure anisometropia without strabismus, and a mixed form where strabismus and anisometropia coexist. Six of our subjects had strabismic amblyopia, four had mixed strabismic/anisometropic amblyopia. During both the fMRI and psychophysics sessions, subjects wore nonmagnetic spectacles to give them corrected acuity based on their refraction. A control group of five normal subjects (average age 29.8 ± 4 years) was also tested. During the scanning sessions, subjects monocularly viewed a stimulus back‐projected into the bore of the scanner and viewed through an angled mirror. The eye not being stimulated was occluded with a black patch that excluded all light from the eye. Subjects DA, DV, GN, MB, LM, HP, OA, and XL participated in Experiment 1. Six of our amblyopic subjects (XL, LM, HP, GN, MG, and EF) and five normal controls took part in Experiment 2. All studies were performed with the informed consent of the subjects and were approved by the Montreal Neurological Institute Research Ethics Committee and complied with the Code of Ethics of the World Association (Declaration of Helsinki).

Table I.

Clinical details of the amblyopic observers participating in the experiment

Obs A/G Type Refraction OA GA ratio CS ratio SQ History
DA 21 F RE strab Ø 20/160 0.73 1.09 ET 15° Dx at 4 y, patching at 4 y for 6 m, Sx at 7 y, no Stereopsis
LE −0.50 DS 20/20
DV 23 F RE +0.25 DS 20/20 0.74 1.0 ET 3° Dx at 5 y, patching for 6 m, No Sx, no Stereopsis
LE mixed +1.50+1.25 85° 20/40
EF 56 M RE +2.00+1.00.180° 20/32 0.48 1.09 ET 6° Dx at 6 y, patching for 1–2 y, No Sx, no Stereopsis
LE strab +2.00+1.00.130° 20/250
GN 30 M RE mixed +3.00+2.00. 30° 20/70 0.78 0.75 ET 8° Dx at 5 y, patching for 3 m, no Stereopsis, Sx REx2 age 10–12 y
LE +2.50+1.00.165° 20/20
HP 33 M RE −1.0 DS 20/25 0.88 0.68 ET 5° Dx at 4 y, patching for 6 m, Sx 5 y, no Stereopsis
LE strab +0.50 DS 20/63
LM 20 F RE mixed +0.25+0.75.180° 20/80 0.83 0.94 ET 6° Dx at 5 y, patching for 2 y, no Stereopsis
LE −3.25 DS 20/25
MB 50 M RE −1.00 DS 20/32 0.96 1.35 ET 3° No Sx, Tx: first glasses at 32 years old, no Stereopsis
LE strab +0.50 DS 20/80
MG 30 F RE strab −0.50 DS 20/100 0.38 0.73 ET 1° Dx at 4 y, patching for 6 m, no Sx, no Stereopsis
LE +0.50 DS 20/15
XL 31 F RE −2.50 DS 20/20 0.29 0.45 ET 15° Dx at 13 y, no Tx, no Stereopsis
LE strab −2.75+0.75. 110° 20/400
OA 27 M RE mixed +4.50−5.00×30° 20/150 0.43 0.67 RET 5° Dx at 3 y, patching 3 y, no Sx
LE −2.00−2.00×150° 20/25
Open in a new tab

M: male, F: female, Obs: observer, A/G: age/gender, OA: optotype acuity, GA: grating, CS: contrast sensitivity at 1 c/deg, Dx: diagnosed, Sx: surgery, Tx: treatment, LE: left eye, RE: right eye, strab: SQ strabismus: A/S age and gender, strabismic amblyopia, DS: dioptre sphere.

Retinotopic Mapping

Using standard radial checkerboard stimuli we performed retinotopic mapping on the fixing and fellow amblyopic eye separately [Li et al., 2007b]. Using an automatic volumetric analysis [Dumoulin et al., 2000, 2003], we defined separately the visual field sign map for fixing and amblyopic eye stimulation and used the average map for the analysis of area boundaries.

Experiment 1

We used a random block design in which three conditions, a medium spatial frequency sinusoidal checkerboard stimulus of 4 c/d (Fig. 1A), a low spatial frequency of 0.5 c/d (Fig. 1B), and control condition (mean luminance) were presented randomly. The temporal frequency was 8 Hz. Each block lasted 15 s and there were eight blocks per run. The attention of the subjects was controlled using a target detection task in which the appearance of a subset of checks (whose position and presentation was chosen randomly) of a higher local contrast/luminance had to be detected (illustrated in Fig. 1A). The same task was performed for test and control conditions. Performance varied between 80 and 97% for amblyopic and normal eye stimulation. As with the retinotopic mapping stimuli, the subject maintained fixation on a central fixation mark.

Figure 1.

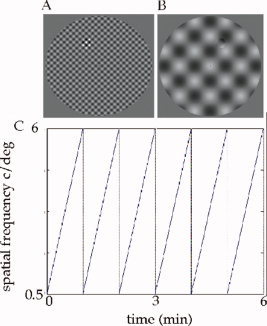
Figure 1

Open in a new tab

Stimuli and experimental design. Illustration of the spatial frequency phase‐encoded design showing the highest (A) and lowest (B) spatial frequencies. If viewed from around 30 cm, the spatial frequency of these stimuli are 6 c/d (A) and 0.5 c/d (B). Note that the diameter of our field size during the experiment was 34°. The cyclic change that occurred in spatial frequency from the lowest to the highest (and vice versa) over the 6‐min run time is shown in (C). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Experiment 2

We used a phase‐encoded design (the spatial frequency changed periodically either from medium to low or from low to medium) in which the spatial frequency of a sinusoidal checkerboard stimulus was gradually varied from 0.5 to 6 c/d over a 1 min period. The temporal frequency of the checkerboard stimulus was 8 Hz. This involved a smooth and gradual change in the spatial frequency of the sinusoidal checkerboard evenly throughout the field. A central fixation point was provided. The stimulus and design matrix are depicted in Figure 1. The attention of the subjects was controlled using a target detection task as described above for the block design. Performance was not significantly different for amblyopic and normal eye stimulation (varied between 78 and 93%).

Image Acquisition

A Siemens 1.5‐T Magnetom scanner was used to collect both anatomical and functional images. Anatomical images were acquired using a rectangular (14.5‐in. × 6.5‐in.) head coil (circularly polarized transmit and receive) and a T1 weighted sequence (TR = 22 ms; TE = 10 ms; flip angle = 30°) giving 176 sagittal slices of 256 × 256 mm3 image voxels. Functional scans for each subject were collected using a surface coil (circularly polarized, receive only) positioned beneath the subject's occiput. Each functional imaging session was preceded by a surface coil anatomical scan (identical to the head coil anatomical sequence, except that 80 × 256 × 256 sagittal images of slice thickness 2 mm were acquired) to later coregister the data with the more homogeneous head‐coil image.

Retinotopic mapping

Functional scans were multislice T2*‐weighted, gradient‐echo, planar images (GE‐EPI, TR = 3.0 s, TE = 51 ms, flip angle = 90°). The image volume consisted of 30 slices orthogonal to the calcarine sulcus. The field of view was 256 × 256 mm2, the matrix size was 64 × 64 with a thickness of 4 mm giving voxel sizes of 4 × 4 × 4 mm3 (128 vol. were collected on a single run). For retinotopic mapping there were four acquisition runs for each subject; eccentricity mapping (fovea to periphery and vice versa), polar mapping (clockwise and counter‐clockwise).

Experiments 1 and 2

The image protocol and functional images were acquired using the same procedure as already described for retinotopic mapping except that image volumes were acquired parallel to the calcarine sulcus. In Experiment 1, the random block design was repeated four times for each eye to enhance activation. In Experiment 2, eight acquisition runs were obtained for each eye; four runs in increasing order (low spatial frequency to medium spatial frequency), and four runs in decreasing order.

Data Analysis

Anatomical images

The global T 1 weighted aMRI scans were corrected for intensity nonuniformity [Sled et al., 1998] and automatically registered [Collins et al., 1994] in a stereotaxic space [Talairach and Tournoux, 1988] using a sterotaxic model of 305 brains [Evans et al., 1993]. The surface‐coil aMRI, acquired in the same session as the functional images, was aligned with the head‐coil aMRI, thereby allowing an alignment of the functional data with a head‐coil MRI and subsequently stereotaxic space. A validation of this method was described in a previous study [Dumoulin et al., 2003]. The aMRIs were classified into gray matter, white matter, and cerebrospinal fluid (CSF), after which the four (gray matter, white matter, left, and right hemisphere) cortical surfaces for all subjects were simultaneously reconstructed at the inner and outer edge of the cortex [Kim et al., 2005; Lerch and Evans, 2005; MacDonald et al., 2000]. All processing steps were automatic and all data are presented in standard stereotaxic space.

Functional images

Dynamic motion correction was performed on all functional volumes using MINC tools [Collins et al., 1994]. The first eight scans of each functional run were discarded due to start‐up magnetization transients in the data. T values were calculated based on the fundamental frequency effects of Fourier transformation [Li et al., 2007a]. For Experiment 2, the design matrix was formed by combining the fundamental frequency effects and the low frequency drift effects. The General linear model (GLM) method was employed to quantify the brain activation. Inference for the effects was obtained using T statistics. Different runs for each eye were combined in terms of a mixed model [Seber and Lee, 2003; Worsley et al., 2002].

Experiment 1

The design matrix was formed by combining medium spatial frequency (4 c/d, 80% contrast), low spatial frequency (0.5 c/d, 80% contrast), and mean luminance conditions (30 cd/m2). The contrast was set to be [1 −1 0] for the comparison of medium (1) with low (−1) spatial frequencies. Both a GLM and a mixed model were employed to quantify the brain activation and inference for the effects was quantified using the T statistic.

Experiment 2

The spatial frequency mapping analysis was conducted using the commercially available Brain Voyager analysis package. Spatial frequency and eccentricity maps for each eye of observers were visualized on inflated representations of each subject's cerebral hemispheres. This allowed visual inspection of the maps without interference from sulci and gyri. Although our phase‐encoded stimulus contained spatial frequencies from 0.5 to 6 c/d, we only tested for voxel preferences within the 0.5–3 c/d range for our mapping analysis. This was because preliminary analyses had shown that the maps generated across the whole spatial frequency range were less interpretable, partly as a consequence of our voxel resolution. This meant that we were unable to replicate previous spatial frequency mapping results [Sasaki et al., 2001] in our control participants when mapping was conducted across the whole 0.5–6 c/d spatial frequency range, whereas reasonable replication was possible when the subset of spatial frequencies that corresponded to those used in the previous study [Sasaki et al., 2001] were used for mapping, i.e. the 0/5–3 c/d range. The exclusion of the highest spatial frequencies had no bearing on the maps produced for the low‐mid spatial frequencies from which we derived conclusions. The relative distributions of spatial frequency preference and eccentricity for each eye of each subject were quantified following the techniques described by [Sasaki et al., 2001]. The eccentricity map for either the dominant or fellow eye of the subject was visualized on the subject's flattened cortical sheets (one for each hemisphere). Following on from the analysis of [Sasaki et al., 2001], a vector was then drawn on the cortical sheet that ran roughly parallel to the horizontal meridian in V1 and spread from the most central representation of the visual field in the map (2°) to the edge of the eccentricity band corresponding to 17° (the largest eccentricity localized). Four vectors were selected per subject, two for each hemisphere; one each for the upper and lower visual fields. Preferred phase responses and associated P values for the eccentricity and spatial frequency stimuli were then calculated for each voxel that fell along a vector in response to simulation from each eye (amblyopic vs. fellow or dominant vs. nondominant) independently. Associated spatial frequency and eccentricity values were then pooled across subjects for each eye (amblyopic, fellow, dominant or nondominant). For each pooled group, pairs of values that did not show a significant preference for both a spatial frequency and an eccentricity (P < 0.05 uncorrected) were excluded from subsequent analysis. The remaining values were subjected to a frequency analysis and for each eccentricity band the spatial frequency that was preferred by the most voxels (peak of the frequency distribution of spatial frequency preferences for that specific eccentricity band) was selected as the spatial frequency preference associated with that eccentricity band for subsequent plotting.

Psychophysics

Eye occlusion and dominance

To test monocular function, we occluded either the fixing or fellow amblyopic eye with a black patch designed to exclude all light. This was done for both the psychophysical testing and for the brain imaging. Under these conditions there is no binocularly‐mediated suppression of the amblyopic eye since all pattern vision in the good eye has been abolished [Harrad and Hess, 1992] and thus our estimates of the reduced activation in the brains of amblyopes is a conservative one as it does not include a binocularly‐suppressive component. Eye dominance was assessed using a standard sighting test [Rosenbach, 1903].

Acuity and contrast sensitivity

For each subject, grating acuity and contrast sensitivity at 1 c/d for optically corrected subjects was established using a method of constant stimuli and a two alternative forced choice (2AFC) paradigm using a VSG 3/4 graphics card and a gamma corrected NEC Multisync XP 17 monitor. The two intervals were presented, one containing a static vertical grating (of 80% contrast for acuity) and variable contrast for contrast sensitivity) and the other a mean luminance. The subject's acuity and or contrast sensitivity (corresponding to 82% correct identification) was measured using a staircase method. The field size had a diameter of 10° at 10 c/d and varied inversely with spatial frequency for the acuity measurement. For the measurement of contrast sensitivity a field size of 10° was used. A central fixation mark was provided for both measurements.

RESULTS

In this study we used both a random block fMRI design and a phase‐encoded design. In the random block design we directly addressed the issue of whether there is an fMRI deficit for stimulus spatial frequencies in the medium–low range for different cortical ROIs. The phase‐encoded design allowed us to use the phase responses to provide information concerning how spatial frequency is mapped across the cortex for the amblyopic eye's input.

Experiment 1—Random Block Design

We used a standard random block design in which there were three stimulus blocks, one comprising a medium spatial frequency stimulus (4 c/d), one containing a low spatial frequency stimulus (0.5 c/d) and a mean luminance condition with a fixation point. The subject performed an attention task involving the detection of the occurrence of randomly positioned regions of lower contrast while maintaining central fixation. The t value associated with both the fellow fixing eye's response and the amblyopic eye's responses was derived for both the low and medium spatial frequency stimuli. Some individual subjects exhibited statistically significant (paired t test; P < 0.05; two‐tailed) reductions in responsiveness (denoted by the dashed box around the initials) in one or more visual areas for the medium spatial frequency stimulus (e.g. DV, LM, MB, GN, and OA) and some of these subjects (DV, LM, and GN) also exhibit statistically significant reductions in activations for the low spatial frequency stimulus in one or more visual areas.

In Figure 2 we plot the differential fMRI activation (i.e. fixing fellow amblyopic eye) for the medium spatial frequency target versus that for the low spatial frequency target across different visual areas for the subjects identified from Experiment 1 who had significant reductions in activations (i.e. DV, LM, MB, GN, and OA). The dotted line is the line of unity slope. Only MB and OA exhibited a greater loss at medium spatial frequencies. In most visual areas, GN exhibited comparable losses for medium and low spatial frequencies and DV and LM exhibited a consistently larger loss for low spatial frequency stimuli, with little or no medium spatial frequency loss.

Figure 2.

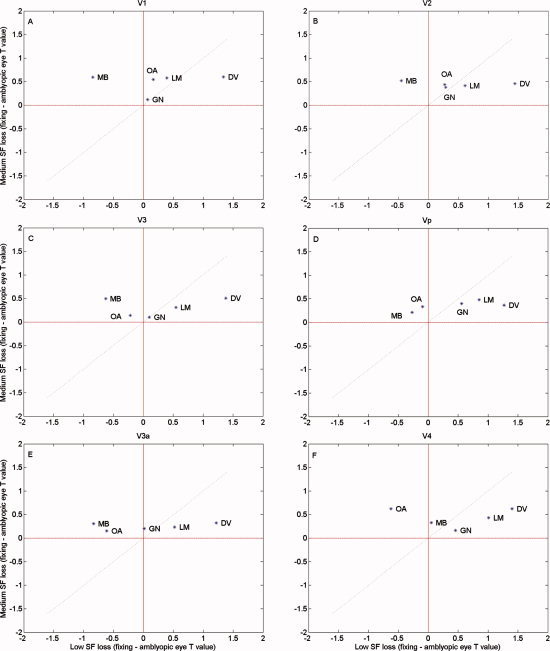
Figure 2

Open in a new tab

Comparison of the deficits at 4 and 0.5 c/d. Comparison of the deficit (t value fixing eye‐T statistic amblyopic eye) for the medium spatial frequency stimulus relative to that for the low spatial frequency stimulus for the random block design for the subjects that showed a significant deficit in Experiment 1. The dashed line has a slope of unity and indicates comparable high/low spatial frequency deficits. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

We examine the correlations between the reductions in fMRI signal (amblyopic/fixing t values) in different visual areas for the medium spatial frequency target and the psychophysically measured contrast sensitivity deficit (amblyopic/fixing contrast sensitivity) within the same spatial frequency range (i.e. 1 c/d) in the amblyopic group as a whole. No significant positive correlations were found in any visual area (r v1 = −0.1281; r v2 = −0.5387; r v3 = −0.5553; r vp = −0.0712; r v3a = −0.1541; r v4 = −0.2030). This was also the case for the low spatial frequency loss. Finally, no significant positive correlations were found in any visual area between the reductions in fMRI activation and the grating acuity deficit.

Experiment 2—Phase‐Encoded Design

To investigate aspects of cortical function that extend beyond simple differences in the activation level we supplemented our block design approach with one involving a phase‐encoded design. Functional data from a phase‐encoded design can provide two sources of additional, complimentary information about cortical function in amblyopia. First, it allows one to assess the way in which spatial frequency is mapped onto the amblyopic cortex by examining the phases of responses [Sasaki et al., 2001] and to ask whether the cortical organization of spatial frequency process is disrupted in amblyopia. The response phase supplies valuable information concerning the global cortical organization for spatial frequency in the amblyopic cortex. Second, it provides a method for assessing the spatial frequency selectivity of the cortical activation in different visual areas. This information concerning the layout of the cortical map for spatial frequency and its selectivity of the fMRI response for spatial frequency that are derived solely from the phase of the responses for the phase‐encoded design compliment the information concerning spatial frequency sensitivity, derived from the magnitude of the responses for the random block design previously described. A measure of how selective the spatial frequency response is in the amblyopic compared with the fellow fixing eye is also important because it may provide an explanation for why we found in our block design experiment that fMRI responses for the amblyopic group as a whole are only subtly, and not significantly, different from those of the fellow fixing eye. If neurons driven by the amblyopic eye have a much broader spatial frequency tuning, then due to a recruitment of responses across the population of broadly‐tuned neurons with different peak spatial frequency, similar or in some cases, greater population responses could be achieved by amblyopic eye stimulation.

Phase responses

A reason for using a phase‐encoded design was to build upon the previous finding for normal vision that spatial frequency is mapped across eccentricity on the cortical surface in an orderly fashion within the spatial range 0.1–2 c/d [Sasaki et al., 2001]. We wanted to know if a map of similar accuracy was present for the connections of the amblyopic eye. Figure 3 shows a comparison between the average phase maps for our eccentricity and spatial frequency phase‐encoded experiments for the dominant and nondominant eyes of normals and the fixing and amblyopic eye of amblyopes. The previous study [Sasaki et al., 2001] of how spatial frequency is mapped across the normal cortex used average maps from eight subjects and for comparative purposes we use the same approach in our amblyopic subjects. It is apparent that the eccentricity maps of normal and amblyopic subjects are qualitatively similar [though see Li et al., 2007a]. A clear spatial frequency map is seen for the normal eyes and for the fixing eye of amblyopes, however a more patchy map is apparent for the amblyopic eye of amblyopes.

Figure 3.

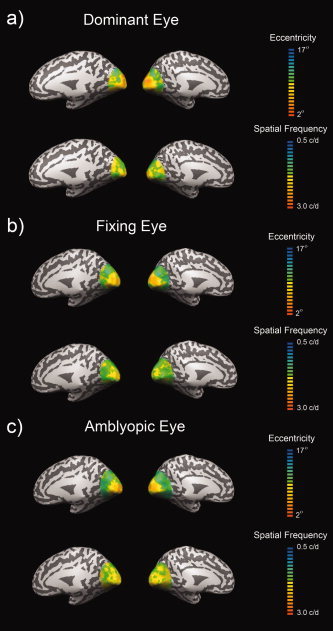
Figure 3

Open in a new tab

The cortical mapping of spatial frequency. The average phase maps shown on inflated left and right hemispheres for the dominant eyes of controls (A), fixing eyes of amblyopes (B) and the amblyopic eyes of amblyopes (C). Maps are presented for both eccentricity (upper row of each panel) and spatial frequency selectivity (lower row of each panel). Maps represent the average of four controls and five amblyopes (four scanning runs per eye for spatial frequency, two runs per eye for eccentricity).

To examine the relationship between stimulus spatial frequency and eccentricity we combined the spatial frequency and eccentricity maps and derived peak preferences along vectors on the flattened cortical sheet that ran parallel to the horizontal meridian in V1 for each hemisphere and for the upper and lower visual fields in a fashion similar (see methods for details) to that of [Sasaki et al., 2001]. These results for the dominant and nondominant eyes of normals and for the fixing and amblyopic eyes of amblyopes are displayed in Figure 4, where the spatial frequency preference is plotted against eccentricity in the visual field.

Figure 4.

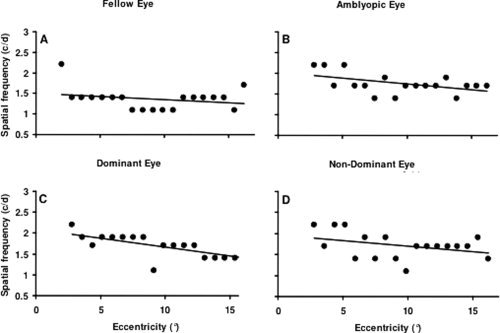
Figure 4

Open in a new tab

Spatial frequency preferences across eccentricity. Peak spatial frequency preference within the 0.5 to 3 c/d range as a function of eccentricity within V1. Data are pooled across upper and lower visual hemifields, hemispheres and subjects and is shown for the fellow fixing (A) and amblyopic eye (B) of amblyopes and the dominant (C) and nondominant (D) eye of controls. Only voxels that showed a significant preference for both a spatial frequency and an eccentricity (P < 0.05) were included in the plots.

The data in Figure 4 has two particular features. First, the spatial frequency preference only declines gradually with eccentricity. These results for normals are not however that dissimilar from those previously reported by [Sasaki et al., 2001]. Second, similar spatial frequency preferences across eccentricity occur for our amblyopic population.

Figure 5 shows histograms of the distribution of spatial frequency preferences among the voxels from normal (dominant and nondominant eye) and amblyopic (fixing and amblyopic eye) cortex. The peak spatial frequency preference is similar for normals and amblyopes, though, if anything, a little higher in the amblyopic group. There is however a clear difference in the number of voxels activated, many fewer voxels are activated by the amblyopic eye compared with the fellow fixing eye (23% fewer voxels for the amblyopic eyes) when the same vectors are applied to the data for the two eyes independently. This was a result of our initial filtering criteria that required a level of statistical significance (P > 0.05 uncorrected) for the phase fits for both eccentricity and spatial frequency. By relaxing these criteria we ascertained that more voxels were rejected for the amblyopic eye due to their response to spatial frequency than due to eccentricity. When only a significant preference for eccentricity was required the number of amblyopic eye voxels was only 1% less than that of the fellow eye, whereas when only a significant preference for spatial frequency was required, this difference increased to 23%. In other words, the maps of amblyopic eyes were noisier in spatial frequency than they were in eccentricity compared with those of normal eyes even when the absolute value of the preference was disregarded and only the presence of a significant preference was required. This is a reflection of the more patchy spatial frequency map that can be seen for the amblyopic eye in Figure 3. There was no pronounced difference in the number of voxels activated between the dominant and nondominant eyes of controls (5.2% less voxels for the nondominant eye).

Figure 5.

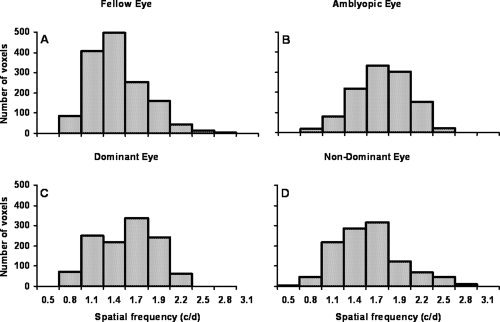
Figure 5

Open in a new tab

Spatial frequency preference distributions. The data from Figure 3 replotted as frequency histograms of the number of voxels with a reliable preference for each spatial frequency. Data is shown for the fellow fixing (A) and amblyopic eyes (B) of amblyopes and the dominant (C) and nondominant eye (D) of controls.

To assess the idea that the spatial frequency selectivity of the cortex is reduced when driven by the amblyopic eye, we undertook an additional region‐of interest analysis using the spatial frequency‐varying stimulus and a phase‐encoded design. We derived t values for the phase‐encoded design to ascertain whether there was a reduced selectivity for spatial frequency. We reasoned that if cells had similar tuning for spatial frequency between fixing and fellow amblyopic eyes then the t value would not be reduced. This intuition is supported by the model predictions in the appendix in which the response of a distributed array of spatial frequency tuned detectors to our phase‐encoded spatial frequency‐varying stimulus is computed. Appendix Figure A1 shows the expected relationship between the bandwidth of the responding detectors and the t‐value computed from their mass response for our phase‐encoded design; the broader the tuning for spatial frequency, the lower the t value for the phase‐encoded response (diagrammatically illustrated in Fig. A2 of the appendix).

The result is shown in Figure 6 where the t value of the fixing eye is plotted against the t value of the amblyopic eye for the different retinotopically mapped areas. The diagonal line represents equivalent responses and the blue line the best fitting line to the average data. The results for each amblyope are shown by initials and if enclosed in a dashed box, are significantly reduced from that of the fellow fixing eye's response (paired t test; P < 0.05; two‐tailed). All subjects show significantly reduced t values in at least one retinotopic visual area, and four out of the six amblyopes (HP, LM, XL, and MG) show a consistent and significant reduction in responses across all visual areas, suggesting that the spatial frequency selectivity is reduced when driven by the amblyopic eye relative to that of the fellow fixing eye. A similar analysis to that already described for Figure 6, but comparing the responses between the dominant and nondominant eyes of normals, is displayed in Figure 7. Normals, unlike the amblyopic eye of amblyopes, do not display a similar reduction in responsiveness for the spatial frequency‐varying stimulation.

Figure 6.

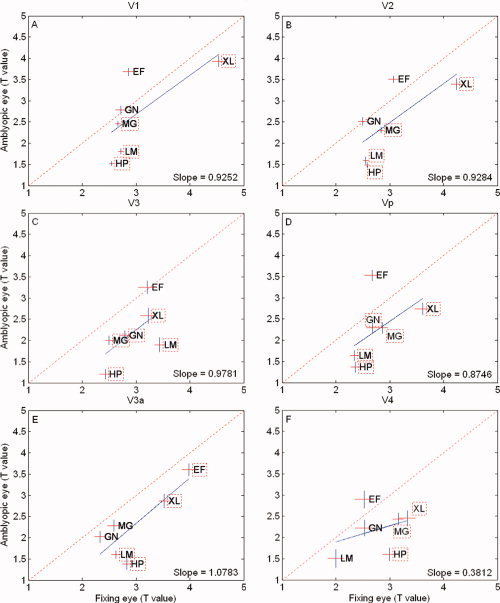
Figure 6

Open in a new tab

Phase‐encoded responses for the amblyopic eye. The t‐value is plotted for the spatial frequency phase‐encoded design for the amblyopic subjects with the fixing eye results on the abscissa and the amblyopic eye results on the ordinate. The dashed line is of unity slope. The solid line represents the best fitting linear function to the amblyopic results. Individual results are given by the subject's initials and when the amblyopic eye's response is significantly different (P = 0.05; two‐tailed) from the fellow fixing eye response, it is surrounded by a dashed box. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 7.

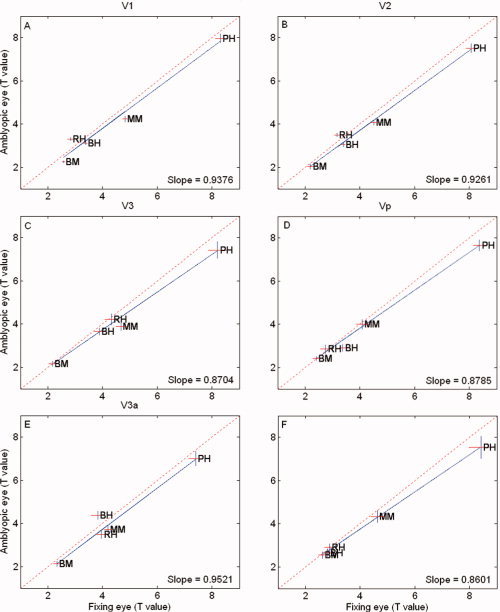
Figure 7

Open in a new tab

Phase‐encoded responses for the normal eye. The t values comparing the dominant and nondominant eyes of normals for the spatial frequency phase‐encoded design. The dashed line is of unity slope and the solid line is the best fitting function to the normal data. Similar interocular activation is seen for normal observers. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

DISCUSSION

Initially, it was thought that the processing deficit in amblyopia only affected the detection of low contrast, high spatial frequency stimuli [Hess and Howell, 1977; Levi, 1991; Levi and Harwerth, 1977]. We now know that there are processing deficits for suprathreshold stimuli of low‐mid spatial frequency in tasks such as global motion, global form, 2nd order global orientation, position‐coding, and shape discrimination. The cortical nature of this processing deficit for low‐mid spatial frequencies is not well understood except that it involves stimuli that are narrowband in spatial frequency and broadband in orientation, in principle similar to the stimuli used here. Although more recent studies have concentrated on the cortical deficit at high spatial frequencies [Barnes et al., 2001; Muckli et al., 2006], there is an indication from the results of Barnes et al. [ 2001] that low‐medium spatial frequency processing deficits are also present for stimuli that are spatial frequency narrowband but orientationally broadband. Here we focus our attention on this low‐medium spatial frequency range for a suprathreshold stimulus composed of two orientations where, on the basis of a wide range of psychophysical tasks [for example, Hess et al., 1999] one might expect to find fMRI anomalies. We show that, while there is a substantial degree of individual variability, there are fMRI anomalies in the processing of orientationally broadband suprathreshold stimuli of low‐medium spatial frequency such that low spatial frequencies are affected equally or, in some cases, to a greater extent than medium spatial frequencies. These anomalies are not confined to area V1, they involve the majority of retinotopically‐mapped visual areas. In addition to a reduction in magnitude (i.e. block design) of response to both medium and low spatial frequencies, it is evident from an analysis of the phase of the response (i.e. phase‐encoded design) that the spatial frequency cortical map [Sasaki et al., 2001] is less well‐defined for the amblyopic input. A further examination of the spatial frequency/eccentricity preference relationship revealed a lack of spatial frequency selectivity in all retinotopic visual areas when driven by the amblyopic eye relative to fellow eye's input (or relative to the responses of normal subjects). Finally, the reduction in activation in the low‐medium spatial frequency range did not correlate with the depth of amblyopia as reflected by the contrast sensitivity deficit for spatial frequencies within this range. This suggests that the fMRI deficit for low‐medium spatial frequencies is not related to the known threshold detection anomaly of spatial frequency and orientational narrowband stimuli but to the processing of suprathreshold stimuli with a broad orientational bandwidth. We have been able to reveal two new features of this cortical loss for low‐mid spatial frequency stimuli that is relevant to the current psychophysical picture; reduced responses for low‐medium spatial frequencies and a loss of spatial frequency selectivity. These deficits affect all retinotopic areas.

The magnitude deficit at low‐medium spatial frequencies

There are two instances in amblyopia in which contrast sensitivity deficits can occur in the low‐medium spatial frequency range. The first was originally reported by Hess and Howell [ 1977] and involves a sub‐population of strabismic amblyopes who exhibit a small (< a factor of 2) reduction in contrast sensitivity at low‐medium spatial frequencies and for whom there are measurable contrast discrimination deficits at suprathreshold contrasts [Hess et al., 1983]. The second involves very severe amblyopes whose high spatial frequency loss can eventually extend into the medium‐low spatial frequency range. Neither of these explanations apply here as we do not find a significant correlation between the fMRI and either the psychophysical threshold loss within this spatial frequency region or the grating acuity deficit. Interestingly, our most severe subject (XL) who had an acuity of 20/400 and a grating acuity of 11 c/d did not exhibit a selective activation loss for either medium or low spatial frequencies in the block design experiment, as might be expected from the psychophysical characteristics of the threshold contrast sensitivity loss.

There are a number of possible explanations why one would not expect the fMRI deficit reported here to reflect the characteristics of the behavioral contrast sensitivity loss. First, the suprathreshold nature of the stimuli used. The present results are for stimuli of suprathreshold contrast whereas contrast sensitivity is solely a threshold measure. Second, the behavioral deficit in amblyopia involves much more than raised contrast thresholds at high spatial frequencies, it also involves elevated positional uncertainty [Hess and Holliday, 1992] elevated global motion sensitivity [Aaen‐Stockdale and Hess, 2008; Simmers et al., 2003] elevated global form sensitivity [Simmers et al., 2005], reduced 2nd order orientation discrimination [Mansouri et al., 2005] and reduced shape sensitivity [Hess et al., 1999], all of which involve suprathreshold, low‐mid spatial frequency components and possibly more importantly, stimuli with a broad orientational bandwidth, similar to the stimulus used here. For example, take the example of global shape processing for which there is evidence of an anomaly in amblyopia [Hess et al., 1999]. There is evidence for considerable intra‐cortical processing and feedback interactions that occur to shape V1 responses and these may be particularly important for the suprathreshold stimuli used here [Dumoulin and Hess, 2006]. When thought of in this way, responses to stimuli composed of more than one orientational component may represent more than just the sum of responses to their individual orientational components. There is evidence that there are processing mechanisms that respond to the conjunctions of Fourier energy, for example, orientation in the present case, and that this represents just the initial stages of the construction of complex stimuli of different shape [Peirce and Taylor, 2006].

The spatial frequency cortical map

There is an indication that the map is not represented with the same fidelity for the connections from the amblyopic eye. This is evident from a comparison of the average maps shown in Figure 3 where a subtle difference in the regular progression from high to low spatial frequency with increasing eccentricity can be observed in the map for the amblyopic eye input. Converging evidence comes from a direct quantification of the how the peak spatial frequency preferences vary with eccentricity (Fig. 4). We found substantially fewer voxels driven by the amblyopic eye that had a reliable preference for a specific spatial frequency. This could be explained by the hypothesis that voxels driven by the amblyopic eye were composed of neurons with less well‐defined spatial frequency preferences compared with that of the normal eye. This could be the result of monocular neurons driven by the amblyopic eye having broader tuning. Another novel finding is that the majority of our amblyopes exhibited significantly reduced responses for an ROI analysis for our phase‐encoded spatial frequency varying stimulus. These results are consistent with the notion (see model predictions in appendix) that amblyopic neurons may be more broadly tuned for spatial frequency and therefore generate a BOLD response with less spatial frequency specificity. Our current psychophysically‐based model of amblyopia involves both binocular [Baker et al., 2007; Mansouri et al., 2008] and monocular neurons. It also involves signal attenuation and increased stochastic noise for amblyopic eye inputs [Baker et al., 2008], the combination of which may result in broader spatial tuning. The current experiment was conducted under monocular viewing and we postulate that more broadly tuned monocular cells contribute to the loss of spatial frequency preferences for voxels driven by the amblyopic eye. We cannot however rule out an explanation based on normally‐tuned cells with a more disordered arrangement with eccentricity within each voxel. However, the more broadly tuned single cell explanation does have neurophysiological support. Studies of strabismic animals have shown that neurons driven by the amblyopic eye are less selective for spatial frequency [Chino et al., 1983; Schmidt et al., 2004], although it has to be said that comparable psychophysical evidence [Hess and Campbell, 1980; Levi and Harwerth, 1982] on strabismic humans is lacking. However, in humans the methods are not only confined to detection threshold (here we use suprathreshold stimuli) but also they necessarily involve indirect measures, such as adaptation [Hess and Campbell, 1980] and masking [Levi and Harwerth, 1982] both of which are open to alternative network‐based interpretations [Meese and Holmes, 2007]. Whatever the cellular explanation, a more broadly‐tuned spatial frequency response for voxels driven by the amblyopic eye may be one reason why it has been so difficult, using fMRI, to demonstrate the selective high spatial frequency loss in amblyopia that is suggested by the psychophysical measurements of contrast sensitivity.

Regional involvement

Our results along with those of [Conner et al., 2007a] do not provide support for the suggestion that V1 and V2 are spared in humans with amblyopia as proposed by [Muckli et al., 2006]. However, in agreement with the results of [Li et al., 2007a], we do find that some individuals exhibit less involvement of V1 and sometimes V2, though this is not a typical finding. Reduced fMRI responses are typically seen in all retinotopic regions of extra‐striate cortex.

Inter‐subject variability

Because of the degree of inter‐subject variability, in the block design in experiment 1 we could not show a statistically significant reduction in the response from the amblyopic eyes as a group compared with the fellow fixing eyes as a group for either low or medium spatial frequency even though individuals within the group did display significant reductions with their amblyopic eye. This was true for the calculation of t values and for % BOLD, so it involves response variability as well as response amplitude. Previous studies have come to the same conclusion and have either compared amblyopic responses from amblyopes with dominant responses [Conner et al., 2007a; Li et al., 2007a from normals or have concentrated on the results of individuals [Barnes et al., 2001; Conner et al., 2007a; Li et al., 2007a; Muckli et al., 2006] rather than that of the group as a whole. The reason for the increased inter‐subject variability for fMRI is not known but our finding that that the spatial frequency selectivity is reduced for the response from the amblyopic eye provides a possible explanation. Even though the responses of individual amblyopic neurons may be reduced this could be offset by an enhanced recruitment of response across the amblyopic neural population due to broader tuning of individual amblyopic neurons.

To illustrate the phase‐locked dependency between BOLD responses and spatial frequency modulation of the stimulus as a function of receptive field spatial frequency bandwidth (i.e., narrow spatial frequency bandwidths exhibiting significant stimulus phase‐locked modulation compared to broad spatial frequency bandwidths), we conducted a simply linear filter analysis. The stimuli used for the spatial frequency mapping consisted of a sinusoidal checkerboard which was varied from 0.5 to 6.0 c/d, which should drive V1 neurons tuned to either vertical or horizontal orientations. For simplicity, we used only the vertical sinusoidal component of that checkerboard constructed in the spatial domain according to:

equation image (1)

with L representing the amplitude of luminance modulation (which was set to 0.5, thereby modulating between 0 and 1) from mean luminance (L m, which was set to 0.5), P representing the period or wavelength, and Inline graphic representing the phase of the sinusoidal modulation. For the current analysis, P was set to produce four sinusoidal gratings of 0.25, 0.5, 1.0, and 2.0 c/d. Using MATLAB (version R2007a) and accompanying Image and Signal Toolboxes (versions 5.4 and 6.7, respectively) each sinusoidal grating, S(x i, y), was in turn subjected to a discrete Fourier transform as follows:

equation image (2)

from which the amplitude spectrum, denoted as:

equation image (3)

was obtained. For filtering purposes, A(u,v) was shifted into polar coordinates, i.e., A(f, θ), where, f and θ represent frequency and orientation respectively. Each amplitude spectrum of each sinusoidal grating was then multiplied by log‐Gabor filters constructed in the Fourier domain:

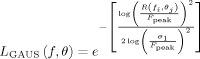equation image (4)

where f i and θj represent any given position in polar coordinates, R represents a given radius vector (i.e., the spatial frequency dimension) taken from A(f, θ), F peak is the central spatial frequency of the log‐Gaussian function, σ1 is the spatial frequency bandwidth of the log‐Gaussian function. The central frequency (F peak) was varied systematically from the lowest spatial frequency available to the highest, while the orientation bandwidth of the log‐Gabor function was fixed at 15° (full width at half height). Each A(f, θ) was multiplied by each log‐Gabor filter set to increasing values of F peak and the output summed. This process was carried out for two different spatial frequency bandwidth settings for the log‐Gabor filters, namely 1.0 and 2.5 octaves, with the outputs plotted in Figure 1A.

To simulate the relationship between the t statistic and the bandwidth of the log‐Gabor filter responses, stochastic noise was added to the log‐Gabor filter responses to the amplitude spectra of two of the gratings described above (0.25 and 0.5 c/d) by systematically varying the bandwidth of the log‐Gabor filters from 0.28 to 2.56 octaves and running independent t‐tests between the output distributions for the 0.25 and 0.5 c/d gratings. This simulation was repeated 50 times, averaged, and plotted in Figure 2A. 379:

Figure A1.

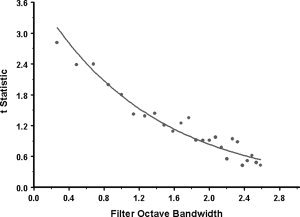
Figure A1

Open in a new tab

Model predictions. Plot showing a simulated relationship between the t values and log‐Gabor filter spatial frequency bandwidth (see the appendix and Fig. A2 of the appendix for more details).

Figure A2.

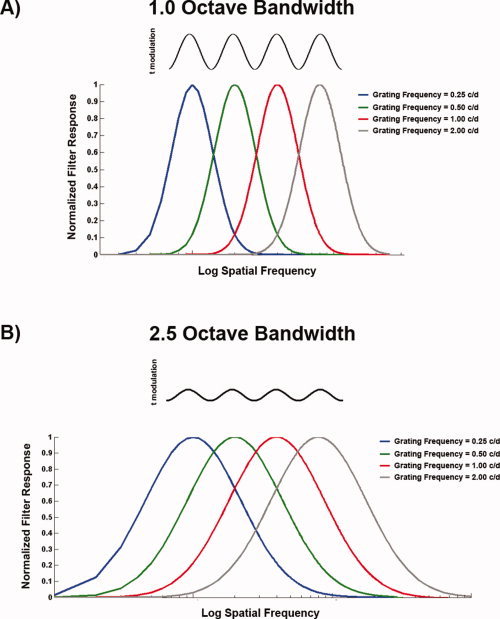
Figure A2

Open in a new tab

Model structure. (A) 1 octave Log‐Gabor filter responses for each of the four sinusoidal gratings described in the appendix. On the ordinate is normalized filter response and on the abscissa is log spatial frequency. Note the degree of overlap which would translate to significantly higher t statistic modulation, thereby increasing the ability to detect significant phaselocking. (B) Identical to (A), except for log‐Gabor filter responses with octave bandwidth set to 2.5. Note the high degree of response overlap which would translate to a lower t value amplitude modulation, thereby limiting the ability to detect significant phase‐locking. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

REFERENCES

  1. Aaen‐Stockdale C, Hess RF ( 2008): The amblyopic deficit for global motion is spatial scale invariant. Vision Res 48: 1965–1971. [DOI] [PubMed] [Google Scholar]
  2. Algaze A, Roberts C, Leguire L, Schmalbrock P, Rogers G ( 2002): Functional magnetic resonance imaging as a tool for investigating amblyopia in the human cortex: A pilot study. J AAPOPS 6: 300–308. [DOI] [PubMed] [Google Scholar]
  3. Anderson SA, Holliday IE, Harding GF ( 1999): Assessment of cortical dysfunction in human strabismic amblyopia using magnetoencephalography. Vision Res 39: 1723–1738. [DOI] [PubMed] [Google Scholar]
  4. Baker DH, Meese TS, Mansouri B, Hess RF ( 2007): Binocular summation of contrast remains intact in strabismic amblyopia. Invest Ophthalmol Vis Sci 48: 5332–5338. [DOI] [PubMed] [Google Scholar]
  5. Baker DH, Meese TS, Hess RF ( 2008): Contrast masking in strabismic amblyopia: Attenuation, noise, interocular suppression and binocular summation. Vision Res 48: 1625–1640. [DOI] [PubMed] [Google Scholar]
  6. Barnes GR, Hess RF, Dumoulin SO, Achtman RL, Pike GB ( 2001): The cortical deficit in humans with strabismic amblyopia. J Physiol (Lond) 533: 281–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Blakemore C, Eggers HM ( 1979): Animal models for human visual development In: Cool SJ, Smith EL, editors. Frontiers in Visual Science. New York: Springer‐Verlag; pp 651–659. [Google Scholar]
  8. Blakemore C, Vital‐Durand F ( 1992): Different neural origins for “blur” amblyopia and strabismic amblyopia. Ophthal Physiol Opt 12: 83. [Google Scholar]
  9. Chino YM, Shansky MS, Jankowski WL, Banser FA ( 1983): Effects of rearing kittens with convergent strabismus on development of receptive‐field properties in striate cortex neurons. J Neurophysiol 50: 265–286. [DOI] [PubMed] [Google Scholar]
  10. Choi MY, Lee KM, Hwang JM, Choi DG, Lee DS, Park KH, Yu YS ( 2001): Comparison between anisometropic and strabismic amblyopia using functional magnetic resonance imaging. Br J Ophthalmol 85: 1052–1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Collins DL, Neelin P, Peters TM, Evans AC ( 1994): Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. J Comput Assist Tomogr 18: 192–205. [PubMed] [Google Scholar]
  12. Conner IP, Odom JV, Schwartz TL, Mendola JD ( 2007a): Monocular activation of V1 and V2 in amblyopic adults measured with functional magnetic resonance imaging. J Aapos 11: 341–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Conner IP, Odom JV, Schwartz TL, Mendola JD ( 2007b): Retinotopic maps and foveal suppression in the visual cortex of amblyopic adults. J Physiol 583 ( Part 1): 159–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Crewther DP, Crewther SG ( 1990): Neural site of strabismic amblyopia in cats: Spatial frequency deficit in primary cortical neurons. Exp Brain Res 79: 615–622. [DOI] [PubMed] [Google Scholar]
  15. Demer JL ( 1997): Positron‐emisson tomographic study of human amblyopia with use of defined visual stimuli. J AAPOPS 1: 158–171. [DOI] [PubMed] [Google Scholar]
  16. Demer JL, von Noorden GK, Volkow ND, Gould KL ( 1988): Imaging of cerebral flow and metabolism in amblyopia by positron emission tomography. Am J Ophthalmol 105: 337–347. [DOI] [PubMed] [Google Scholar]
  17. Dumoulin SO, Hess RF ( 2006): Modulation of V1 activity by shape: Image‐statistics or shape‐based perception? J Neurophysiol 95: 3654–3664. [DOI] [PubMed] [Google Scholar]
  18. Dumoulin SO, Hoge RD, Achtman RL, Baker CL, Hess RF, Evans AC ( 2000): Volumetric retinotopic mapping without cortical surface reconstruction. NeuroImage 11: s613. [Google Scholar]
  19. Dumoulin SO, Hoge RD, Baker CL, Hess RF, Achtman RL, Evans AC ( 2003): Automatic volumetric segmentation of human visual retinotopic cortex. NeuroImage 18: 576–587. [DOI] [PubMed] [Google Scholar]
  20. Evans AC, Collins DL, Mills SR, Brown ED, Kelly RL, Peters TM ( 1993): 3D statistical neuroanatomical models from 305 MRI volumes Proc IEEE‐nuclear science symposium and medical imaging conference. pp. 1813–1817. [Google Scholar]
  21. Goodyear BG, Nicolle DA, Humphrey GK, Menon RS ( 2000): BOLD fMRI response of early visual areas to perceived contrast in human amblyopia. J. Neurophysiol 84: 1907–1913. [DOI] [PubMed] [Google Scholar]
  22. Gstalder RJ, Green DG ( 1971): Laser interferometric acuity in amblyopia. J Pediat Ophthalmol 8: 251–256. [Google Scholar]
  23. Harrad RA, Hess RF ( 1992): Binocular integration of contrast information in amblyopia. Vision Res 32: 135–2150. [DOI] [PubMed] [Google Scholar]
  24. Hess RF, Howell ER ( 1977): The threshold contrast sensitivity function in strabismic amblyopia: Evidence for a two type classification. Vision Res 17: 1049–1055. [DOI] [PubMed] [Google Scholar]
  25. Hess RF, Campbell FW ( 1980): A preliminary investigation of neural function and dysfunction in amblyopia—II. Activity within an amblyopic “channel.” Vision Res 20: 755–756. [DOI] [PubMed] [Google Scholar]
  26. Hess RF, Holliday IE ( 1992): The spatial localization deficit in amblyopia. Vision Res 32: 1319–1339. [DOI] [PubMed] [Google Scholar]
  27. Hess RF, Bradley A, Piotrowski L ( 1983): Contrast‐coding in amblyopia. I. Differences in the neural basis of human amblyopia. Proc R Soc Lond B Biol Sci 217: 309–330. [DOI] [PubMed] [Google Scholar]
  28. Hess RF, Wang Y‐Z, Demanins R, Wilkinson F, Wilson HR ( 1999): A deficit in strabismic amblyopia for global shape detection. Vision Res 39: 901–914. [DOI] [PubMed] [Google Scholar]
  29. Imamura K, Richter H, Lennerstrand G, Rydberg A, Andersson J, Schneider H, Watanabe Y, Langstrom B ( 1997): Reduced activity in the extra‐striate visual cortex of individuals with strabismic amblyopia. Neurosci Lett 225: 173–176. [DOI] [PubMed] [Google Scholar]
  30. Kabasakal L, Devranoglu K, Arslan O, Erdil TY, Sonmezoglu K, Uslu I, Tolunm H, Isitman AT, Ozker K, Onsel C ( 1995): Brain SPECT evaluation of the visual cortex in amblyopia. J Nucl Med 36: 1170–1174. [PubMed] [Google Scholar]
  31. Kim JS, Singh V, Lee JK, Lerch J, Ad‐Dab'bagh Y, MacDonald D, Lee JM, Kim SI, Evans AC ( 2005): Automated 3‐D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. NeuroImage 27: 210–221. [DOI] [PubMed] [Google Scholar]
  32. Kiorpes L, McKee SP ( 1999): Neural mechanisms underlying amblyopia. Curr Opin Neurobiol 9: 480–486. [DOI] [PubMed] [Google Scholar]
  33. Kiorpes L, Kiper DC, O'Keefe LP, Cavanaugh JR, Movshon JA ( 1998): Neuronal correlates of amblyopia in the visual cortex of macague monkeys with experimental strabismus and anisometropia. J Neurosci 18: 6411–6424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lee KM, Lee SH, Kim NY, Kim CY, Sohn JW, Choi MY, Choi DG, Hwang JM, Park KH, Lee DS, et al. ( 2001): Binocularity and spatial frequency dependence of calcarine activation in two types of amblyopia. Neurosci Res 40: 147–153. [DOI] [PubMed] [Google Scholar]
  35. Lerch JP, Evans AC ( 2005): Cortical thickness analysis examined through power analysis and a population simulation. NeuroImage 24: 163–173. [DOI] [PubMed] [Google Scholar]
  36. Levi DM ( 1991): Spatial vision in Amblyopia In: Regan D, editor. Vision and Visual Dysfunction. Boston: CRC Press; pp 212–238. [Google Scholar]
  37. Levi M, Harwerth RS ( 1977): Spatio‐temporal interactions in anisometropic and strabismic amblyopia. Invest Ophthalmol Vis Sci 16: 90–95. [PubMed] [Google Scholar]
  38. Levi DM, Harwerth RS ( 1982): Psychophysical mechanisms in humans with amblyopia. Am J Optom Physiol Opt 59: 936–951. [DOI] [PubMed] [Google Scholar]
  39. Li X, Dumoulin SO, Mansouri B, Hess RF ( 2007a): Cortical deficits in human amblyopia: Their regional distribution and their relationship to the contrast detection deficit. Invest Ophthal Vis Sci 48: 1575–1591. [DOI] [PubMed] [Google Scholar]
  40. Li X, Dumoulin SO, Mansouri B, Hess RF ( 2007b): The fidelity of the cortical retinotopic map in human amblyopia. Eur J Neurosci 25: 1265–1277. [DOI] [PubMed] [Google Scholar]
  41. MacDonald D, Kabani N, Avis D, Evans AC ( 2000): Automated 3‐D extraction of inner and outer surfaces of cerebral cortex from MRI. NeuroImage 12: 340–356. [DOI] [PubMed] [Google Scholar]
  42. Mansouri B, Allen HA, Hess RF ( 2005): Detection, discrimination and integration of second‐order orientation information in strabismic and anisometropic amblyopia. Vision Res 45: 2449–2460. [DOI] [PubMed] [Google Scholar]
  43. Mansouri B, Thompson B, Hess RF ( 2008): Measurement of suprathreshold binocular interactions in amblyopia. Vision Res 48: 2775–2784. [DOI] [PubMed] [Google Scholar]
  44. Meese TS, Holmes DJ ( 2007): Spatial and temporal dependencies of cross orientation suppression in human vision. Proc R Soc B 274: 127–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Movshon JA, Eggers HM, Gizzi MS, Hendrickson AE, Kiorpes L, Boothe RG ( 1987): Effects of early unilateral blur on the macaque's visual system. III. Physiological observations. J Neurosci 7: 1340–1351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Muckli L, Kiess S, Tonhausen N, Singer W, Goegel R, Sireteanu R ( 2006): Cerebral correlates of impaired grating perception in individual psychophysically assessed human amblyopes. Vision Res 46: 506–526. [DOI] [PubMed] [Google Scholar]
  47. Peirce JW, Taylor LJ ( 2006): Selective mechanisms for complex visual patterns revealed by adaptation. Neuroscience 141: 15–18. [DOI] [PubMed] [Google Scholar]
  48. Roelfsema PR, Koenig P, Engel AK, Sireteanu R, Singer W ( 1994): Reduced synchronization in the visual cortex of cats with strabismic amblyopia. Eur J Neurosci 6: 1645–1655. [DOI] [PubMed] [Google Scholar]
  49. Rosenbach O ( 1903): Ueber monokulare Vorherrschaft beim binikularen Sehen. Munchener Medizinische Wochenschriff 30: 1290–1292. [Google Scholar]
  50. Sasaki Y, Hadjikhani N, Fischl B, Liu AK, Marrett S, Dale AM, Tootell RB ( 2001): Local and global attention are mapped retinotopically in human occipital cortex. Proc Natl Acad Sci USA 98: 2077–2082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Schmidt KE, Singer W, Galuske RA ( 2004): Processing deficits in primary visual cortex of amblyopic cats. J Neurophysiol 91: 1661–1671. [DOI] [PubMed] [Google Scholar]
  52. Seber GAF, Lee AJ ( 2003): Linear Regression Analysis, 2nd ed Wiley‐Interscience; pp 97–118. [Google Scholar]
  53. Simmers AJ, Ledgeway T, Hess RF, McGraw PV ( 2003): Deficits to global motion processing in human amblyopia. Vision Res 43: 729–738. [DOI] [PubMed] [Google Scholar]
  54. Simmers AJ, Ledgeway T, Hess RF ( 2004): The influences of visibility and anomalous integration processes on the perception of global spatial form versus motion in human amblyopia. Vision Res 45: 449–460. [DOI] [PubMed] [Google Scholar]
  55. Simmers AJ, Ledgeway T, Hess RF ( 2005): The influences of visibility and anomalous integration processes on the perception of global spatial form versus motion in human amblyopia. Vision Res 45: 449–460. [DOI] [PubMed] [Google Scholar]
  56. Sled JG, Zijdenbos AP, Evans AC ( 1998): A non‐parametric method for automatic correction of intensity non‐uniformity in MRI data. IEEE Trans Med Image 17: 87–97. [DOI] [PubMed] [Google Scholar]
  57. Talairach J, Tournoux P ( 1988): Coplanar Stereotaxic Atlas of the Human Brain. New York: Thieme. [Google Scholar]
  58. Worsley KJ, Liao C, Aston J, Petre V, Duncan GH, Evans AC ( 2002): A general statistical analysis for fMRI data. NeuroImage 15: 1–15. [DOI] [PubMed] [Google Scholar]

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES