Abstract
We propose a novel cerebral source extraction method (functional source separation, FSS) starting from extra‐cephalic magnetoencephalographic (MEG) signals in humans. It is obtained by adding a functional constraint to the cost function of a basic independent component analysis (ICA) model, defined according to the specific experiment under study, and removing the orthogonality constraint, (i.e., in a single‐unit approach, skipping decorrelation of each new component from the subspace generated by the components already found). Source activity was obtained all along processing of a simple separate sensory stimulation of thumb, little finger, and median nerve. Being the sources obtained one by one in each stage applying different criteria, the a posteriori “interesting sources selection” step is avoided. The obtained solutions were in agreement with the homuncular organization in all subjects, neurophysiologically reacting properly and with negligible residual activity. On this basis, the separated sources were interpreted as satisfactorily describing highly superimposed and interconnected neural networks devoted to cortical finger representation. The proposed procedure significantly improves the quality of the extraction with respect to a standard BSS algorithm. Moreover, it is very flexible in including different functional constraints, providing a promising tool to identify neuronal networks in very general cerebral processing. Hum Brain Mapp, 2006. © 2006 Wiley‐Liss, Inc.
Keywords: blind source separation (BSS), functional constraint, magnetoencephalography (MEG), finger cortical representation
INTRODUCTION
Physiological activity in the brain can be evaluated by noninvasive techniques based on measurement of the electric or magnetic field generated by electrical neuronal currents (e.g., electroencephalogram [EEG]; magnetoencephalogram [MEG]). Such neurophysiological techniques, by allowing direct investigation of neuronal pool activity when at least part of the constituent cells fire synchronously, obtain measures with the same time resolution as the cerebral processing itself. The crucial problem is to gain access to the inner neural code starting from the extracranial recorded EEG and MEG raw signals: recorded cerebral signals related to significant activity are mixed and embedded in unstructured noise and in other physiological signals nonrelevant to the desired observation. The main approach has been, after applying procedures to enhance signal‐to‐noise ratio (e.g., stimulus‐related averaging) to solve the so‐called inverse problem, i.e., to use Maxwell's equations to calculate spatial distribution of the intracerebral currents starting from the magnetic or electric field detected in a wide enough area of the scalp surface. This problem does not permit a unique solution. For this reason, it is necessary to acquire supplementary information [Del Gratta et al., 2001], i.e., to define the parameters of the forward problem, to obtain position, intensity, and direction of the modeled cerebral currents (single and multiple dipoles [Scherg and Berg, 1991], music [Mosher et al., 1992], RAP music [Mosher and Leahy, 1999], minimum norm estimates [Hämäläinen and Ilmoniemi, 1994], low‐resolution brain electromagnetic tomography (LORETA) [Pascual‐Marqui et al., 1995], and synthetic aperture magnetometry (SAM) [Vrba and Robinson, 2001]. Currently, no universally accepted criteria exist to define adequate model except in very specific cases.
In the last decade, a different approach has been introduced in the MEG/EEG community, based on exploiting statistical properties of sources composed in the observed signals: extraction of information from such signals amounts to blind separation of sources in presence of noise and interferences. To tackle such a task, blind source separation (BSS) and particularly independent component analysis [ICA; Hyvärinen et al., 2001; Cichocki and Amari, 2002] were proposed.
ICA assumes that sources are statistically mutually independent; to extract them from the recorded mixture a measure of non‐Gaussianity is maximized (e.g., kurtosis) since, by means of the Central Limit Theorem, it has been shown that a linear transformation of the data that maximizes non‐Gaussianity leads to independence as well.
Several studies have proved its effectiveness in removing artifacts and extracting relevant activations from MEG and EEG signals [Barbati et al., 2004; Ikeda and Toyama, 2000; Makeig et al., 1996; Vigario et al., 2000; for up‐to‐date reviews see Cichocki, 2004; Choi and Cichocki, 2005; James and Hesse, 2005]. BSS and ICA algorithms do not solve the inverse problem but they estimate complete source time courses for task‐related features description and provide information that could be used to estimate the source position in a successive step.
A first challenging issue in BSS neurophysiologic applications is the choice of the contrast function used to extract sources: the non‐Gaussianity assumption in the ICA model and the imposition of an orthogonality constraint between extracted components (ICs) produce source estimates that are active during short time intervals with minimal overlap. The ICA technique therefore seems to be effective for separating neuronal signals corresponding to sources that exhibit burst behavior, coming from spatially distinct compact sources. The magnetic field patterns of these ICs are close to those produced by isolated current dipoles [Makeig et al., 2004; Moran et al., 2004]. In this way, ICA achieves both temporal and spatial separation of source activity and can significantly enhance imaging accuracy [Moran et al., 2004; Zhukov et al., 2000]. ICA, however, is insensitive to the time ordering of the data points; other BSS algorithms have been claimed recently as more suitable for cerebral source separation by exploiting second‐order statistics of the source signals to decompose the recorded mixture, e.g., minimizing a set of time‐lagged cross‐correlations [Tang et al., 2004]. At present, many different BSS packages are available, implementing both high‐order ICA algorithms and second‐order BSS techniques; validation of obtained results have to be investigated case by case.
A second key point in applications is how to assign the neurophysiological and neuroanatomical meaning and interpretation to the extracted sources, because often “interesting” characteristics are not separated effectively in a single component but can remain partially mixed or split into more than one component. Usually, a post‐extraction analysis of spectral and spatial IC properties is applied to select the relevant ones, leading to the definition of clusters of “similar” components with respect to some criteria [Himberg et al., 2004; Barbati et al., 2005; Makeig et al., 2004]. The necessity of this post‐processing is the consequence of the blindness of the approach, because BSS/ICA does not take information into account other than the statistics of the data. The advantage is the generality of the assumptions that make these techniques powerful and flexible tools with respect to hypothesis‐driven procedures, which are highly dependent on the accuracy of a predefined model/template.
Sometimes, however, quite accurate information on some parameters of the signals that we want to separate is known: for this reason semi‐blind ICA algorithms have been developed recently. In Papathanassiou and Petrou [2002], the prior knowledge of the autocorrelation function of a source is used to extract it first, using a gradient optimization scheme. In Lu and Rajapakse [2005], the authors proposed a constrained optimization by means of Lagrange multipliers; this algorithm (cICA) allowed accounting for rough knowledge of the time‐course of a functional magnetic resonance imaging (fMRI) source to extract it first. Similar results were obtained in Calhoun et al. [2005] where a semi‐blind ICA approach, derived from the INFOMAX algorithm [Bell and Sejnowski, 1995], was developed.
The Bayesian approach has been presented as a comprehensive theoretical framework for including prior knowledge about sources [Knuth, 1999]; a family of denoising source separation algorithms (DSS) has been introduced recently, ranging from almost blind to highly specialized source extraction, employing additional information [Särelä and Valpola, 2005].
On this route, some of the authors have developed a semi‐blind ICA algorithm that makes it possible to introduce different functions as constraint, allowing also nondifferentiable ones. This procedure has been demonstrated effective on artificial and real fMRI data [Valente et al., 2005].
In the present work, the procedure developed by Valente et al. [2005] is exploited to extract cerebral sources including directly in the separating algorithm information about neuronal activation properties. To assess the efficiency of the approach, a very simple experiment was considered: MEG cerebral activity was recorded during separate little finger, thumb, and median nerve galvanic stimulation. To extract sources corresponding to single finger cortical representation during different activation states, a proper functional constraint was introduced within the separating algorithm and applied to data recorded during the alternated stimulation of thumb, little finger, and median nerve. A further step was then made, removing the orthogonality constraint. In fact, in the specific and restricted cortical region of interest, neural networks are highly spatially interconnected and superimposed and temporal overlap of finger sources activation could be reasonably hypothesized, particularly during nerve stimulation.
Both the proposed separating algorithm versions, defined respectively as functional component analysis (FCA, the orthogonal one) and functional source separation (FSS, the non‐orthogonal) were compared to a standard ICA algorithm [fastICA; Hyvärinen et al., 2001]. Performances were judged based on the extracted sources spatial positions and functional activation properties during the three different stimuli.
MATERIALS AND METHODS
Experimental Setup
Fifteen healthy volunteers (mean age, 31 ± 2 years, seven females and eight males) were enrolled for the study.
Somatosensory evoked fields (SEFs) were carried out in analogy with standard and widely accepted procedures [Hari et al., 1984]. In brief, measurements were performed inside a magnetically shielded room (Vacuumschmeltze GmBH), using a 28‐channel system [Foglietti et al., 1991; Tecchio et al., 1997], the active channels being distributed regularly on a spherical surface (13.5 cm of curvature radius; out of 28 channels, three channels were balancing magnetometers devoted to noise reduction) and covering a total area of about 180 cm2. The noise spectral density of each magnetic sensor was 5–7
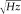 at 1 Hz.
at 1 Hz.
The right little finger, thumb, and median nerve at wrist were separately stimulated for three minutes by 0.2‐msec electric pulses, with an interstimulus interval of 631 msec. Intensities were set at about twice the subjective threshold of perception for fingers (via ring electrodes) and just above motor threshold, i.e., thumb twitch, for the nerve at the wrist (via surface disks). Brain magnetic fields were recorded via a single positioning on the hemisphere contralateral to the stimulated side, by centering the recording apparatus over the C3 site of the International 10–20 electroencephalographic system.
The entire MEG procedure (preparation and recording) lasted about 30 min; subjects had signed an informed consent and the experimental protocol followed the standard ethical directives of the declaration of Helsinki.
Data were filtered through a 0.16–250‐Hz bandpass and gathered at 1,000‐Hz sampling rate for offline processing, resulting for each subject in a data matrix of size 25 × 540,000 points.
ICA with Prior Information
ICA applies to blind decomposition of a set of signals X that is assumed to be obtained as a linear combination (through an unknown mixing matrix A) of statistically independent non‐Gaussian sources S:
| (1) |
Sources S are estimated (up to arbitrary scaling and permutation) by independent components Y as:
| (2) |
where the unmixing matrix W is to be estimated along with the ICs.
Of course, the decomposition problem (equation 2) has more unknowns that equations, so that the estimation relies on additional information, namely the statistical independence of sources. ICA can therefore be viewed as an optimization process that maximizes independence as described indirectly by a suitable contrast function.
Biomedical signals can often be assumed as generated through a linear mixing process as equation (1), where independent sources are supposed to model activities (of the brain in this case) that originate from separate causes. In fact, strict independence of such sources is probably in many cases unrealistic, but using such hypothesis has proved very effective in many contexts, even if a posteriori we may observe that perfect independence is never achieved.
In Valente et al. [2005], a modified ICA procedure has been proposed that explicitly uses additional information to bias the decomposition algorithm towards solutions that satisfy physiological assumptions, instead of extracting sources only based on their signal's statistical independence. The method is based on optimizing a modified contrast function:
| (3) |
where J can be any function normally used for ICA (in our case kurtosis), whereas H accounts for the prior information we have on sources. Parameter λ is used to weigh the two parts of the contrast function. If λ is set to zero, maximization of F leads to pure independence. The optimization is performed by simulated annealing [Kirkpatrick et al., 1983] so that function H can have any form (e.g., it does not need to be differentiable). Performance of the algorithm can be in general quite sensitive to the choice of λ, as the optimization is driven by different criteria and one of the two might prevail excessively (multiobjective optimization). For this reason, it is often useful to choose a saturating H function that is active only in an appropriate vicinity of good solutions. Such strategy actually amounts to performing constrained optimization, where H imposes a restriction to a region of search space where J is optimized freely. Further details on the implemented version of the simulated annealing optimization are given in Appendix A.
Functional Constraints
To identify neural networks devoted to individual finger central representation, the reactivity to the stimuli was taken into account. It was defined as follows: the evoked activity (EA) was computed separately for the three sensorial stimulations by averaging signal epochs centered on the corresponding stimulus (EAL, little finger; EAT, thumb; EAM, median nerve).
The reactivity coefficient (Rstim) was then computed as:
| (4) |
with stim = T, L, M and t = 0 corresponding to the stimulus arrival. The time interval ranging from 20 to 40 msec includes the maximum activation [Allison et al., 1980; Tecchio et al., 1997] and the baseline (no response) was computed in the prestimulus time interval (−30 to −10 msec). The constraint function Hstim is then chosen as:
| (5) |
where
| (6) |
and k is a suitable parameter measuring the required minimum response. In the present application we chose k and λ heuristically, based respectively on subject data characteristics and a preliminary study on a test case. Parameter settings depend on the specific experimental set up; however, the procedure can be made automatic, as discussed in Appendix B. The shape of function ϕ is such that the constraint is inactive when response is greater than k, so as to define an admissible region where the optimization is only driven by J. Where response is smaller, if λ is large enough, Hstim dominates the search. A constrained optimization procedure therefore is obtained. To estimate the time behavior of the neural networks devoted to the two finger cortical representations during different activation states, each functional source was extracted using data along the entire recording period, alternating the two fingers and median nerve separate stimulation. Details on the parameter settings and algorithm performance are given in Appendix B.
Orthogonal (FCA) and Non‐Orthogonal (FSS) Source Extraction
To separate contributions representing individual fingers, the proposed FCA procedure was applied as follows: first, a single component was extracted using the constraint HL and obtaining the functional component describing the time evolution of the little finger cortical representation: FCL. After projecting residuals on the orthogonal space with respect to the extracted component, the procedure was repeated using HT to obtain FCT, the functional component describing the thumb source, as independent as possible with respect to the little finger source. This constraint sequence was motivated by the fact that thumb representation is physiologically larger than is the little finger one. By operating in this way, we therefore meant to favor extraction of the naturally weaker component first. Operating in reverse order, the little finger component could not be extracted satisfactorily, because the orthogonalization almost cancelled it.
Based on this experience, which shows that relevant components are not independent (and in particular not uncorrelated) in the second version of the proposed algorithm FSS, the procedure was repeated identically but the orthogonalization step was skipped, producing a non‐orthogonal functional source estimate for the thumb identification (FST). The little finger source FSL is virtually identical to FCL. In this case, the order of extraction is not significant because the procedure is applied each time to the original data. The non‐orthogonal approach has already been introduced in the BSS literature [Inki and Hyvärinen, 2002; Yeredor, 2002; Ziehe et al., 2004], both from a theoretical point of view to generalize joint diagonalization procedures to the case of a non‐orthogonal diagonalization matrix, and in applications, particularly in image modeling, to estimate overcomplete ICA bases (i.e., when the number of sources is greater than number of mixtures); in a deflationary extraction scheme, after the estimation of a component, the successive IC is searched in a space that is “quasi‐orthogonal” to the initial one. In the present work, the non‐orthogonal version of the procedure has been implemented according to considerations about the nature of the neural network under study; it is well known that finger sources are highly interconnected spatially and superimposed.
Results obtained by FCA and FSS were compared with ICs estimated by a widely used separating ICA algorithm (fastICA, freely available at http://www.cis.hut.fi/projects/ica/fastica/).
Source Localization and Activity Extraction Comparisons
As a main criterion to evaluate the goodness of extracted components in representing individual fingers, we observed their spatial position. To this aim, sources representing little finger (FCL; FSL) and thumb (FCT; FST) were separately retroprojected, so as to obtain their field distribution, as follows:
| (7) |
where as is the estimated mixing vector (column of matrix A) for the functional source ys (y = FS, FC, IC; s = T, L) and MEG_recs are the retro‐projection on the sensor channels of the estimated ys source.
A moving equivalent current dipole (ECD) model inside a homogeneous best‐fitted sphere was used. ECD coordinates were expressed in a right‐handed Cartesian coordinate system defined based on three anatomical landmarks (x‐axis passing through the two preauricolar points directed rightward, the positive y‐axis passing through the nasion, the positive z‐axis is consequently defined). Only sources with a goodness‐of‐fit exceeding 80% were accepted. The field distribution obtained by retro‐projecting only one component is time invariant up to a scale factor; consequently, the subtending current distribution (ECD position in our case) is time‐independent. The same retro‐projection was performed also for all the fastICA estimated components. To have a benchmark for finger somatosensory source position, known markers of signal arrival in the primary sensory cortex, occurring at around 20 and 30 msec from the stimulus (M20, M30 [Allison et al., 1991; Hari and Kaukoranta, 1985; Tecchio et al., 1997]), were calculated by standard procedure of averaging original MEG channel signals and computing corresponding ECDs.
General linear models (GLM) for repeated measures were estimated to test for differences in source localization and source reactivity across subjects: as dependent variables respectively, the 3‐D coordinates vectors (x, y, z) and 3‐D reactivity vectors (RT, RL, RM) were used, with the two levels Finger (thumb, little finger) as within‐subjects factor. Because FSL and FCL are practically identical, only FSL has been considered in the statistical analysis.
To check for the level of residual response to the stimulation after sources extraction, we defined a “discrepancy response” index as follows:
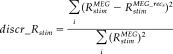 |
(8) |
where, as defined in equation (4), Rstim MEG is the reactivity index computed on MEG data during finger stimulation (stim = L, T) and Rstim is the reactivity index of reconstructed MEG data with the s finger source (s = L, T) during its corresponding stimulation; the index i runs upon the four channels of minimal and maximal amplitude at M20 and M30 latencies. In fact, the dipolar field distribution generated at these peak latencies are well described by their minimum/maximum values [Tecchio et al., 2005]. Obtained indices for little finger and thumb (discr_RL; discr_RT) were computed and compared between the proposed FCA/FSS procedures and fastICA.
Basic ICA Model Features Comparison: Non‐Gaussianity and Basis Vectors Angles
As the proposed procedures include in the cost function physiological constraints, it is interesting to evaluate the trade‐off between non‐Gaussianity maximization and the introduced constrained optimization. For this reason, kurtosis values of the FCA, FSS sources, and the corresponding fastICA components across subjects were compared.
In this way, we could also evaluate how the functional characteristics of the estimated sources, summarized by the constraints, go with the non‐Gaussianity assumption of the basic ICA model.
Moreover, as FSS leaves out the basis vector orthogonality, the angles between FSL and FST basis vectors were evaluated as an additional indication that the algorithm did not estimate several times the same components.
RESULTS AND DISCUSSION
Source Localization
Dipole coordinates (x, y, z) were computed from the retro‐projected FCA and FSS components in our 15‐subject group. We have to note that in four subjects localization of the retro‐projected FCT was not possible (variance explained <0.8, dipole not accepted); instead, localization of the retro‐projected FST was acceptable for all examined subjects (Table I).
Table I.
Spatial and reactivity components characteristics
| Sources | Successful cases | Explained variance | Position (mm) | Reactivity | ||||
|---|---|---|---|---|---|---|---|---|
| x | y | z | RL | RT | RM | |||
| FSS | ||||||||
| FSL | 15 | 0.95 ± 0.04 | −33 ± 10 | 6 ± 12 | 99 ± 14 | 12.7 ± 4.9 | 7.7 ± 5.6 | 18.8 ± 12 |
| FST | 15 | 0.97 ± 0.03 | −38 ± 10 | 10 ± 13 | 90 ± 10 | 6.3 ± 5.1 | 13.4 ± 4.8 | 18.3 ± 12.6 |
| FCA | ||||||||
| FCL | 15 | 0.95 ± 0.04 | −33 ± 10 | 5 ± 12 | 99 ± 13 | 12.7 ± 4.9 | 7.7 ± 5.5 | 18.9 ± 12 |
| FCT | 11 | 0.95 ± 0.05 | −41 ± 10 | 11 ± 12 | 87 ± 11 | 1.2 ± 0.8 | 10.7 ± 3.1 | 10.0 ± 6.0 |
| fastICA | ||||||||
| ICL | 6 | 0.96 ± 0.04 | −36 ± 12 | 9 ± 23 | 96 ± 11 | 7.5 ± 5.9 | 4.4 ± 5.1 | 11.4 ± 11.3 |
| ICT | 6 | 0.95 ± 0.03 | −41 ± 14 | 16 ± 43 | 79 ± 20 | 2.5 ± 3.9 | 6.3 ± 2.7 | 11.1 ± 14.2 |
| ICT;L | 9 | 0.93 ± 0.08 | −39 ± 13 | 7 ± 10 | 97 ± 12 | 7.9 ± 3.7 | 7.3 ± 5.1 | 16.7 ± 16.6 |
| MEG data | ||||||||
| M20L | 12 | 0.94 ± 0.06 | −34 ± 9 | 7 ± 14 | 99 ± 9 | |||
| M20T | 15 | 0.96 ± 0.02 | −42 ± 8 | 11 ± 11 | 91 ± 10 | |||
| M30L | 11 | 0.97 ± 0.02 | −31 ± 8 | 4 ± 10 | 97 ± 9 | |||
| M30T | 12 | 0.97 ± 0.03 | −33 ± 8 | 6 ± 13 | 89 ± 12 | |||
Values are mean ± SD. Successful cases, number of subjects with successful localizations (>80%); Position, coordinates of ECDs; Reactivity, sources reactivity indexes to the three stimulations RL, RT, RM, pure numbers. M20L, M20T, M30L, M30T positions computed on MEG data are reported for comparison.
Factor Finger resulted significant in FSL versus FCT and versus FST (Table II), corresponding in both cases to the estimated thumb source significantly lateral, anterior, and lower with respect to the little finger source, in agreement with the well‐known homuncular finger somatotopy. The same relative positions were found with M20 and M30 ECD when stimulating thumb and little finger, respectively (Tables I, II).
Table II.
Statistical analysis on source positions and reactivity
| Subjects | Position (mm) | P | Reactivity | P | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sources | x | y | z | RL | RT | RM | ||||
| FSL (FCL) | FCT | 11 | 6 ± 12 | −4 ± 14 | 14 ± 9 | 0.002 | 10.8 ± 4.8 | −5.1 ± 3.9 | 5.8 ± 11.1 | <0.0001 |
| FST | 15 | 5 ± 13 | −4 ± 14 | 9 ± 12 | 0.003 | 6.3 ± 4.1 | −5.7 ± 3 | 0.4 ± 6.2 | <0.0001 | |
| ICL | ICT | 6 | 5 ± 17 | −7 ± 37 | 18 ± 21 | 0.2 | 5 ± 4.9 | −1.8 ± 7 | 0.3 ± 19 | >0.5 |
| ICT;L | ICT a | 9;6 | 2 ± 7 | −9 ± 14 | 18 ± 8 | >0.1 | 5.3 ± 2.3 | 1.1 ± 2.5 | 5.6 ± 7.7 | >0.1 |
| ICL a | 9;6 | 3 ± 7 | −2 ± 14 | 0 ± 8 | >0.1 | 0.4 ± 2.3 | 2.9 ± 2.4 | 5.3 ± 7.7 | >0.1 | |
| M20L | M20T | 12 | 9 ± 8 | −2 ± 13 | 9 ± 8 | 0.001 | ||||
| M30L | M30T | 11 | 3 ± 5 | 0 ± 11 | 10 ± 8 | 0.03 | ||||
Values are mean ± SD differences in sources ECDs coordinates and evoked activity indexes RT, RL and RM. Difference in position for M20L versus M20T and M30L versus M30T are also reported. Results of GLM models evaluating contrasts between sources in position and reactivity across subjects are summarized in the corresponding P value columns (Pillai's trace within‐subject effect).
Indicates different groups of subjects tested in the fastICA case (ANOVA test with Bonferroni correction for multiple comparisons).
Components obtained by fastICA failed in more than half of cases (9 of 15) to separate thumb (ICT) and little finger (ICL) response: in those cases a unique IC was selected that responded best to both stimulations and localized with more than 80% of variance explained (ICT;L, Table I). Testing the 6 subjects for whom thumb and little finger response was separated by fastICA, factor Finger was not significant at the standard threshold P value of 0.05. Moreover, dipole coordinates of the retro‐projected mixed source corresponding to ICT;L with respect to ICL and ICT were not significantly different (using Bonferroni post‐hoc comparisons, all P values were greater than 0.05, Table II).
Due to a very poor signal to noise ratio in 3 cases, where a noise reduction preprocessing algorithm should have been applied in addition to standard average in the localization procedure, localization of M20 component was unsuccessful. On the other hand, FSS algorithm source positions were successfully determined for all 15 examined subjects, even in the cases of very noisy data. Moreover, it could be noted that FSL and FST lie in‐between their respective M20 and M30 positions (Table I, Fig. 1), in agreement with the constraint time window definition (see equation 4), which includes both M20 and M30 latencies.
Figure 1.
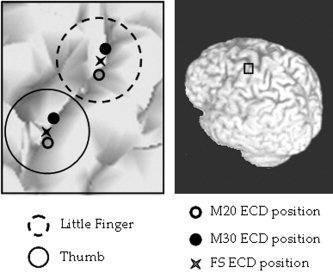
Position in one representative subject of thumb (solid circle area) and little finger (dotted circle area) sources. Positions of M20 (empty circle), M30 (filled circle) and the extracted source with the FSS procedure (star) are shown. It can be noted the in‐between position of the estimated functional source with respect to its corresponding M20 and M30 ECDs.
Activity Extraction Comparisons
Source reactivity
The activity of the source representing a finger is compared when stimulating the finger itself with respect to when the other finger or the median nerve is stimulated. To do this, the above‐defined indexes RL, RT and RM describing, respectively, the responsiveness to little finger, thumb and median nerve stimulation, were all considered for each of the three estimated functional components (FSL, FCT, and FST) and for the selected fastICA ones (ICL, ICT, and ICT;L, Table I).
Factor Finger resulted significant in FCL versus FCT in the corresponding stimulation periods, indicating a lower response of the FCL with respect to FCT during thumb stimulation and a higher response of the FCL with respect to FCT during little finger stimulation. The same behavior was observed in comparing FSL versus FST (Table II, Fig. 2), as expected. A significant difference between the two methods emerged when considering the contrasts between reactivity levels in RM versus RT respectively for FCT and FST: only in this latter a higher evoked activity to the median nerve stimulation with respect to the thumb stimulation itself was present, in agreement with the physiology of the hand innervation (paired t test, for FST P = 0.04; for FCT P = 0.68). In fact, it is well known that stimulating directly a nerve, all the proprioceptive and the superficial perception fibers of innervated districts are recruited; therefore, the cerebral source representing the thumb, innervated by the median nerve, is expected to be more reactive to the stimulation of this nerve with respect to the cutaneous stimulation obtained by ring electrodes. Moreover, median nerve stimulation over the motor threshold induces a partial stimulation of the ulnar nerve (innervating the little finger) and consequently of the little finger proprioceptive and superficial perception fibers. For this reason, it is not surprising that a higher reactivity to the median nerve stimulation was also found for FSL (RM versus RL; paired t test P = 0.02).
Figure 2.
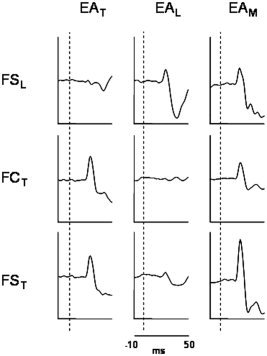
Temporal evoked activity of the extracted finger sources (little finger and thumb) by the two proposed procedures (FCA: FCL = FSL, FCT; FSS: FSL, FST) during the stimulation of thumb (EAT), little finger (EAL), and median nerve (EAM) for one subject. To be noted the selective reactivity of each finger source to the respective finger stimulation; moreover, the FST reaction to the median nerve stimulation was even higher than to the stimulation of the thumb itself.
Testing the six subjects with finger sources separated by fastICA, factor Finger resulted globally not significant, with similar reactivity levels for the two sources across different stimulations. In addition, testing the mixed source ICT;L versus ICT and ICL, no significant differences in reactivity were detected (Table II).
Residual response levels evaluation
The level of residual finger response to the corresponding stimulation after sources extraction (i.e., the discrepancy response indices distribution values across subjects: discr_RL and discr_RT, see equation [8]) was investigated. This comparison has been made in terms of relative performance between the three algorithms tested. Discrepancy reactivity was significantly lower for the FSS procedure with respect to both its orthogonal version FCA and fastICA, indicating the more satisfactory performance of the FSS procedure in extracting activity of interest; instead, no significant difference in discr_RT mean values was found between FCA and fastICA (Table III). Low mean discrepancy reactivity values for FSS (6% of residual response for the little finger and 3% for the thumb with respect to the original averaged MEG data) indicate that the two extracted finger sources described practically all the evoked response contained in the original data matrix.
Table III.
Discrepancy response levels
| Method | discr_R L | discr_R T | Contrast | P | |
|---|---|---|---|---|---|
| discr_R L | discr_R T | ||||
| FCA | 0.06 ± 0.07 | 0.22 ± 0.21 | FCA vs. FSS | — | 0.04 |
| FSS | 0.06 ± 0.07 | 0.03 ± 0.04 | FCA vs. fastICA | 0.004 | 0.3 |
| fastICA | 0.28 ± 0.27 | 0.32 ± 0.28 | FSS vs. fastICA | 0.004 | 0.001 |
Mean ± SD for the two finger discrepancy indices in the three considered algorithms are reported. Results of ANOVA test (with Bonferroni correction for multiple comparisons in the thumb case) are summarized for the corresponding contrast in the P value columns.
Basic ICA Model Features Comparison
Non‐Gaussianity
When comparing kurtosis values between FCA and FSS finger sources with respect to the fastICA ones, we found that kurtosis was significantly higher for fastICA than for FCA and FSS, and that these last two were not significantly different (FCA versus fastICA, P = 0.03; FSS versus fastICA, P = 0.01; FCA versus FSS, P = 0.8; Bonferroni‐corrected multiple comparisons). This result was not surprising, due to the introduction of the functional constraint in FCA and FSS in addition to the kurtosis maximization. An interesting finding has been obtained when comparing kurtosis values between finger sources and residual components for FCA versus fastICA. For FCA, residual components are defined as all the components extracted orthogonally to the first two, without activating the functional constraints (λ = 0). For fastICA, they are defined as the remaining ICs, having removed ICL, ICT and ICT;L. From both methods the components with abnormal kurtosis values, marked as artefacts, were removed [Barbati et al., 2004]. In both cases, kurtosis values were significantly higher for the finger sources than for the residual components (FCA, P = 0.01; fastICA, P < 0.0001), indicating that higher kurtosis values are associated with functional source properties. We could not make this check between sources and noise for the FSS procedure, because without imposing the functional constraints and without the orthogonality condition, no further source extraction was feasible after the first two.
Basis vector angles
As an additional indication that FSS algorithm did not estimate several times the same components, due to the absence of the orthogonality constraint, the angles between basis vectors couples of FSLs and FST were computed across subjects. The median angle obtained (63 degrees), the interquartile range of this distribution (42–79 degrees), and the minimum at 25 degrees, indicated that the great majority of these angles were quite large, i.e., a difference in basis vectors was obtained even in absence of the orthogonality constraint.
CONCLUSIONS
In the present work, a functional source separation (FSS) technique has been introduced in the context of neurophysiologic applications using MEG recordings. Adding to a kurtosis‐based cost function physiological constraints defined on the expected temporal behavior of cerebral sources of interest, we exploited in the proposed extraction procedure information both about the source statistical distribution (time‐independent) and the temporal structure of the cerebral activity.
It has been demonstrated how addition of appropriate information to a separating algorithm and the removal of the orthogonality constraint allow distinguishing more satisfactorily activity from neural networks devoted to individual finger representation with respect to a standard ICA algorithm. In fact, the proposed procedure proved able to extract in all cases somatotopically consistent sources. Moreover, by removing the orthogonality constraint, the obtained source has been proved to express more physiologically plausible activation properties with respect to their orthogonal version and a standard ICA model. The provided sources are suitable to describe ongoing activity time courses, which allows for example trial‐by‐trial analysis, instead of describing the activations by averaging all sensor channels and only in specific instances, as usually done in the standard procedures. The obtained activation properties highlight the ability of the extracted sources in describing complex and interconnected cerebral networks. Nonetheless, the FSS procedure was characterized by minimal residual activity.
The proposed approach, consisting of a sequential estimation, with sources obtained one‐by‐one in each stage applying different criteria, is very useful also from another point of view: extracting different components with defined required properties leaves out the problematic and subjective step of a posteriori identification and classification of estimated components.
In summary, the proposed FSS approach, by adding functional constraints to standard ICA and not requiring orthogonality between extracted sources, provided solutions always correctly positioned, reacting properly neurophysiologically and with negligible residual activity. This procedure is very flexible in including different functional constraints, providing a promising tool to identify neuronal networks in very general cerebral processing.
Acknowledgements
We thank Professor GianLuca Romani, Professor Vittorio Pizzella, Dr. Patrizio Pasqualetti, and TNFP Matilde Ercolani for their continuous support.
APPENDIX A.
Simulated Annealing
Simulated annealing (SA) is a well known global optimization technique [Kirkpatrick et al., 1983] inspired to statistical mechanics. It simulates the behavior of a liquid that freezes slowly: if the process is slow enough, it will be possible to create crystals in the structure (minimum energy configuration). Starting from these principles, it is possible to optimize by SA almost any kind of contrast function, because it does not require the knowledge of its derivatives. The optimization process is based on the perturbation of a given solution, according to the concepts of temperature, statistical equilibrium and probabilistic acceptance.
Consider the problem of maximizing S(w) and choose a starting solution (state) w1. Let S1 = S(w1). A new state w2 is generated perturbing w1 by means of a suitable rule and the value S2 = S(w2) is evaluated. If S2>S1 the new solution w2 is accepted, while if S1>S2 it is accepted with probability p=min{1,exp(−(S1−S2)/T)}, where T is the control parameter called Temperature (according to the physical formulation). Accepting the new solution means that the system moves to the new state w2. At large values of T, the probability p of accepting less‐optimal (lower S) solutions will be high; as the temperature decreases, the system will accept fewer such solutions. The optimization is carried out following this scheme: the system starts at a high temperature (such that most of the perturbations will be accepted anyway) and at that temperature, it generates a number of states such that the statistical equilibrium is reached.
Subsequently, the temperature is decreased according to an appropriate criterion (cooling schedule), and the procedure continues as before until a suitable stopping criterion halts the process. If the cooling schedule is slow enough (logarithmic), the algorithm is statistically guaranteed to reach a global optimum (with probability 1). Such theoretically correct cooling schedule is too slow to be applied in practice, however, so that normally a geometric schedule is applied.
SA optimization has two advantages over traditional techniques (such as gradient‐based): it does not require the use of derivatives and, if properly set, it reaches the global maximum. Although it is considerably slower if compared with those techniques, in the present application this is not a relevant drawback, because only a limited number of components have to be extracted. In fact, in this work emphasis has been placed on proving effectiveness of the constrained optimization approach, and to evaluate different options we privileged flexibility of the algorithm on the choice of constraint function over speed.
In the present application, we whitened data and for each functional constraint we started from an initial random w unmixing coefficients vector (equation [2]) and the contrast function in equation (3) was maximized by perturbing w. An optimal wopt was found at the end of the optimization process and the corresponding source was recovered from it. We implemented a decrease rate for the temperature, such that Tt+1=Ttα, with α = 0.7. The algorithm terminated when, comparing the optimal solutions at two consecutive temperatures, the norm of the difference of the unmixing coefficients w (or of the sum, because both w and −w correspond to the same source) was under a fixed threshold (ε = 10−4). We implemented a procedure to automatically set the initial temperature T0. Starting from a random initial temperature TR, we kept trace of the number of accepted (A) and rejected (R) state transitions. The ratio ρ = A/(A + R) was computed after the system had reached the equilibrium, and the following criterion to set up the starting temperature T0 was used: if ρ < 0.8, the system was not warm enough and the optimization could be not reliable, then we set TR = 1.5TR. If ρ > 0.9 the system was considered too warm and the optimization may take more time than needed, then TR = 0.9TR; if 0.8 ≤ ρ ≤ 0.9, then T0 = TR. In this way, the optimization does not need further temperature set up even when parameters λ and k are changed, because the optimal starting temperature is estimated according to the used dataset and the specific contrast function.
APPENDIX B.
Parameter Settings and Execution Time
In this appendix we specify how the values of parameters λ and k have been determined in the present application. Information about dimension of the data and the average execution time are given at the end of this section.
-
a1
A preliminary standard ICA extraction is made, setting λ = 0; it is equivalent to maximize only the independence constraint (kurtosis).
-
a2
Kurtosis values and Rstim (stim = T,L; as defined in equation [4]) of all extracted components are evaluated. After applying a switching system to remove artifacts (resulting for example in very extreme kurtotic components [Barbati et al., 2004]), the maximum values of kurtosis and Rstim are selected among the retained components. To set k values, the initial steps (a1) and (a2) have been performed for each subject, and corresponding maximum Rstim values obtained have been assigned as initial k values in the FCA and FSS algorithms.
-
a3
λ is fixed so as to make the functional constraint (λ*Hstim) approximately three orders of magnitude greater than kurtosis (J).
The result of the λ setting procedure has been observed to be quite general and suitable for all examined subjects, because the algorithm showed low sensitivity to this parameter; therefore, in our experimental setting the same value was used in all cases: λ = 1,000.
The size of the data matrices was 25 rows × 540,000 time points for each subject; the general calculator characteristics were a CPU of 3.2 GHz with 1.0 GB RAM. The average execution time over the extractions for the thumb source resulted 114 sec. and for the little finger source, 105 sec. The fastICA average execution time to extract all components was about 192 sec.
REFERENCES
- Allison T, Goff WR, Williamson PD, Vangilder G. 1980. On the neural origin of the early components of the human somatosensory evoked potentials In: Desmedt JD, editor. Progress in clinical neurophysiology. Karger: Basel; p 51–68. [Google Scholar]
- Allison T, McCarthy G, Wood CC, Jones SJ (1991): Potentials evoked in human and monkey cerebral cortex by stimulation of the median nerve. A review of scalp and intracranial recordings. Brain 114: 2465–2503. [DOI] [PubMed] [Google Scholar]
- Barbati G, Porcaro C, Zappasodi F, Rossini PM, Tecchio F (2004): Optimization of ICA approach for artifact identification and removal in MEG signals. Clin Neurophysiol 115: 1220–1232. [DOI] [PubMed] [Google Scholar]
- Barbati G, Porcaro C, Zappasodi F, Tecchio F (2005): An ICA approach to detect functionally different intra‐regional neuronal signals in MEG data In: Computational Intelligence and Bioinspired Systems Lecture Notes in Computer Science (LNCS 3512). p 1083–1090 IWANN ‘05, Barcelona (Spain). [Google Scholar]
- Bell AJ, Sejnowski TJ (1995): An information‐maximization approach to blind separation and blind deconvolution. Neural Comput 7: 1129–1159. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Stevens MC, Kiehl KA, Pekar JJ (2005): Semi‐blind ICA of fMRI: a method for utilizing hypothesis‐derived time courses in spatial ICA analysis. Neuroimage 25: 527–538. [DOI] [PubMed] [Google Scholar]
- Choi S, Cichocki A (2005): Blind source separation and independent component analysis: a review. Neural Inform Process 6: 1–57. [Google Scholar]
- Cichocki A (2004): Blind signal processing methods for analyzing multichannel brain signals. Int J Bioelectromagn 6: 1. [Google Scholar]
- Cichocki A, Amari SI (2002): Adaptive blind signal and image processing. Chichester: John Wiley and Sons. [Google Scholar]
- Del Gratta C, Pizzella V, Tecchio F, Romani GL (2001): Magnetoencephalography–a non invasive brain imaging method with 1 ms time resolution. Rep Prog Phys, 64: 1759–1814. [Google Scholar]
- Foglietti V, Del Gratta C, Pasquarelli A, Pizzella V, Torrioli G, Romani GL, Gallagher W, Ketchen MB, Kleinasser AW, Sandrom RL (1991): 28‐channel hybrid system for neuro‐magnetic measurements. IEEE Trans MG 27: 2959–2962. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Ilmoniemi RJ (1994): Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput 32: 35–42. [DOI] [PubMed] [Google Scholar]
- Hari R, Kaukoranta E (1985): Neuromagnetic studies of somatosensory system principles and examples. Prog Neurobiol 24: 233–236. [DOI] [PubMed] [Google Scholar]
- Hari R, Reinikanen Km Hamalainen M, Ilmoniemi R, Penttinen A, Salminen J, Teszner D (1984): Somatosensory evoked magnetic fields from SI and SII in man. Electroencephalogr Clin Neurophysiol 57: 254–263. [DOI] [PubMed] [Google Scholar]
- Himberg J, Hyvarinen A, Esposito F (2004): Validating the independent components of neuroimaging time series via clustering and visualization. Neuroimage 22: 1214–1222. [DOI] [PubMed] [Google Scholar]
- Hyvärinen A, Karhunen J, Oja E. 2001. Independent component analysis. New York: John Wiley and Sons. [Google Scholar]
- Ikeda S, Toyama K (2000): Independent component analysis for noisy data—MEG data analysis. Neural Networks 13: 1063–1074. [DOI] [PubMed] [Google Scholar]
- Inki M, Hyvärinen A, (2002): Two methods for estimating overcomplete independent component bases. In: Proc. Int. Workshop on Independent Component Analysis and Blind Signal Separation (ICA2001), San Diego, California, 2001.
- James CJ, Hesse CW, (2005): Independent component analysis for biomedical signals. Physiol Measur 26: 15–39. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick S, Gelatt CD Jr, Vecchi MP, (1983): Optimization by simulated annealing. Science 220: 671–680. [DOI] [PubMed] [Google Scholar]
- Knuth KH. 1999. A Bayesian approach to source separation. In: Cardoso JF, Jutten C, Loubaton P, editors. Proceedings of the First International Workshop on Independent Component Analysis and Signal Separation: ICA’99, Aussios, France. p 283–288.
- Lu W, Rajapakse J (2005): Approach and applications of constrained ICA. IEEE Trans Neural Networks 16: 203–212. [DOI] [PubMed] [Google Scholar]
- Makeig S, Bell AJ, Jung TP, Sejnowski TJ. 1996. Independent component analysis of electroencephalographic data In: Jordan MI, Kearns MJ, Solla SA, editors. Advances in neural information processing systems, Vol. 8 Cambridge, MA: MIT Press; p 145–151. [Google Scholar]
- Makeig S, Debener S, Onton J, Delorme A (2004): Mining event‐related brain dynamics. Trends Cogn Sci 8: 204–210. [DOI] [PubMed] [Google Scholar]
- Moran JE, Drake CL, Tepley N (2004): ICA method for MEG imaging. Neurol Clin Neurophysiol 72:BIOMAG 2004. [PubMed] [Google Scholar]
- Mosher JC, Leahy RM (1999): Source localization using recursively applied and projected (rap) music. IEEE Trans Signal Process 47: 332–345. [DOI] [PubMed] [Google Scholar]
- Mosher JC, Lewis PS, Leahy RM (1992): Multiple dipole modeling and localization from spatiotemporal MEG data. IEEE Trans Biomed Eng 39: 541–557. [DOI] [PubMed] [Google Scholar]
- Papathanassiou C, Petrou M (2002): Incorporating prior knowledge in ICA. Digital Signal Processing 2002. IEEE 14th Int. Conf. On, 2, 761–764.
- Pascual‐Marqui R D, Michel CM, Lehman D (1995): Low resolution electromagnetic tomography: a new method for localizing electrical activity in the brain. Int J Psychophysiol 18: 49–65. [DOI] [PubMed] [Google Scholar]
- Särelä J, Valpola H (2005): Denoising source separation. J Machine Learn Res 6: 233–272. [Google Scholar]
- Scherg M, Berg P (1991): Use of prior knowledge in brain electromagnetic source analysis. Brain Topogr 4: 143–150. [DOI] [PubMed] [Google Scholar]
- Tang AC, Sutherland MT, McKinney CJ (2004): Validation of SOBI components from high‐density EEG. Neuroimage 25: 539–553. [DOI] [PubMed] [Google Scholar]
- Tecchio F, Rossini PM, Pizzella V, Cassetta E, Romani GL (1997): Spatial properties and interhemispheric differences of the sensory hand cortical representation: a neuromagnetic study. Brain Res 29: 100–108. [DOI] [PubMed] [Google Scholar]
- Tecchio F, Zappasodi F, Pasqualetti P, Rossini PM (2005): Neural connectivity in hand sensorimotor area: an evaluation by evoked fields morphology. Hum Brain Mapp 24: 99–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valente G, Filosa G, De Martino F, Formisano E, Balsi M (2005): Optimizing ICA using prior information. Proc. in BPC'05: Biosignals Processing and Classification—The International Conference on Informatics in Control, Automation and Robotics, Barcelona, Spain. p 27–34.
- Vigario R, Sarela J, Jousmaki V, Hamalainen M, Oja E (2000): Independent component approach to the analysis of EEG and MEG recordings. IEEE Trans Biomed Eng 47: 589–593. [DOI] [PubMed] [Google Scholar]
- Vrba J, Robinson SE (2001): Signal processing in magnetoencephalography. Methods 25: 249–271. [DOI] [PubMed] [Google Scholar]
- Yeredor A (2002): Non‐orthogonal joint diagonalization in the least‐squares sense with application in blind source separation. IEEE Trans Signal Process 50: 1545–1553. [Google Scholar]
- Zhukov L, Weinstein D, Johnson C (2000): Independent component analysis for EEG source localization. IEEE Eng Med Biol Magn 19: 87–96. [DOI] [PubMed] [Google Scholar]
- Ziehe A, Kawanabe M, Harmeling S, Müller KR (2004): A fast algorithm for joint diagonalization with non‐orthogonal transformations and its application to blind source separation. J Machine Learn Res 5: 801 –818. [Google Scholar]


