Detecting functional nodes in large‐scale cortical networks with functional magnetic resonance imaging: A principal component analysis of the human visual system

Abstract

This study aimed to demonstrate how a regional variant of principal component analysis (PCA) can be used to delineate the known functional subdivisions of the human visual system. Unlike conventional eigenimage analysis, PCA was carried out as a second‐level analysis subsequent to model‐based General Linear Model (GLM)‐type functional activation mapping. Functional homogeneity of the functional magnetic resonance imaging (fMRI) time series within and between clusters was examined on several levels of the visual network, starting from the level of individual clusters up to the network level comprising two or more distinct visual regions. On each level, the number of significant components was identified and compared with the number of clusters in the data set. Eigenimages were used to examine the regional distribution of the extracted components. It was shown that voxels within individual clusters and voxels located in bilateral homologue visual regions can be represented by a single component, constituting the characteristic functional specialization of the cluster(s). If, however, PCA was applied to time series of voxels located in functionally distinct visual regions, more than one component was observed with each component being dominated by voxels in one of the investigated regions. The model of functional connections derived by PCA was in accordance with the well‐known functional anatomy and anatomical connectivity of the visual system. PCA in combination with conventional activation mapping might therefore be used to identify the number of functionally distinct nodes in an fMRI data set in order to generate a model of functional connectivity within a neuroanatomical network. Hum Brain Mapp, 2006. © 2006 Wiley‐Liss, Inc.

INTRODUCTION

Conventional activation mapping in functional magnetic resonance imaging (fMRI) involves the reduction of the complex pattern of brain activation (i.e., fMRI time series) to a single test parameter (e.g., F‐, t‐statistic, Fundamental Power Quotient (FPQ) [Friston et al., 1995; Bullmore et al., 1996a; Cox, 1996]). This test parameter indicates the goodness of fit between the observed fMRI time series and the response predicted on the basis of the experimental paradigm at each intracerebral voxel. Following the statistical inference of the parameter, an activation map identifying voxels whose goodness of fit exceeds a chosen threshold (e.g., P < 0.001) is computed.

The reduction of the time series to a single parameter limits the extent to which significantly activated voxels can be interpreted in terms of their specific functional involvement. The identification or classification of voxels with the same functional role can only be achieved if the statistical parameter uniquely identifies the set of parameters characterizing each time series (e.g., amplitude, onset, width). This implies that voxels with the same statistical parameters also exhibit undistinguishable time series and are thus functionally homogeneous.

Parameters that are most commonly used in conventional activation mapping, however, do not offer a unique representation of the set of parameters characterizing the fMRI time series at each cerebral voxel. Instead, different combinations of the temporal characteristics of the fMRI time series in combination with signal intensity differences can result in the same goodness of fit. For instance, in a periodic response paradigm, voxel i whose response is shifted in time by +Δt relative to the stimulation paradigm will exhibit the same test parameter as voxel j, whose response is shifted by −Δt. Despite the fact that both voxels are “somehow” related to the stimulation paradigm, the phase difference suggests a different functional involvement. The inference of the functional specialization of voxels or brain regions on the basis of a single test parameter can thus be compared to solving an inverse problem. Although voxels in several cortical regions might appear activated in response to a stimulation paradigm, not all voxels are inevitably functionally homogeneous.

The question of time series representation by a single or a set of few parameters is naturally closely related to the parameters of the employed model. One possible solution for finding a more unique representation in General Linear Model (GLM)‐type analysis is thus the use of more flexible time series models. Additional regressors might, for instance, be included to account for delays in signal onset, or variations in signal widths [e.g., Woolrich et al., 2004]. Ultimately, however, the characterization of the observed time series is only as good as the a priori specified model, and parameters not accounted for by the model will not affect the goodness of fit.

In this study, we used a novel approach to investigating functional connectivity among voxels in response to a visual stimulation paradigm. This approach combines the strengths of a model‐driven analysis with the advantages of a model‐free technique. Initially, conventional activation mapping was used to identify voxels with activation somehow related to the stimulation paradigm. Principal component analysis (PCA) was then employed as a second‐level analysis in order to subdivide further the detected voxels into functionally specialized units (i.e., functional nodes).

PCA has previously been applied to a wide range of problems in the analysis of fMRI data such as the identification of an average pattern of response in regions of interest [Buchel and Friston, 1997; Fletcher et al., 1999] and the reduction of noise in the fMRI time series [Thomas et al., 2002]. Variants of PCA such as the closely related eigenimage analysis have also been used to investigate functional connectivity in spatially distributed neural systems [Friston et al., 1993; Bullmore et al., 1996b]. The mathematical rationale behind PCA has been described in detail elsewhere [Andersen et al., 1999]. In brief, PCA aims to describe coherent signal variations in a multivariate data set in terms of a set of uncorrelated variables, i.e., principal components (PCs) or eigenvectors. These are particular linear combinations of the original variables derived in descending order of importance. Unlike most univariate analyses, PCA does not rely on any a priori‐defined parameters but detects specific experimental effects on the basis of a specific criterion (i.e., maximization of variance and orthogonality of components).

It was the aim of this study to investigate functional homogeneity of voxels within and between significantly activated clusters in the human visual system using PCA. The use of PCA in this investigation differed from conventional PCA in several aspects. First, the PCA utilized here was not applied to the entire multivariate fMRI data set but was employed as a second‐level analysis subsequent to functional activation mapping [Pedersen et al., 1994]. Although this approach limits the exploratory power, it decreases the probability that some of the maintained eigenimages reflect structured noise rather than “real” functional connectivity [McKeown et al., 2003]. Second, the analysis was build up in a hierarchical fashion, starting from the level of individual visual clusters up to the network level comprising two or more functionally and anatomically distinct visual regions. On each level of the network, the number of significant components was identified on the basis of the component eigenvalue displays. Finally, the eigenimages and component loadings matrices were created in order to assess the spatial distribution of the components. The model‐driven functional classification of visual voxels resulting from the PCA was then compared to known functional subdivisions of the system.

MATERIALS AND METHODS

Subjects

Seven female right‐handed volunteers between 20 and 30 years of age were recruited from the general population. All subjects were in good general health without a history of neurological or psychiatric disorders and exhibited normal eyesight and color perception. Written consent was provided by all subjects. All participants were given full instructions before the scanning session. The study was approved by the Bethlem Royal and the Maudsley NHS Trust Ethics (Research) Committee.

Stimuli

The purpose of the experimental paradigm was to elicit significant functional activation in at least three anatomically and functionally distinct visual regions. These were the color‐responsive area V4, the motion‐sensitive area V5/MT, as well as early visual regions such as V1 and V2/3. These regions were subsequently subject to PCA to generate a model of functional connectivity in the visual system. The visual stimuli used to generate BOLD images in several different regions of the visual cortex were square wave gratings within an overall circular shape presented in front of an isoluminant gray background. On the basis of a factorial experimental design, which consisted of two factors (movement and color), four different stimuli were generated: (1) stationary, black and white; (2) moving, black and white; (3) stationary, red and green; and (4) moving, red and green.

In order to maximize the contrast sensitivity of the BOLD response, a spatial frequency of 2.2 cycles/degree in the no‐movement conditions and a temporal frequency of 9 Hz/degree in the movement conditions were used in this investigation. These parameters have previously been shown to elicit maximal BOLD responses in the primary visual system [Singh et al., 2000]. Movement was induced by moving the bars of the grid downward within the overall circular shape. As baseline condition, a white fixation cross in front of the same isoluminant background was presented. During the task, subjects were instructed to focus their eye gaze on the center of the screen at the same position at which the fixation cross was presented. The stimuli were generated using Microsoft Visual Basic (Microsoft, Redmond, WA) with the OpenGL graphics library. A computer‐controlled projector system was used to display the images onto a screen placed across the bore of the magnet 3.4 m from the subjects' eyes and viewed through a prismatic mirror. The diameter of each circle was 0.297 m. This value was chosen to adjust the visual angle to 5°. The background luminance was held at a constant value during the length of the experiment and equaled the ambient darkness inside the bore of the MR scanner with the room light extinguished.

Experimental Paradigm

Event‐related fMRI with constant stimulus duration (SD = 2 s) and randomized interstimulus interval (ISI) was used in this investigation. The randomization of the ISIs was based on a Poisson distribution with a mean of 9 s. The shortest ISI was 4 s and the maximal ISI was 14 s. The average ISI of 9 s is close to the empirically optimal ISI at a constant SD of 2 s [Bandettini and Cox, 2000]. All trials were presented in fully randomized order with the aim of avoiding habituation and expectancy effects. Stimuli were presented in a single run lasting 8 min and 36 s. During this run, 14 trials per condition were presented in random order (total number of trials per run = 56). In half of the trials, stimuli were presented in a jittered fashion at a stimulus onset asynchrony (SOA) of 1 s in order to achieve a better characterization of the hemodynamic response (i.e., increased sampling frequency).

Data Acquisition

Whole brain gradient echo planar MR images were acquired using a 1.5 Tesla GE Signa Neuro‐optimized System (General Electric, Milwaukee, WI) fitted with 40 mT/m high‐speed gradients at the Maudsley Hospital in London. Foam padding and a forehead strap were used to limit head motion. Daily quality assurance was carried out to ensure high signal‐to‐ghost ratio, high signal‐to‐noise ratio, and excellent temporal stability using an automated quality control procedure [Simmons et al., 1999]. A quadrature birdcage head coil was used for radiofrequency transmission and reception.

At the beginning of each session, an inversion recovery EPI data set was acquired at 43 near‐axial 3 mm thick planes parallel to the AC‐PC line: TE = 73 ms, TI (inversion time) = 180 ms, TR = 16 s, in‐plane resolution = 1.72 mm, interslice gap = 0.3 mm. This higher‐resolution EPI data set provided whole brain coverage and was later used to register the fMRI data sets acquired from each individual subject in standard stereotaxic space. During the functional scan, 258 T2*‐weighted images depicting BOLD contrast [Ogawa et al., 1990; Kwong et al., 1992] were acquired over 8.44 min at each of 25 near‐axial noncontiguous 5 mm thick planes parallel to the intercommissural (AC‐PC) line: TE = 40 ms, TR = 2,000 ms, theta = 80°, in‐plane resolution = 3.75 mm, interslice gap = 0.5 mm.

Data Analysis

Brain activation mapping

Image processing and statistical analysis were carried out using the in‐house analytical package XBAM, developed at the Institute of Psychiatry. Prior to the time series analysis, the data were processed to remove low‐frequency signal changes and motion‐related artifacts. This was done by realignment using tricubic spline interpolation followed by regression of each realigned fMRI time series on a second‐order polynomial function of lagged and concomitant positional displacements of the subject's head [Bullmore et al., 1996b; Brammer et al., 1997].

Responses to the experimental paradigms were then detected by time series analysis using gamma variate functions (peak responses weighted between 4 and 8 s) convolved with the experimental design to model the blood oxygen level‐dependent response. This time series analysis involved regressing the motion‐corrected fMRI time series on the predicted time series at each voxel i, where the prediction was made on the basis of a linear model (i.e., modeled time series is a linear combination of the convolved contrast vector). For a single experimental condition, the regression equation can thus be formalized as

(1)

where y_i denotes the observed intensity value at voxel i, ${}_{\text{μ}}^{\mathit{\text{i}}}$ is the mean of the time series, a _i equals the amplitude of the first convolution with a peak response at 4 s, and indicates the error term (i.e., 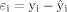with 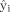denoting the predicted signal intensity value).

Following least squares fitting of this model, a goodness‐of‐fit statistic [the sum of squares (SSQ) ratio] and a measure of the mean power of neural response (effect size or ES) was computed at each voxel i. This was the ratio of the sum of squares of deviations from the mean intensity value due to the model (fitted time series) divided by the sum of squares due to the residuals (original time series minus model time series). Assuming that n equals the number of data points in the whole fMRI time series, the SSQ index for each voxel i can be formalized as

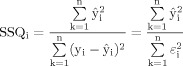(2)

To ascertain the distribution of SSQ under the null hypothesis of no experimental effect, the observed time series were then randomly permutated using a waveled‐based resampling method [Bullmore et al., 2001], and the models were refitted to the resampled data. This process was repeated 20 times at each voxel to derive the distribution of SSQ ratios under the null hypothesis. The observed and the randomized SSQ maps for each subject were then registered in the standard space of Talairach and Tournoux [1988]. If the observed SSQ ratio at a voxel exceeded the 95th percentile of the distribution of the 20 randomized maps, then the null hypothesis was refuted by a one‐tailed test at the voxel with probability of type I error = 0.05. This method has been shown to give excellent control of nominal type I error rates in fMRI data from a variety of scanners. Activations for any contrast at any required P value can then be determined by obtaining the appropriate critical values from the null distribution [Bullmore et al., 1996b]. The statistical maps displaying the two main effects (color/motion) were used to identify regions of interest in the visual system. These ROIs were then subject to PCA.

General model assumptions and hypotheses

In this study, PCA was employed as a meta‐analysis of the time series extracted from voxels displaying significant functional activation in the primary visual system. It was the aim of the analysis to generate a model of functional connections within the visual network by clustering voxels with the same functional specialization into functional nodes and by comparing the number of functional nodes k with the number of anatomically defined clusters v. The number of clusters v was thus not necessarily assumed to be equal to the number of functional nodes k. Three possible scenarios might thus be subject to interpretation.

First, the number of clusters equals the number of functional nodes (v = k). In this case, all clusters are functionally distinct and exhibit their own functional specialization. On the other hand, if voxels within an individual cluster are examined, a single significant component indicates that all voxels within the cluster are functionally homogeneous. The second possible outcome is that the number of clusters exceeds the number of functional nodes (v > k). Here, (v − k) clusters are not functionally distinct but share variance with the k functional nodes. The last possibility is that the number of nodes could exceed the number of clusters (k > v). This result indicates that not all anatomically different clusters in the data set are functionally homogeneous, but that at least one cluster should be subdivided into separate functional nodes.

The number of clusters was simply inferred from the functional activation maps for each individual subject, and the number of functional nodes was assumed to equal the number of significant principal components in the data set. The number of significant components was identified on the basis of the Eigenspectra of the data covariance matrix assuming a minimal required signal‐to‐noise ratio (SNR).

To test these basic assumptions empirically, PCA was carried out on different levels of the visual network, starting from the level of individual clusters up to the network level comprising two or more functionally and anatomically distinct regions. Functional connectivity was therefore examined in a hierarchical fashion by applying singular value decomposition (SVD) to a different covariance matrix in each analysis run. On each network level, the number of significant components as well as their regional distribution was examined.

In the first analysis run, PCA was carried out across the motion‐corrected fMRI time series extracted from voxels located within a single significantly activated cluster. If all voxels within the cluster are indeed functionally homogeneous, as would be expected from the known functional and anatomical organization of the visual system, a single significant component should be observed. In the second analysis run, PCA was applied to voxels located in bilateral homologue visual regions. Bilateral homologue visual regions are known to exhibit the same functional specialization despite being spatially separated and should therefore be presented by a single component. In the third run, PCA was carried out across voxels located in two anatomically distinct visual regions within one hemisphere. If these regions are also functionally distinct, more than one significant component should be observed and each component should be dominated (i.e., high factor loadings) by voxels within each region. The following regional combinations were analyzed simultaneously: V1 in combination with V2/3, V1 in combination with V5/MT, and V2/3 in combination with V5/MT. In addition, each visual region was analyzed in combination with voxels in a control area located in the region of the temporal pole of the ipsilateral hemisphere. This control region was chosen because it is anatomically connected with the visual system but did not exhibit significant functional activation during the paradigm. Finally, PCA was carried out across voxels in three different visual regions (e.g., V1, V2/3, V5/MT) located within the same slice.

In order to minimize the effects of data preprocessing (e.g., interslice interpolation, rendering of images to template), PCA was applied to voxel time series within individual slices and subjects.

Mathematical framework

The mathematical model was build on the mathematical framework of general factor analytical models, where a data matrix X is reconstructed by a linear combination of a set of underlying factors (i.e., principal components). Suppose that n denotes the number of data points in the fMRI time series (n = 258), and P the number of voxels included into the analysis, the mathematical model can be formalized as

(3)

where X is a matrix of signal intensity values, F denotes the factor scores, A is a matrix of factor loadings (i.e., contribution of a factor to the time series at a particular voxel location), and E is a matrix of residuals. k is a scalar denoting the number of significant components. In the context of this study, the term component is used in the sense of a “latent” factor, which is the overall functional specialization of a particular brain region. Hence, the matrix of factor scores F contains the region‐specific characteristic time series, which more or less resembles the observed time series of all voxels within a specific region.

To accommodate the number of anatomically distinct brain regions v (i.e., clusters), the model was extended by an indicator function I _{voxel i}: cluster v{1, 0} denoting the presence of a voxel in a particular cluster so that

(4)

with

The time series of voxel i may therefore be generalized to the form

(5)

with 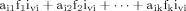being the common part of x _i, which is shared with all other voxels within cluster v.

Singular value decomposition

The matrix of factor scores F and of factor loadings A were obtained with singular value decomposition (SVD), which was used to find r orthogonal principal eigenvectors with r = min(n, p), ranked in descending order of importance. SVD of an arbitrary (n × p) data matrix X is based on the following theorem of linear algebra:

(6)

where U _(n×r) is an orthogonal matrix, Λ_(r×r) is a diagonal matrix with positive or zero elements λ_r (singular values or eigenvalues), and 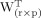containing the eigenvectors of X in its rows.

SVD can be carried out in the spatial as well as in the temporal domain. In the spatial domain, voxels represent variables and volumes constitute observations. The spatial covariance structure S_vox is thus a square matrix with the dimension (p × p), with S_vox ∝ X^TX. On the basis of Eq. (6), it can be shown that

(7)

To obtain the factor loadings matrix A, indicating the correlation between a voxel with the factor, the column vectors of W containing the principal eigenvectors were multiplied by the associated singular values λ_r. Thus,

(8)

The principal factors with unit variance were derived from the principal components as follows:

(9)

where B denotes the matrix of factor score coefficients. Finally, the factor scores (i.e., eigentime series) were computed by

(10)

where Z denotes X converted to standard score form.

Identification of number of significant components

As pointed out above, SVD of an arbitrary data matrix X leads to r orthogonal PCs, ranked in descending order of importance, with r = min(n, p). Therefore, if all PCs are extracted, r equals the number of voxels in the analysis and no clustering occurs. To identify the number of significant components k only, which indicated the number of functional nodes, at least the first two of the following criteria had to be fulfilled.

One, only components with eigenvalues greater than or equal to 1 (λ² > 1.00) were retained for further analysis, thus explaining more variance than a single voxel (considering that the variance of standardized variables or voxels equals 1.00). This criterion is conventionally used for determining the number of factors to be extracted in factor analysis and is also known as Kaiser's rule [Kaiser, 1958].

Two, only those components whose eigenvalues fell before the last large drop on the so‐called SCREE diagram or eigenvalue spectrum were included. This criterion is also known as the elbow criterion [Cattell, 1966]. The eigenvalue spectra were derived by plotting the squared diagonal elements λ² of Λ against their rank order in terms of size. Each eigenvalue is equal to the variance of the corresponding principal component, and the sum of eigenvalues is equal to the total variance of X. Therefore, a plot of

(11)

against k can be used to show the cumulative percentage of total variance in X accounted for by the first k PCs [Bullmore et al., 1996b].

Three, if SCREE plots indicated a single underlying PC, then the ratio of the difference in explained variance between the first PC pair (Δ₁ = %_{expl, 1st PC} − %_{expl, 2nd PC}) and the second PC pair (Δ₂ = %_{expl, 2nd PC} − %_{expl, 3rd PC}) must exceed a factor of 3.00 (Δ₁/Δ₂ ≥ 3.00). Using the squared diagonal elements λ² of Λ, this criterion can also be formalized as

(12)

where λ${}_{\text{1}}^{\text{2}}$ equals the percentage of explained variance by the first PC, λ${}_{\text{2}}^{\text{2}}$ equals the percentage of explained variance by the second PC, and so forth. If SCREE plots indicated two underlying PCs, then the ratio of the difference in explained variance between the second PC pair and the third PC pair had to exceed a factor of 3.00. In parallel to Eq. (10), this can be expressed as

(13)

If more than two PCs were significant, the criterion was analogous. This criterion was chosen to quantify further the size of the last drop on the SCREE plot. The value of 3.0 was chosen arbitrarily, indicating the required SNR expected in the visual system. It is, however, important to point out that this ratio might change depending on the cortical system under investigation as well as the field strength of the scanner.

In order to enable a better interpretability of the extracted PCs, the factor loadings matrix A was subject to an orthogonal factor rotation using the VARIMAX criterion. A detailed description of the mathematical algorithms involved in this rotation is provided by Kaiser [1958]. VARIMAX rotation has been used in PCA of fMRI data before [Andersen et al., 1999; Thomas et al., 2002]. Pearson correlation coefficients between the voxel factor loadings on the first PC and the level of functional significance indicated by the SSQ values described in Eq. (2) were calculated. This was done with the aim of showing that the first PC represents signal due to the experimental stimulation and not due to structured noise.

Spatial distribution of components

To examine the spatial distribution of the components, eigenimages and component displays were created. The first two eigenimages were displayed for each of the extracted components. The orthogonal axes of each eigenimage encoded the anatomical {x, y} coordinates of each voxel. The color of each voxel in the ROIs encoded the size of the factor loadings on the first two components. The color maps of voxels in ROIs were superimposed onto the average intensity image. Two different color palettes were used for displaying the size and the prefix of the factor loadings. An orange‐to‐yellow color palette displayed the size of positive factor loadings, whereas a blue‐to‐turquoise color palette represented the size of negative factor loadings. In addition, the matrix of factor loadings was displayed using two‐dimensional component plot. In contrast to the eigenimages, the orthogonal axis of a component plot encoded the size of a voxel's factor loading on each of the two extracted components. The color of individual voxels encoded the regional origin of the voxel.

Finally, in order to assess whether spatial proximity of investigated clusters could be a contributing factor to establishing significant components, the Euclidean distances between the centers of mass of each cluster were calculated. The center of mass for each individual cluster was calculated as the average {x} and {y} column vector containing coordinates of each voxel within a particular cluster. The distance d between points x and y in a Euclidean space ℜⁿ is given by

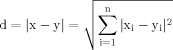(14)

Thus, in the plane, the distance between the center of mass with the coordinates (x₁, y₁) and (x₂, y₂) was calculated as

(15)

The squared Euclidean distance d ²(x, y) between clusters was taken as a measure of spatial distance between the ROIs. In order to test whether there is a statistically significant difference in squared Euclidean distance between voxels in ROIs with a one‐ or two‐component solution, a Wilcoxon signed‐rank test for dependent samples was carried out considering the small sample size.

RESULTS

Functional Connectivity on Cluster Level

Number of principal components

The foci of significant functional brain activation in the visual system, from which the motion‐corrected time series were extracted, are summarized for individual subjects in Table I.

Table I.

Foci of functional brain activation in the visual system for individual subjects

Region definition	Subject 1		Subject 2		Subject 3		Subject 4		Subject 5		Subject 6		Subject 7
	Tal (x, y, z)	SSQmax	Tal (x, y, z)	SSQmax	Tal (x, y, z)	SSQmax	Tal (x, y, z)	SSQmax	Tal (x, y, z)	SSQmax	Tal (x, y, z)	SSQmax	Tal (x, y, z)	SSQmax
V1 L	−25, −89, 4	0.202	−15, −93, 15	0.239							−15, −82, 4	0.359	−21, −86, −13	0.369
V1 R	15, −89, 4	0.280	17, −86, 15	0.216					7, −73, 9	0.304	43, 10, 9	0.233	17, −86, −13	0.314
V2/3 L	−21, −80, 15	0.353			−17, −82, 9	0.245			−21, −80, 15	0.195	−21, −76, 20	0.269	−21, −82, −2	0.251
V2/3 R	25, −82, 15	0.362	28, −80, 9	0.460			25, −82, 9	0.274	21, −76, 15	0.193	36, −73, 5	0.274	21, −86, 4	0.386
V4 L			−11, −73, 4	0.267	−36, −76, −13	0.276			−32, −67, −13	0.487	−21, −63, −7	0.301
V4 R	32, −67, −2	0.233	25, −76, −2	0.341	28, −80, −13	0.230	25, −69, −13	0.423	36, −67, −13	0.309	32, −63, −7	0.332	50, −56, −7	0.381
V5/MT L	−36, −73, 20	0.344			−40, −60, −2	0.421					−43, −60, −2	0.313	−47, 67, −7	0.281
V5/MT R	36, −60, 15	0.232	43, −56, 4	0.328	40, −67, −2	0.437	47, −63, −2	0.311	25, −50, 4	0.221	47, −46, −2	0.487	36, −69, −2	0.297

The cluster in the largest goodness‐of‐fit index (SSQ, P ≤ 0.01) for each visual region is reported. Talairach coordinates refer to the center of mass of the cluster with the largest SSQ index.

In all 10 investigated clusters, factor eigenvalue plots (SCREE plots) suggested a prominent one‐factor solution when PCA was carried out across voxels within a significantly activated visual cluster. According to the postulated criteria that had to be satisfied in order to establish the significance of a component in relation to those resulting from random variations in the data set, the SCREE plots for individual clusters revealed only one component whose eigenvalue fell before the last large drop of eigenvalues. Furthermore, this component exhibited an eigenvalue larger than 1.0, thus accounting for more variance in the data set than introduced by a single voxel time series. While the eigenvalues of the components falling below the last large drop decreased linearly with the component number, the first PC explained at least five times more variance than the second PC. The results of all selected clusters are summarized in Table II.

Table II.

Summary results of the PCA carried out across voxels within significantly activated visual clusters

Cluster ID	Region definition	Number of voxels within cluster	% variance first PC	% variance second PC	% variance third PC	Ratio*	Correlations factor loading/SSQ**
1a	V1	9	31.38	15.79	13.67	7.35	0.834
2a	V1	11	30.93	12.79	11.90	20.38	0.882
3a	V1	15	26.35	11.40	11.03	40.41	0.759
4a	V2/3	9	33.01	14.81	12.46	7.74	0.828
5a	V2/3	13	31.98	14.10	10.70	5.26	0.833
6a	V4	31	23.21	7.33	6.80	29.96	0.778
7a	V4	21	32.21	9.72	7.62	10.71	0.869
8a	V5/MT	17	24.551	11.34	10.00	9.86	0.747
9a	V5/MT	14	25.92	12.81	11.26	8.46	0.942
10a	V5/MT	11	28.85	13.73	12.85	17.18	0.746

^*Ratio difference in explained variance between the first PC and the second PC pair.

^** P < 0.01, two‐tailed.

^aOne‐component solution.

On average, the first PC explained 28.84% ± 3.56% of the total variance in the data set, the second principal component explained a mean percentage of 12.38% ± 2.52%, and the third principal component explained 10.82% ± 2.19% of the total variance. The ratio of explained variance between the first and the second component was at least 5.26 times larger than between the explained variance of the second PC pair. Figure 1B shows the component eigenvalue displays and the eigentime series (Fig. 1C) of a representative cluster located in visual area V5/MT. The existence of a single significant component for voxels within visual clusters indicates that all voxels within the cluster are functionally homogeneous and thus represent a single functional unit. The hemodynamic responses in all voxels within the cluster can be reduced to a single time series, the first eigentime series, representing the overall functional activation within the cluster. This finding offers direct empirical evidence for an often‐made hypothetical assumption in conventional activation mapping, namely, that voxels within a cluster are functionally homogeneous and thus representing a single functional unit or cluster.

Figure 1.

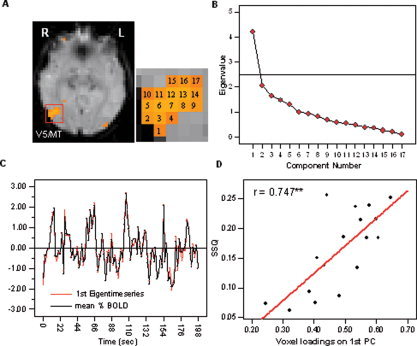
A: Results of the PCA carried out across voxels within a significantly activated cluster in V5 for a representative subject. B: The SCREE plot indicated that only one component fell above the last large drop on the display and exhibited an eigenvalue larger than 1.0. C: The first eigentime series is very similar to the average observed time series within the cluster. D: There was a significant positive correlation between the voxel factor loadings on the first component and the level of significance (SSQ index) indicated by the functional activation map. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Correlations between SSQ values and factor loadings

One of the main problems of PCA is the separation of signal related to the stimulation paradigm from signal components reflecting noise. PCs are derived from a data set in descending order of importance, each component accounting for as much partial variance as possible. Any signal variations, which are in some way correlated across voxels or volumes, could thus be represented by a PC. Due to the existence of colored noise components in the fMRI time series [Bullmore et al., 2001], it is possible that several of the retained eigenimages reveal brain regions with similar noise properties rather than areas with a similar functional specialization [Pedersen et al., 1994]. However, components reflecting noise cannot be separated from components representing functional connectivity since PCA does not utilize information concerning the stimulation paradigm. To address this issue, the results of the model‐free PCA were compared with the model‐dependent functional activation mapping using bivariate correlation analysis.

In all 10 investigated clusters, the voxel factor loadings on the first principal component were significantly positively correlated with their statistical test parameter (SSQ ratio) extracted from the individual brain activation maps. Thus, higher factor loadings of individual voxel on the first principal component were accompanied by high levels of significance. The highest correlation coefficient was observed in visual area V5/MT (r = 0.942; P < 0.01). The correlation coefficient was also highly significant when the analysis was carried out across all 10 investigated clusters (r = 0.79; P < 0.01). The relationship between SSQ values and the factor loadings across all investigated clusters is displayed in Figure 2. See Figure 1D for scatter plots of the representative cluster located in visual area V5/MT. Because the SSQ ratio indicates the standardized level of response to the stimulation paradigm, it can be concluded that the retained PCs do indeed reflect the degree of functional homogeneity between voxels rather than correlated noise.

Figure 2.

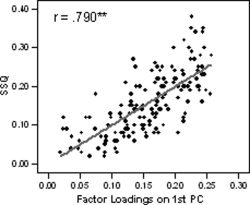
Correlation between voxel factor loadings on the first principal component and the level of significance (SSQ index) in the functional activation maps across all investigated clusters.

Functional Connectivity Between Voxels in Bilateral Homologue Visual Areas

In the next analysis step, PCA was applied to voxels located in bilateral homologue visual regions. These regions are known to exhibit the same functional specialization and are spatially far apart. As would be expected on the basis of the outlined rationale, applying PCA to a set of motion‐corrected time series extracted from voxels in bilateral homologue visual regions led to very similar results as the ones reported for voxels within significantly activated clusters.

Number of components

Summary results of the PCA for bilateral homologue visual regions are shown in Table III. In eight out of nine investigated cluster pairs, SCREE plots revealed only one component whose eigenvalue fell before the last large drop on the display. All cluster pairs with a clear one‐component solution also exhibited a ratio of explained variance between the first two component pairs of a value larger than 3.00. A minimum ratio difference of 5.93 was observed in visual area V2/3, and a maximum ratio difference of 25.45 was observed in visual area V1. On average, the first principal component explained 23.71% ± 4.82% of the total variance in the data set, the second principal component explained a mean percentage of 9.63% ± 2.04%, and the third principal component explained 7.99% ± 1.98% of the total variance. SCREE plots of two representative homologue clusters in V2/3 and V5/MT within the same subject are shown in Figure 3.

Table III.

Results of the PCA carried out across voxels in bilateral homologue areas of the visual system

Cluster ID	Region definition	Total number of voxels	% variance first PC	% variance second PC	% variance third PC	Ratio*
1a	V1	31	20.38	6.89	6.36	25.45
2b	V1	102	17.09	10.583	4.716	1.11
3a	V2/3	18	26.87	10.07	8.38	9.94
4a	V2/3	18	25.63	11.63	9.27	5.93
5a	V2/3	17	26.40	10.57	9.84	21.68
6a	V4	32	19.06	6.79	5.87	13.34
8a	V5/MT	22	22.55	8.41	7.75	21.42
9a	V5/MT	15	31.72	12.11	10.17	10.11

^*Ratio difference in explained variance between the first PC pair and the second PC pair.

^aOne‐component solution.

^bTwo‐component solution.

Figure 3.

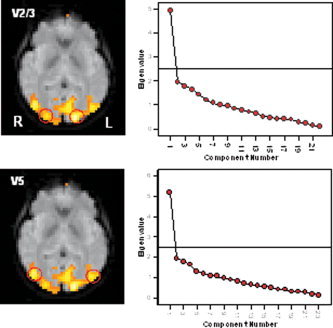
Results of the PCA carried out across voxels located in bilateral homologue visual regions in V2/3 (top) and V5/MT (bottom) for a representative subject. In both cases, only one significant component was observed on the basis of the SCREE plots (right). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

In one out of the nine investigated cluster pairs (cluster ID 2 in Table III), the SCREE plot revealed more than one significant underlying component. This cluster contained voxel time series extracted from visual area V1 in both hemispheres. Here, the percentage of explained variance decreased from 17.09% to 10.58% between the first and the second PC, and from 10.58% to 4.71% between the second and the third PC. The ratio difference of explained variance between component one and two was thus very low at 1.11, and fell below the set criterion of a value of 3.00.

These findings are in accordance with the assumption that the number of significant PCs indicates the number of functionally specialized units in the data set. Although both clusters were spatially far apart, both homologue visual clusters were classified as one functional unit.

Component Structure of an fMRI Data Set Containing Time Series From Two or More Anatomically Distinct Visual Regions

So far, the reported subspace of significant components was one‐dimensional. In order to show that PCA is sensitive enough to detect functional differences between voxels subsequent to brain activation mapping, PCA was carried out across two different regions of the visual system within the same hemisphere. Three possible combinations of visual regions were subject to PCA: V1 in combination with V5/MT, V2/3 in combination with V5/MT, and V1 in combination with V2/3. A summary of the results can be found in Table IV.

Table IV.

Results of the PCA carried out across voxels located in two different areas of the visual system

Cluster ID	Regions included	Total number of voxels	% variance first PC	% variance second PC	% variance third PC	% variance fourth PC	Ratio 1*	Ratio 2**
1a	V1, V5/MT	20	26.75	11.68	7.15	6.31	3.33	5.39
2a	V1, V5/MT	24	21.01	13.06	7.79	6.78	1.51	5.22
3a	V1, V5/MT	10	25.65	17.78	10.97	9.81	1.16	5.87
4a	V1, V5/MT	22	19.95	13.11	7.42	6.93	1.20	11.61
5b	V2/3, V5/MT	20	29.00	10.34	8.83	6.56	12.36
6b	V2/3, V5/MT	24	19.49	9.09	7.73	7.55	7.65
7b	V2/3, V5/MT	17	22.91	11.35	10.47	9.05	13.14
8b	V1, V2/3	16	24.42	11.89	9.83	8.16	6.08
9b	V1, V2/3	18	29.47	10.20	7.73	6.84	7.80

^*Ratio difference in explained variance between the first PC pair and the second PC pair.

^**Ratio difference in explained variance between the second PC pair and the third PC pair.

^aTwo‐component solution.

^bOne‐component solution.

Number of components

As can be inferred from Table IV, the number of PCs was highly dependent on the specific ROIs included in the analysis. In all five investigated regional combinations in which visual area V2/3 was analyzed in combination with V1 (n = 2) or V5/MT (n = 3), SCREE plots revealed that only one component explained nonrandom variance. On average, the first PC explained 25.06% ± 4.21% of the total variance in the data set, the second PC explained a mean percentage of 10.57% ± 1.09%, and the third PC explained 8.91% ± 1.23% of the total variance. The ratio of explained variance between the first and the second component was at least 6.8 times larger than between the percentage of explained variance between the second component pair. A maximal increase in explained variance by a factor of 13.14 was observed in cluster 7, which analyzed V2/3 in combination with V5/MT.

More than one significant PC were found when PCA was applied to voxels located in two functionally distinct visual areas such as V1 in combination with the motion‐sensitive area V5/MT. In all four investigated cluster pairs, SCREE plots suggested two significant components falling below the last large drop. Overall, the first component explained a mean percentage 23.34% ± 3.36% of the total variance in the data set. On average, the second component explained additional variance of 13.91% ± 2.67%. Thus, about 27% of the total variance could be explained by the first two PCs. On the whole, the third principal component explained additional variance of 8.33% ± 1.77%. Furthermore, the ratio difference of explained variance between the second and third component was at least 5.22 times larger than the ratio difference of explained variance between the third and fourth components. Summary results of the analysis of voxels in V1 in combination with V5/MT are displayed in Figure 4.

Figure 4.

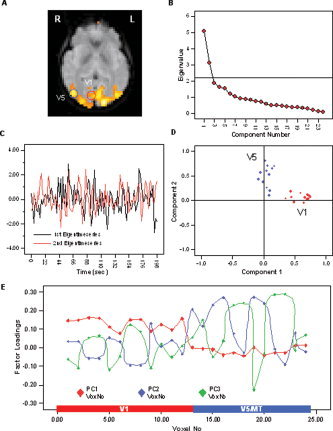
A: Results of the PCA carried out across voxels in V1 in combination with voxels in V5 for a representative subject. B: The SCREE plot indicated two significant components falling above the last large drop of eigenvalues and exhibiting an eigenvalue larger than 1.0. C: Display of the first and second eigentime series. D: Factor loading display following orgothonal component rotation using the VARIMAX criterion. Voxels in V1 exhibit high loadings on the first PC but low correlation with the second PC, whereas voxels in V5/MT exhibit high loadings on the second and low loadings on the first PC (i.e., simple structure). First eigentime series therefore represents an average pattern of functional activation in V1, and the second eigentime series represents activation in V5. E: Factor loadings display on the extracted first four components, while only the first two components met the outlined criteria. Voxels in area V1 are indicated by the blue bar, voxels in V5/MT are indicated by the red bar. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 4 further indicates that when additional components are recruited despite not meeting the outlined criteria, the functional classification of voxels is still meaningful. Figure 4E displays the factor loadings profiles of voxels in V1 and V5/MT on the first four components, while only the first two met the outlined criteria. The graph shows that, overall, voxels in V1 display high loadings on PC 1 and 4, but exhibit low factor loadings on PC 2 and 3. Voxels in V5/MT, on the other hand, have low loadings on PC 1 and 4 while displaying high loadings on PC 2 and 3. This suggests that PCA is potentially quite sensitive to differences in the temporal characteristics of the fMRI time series. It is, however, an entirely different question whether this difference is significant (i.e., should voxels in V1 and V5/MT be further subdivided into functionally distinct units?).

When PCA was carried out across one of the visual ROIs (i.e., V1, V2/3, and V5/MT) in combination with the control region located in the region of the temporal pole, two significant components were observed. SCREE plots resulting from the PCA across voxels in V2/3 in combination with V5/MT as well as in combination with the control region are shown in Figure 5 for a representative subject.

Figure 5.

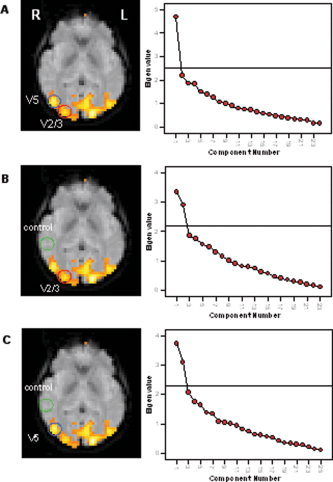
Results of the PCA carried out across V2/3 in combination with V5 and the control regions for a representative subject. A: SCREE plot following the analysis of voxels in V2/3 in combination with V5/MT revealed only one significant component. B and C: Two significant components were observed when V2/3 or V5/MT was analyzed in combination with the control region. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

To simplify the regional interpretation of the two extracted components, VARIMAX rotation was carried out and component plots as well as eigenimages were displayed. The rotated factor loading display (Fig. 4D) indicated that the two components are determined by regional signal variations. All voxels extracted from visual area V1 exhibited high factor loadings on the first component exclusively, while all voxels extracted from V5/MT exhibited high factor loadings on the second component. Therefore, a simple structure of the factor loadings matrix was achieved. The first and second eigentime series are displayed in Figure 4C. Because voxels in V1 exhibited high factor loadings on the first PC, the first eigentime series represents functional activation in V1, and the second eigentime series represents activation in V5/MT.

Euclidean distance between ROIs

In order to test whether spatial proximity between investigated cluster pairs could be a contributing factor in ascertaining differences in the number of components, the squared Euclidean distances between the centers of mass of each cluster were statistically compared. The results indicated that the number of significant components does not seem to be directly related to the spatial distance between the clusters. Although the squared Euclidean distance between the center of mass in V2/3 clusters as compared to V1 or V5/MT (median distance = 22.72 mm) was smaller than between the center of mass in V1 as compared to V5/MT (median distance = 34.54 mm), the Wilcoxon signed‐rank test across all nine investigated cluster pairs showed that there was no significant difference in the spatial distance between investigated cluster pairs resulting in a one‐component solution (n = 5) and cluster pairs resulting in a two‐component solution (n = 4; Wilcoxon Z = −1.461; P < 0.15). Taking into account the results of the PCA over bilateral homologue visual areas as well as the results reported in this section, it seems unlikely that the number of significant PCs can be explained by the spatial distance (or proximity) between voxels (or clusters) exclusively.

PCA across voxels in V1, V2/3, and V5/MT within one hemisphere

In the final analysis step, PCA was carried out across voxels time series extracted from three distinct visual regions. To avoid possible slice timing issues, the analysis was restricted to significantly activated voxels within an individual slice. Significant functional activation in three distinct visual regions (e.g., V1, V2/3, and V5/MT) within the same slice was, however, observed in only one out of the seven subjects. Therefore, the results presented in the following chapter should be considered as preliminary needing further validation.

Figure 6 summarizes the results of the PCA across voxels in V1, V2/3, and V5/MT in the right hemisphere. Although three anatomically distinct visual regions were included, only two components exhibited eigenvalues falling before the last large drop on the SCREE plot (Fig. 6B) and exhibiting eigenvalues larger than 1.00; 17% of the total variance was explained by the first PC, 9.84% by the second PC, and 7.2% by the third PC. The ratio of explained variance between the second and the third component pair was 2.65, thus being just below the set threshold of 3.00. In order to explore the regional classification of the components, the factor loadings matrix was rotated. A visual display of the rotated factor loadings matrix is shown in Figure 6C. After orthogonal rotation, voxels located in area V5/MT exhibited generally high positive factor loadings on the first PC, and low negative factor loadings on the second PC. Voxels located in area V1 exhibited predominantly high positive factor loadings on the second PC, and low negative loadings on the first PC. A large percentage of voxels in area V2/3 displayed low or medium factor loadings on both PCs. The regional separation of the components can also be seen in the eigenimages (Fig. 6D), which incorporated all significantly activated visual voxels in the right hemisphere. The BOLD response functions for each of the four stimulation conditions were extracted from the first and second eigentime series and displayed in Figure 6E. Because the first PC was dominated by voxels in V5/MT, the first eigentime series represented mainly functional activation in V5/MT, and the second eigentime series indicated the pattern of response in V1. The response functions on the basis of the first eigentime series clearly highlighted the selective responsiveness for moving stimuli (condition 2 and 4) in visual area V5/MT (i.e., presence of a characteristic BOLD response following visual motion exclusively). In V1, a characteristic response was present in all conditions.

Figure 6.

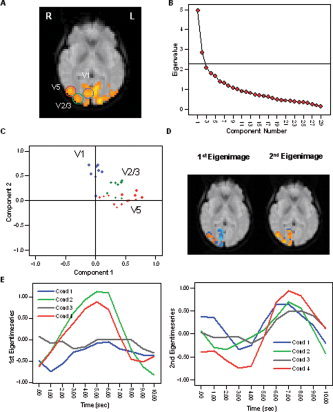
A: Results of the PCA carried out across voxels in V2/3, V1, and V5/MT for a representative subject. B: The SCREE plot indicated two significant components falling above the last large drop of eigenvalues and exhibiting an eigenvalue larger than 1.0. C: The factor loadings display after VARIMAX rotation indicates that voxels in V5/MT exhibit generally high loadings on the first PC, and voxels in V1 exhibit high loadings on the second PC. Voxels in V2/3 show medium loadings on both components. D: A regional classification of the components can also be observed in the eigenimages. Positive factor loadings are displayed in orange; negative loadings are displayed in blue. E: Average BOLD responses for each stimulation condition extracted from the first (left) and second (right) eigentime series. The responses based on the first eigentime series, which represents the average pattern of response in V5/MT, clearly highlight the response selectivity for moving stimuli (conditions 2 and 4). The second eigentime series representing functional activation in V1 indicates a characteristic response in all stimulation conditions. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Very similar results were observed in the right hemisphere. Here, two components fell before the last large drop on the SCREE plot whose eigenvalues were above 1.00; 23.78% of the total variance in the data set was explained by the first PC, 9.2% were explained by the second PC, and 6.8% by the third PC. The ratio of explained variance between the first and the second component pair was 6.32. The ratio of explained variance between the second and the third component pair was 2.4, thus being slightly below the set threshold. Following orthogonal rotation of the loadings matrix, a similar pattern of functional connectivity emerged as described in the right hemisphere. Voxels in area V5/MT are predominantly correlated with the first PC, whereas voxels in V1 are predominantly correlated with the second PC. Voxels in V2/3 displayed medium correlations with both components.

These findings indicate that significantly activated visual voxels identified by conventional activation mapping are not functionally homogeneous, but can further be classified according to their functional specialization by PCA. As expected, voxels in V1 and V5/MT were classified into two different functional units. Voxels in V2/3, however, did not reveal an additional component and were associated with both the PC for V1 and the PC for V5/MT.

DISCUSSION

This study aimed to demonstrate how a regional variant of principal component analysis can be used to delineate the known functional subdivisions of the human visual system. Unlike conventional PCA [e.g., Hansen et al., 1999; Viviani et al., 2005], PCA was not applied to the entire fMRI data set but was carried out on several levels of a cortical network. On each level, the number of significant components was first identified by means of several criteria. Voxels were then allocated to clusters on the basis of a common functional involvement. The model of functional connectivity in the visual system derived by PCA was in agreement with its well‐known functional specialization and anatomical connectivity.

Methodological Considerations

The regional variant of PCA used in this investigation should be distinguished from local PCA (LPCA) originally described by Lai and Fang [1999]. These authors used the term “local” to describe a PCA carried out across a single voxel time series in combination with the signal obtained in the neighborhood of each voxel [Lai and Fang, 1999]. Furthermore, it should be distinguished from hierarchical regional PCA (HRPCA), which has been used to model object shape deformations in medical images [e.g., Hamarneh et al., 2004]. The use of the terms “hierarchical” and “regional” in this context, however, differs from their use in the present study. In HRPCA, the overall model of an anatomical structure is broken down into a set of subprofiles, which are described by a set of shape measures (length, orientation, thickness). Structure deformations are implemented as deformation operators and act on the shape profiles. PCA is then performed on a set of shape profiles in order to detect the main modes of variation of landmark positions as well as the amount of variation. The term “hierarchical” is used to highlight that each subprofile displays a different length (multiscale) and position (multilocation), hence the term “regional.” In the present study, the term “region” was chosen to point out that PCA was applied to ROIs, which were previously selected on the basis of the activation maps. The term “hierarchical” was used to highlight that PCA was carried out on different levels of the visual system (i.e., cluster level, network level). Therefore, although the overall use of HPCA and the here‐used PCA is similar in that both achieve data reduction, their terminology is not compatible and the type of data to which PCA is applied is different (i.e., spatial coordinates vs. time series).

In the presented study, PCA was carried out as a second‐level analysis subsequent to functional activation mapping. The selection of ROIs prior to PCA (hence the term “regional”) has been previously suggested [Pedersen et al., 1994; Backfrieder et al., 1996]. There are several advantages of following an ROI approach. Although PCA can be used to overcome some of the limitations of an ROI approach, a trade‐off exists between its exploratory power and the interpretability of the results. The number of significant components (i.e., PCs explaining above‐random variance) as well as their functional identity are not known a priori and require posthoc interpretation [Hansen et al., 1999; McKeown et al., 2003]. Due to the model‐free character, however, PCA is unable to distinguish PCs representing correlated noise from PCs representing stimulus‐related functional connectivity. Furthermore, maximal exploratory power can only be achieved when no data reduction occurs and all possible eigenimages are maintained. The number of possible eigenimages equals the number of voxels in the data set if PCA is carried out in the spatial domain and equals the number of volumes if PCA is applied in the temporal domain. If no restrictions limiting the model‐free and data‐driven character of PCA are introduced, the interpretability of the eigenimages is thus virtually impossible.

Using PCA as an ROI analysis enhanced the interpretability of the eigenimages in the following aspects. Initially, the dimensionality of the data set was reduced by including only those voxels whose goodness of fit exceeded the set threshold. Furthermore, significantly activated voxels generally exhibit a high signal‐to‐noise ratio. This not only increased the statistical power of the analysis but also decreased the probability that the most dominant PCs reflected structured noise. This assumption was supported by the observation that within significantly activated clusters, the voxel factor loadings on the first PC were positively correlated with the test parameter indicating the level of response associated with the stimulation paradigm in the functional activation maps (i.e., SSQ ratios). On the basis of this finding, it was concluded that the PCs detected by PCA do indeed reflect real functional connectivity rather than correlated noise.

The space of possible PCs was then further reduced to a subspace of significant components by applying various criteria to the component eigenvalue displays. Two main criteria had to be satisfied for a component to be significant: the Kaiser criterion [Kaiser, 1958] and the “elbow” criterion [Cattell, 1966]. Although both criteria are well established in the literature, the interpretation of eigenvalue displays is not straightforward and likely to be subjective. The reasons why a combination of these criteria was chosen over other alternative techniques were the following. Despite being very reliable and objective (i.e., PCs with an eigenvalue larger than 1.0 are significant), Kaiser's rule is very rigid and tends to overestimate the number of components. Only by combining Kaiser's rule with more informal criteria (e.g., the elbow criterion) can an accurate identification of the number of components be achieved. Secondly, formal statistical tests for determining the component number can only be employed under certain conditions. Most of these formal tests (e.g., chi‐square test) are based on the analysis of the residuals. The chi‐square test is available if maximum‐likelihood (ML) or generalized least‐squares (GLS) methods are chosen for factor extraction. It follows a confirmatory rather than exploratory approach as the number of factors has to be specified a priori, after which these components are fitted to the observed data. If the residuals between the hypothesized and the observed factor structure are too large, the chi‐square test becomes significant and the testing procedure needs to be repeated. There are, however, two important disadvantages of this technique. The chi‐square test statistic is calculated under the assumption of joint multivariate normal distribution. It is, however, still highly discussed whether the fMRI time series is normally distributed. Second, the chi‐square test statistic is very sensitive to sample size, i.e., a large sample size might result in a statistical significance. Thus, if the chi‐square test is used exclusively, the number of components will be overestimated by far. The question of how many PCs should be retained has been raised previously by Hansen et al. [1999]. The authors identified the number of PCs by minimizing the generalization error. This procedure is computationally very demanding. It would, however, be interesting to compare the number of significant PCs found in this investigation with the technique outlined by Hansen et al. [1999].

For display purposes and to achieve a better regional interpretability of the derived components, the factor loadings matrix underwent rotation using the VARIMAX criterion. Orthogonal factor rotation does not alter the overall structure of a solution (i.e., number of significant components) and leads to an identical prediction for the covariance matrix of the observed variables as the unrotated solution. By redistributing the factor loadings, voxels are classified in mutually exclusive brain regions, which can then easily be interpreted. Due to reasons of simplicity and generalizability, orthogonal factor rotation (uncorrelated components) was preferred to oblique rotation (correlated components). Alternatively, oblique factor rotation might be used in prospective research to provide a model that best fits the data as well as to enhance the biological plausibility of PCA.

Here the more traditional PCA was preferred to the more recent independent component analysis (ICA) [McKeown et al., 1998; Calhoun et al., 2001; Thomas et al., 2002; Beckmann et al., 2005]. Although both of these data‐driven methods aim to decompose a set of signals into a set of underlying sources, the criterion used for the decomposition is very different. Whereas PCA identifies underlying variables uncorrelated with each other, ICA assumes that source signals are also statistically independent (i.e., signal in ROI 1 does not contain any information about the signal in ROI 2). One of the key issues addressed in the present study was the identification of the number of significant components. As with PCA, the number of sources in ICA is unknown and needs to be estimated. The most widely used techniques for estimating the number of independent components (ICs), however, namely, the Akaike's information criterion (AIC) and the minimum description length criterion (MDL), are based on PCA [McKeown et al., 1998; Calhoun et al., 2001]. Both criteria make a decision by trading off the error in the model (i.e., residual variance) with the complexity of the model (i.e., degrees of freedom, dfs). The basic principle for deriving significant components in ICA and in this investigation is thus very similar (i.e., maintaining components that explain maximal variance by disregarding eigenvectors with the smallest eigenvalues). Contrary to the criteria in the present study, however, AIC and MDL assume that signals have a Gaussian distribution, an assumption that might not be met using fMRI data. Furthermore, PCs can be rotated in order to find a more interpretable set of factors without affecting the zero correlations between the factors, whereas ICs are uniquely identified and cannot be rotated. Despite the fact that PCA seems more suitable for identifying the number of significant components, to what extent ICA might lead to a better spatial or temporal separation of the components ought to be addressed by future research.

Functional Classification of Voxels in Human Visual System by PCA

This investigation was motivated by the notion that not all significantly activated voxels in conventional activation maps have to be functionally homogeneous and can be further classified into functional units by PCA. The number of functionally specialized units in a data set was assumed to equal the number of significant components. The data provided good evidence for this assumption.

It was first shown that the subspace of significant PCs was one‐dimensional if PCA was applied to a data set comprising voxels located in the same visual cluster. This finding offers direct empirical evidence for a frequently made hypothetical assumption in conventional univariate activation mapping, namely, that voxels within a cluster are functionally homogeneous and thus representing a single functional unit or cluster. The high degree of local connectivity further indicates that the univariate analysis of voxels within clusters is redundant, but that the time series of voxels within the cluster can be reduced to a single time series (i.e., the first eigentime series), which represents the overall functional activation in the cluster.

Second, a single underlying PC was also observed when PCA was carried out across time series extracted from bilateral homologue visual regions. Homologue visual regions are known to exhibit the same functional specialization [e.g., Wandell and Wade, 2003] and are spatially separated. This finding not only offered a direct validation of the technique but also refuted the argument that the number of PCs might be influenced by the spatial distance between selected voxels. On the cluster level, one would naturally expect a high degree of functional connectivity because all voxels within a cluster belong to the same anatomical region. However, rather than assuming that these voxels exhibit the same functional specialization, several methodological reasons might account for a high local connectivity. Due to technical reasons, the noise components in proximate voxels are more similar than noise components in spatially remote voxels. Furthermore, the intrinsic noise properties (e.g., signal‐to‐noise ratio) of anatomically defined ROIs differ between brain regions, which could enhance functional connectivity within ROIs. Finally, fMRI data sets are generally spatially smoothed either involuntarily (e.g., spatial blurring induced by realignment of images to template, or motion correction) or voluntarily (e.g., by smoothing filter). Despite the fact that the images were not intentionally smoothed with a smoothing filter in this investigation, the voxel time series were extracted from the motion‐corrected registered images. Smoothing induced by the spatial realignment could therefore not be excluded. However, a single significant PC was also observed in bilateral homologue regions, which are spatially too far apart to be smoothed in a similar fashion. The effect of smoothing was therefore considered negligible.

So far, the subspace of significant PCs considered has been exclusively one‐dimensional. Further analysis of two or more distinct visual areas, however, demonstrated that the number of PCs did indeed depend on the degree of functional heterogeneity between clusters. Based on current knowledge of the visual system, the strongest degree of functional heterogeneity was expected between the striate cortex or V1, which is involved in the initial encoding of a visual stimulus [e.g., Livingstone and Hubel, 1988; Sincich and Horton, 2004] and the motion‐sensitive area V5 also known as MT [Zeki, 1974; Watson et al., 1993; Tootell et al., 1995]. As hypothesized, two significant PCs were observed when voxels in V1 were analyzed in combination with voxels in V5/MT. Mathematically, PCs explain successive maximal variance in a data set subject to being uncorrelated or orthogonal. Therefore, the existence of a second component implies that the percentage of uncorrelated variance between V1 and V5/MT is considerably large (i.e., above random). Since each PCs was dominated by voxels in either V1 or V5/MT (i.e., simple structure), one can conclude that both regions must be functionally distinct. As can be inferred from the eigentime series, a likely explanation for the existence of two separate components for voxels in V1 and V5/MT could be the selective responsiveness of V5/MT following the presentation of moving stimuli, whereas voxels in V1 displayed a characteristic response in all conditions. A second component was, however, absent when voxels in V2/3 were analyzed simultaneously with voxels in V1 or V5/MT. Along the same line, one could argue that the absence of a second component implies that the percentage of variance explained by the second PC (and uncorrelated with the first PC) was negligible. This suggests that voxels in V2/3 seem to share variance with both V1 as well as V5/MT and should be considered to be one functional unit.

The absence of an additional component for V2/3 cannot be explained by issues surrounding the sensitivity of PCA. A two‐dimensional subspace of PCs was also observed when voxels in V2/3, as well as in V5/MT and V1, were analyzed in combination with a control region in the area of the temporal pole. Although likely to be anatomically connected with visual areas, voxels in this region did not display significant activation related to the stimulation paradigm and were therefore not expected to display a significant degree of functional connectivity.

In the final analysis step, it was demonstrated that the simultaneous analysis of voxels in V1, V2/3, and V5/MT revealed two significant components. The two components were dominated either by voxels in V1 or V5/MT exclusively, whereas voxels in V2/3 displayed medium correlations (i.e., factor loadings) with both PCs. One could therefore conclude that visual region V2/3 might represent a mediating area transmitting information between V1 and V5/MT. This finding is compatible with current neuroanatomical models of visual motion perception. These models are based on the magnocellular or M system. The M pathway assumes that the perception of moving stimuli originates in the retinal Pα cells, which project through the two lower layers of the Lateral Geniculate Nucleus (LGN) to neurons in layer 4Cα of the striate cortex. From there, information is conveyed to neurons in layer 4B. Neurons in layer 4B in turn project directly to V5/MT and indirectly via neurons in the thick cytochrome oxidase stripes of V2 [Maunsell and Van Essen, 1983]. The model of functional connections revealed by LPCA seems to be compatible with the indirect pathway involving projection from V1 to V5/MT via V2/3. It is, however, essential to point out that the proposed model of functional connectivity (i.e., “temporal correlations between spatially remote neurophysiological events” [Friston et al., 1993]) among visual areas V1, V2/3, and V5/MT does not allow conclusions on the effective connections between these areas (i.e., the influence that one neural system exerts over another either directly or indirectly [Friston et al., 1993]. For example, the data do not allow inference of whether visual information is processed by virtue of projections from V1 to V5/MT through V2/3 or vice versa. The direction in which the information is processed within these network components needs to be further established by alternative statistical techniques such as regression models or structural equation modeling (SEM).

There is evidence that the type of data processing carried out prior to the computation of the covariance matrix strongly affects the nature of the information and the patterns constituting the individual eigenimages. For instance, Andersen et al. [1999] pointed out that the potential misregistration of signals along the outer edge of the brain might introduce a large amount of variance, thereby influencing the direction of the PCs in the data space. In order to minimize the effects of data preprocessing (e.g., interslice interpolation, rendering of images to template), PCA was applied to voxel time series within individual slices and subjects. Simultaneous activation of visual areas V1, V2/3, and V5/MT within a single slice was, however, observed in one individual subject only (although in both hemispheres). Hence, the results of the simultaneous analysis of V1, V2/3, and V5/MT ought to be regarded as preliminary in nature and need to be replicated in prospective research.

PCA Applied to ROIs: A Generic Tool for Inferring Functional Homogeneity?

This study aimed to introduce an alternative approach to using PCA on fMRI data set in order to assess functional homogeneity within and between clusters of significant functional activation. The basic analytical framework was applied to the human visual system to demonstrate that the known functional subdivisions can be delineated by the proposed use of PCA. So far, however, the presented analytical framework seems more of a case study (i.e., the application of the employed analysis to a specific cortical system) rather than a generic analysis approach. In order to postulate the approach as a generic image analysis tool, future research is needed to address the following aspects.

To receive a first impression of the validity of the model, PCA was applied to fMRI data on the human visual system, which generally displays a high signal‐to‐noise ratio in comparison to other systems (i.e., neurocognitive networks). It thus remains to be shown that PCA performs equally well in other cortical networks with a lower signal‐to‐noise ratio, such as fMRI data sets coming from cognitive studies. An issue related to the specificity of the model is its statistical sensitivity. In the present study, it was demonstrated that PCA was able to distinguish between fMRI time series extracted from two functionally distinct visual regions (e.g., V1 and V5/MT) and that it is potentially quite sensitive even if components are extracted, which do not meet the outlined criteria. However, no formal attempt has yet been made to quantify numerically how different two time series have to be in order to be represented by a different component. This could best be addressed using stimulation studies, where the correlation coefficients between time series can be altered arbitrarily to examine the effects of this on the number and regional distribution of the components. Finally, the analysis was performed for each subject separately and within individual slices. Although this approach minimizes the as yet unknown effects of data preprocessing (e.g., slice‐timing correction, spatial normalization) on the correlation coefficient between the fMRI time series, it is unsuitable for inferring long‐range connectivity or for the comparison of different subject groups. More work is therefore needed in order to investigate the effects of preprocessing and to specify the outlined analytical framework on the group level.

CONCLUSIONS

To conclude, this study addressed an important problem of univariate functional activation mapping, which is the allocation of voxels to clusters on the basis of a common functional involvement. It was demonstrated that not all voxels in a conventional activation map are functionally homogeneous but can be further classified into functional units by PCA. The model of functional connectivity in the visual system derived by PCA was in accordance with its well‐known functional anatomy and anatomical connectivity, thus offering a direct validation of the technique. Unlike the cognitive subtraction technique, PCA is sensitive to temporal aspects of the time series (i.e., latency of the response) and does not rely on a model the hemodynamic response. This makes PCA particularly suitable for the investigation of brain regions whose response characteristics are less well established. By applying cognitive subtraction in a voxel‐by‐voxel fashion, a functional separation rather than classification can be achieved. PCA, however, allows for both functional separation as well as functional classification.