Simplified intersubject averaging on the cortical surface using SUMA

Abstract

Task and group comparisons in functional magnetic resonance imaging (fMRI) studies are often accomplished through the creation of intersubject average activation maps. Compared with traditional volume‐based intersubject averages, averages made using computational models of the cortical surface have the potential to increase statistical power because they reduce intersubject variability in cortical folding patterns. We describe a two‐step method for creating intersubject surface averages. In the first step cortical surface models are created for each subject and the locations of the anterior and posterior commissures (AC and PC) are aligned. In the second step each surface is standardized to contain the same number of nodes with identical indexing. An anatomical average from 28 subjects created using the AC–PC technique showed greater sulcal and gyral definition than the corresponding volume‐based average. When applied to an fMRI dataset, the AC–PC method produced greater maximum, median, and mean t‐statistics in the average activation map than did the volume average and gave a better approximation to the theoretical‐ideal average calculated from individual subjects. The AC–PC method produced average activation maps equivalent to those produced with surface‐averaging methods that use high‐dimensional morphing. In comparison with morphing methods, the AC–PC technique does not require selection of a template brain and does not introduce deformations of sulcal and gyral patterns, allowing for group analysis within the original folded topology of each individual subject. The tools for performing AC–PC surface averaging are implemented and freely available in the SUMA software package. Hum Brain Mapp, 2005. © 2005 Wiley‐Liss, Inc.

INTRODUCTION

The human cerebral cortex consists of a large, continuous sheet of tissue that is folded with deep involutions to fit inside the skull. While functionally the cortex is organized along its two‐dimensional (2‐D) surface, common noninvasive methods for examining cortex, such as MRI, produce 3‐D data. In order to bridge this dimensional gap, models of the cortical surface can be constructed from anatomical MRI data. These models are useful as a framework for the visualization and analysis of functional properties of cortex obtain with fMRI.

fMRI studies commonly use intersubject average activation maps created not on the surface but in the 3‐D volume. Each subject's brain is standardized, often to a template related to that of Talairach and Tournoux [1988], and averages are computed at each location in standard volumetric space. While volume‐averaging techniques are simple and reliable [Collins et al., 1994], they suffer from a key limitation. Functional brain regions, such as core areas of auditory cortex, are tied to locations on the cortical surface, such as Heschl's gyrus on the planum temporale. Because of intersubject variability in cortical folding patterns, these anatomical landmarks do not occupy the same location in standard volumetric space across subjects. Conversely, anatomical regions that are distant on the cortical surface (such as superior temporal gyrus and inferior frontal cortex) may occupy the same location in volumetric space. When averaging of functional data is performed in volumetric space, this anatomical variability results in decreased statistical power and poor quality averages.

A number of methods have been developed to apply information about cortical folding from surface models to the problem of intersubject averaging. For intersubject functional averages, several groups have proposed hybrid methods that combine volume averaging with information from a single canonical surface model, such as the Visible Man brain [Van Essen and Drury, 1997] or the Colin brain [Holmes et al., 1998]. Intersubject volume averages can be created, registered to the canonical surface model, and then visualized on the surface or compared with other datasets [Van Essen, 2002]. Kiebel and Friston [2002] proposed the use of anatomical priors based on the canonical surface model to apply different smoothing kernels to different locations in standard space during the volume‐averaging process. These approaches are valuable because they do not require the creation of a cortical surface model for each individual subject. Ultimately, they suffer from many of the same problems as volume averaging because the assumption is made that each individual's cortical surface is approximated by the canonical surface model. Because of the large individual differences in folding patterns, it is beneficial to construct a cortical surface model for each individual. Fortunately, there have been a number of recent advances in techniques underlying surface creation, including skull‐stripping [Segonne et al., 2004], topology correction [Fischl et al., 2001; Han et al., 2002; Kriegeskorte and Goebel, 2001; Shattuck and Leahy, 2001], extraction of the surfaces [Dale et al., 1999; MacDonald et al., 2000; Thompson et al., 2003], and unfolding [Drury et al., 1996; Fischl et al., 1999a; Wandell et al., 2000]. These advances have resulted in the availability of a number of software packages, including FreeSurfer (online at http://surfer.nmr.mgh.harvard.edu/) [Dale et al., 1999; Dale and Sereno, 1993; Fischl et al., 1999a], SureFit [Van Essen et al., 2001], BrainVoyager (http://www.brainvoyager.com) BrainSuite [Shattuck and Leahy, 2002], and CRUISE [Han et al., 2004] that allow rapid creation of topologically correct surfaces from T₁‐weighted MR images, making it feasible to construct surface models for each individual subject in an fMRI study.

Once surface models for each subject are available, the key issue becomes selecting a method for intersubject averaging. Surface morphometry methods detect anatomical changes in surfaces that occur over time or between patient populations [Chung et al., 2001, 2003; Liu et al., 2004; Shen et al., 2002; Thompson and Toga, 2002]. Some of these techniques rely on manual identification of sulci and gyri that are then warped to a template [Liu et al., 2004; Thompson et al., 2003, 2004; Van Essen et al., 2001]. A widely used surface‐averaging technique applied to functional data was proposed by Fischl et al. [1999b]. In this method the anatomical folding pattern of each surface is used to morph that surface to a template brain. Functional data from the individually morphed brains are then averaged in a standard spherical (2‐D) space. These surface‐based averages were reported to yield intersubject averages superior to those obtained from traditional volume averages. However, morphing methods like those proposed by Fischl and similar methods [Chung et al., 2003; Liu et al., 2004; Thompson et al., 2003] have some disadvantages. First, the morphing algorithms are complex, high‐dimensional operations that are computationally intensive. They require the selection of a template brain, to which all individual subjects are mapped. If the template is not a good match to the individual subjects (for instance, in developmental studies or clinical populations) or if the parameters for the morph are not optimized, morphing methods may produce unexpected results, such as heavily distorted sulcal and gyral patterns.

We describe a method that combines the simplicity of volume‐based normalization with the advantages of purely surface‐based averages in a two‐step process. First, a cortical surface model is created for each individual subject and aligned along the anterior and posterior commissure (AC–PC) axis, as in the first step of the traditional Talairach transformation. Second, each individual surface is standardized to contain the same number of surface nodes with identical node indexing. This occurs by unfolding the surface to a sphere, resampling to a projected standard icosahedron, and refolding the icosahedron to the original space of the cortical surface model. The result of this regularization is that any given node index corresponds to the same (or nearby) cortical location on each surface. Intersubject averaging is then a simple matter of comparing values at every node index in the original folded conformation of each brain.

The method proposed here has some conceptual similarity to a technique described for anatomical comparisons [Chung et al., 2003; MacDonald et al., 2000] in which a standard mesh is created first, then warped to fit the cortical anatomy of each individual subject. The result is similar, in that a given node (or point on the mesh) corresponds to a similar anatomical location in each subject. However, accurate warping of a standard mesh to the complex and deep folding pattern of human cortex can be difficult. From a practical standpoint, it is simpler and more flexible to convert an already created whole‐brain cortical surface models (available from a variety of sources) to a standard indexing system via icosahedral tessellation.

The results of applying this AC–PC technique to anatomical and functional datasets are illustrated. A large increase in statistical power, compared with volume‐based averaging applied to the same dataset, was observed. Surprisingly, the results from the simple AC–PC method were similar to those obtained with more complex morphing methods. Because the AC–PC technique is simple and does not require the choice of a template brain or the distortion of anatomical features, it may help to promote the use of intersubject surface averages in fMRI studies.

SUBJECTS AND METHODS

Human Subjects and MR Data Collection

Twenty‐eight subjects underwent a complete physical examination and provided informed consent. Subjects were compensated for participation in the study and anatomical MR scans were screened by the NIH Clinical Center Department of Radiology in accordance with the NIMH‐IRP human subjects committee. MR data were collected on a General Electric 3 T scanner.

Surface Creation

Surface models were analyzed in SUMA [Saad et al., 2004], a component of the AFNI package (online at http://afni.nimh.nih.gov). SUMA does not create cortical surface models but can process surfaces generated by several packages, including SureFit, FreeSurfer, and BrainVoyager. All surfaces in this study were created from an average of one to five high‐resolution MP‐RAGE anatomical scans using FreeSurfer [Dale et al., 1999; MacDonald et al., 2000; Thompson et al., 2003].

Surface Standardization

In order to prepare the surfaces for intersubject averaging a two‐step standardization process was performed. The programs developed to perform the standardization are now freely available in the AFNI distribution and their usage is described in the online documentation.

In the first step, each subject's surface was aligned (Fig. 1A). Markers were manually placed on both the AC and PC and in the mid‐sagittal plane in the subject's anatomical volume dataset. The brain volume was then translated and rotated so that the subject's AC and PC aligned with the AC–PC line in canonical Talairach space [Talairach and Tournoux, 1988]. While this step required minimal human interaction (<5 min per subject), automated procedures for AC–PC alignment are also available. The AC–PC transformation was then applied to the subject's surface (in both folded and spherical forms) to create an AC–PC aligned cortical surface model. Although this step aligned the surfaces, raw surface models have several properties that make them unsuitable for cross‐subject averaging. Raw surfaces vary greatly in the number of nodes (surface elements) for each subject, and the correspondence between node index and physical location in the cortex can be highly irregular. This often occurs during the topology‐fixing stage of surface creation, in which small errors in the surface are corrected by the insertion of new nodes whose indices differ greatly from adjacent nodes.

Figure 1.

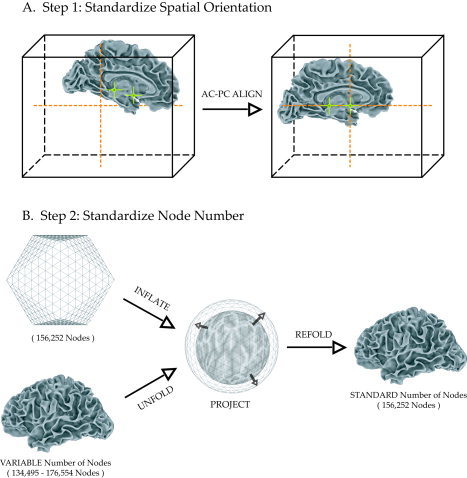
Two‐step process for creating standard individual subject surfaces. A: Spatial orientation is standardized by aligning the anterior and posterior commissures (AC and PC) to the center of standard space by translating and rotating the surface. An additional mid‐sagittal point (not shown) is used to define the plane. B: Node number is standardized by resampling to a projected standard icosahedron and refolding to the original space of the cortical surface model. When initially created, surface models contain variable numbers of nodes across subjects (left bottom). An icosahedron is tessellated to a standard number of nodes (left top). The icosahedron and the AC–PC aligned surface model are inflated to spheres (middle). The unfolded spherical representation of the surface model is mapped onto the inflated icosahedron, which is then refolded, resulting in a representation of the brain surface in its original state with a standard number of nodes (right).

To fix these problems and to reduce intersubject variability in folding patterns, in the second step of standardization the number of nodes (and node numbering scheme) in each subject's surface was standardized using icosahedral tessellation and projection (Fig. 1B). Each individual surface was unfolded and inflated to a sphere using the FreeSurfer mris_sphere routine [Dale et al., 1999; Fischl et al., 1999a]. Then an icosahedron was created and tessellated to a linear depth of 125 (each edge had 125 divisions, and therefore contained 126 parts) resulting in 156,252 nodes in the entire icosahedron. The tessellated icosahedron was then inflated to a sphere. Next, the spherical icosahedron was projected onto the unfolded, spherical representation of the subject's AC–PC aligned cortical surface. For each node on the inflated icosahedron, nearby nodes on the inflated spherical surface were selected. Finally, the coordinates of these surface nodes on the original (folded) brain were interpolated using a barycentric (area‐weighted) coordinate scheme and assigned to the icosahedral node [Saad et al., 2004]. This resulted in a surface with the same number of nodes as the icosahedron but with a folded spatial configuration. The standardized surfaces closely matched the original surfaces, with a mean distance between the original and standardized surfaces of 2 × 10⁻⁵ mm [Saad et al., 2004]. All intersubject averaging was done on the standardized nodes in the original folded cortical configuration of each subject, not in the inflated (or otherwise distorted by morphing) spherical surface model.

fMRI Experiment

In eight subjects, gradient‐recalled‐echo echo‐planar volumes were acquired with echo time (TE) of 30 ms, repetition time (TR) of 3 s, and 3.75 mm in‐plane resolution. Each volume contained 24 axial slices (slice thickness of 4.5 or 5.0 mm as necessary to cover the entire cortex) with 132 volumes per scan series and 8 to 10 scan series per subject. Stimuli for the fMRI experiment consisted of video clips of moving manipulable objects (e.g., a hammering hammer), auditory recordings of these objects (e.g., “bang‐bang‐bang”), or simultaneously presented videos and recordings. An event‐related design was used, with each trial containing distinct sensory stimulation and behavioral response epochs, allowing separate estimation of the response to the stimulus and response in each voxel using AFNI 2.50 [Cox, 1996]. The first two volumes in each scan series, collected before equilibrium magnetization was reached, were discarded. Then all volumes were registered to the volume collected nearest in time to the high‐resolution anatomy. Next, a spatial filter with a root‐mean‐square width of 4 mm was applied to each echo‐planar volume. The response to each stimulus category was estimated using a deconvolution method which made no assumptions about the shape of the hemodynamic response. Individual subject activation maps were created by using the overall experimental‐effect (all regressors of interest) to find voxels showing a response to any type of stimulus at a threshold of P < 10⁻⁶ to correct for the multiple comparisons produced by 20,000–25,000 intracranial functional voxels. A more liberal threshold of P < 0.05 was used to isolate individual ROIs (see below). For more details on the fMRI experiment, please see Beauchamp et al. [2004b].

Intersubject Surface Averaging

After the standardization process each individual subject cortical surface contained the same number of nodes. In addition, these nodes were in approximate spatial alignment, so that each node with a given index (in the range of 1–156,252) corresponded, insofar as the surfaces were brought into alignment by the method, to a similar brain location in each subject. Therefore, intersubject averaging could be performed by simply averaging the values of interest across subjects at each node index.

To average structural data, the spatial xyz coordinates associated with a given node index were averaged across subjects (Fig. 2, right). To average functional data, individual surface functional maps were created using an intersection algorithm in SUMA. For each subject, each node on the surface was assigned the t‐statistic corresponding to the original (uninterpolated) functional voxel which it intersected. Then the t‐statistic at each node index was averaged across subjects (Fig. 3B, right).

Figure 2.

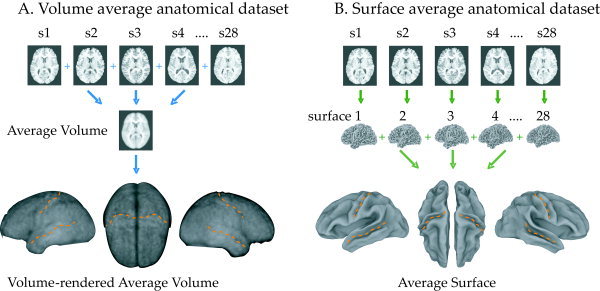
Comparison of volume (A) and surface (B) intersubject averaging techniques with anatomical MR data. A: Whole‐brain anatomical scans from 28 subjects (top row) were transformed into standard space and the intensity was averaged in each voxel, creating a volume‐averaged anatomical dataset (middle row). A volume renderer was used to create a lateral view of the average left hemisphere, a top‐view of both hemispheres, and a lateral view of the right hemisphere (bottom row). Orange dashed lines indicate the approximate location of central sulcus and superior temporal sulcus. B: For the surface average, the same anatomical datasets were used to create cortical surface models (middle row). Each surface was then standardized (see Fig. 1) and the position of each node was averaged in space to create a surface‐average anatomical dataset (bottom row).

Figure 3.

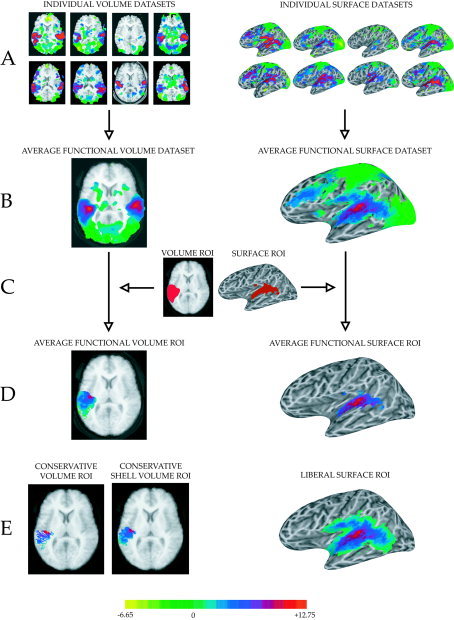
Comparison of volume (left column) and surface (right column) intersubject averaging techniques on BOLD fMRI data from auditory cortex. fMRI data (in color, overlaid on anatomical data, shown in gray scale) represents the t‐statistic of the contrast of the response to auditory vs. visual stimulation. Auditory cortex, in the planum temporale, shows a strong positive value for this contrast (red color, color scale shown at bottom of figure). A: Left: Functional datasets from each individual subject (n = 8) were Talairach transformed (slices shown at z = 10 mm). Right: Cortical surface models were created for each individual subject and functional data was mapped from the volume to the surface. B: Left: The average volume dataset was created by averaging the t‐statistic (for functional) or intensity (for anatomical) values at each location in Talairach space across subjects. Right: The average surface dataset was created by averaging the t‐statistic at each standardized node (displayed on an individual subject surface). C: A region of interest (ROI) for auditory cortex was created from the functional intersubject average volume and surface datasets. D: The auditory cortex ROI was applied to average volume (left) and surface (right) datasets. E: Alternative ROIs for comparison. Left: More conservative volume ROI created by surface gray‐white intersection algorithm. Middle: More conservative volume ROI created by cortical shell intersection algorithm. Right: Liberal surface ROI created by selecting all nodes intersecting the volume ROI in any of the individual subjects.

Volume Data Averaging

Each subject's anatomical dataset was converted to standard space using stereotactic normalization [Talairach and Tournoux, 1988] with 1 mm³ resolution in AFNI. To average anatomical data, the intensity at each location in Talairach space was averaged (Fig. 2 left). To average functional data, the t‐statistic at each location in standard space was averaged (Fig. 3B, left).

Spherical Morphing

As an additional source of comparison, intersubject averaging was performed using the MGH FreeSurfer tools [Dale et al., 1999; Fischl et al., 1999a]. Using the mris_register [Fischl et al., 1999b] routine, each individual subject's surface was registered to the FreeSurfer average7 template prior to node number standardization. Standardization and averaging were then performed on the surfaces as described above.

Region of Interest (ROI) Creation

Because the fMRI dataset contained auditory, motor, and visual components, ROIs were created in auditory, motor, and visual cortex. Benchmark ROIs were first created in the average volume dataset, then applied to each individual subject, giving measurements from roughly the same brain area in each subject [Buckner et al., 2000]. While it is possible to create separate ROIs for the surface and volume, this complicates comparisons between surface and volume because of possible confounds (for instance, if surface ROIs were systematically smaller or larger than volume ROIs, the comparison between surface and volume might be biased).

The benchmark auditory cortex ROI was created by finding active voxels in and near Heschl's gyrus, the location of core areas of auditory cortex [Hackett et al., 2001]. More precisely, the ROI contained all contiguous voxels in the functional average volume dataset (Fig. 3B, left) that showed a significant overall experimental effect (F > 8.23, P < 10⁻⁶) and a significant (P < 0.05) preference for auditory compared with visual stimuli. The benchmark motor cortex ROI was created by selecting all contiguous voxels in the region of the left central sulcus that showed a significant experimental effect (F > 8.23, P < 10⁻⁶) and a significant (P < 0.05) preference for the response epoch of the trial compared with the visual epoch. The benchmark visual cortex ROI contained all contiguous voxels in left occipital lobe (Talairach z, −20 < z < 35) that showed an experimental effect and a significant preference (P < 0.05) for the visual compared with the auditory stimulus epochs.

These benchmark volume ROIs (shown for auditory cortex in Fig. 3C, left) became the reference on which all other individual and average ROIs were based. For each region (auditory, motor, or visual) the volume ROI was intersected with each subject's standardized cortical surface, producing a list of nodes for each subject. Surface nodes that were present in every subject were used to create the surface ROI (Fig. 3C, right). Finally, these ROIs were applied to the functional datasets (Fig. 3B) to create functional volume and surface ROIs (Fig. 3D, left and right).

Alternative ROIs

This procedure was relatively straightforward and similar to that used in previous studies. However, due to the lack of a one‐to‐one correspondence between volume and surface elements, there are many equally reasonable ways to construct corresponding volume and surface ROIs. If a typical fMRI activation profile is assumed (in which a few voxels with very high significance are surrounded by voxels with less significance) ROI creation methods that are more liberal (include more elements) will give lower mean/median statistics, while ROI creation methods that are more conservative (include fewer elements) will give higher mean/median statistics. To determine the dependence of surface vs. volume comparisons on the method used to create ROIs, statistics were calculated for liberal auditory cortex surface ROIs and conservative auditory cortex volume ROIs. While in the initial surface analysis only those nodes found in every subject were included in the ROI, for the liberal surface ROI nodes found in any subject were included in the ROI (Fig. 3E, right). In the initial volume analysis, all voxels in the volume ROI were included. For the first conservative volume ROI, only those voxels intersected by the surface ROI in at least one subject volume were included (Fig. 3E, left). For the second conservative volume ROI, an additional restricted volume ROI was created that included only those voxels intersected by the cortical shell ROI (the surface ROI applied across gray matter, from gray‐white boundary to pial surface) in at least 3 of 8 subjects (Fig. 3E, middle). Additional ROIs were also created by varying this “x of 8” intersection criterion, with similar results. Only the data with the “3 of 8” criterion is reported because it produced an ROI whose volume most closely matched the volume of the mean of the individual subject cortical shell ROIs.

RESULTS

Intersubject Averaging of Anatomical Data: Surface vs. Volume

Using the AC–PC standardization method, 28 individual subject cortical surface models were created and averaged to produce an average surface dataset. For comparison, anatomical volumes from the same subjects were Talairach transformed and averaged to produce an average volume dataset. To give a qualitative impression of the differences between surface and volume intersubject averages, the two were visualized (Fig. 2). Anatomical features in the 28‐subject average volume dataset were markedly blurred, with only the lateral sulcus (Sylvian fissure) clearly visible in the volume rendering. In contrast, most major sulci and gyri were visible in the average surface dataset, including the central sulcus and the superior temporal sulcus.

Intersubject Averaging of Functional Data: Surface vs. Volume

An auditory cortex ROI was applied to the surface and volume average functional datasets and activation statistics were calculated (Fig. 4A). The mean t‐statistic from the surface average (t = 7.00, 99% confidence interval 6.58–7.42) was significantly greater than the mean t‐statistic from the volume average (t = 2.92, 2.68–3.17, P < 10⁻¹⁰). The surface average also produced significantly better results as measured by the maximum and median statistics (surface vs. volume maximum t = 12.62 vs. 9.50, surface vs. volume median t = 6.96 vs. 2.64).

Figure 4.

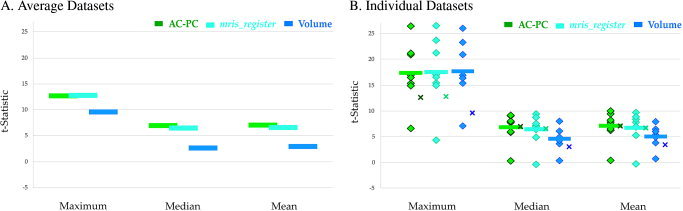
Statistical comparisons on functional data averaged with three different methods. A: The auditory cortex ROI was applied to surface and volume average datasets (see Fig. 3) and the maximum, median, and mean t‐statistics were calculated. The variability of each estimate was low: SD less than or equal to the thickness of each bar. Green symbols show the result of the AC–PC surface averaging method. Light blue symbols show the result of the mris_register surface averaging method [Fischl et al., 1999b]. Dark blue symbols show the volume average results. B: The surface average ROI was applied to each individual surface, and the volume average ROI was applied to each individual volume, generating maximum, median, and mean t‐statistics for each subject (same color scale as A). The average of these individual values (thick bars) provides an estimate of the ideal average value (assuming perfect intersubject alignment). This ideal value can be compared with the actual value obtained from surface and volume averages taken from A (shown with “x” symbols).

While more significance is notable, one might ask what the true average should be. While there is no “gold standard” or perfect method for intersubject averaging, the results of an ideal averaging method can be estimated. If intersubject alignment were perfect (and activation patterns identical across subjects) the voxels showing maximum activation within the ROIs would align perfectly and the maximum value of the average dataset ROI would be the same as the average of the maximums of the individual subject ROIs. Therefore, the difference between the maximum in the average dataset and the mean of the individual subject maximums provides one measure of the accuracy of the intersubject alignment (maximum value in average dataset much lower than average of individual maximums ∼ poor alignment, similar values ∼ good alignment). To assess this difference, ROIs from the average surface and volume datasets were applied to each individual surface and volume datasets (Fig. 4B). As expected, the average of the maximums in the individual surface and volume datasets (the theoretically perfect method) was higher than the maximum in the average datasets. However, the intersubject surface average was a closer approximation to the average of the individual surface ROIs (intersubject vs. individual maximum t = 12.62 vs. 17.35) than the intersubject volume average was to the average of the individual volume ROIs (intersubject vs. individual maximum t = 9.50 vs. 17.78). This suggests that averaging on the surface more closely aligns functionally similar regions across subjects.

The same comparison can be performed for the median and mean statistics. The intersubject surface average values were similar to the values obtained by averaging across the individual subject ROIs (intersubject vs. individual median t = 6.96 vs. 6.72, intersubject vs. individual mean t = 7.00 vs. 7.00), while the volume intersubject ROI was considerably lower than the individual subject volume ROIs (intersubject vs. individual median t = 2.64 vs. 4.18, intersubject vs. individual mean t = 2.92 vs. 4.67). These results also suggest that intersubject surface averaging more closely aligns functionally homologous regions and provides a more accurate approximation to individual subject activation maps.

Surface vs. Volume Averaging With Alternative Auditory Cortex ROIs

To ensure that these results were not solely due to the exact definition of the auditory cortex ROI, the same analyses were carried out with different ROIs. The liberal surface ROI was much larger (427.2%) than the original surface ROI, and encompassed many weaker areas of activation outside the central peak of activity (Fig. 3E). Even so, the maximum and mean statistics were still greater than the volume ROI (liberal surface vs. volume maximum t = 12.62 vs. 9.50, liberal surface vs. volume mean t = 3.32 vs. 2.92) and the median was similar to the volume ROI (liberal surface vs. volume median t = 2.62 vs. 2.64). For the conservative volume ROIs, information about the individual subject surface geometry was used to constrain the voxels contributing to the intersubject volume average, eliminating weaker activations (see Subjects and Methods). However, both conservative volume ROIs still had lower maximum, median, and mean statistics than those of the surface ROI (first conservative volume ROI: surface vs. volume maximum t = 12.62 vs. 9.50, surface vs. volume median t = 6.96 vs. 3.31, surface vs. volume mean t = 7.00 vs. 3.41; second conservative volume ROI: surface vs. shell volume maximum t = 12.62 vs. 9.50, surface vs. shell volume median t = 6.96 vs. 3.97, surface vs. shell volume mean t = 7.00 vs. 4.09).

Comparisons Using Motor and Visual ROIs

The relative statistical power of surface and volume averaging methods was examined in two additional ROIs located in visual and motor cortices. The maximum, median, and mean statistics were greater for surface compared with volume averages in both visual cortex (surface vs. volume maximum t = 15.6 vs. 10.0, surface vs. volume median t = 7.0 vs. 3.2, surface vs. volume mean t = 8.2 vs. 3.2) and motor cortex (surface vs. volume maximum t = 10.8 vs. 8.5, surface vs. volume median t = 7.7 vs. 6.1, surface vs. volume mean t = 7.8 vs. 5.9).

Node and Voxel Correspondence Across Subjects

One reason for the superiority of surface vs. volume intersubject averaging is better alignment of anatomical elements across subjects. In order to quantify this advantage, an intersection comparison was performed between surface and volume mapping to determine how often corresponding elements were found in different individual subjects (Fig. 5). Each individual surface ROI contained different numbers of nodes and different node spatial placements, depending on the cortical geometry of that subject. Due to the one‐to‐one correspondence of node index across subjects, the total number of node indices present in one or more individual subject ROIs was summed and used as the denominator in the intersection fraction (total node‐count). Then, for each of these node indices the number of individual surface ROIs that contained it was counted (subject‐count). The intersection fraction was calculated as the number of nodes with a given subject‐count, divided by the total node‐count. As shown in Figure 5A, this fraction decreases as the subject‐count increases. By definition, all nodes are found in at least one subject ROI, for an intersection fraction of 100%, while only 22% of the nodes were found in all eight subject ROIs. More than 50% of the total nodes were found in five subject ROIs.

Figure 5.

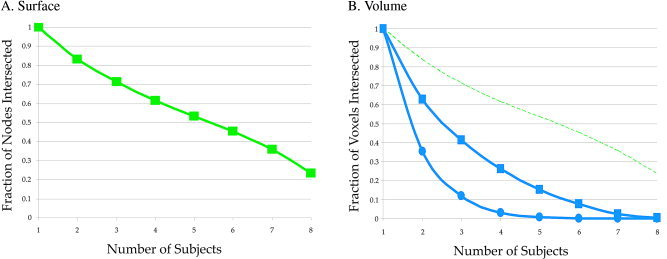
Correspondence of ROI constituents across subjects for surface (A) and volume (B) averages. A: The auditory cortex volume ROI (Fig. 3C, left) was intersected with the surface models from eight subjects, creating eight distinct surface ROIs. The proportion of nodes found in multiple individual subjects was tallied (100% of nodes found in at least one subject, 22% of nodes found in all eight subjects). B: The auditory cortex surface ROI (Fig. 3C, right) was intersected with the volume datasets of eight subjects, creating eight distinct volume ROIs. The proportion of Talairach locations found in multiple individual subjects was tallied. Volume ROIs calculated with a gray‐white matter intersection algorithm (blue circles) and a cortical shell intersection algorithm (blue squares). Surface ROI from A shown for comparison (dashed green line).

The same comparison was performed for the volume average by mapping the average surface ROI to the volume in each individual subject, creating eight distinct volume ROIs. These ROIs contained different numbers of voxels and different voxel locations, depending on the cortical geometry of each subject. The total number of locations present in one or more individual subject ROIs was summed and used as the denominator in the intersection fraction. In contrast to the surface intersection curve, which showed an approximately linear decrease with increasing subject number, the volume intersection fell off sharply with increasing subject number (Fig. 5B). More than 50% of the total locations were found in only one subject, and no corresponding locations were found for a subject‐count greater than 4.

This low correspondence was in part due to the fact that volume‐to‐surface mapping was performed using the cortical surface created from the gray/white matter boundary. This means that any given surface ROI maps to a thin shell of voxels in the volume, which are unlikely to intersect across subjects. To circumvent this problem, an alternative surface‐to‐volume mapping was performed using a thickened shell surface model that spanned gray matter from the gray/white boundary to the pial surface. This mapping improved intersubject correspondence, but most locations were still found in only two of eight subjects (Fig. 5B). Surface node correspondence was much better than volume correspondence using either method.

Intersubject Averaging of Functional Data: Different Surface Methods

In the simplified AC–PC surface averaging method, no explicit steps were performed to ensure anatomical or functional correspondence between nodes with the same node index in different subjects. Methods to align cortical surfaces [Thompson et al., 1996; Van Essen et al., 1998] usually involve fluid deformation or morphing of individual surfaces. In order to compare the AC–PC method to these more complex algorithms, the FreeSurfer program mris_register [used in Fischl et al., 1999b] was used to morph the cortical surface models to a predefined template, and these morphed surface models were then used to create a morphed surface average. Maximum, median, and mean statistics were calculated using the auditory cortex ROI for AC–PC and mris_register surface averages (Fig. 4A). Compared to the large differences between AC–PC surface and volume averages, the AC–PC and mris_register surface averages gave very similar results. The AC–PC average had slightly lower maximum values (AC–PC vs. mris_register maximum t = 12.62 vs. 12.70) but slightly higher median and mean values (median t = 6.95 vs. 6.46, mean t = 7.00 vs. 6.58). As was done with the volume average, theoretical‐ideal averages were calculated using ROI values from individual subjects that had undergone AC–PC or mris_register standardization (Fig. 4B). Again, the AC–PC and mris_register results were nearly identical. The similarity is apparent in a cortical surface rendering of the entire auditory cortex ROI (Fig. 6A). Motor and visual cortex ROIs averaged using AC–PC and mris_register were also very similar, both qualitatively (Fig. 6B,C) and quantitatively (motor cortex: AC–PC vs. mris_register maximum t = 10.9 vs. 11.6, median t = 7.7 vs. 7.5, mean t = 7.8 vs. 7.7; visual cortex: maximum t = 15.6 vs. 13.0, median t = 7.9 vs. 7.9, mean t = 8.2 vs. 7.9).

Figure 6.

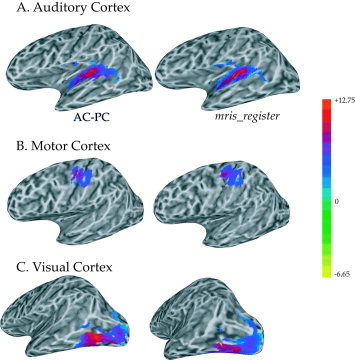
Auditory (A), motor (B), and visual (C) cortex ROIs applied to functional averages created with two surface‐averaging techniques, AC–PC and mris_register. A: Surface ROIs for auditory cortex generated with AC–PC alignment (left) and mris_register morphing (right). Colors represent t‐statistic of functional contrast (color bar at right, same for A, B, C). B: Surface ROIs for motor cortex. C: Surface ROIs for visual cortex.

Intersubject Averaging of Anatomical Data

To assess the AC–PC averaging method on purely anatomical data, an average brain was constructed from 28 AC–PC aligned brains (Fig. 7A). For every node position the standard deviation of the distance between each individual subject and the average brain was calculated (Fig. 7B). The standard deviation was relatively small (averaged across nodes, 3.9 ± 0.9 mm SD). The largest standard deviation was observed in regions far from the AC–PC landmarks used in the alignment, such as the vertex.

Figure 7.

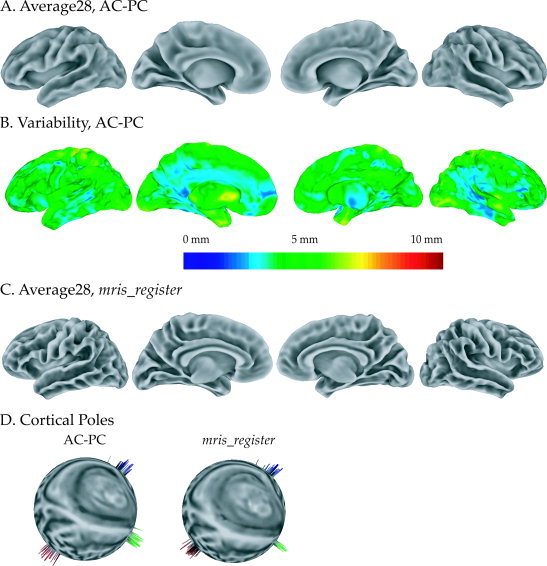
Comparisons of anatomical averages created with two surface averaging techniques, AC–PC and mris_register. A: An average surface was created by averaging the location of each node across 28 subjects following AC–PC standardization. From left to right, left hemisphere (lateral and medial), right hemisphere (medial and lateral). B: The standard deviation between individual subjects and the average surface was calculated at each location on the surface and mapped to the average surface (color scale shows distance). C: Average surface created by averaging the same 28 subjects using mris_register standardization. D: Location of cortical poles following AC–PC (left) and mris_register (right) alignment. Temporal poles (green), occipital poles (red), and frontal poles (blue) were manually selected in each individual subject. The standard node index of each pole following registration is plotted on a spherical left hemisphere. Each spike (shown projecting normal to the surface for visibility) represents an individual subject.

An average of the same 28 brains was constructed using mris_register (Fig. 7C). To quantify the difference between the AC–PC and mris_register averages, anatomical landmarks were selected in each subject and their position was measured after alignment. The frontal, temporal, and occipital poles were chosen because of their unambiguous location. The position of the poles was measured in spherical coordinates on the template sphere (for the mris_register average) or on the sphericalized icosahedron (for the AC–PC average) as shown in Figure 7D. Given spherical coordinates (r, theta, phi) of a landmark for each subject, the standard deviation (SD) of theta and phi measure the variance of the landmark and provides an estimate of the intersubject variability that remains following intersubject alignment (the value of the radius, r, is fixed and depends arbitrarily on the inflation parameters, while the absolute values of theta and phi depend on the orientation of the mris_register template sphere). For the mris_register average, the SD of theta of the (temporal, frontal, occipital) poles was (5.8°, 6.0°, 6.4°), averaged across left and right hemispheres, and the SD of phi was (3.7, 5.5, 5.4). For the AC–PC average, the SD of theta was (9.0, 3.3, 4.2) and of phi was (3.6, 5.2, 4.4). A paired t‐test across poles and hemispheres did not show a significant different between the two averages for either theta (P = 0.8) or phi (P = 0.2).

DISCUSSION

We describe a simple two‐step method for aligning and standardizing surface models from different individual subjects. Anatomical averages using this AC–PC method were qualitatively superior to Talairach volume averages. This improvement was also observed for a functional dataset. Auditory, visual, and motor cortex ROIs showed higher test statistics for surface compared with volume averages. These results are consistent with those of Fischl et al. [1999b], who found improvements over volume averages for surface averages created using the mris_register morphing algorithm.

Reasons for the Superiority of Surface Averaging

For a variety of surface and volume ROIs, better results were observed for surface than volume averaging, suggesting that surface averaging provides better alignment across subjects (accounting for anatomical variability) than does volume averaging, resulting in better average functional maps.

Even in individual subjects, the mean and median t‐statistic from the surface ROI was higher than the mean and median from the volume ROI. An obvious explanation for this is that the volume ROI includes both parenchyma, containing active neurons, and white matter, inactive in BOLD fMRI. In contrast, the mapping process used to create the individual subject functional surface datasets ensures that primarily gray matter voxels are mapped to the surface. On average, only 26.3 ± 1.5% of the voxels in each subject's volume ROI intersected the surface (and therefore were likely to be active in BOLD fMRI).

Cortical folding patterns are highly variable across subjects, and so any given anatomical location (such as the fundus of the STS) is unlikely to align precisely from subject to subject in the volume. Because intersubject averaging is done on node indices assigned after the brains are unfolded to a sphere, intersubject differences in the depths of sulci and the details of folding patterns are eliminated as a source of variability. This can be also be examined from the perspective of a reduction in dimensionality. In the 3‐D volume, a distance of a few mm in standard space can traverse very large distances in cortical space (e.g., from anterior temporal cortex to inferior frontal cortex). Because intersubject alignment is inherently only accurate to several mm, the inevitable result is that functional data from very different brain regions are averaged, decreasing statistical power. On the 2‐D surface, distances of a few mm traverse only a limited distance in brain space (e.g., from the fundus of the STS to the banks of the STS). Even with inaccuracies in intersubject alignment of a few mm, there is a much greater chance that functionally homologous regions will be averaged.

To gain a better understanding of these effects, the volume ROI was made more conservative by requiring that voxels in the ROI be located in gray matter in increasing numbers of subjects. That is, voxels were included in the ROI only if they intersected the surface in one of eight, two of eight, to eight of eight subjects. As the volume ROI grew more and more restrictive, the activation statistics approached those of the surface average. At the limit, since the mapping between standard space locations and surface nodes is known for each subject, the surface average could be exactly duplicated in the volume by averaging together those voxels in each subject that mapped to the same surface node. It should be noted that this is only possible if a surface model is available for every subject, and hence is not an argument in favor of volume vs. surface averaging.

Another reason for the superiority of AC–PC averaging is that there is no explicit need for brain scaling. Unlike Talairach normalization, in which different portions of the brain receive different amounts of affine stretching, the folding of the standardized icosahedron into the shape of the original cortical surface model effectively creates a scale‐invariant brain, removing another source of intersubject variability. There are other advantages to performing fMRI analysis on the cortical surface as well. For instance, because many fewer voxels are mapped to the cortical surface than exist in the volume, the denominator in the Bonferroni correction is much lower, allowing a lower threshold for the same statistical significance [Andrade et al., 2001]. In the present datasets, only 1.86 ± 0.10% of the voxels in each subject's volume dataset mapped to the cortical surface.

It should be noted that the standard space used to create the volume average was that of Talairach and Tournoux, a simple and commonly used transformation. Other methods of volume normalization that involve higher dimensional volume warping would likely improve intersubject correspondence in the volume and so reduce the advantage of surface averaging. However, because these methods do not take into account cortical folding patterns, it is unlikely that they could completely match the performance of the surface average [Thompson and Toga, 2002].

Comparing the AC–PC Method With Other Surface Averaging Techniques

Both AC–PC and mris_register surface‐averaging techniques offered large improvements over volume averages, but there was little difference between the surface methods. On practical grounds, morphing techniques such as mris_register require a template, which is a concern for clinical and developmental studies for which an ideal template may not be available. In contrast, the AC–PC method does not require a template. In addition, the AC–PC method allows intersubject statistics to be performed in the original folded configuration of the brain, preserving any inherent variation that may be of interest, such as anatomical differences in sulcal depths between patient populations.

One might expect that a method that actively aligns sulcal and gyral landmarks (such as mris_register) would produce better functional averages than the AC–PC method. Surprisingly, we found similar results for the two methods. This suggests that the most important reason for the superiority of surface averaging is the reduction in dimensionality from three dimensions (for volume averaging) to two dimensions (for surface averaging), with additional alignment based on anatomical landmarks patterns adding little. This idea is supported by recent evidence showing that, across species, aligning only anatomical landmarks does a poor job of aligning functionally homologous regions, while adding the location of identified areas (such as area MT) gives better results [Orban et al., 2004; Van Essen, 2004]. In future studies, it will be important to explore the use of appropriate fMRI localizers to produce better alignment of functionally homologous regions and improved intersubject averages.

CONCLUSIONS

The match between the spatial resolution of the technique and the resolution of intersubject averaging methods will become even more important as fMRI reaches higher and higher spatial resolutions [Beauchamp et al., 2004a]. Because volume‐averaging methods are barely adequate for fMRI studies at standard resolution, they are certain to be a handicap for high‐resolution fMRI studies. In contrast, the surface models used in surface averaging techniques can be created and aligned with high spatial resolution.

For the normal population used in the present validation, the AC–PC method resulted in greater statistical power compared with traditional volume‐based normalization, and gave results comparable to methods that actively align major sulci and gyri. It will be interesting to further validate the method in different clinical populations and in fMRI studies with different experimental tasks and different numbers of subjects, and to study the effect of different techniques for unfolding individual surface models to a sphere.

The software for performing AC–PC averaging is freely available and is compatible with surfaces created by several standard packages. Because of the large improvements in statistical power for surface compared with volume averages documented in this study and in Fischl et al. [1999b], the use of surface averages should be considered in fMRI studies whenever cortical surface models are available.