Motion correction and the use of motion covariates in multiple‐subject fMRI analysis

Abstract

The impact of using motion estimates as covariates of no interest was examined in general linear modeling (GLM) of both block design and rapid event‐related functional magnetic resonance imaging (fMRI) data. The purpose of motion correction is to identify and eliminate artifacts caused by task‐correlated motion while maximizing sensitivity to true activations. To optimize this process, a combination of motion correction approaches was applied to data from 33 subjects performing both a block‐design and an event‐related fMRI experiment, including analysis: (1) without motion correction; (2) with motion correction alone; (3) with motion‐corrected data and motion covariates included in the GLM; and (4) with non–motion‐corrected data and motion covariates included in the GLM. Inclusion of covariates was found to be generally useful for increasing the sensitivity of GLM results in the analysis of event‐related data. When motion parameters were included in the GLM for event‐related data, it made little difference if motion correction was actually applied to the data. For the block design, inclusion of motion covariates had a deleterious impact on GLM sensitivity when even moderate correlation existed between motion and the experimental design. Based on these results, we present a general strategy for block designs, event‐related designs, and hybrid designs to identify and eliminate probable motion artifacts while maximizing sensitivity to true activations. Hum. Brain Mapp, 2006. © 2006 Wiley‐Liss, Inc.

INTRODUCTION

Motion correction is a common step in preprocessing functional magnetic resonance imaging (fMRI) data in which small (∼1 mm) frame‐to‐frame head movement is estimated and removed. The term “motion correction” is used commonly to mean both the estimation of the rigid body movement parameters and the subsequent application of the estimated motion transforms to realign the time series of brain images. It has been shown that even small head motion can create artifacts in activation maps when analyzing fMRI data, particularly when the motion is correlated with the activation paradigm [Field et al.,2000; Hajnal et al.,1994]. The overall goal of motion correction in fMRI data analysis is to maximize sensitivity to true activations in the ensuing statistical parametric map while minimizing false activations related to motion.

Jiang et al. [1995] adapted the automated image registration [AIR; Woods et al.,1992] methods of image registration for motion correction of an fMRI time series by comparing each image in the time series to the first (reference image) and minimizing the variance of the ratio of the voxels of the two images. This approach, still commonly used today, gives a set of 6 parameters (x, y, and z translations and rotations) with which to realign each image of the time series. Images are then resliced and voxel intensities are determined from an interpolation scheme using neighboring voxel values.

Current methods have refined earlier approaches by iteratively maximizing a similarity measure between each time point and a reference image, which is typically either the first, middle, or last in the series, or else to a template image that is representative of all images in the series. Traditionally, the last step in motion correction is to reslice each image to match the reference image using the estimated parameters. Commonly used motion correction tools include AIR [Woods et al.,1992,1998a, b], AFNI 3dvolreg [Cox,1996], FSL mcflirt [Jenkinson et al.,2002], and statistical parametric mapping (SPM) realign tools [Friston et al.,1995].

Current approaches to motion correction are imperfect, however, in part because a change in head position can cause changes in the magnetic field, leading to nonlinear, time‐varying distortion of the brain image [Friston et al.,1996]. In addition, motion occurring within the time that it takes to acquire a brain volume (e.g., the repetition time [TR], commonly on the order of 2–3 s) cannot be detected properly and characterized by the realignment methods, as they assume each scan is a single time point. It thus cannot be assumed that all motion has been removed by application of current motion‐correction algorithms [Friston et al.,1996]. Uncorrected motion will tend to cause signal changes in the time series of particular voxels (most commonly those close to tissue boundaries) that depending on the relative timing of motion and the experimental paradigm might lead to artifactual activations. Residual image motion will also have an impact on the sensitivity of analysis to detect true activations by adding to the unmodeled error variance. The extent to which motion produces artifactual activations and decreases statistical sensitivity in regions of true activation depends on the experimental design and the nature of the experimental task. For interactive tasks (e.g., those requiring a button press response), it is common that some head motion will correlate with the presentation of task stimuli. Even in passive tasks, subjects have a greater tendency to move their head when viewing stimuli, as opposed to rest or intertrial periods. For block designs, sustained periods of head displacement may correspond highly with expected sustained hemodynamic responses during stimulus blocks. It is this correlation between head displacement and the experimental task that can lead to artifactual activations, particularly in areas of the brain with spatially heterogeneous signal intensity (e.g., tissue boundaries). In this case, it may be difficult to detect if activations are true or artifactual [Field et al.,2000]. Event‐related experimental designs can aid in reducing the problem of motion artifacts [Birn et al.,1999; Josephs et al.,1997; Zarahn et al.,1997]. If the task is a brief response to a randomly spaced stimulus as opposed to a prolonged block of stimuli, motion induced by responding to the task will have a different temporal shape than the lagged, smooth hemodynamic response of the blood oxygenation level‐dependent (BOLD) signal. Signal change due to motion therefore will not be as highly correlated with the general linear model (GLM) regressors used to model task‐related signal changes, reducing the risk of false activations due to motion. Even when motion is uncorrelated with the predicted hemodynamic response, however, the problem remains that residual motion‐induced fluctuations in the magnetic resonance (MR) signal will decrease the reliability of the GLM parameter estimates and therefore decrease statistical sensitivity.

One solution to this is to include vectors of motion estimates as “nuisance variables” (covariates of no interest) in the single‐subject single‐run GLM to account for the variance due to motion. In simple terms, the GLM for analysis of a single subject's data can be specified for each voxel as y = βX + γM + ε, where y is the vector of measured signal samples, X is the design matrix, which incorporates the time series representing each modeled experimental effect, M is a matrix incorporating one or more time series of estimated motions, ε is a residual, or unexplained signal vector, and β and γ are the parameter vectors to be estimated. The matrix M could either incorporate multiple estimates of motion (e.g., three translations and/or three rotations), or might more simply consist of a single global estimate of absolute estimated motion (e.g., the root mean square value of separate motion estimates). Using this general technique, Friston et al. [1996] found that if activations are detected before correcting for movement then they are likely to be real (assuming that they are orthogonal to movement effects). For these types of activations, including motion parameters as covariates of no interest should increase the statistical sensitivity; however, the assumption that motion is orthogonal to a task does not always hold. When estimated motion is correlated with the task design, inclusion of motion estimates as covariates of no interest can reduce the significance of real clusters of activation, because the motion estimator can “steal” variance from the regressor(s) modeling the real hemodynamic response. It is unclear what the magnitude of correlation between motion and task design must be for this to have a noticeable impact on statistical significance. Field et al. [2000] have shown in a phantom study that motion parameters with a correlation coefficient to the paradigm of approximately 0.5 can cause spurious activations.

In this study, we compared the effects of different motion correction strategies on multiple‐subject t‐statistic images for both a rapid event‐related design and a block design. Many studies on motion correction in the past have used a first‐level analysis of individual subject data to investigate the validity of motion correction procedures. [Birn et al.,1999; Field et al.,2000; Friston et al.,1996; Grootoonk et al.,2000; Jiang et al.,1995; Morgan et al.,2001]. Ultimately, however, the effect of motion correction and analysis techniques on group data analysis is of more relevance to most researchers. Given the large between‐subject variability in brain anatomy and function, it is not obvious to what extent results measured at the individual subject level will generalize to group data. This study adds to existing research by examining the downstream effects of individual‐subject motion correction and covariate analysis on activation clusters at the multiple‐subject statistical level.

Results from three different motion correction processing pathways were compared to statistical images derived from non–motion‐corrected images. These pathways included: (1) standard motion correction, consisting of estimation followed by realignment of data (MC); (2) motion estimation and realignment of the images, then including the motion estimates as covariates of no interest in the individual subject GLM (MC+COV); and (3) motion estimation without realigning the images, but including the motion parameters as covariates of no interest in the GLM (NONMC+COV). We demonstrate that a combination of these methods can effectively remove apparent activation likely due to motion artifact at the multiple‐subject level of fMRI data analysis while maintaining good sensitivity to activations likely to be true activations, particularly for block‐design paradigms.

SUBJECTS AND METHODS

Forty healthy human subjects were recruited through the local newspaper and chosen by phone screening with an MRI compatibility form and the Edinburgh Handedness Survey. The goal was to obtain a sample representative of the “normal” types of subjects recruited as controls from the population at large. Subjects ranged in age from 18–50 years, with number and sex balanced within each decade: 18–29 years, 8 males and 6 females; 30–39 years, 6 males and 6 females; and 40–50 years, 8 males and 6 females. Before participating, each subject gave informed consent. UW‐Madison's Human Subjects Committee approved the study paradigm. These data are part of the Wisconsin Neuroimaging Tool Evaluation Resource (WINTER) dataset used to explore fMRI methodology and data analysis issues.

Functional and anatomic MRI data were acquired. The functional tasks included a multi‐condition block design task, the N‐back task [Casey et al.,1998; Cohen et al.,1997; Smith et al.,1996] (consisting of 0‐, 1‐ and 2‐back trials, 51 s per block with 10 s of rest between each block and three blocks of each condition) and a rapid event‐related task, the Go/NoGo task [Garavan et al.,1999; Liddle et al.,2001], consisting of random intertrial interval (ITI) between 1.5 and 3.5 s, 120 Go trials, and 30 NoGo trials. Functional images were acquired using a GE/Signa 3T MRI scanner (General Electric Medical Systems, Waukesha, WI) with a gradient echo echo planar imaging (EPI) sequence (64 × 64 in‐plane resolution, 240 mm filed of view [FOV], repetition time [TR]/echo time [TE]/flip angle = 2,000 ms/30 ms/90 degrees, 30 × 4 mm interleaved sagittal slices with a 1‐mm interslice gap; 252 whole brain images per scan run for the N‐back task, 203 whole brain images per scan run for the Go/NoGo task). The signal‐to‐noise ratio (SNR) of the functional image data averaged over all subjects and over the entire brain volume was 130 ± 50, with a range of 80–250. This value includes regions of the brain with substantial inhomogeneity (dropout) artifact so there is substantial spatial variation. Anatomical scans consisted of a high resolution 3D T1‐weighted inversion recovery fast gradient echo image (inversion time = 600 ms, 256 × 256 in‐plane resolution, 240 mm FOV, 124 × 1.1‐mm axial slices), a T1‐weighted spin echo coplanar image with the same slice position and orientation as the functional images, used for coregistration of functional data (256 × 256 in‐plane resolution, 240 mm FOV, 30 × 4‐mm sagittal slices with a 1‐mm gap), and a T2‐weighted fast spin echo image, used for stripping the skull off the T1‐weighted images before coregistration (256 × 256 in‐plane resolution, 240 mm FOV, 81 × 2‐mm sagittal slices).

MRI EPI‐BOLD data were reconstructed using epirecon, a program made available by GE Medical Systems to certain research facilities using its MRI scanners. Reconstructed functional data were converted to AFNI format and then slice‐time corrected to remove differences in the acquisition time of different slices. Ideally, slice‐time correction and motion correction should be carried out in combination, because motion can occur during acquisition of a single brain volume, thus causing a shift in the position of some acquired slices but not in others. Currently there are no widely available techniques that combine the two preprocessing steps. By performing slice‐timing correction before motion correction it is thus possible that interpolation artifacts might be introduced into voxel time series that will effect subsequent GLM analyses. Such a correction is warranted, however, given the relatively large difference in acquisition time between adjacent slices for an interleaved acquisition such as that used here (approximately 650 ms), particularly for the event‐related design, in which fairly rapid changes to the BOLD signal are expected. (With a more sophisticated, slice‐dependent analysis of rapid, event‐related data, inclusion of covariates might be expected to have a somewhat greater impact.) Previous work [Oakes et al.,2005] has demonstrated that AFNI yields equivalent group‐wise results to several other leading motion‐correction packages but is faster to execute. Furthermore, the sinc‐like interpolation algorithm used by AFNI introduces substantially less spatial smoothing than does other comparable software packages. Motion parameters were estimated and each time series underwent realignment using AFNI's 3dvolreg command. After the estimated motion parameters were visually inspected, subjects with extreme motion (>4 mm translation, >5 degrees rotation) were eliminated. These values were based on their match with the voxel size with consideration also for expectations of the spatial resolution of BOLD responses and the inherent variability between subjects in brain anatomy. With smaller voxel sizes and better (e.g., nonlinear) coregistration techniques, it is possible that smaller motions would have a more noticeable impact and thus a lower threshold would be warranted. Thirty‐three subjects deemed to have tolerable motion were retained. Data were then converted to ANALYZE format before using fmristat [Worsley,2002] for the GLM analysis (although currently fmristat is able to use AFNI‐formatted data directly with a recently added MATLAB toolbox).

In the first‐level analysis, each condition of the task was modeled as a regressor for the GLM formed by convolving a boxcar (for block design) or delta function (for event‐related design) with an ideal hemodynamic response function. This first‐level analysis was run for four different processing pathways using fmristat: (1) as a baseline for comparison, no motion correction was carried out (NONMC); (2) the realigned images were analyzed but no covariates of no interest were included (MC); (3) the realigned images were analyzed and the motion parameters were included in the GLM as covariates of no interest (MC+COV); and (4) the non‐realigned images were analyzed and the motion parameters were included as covariates of no interest (NONMC+COV)

Additionally, several alternative covariates of no interest derived from the estimated motion parameters were tested. They included: a weighted sum of squares; linearly detrended motion parameters; orthogonalized motion parameters; derivatives of the motion parameters; and both the derivatives and the motion parameters themselves. These options lent no additional insight or sensitivity to the resulting statistical images and were not pursued further, although it is possible that with other experimental designs or with different subject populations, such estimates might yield additional improvements.

From the first‐level analysis, contrast maps were generated for parameter estimates between pairs of conditions. These maps were then registered to an Montreal Neurological Institute (MNI) template via a coplanar high‐resolution T1 intermediary image using FLIRT software [Jenkinson et al.,2002]. To define clusters of interest, a group analysis was run on the non–motion‐corrected images from all 33 subjects. Clusters of activation were selected from these images by thresholding the t‐maps at t = 2.0 (P < 0.054 uncorrected). A liberal threshold was chosen deliberately to allow for measurement of the degree to which voxels that were only marginally significant before motion correction became more significant after motion correction (in the case of true activations) or less significant (in the case of artifacts). Given that activated voxels might change position slightly with motion correction, identifying initial regions of interest (ROIs) with a liberal threshold of P < 0.05 allowed us to be overly inclusive for voxels of marginal significance around the edges of the cluster. This ensured that for the subsequent analyses using a threshold of P < 0.01, small shifts in the cluster location would not cause parts of the cluster to move outside of the originally defined ROI. Six clusters from the event‐related task and five from the block design task were chosen to include a variety of shapes, sizes, locations, and maximal t‐values (see Fig. 1 and Table I). Based upon existing literature on the two tasks, all clusters (except one; see Fig. 2) were chosen to be physiologically plausible activations. For the event‐related task (Go/NoGo), activation clusters were identified bilaterally in temporoparietal cortex, inferior frontal gyrus, anterior cingulate, and left motor cortex. These brain regions have been found to make up part of a network involved in manual response selection and inhibition [e.g., Liddle et al.,2001]. For the block‐design task (N‐back), clusters were identified bilaterally in the middle and inferior frontal gyri, as well as bilateral middle and superior temporal gyri, consistent with previous research on working memory tasks similar to this one [Cohen et al.,1997]. In addition, a cluster was identified as a probable motion artifact, running in a narrow strip around the left anterior cortical surface (Fig. 2). A binary mask was then created for each cluster and used to extract results for each subsequent analysis.

Figure 1.

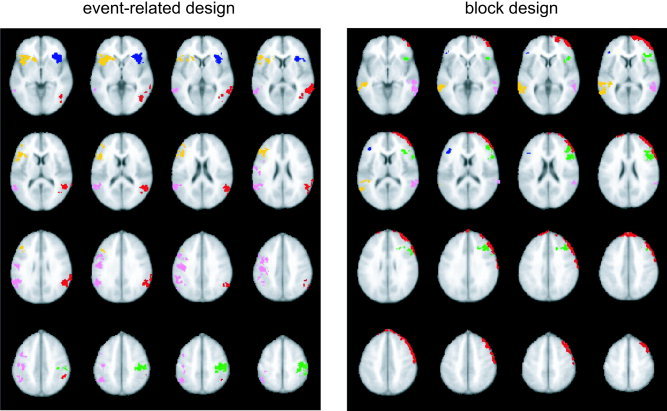
Clusters that were identified and included in the motion correction analysis for the event‐related design (left) and the block design (right). For the event‐related design, these were clusters in the left prefrontal (dark blue), right prefrontal (yellow), left parietal (red), right parietal (pink), left motor (green), and anterior cingulate (light blue) regions. For the block design, clusters were identified in the right prefrontal (dark blue), left prefrontal (green), left temporal (pink), and right temporal (yellow) regions. In addition, a cluster in left prefrontal cortex was attributed to a motion artifact (red). All images are in radiological convention (i.e., right side of image = left side of brain).

Table 1.

Details of the six ROIs examined in the event‐related (Go/NoGo) and block design (N‐back) datasets

ROI location	Design	Volume (mm3)	Maximum T
Anterior cingulate	Event	21,700	5.28
Left parietal	Event	12,300	4.81
Right temporoparietal	Event	16,300	4.41
Left inferior frontal	Event	7,800	5.06
Right inferior frontal	Event	11,400	6.06
Motor Cortex	Event	12,000	4.56
Left middle frontal	Block	8,900	4.91
Left temporal	Block	9,700	4.85
Right temporal	Block	5,500	5.28
Right inferior frontal	Block	700	3.78
Left frontal (motion artifact)	Block	22,600	5.66

All event‐related clusters were based on the go vs. no‐go contrast. For the block design, all clusters were based on the 2‐back vs. 1‐back contrast, except for the right inferior frontal cluster and left frontal (motion) cluster, which were based on the 2‐back vs. 0‐back contrast.

Figure 2.

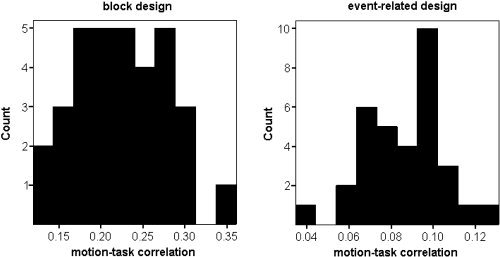
Histograms of correlations between estimated motion and the experimental task model for the block design (left) and the event‐related design (right).

To examine the effects that motion correction and including motion covariates in the GLM had on final analysis results, we focused on both individual contrast estimates as well as overall group statistics. The individual contrast estimates are affected most directly by the different motion correction procedures, because ideally both motion correction and inclusion of motion covariates should decrease noise, thus making contrast estimates more reliable. The contrast estimates are also what is input to higher‐level group analysis and are thus most relevant to the ultimate group‐level results. Mean contrast values were extracted for each cluster of interest for each type of motion‐correction pathway, and then entered into a mixed‐effects GLM with subject as a random factor and motion correction and inclusion of covariates as fixed factors. Because motion correction shifts the position of voxels, comparison of mean contrast values for a given ROI involves comparison of slightly different sets of voxels, although this difference will be small relative to the size of the ROIs.

To compare the processing pathways at the multiple‐subject level, a group analysis with all 33 subjects was run to produce one statistical image for each processing pathway for each design type. Using the binary mask created with the non–motion‐corrected images (NONMC pathway), clusters were extracted from each of the other multiple subject statistical images (MC, MC+COV, and NONMC+COV). Two groupwise summary statistics were used in evaluating each motion correction pathway: (1) the maximum t‐value of the cluster; and (2) the cluster volume after thresholding at P < 0.01. This threshold value was chosen because it is commonly used as a voxelwise threshold for cluster‐based correction for multiple comparisons, using Monte Carlo simulations, permutation techniques [Hayasaka and Nichols,2003; Holmes et al.,1996], or random field theory (Worsley et al.,1996) to determine the minimum number of contiguous voxels that exceed a given (uncorrected) voxelwise threshold, such that the cluster of active voxels meets a given corrected α level (these techniques take into account the spatial correlation within datasets and so result in a more accurate corrected threshold than do Bonferroni corrections). These indices were then compared using a mixed‐model GLM with cluster as a random factor, and motion correction and inclusion of covariates as fixed factors.

RESULTS

Figure 2 shows histograms of the correlation magnitude between the estimated motion and the model of the task time course (maximum of the correlations with the three condition regressors for the block design and correlation with the Go condition for the event‐related design) for each subject, averaged over the six motion parameters. As expected, the block design motion parameters had much higher correlations with the task (mean correlation = 0.22, standard deviation [SD] = 0.06, maximum = 0.36) than did the event‐related design (mean correlation = 0.09, SD = 0.02, maximum = 0.13). In fact, the correlations were universally higher for the block design than for the event‐related design, which supports previous studies showing that event‐related designs decrease temporal correlations with subject movement [Birn et al.,1999].

Individual Subject Analyses

For the event‐related design, there was no significant main effect of applying motion correction (F[1,32] = 1.79, P = 0.19), nor an effect of including motion estimates as covariates (F[1,32] < 1). Linear regression was then used to assess the degree to which the correlation between motion estimates and task model for a given subject predicted the impact on that subject's contrast estimates of including motion covariates. The magnitude of correlation between estimated motion and the task model did not relate significantly to the change in contrast estimates with inclusion of motion covariates (r = 0.17, P = 0.35).

For the block design, there was no significant effect of applying motion correction (F[1,32] < 1), but including motion estimates as covariates significantly reduced the mean contrast estimates (F[1,32] = 23.6, P < 0. 0001), indicating a generally deleterious effect of including motion covariates. As with the event‐related design, the magnitude of correlation between estimated motion and the task model did not relate significantly to the change in contrast estimates with inclusion of motion covariates (r = 0.08, P = 0.65). Although including motion estimates as covariates had a consistent (negative) impact on contrast estimates, the magnitude of correlation between estimated motion and the task model thus did not relate to the amount by which contrast estimates were affected.

Group Analyses

Figure 3 shows both the cluster size and the maximum t‐value of each cluster, for both the event‐related and block designs in the group analyses. For the event related design (upper graphs in Fig. 3) there was a significant increase in maximum t‐values when including motion covariates as opposed to not including them (F[1,5] = 30.1, P = 0.003), but no overall difference when motion correcting versus not motion correcting (F[1,5] = 1.03, P = 0.35). Cluster size increased significantly when using motion covariates (F[1,5] = 39.9, P = 0.001) and increased when applying motion correction (F[1,5] = 12.3, P = 0.017), although the impact of covariates was greater than that using motion correction.

Figure 3.

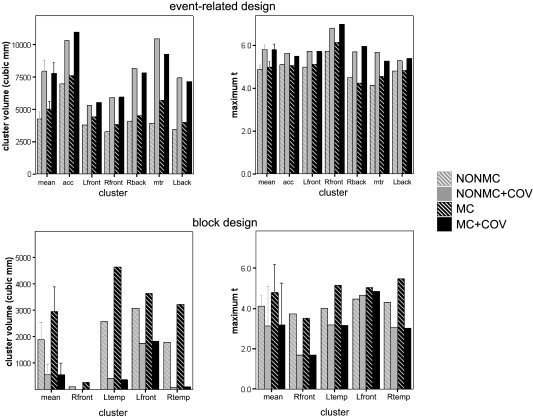
Thresholded cluster volumes (left) and maximum t‐statistics (right) for the event‐related design (top) and the block design (bottom). Gray bars represent results for non–motion‐corrected images (NONMC), black bars represent motion‐corrected images (MC); cross‐hatched bars represent no use of motion covariates (NOCOV), solid bars denote use of motion covariates (COV). Bars show results for individual clusters, as well as means across clusters (left‐most columns in each graph).

The block design task (lower graphs in Fig. 3) shows a distinctly different pattern. Inclusion of motion covariates decreased both the maximum t‐statistic (F[1,3] = 8.19, P = 0.064) and cluster volume (F[1,3] = 8.17, P = 0.065; we report results of marginal significance here, because there is little risk in falsely rejecting the null hypothesis that all motion correction techniques are equivalent, but potentially much to be lost from falsely accepting the null). Motion correction increased cluster size (F[1,3] = 6.7, P = 0.081) with the best results, both in terms of maximum t‐statistic and cluster volume, obtained by using motion correction with no covariate (as evidenced Fig. 4 and by the covariate by motion correction interaction F[1,3] = 6.87, P = 0.074 for maximum t; F[1,3] = 8.46, P = 0.056 for cluster volume). The fact that motion correction alone produced an increase in t‐statistics and cluster volume (compared to no motion correction) is evidence that these clusters were indeed real activations rather than motion‐related artifacts, because correcting for motion would decrease the significance of artifactual clusters. The reduction of activation when including motion covariates is evidence that the detected motion was correlated with real activation in these brain regions, and thus the motion covariates were collinear with the model task regressors.

Figure 4.

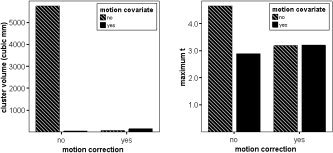
Group analysis cluster volume (left) and maximum t‐statistic (right) for the left frontal motion artifact cluster, as a function of applying motion correction and including motion estimates as general linear model (GLM) covariates.

Figure 4 shows the effects of applying motion correction and of including motion estimates as GLM covariates on the maximum t‐value and cluster size of the cluster identified to be a motion artifact (see Fig. 1) in the block‐design study. Applying motion correction, including motion estimates as covariates, or a combination of both had a similar effect in reducing both cluster size and the maximum t‐value. Of particular relevance to devising a general strategy for dealing with motion in fMRI data is how the effect on this artifactual cluster of applying motion correction alone differs from the effect on real activation clusters. In this case cluster activation was reduced, whereas with the real clusters activation was increased.

DISCUSSION

A significant effect on group analysis t‐values and cluster sizes was realized depending on whether or not covariates of no interest were included in the GLM design; however, this effect depended on the experimental design. In our study, we used archetypes of both a rapid event‐related study and a three‐condition block design (a further investigation could include a well‐spaced event‐related design, or a hybrid event‐related/block design). As shown in Figure 3, including confounds increased the sensitivity (as measured by the maximum t‐value in group analysis) compared to motion correction alone only for the event‐related design. Notably, the event‐related design exhibits a low correlation between the movement parameters and the design model. Individual subject analyses of event‐related data showed no consistent effect of including covariates. With uniformly low correlation between estimated motion and the task, the degree to which including motion estimates as covariates improves GLM sensitivity presumably has more to do with individual differences such as image signal gradients in or near regions of activation. A given amount of motion in a subject with large signal gradients thus might have a greater impact than would the same motion in subjects with relatively uniform image signal intensity. From these analyses it would seem that small, inconsistent improvements in individual subject contrast estimates with the use of motion covariates can nevertheless lead to significantly more sensitive group‐level analyses.

Conversely, including the covariates in the analysis of block‐design data reduced the sensitivity of the group t‐statistic results, consistent with the effect of including covariates for individual subject contrast estimates. These results highlight what has been identified as a particular weakness of block designs [Birn et al.,1999], namely that subject motion is often correlated with the experimental paradigm. Including motion estimates as covariates of no interest in such cases has the effect of stealing much of the variance that may be due to actual activations, leaving little extra variance to be assigned to the model and consequently limiting the magnitude of the final t‐statistic parameter. Field et al. [2000] found correlations of approximately 0.5 can have a deleterious effect when including motion estimates as covariates. In this study, however, the mean correlation between estimated motion and the block‐task design, although higher than for the event‐related design, was only 0.2. For this specific block design there was only 10 s of rest between consecutive “on” periods; with longer rest periods one might expect greater correlation between motion covariates and the task design. This work thus demonstrates that such paradigm‐correlated motion can have an appreciable effect, even when the correlation is relatively low (i.e., in the range of r ∼ 0.2). Interestingly however, the magnitude of correlation between the estimated motion and the experimental task did not predict the impact of including covariates on individual subject contrast estimates. For group analysis involving a moderate degree of task‐correlated motion, including covariates thus will have a detrimental effect on group analysis results, but it is not possible to use the degree of correlation for any one subject to determine whether inclusion of covariates would be advantageous. In this case, applying motion correction but not including motion covariates in the statistical model is the safer way to optimize the sensitivity to true activations.

The main problem with such an approach is that the residual effects of motion that remain even after careful motion correction has been carried out can give rise to spurious apparent activations. Although artifactual activations that commonly appear along brain edges are identified easily by visual inspection, the risk is that other artifacts might exist within the brain and be accepted as true activations. We observed an increase in the magnitude and extent of activation for real activation clusters for the motion‐corrected images as contrasted with non–motion‐corrected images, but a corresponding reduction in activation for artifactual clusters. One way to identify artifactual from real activations would thus be to carry out analysis both with motion‐corrected and non–motion‐corrected images, and mark those activations that decrease in significance with motion correction as probable motion artifacts to be excluded from further analysis. With rapid motion correction now possible with current computers, such a dual analysis approach is relatively straightforward and easily automated.

For the rapid event‐related design, we observed an increase in activation magnitude and extent with the inclusion of motion covariates. For similar designs, including motion covariates would thus seem warranted as part of a standard analysis path. For slightly different designs, however, the decision of whether or not to include covariates is not so clear. Factors such as the nature of the task itself, the relative randomization of trials or blocks, the velocity of rapid motion, and the robustness and strength of real activation will all affect how the inclusion of motion covariates impacts the statistical results. For example, for slower event‐related designs, there is a greater risk that estimates of motion will correlate more highly with modeled hemodynamic responses, and thus begin to have a deleterious effect on statistical sensitivity. Hybrid fMRI designs, in which randomized sequences of single events are presented within extended blocks of specific task or contextual conditions, are also likely to demonstrate some degree of correlation between motion and modeled responses. In such cases, it is difficult to know a priori whether including motion covariates will increase or decrease sensitivity. Comparison of analysis results both with and without motion covariates would be an appropriate way to maximize detection sensitivity, with the experimenter choosing the results with greatest activation. Care must be made to screen for artifactual activations as described above, however, because reduced activation with the inclusion of covariates could indicate either the deleterious effects of task‐correlated motion covariates on estimates of true activation or the beneficial effects of motion covariates in reducing artifactual activation.

One possibility that has not been addressed in the current study is that strong task activation in an extended region of the brain might lead to spurious motion estimates. This is a possibility with motion‐correction algorithms that calculate a difference measure between different image frames based upon the image intensity data. Most current motion‐correction algorithms go some way to addressing this problem with the use of magnitude‐invariant difference measures such as normalized correlation ratio or mutual information. Should spurious motion estimates still arise from real brain activation, however, the effect might be that task‐correlated motion is introduced into the data. This could lead to artifactual activations if no motion covariates are used, and reduction of true activations when including motion covariates. One possibility would be to use a thresholded brain mask to estimate motion, although the problem with such a technique is that it is extremely sensitive to small signal changes at the edges of the mask (which might be due to motion, noise, or brain activation). Another possibility would be to re‐estimate motion after having masked out areas of possible activation derived from an individual's GLM results. Experimenters might choose to try this if their statistics show large areas of activation in one region of the brain and they observe strong correlations between estimated motion and the task design (in this study such high correlations were not observed), and thus suspect that estimates of motion might themselves be artifacts.

Given these considerations, the following strategy is proposed for a range of task designs, to separately identify clusters that are likely to be false activations related to a residual motion artifact while optimizing statistical sensitivity for real activations:

• 1Analyze group data (i.e., second‐level analysis) using the non–motion‐corrected images (NONMC) and identify clusters of activation.
• 2Analyze group data a second time, including the motion parameters as nuisance variables at the first‐level analysis (MC+COV). (The data we report here indicate that NONMC+COV could equally be used in place of MC+COV).
• 3Compare the activated clusters of MC+COV (step 2) to NONMC (step 1). If clusters of interest in MC+COV are unchanged or increase in significance, then they are most likely real activations, and motion has been properly accounted for. Clusters in MC+COV that show decreases in size or mean t‐value, however, are either due to an artifact related to motion or else the motion parameters are sufficiently correlated with the task that they account for some of the real activation variance, thus reducing the significance of true activations.
• 4To identify which of the clusters showing a t‐value decrease in step 3 are most probably artifactual, run the group analysis a third time using the motion‐corrected images but without the motion parameters as covariates at the first level (MC). In this case, true activations show an increase in significance, because removal of actual motion from the image sequence reduces error variance in the activated voxel time series. Artifacts caused by motion, however, should show a decrease in significance due to the reduction in image motion, and can be excluded from further analysis.

This procedure has the potential to increase the statistical significance of real clusters of activation even when motion is correlated with the experimental design, while identifying probable artifactual clusters caused by motion. Although such a multistage procedure might seem unwieldy and slow, with automated batch processing via scripts and with modern desktop computers it can be accomplished in a reasonable time. If speed is an issue, then one may use a fast GLM estimation technique (e.g., one using simple ordinary least squares [OLS]), such as that provided in AFNI [Cox et al.,1996]) to identify and mask out motion artifacts before proceeding to a more rigorous analysis. It is worth noting that although this multi‐step procedure should prove useful in identifying and eliminating probable motion artifacts, the experimenter should still base the final decision not only upon the impact of motion correction and the inclusion of covariates but also upon a priori expectations of regions of activation, cluster shape, and size (i.e., being wary of rim effects), and close examination of the data itself.

A multistep analysis process such as that described above was not necessary for the event‐related design examined in this study, because inclusion of motion covariates increased sensitivity for all event‐related clusters. Nevertheless, the procedure outlined above would be advisable with event‐related designs, particularly in cases where the experimenter is unsure whether the correlation between the experimental design and subject motion is sufficient to cause problems when including motion covariates. It is likely that such a multistep procedure would also be appropriate for widely spaced event‐related experiments, as well as mixed event‐related/block designs (i.e., “hybrid” designs [Donaldson et al.,2001]), in which the hemodynamic response to at least some of the experimental events or periods might have similar temporal characteristics to subject motion.

CONCLUSIONS

Subject motion, whether correlated to the design model or not, can have a significant impact on the sensitivity of group‐level fMRI data analysis. The judicious inclusion of motion parameters as nuisance covariates in the first level GLM can improve sensitivity as measured by t‐values and cluster sizes, as well as improve the detection and elimination of spurious activations.

This study, using archetypes of a block design and a rapid event‐related design along with various motion‐correction processing pathways, demonstrates the benefits and drawbacks of including the estimated motion parameters as covariates of no interest in the first‐level GLM. In a rapid event‐related design where motion parameters show little or no correlation with the model, it is generally beneficial to include motion estimates in the GLM. In a block design, or more generally a design in which motion parameters are even moderately correlated (r ∼ 0.2 or greater) with the model, including the motion parameters as covariates can reduce the sensitivity for detecting activations. Without the inclusion of motion estimates in the GLM, however, motion artifacts may persist. The series of processing steps proposed in this work permits the identification of probable false activations caused by motion while maximizing the sensitivity to activations likely to be of true experimental interest.