How does spatial extent of fMRI datasets affect independent component analysis decomposition?

Abstract

Spatial independent component analysis (sICA) of functional magnetic resonance imaging (fMRI) time series can generate meaningful activation maps and associated descriptive signals, which are useful to evaluate datasets of the entire brain or selected portions of it. Besides computational implications, variations in the input dataset combined with the multivariate nature of ICA may lead to different spatial or temporal readouts of brain activation phenomena. By reducing and increasing a volume of interest (VOI), we applied sICA to different datasets from real activation experiments with multislice acquisition and single or multiple sensory‐motor task‐induced blood oxygenation level‐dependent (BOLD) signal sources with different spatial and temporal structure. Using receiver operating characteristics (ROC) methodology for accuracy evaluation and multiple regression analysis as benchmark, we compared sICA decompositions of reduced and increased VOI fMRI time‐series containing auditory, motor and hemifield visual activation occurring separately or simultaneously in time. Both approaches yielded valid results; however, the results of the increased VOI approach were spatially more accurate compared to the results of the decreased VOI approach. This is consistent with the capability of sICA to take advantage of extended samples of statistical observations and suggests that sICA is more powerful with extended rather than reduced VOI datasets to delineate brain activity. Hum Brain Mapp, 2005. © 2006 Wiley‐Liss, Inc.

INTRODUCTION

In functional magnetic resonance imaging (fMRI), univariate and multivariate statistics are used to read out different blood oxygenation level‐dependent (BOLD) signals from the acquired time series. Univariate methods, both hypothesis‐driven [Bandettini et al., 1993; Friston, 1996] and data‐driven [Baumgartner et al., 2000], enable detection and signal characterization through an estimation procedure that is repeated identically at each individual volume element (voxel). The spatial accuracy of the results from univariate methods is not affected by the selection of the region of analysis (ROI); univariate approaches, testing each single brain voxel independently, neither exploit at all nor fully characterize the co‐activation phenomena within the same neurophysiological pattern. This lack of consideration of spatial interactions inspired the utilization of multivariate methods for detection and estimation of spatial activation and temporal dynamics of the brain. Multivariate techniques have been verified and adopted for functional connectivity pattern analysis of distributed regions in the brain during cognitive tasks, such as human memory [Fletcher et al., 1996] and resting state [Van de Ven et al., 2004]. This task is accomplished by estimating suitable second‐ or higher‐order statistical entities on the relationships among subsets of brain voxels or time points.

Multivariate methods try to aggregate the voxels in spatiotemporal patterns of activity based on a common time course and a common spatial distribution of a given effect. In general, the relationships between voxel time courses are estimated in the spatial covariance of the measured signals, whose processing reveals the modes of signal variability.

Independent component analysis (ICA) is a popular and highly studied technique of multivariate (data‐driven) analysis of multidimensional datasets. It transforms the measured time series into components that are as statistically independent from each other as possible [Comon, 1994]: the independent components (ICs).

Statistical independence can be considered a plausible assumption in many neuroimaging applications, because neuronal responses that have distinct causes are likely to generate regionally specific effects on the measured signals and it is plausible that these effects do not overlap systematically, which gives rise to approximately statistically independent observations [Brown et al., 2001]. So far, the application of the ICA model to data from different neuroimaging modalities has provided important insights about fundamental spatiotemporal dynamics of the human visual [Makeig et al., 2002] and auditory systems [Seifritz et al., 2002].

ICA can be applied to fMRI data in two different ways, namely spatial ICA [McKeown et al., 1998b] and temporal ICA [Biswal and Ulmer, 1999]. In spatial ICA (sICA), statistical independence is assumed for the distribution in space of the extracted sources of signal change: the signal sources are independent in their spatial locations rather than in their time profile that can exhibit high mutual correlations. In temporal ICA (tICA), the sources are assumed to be independent across time. These two variants are described and compared in Calhoun et al. [ 2001a].

Considering a typical 3D fMRI dataset, the spatial and temporal dimensions of the statistical samples suggest the use of the sICA for 3‐D pattern generation, whereas tICA can reveal the presence of multiple dynamics in an anatomically or functionally selected region of interest [ROI; Calhoun et al., 2001a; Seifritz et al., 2002]. From the perspective of statistical power, sICA has the best potential for a robust representation of whole‐brain fMRI datasets because of the sample sizes achievable. The statistical power of sICA can be as high as to enable useful sICA decomposition even using few time points of a single slice fMRI time‐series [Esposito et al., 2003].

In multislice 3‐D fMRI experiments, the data matrix is filled by a suitable vectorization of all voxels from all slices. The selection of voxels in sICA may affect the outcome of the decomposition in two opposite ways: statistical and informative. From the statistical point of view increasing the number of voxels increases the power of the sICA analysis as a method that exploits spatial statistics. From the informative point of view, excluding or including a region in the data selection step may crucially change the actual number of neurologically relevant signal sources or their statistical characterization. These two situations are thought to produce antithetic effects on ICA decompositions. The purpose of this study is to evaluate and compare two different approaches of selecting raw data before the computational stage: reduced versus increased volumes of interest (VOI).

To achieve this purpose and to keep the analysis as close as possible to the real case of a common fMRI experiment, the slice of acquisition was preferentially chosen as the elementary degree of freedom that is available to the user to define the VOI; besides, in a separate moment, an anatomically and functionally guided selection of the volume was applied along the three spatial dimensions. In this sense, selecting a volume of just one slice at a time could involve better performances because of the reduced influence of “extra‐slice” sources of signal change (whose foci of influence are located in a different slice) on the “intra‐slice” sources (whose foci of influence are located in that slice). In other words, given the same number of time points, the mixtures are “simpler.” Selecting a bigger volume of data (so increasing the computational load), however, gathers additional statistical observations even for the intra‐slice sources, which helps ICA to extract the corresponding component. Of course, more sources will have the chance to be estimated in this enlarged domain but the temporal dimensionality of the dataset is not changed.

This fundamental trade‐off makes the choice of a data selection approach non‐trivial and justifies an analytical investigation of the true extent to which the performances could be affected by the spatial configuration of the dataset. After having investigated in a previous study the effect of the temporal dimension on the ICA output [Esposito et al., 2003], we thus focused here on the spatial extent.

SUBJECTS AND METHODS

Data Acquisition

Imaging parameters

In this study, informed consent was obtained from three right‐handed healthy volunteers (all female; age range 24–34 years) who participated in three sessions of a dominant hand finger‐tapping, visual, and auditory fMRI experiment. Whole‐brain images were acquired on a 3 Tesla superconducting SIGNA MR scanner (General Electric Medical Systems, S. Giovanni Rotondo, Foggia, Italy) using a standard circularly polarized head coil. After localizer scans, we acquired T1‐weighted structural volumes consisting of 184 sagittal slices covering the entire brain (field of view 250 × 250 mm², matrix 256 × 256 pixels, and slice thickness 1 mm). For fMRI, we used conventional single‐shot echo‐planar image sequence (volume repetition time 1,000 ms, interslice time 71 ms, field of view 240 × 240 mm²; matrix 64 × 64 pixels, and slice thickness 7 mm). A functional slab consisted of 14 contiguous slices, which were positioned parallel to the bi‐commissural plane and covered the primary motor, supplementary motor, and occipital cortex areas. In total, 180 fMRI volumes (180 s) were acquired three times during one experimental session. Twenty dummy (discarded acquisitions) scans were carried out at the beginning to allow for longitudinal equilibrium, after which the paradigm was automatically triggered to start by the scanner.

Experimental paradigms

As shown in Figure 1, visual and auditory stimuli were presented alternating across the three experimental runs. Stimuli were separated by a nonstimulation interval ranging between 10 and 20 s using the stimulation software package Presentation (http://www.neuro-bs.com; Version 0.91). A white cross on a black background was visible during the experiment (not only during the visual interstimulus intervals). The imaging series consisted of an alternating 20‐s rest epoch (no auditory stimulation) with a 20‐s auditory activation epoch repeated 12 times in total for all the sessions. The acoustic stimulus consisted of a train of 20 bursts of 3.4 kHz, which lasted 20 s and alternated every 20 s. There were three different auditory conditions (Fig. 1): the stand‐alone auditory one (pattern A) and the other two, which were auditory stimuli with a distracting visual stimulus that lasted 10 s, starting 5 s after the auditory stimulus onset. The visual stimuli consisted of a flickering checkerboard at a fixed luminance contrast level, which was in one case on the left side of the screen (pattern B) and in the other on the right side (pattern C). The participants looked into a mirror to see a screen subtending approximately 25 degrees of visual field in which the figures were back‐projected. The subject had to press a fiberoptically‐monitored button panel when he/she listened to the acoustic stimuli. The button was controlled by the index finger of the right hand. We recorded reaction times for each item for all the participants to get a feedback of the answers and a measure of accuracy of response.

Figure 1.

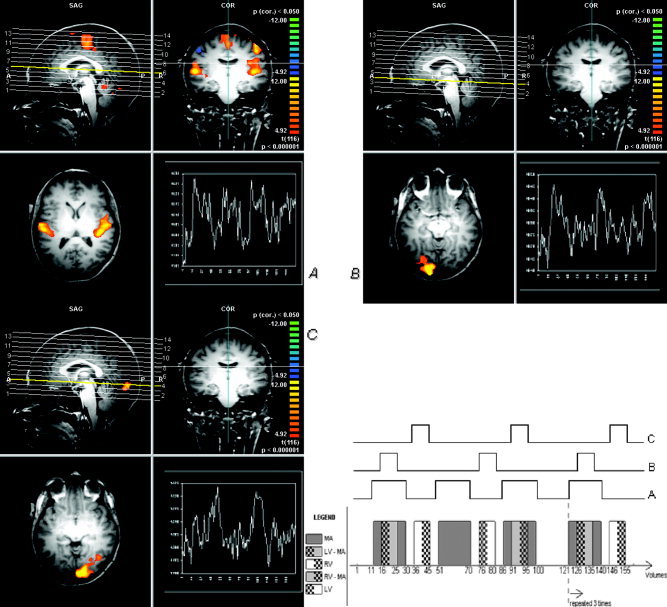
Schematic presentation of the sequential epoch stimulation. Variously combined, AM, LV, and RV represent auditory‐motor, left visual, and right visual, respectively. Given that there is no significant confounding effect on each other, three main patterns (A–C) of behavioral‐related activation can be considered. In this example, pattern A through pattern C can be utilized as a model function for general linear model analysis to detect the areas of activation corresponding to auditory‐motor predictor in general (A), left visual predictor (B), and right visual predictor (C). Representative multiple regression analysis using patterns A, B, and C model functions within the whole brain are shown below. White graphs indicate representative time series of active voxels (P‐corrected < 0.001) BOLD signal. The activation areas are subsequently identified as the primary motor cortex and primary auditory cortex for the pattern A, and lateralized primary visual areas (V1) for patterns B and C.

Data Models

Reduced and increased sample data selection methods

The selection of the voxels included in the analysis is typically carried out based on intensity histograms of the mean signal or using anatomically relevant segmentation of the data [cortex‐based ICA; Formisano et al., 2004].

We investigated the effects of reducing or increasing the spatial extent of the dataset (increased VOI [iVOI]; reduced VOI [rVOI]) by including or excluding an adequate sampling of multiple concurrent hemodynamic sources in the data matrix. Two different approaches to vary the spatial extent of the sample were used. In the first approach, the single slice of acquisition was chosen as the unitary step and the VOI was increased or reduced slice by slice along the z‐axis. In the second approach, an anatomically and functionally guided selection of the region of interest was made along a 3D volume, based on the inspection of a skilled fMRI neuroradiologist and on data by previous fMRI experiments.

In this sense, the problem has a close connection with the natural choice posed to an MR experimenter of including or excluding single or multiple slices during the acquisition and analysis steps. This choice has both technical and methodological relevance and helps the experimenter in making decision about critical slice‐based sampling of the brain as well as post‐hoc evaluations of ICA outcomes.

For this study, an illustrative multislice whole‐brain acquisition has been designed during a mixed visual, auditory, and motor experimental paradigm with slices encompassing visual, auditory, and motor cortices. For the analyses we selected a reduced dataset (rVOI) by covering an area expected to comprise only one of the three analyzed systems. This allowed us to observe preferentially one of four foci (left visual, right visual, auditory, and motor) of BOLD activity resulting in one main source of signal change in the data. Alternatively, by selecting a bigger spatial volume for the same ICA run, more spatial observations were evident for the sources and more than two sources had to be separated. The goal of this experimental paradigm was to test spatial ICA on whole‐brain functional MRI time series containing multiple sources of consistently task‐related in anatomically disparate and well‐separated regions such as the visual areas, the auditory areas and the motor areas. This framework aims at investigating the conditions of reducing the volume of interest of the ICA analysis in a way that excludes from the data matrix both one independent source (leaving at least another independent source), as in the case of the visual and the audio‐motor source, and a spatially separated part of the same independent source. This was made possible by using temporally overlapping auditory and motor sources.

Models and methods of sICA

The basic goal of ICA is to solve the blind source separation (BSS) problem by expressing a set of random vectorial observations as linear combinations of statistically independent latent source scalar variables. In the field of fMRI, ICA has been applied since the publication of two seminal articles [Calhoun et al., 2001a; McKeown et al., 1998b]. It pursues maximally independent components by maximizing the joint entropy of suitably transformed component maps so that the mutual information between different components is minimized, finally reducing the redundancy between the distributions of map values for different components.

The raw data from each participant was arranged into a (P × T) matrix with P voxels measured at T different time points and entered into a spatial ICA analysis. Principal component analysis (PCA) was employed as a data reduction step before the estimation of N<T components. This step is usually carried out heuristically or analytically with the attempt of limiting the under‐decomposition or over‐reduction (thus excluding important signal contribution to the measured variance) and the over‐fitting of the data (causing clusters of voxels belonging to the same generative source to be fragmented into multiple different spatial maps). Different methods for estimating the optimal number of components to be extracted have been already proposed [e.g., see Beckmann and Smith, 2004; Calhoun et al., 2001a]. We applied the PPCA method [Beckmann and Smith, 2004] and found out an optimal choice at n = 34 ICs (on average).

The component maps were automatically inspected based on their spatial [Formisano et al., 2002] and anatomical [Van de Ven et al., 2004] structure and identified as left visual (LV; C_{left visual, j}), right visual (RV; C_{right visual, j}), and auditory‐motor (AM; C_{auditory‐motor, j}), for each jth participant for every spatial configuration from rVOI to iVOI.

Models and methods of general linear model (multiple regression analysis)

The general linear model (GLM), first introduced in analyzing brain imaging data by Friston et al. [ 1990], is the conventional analysis method for most study designs [Laurienti et al., 2003]. In the GLM (also known as multiple regression analysis), a linear combination of several regressor variables (predictor or explanatory variables) are used to “predict” the variation of an observed signal time course. GLM analysis is carried out independently for the time course at each individual voxel, and the results of GLM analysis for a voxel time course are the estimates for the regression coefficients (estimated by the least squares method [LSM] to minimize error values) that make the predicted values as close as possible to the measured values.

Data Analysis

To define suitable benchmark maps for a receiver operator characteristic (ROC)‐based comparison [Skudlarski et al., 1999] of rVOIs and iVOIs in ICA, each dataset was first analyzed with the GLM analysis tool with Brain Voyager 2000 (Brain Innovation, Maastricht, The Netherlands; online at http://www.brainvoyager.com).

Preprocessing

Whole‐brain images were first corrected for timing differences between the slices using sinc interpolation to reduce potential misinterpretable effects due to the sequential scanning of slices [van de Moortele et al., 1997] and then were motion corrected to compensate for head movement. Images were spatially normalized to Talairach and Tournoux space [ 1988] after warping different subject anatomies onto the same template. Data were temporally smoothed by applying a linear trend removal (slow‐frequency drift removal) and a high‐pass filter for three cycles (to remove nonlinear drifts). This filter converts the time series at each voxel in the frequency domain and then removes low frequencies. The frequency domain representation is then converted back in the time domains, which looks then as before except that low‐frequency drifts are no longer visible. Finally, data were spatially smoothed by applying a Gaussian kernel of 2 mm full‐width at half maximum to each acquired slice; the effect of this step is to reduce high‐frequency spatial fluctuations in the images.

General linear model

Data from each participant was entered into GLM single‐subject analysis framework using Brain Voyager 2000. The conventional multiple regression analysis was carried out on each voxel of every subject separately using Brain Voyager 2000 with one regressor for each of the four conditions, each consisting of a box‐car convolved by the standard Brain Voyager 2000 canonical hemodynamic response function (HRF), which consists of a gamma function. Furthermore, voxels lying outside the brain were removed by limiting to 500 the image intensity thresholding of every subject.

Independent component analysis

To avoid any potential influence of the preprocessing steps on data quality and intrinsic spatiotemporal correspondence, the preprocessing steps in ICA as well as in the GLM analysis were limited to the intensity thresholding and the gaussian spatial smoothing. ICA runs based on the fixed‐point algorithm in deflation mode [Hyvärinen, 1999a and 2001] were started from Brain Voyager 2000 using the cortex‐based ICA module, without specifying any mask (i.e., volume‐based ICA). Instead, the performance evaluation procedures were implemented in MATLAB, using the output of Brain Voyager 2000.

The fixed‐point algorithm aims at solving the ICA problem through a linear transformation that minimizes the mutual information of the components by finding the directions of maximum negentropy. In this algorithm, suitable approximations of the negentropy introduced in [Hyvärinen, 1998] are used to derive objective functions for the optimization [Hyvärinen, 1999b].

Selecting ICs that contain cortical or subcortical functional units is often a problem in the interpretation of fMRI‐ICA results, as many components also represent artifacts (e.g., scanner and echo‐planar imaging (EPI)‐related noise, subject movement, breathing, and artery pulsation). Previous applications of ICA could identify relevant ICs by post‐hoc correlation of the IC time courses to the event or epoch timing [Calhoun et al., 2001a; Gu, 2001; McKeown, 2000], selecting them according to their spatial and temporal nature [Calhoun et al., 2002] or by predicting that functionally corresponding areas in different subjects should have temporally correlated activity time courses as identical stimuli activate same regions in the same way across subjects [Bartels and Zeki, 2004]. In this study, we found that each selected IC had always an associated time course that was well correlated to the BOLD signal of the most significant voxels (i.e., maximal voxel time course), r(AM) = 0.896 ± 0.095, r(LV) = 0.902 ± 0.074, r(RV) = 0.882 ± 0.089 across subjects and VOIs. The ICs thus could be selected both according to the correlation of their time courses with the GLM regressors and according to the anatomical correspondence of their most significant voxels with the GLM maps. The IC time courses are normally provided by ICA decompositions as columns of the mixing matrix, in turn reconstructed by pseudo‐inversion of the estimated unmixing matrices. Apart from difference in the sign of the activity, how much these waveforms visually describe the time courses of the regions of activity depends also on the distribution of values in the spatial map and may be often poorly correlated with the data even in the highest voxels in the IC maps. For these reasons, it is sometimes reported the region‐of‐activity (ROA) time course instead of the IC time course [see also Duann et al., 2002].

In both the rVOI and the iVOI approach, the selection and assignment of components with similar sources for the identification was unambiguous and straightforward in all areas because the individual maps proved to be highly correlated with the GLM (for separate subjects) as presented in Figure 1 (P corrected < 0.05), even if in the approach with increased volumes we found out that either multiple or single foci could be present in a single extracted component map.

Quantification and comparison of the approaches' performance

We used the ROC method to compare the efficacy of the two approaches in estimating the activation map from a single subject. ROC is based on the optimization of the true‐positive ratio (portion of correctly detected activations to all added activations) to the false‐positive ratio (portion of pixels that were incorrectly recognized as active in all pixels without added activation). We evaluated specificity and sensibility of the two sICA approaches in estimating the spatial layout of the task‐related effects using multiple regression analysis maps as benchmarks.

To distinguish significantly contributing voxels, ICA maps were scaled to the spatial z‐scores, computed as the number of standard deviations from the map mean [McKeown et al., 1998b]. These parameters are useful for descriptive purposes only and do not provide intrinsic confidence levels for statistical thresholding. For the figures, we thus chose the threshold of the z‐maps using a gaussian mixture model (GMM) of the histograms [see Beckmann and Smith, 2004], accepting as active voxels with an estimated posterior probability of activation exceeding a value of 0.5.

Following the ROC procedure, a curve is traced by finding the corresponding false‐positive fraction (FPF) and the false‐negative fraction (FNF) at varying thresholds for the selected ICA z‐map (i.e., z‐map threshold varying 0–10). In this way, the results of our analysis will be independent of the z‐threshold, which is not a rigorous statistical concept by itself [see Beckmann and Smith, 2004]. To produce a single quantitative figure of merit for each ROC curve, we used the mean of the ROC curve over the limited range of false‐positive ratio between 0 and 0.1 [Skudlarski et al., 1999]. The somewhat arbitrary threshold 0.1 was chosen in relation to an empirical working regime of fMRI data analysis: staying within the value of 0.1 ensures that the ratio of false activations is much smaller than the ratio of true activations [see Fadili et al., 2000].

RESULTS AND DISCUSSION

For each dataset or each run and session, the carried out analysis provided results that were highly consistent across subjects, suggesting an adequate level of generality of the outcomes. ICA revealed the same activity patterns as the GLM analysis did carried out with Brain Voyager 2000 in the occipital lobe (visual component) and in the auditory and motor cortices (auditory‐motor component). This shows that ICA can segregate regions that are activated by stimulus epochs occurring both simultaneously and asynchronously. Each of these ICs had a time course that closely matched the BOLD signal time course of the active voxels revealed by GLM in the corresponding region. Results were well reproducible across subjects, in that the IC time courses were well correlated to GLM predictors: r(AM) = 0.730 ± 0.179, r(LV) = 0.763 ± 0.179, and r(RV) = 0.684 ± 0.173, across subjects and VOIs.

The rVOI and iVOI approaches exhibited different results for the components associated with the auditory‐motor sources (multiple sources activated) and similar results for the visual components (single sources activated).

Specifically, as expected based on the timing of the sensory stimulation, separate task‐related maps contained the relative hemi‐visual sources. Furthermore, audio‐motor task‐related maps contained task‐related single foci (only “auditory” or only “motor” component) in the rVOI and multiple foci of brain activity (“auditory‐motor” components) in the iVOI datasets. Including or not including a region of interest in ICA data selection (by selecting bigger or smaller volumes of data) may crucially affect the extraction of targeted source signals. The auditory‐motor source was best estimated on the maximal iVOI whereas a spatially reduced dataset that comprised only the auditory slices was less accurate in estimating the same auditory components. This suggests that when the observations of the fMRI mixtures are drawn from a native auditory‐motor (multiple foci) source, the iVOI approach actually takes advantage of some form of signal interaction between the multiple foci of activity in the conceptually unique component that is not exploited in the rVOI (Fig. 2B). Additional slices in the motor cortex globally improve the estimate of the auditory‐motor components but do not affect the estimate of the visual components (Fig. 2A; Fig. 3). Despite the improved spatiotemporal accuracy, because of the highly similar regional time courses the iVOI decompositions exhibited a substantially poor functional segregation, providing a single‐component instead of a two‐component model of the observed functional connectivity in the two spatially separate systems. In general, ICA provides a better functional segregation in event‐related designs [see Calhoun et al., 2001b; Formisano et al., 2004] where the measured interregional differences in the time‐courses are more systematic.

Figure 2.

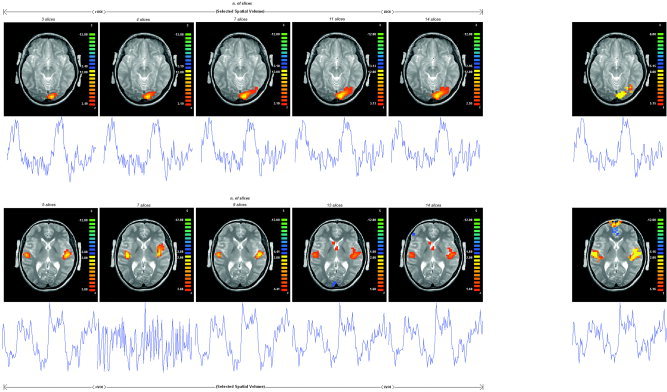
Consistently task‐related components. ICA decomposition of each session produced a component to which the activated voxels time course well resembled the task block structure (r[a] = 0.66 ± 0.09 and r[b] = 0.61 ± 0.06). ICA component map active voxels (posterior probability images thresholded at 0.5) are displayed in the original 2D image matrix (fMRI images) for Subject 1 by selecting five different VOI configurations. More spatial observations (iVOI) improve the spatial accuracy of the extracted components (with respect to the GLM benchmark). A: Result for the right visual task. The ICA maps look like much performing to GLM maps already when we build up a VOI of seven slices. B: Comparison of consistently task‐related component maps for auditory‐motor task. The ICA maps get the top performing to GLM maps only when we build up a complete VOI.

Figure 3.

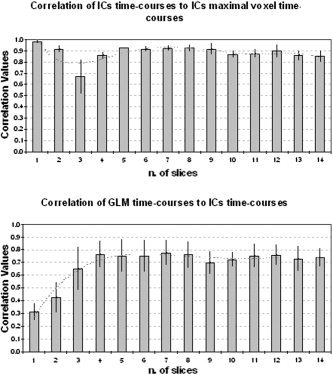
The panels show the correlation values of IC time courses vs. time courses of IC maximal voxel and vs. GLM regressors time courses, across VOIs, averaged on subjects.

The visual inspection of the components generated by sICA decompositions confirmed the ROC measures and revealed the different technical quality of iVOI and rVOI maps. Both rVOI and iVOI ICA as well as GLM maps clearly show clusters of cortical activity corresponding to the main areas expected to be activated by the auditory‐motor, left visual, and right visual tasks. For the purpose of a reliable selection of the task‐related ICs, the ROI‐based selection criterion [Van de Ven et al., 2004] was used and the output was confirmed by the temporal references. The auditory‐motor pattern (Fig. 1, see A) resulted in an wide network of activations that included a very large cluster in the primary motor cortex spanning the left pre‐ (supplementary motor area; SMA), medial‐ (premotor cortex), middle‐ (prefrontal cortex), and postcentral (pre‐SMA) gyrus (Brodmann area [BA] 4, 6, 46, 2, respectively) and an extended region of activation in the insula (basal ganglia; BA 13). The peak of activation was found in BA 42 (superior temporal gyrus; STG) consistent with the activation of the auditory area in primary auditory cortex (Heschl's convolutions). In the left visual pattern (Fig. 1, see B) the activated regions were the inferior (BA 17) and middle occipital gyrus (BA 18), the fusiform gyrus (BA 19), and the cuneus (BA 17), consistent with activation of the primary visual cortex (V1). Finally in the right visual pattern (Fig. 1, see C), the activated regions were similar to the pattern (B) and included the lingual gyrus (BA 18).

McKeown et al. [ 1998b] compared sICA with other data‐driven methods and showed that sICA performs best in isolating voxels whose activity time courses correlate with distinct task conditions or with artifacts. We observed that for every subject, the C_{left visual, j} and C_{right visual, j} are components more easily extracted than are C_{auditory‐motor, j} (Fig. 3); in fact, they fit better to the multiple regression analysis maps.

The GLM analysis and ICA decomposition exhibited clearly different behavior with respect to the changes of the threshold. In fact, threshold proved to be a critical parameter for the ROC power evaluation, particularly related to filtering properties of ICA not present in standard multiple regression analysis. We found an acceptable threshold trade‐off between statistical significance and the accuracy of activation patterns in using a corrected significance of P < 0.01 for the GLM, but in the ROC analysis a pixel is considered active only when a certain number of its closest neighbors (20) are active as well. In this approach, pixels on the border of activated regions are not treated as activated even for an extremely low threshold level. In such circumstances, the true‐positive ratio is always significantly smaller than one. This may offset the high efficiency of such a filter in the more interesting regime of a more realistic and higher threshold. Despite the obvious suboptimality of multiple regression analysis as a benchmark, we have used it to achieve a simple standardization of the results.

The measures of spatial accuracy revealed that the iVOI approach can ensure superior performances in terms of ROC power than the rVOI one can. Figure 4 and Tables I and II show ROC results on auditory‐motor and visual activation data averaged across subjects and sessions. Those results indicate that by increasing the number of voxels we strengthen sICA power to identify clusters of activation, or at least, if more spatial observations are available for covariant sources the decomposition will produce more accurate components (Fig. 2A,B).

Figure 4.

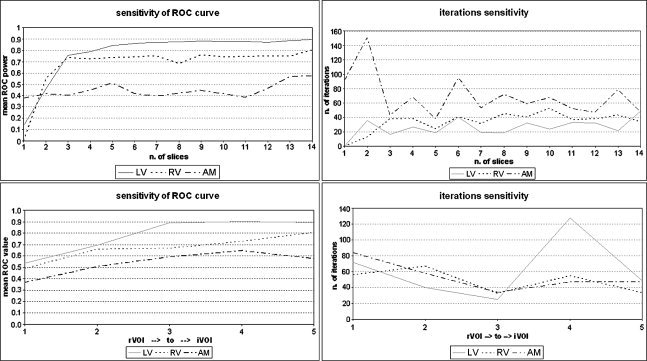
The left panels present the mean measure of the ROC curve as a function of the selected increasing VOI (from slice 1 to 14 for the slice‐based approach in the upper panel and five functional‐based VOIs in the lower panel), for the three main functional activities (auditory‐motor [AM], left visual [LV], and right visual [RV]). The curves were obtained from the whole ROC curve using only 0–0.1 false positive ratio regions as used in this article. We used three different imaging sessions and the results are reported for the three sessions averaged out. The measures of spatial accuracy revealed that the iVOI approach can ensure superior performances in terms of ROC power than the rVOI one can: by increasing the number of voxels, the extracted independent components perform better to multiple regression analysis benchmarks. We noticed that for the C_{auditory‐motor, j} in the slice‐based approach, including additional spatial volumes with new sources causes a transitory slow down in the mean ROC value, which rises again by including further extra spatial volumes, useful for the auditory‐motor component. Specifically, this fall occurs when including the extra auditory area (slice 7) until when including the motor area (slice 11). The graphs on the right represent the mean number of iterations necessary for extracting the representative independent components as function of the selected increasing VOI for the three main functional activities (AM, LV, RV). The number of iterations for extracting the best ROC power task‐related extracted components in the iVOI approach is on the average lower than that in the rVOI approach. Furthermore, in the slice‐based approach, including additional spatial volumes with new sources causes a transitory rise in the number of iterations, which goes again down by including further extra spatial volumes, useful for the auditory‐motor component C_{auditory‐motor, j}. The number of iterations seems to be affected by the structure of the sample used in spatial ICA in a way that the more information about the sources affecting the data, the faster (and more accurate) the estimation is.

Table I.

Mean ROC scores for VOI along z for three subjects

Slices	1st Session			2nd Session			3rd Session			All 3 Sessions
	CLV	CRV	CAM	CLV	CRV	CAM	CLV	CRV	CAM	CLV	CRV	CAM
1	0.085	0.000	0.356	0.120	0.000	0.390	0.196	0.000	0.378	0.134	0.000	0.375
2	0.491	0.505	0.438	0.464	0.539	0.352	0.434	0.596	0.469	0.463	0.547	0.420
3	0.784	0.758	0.434	0.724	0.733	0.377	0.763	0.710	0.404	0.757	0.733	0.405
4	0.758	0.731	0.454	0.799	0.688	0.455	0.805	0.759	0.443	0.787	0.726	0.451
5	0.843	0.745	0.514	0.839	0.692	0.516	0.843	0.772	0.510	0.842	0.737	0.513
6	0.881	0.749	0.327	0.846	0.723	0.508	0.854	0.753	0.419	0.860	0.742	0.418
7	0.892	0.766	0.353	0.866	0.719	0.422	0.849	0.770	0.421	0.869	0.752	0.399
8	0.886	0.764	0.434	0.875	0.509	0.397	0.857	0.777	0.442	0.873	0.683	0.424
9	0.904	0.780	0.363	0.883	0.736	0.516	0.857	0.759	0.466	0.881	0.758	0.448
10	0.878	0.764	0.407	0.893	0.705	0.403	0.859	0.758	0.447	0.877	0.743	0.419
11	0.882	0.761	0.300	0.889	0.719	0.388	0.858	0.758	0.459	0.877	0.746	0.382
12	0.856	0.771	0.501	0.890	0.715	0.429	0.865	0.758	0.464	0.870	0.748	0.464
13	0.888	0.773	0.583	0.895	0.729	0.545	0.868	0.749	0.580	0.884	0.750	0.569
14	0.896	0.841	0.605	0.912	0.803	0.573	0.879	0.770	0.555	0.896	0.805	0.578

All subjects mean ROC measures as a function of the selected increasing VOI (from 1 to 14 slices), for the three main related extracted components (C_{left visual} [C_LV]; C_{right visual} [C_RV]; C_{auditory‐motor} [C_AM]) along a mean of all sessions, by using only 0–0.1 false‐positive ratio regions.

Table II.

Mean ROC scores for VOI along xyz for three subjects for all three sessions

VOI	CLV	CRV	CAM
1	0.537	0.491	0.368
2	0.693	0.658	0.507
3	0.891	0.666	0.592
4	0.900	0.727	0.646
5	0.896	0.805	0.578

All subjects mean ROC measures as a function of the selected increasing VOI: an anatomically and functionally informed selection of the region of interest that is made variable along all the three spatial dimensions, for the three main related extracted components (C_{left visual} [C_LV]; C_{right visual} [C_RV]; C_{auditory‐motor} [C_AM]) along a mean of all sessions using only 0–0.1 false positive ratio regions.

Furthermore, we noticed that the number of iterations for extracting the best ROC power task‐related components in the iVOI approach was on average lower than that in the rVOI approach (Fig. 4; Tables III and IV). This indicates that selecting a bigger spatial volume of data and making more statistical observations available for source estimation may render the ICA extraction easier from the algorithmic point of view. Moreover, we noticed that incrementally adding subvolumes of data with new active sources altered the number of iterations as a function of the actual spatial coverage of the new sources. More in detail, a transient rise in the number of iterations was observed when including the auditory area or the motor area in the iVOI audiomotor component. The number of iterations thus seems to be affected by the structure of the sample used in sICA in a way that the more information about the sources affecting the data we use, the faster (and more accurate) the estimation is. More spatial observations available for both single and multiple sources produce an average decrease in the number of iterations, provided that these additional observations actually enforced the statistical ICA efficiency in the extraction of those sources (i.e., voxels that fit those sources in terms of their multivariate spatiotemporal profiles). When additional observations only increase the complexity of the mixture rather than “enforcing” the structure of “already” extractable components or allowing the identification of new components, these act as noisy, confounding observations and the unmixing process of ICA is less effective and accurate.

Table III.

Mean number of iterations for VOI along z

Slices	1st Session			2nd Session			3rd Session			All 3 Sessions
	CLV	CRV	CAM	CLV	CRV	CAM	CLV	CRV	CAM	CLV	CRV	CAM
1	0.00	0.00	99.00	0.00	0.00	85.67	0.00	0.00	89.50	0.00	0.00	91.39
2	36.33	0.00	212.67	49.33	37.67	128.67	20.33	0.00	111.67	35.33	12.56	151
3	11.33	42.67	37.00	14.67	25.67	55.67	23.00	44.33	37.33	16.33	37.56	43.33
4	41.33	49.33	43.33	15.67	29.33	111.33	23.00	36.33	49.33	26.67	38.33	68.00
5	22.67	26.67	37.33	15.67	20.00	23.33	18.67	26.67	52.00	19.00	24.44	37.56
6	46.00	19.67	51.00	20.00	70.67	95.00	53.67	33.00	137.67	39.89	41.11	94.56
7	25.67	24.00	69.67	17.00	37.33	33.00	15.67	33.67	57.00	19.44	31.67	53.22
8	25.00	31.33	46.67	17.67	79.33	46.67	14.00	24.33	123.67	18.89	45.00	72.33
9	23.33	29.67	35.33	39.67	52.00	50.00	32.33	40.33	91.00	32.11	40.67	58.78
10	19.67	73.67	34.67	23.00	56.67	76.00	23.67	27.67	92.67	23.33	52.67	67.78
11	36.00	24.00	53.33	48.67	56.00	51.00	29.67	30.67	53.00	32.67	36.89	52.44
12	32.22	31.00	59.00	31.33	52.33	34.33	29.33	29.33	48.00	32.22	37.56	47.11
13	21.33	35.33	101.33	23.67	54.67	93.00	20.33	40.33	40.67	21.33	43.44	78.33
14	48.78	23.00	54.33	36.67	52.00	50.00	85.67	26.67	36.67	48.78	33.89	47.00

All subjects mean number of iterations as a function of the selected increasing VOI (from 1 to 14s), for the three main related extracted components (C_{left visual} [C_LV]; C_{right visual} [C_RV]; C_{auditory‐motor} [C_AM]) along distinct sessions and showing a mean of all sessions.

Table IV.

Mean number of iterations for VOI along xyz for three subjects for all three sessions

VOI	CLV	CRV	CAM
1	72.00	56.33	84.00
2	40.00	67.00	58.00
3	25.00	33.00	34.00
4	128.00	55.00	47.00
5	48.78	33.89	47.00

All subjects mean number of iterations as a function of the selected increasing VOI along all the three spatial dimensions, for the three main related extracted components (C_{left visual} [C_LV]; C_{right visual} [C_RV]; C_{auditory‐motor} [C_AM]) along a mean of all sessions.

These considerations imply important consequences for the practical application of ICA to protocols in which synchronous spatially independent multiple sources are investigated with respect to how the computational load and the accuracy of the layout are affected. This aspect becomes crucial in a real‐time ICA [Esposito et al., 2003], in which the trade‐off of space and time source sampling is at its extreme grade.

CONCLUSIONS

The aim of this article was to explore the performance of multiple ways to select the data sample for sICA in multicondition experimental designs, to provide quantitative information concerning their impact in the processing of fMRI data, and to suggest their choice based on specific application problems. We have experimentally compared two methods for voxel selection when constructing the ICA observation matrix from the acquired slice time‐series and compared the rVOI and the iVOI for sICA decompositions. Estimation and accuracy performances in extracting task‐related activation maps from multiple condition block‐design fMRI datasets were considered within a multicondition experimental framework. The performances of the iVOI approach were almost always better compared to that of the rVOI. Although the rVOI approach was faster in extracting the individual sources because of the reduced size of the input data matrix, the iVOI approach was more powerful in terms of appropriate separation and estimation of multiple sources in a single decomposition.

The spatial extent of a dataset is a major issue for off‐line and real‐time ICA applications in relation to the experimental design. In fact, especially with a temporally reduced observation window, it is essential to predict how the spatial structure of the sample will be affected by the number of sources and their spread across space. In our off‐line application, even when both types of data selection worked properly, the iVOI approach also exhibited a specific superiority in the efficacy of ICA component extraction, a relevant point for further work in the context of real‐time ICA.