Abstract
A prominent theory in neuroscience suggests reward learning is driven by the discrepancy between a subject's expectation of an outcome and the actual outcome itself. Furthermore, it is postulated that midbrain dopamine neurons relay this mismatch to target regions including the ventral striatum. Using functional MRI (fMRI), we tested striatal responses to prediction errors for probabilistic classification learning with purely cognitive feedback. We used a version of the Rescorla‐Wagner model to generate prediction errors for each subject and then entered these in a parametric analysis of fMRI activity. Activation in ventral striatum/nucleus‐accumbens (Nacc) increased parametrically with prediction error for negative feedback. This result extends recent neuroimaging findings in reward learning by showing that learning with cognitive feedback also depends on the same circuitry and dopaminergic signaling mechanisms. Hum Brain Mapp, 2005. © 2005 Wiley‐Liss, Inc.
Keywords: functional MRI, probabilistic feedback, Rescorla‐Wagner model, reward, basal‐ganglia
INTRODUCTION
In a recent neuroimaging study we investigated the neural correlates of classification learning by separately modeling the BOLD response to stimulus/response, delay period, and feedback (positive or negative) for each trial [Aron et al., 2004]. We reported that stimulus/response and positive or negative feedback, but not the delay period, all led to significant activation of a network of regions comprising the mesencephalic dopamine system, including midbrain, ventral striatum, and orbital and medial frontal cortex. Those results are consistent with the hypothesis that midbrain dopamine neurons code the mismatch between expected and actual reward outcomes and then relay this to target regions in order to drive the subject's learning [see for review, Schultz, 2002]. Here we report a further analysis of those data, investigating more directly whether a prominent target of midbrain DA neurons, the ventral striatum, is activated parametrically according to the level of prediction error on each trial.
The striatum, comprising caudate, putamen, and nucleus accumbens (Nacc), has been heavily implicated in the processing of expectations and rewards/outcomes by lesion and neurophysiological studies [e.g., Cardinal et al., 2001; Schoenbaum and Setlow, 2003; Schultz et al., 1992; Setlow et al., 2003] and is activated in a number of recent neuroimaging studies related to processing primary (e.g., gustatory) rewards [Berns et al., 2001; McClure et al., 2003; O'Doherty et al., 2003, 2004; Pagnoni et al., 2002], conditioned rewards (e.g., money) [Breiter et al., 2001; Delgado et al., 2000; Elliott et al., 2000; Haruno et al., 2004; Knutson et al., 2001a, b; Tanaka et al., 2004], and pain [Becerra et al., 2001; Jensen et al., 2003; Seymour et al., 2004]. Several such neuroimaging studies have used temporal‐difference reinforcement learning models to estimate prediction errors underlying either classical [McClure et al., 2003; O'Doherty et al., 2003] or instrumental conditioning [O'Doherty et al., 2004; Tanaka et al., 2004], finding that activity in the ventral striatum correlates with prediction error.
The classification learning paradigm used by Aron et al. [2004] differs from these tasks in employing purely informational feedback (i.e., no primary or conditioned rewards). On each trial a subject predicts one of two possible outcomes and is then simply shown the “correct” outcome. Depending on a match/mismatch of the prediction and outcome, the trial is coded as “positive” or “negative” feedback. Here we used an adaptation of the well‐known Rescorla‐Wagner (RW) reinforcement learning model [Rescorla and Wagner, 1972] to estimate prediction errors for each trial and subject. The Rescorla‐Wagner model does not include representations of time within a trial, as do temporal‐difference models, but it has been shown to accurately capture many aspects of probabilistic category learning [Gluck, 1991; Gluck and Bower, 1988], of which our task is one example. More importantly, as demonstrated by Gluck and colleagues, the RW model can be simply extended to incorporate certain properties that likely reflect human learning, such as association strengths that depend on errors and reinforcements in a frequency‐driven manner, and the possibility that stimulus‐response associations can interact in subtle ways, either when stimuli are paired together or when stimuli are associated with more than one type of response. Other functional MRI (fMRI) studies have also been motivated by aspects of the RW model. For example, Fletcher et al. [2001] showed differences in neural response to the unexpected presence or absence of outcomes, which are represented by distinct learning rates in the RW model.
Here we used the prediction errors from the model as regressors in an analysis of the subjects' fMRI data. We examined whether the ventral striatum, which has shown sensitivity to prediction errors for primary or conditioned rewards, would be activated according to the level of prediction error even when the outcomes were purely informational.
SUBJECTS AND METHODS
Participants
An extended analysis of imaging and behavioral data was undertaken for the 15 subjects reported in Aron et al. [2004]. All subjects gave informed consent according to a Massachusetts General Hospital Human Subjects Committee protocol.
Category Learning: The Behavioral Task
The classification learning task [Aron et al., 2004; also see Knowlton et al., 1994; Poldrack et al., 2001] consisted of six blocks of 25 trials each, for 150 trials total. Each subject was instructed to pretend that they were working in an ice‐cream store, and that they were to learn to predict which individual figures preferred vanilla or chocolate ice cream. On each trial the subject was presented with a toy figure (Mr. Potatohead, Playschool/Hasbro) with several features that could be present or absent (hat, eyeglasses, moustache, and bowtie). Each combination of features constituted a particular “stimulus” and there was always at least one feature present, but never all four, giving a total of 14 stimuli. The stimuli and outcomes were chosen such that the marginal conditional probabilities of the chocolate/vanilla outcomes given the individual features were 0.85/0.15, 0.66/0.34, 0.44/0.56, and 0.24/0.76 (Table I).
Table I.
Stimuli as well as objective/empirical/model‐based probabilities for the chocolate (as opposed to vanilla) outcome
| Stimulus | Features | P(choc) | |||||
|---|---|---|---|---|---|---|---|
| Moustache | Hat | Glasses | Bowtie | Objective | Subjects' responses | Model outputs | |
| 1 | 0 | 0 | 0 | 1 | 0.94 | 0.81 | 0.89 |
| 2 | 0 | 1 | 0 | 0 | 0.75 | 0.56 | 0.63 |
| 3 | 0 | 1 | 0 | 1 | 0.91 | 0.84 | 0.83 |
| 4 | 0 | 0 | 1 | 0 | 0.12 | 0.32 | 0.27 |
| 5 | 0 | 0 | 1 | 1 | 0.88 | 0.72 | 0.70 |
| 6 | 0 | 1 | 1 | 0 | 0.50 | 0.30 | 0.49 |
| 7 | 0 | 1 | 1 | 1 | 0.94 | 0.62 | 0.75 |
| 8 | 1 | 0 | 0 | 0 | 0.07 | 0.13 | 0.17 |
| 9 | 1 | 0 | 0 | 1 | 0.50 | 0.43 | 0.50 |
| 10 | 1 | 1 | 0 | 0 | 0.17 | 0.11 | 0.29 |
| 11 | 1 | 1 | 0 | 1 | 0.71 | 0.32 | 0.60 |
| 12 | 1 | 0 | 1 | 0 | 0.07 | 0.14 | 0.20 |
| 13 | 1 | 0 | 1 | 1 | 0.60 | 0.38 | 0.40 |
| 14 | 1 | 1 | 1 | 0 | 0.14 | 0.12 | 0.23 |
Fourteen stimuli (with different frequencies) were shown over 150 trials. Each stimulus consisted of one to three features (moustache, hat, glasses, bowtie) for the Mr Potatohead feedback‐driven category learning task. The last two columns show the observed responses from subjects and the average responses from the model over the last 100 trials only.
The timing of events within and between trials was optimized to permit separation of hemodynamic responses to different events. Stimulus presentation lasted 2.5 s, within which time the subject responded with a left button press for chocolate or a right button press for vanilla. There followed a variable interval of visual fixation (0.5–6 s, mean = 2 s), after which feedback was presented (2 s) by showing the stimulus figure holding either a vanilla or chocolate ice cream cone. The interval between the feedback offset and onset of the next stimulus varied between 2–16 s (mean = 7.7 s).
Estimating the Prediction Error: Mathematical Modeling
We implemented a version of the Rescorla–Wagner model [1972], as modified by Gluck and Bower [1988], consisting of 14 input nodes with weighted connections to two output nodes. Four of the input nodes modeled the presence/absence of a particular individual feature and the remaining 10 modeled the presence/absence of the 10 possible combinations of two or three features [Gluck 1991; Gluck and Bower 1988].
On each trial, the activity for each output node was computed as:
and the weight change for that trial computed as:
where i = 1 or 2 indexes the output node, j = 1…14 indexes the input node, O i is the i‐th output node, V ij is an association weight to i from j, I i = 1 or 0 is the i‐th input node, ϵ is the learning rate, λi = 1 or 0 is the target value for the i‐th output node indicating the actual outcome (presented in the feedback), and Z i = 0 or 1 indicates the category chosen by the subject on that trial. The intent of adding the Z i factor in the weight update equation was to make the model a simulation of individual subjects. In other words, by forcing the model to make the same choice that the subject made on each trial, the model received the same teaching signal as the subject—namely, the actual trial outcome. It is interesting to point out that including the Z i factor creates a biologically plausible Hebbian learning rule if we interpret the terms as presynaptic, I j, postsynaptic, Z i, and dopaminergic, λi–O i, activity [e.g., Schultz, 2002].
The model was first run to find a reasonable learning parameter (ϵ). Weights were initialized to small values (±0.5), model responses were chosen according to the largest output node (i.e., Z 1 = 1 if O 1 > O 2, or Z 2 = 1 if O 2 > O 1), and a learning rate was found such that average performance across 50 instantiations of the model matched overall average human performance (ϵ = 0.02). This particular learning rate was then used when modeling prediction errors for each subject (one model per subject) in the second stage. In this latter stage, weight values were initialized to zero because nonzero values would have introduced some response bias. Variation across subjects was ensured because the variable Z i indicated which output node was chosen by the subject on each trial (i.e., Z 1 = 1 if category 1 was chosen by subject, Z 1 = 0 if the other category was chosen). The mean square prediction error (MSPE) from the model was computed on each trial as:
This error signal was used to create a parametric regressor for the fMRI analysis, separately for positive and negative feedback trials.
Functional MRI Methods
Preprocessing and statistical analysis of the fMRI data were performed using SPM99 software (Wellcome Dept. of Cognitive Neurology, London) and included slice timing correction, motion correction, spatial normalization to the MNI305 (Montreal Neurological Institute) stereotactic space (using linear affine registration followed by nonlinear registration, resampling to 3 mm cubic voxels), and spatial smoothing with an 8 mm Gaussian kernel. Stimulus, positive feedback, negative feedback, and delay (a boxcar starting at stimulus‐offset and lasting the delay duration) were modeled using the canonical hemodynamic response function and its temporal derivative. Low‐frequency signal components (66 s cutoff) were treated as confounding covariates. The model‐fit was performed individually for each subject. Contrast images were generated for each of the four event types (against the implicitly modeled baseline/fixation), as well as for contrasts between event types, as reported in Aron et al. [2004]. The contrast images were then used in a second‐level analysis, treating subject as a random effect. For current purposes, for each subject, we entered MSPE from the model as a parametric modulation regressor separately for positive and negative feedback trials (e.g., for each positive feedback trial, the corresponding MSPE value from the model for that trial was entered as a regressor), and these were orthogonalized with respect to corresponding positive and negative feedback regressors. Contrast images, representing increases of activation with increases in MSPE, as well as those representing decreases of activation with increases in MSPE, were generated separately for positive and negative feedback and entered into a second‐level analysis treating subject as a random effect.
Statistical Analyses of Imaging Contrasts
Given the importance of the basal‐ganglia in feedback‐driven learning (see Introduction) and the importance of having appropriate statistical sensitivity, our prime statistical analysis of the group contrasts was performed using small‐volume correction within a box‐shaped region of interest (ROI) encompassing the entire basal‐ganglia, with dimensions 64 mm wide (x‐direction), 44 mm deep (y‐direction), and 43 mm high (z‐direction), and centered on the basal‐ganglia at 0,0,0 in MNI coordinates. Within this region, correction for multiple comparisons was accomplished using small volume correction based on Gaussian random field theory in SPM99. For completeness, we also report statistical analyses corrected at the whole‐brain level using Gaussian random field theory.
RESULTS
Category Learning: Behavior
Across six blocks subjects achieved a mean score of 66.4 ± 7.4% correct [see Aron et al., 2004, for details]. Accuracy and RT data were analyzed using ANOVA with session as a repeated measure. There was a significant increase in accuracy, F(5,75) = 2.714, P = 0.032, and a marginally significant decrease in RT, F(5,75) = 2.087, P = 0.091, consistent with learning across sessions.
Comparing Model Performance to Subject Performance
Just as subjects quickly learned the classification task (i.e., achieved >60% correct performance by the end of block 1), prediction errors in the model declined steadily from near 0.5 (for guessing) (Fig. 1), and all subjects (as well as the model) converged on similar correct responses for higher frequency associations. By trial 50, peaks in MSPE began to appear, which indicate occurrences of stronger predictions from the model in combination with negative feedback. The subject/model relation was assessed more quantitatively by comparing whether output values from the model, when trained with the subjects' actual responses, matched subject choices. Over the last 100 trials, responses based on model predictions were significantly correlated with subjects' actual responses (average R = 0.48, P = 0.011, 100 trials). Moreover, when there was a relatively large difference between output values within the model (i.e., larger than the mean output difference across the last 100 trials), the correlations were much larger (R = 0.64, P = 0.015, 47.2 ± 6.1 trials). The highest MSPE values (near 0.7) occurred for trials later in training in which the prediction was strong but negative feedback occurred. Therefore, after some initial guessing period most trials with positive feedback had relatively low MSPE, while trials with negative feedback were associated with large MSPE.
Figure 1.
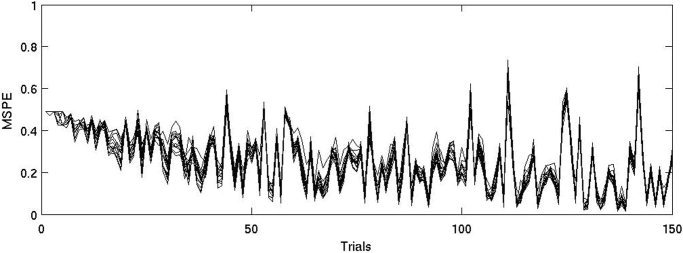
The MSPE from the individual subject models across trials. Early in training errors are near 0.5 with little variation due to the fact that weights are initialized to 0 and only subject responses produce variation. By trial 50, peaks in MSPE begin to appear, which indicate the occurrence of stronger predictions from the model in combination with negative feedback. Also, by this time all subject‐models have converged on similar responses, which merely reflects good performance and that the model is driven by frequency of stimulus‐outcome observations.
Correlating Brain Activity With the Model Estimate of the Prediction Error
Prediction errors on negative feedback trials
There was a single large cluster comprising 91 voxels within the basal‐ganglia ROI which was significant at P = 0.029 (corrected for multiple comparisons). This cluster included three prominent basal‐ganglia foci (Fig 2): a medial caudal focus (peak MNI coordinates: −6, 3, −6, Z = 3.16), and two lateral anterior foci (peak MNI: −15, 18, −3 and 15, 18, 0, Z = 3.56 for both). An atlas of deep brain structures [Duvernoy, 1999] placed the medial caudal focus squarely within the Nacc, while the two lateral anterior foci lay close to the Nacc, but more specifically in ventral striatum where Nacc, caudate, and putamen merge. There were no regions that were significantly negatively correlated with prediction error.
Figure 2.
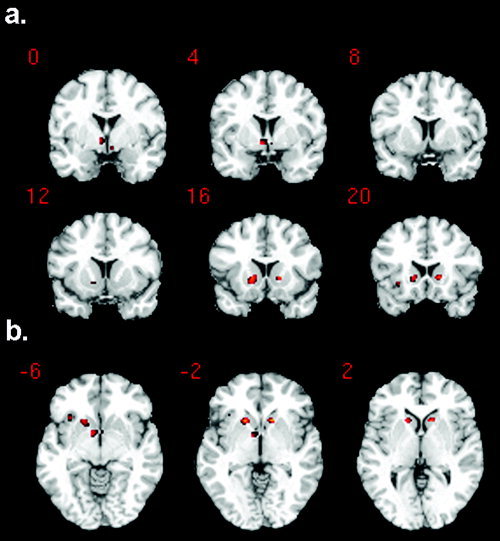
Ventral striatal (including nucleus accumbens, Nacc) activation is significantly correlated with increasing prediction errors on negative feedback trials. a: Activation foci overlaid on a standard structural image in the coronal plane. Y coordinates are shown for MNI space: i.e., distance anterior to the anterior commissure (in mm). There is a medial caudal focus and two anterior lateral foci. The medial caudal focus is highly consistent with the nucleus accumbens, as shown in the anatomical atlas of Duvernoy [1999]. b: The same foci are shown overlaid on axial slices. Z coordinates are now shown for MNI space.
Prediction errors on positive feedback trials
There were no regions whose activity was significantly correlated either positively or negatively with positive prediction error.
Contrast of negative and positive feedback trials
Our prior report [Aron et al., 2004] established that positive and negative feedback trial components both led to significant activation of the ventral‐striatal region (see fig. 3 in that article). Here we assessed the contrast of positive and negative feedback within the basal‐ganglia ROI. There was no significant difference in activation or deactivation at P < 0.01 (voxel level uncorrected) and P < 0.05 cluster corrected.
Whole brain analysis
For completeness, we performed a whole brain analysis with a map thresholded at P < 0.01 (voxel level) and P < 0.05 (cluster corrected). We found significant clusters representing positive correlations between activity and prediction errors for negative feedback trials in medial dorsal cerebellum (size = 334 voxels, t = 7.1, MNI: −15, −45, −12), cuneus (788 voxels, t = 5.46, MNI: 15, −72, 18) and pre/post‐central gyrus (218 voxels, t = 4.97, MNI: 45, −24, 45), and a significant cluster representing a positive correlation between activity and prediction errors for positive feedback trials in cerebellum extending into lingual gyrus (291 voxels, t = 4.15, MNI: −33, −42, −12). Other studies have also occasionally reported learning‐related activations in cuneus, paracentral regions, or cerebellum [Berns et al., 2001; Haruno et al., 2004; O'Doherty et al., 2003; Volz et al., 2003]. Speculatively, such foci are involved in motor‐related coordination and learning. However, as these foci are not obviously explicable with respect to classic reward systems and the wider dopaminergic system, we do not discuss them further. Other studies have also reported frontal or parietal activations related to prediction errors [O'Doherty et al., 2003; Volz et al., 2003]. We too, in our prior report, found frontal and parietal activations for positive or negative feedback [Aron et al., 2004]. However, in our current analysis there were no other clusters of activity that were significantly correlated either positively or negatively with prediction error on positive or negative feedback trials.
DISCUSSION
The results show that activity in the ventral striatum, as measured with BOLD fMRI during classification learning, was significantly correlated with the degree of prediction error estimated from a Rescorla‐Wagner associative learning model. This is consistent with other results showing that ventral striatum is sensitive to prediction errors during learning with primary or conditioned reinforcers, and extends them by suggesting generality for both primary reinforcers and informational feedback.
The ventral striatal activations in the present study were located in a medial caudal focus, consistent with the location of the Nacc [Duvernoy, 1999], while the two anterior lateral foci were less clearly localized to Nacc. The medial caudal Nacc focus (−6, 3, −6), was close to that reported in studies comparing predictable with unpredictable events [e.g., Berns et al., 2001, MNI: 0, 4, −4; see for an ROI analysis Pagnoni et al., 2002; Volz et al., 2003, MNI: −12, 12, −3], and a study comparing a salient (behaviorally relevant) unrewarded outcome vs. a nonsalient one [Zink et al., 2003, MNI: −12, 8, −12]. A study looking at temporal difference prediction errors in instrumental learning also reported Nacc activation but at a more remote locus [O'Doherty et al., 2004, MNI: 6, 14, −2], while two studies analyzing temporal difference prediction errors in classical learning paradigms reported striatal activity in the ventral putamen rather than Nacc [McClure et al., 2003; O'Doherty et al., 2003]. Other studies have reported ventral striatal/Nacc activations, usually at locations more similar to the lateral foci here (MNI: −15, 18, −3 and 15, 18, 0), for contrasts of reward vs. nonreward [Knutson et al., 2001b], active vs. passive receipt of reward [Zink et al., 2004], and size of monetary outcome [Breiter et al., 2001]. Therefore, one of our ventral striatal foci was consistent with the anatomical location of Nacc as well as with reported Nacc activations in prior neuroimaging studies, especially those contrasting unpredictable with predictable events, while the two lateral foci were consistent with several other reported ventral striatal activations, some of which involved monetary rewards and at least one that involved primary rewards.
A challenge in relating the present findings to neurophysiological data is that our results show increased striatal signal in response to unexpected negative feedback, whereas single‐unit recordings of dopaminergic cells in the midbrain generally find increased firing in response to unexpected reward and decreased firing in the absence of reward [Hollerman and Schultz, 1998]. There are a number of possible reasons for this discrepancy. First, fMRI signals are better correlated with local field potentials (reflecting synaptic input and local interneuron processing) than with spiking activity (which is what the neurophysiology measures) [Logothetis, 2003]. Therefore, the observation of increased fMRI signal in the ventral‐striatum leaves unknown many features of the underlying activity (e.g., projection neurons vs. interneurons). Second, it is possible that our result does not even reflect dopaminergic signals, but rather arises from some other source such as projections to the region from other neurons or interneurons within ventral striatum/Nacc. However, we note that patients with impaired dopaminergic systems are impaired on this task [Beninger et al., 2003; Knowlton et al., 1996; Shohamy et al., 2004]. Third, the presence of negative feedback could imply the absence of expected positive feedback, which is associated with decreased firing of dopamine cells [Hollerman and Schultz, 1998]. Imaging results are mixed regarding the effects of reward omission: Some fMRI studies do report decreases in ventral striatum related to the absence of expected reward [Knutson et al., 2001b; O'Doherty et al., 2003], but other studies do not [McClure et al., 2003; Pagnoni et al., 2002], and some report it only in relation to positive outcomes [cf. Ullsperger and von Cramon, 2003]. In brief, the source of discrepancy between neurophysiological findings and neuroimaging findings of striatal activation, as well as different directions of striatal activation for different tasks, remains to be fully understood.
Although the current analysis only examined activity in the basal‐ganglia correlated with prediction error, our prior study found that midbrain activation for negative feedback trials was significantly correlated (across subjects) with ventral striatal, orbital, and medial frontal foci [Aron et al., 2004]. This was consistent with proposals that a widespread mesencephalic dopamine network underlies reinforcement learning [e.g., Holroyd and Coles, 2002]. While the interactions of this network remain to be better characterized, Nacc activation in the absence of explicit reward fits proposals that the ventral striatal response is best related to salience, novelty, or behavioral relevance of the feedback rather than its putative hedonic or punishment value [Horvitz, 2000; Tricomi et al., 2004; Zink et al., 2003, 2004]. However, it is also possible that this response represents an internalized form of disappointment or aversion in the face of a difficult cognitive challenge. The Nacc is indeed necessary for some forms of aversive learning [Schoenbaum and Setlow, 2003], and neurons in Nacc fire to both rewarding and aversive stimuli [Setlow et al., 2003]. Imaging studies have also shown activity in the ventral striatum for aversive stimulation [e.g., Becerra et al., 2001; Jensen et al., 2003; Seymour et al., 2004]. Interestingly, recent evidence suggests that dopaminergic neurons are inhibited by aversive stimuli and some other, not yet identified neurons respond instead [Ungless et al., 2004]. It is unknown if such activity could reflect prediction errors or account for the discrepancies in increasing vs. decreasing activity to the absence of positive rewards.
We note that the present analysis only showed a significant correlation between ventral striatal activation and prediction error for negative feedback trials (not positive feedback trials). Our examination of the time‐course of MSPE for the subject‐models showed that the highest MSPE values (near 0.7) occurred for trials later in training in which the prediction was strong but negative feedback occurred (Fig. 1). Consequently, after some initial guessing period, most trials with positive feedback have relatively low MSPE, and this probably reduced our power to detect neural activation correlated with these errors. Thus, it is presently unclear whether the Nacc response observed here relates uniquely to prediction errors on negative feedback trials or whether it is a general feature of feedback‐driven learning regardless of the valence of feedback.
In conclusion, we have confirmed prior reports of Nacc response for a contrast of unpredictable vs. predictable events [Berns et al., 2001; Pagnoni et al., 2002; Volz et al., 2003], demonstrated that it varies parametrically with level of prediction error, and shown that it also applies in the case of classification learning, even when outcomes are purely informational and only probabilistically related to stimuli. As we have pointed out, the relationship between Nacc, negative feedback, and dopaminergic signals is not fully understood. That caveat notwithstanding, our results suggest that Nacc integrates frequency‐driven predictions, anticipated outcomes, and feedback, which could be used for the purpose of monitoring learning and guiding behavior, for both primary rewards and informational feedback
Acknowledgements
We thank Mark Gluck for comments.
REFERENCES
- Aron AR, Shohamy D, Clark J, Myers C, Gluck MA, Poldrack RA (2004): Human midbrain sensitivity to cognitive feedback and uncertainty during classification learning. J Neurophysiol 92: 1144–1152. Epub 2004 Mar 10. [DOI] [PubMed] [Google Scholar]
- Becerra L, Breiter HC, Wise R, Gonzalez RG, Borsook D (2001): Reward circuitry activation by noxious thermal stimuli. Neuron 32: 927–946. [DOI] [PubMed] [Google Scholar]
- Beninger RJ, Wasserman J, Zanibbi K, Charbonneau D, Mangels J, Beninger BV (2003): Typical and atypical antipsychotic medications differentially affect two nondeclarative memory tasks in schizophrenic patients: a double dissociation. Schizophr Res 61: 281–292. [DOI] [PubMed] [Google Scholar]
- Berns GS, McClure SM, Pagnoni G, Montague PR (2001): Predictability modulates human brain response to reward. J Neurosci 21: 2793–2798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiter HC, Aharon I, Kahneman D, Dale A, Shizgal P (2001): Functional imaging of neural responses to expectancy and experience of monetary gains and losses. Neuron 30: 619–639. [DOI] [PubMed] [Google Scholar]
- Cardinal RN, Pennicott DR, Sugathapala CL, Robbins TW, Everitt BJ (2001): Impulsive choice induced in rats by lesions of the nucleus accumbens core. Science 292: 2499–2501. Epub 2001 May 24. [DOI] [PubMed] [Google Scholar]
- Delgado MR, Nystrom LE, Fissell C, Noll DC, Fiez JA (2000): Tracking the hemodynamic responses to reward and punishment in the striatum. J Neurophysiol 84: 3072–3077. [DOI] [PubMed] [Google Scholar]
- Duvernoy HM (1999): The human brain: surface, blood supply, three‐dimensional sectional anatomy. New York: Springer. [Google Scholar]
- Elliott R, Friston KJ, Dolan RJ (2000): Dissociable neural responses in human reward systems. J Neurosci 20: 6159–6165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher PC, Anderson JM, Shanks DR, Honey R, Carpenter TA, Donovan T, Papadakis N, Bullmore ET (2001): Responses of human frontal cortex to surprising events are predicted by formal associative learning theory. Nat Neurosci 4: 1043–1048. [DOI] [PubMed] [Google Scholar]
- Gluck MA (1991): Stimulus‐generalization and representation in adaptive network models of category learning. Psychol Sci 2: 50–55. [Google Scholar]
- Gluck MA, Bower GH (1988): Evaluating an adaptive network model of human learning. J Mem Lang 27: 166–195. [Google Scholar]
- Haruno M, Kuroda T, Doya K, Toyama K, Kimura M, Samejima K, Imamizu H, Kawato M (2004): A neural correlate of reward‐based behavioral learning in caudate nucleus: a functional magnetic resonance imaging study of a stochastic decision task. J Neurosci 24: 1660–1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollerman JR, Schultz W (1998): Dopamine neurons report an error in the temporal prediction of reward during learning. Nat Neurosci 1: 304–309. [DOI] [PubMed] [Google Scholar]
- Holroyd CB, Coles MG (2002): The neural basis of human error processing: reinforcement learning, dopamine, and the error‐related negativity. Psychol Rev 109: 679–709. [DOI] [PubMed] [Google Scholar]
- Horvitz JC (2000): Mesolimbocortical and nigrostriatal dopamine responses to salient non‐reward events. Neuroscience 96: 651–656. [DOI] [PubMed] [Google Scholar]
- Jensen J, McIntosh AR, Crawley AP, Mikulis DJ, Remington G, Kapur S (2003): Direct activation of the ventral striatum in anticipation of aversive stimuli. Neuron 40: 1251–1257. [DOI] [PubMed] [Google Scholar]
- Knowlton BJ, Squire LR, Gluck MA (1994): Probabilistic category learning in amnesia. Learn Mem 1: 106–120. [PubMed] [Google Scholar]
- Knowlton BJ, Mangels JA, Squire LR (1996): A neostriatal habit learning system in humans. Science 273: 1399–1402. [DOI] [PubMed] [Google Scholar]
- Knutson B, Adams CM, Fong GW, Hommer D (2001a): Anticipation of increasing monetary reward selectively recruits nucleus accumbens. J Neurosci 21: RC159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knutson B, Fong GW, Adams CM, Varner JL, Hommer D (2001b): Dissociation of reward anticipation and outcome with event‐related fMRI. Neuroreport 12: 3683–3687. [DOI] [PubMed] [Google Scholar]
- Logothetis N (2003): The underpinnings of the BOLD functional magnetic resonance imaging signal. J Neurosci 23: 3963–3971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure SM, Berns GS, Montague PR (2003): Temporal prediction errors in a passive learning task activate human striatum. Neuron 38: 339–346. [DOI] [PubMed] [Google Scholar]
- O'Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ (2003): Temporal difference models and reward‐related learning in the human brain. Neuron 38: 329–337. [DOI] [PubMed] [Google Scholar]
- O'Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ (2004): Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science 304: 452–454. [DOI] [PubMed] [Google Scholar]
- Pagnoni G, Zink CF, Montague PR, Berns GS (2002): Activity in human ventral striatum locked to errors of reward prediction. Nat Neurosci 5: 97–98. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Clark J, Pare‐Blagoev EJ, Shohamy D, Moyano JC, Myers C, Gluck MA (2001): Interactive memory systems in the human brain. Nature 414: 546–550. [DOI] [PubMed] [Google Scholar]
- Rescorla R, Wagner A (1972): A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement In: Black A, Prokasy W, editors. Classical conditioning II: current research and theory. New York: Appleton Century Crofts; p 64–99. [Google Scholar]
- Schoenbaum G, Setlow B (2003): Lesions of nucleus accumbens disrupt learning about aversive outcomes. J Neurosci 23: 9833–9841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W (2002): Getting formal with dopamine and reward. Neuron 36: 241–263. [DOI] [PubMed] [Google Scholar]
- Schultz W, Apicella P, Scarnati E, Ljungberg T (1992): Neuronal activity in monkey ventral striatum related to the expectation of reward. J Neurosci 12: 4595–4610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setlow B, Schoenbaum G, Gallagher M (2003): Neural encoding in ventral striatum during olfactory discrimination learning. Neuron 38: 625–636. [DOI] [PubMed] [Google Scholar]
- Seymour B, O'Doherty JP, Dayan P, Koltzenburg M, Jones AK, Dolan RJ, Friston KJ, Frackowiak RS (2004): Temporal difference models describe higher‐order learning in humans. Nature 429: 664–667. [DOI] [PubMed] [Google Scholar]
- Shohamy D, Myers CE, Grossman S, Sage J, Gluck MA, Poldrack RA (2004): Cortico‐striatal contributions to feedback‐based learning: converging data from neuroimaging and neuropsychology. Brain 127: 851–859. Epub 2004 Mar 10. [DOI] [PubMed] [Google Scholar]
- Tanaka SC, Doya K, Okada G, Ueda K, Okamoto Y, Yamawaki S (2004): Prediction of immediate and future rewards differentially recruits cortico‐basal ganglia loops. Nat Neurosci 7: 887–893. Epub 2004 Jul 4. [DOI] [PubMed] [Google Scholar]
- Tricomi EM, Delgado MR, Fiez JA (2004): Modulation of caudate activity by action contingency. Neuron 41: 281–292. [DOI] [PubMed] [Google Scholar]
- Ullsperger M, von Cramon DY (2003): Error monitoring using external feedback: specific roles of the habenular complex, the reward system, and the cingulate motor area revealed by functional magnetic resonance imaging. J Neurosci 23: 4308–4314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ungless MA, Magill PJ, Bolam JP (2004): Uniform inhibition of dopamine neurons in the ventral tegmental area by aversive stimuli. Science 303: 2040–2042. [DOI] [PubMed] [Google Scholar]
- Volz KG, Schubotz RI, Von Cramon DY (2003): Predicting events of varying probability: uncertainty investigated by fMRI. Neuroimage 19: 271–280. [DOI] [PubMed] [Google Scholar]
- Zink CF, Pagnoni G, Martin ME, Dhamala M, Berns GS (2003): Human striatal response to salient nonrewarding stimuli. J Neurosci 23: 8092–8097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zink CF, Pagnoni G, Martin‐Skurski ME, Chappelow JC, Berns GS (2004): Human striatal responses to monetary reward depend on saliency. Neuron 42: 509–517. [DOI] [PubMed] [Google Scholar]


