Scaling behaviour in steady-state contracting actomyosin networks

Abstract

Contractile actomyosin network flows are crucial for many cellular processes including cell division and motility, morphogenesis and transport. How local remodeling of actin architecture tunes stress production and dissipation and regulates large-scale network flows remains poorly understood. Here, we generate contracting actomyosin networks with rapid turnover in vitro, by encapsulating cytoplasmic Xenopus egg extracts into cell-sized ‘water-in-oil’ droplets. Within minutes, the networks reach a dynamic steady-state with continuous inward flow. The networks exhibit homogeneous, density-independent contraction for a wide range of physiological conditions, implying that the myosin-generated stress driving contraction and the effective network viscosity have similar density dependence. We further find that the contraction rate is roughly proportional to the network turnover rate, but this relation breaks down in the presence of excessive crosslinking or branching. Our findings suggest that cells use diverse biochemical mechanisms to generate robust, yet tunable, actin flows by regulating two parameters: turnover rate and network geometry.

The dynamic organization of cellular actin networks emerges from the collective activities of a host of actin-associated proteins, including factors that stimulate actin assembly and disassembly, various crosslinkers and filament binding proteins which define the local network architecture, and myosin motors that generate contractile forces ^1–5. Myosin activity can drive global contraction and generate actin network flows, which play a crucial role in cell division, polarization and movement. For example, cell division is driven by the contraction of the cytokinetic ring, which is a quasi-1D contractile actomyosin network ⁶. Contractile flows in the actin cortex are essential for cell polarization ⁷, while bulk actin network flows are crucial for localization of cellular components during the early stages of embryo development ⁸. Continuous retrograde actin flows were further shown to provide the basis for amoeboid cell motility, the primary mode of motility observed in vivo for cells moving in a confined 3D geometry ^{9, 10}. In all these examples, there is limited quantitative understanding of what determines the contractile network behavior, and in particular what governs the rate of network flow. Both the force generation within actomyosin networks and their viscoelastic properties depend in non-trivial ways on the architecture and turnover dynamics of the network ^11–17. Conversely, the network architecture and dynamics are influenced by the stress distribution in the network and the flows it generates ^17–20. As such, understanding how the microscopic dynamics of actin and its associated proteins shape the large-scale structure and flow of contracting actomyosin networks remains an outstanding challenge.

The study of contracting actomyosin networks has primarily focused on the interplay between myosin motor activity and network connectivity ^{14, 18, 21}. Experiments with reconstituted networks assembled from purified actin, crosslinkers and myosin motors established the conditions required for large-scale global contraction ^{12, 18, 22–26}. However, in the absence of rapid network turnover, myosin-motor activity led to transient and essentially irreversible contraction; this is very different from the persistent actin flows in living cells, which exhibit continuous recycling of network components. Recent theoretical modeling and simulation studies have started to explore how rapid turnover influences force production, dissipation and the dynamic spatio-temporal organization of contracting actomyosin networks ^{15, 16, 27–29}. In particular, these simulations suggest that rapid turnover is essential for generating persistent flows, allowing the network to continuously produce active stress and dissipate elastic stress, while maintaining its structural integrity ¹⁵.

Experimental efforts to study contracting actomyosin networks have been hampered by the lack of suitable model systems. In vitro reconstituted networks with limited turnover cannot sustain persistent network flows, so their contraction is necessarily transient, whereas in vivo studies on contracting networks are limited by the difficulties of measuring actin dynamics in complex cell geometries and the ability to control and vary system parameters. Here we leverage the unique benefits of an in vitro reconstitution system based on cell extracts that provides both myosin activity and physiological actin turnover rates, to investigate how the interplay between actin assembly and disassembly, myosin motor activity and network connectivity, determine large-scale structure and dynamics of contracting actomyosin networks. Importantly, the rapid turnover in our system allows the networks to attain a dynamic steady-state characterized by persistent contractile flows and a self-organized, radially symmetric density distribution.

Using this system, we quantitatively characterize actin network turnover and flow and systematically investigate the emerging network properties. We find that under a broad range of physiological conditions, the networks contract homogeneously, despite large spatial variations in network density. The emergence of a density-independent contraction rate is surprising since the internal force generation in actin networks and their viscoelastic properties are strongly dependent on network density ^{13, 30, 31}. Theoretical modeling using ‘active fluid theory’ suggests that the homogeneous contraction arises from a scaling relation between the active stress and the effective viscosity in these self-organized networks. We further find that the contraction rate is roughly proportional to the network turnover rate as we alter the dynamics of the system by changing its composition. This correlation breaks down when we add branching or crosslinking factors in comparable amounts to their endogenous concentrations ³². Together, these results show how physiological rates of actin turnover influence force production and dissipation in cellular actomyosin networks, demonstrating that the rate of network flow depends both on the actin turnover rate and on the local network architecture.

Reconstituting steady-state contracting actomyosin networks

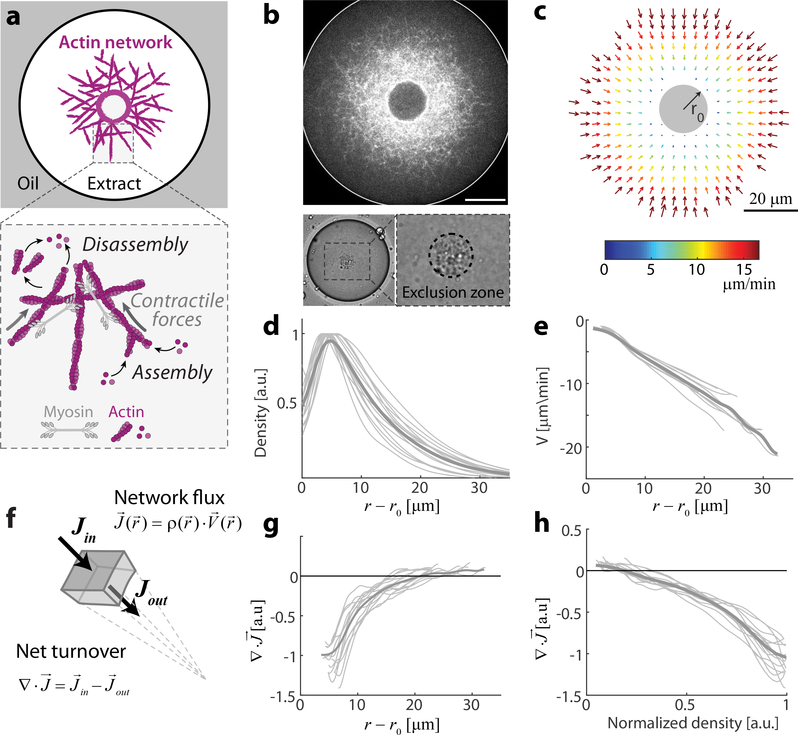
To generate contractile actin networks, we encapsulate cytoplasmic Xenopus egg extract in water-in-oil emulsion droplets ^33–35. Endogenous actin nucleation activities induce the formation of a bulk network, which undergoes myosin-driven contraction ^{18, 36}. Within minutes after droplet formation, the system assumes a dynamic steady-state characterized by an inward network flow and a stationary network density that decreases toward the periphery (Figs. 1, S1; Movie 1). This steady-state is made possible by the rapid turnover in the system, such that the inward network flux is balanced by a diffusive flux of disassembled network components back to the periphery. The inward network velocity approaches zero at the boundary of a dense spherical ‘exclusion zone’ which forms at the center of the droplet. This exclusion zone appears within minutes, as the network contracts and accumulates particulates from the (crude) extract, condensing this material into a spheroid (Fig. 1b, S1e). The simple geometry and persistent dynamics of our system facilitate quantitative analysis of actin network turnover and flow. The network density and flow attain a radially-symmetric pattern (Fig. 1b,c), which remains at steady-state for more than half an hour (Fig. S1).

Figure 1. Quantitative analysis of actin network flow and turnover.

Bulk contracting actomyosin networks are formed by encapsulating Xenopus extract in water-in-oil droplets. The network is labeled using a low concentration of GFP-Lifeact, which does not significantly alter the network (see Methods), and imaged by time-lapse spinning-disk confocal microscopy. Images are acquired at the mid-plane of the droplets, where the network flow is approximately planar due to the symmetry of the set up. The system reaches a dynamic steady-state characterized by a radially-symmetric inward flow. (a) Schematic of the actin network inside a water-in-oil droplet, illustrating the actin turnover dynamics and myosin-driven contraction. (b) Top: Spinning disk confocal image of the equatorial cross section of a network labeled with GFP-Lifeact. Bottom: Bright-field images of a droplet showing the aggregate of particulates that forms an exclusion zone around the contraction center. (c) The network velocity field for the droplet shown in (b), as determined by correlation analysis of the time-lapse movie (Movie 1). (d) The actin network density as a function of distance from the contraction center. The thin lines depict data from individual droplets, and the thick line is the average density profile. The density is normalized to have a peak intensity =1. (e) The radial velocity as a function of distance from the contraction center. The inward velocity increases linearly with distance. (f-h) Analysis of net actin network turnover. (f) Schematic illustration showing that at steady-state, the divergence of the actin network flux is equal to the net network turnover rate. The network flux is equal to the product of the local network density and velocity J(r) = ρ(r)V(r). (g) The divergence of the network flux, $\nabla \cdot \overrightarrow{J}\left(r\right)$ (see Methods), is plotted as a function of distance from the contraction center, showing the spatial distribution of the net turnover. Negative values (at smaller r) correspond to net disassembly, while positive values (near the droplet’s periphery) indicate net assembly. (h) The divergence of the network flux is plotted as a function of the local actin network density. The net turnover decreases roughly linearly with actin network density.

The network contraction rate is density-independent

Interestingly, the inward flow velocity, V, varies nearly linearly as a function of distance from the inner boundary, V ≈ −k(r−r₀), with k a constant, r the radial coordinate, and r₀ the radius of the exclusion zone (Fig. 1e). A linear velocity profile with V ~ −kr is a signature of uniform global contraction; in a homogeneously contracting network, the relative velocity between two points is directly proportional to their distance, so the radial network flow velocity depends linearly on the radial distance from the stationary contraction center (see Supplementary Information). The contraction rate in this case can be determined from the slope of the linear fit for the inward radial velocity as a function of distance, and is equal to k=0.65 ±0.15 min⁻¹ (mean±std, N=39; Fig. S2a). This constant rate of contraction is a global characteristic of the self-organized network dynamics, and is not dependent on the geometry of the droplet (Fig. S3).

In general, the relationship between the network contraction rate and network density is non–trivial, since the active stress driving contraction and the viscoelastic properties of the network are both density-dependent ^{13, 30, 31}. Our observation that the self-organized dynamics in the system lead to a local contraction rate that is uniform (Fig. S3e), despite large spatial variations in network density, is thus surprising. As shown below, homogeneous network contraction is observed for a range of different conditions, suggesting that the density-independent contraction is a manifestation of an inherent scaling relation in the system, rather than the result of fine-tuning of parameters.

Measurements of net actin turnover

We can infer the net rate of actin turnover taking into account the conservation of actin subunits described by the continuity equation, $\frac{\partial \rho }{\partial t}+\nabla \cdot \overrightarrow{J}=\text{net}\text{turnover}$, where ρ is the network density, $\overrightarrow{V}$ is the network velocity, and $\overrightarrow{J}=\rho \overrightarrow{V}$ is the network flux (Fig. 1f). The network density and velocity fields in our system are at steady-state, so the net turnover (i.e. the difference between local assembly and disassembly) will be equal to the divergence of the network flux. Using the measured network density and flow, we determine the spatial distribution of network turnover ($\nabla \cdot \overrightarrow{J}\left(r\right)$; Fig. 1g). We find that the network undergoes net disassembly (i.e. $\nabla \cdot \overrightarrow{J}<0$) closer to the contraction center in regions with higher network density, and net assembly (i.e. $\nabla \cdot \overrightarrow{J}>0$) toward the periphery where the network is sparse. The net turnover can also be plotted as a function of the local network density, showing that disassembly increases with network density (Fig. 1h). We can approximate the relation between network turnover and density by a linear fit: $\nabla \cdot \overrightarrow{J}\left(\rho \right)~\alpha -\beta \rho$. This linear relation describes the simplest model for actin turnover, with a constant assembly term and disassembly that is proportional to local network density. The net turnover rate, β, can be estimated from the slope of the linear fit to the divergence of network flux as a function of network density (Fig. S2a; see Methods), which is equal to β= 1.4 ±0.3 min⁻¹ (mean±std, N=39; Fig. S2a).

Modeling contracting actomyosin networks as an active fluid

To understand the origin of the homogeneous contractile behavior we turned to modeling using active fluid theory ^{37, 38}. The actomyosin network is described as an active isotropic viscous fluid characterized by a density ρ and a velocity field V. The network dynamics are governed by two equations, one for mass conservation (continuity equation) and one for momentum conservation (force balance equation). At steady-state the force balance equation can be written as ∇⋅σ = ∇⋅(σ_A + σ_VE) = f_D, where σ_A is the active stress, σ_VE is the effective viscoelastic network stress, and f_D is the friction with the surrounding fluid. The viscoelastic contribution is dominated by the viscous stress (Supp. Information), and estimates indicate that the friction with the fluid is negligible (Supp. Information). Hence, the myosin-generated active stress which drives contraction, is largely balanced by the viscous network stress resisting it: ∇⋅(σ_A + σ_V) ≈ 0. Assuming that the actomyosin network is an isotropic compressible viscous continuum in a spherically-symmetric system, we obtain, $\frac{\partial }{\partial r}\left({\sigma }_A+2\mu \frac{\partial V}{\partial r}+\lambda \nabla \cdot V+4\mu \frac{V}{r}\right)=0$, where λ and μ are the bulk and shear network viscosities, respectively ³⁹. The periphery of the network at large radii typically does not reach the water-oil interface and the friction with the cytosol is negligible, so we take stress-free boundary conditions for the outer rim of the network. Integrating over r and taking into account this boundary condition at large r, we obtain: $-\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}V\right)=\frac{{\sigma }_A}{2\mu +\lambda }$. Both the active stress and the network viscosities are expected to vary considerably, since the network density is spatially variable. However, if their ratio remains constant, $\frac{{\sigma }_A\left(r\right)}{2\mu \left(r\right)+\lambda \left(r\right)}=c$, the velocity profile will be linear $\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}V\right)=-c\to V=-\frac{c}{3}r$, and the network will contract homogeneously with a contraction rate equal to k = c/3. This analysis indicates that when the active stress and the effective viscosities scale similarly with density, so their ratio remains constant, the local contraction rate becomes density-independent and the network will contract homogeneously as observed (Fig. 1). The ratio between the active stress and the effective viscosity, $\frac{{\sigma }_A}{2\mu +\lambda }$, can then be deduced from the measured velocity profile and is found to be ~1min⁻¹ (Fig. S3e).

Influence of auxiliary proteins on network dynamics

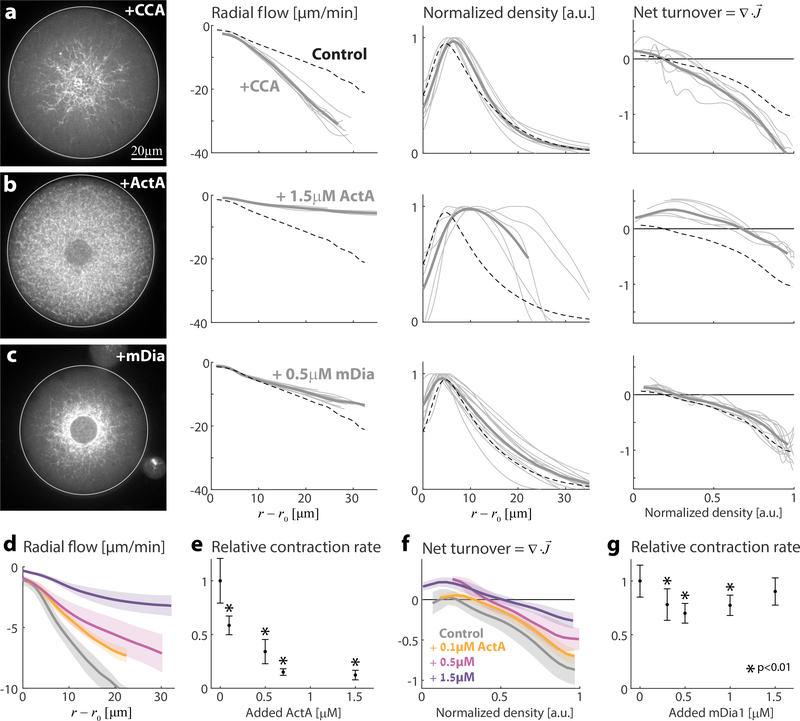
The network dynamics can be modified by supplementing the extract with various components of the actin machinery. Actin disassembly can be enhanced by the combined action of the severing/depolymerizing protein Cofilin together with Coronin and Aip1, which have recently been shown to work in concert to enhance actin disassembly in vitro even under assembly-promoting conditions (e.g., physiological conditions with high actin monomer concentrations as present in our system) ⁴⁰. The addition of these three proteins (CCA: Cofilin, Coronin, and AIP1) together in the reconstituted system (Fig. 2a; Movie 2) induces a ~1.5-fold increase in the net actin turnover (β= 2.1 ±0.3 min⁻¹, N=7). Addition of Cofilin, Coronin, or Aip1 individually does not enhance turnover (Fig. S4), illustrating that their combined activity is required for promoting disassembly under physiological conditions. The presence of CCA also leads to faster network contraction (Fig. 2a). Under these conditions the network still contracts homogeneously, with a linear velocity profile, but at an increased rate of k= 1.3 ±0.15 min⁻¹ (N=7). Similar effects are observed when actin assembly is restricted with Capping Protein that caps free barbed ends (Fig. S5), whereas slowing actin filament disassembly with low levels of Phalloidin has the opposite effect (Fig. S6a).

Figure 2. Influence of assembly and disassembly factors on actin network architecture, flow and turnover.

Contractile actin networks are generated by encapsulating Xenopus extract supplemented with different assembly and disassembly factors. In all cases, the system reaches a steady-state within minutes. The inward contractile flow and actin network density were measured (as in Fig. 1). (a-c) The steady-state network behavior is shown for samples supplemented with (a) 12.5μM Cofilin, 1.3μM Coronin and 1.3 μM Aip1 (see Movie 2); (b) 1.5μM ActA (see Movie 3); (c) 0.5μM mDia1. For each condition, a spinning disk confocal fluorescence image of the equatorial cross section of the network labeled with GFP-Lifeact (left) is shown, together with graphs depicting the radial network flow and density as a function of distance from the contraction center (middle), and the net actin turnover as a function of network density (right). The thin grey lines depict data from individual droplets, and the thick line is the average over different droplets. The dashed lines show the results for the control unsupplemented sample. (d-g) The concentration-dependent effects of adding ActA (d-f) and mDia1 (g) on network dynamics. (d) The radial network flow is plotted as a function of distance from the contraction center. For each ActA concentration, the mean (line) and std (shaded region) over different droplets are depicted. (e) The network contraction rate in individual droplets is determined from the slope of the fit to the radial network flow as a function of distance. For each ActA concentration, the contraction rate was averaged over different droplets (0μM, N=15; 0.1μM, N=4; 0.5μM, N=3; 0.7μM, N=4; 1.5μM, N=4). To obtain the relative contraction rates, these values were divided by the average contraction rate for the unsupplemented control sample. The relative network contraction rate (mean±std) is plotted as a function of the added ActA concentration. (f) The net actin turnover rate, determined from the divergence of the flux, is plotted as a function of network density for the different ActA concentrations. (g) The relative network contraction rates (mean±std; as in Fig. 2e) are plotted as a function of the added mDia1 concentration. For each mDia1 concentration, the contraction rate was averaged over different droplets (0μM, N=14; 0.1μM, N=12; 0.5μM, N=12; 0.7μM, N=12; 1.5μM, N=10). In (e) and (g), the measured contraction rates in each condition were compared to the control sample (0μM) using the Mann–Whitney test. Conditions for which the contraction rates were statistically different from the control are indicated (*).

Actin assembly can be enhanced by adding nucleation-promoting factors (Fig. 2b-g; Movie 3). Adding increasing amounts of ActA, which activates the Arp2/3 complex to nucleate branched actin filaments, has a dramatic effect on actin network distribution and flow. The rate of contraction gradually decreases and the spatial extent of the network increases with increasing concentrations of ActA, until at high concentrations (1.5μM) contraction nearly stops and the network fills the entire droplet (Fig. 2b,d,e). Supplementing the extract with mDia1, which nucleates unbranched actin filaments, has a qualitatively different effect (Fig. 2c,g). The dependence of the contraction rate on the concentration of mDia1 becomes non-monotonic: adding mDia1 up to a concentration of 0.5 μM leads to a small decrease in the contraction rate, but further addition of the nucleator reverses the trend and the contraction rate increases. At high mDia1 concentrations (~1.5 μM), the contraction rate returns to values close to the control sample, but the network appearance is very different, with a strong diffuse background signal, likely due to the presence of many dissociated filaments. In both cases, the net turnover rate remains largely unchanged (Fig. S7a,b).

The different dependence of the contraction rate on the amount of protein added for the two types of nucleation promoting factors is likely related to the inherent difference in the connectivity of the nucleated filaments. Arp2/3 mediated nucleation creates a filament that is physically connected to an existing filament through a branch junction. In contrast, mDia1 nucleates filaments in solution which must subsequently be crosslinked to other filaments to become associated with the network. As such, high levels of Arp2/3 activation generate highly connected networks consisting of densely branched filaments, whereas enhanced mDia1 activity results in many unconnected filaments.

Our results (Figs. 1–2) demonstrate that confined contractile actin networks with rapid turnover can attain a dynamic steady-state over a wide range of parameters. Reaching a steady-state does not require fine-tuning of parameters; rather the system dynamically adapts the overall assembly/disassembly rates to be equal. This can be done, e.g., through variations in the fraction of actin associated with the network, which will induce changes in the actin monomer concentration and assembly dynamics, until the assembly processes balance disassembly. The characteristics of the steady-states obtained vary considerably as a function of system composition, whereby the rate of network contraction and/or the turnover rate changes over a few-fold range following the addition of different components of the actin machinery (Figs. 2, S4-S6). Surprisingly, the network flow maintains a nearly linear velocity profile under a variety of different conditions. Thus, while the rate of network contraction depends on the composition of the system, the local contraction rate for a given condition (which is equal in the active fluid model to the ratio between the active stress and the effective viscosities) is homogeneous, across a range of network densities.

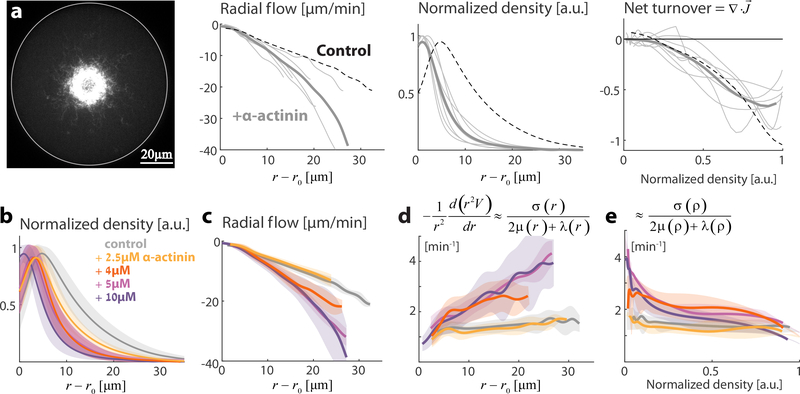
The active fluid model also implies that a non-linear contraction velocity profile indicates that the ratio between the active stress and the effective viscosity varies in space and is hence density-dependent. We find such behavior when we supplement the extract with sufficiently high concentration of crosslinkers such as α-Actinin (Fig. 3; Movie 4). We can infer the density-dependence of the ratio between the active stress and the effective viscosity from the spatial variation in the local contraction velocity (Fig. 3e). We find that the ratio between the active stress and the viscosity, for high α-Actinin concentration (>4μM), decreases with density, indicating that non-linear contributions as a function of density in the active stress, the viscosity, or both, become important. Addition of the filament bundler Fascin had a different effect; Actin network contraction remained homogeneous but at a reduced rate (Fig. S6b), and the net turnover rate was lower. The difference between α-Actinin and Fascin is likely related to differences in their actin binding properties ⁴¹.

Figure 3. Influence of crosslinking on actin network dynamics.

Contractile actin networks are generated by encapsulating Xenopus extract supplemented with different concentrations of the actin crosslinker α-Actinin. The inward contractile flow and actin network density were measured (as in Fig. 1). (a) The steady-state network behavior is shown for a sample supplemented with 10 μM α-Actinin (see Movie 4). A spinning disk confocal fluorescence image of the equatorial cross section of the network labeled with GFP-Lifeact (left) is shown, together with graphs depicting the inward radial network flow and network density as a function of distance from the contraction center (middle) and the net actin turnover as a function of network density (right). The thin grey lines depict data from individual droplets, and the thick line is the average over different droplets. The dashed lines show the results for the control unsupplemented sample. The network contracts in a non-homogeneous manner, reflected by the non-linear dependence of the radial network flow on the distance from the contraction center. (b,c) The concentration-dependent effect of α-Actinin on network density and flow. The network density (b) and radial flow (c) are plotted as a function of distance from the contraction center. For each α-Actinin concentration, the mean (line) and std (shaded region) over different droplets are depicted. The position of the network density peak moves towards the inner boundary with increasing α-Actinin concentrations, and the radial velocity becomes a non-linear function of the distance from the contraction center. (d) The derivative of the radial velocity, $-\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}V\right)$, is plotted as a function of distance from the contraction center. This function becomes position-dependent for α-Actinin concentrations ≥ 4μM. According to the model, this derivative should be approximately equal to the ratio between the active stress and the effective network viscosities, $\frac{{\sigma }_A\left(r\right)}{2\mu \left(r\right)+\lambda \left(r\right)}$. (e) The derivative of the radial velocity, $-\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}V\right)$, is plotted as a function of network density. According to the model, this derivative should be approximately equal to the ratio between the active stress and the effective network viscosities, $\frac{{\sigma }_A\left(\rho \right)}{2\mu \left(\rho \right)+\lambda \left(\rho \right)}$. For α-Actinin concentrations ≥4μM this ratio becomes density-dependent, indicating that the scaling relation between the active stress and the effective viscosity no longer holds.

Network dynamics as a function of contraction and turnover rates

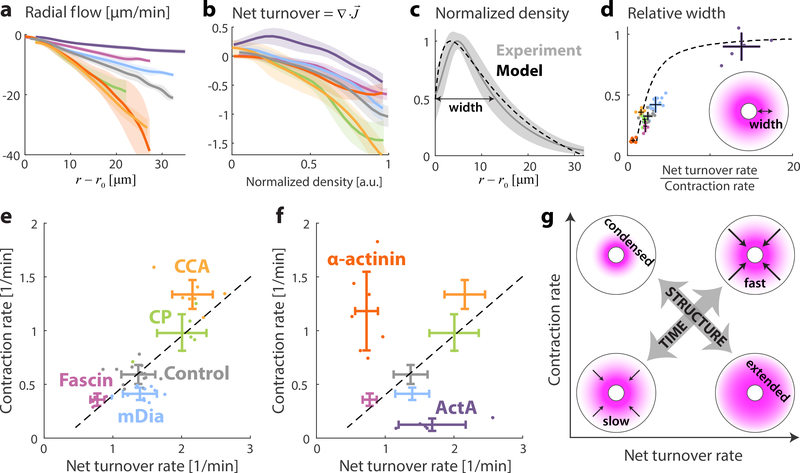
The addition of different actin regulators (e.g. nucleation promoting factors, disassembly factors, bundlers or crosslinking proteins) at concentrations comparable to their endogenous concentration ³², allowed us to explore contracting networks over a wide range of physiologically-relevant conditions (Fig. 4). The contraction and turnover rates were estimated from the slopes of linear fits of the velocity as a function of distance (k) and the net turnover as a function of density (β), respectively (Fig. 4a,b, S2). The network dynamics can thus be characterized by two time scales, (1) the contraction time (k⁻¹), and (2) the actin turnover time (β⁻¹), which have the same order of magnitude (~1 min). The diffusion time across the system provides a third timescale (τ_D~R²/6D, where R is the droplet radius and D~15 μm²/s is the diffusion coefficient of actin monomers in the cytosol ⁴²). However, for droplets in the size range considered here (R<65 μm), the diffusion time is < 1min. In this case, diffusion is sufficient to redistribute network components across the system, and the behavior of the system is primarily governed by the contraction and turnover time scales.

Figure 4. Characteristics of contractile actin networks with turnover.

The contracting flows and actin turnover were measured for contractile actin networks formed under different conditions, including 80% extract (control; grey) and samples supplemented with 1.5μM ActA (purple); 2.6μM Fascin (magenta); 0.5μM mDia1 (cyan); 10μM α-Actinin (red); 0.5μM Capping Protein (green); or 12.5μM Cofilin, 1.3μM Coronin and 1.3 μM Aip1 (orange). (a) The radial network flow rate is plotted as a function of distance from the contraction center. For each condition, the mean (line) and std (shaded region) over different droplets are depicted. (b) The net actin turnover as a function of network density is plotted for different conditions. The contraction rate and turnover rate are determined for each droplet from the slopes of linear fits to the radial network flow as a function of distance, and the net turnover as a function of density, respectively (see Methods, Fig. S2). (c) The measured network density profile for the control sample is compared to the predictions of a model which assumes constant turnover and contraction rates (Supp. Information). The measured density distribution (mean and std) nicely matches the model predicted distribution based on the average values of the turnover and contraction rates, β= 1.4 min⁻¹ and k=0.65 min⁻¹ (dashed line). (d) The relative width of the network profile (quantified as the distance between the inner boundary and the position where the network reaches half its maximal value, normalized by the droplet’s radius) is plotted as a function of the ratio between the net turnover rate and the contraction rate. The dots depict values for individual droplets and the error bars show the mean and std for all the droplets examined for each condition. The model results (dashed line; Supp. Information) predict the increase of the network width as a function of the ratio between the net turnover rate and the contraction rate. (e,f) Scatter plots of the contraction rate and net turnover rate for different conditions. For each condition, the dots depict values for individual droplets and the error bars show the mean and std for all the droplets examined for each condition. (e) The contraction rate is correlated with the turnover rate for the conditions examined (Pearson correlation=0.76, p<10⁻⁸). The dashed line depicts a linear fit. (f) The correlation between the contraction rate and the turnover rate breaks down for samples with added ActA or α-Actinin. (g) Schematic illustration of the behavior of networks with constant contraction and turnover rates. Increasing the contraction and turnover rates proportionally leads to faster network dynamics but the network density profile remains the same, whereas changes in the ratio between the contraction and turnover rates leads to significant modifications in network structure (Supp. Information).

We consider the characteristic network dynamics over a range of conditions (Fig. 4). For many conditions (e.g. addition of CCA, Fascin, mDia1, Capping Protein), the network contraction rate is correlated with the net turnover rate (dashed line; Fig. 4e), such that their ratio remains nearly constant. As a result, the large-scale density profiles of the contracting networks are similar, while the dynamics are faster or slower depending on the magnitude of the contraction and turnover rates (see Supp. Information; Fig. 4g). Adding crosslinkers (α-Actinin) or enhancing branching activity (ActA) leads to deviations in the ratio between the turnover rate and contraction rate (Figs. 4e, S8), which are reflected by large-scale changes in network structure (Fig. 4g); A lower ratio (stronger contraction) results in compact networks concentrated around the contraction center as observed with α-Actinin (Fig. 3), whereas a larger ratio results in more extended networks as seen with ActA (Fig. 2b). The local modifications in network architecture generated by increasing the density of filament branch junctions or crosslinks, are thus translated to global changes in the overall network structure.

The behavior of contracting actomyosin networks arises from the interplay between the active stress generated within the network and the viscoelastic stress of the network. Both the force generation and the dissipation depend on the microscopic details of the network organization which are determined by the activity of a host of actin regulatory proteins. We have developed an experimental system where we can systematically investigate the emergent behavior of contracting networks at steady-state and quantitatively characterize network flow and turnover in the presence of physiological rates of actin turnover. Our findings imply that the active stress and the effective network viscosity scale similarly with network density, so their ratio becomes density-independent, leading to homogeneous network contraction. We further find that the contraction rate is roughly proportional to the actin turnover rate for a range of conditions (Fig. 4e). Simulation studies of actomyosin networks in the presence of rapid turnover ^{15, 43}, show that viscous dissipation in the network will be dominated by filament breaking and disassembly, so the effective viscosity is expected to be inversely proportional to the turnover rate. This is consistent with our results, since according to the active fluid model, the contraction rate should be inversely proportional to the effective viscosity. Thus, if viscosity is inversely proportional to the turnover rate, the contraction rate will be proportional to the turnover rate.

Our observations provide new insights into the relationship between network density and flow in contracting actomyosin networks. This relationship has been studied in vivo e.g. in the context of the cytokinetic ring ⁶. Our results suggest that a constant contraction rate can arise, even if the network density changes over time, if the production and dissipation of internal stress in the cytokinetic ring exhibit similar scaling with network density as observed here. Furthermore, the rate of constriction would be expected to decrease when actin disassembly processes are slowed down, as observed ⁴⁴. More generally, the ability to study contracting actomyosin networks with physiological actin turnover rates in vitro, as demonstrated here, can provide further insight into the behavior of actomyosin networks in vivo and promote quantitative understanding of cellular dynamics.

Materials and Methods

Cell extracts, Proteins and Reagents

Concentrated M-phase extracts were prepared from freshly laid Xenopus laevis eggs as previously described ^34–36. Briefly, Xenopus frogs were injected with hormones to induce ovulation and laying of unfertilized eggs for extract preparation. The eggs from different frogs were pooled together and washed with 1× MMR (100 mM NaCl, 2 mM KCl, 1mM MgCl₂, 2 mM CaCl₂, 0.1 mM EDTA, 5 mM Hepes, pH 7.8), at 16^oC. The jelly envelope surrounding the eggs was dissolved using 2% cysteine solution (in 100 mM KCl, 2 mM MgCl₂, and 0.1 mM CaCl₂, pH 7.8). Finally, eggs were washed with CSF-XB (10 mM K-Hepes pH 7.7, 100 mM KCl, 1 mM MgCl₂, 5 mM EGTA, 0.1 mM CaCl₂, and 50 mM sucrose) containing protease inhibitors (10 μg/ml each of leupeptin, pepstatin and chymostatin). The eggs were then packed using a clinical centrifuge and crushed by centrifugation at 15000g for 15 minutes at 4 ^oC. The crude extract (the middle yellowish layer out of three layers) was collected, supplemented with 50 mM sucrose containing protease inhibitors (10 μg/ml each of leupeptin, pepstatin and chymostatin), snap-frozen as 10 μl aliquots in liquid N₂ and stored at −80 ^oC. Typically, for each extract batch a few hundred aliquots were made. Different extract batches exhibit similar behavior qualitatively, but the values of the contraction and net turnover rates vary (Fig. S9). All comparative analysis between conditions was done using the same batch of extract.

ActA-His was purified from strain JAT084 of L. monocytogenes (a gift from Julie Theriot, Stanford University) expressing a truncated actA gene encoding amino acids 1–613 with a COOH-terminal six-histidine tag replacing the transmembrane domain, as described in ^{34, 35}. Purified proteins were aliquoted, snap-frozen in liquid N₂, and stored at −80°C until use.

Cor1B and AIP1 were expressed and purified from transfected HEK293T cells (ATCC). Cells were grown on plates at 37°C under a humidified atmosphere containing 5% CO₂ in Dulbecco’s modified Eagle’s medium (DMEM), supplemented with 10% (v/v) heat-inactivated foetal bovine serum, glucose (4.5 g/l), penicillin (100 units/ml) and streptomycin (100 μg/ml). Cells at 30–40% confluence were transiently transfected using 25 kDa linear polyethylenimine (Polysciences, Warrington, PA). 72 h post-transfection, cells were harvested in PBS, pelleted by centrifugation at 1,000 × g for 5 min, and lysed by repeated freeze-thawing in 20 mM Tris/HCl pH 7.5, 150 mM NaCl, 1% (v/v) Triton X-100 and a standard cocktail of protease inhibitors (Roche, Germany). After a 30 min incubation on ice, cell lysates were cleared by centrifugation at 20,000 × g at 4°C and incubated with Ni²⁺-NTA beads (Qiagen, Valencia, CA) for 90 min at 4°C in the presence of 20 mM imidazole. After washing with Buffer A (20 mM Tris pH 7.5, 300 mM NaCl, 50 mM imidazole and 1 mM DTT), proteins were eluted in Buffer A supplemented with 250 mM imidazole, concentrated, and purified further on a Superose 6 gel filtration column (GE Healthcare Biosciences, Pittsburgh, PA) equilibrated in Buffer B (20 mM Tris pH 8.0, 50 mM KCl and 1 mM DTT). Purified proteins were concentrated, aliquoted, snap-frozen in liquid N₂, and stored at −80°C until use.

Human Cofilin-1 (Cof1) was expressed in BL21 (DE3) E. coli by growing cells at 37°C in TB medium to log phase, then inducing expression with 1 mM isopropyl β-D-1-thiogalactopyranoside (IPTG) at 18°C for 16 h. Cells were harvested by centrifugation and stored at −80°C, then lysed by sonication in 20 mM Tris pH 8.0, 50 mM NaCl, 1 mM DTT and protease inhibitors. Lysates were cleared by centrifugation at 30,000 × g for 20 min, and applied to a 5 ml HiTrap HP Q column (GE Healthcare Biosciences). The flow-through containing Cof1 was collected and dialyzed into 20 mM Hepes pH 6.8, 25 mM NaCl and 1 mM DTT. Next, the protein was applied to a 5 ml HiTrap SP FF column (GE Healthcare Biosciences) and eluted with a linear gradient of NaCl (25 to 500 mM). Fractions containing Cof1 were concentrated and dialyzed into Buffer B, aliquoted, snap-frozen in liquid N₂, and stored at −80°C until use.

α-Actinin was purchased from Cytoskeleton Inc., and reconstituted to final concentration of 40μM with water. Fascin was purchased from Prospec, dialyzed against Hepes pH 7.5 and reconstituted to final concentration of 20μM in XB buffer with 50mM Hepes.

Actin networks were labeled with GFP-Lifeact (the construct was a gift from Christine Field, Harvard Medical School). GFP-Lifeact was purified and concentrated to a final concentration of 252μM in 100mM KCL, 1mM MgCl2, 0.1mM CaCl2, 1mM DTT and 10% Sucrose.

Skeletal actin was purified from chicken skeletal muscle using standard protocols. Actin was chemically labeled with Alexa Fluor 488 Carboxylic Acid Succinimidyl Ester (Molecular Porbes) in filamentous form, and subsequently purified by two cycles of polymerization and depolymerization. We used a labeling ratio of ~60%.

Emulsion preparation

An aqueous mix was prepared by mixing the following: 8μl crude extract, 0.5 μl 20× ATP regenerating mix (150mM creatine phosphate, 20mM ATP, 20mM MgCl2 and 20mM EGTA), 0.5 μM GFP-Lifeact and any additional proteins as indicated. The final volume was adjusted to 10 μL by adding XB (10 mM Hepes, 5 mM EGTA, 100 mM KCl, 2 mM MgCl₂, 0.1 mM CaCl₂ at pH 7.8). The concentration of the endogenous components of the actin machinery in the mix can be estimated based on ³². The total actin concentration is estimated to be ~20 μM. Labeled actin was used to directly visualize the actin density (Fig. S1g) at a final concentration of 1.5μM in the emulsion mix, which is <10% of the endogenous actin in the extract. The ATP regeneration mix enables the system to continuously flow for more than 1–2 hours.

Emulsions were made by adding 1–3% (v/v) extract mix to degassed mineral oil (Sigma) containing 4% Cetyl PEG/PPG-10/1 Dimethiocone (Abil EM90, Evnok Industries) and stirring for 1 min on ice. The mix was then incubated for an additional 10 min on ice to allow the emulsions to settle. Samples were made in chambers assembled from two passivated coverslips separated by 30 μm-thick double stick tape (3M), sealed with vaseline:lanolin:paraffin (at 1:1:1) and attached to a glass slide. Passivation was done by incubating cleaned coverslips in silanization solution (5% dichlorodimethylsilane in heptane) for 20 minutes, washing in heptane, sonicating twice in DDW for 5 minutes and once in ethanol for 5 minutes, and drying in an oven at 100 ^oC. Droplets with radii in the range of 25–65 μm were imaged 10–60 min after sample preparation.

Microscopy

Emulsions were imaged on a 3I spinning disk confocal microscope running Slidebook software, using a 63× oil objective (NA=1.4). Images were acquired using 488nm laser illumination and appropriate emission filters at room temperature. Images were collected on an EM-CCD (QuantEM; Photometrix). Time lapse movies of emulsions were taken at the equatorial plane, so the network velocity is within the imaging plane.

Analysis

The steady-state density and velocity distributions were determined from time lapse movies of contracting networks. The movies were acquired at the droplets’ equatorial planes where the distributions exhibit radial symmetry for the squished geometry and spherical symmetry for the spherical geometry (see Fig. S3). The movies were taken at time intervals of 2.5–10 sec (depending on network speed) with 512×512 pixels per frame at 0.2054 μm/pixel. Background subtraction and corrections for uneven illumination field were done by subtracting the mean intensity of images of droplets without a fluorescent probe, and dividing by a normalized image of the illumination field distribution. To determine the illumination field distribution, we imaged very large droplets (larger than the field of view) with uniform probe distribution generated by inhibiting actin polymerization with 6.6 μM Capping Protein and no ATP regeneration mix. Bleach correction was done by dividing the entire image by a constant factor determined from an exponential fit to the total image intensity as a function of time. The differences in the refractive index of the oil and the extract within the droplets, distorts the intensity near the edge of the droplets. To correct for this, we measured the fluorescence intensity as a function of distance from the edge for droplets with uniform probe distribution (as above). The correction as a function of distance from the edge of the droplet was determined by averaging the measured intensity near the edge for ~50 droplets. The fluorescence signal was corrected for edge effects by dividing by this correction function.

The velocity distribution (Fig. 1c) was extracted using direct cross-correlation analysis based on PIVlab code ⁴⁵ written in matlab with modifications. The movies were first preprocessed to enhance contrast using contrast limited adaptive histogram equalization (CLAHE) and high pass filter in Matlab. Cross-correlation was done on overlapping regions, 30×30 pixels in size, on a grid with 10 pixel intervals. To avoid artefacts associated with padding the boundaries in the correlation analysis, the 30×30 correlation analysis was done using 60×60 windows from the original images and no padding was used. The correlation functions from pairs of consecutive images from the movie was averaged over time (between 5–40 consecutive image pairs). The peak of the time-averaged correlation function was determined by fitting a 2D Gaussian, and the local velocity in each correlation region was determined from the shift of the Gaussian’s peak from the origin. To automatically exclude spurious correlations, we considered only regions in which the fit was to a Gaussian with a single peak that is more than 3 pixels away from the window boundary, has a peak amplitude that is larger than 5–20% (depending on the conditions used) of the average correlation peak value, and has a width (at 70% height) which is less than 20 pixels. To further remove spurious correlations at large radii (where the network density is close to background levels, and hence the correlation signal is weak) we excluded velocity vectors whose angular component was larger than a threshold. The radial velocity was determined by averaging the velocities as a function of distance from the contraction center, for radii for which the velocity was determined for more than half the relevant grid points.

The contraction rate for each droplet was determined from the slope of the linear fit to the radial velocity as a function of distance from the contraction center. The fit range was taken to be between the radius where the network intensity peaks near the inner boundary and the largest radius for which the network velocity could be determined reliably. The error in the contraction rate in individual droplets was estimated as the half-width of the 95% confidence interval for the slope values determined using Matlab (Fig. S2). Since the maximal error in determining the slope of the fit was smaller than the variability between droplets made with the same composition, we report the standard deviation among droplets as a measure of the variability for each condition. The radius of the inner boundary (r₀ ) was determined as the intersection point of the linear fit to the velocity with the x-axis.

The network density was determined by averaging the corrected fluorescence signal over different angles and over time (typically 20–40 frames) to obtain the probe density distribution as a function of distance from the contraction center. The measured probe distribution reflects the sum of signals emanating from the network bound probe and from the diffusing probe. To approximate the network bound probe density we subtracted the measured signal near the periphery of the droplet, which is equivalent to assuming that the network density approaches zero near the periphery and that the diffusing probe is distributed uniformly.

Analysis of the net turnover of the network is based on the continuity equation at steady-state, $\nabla \cdot \overrightarrow{J}=\text{net}\text{turnover}$. The network flux is the product of the network density and velocity, $\overrightarrow{J}\left(r\right)=J\left(r\right)\widehat{r}=\rho \left(r\right)V\left(r\right)\widehat{r}$. The divergence of the flux is calculated assuming spherical-symmetry as, $\nabla \cdot \overrightarrow{J}(r)=\frac{1}{r^2}\frac{d\left(r^2\rho (r)V\left(r\right)\right)}{dr}$. The divergence of the flux was also plotted as a function of the local density ρ, and fit to a linear function $\nabla \cdot \overrightarrow{J}(\rho )\approx \alpha -\beta \rho$. The fit was done on the density range for which the system undergoes net disassembly (i.e. $\nabla \cdot \overrightarrow{J}(\rho )<0$). The net turnover rate reported was determined as the slope of the linear fit of the divergence of the flux as a function of the network density (β). The error in the turnover rate in individual droplets was estimated as the half-width of the 95% confidence interval for the slope values determined using Matlab (Fig. S2). Since the typical error in determining the slope of the fit was smaller than the variability between droplets made with the same composition, we report the standard deviation among droplets as a measure of the variability for each condition. The contraction and turnover rates between the unsupplemented control sample and other conditions were statistically compared using the Mann–Whitney test.