Abstract
The age‐related trends of the width and the depth of major cortical sulci were studied in normal adults. Ninety healthy subjects (47 males, 43 females) age 20–82 years were evaluated. Measurements of average sulcal width and depth in 14 prominent sulcal structures per hemisphere were performed with high‐resolution anatomical MRI. The average sulcal width increased at a rate of about 0.7 mm/decade, while the average sulcal depth decreased at a rate of about 0.4 mm/decade. Sulcal age‐related trends were found to be highly influenced by gender in the superior temporal, collateral, and cingulate sulci (P < 0.05), with males showing more pronounced age‐related change in sulcal width than females. Sulcal structures located in multimodal cortical areas showed more profound age‐related changes than sulcal structures in unimodal cortical areas (P < 0.05). Hum Brain Mapp, 2005. © 2005 Wiley‐Liss, Inc.
INTRODUCTION
Histological studies of postmortem samples and modern, noninvasive imaging research indicate significant age‐related alterations of human cerebral cortex. Regional trends of age‐related morphological changes observed from histological studies reveal that multimodal areas of the cortex showed much larger age‐related alterations than unimodal sensory and that motor areas and multimodal cortical regions show changes much earlier than unimodal sensory and motor cortical regions [Duan et al., 2003; Flood and Coleman, 1988; Morrison and Hof, 1997]. Whole‐brain histological studies, while providing the most precise and comprehensive information, are difficult to perform in humans due to the cost and effort of processing full‐size histological sections and scarcity of postmortem samples [Amunts et al., 2001; Zilles et al., 2002]. Early neuroimaging studies reported global morphological alterations associated with senescence such as shrinkage of the cerebrum, ventricular dilation, and decrease in brain‐parenchyma fractions [Freedman et al., 1984; Pfefferbaum et al., 1990; Steiner et al., 1985]. Advances in high‐resolution, structural MR imaging paved the way for systematic and regionalized studies of morphology of cortical aging.
Raz et al. [1997] performed the first comprehensive neuroimaging study that quantified a complex regional pattern of age‐related morphological changes in a sample of subjects ages 18–78 years. Cortical gray matter (GM) volumes were measured in a large number of regions that were manually traced on the high‐resolution anatomical MR images. A significant age‐related decline in GM volumes was seen, with the highest rate of loss observed in multimodal areas, such as superior frontal and dorsolateral prefrontal cortices. Similarly, Sowell et al. [2002, 2003] reported that gray matter density (GMD), an indicator of cortical gray matter thickness, declined sharply with age in subjects ages 7–87. Regional trends of age‐related GMD decline were analogous to the trends reported by Raz et al. [1997], with multimodal areas showing the largest and the earliest decline. Techniques used by Raz et al. [1997] and Sowell et al. [2002, 2003] were based on manual tracings that were very labor‐intensive. Good et al. [2001] utilized an automated analysis method called voxel‐based morphometry (VBM) [Ashburner and Friston, 2000; Wright et al., 1995] to study morphology of senescence in healthy subjects ages 18–80 years. They observed a significant age‐related decline in overall GM volume but did not observe an accelerated GM decline for the frontal lobe areas. This is possibly due to much lower spatial resolution and lower sensitivity of VBM analysis compared to the methods employed by Raz et al. [1997] and Sowell et al. [2002, 2003].
Most anatomical studies of brain aging have quantified morphological trends based on the regional GM/WM (white matter) volumes/densities and have a common shortcoming due to the fact that MRI contrast between GM and WM tissues deteriorates with age. The contrast mechanism of a low flip angle, short TR, T 1‐weighted, spoiled gradient echo sequence commonly used for anatomical MR imaging has a complex, nonlinear dependence on the tissue's proton density and T 1‐relaxation times [Haacke, 1999]. Excellent WM/GM MRI contrast is easily achievable in early adulthood when the T 1 relaxation times and proton densities for WM and GM tissues are most different. Unfortunately, GM/WM MRI contrast deteriorates with age due to the reduction in difference between both the T 1 relaxation time and proton density, possibly due to reduction of the brain tissue's water content, thus presenting challenges in achieving an age‐independent GM/WM contrast [Breger et al. 1991; Chang et al., 1996; Cho et al., 1997; Steen et al., 1995].
The age‐related “widening” of cortical sulci and the subsequent filling‐up of freed space by cerebrospinal fluid (CSF) is a well‐described phenomenon. Its nature is yet unknown but it is thought that the atrophy of the underlying WM and GM results in reduction of gyral thickness and causes dilation of cortical sulci [Jernigan et al., 2001; Magnotta et al., 1999; Symonds et al., 1999]. While visual assessments of “widening” of cortical sulci have long been used to diagnose regional cortical atrophy, to our knowledge there has not been a systematic study that quantified regional sulcal age‐related trends in normal aging. Here we studied age‐related changes in sulcal width and depth in the primary and secondary cortical furrows using an automated sulcal analysis, BrainVisa (online at http://www.brainvisa.info). This analysis is based on MRI contrast between GM and CSF which remains stable through the life‐span. The T 1 relaxation time of CSF is three to four times longer and the proton density of CSF is approximately 50% higher than the T 1‐relaxation time and proton density of GM and WM. Thus, while the WM and GM contrast deteriorates with age, the GM/CSF contrast remains constant, allowing for age‐independent measurements.
SUBJECTS AND METHODS
Subjects
We performed sulcal analysis on 90 high‐resolution, anatomical MRI scans collected from subjects ages 20–82. The subject's age, gender, and handedness data is summarized in Table I. Subjects were recruited as part of the International Consortium on Brain Mapping (ICBM) [Mazziotta et al., 1995, 2001] project and their medical history was reviewed to rule out any endocrinal, neurological, and/or psychiatric illnesses. All subjects underwent a complete neurological examination and neurocognitive testing to qualify for imaging. Elderly subjects (ages 76–82) were also thoroughly examined by a psychiatrist and a cognitive neuropsychologist to rule out dementia and psychiatric disorders. All subjects were imaged at the Research Imaging Center on the Elscint/GE Prestege 2‐T MRI scanner using a high‐resolution (isotropic 1 mm3), 3‐D, spoiled gradient recalled echo sequence optimized for white matter/gray matter contrast, published as a part of a multicenter imaging protocol [Mazziotta et al., 2001].
Table I.
Subject demographics
| Age range (yr) | Subjects (n) | Mean age (yr) | Left handed (n) | Gender, n (M/F) | Age of male subjects (mean ± SD) | Age of female subjects (mean ± SD) |
|---|---|---|---|---|---|---|
| 20–29 | 20 | 24.5 ± 2.9 | 3 | 10/10 | 24.2 ± 3.3 | 25.1 ± 2.3 |
| 30–39 | 20 | 33.1 ± 2.5 | 2 | 13/7 | 32.7 ± 2.8 | 33.3 ± 2.4 |
| 40–49 | 20 | 44.3 ± 2.8 | 2 | 9/11 | 44.5 ± 2.8 | 44.8 ± 3.3 |
| 50–60 | 20 | 53.5 ± 2.7 | 3 | 11/9 | 53.2 ± 2.3 | 53.6 ± 3.1 |
| 76–82 | 10 | 79 ± 2.6 | 0 | 4/6 | 78 ± 3.2 | 81.1 ± 1.2 |
Preprocessing
Preprocessing of images for sulcal measurements included the following steps: removal of nonbrain tissue, registration to the Talairach frame, RF inhomogeneity correction, brain tissue partial‐volume segmentation, and sulcal extraction and verification.
Removal of nonbrain tissue
The nonbrain brain tissues such as skin, muscle, fat, etc., were removed using the automated skull‐stripping procedure BET [Smith, 2002], which is provided as an add‐on for the MEDx software package (Sensor Systems, Sterling, VA). The extracted brain images were cropped at the level of the brain stem.
Registration to talairach frame
All brain images were globally, spatially normalized to the Talairach coordinate system to remove gross differences in brain size and orientation. Automated, nine‐parameter (three rotations, three scales, and three translations) Convex Hull global spatial normalization software [Lancaster et al., 1999] was used to register all images into the Talairach reference frame. The midline and AC–PC alignments were manually verified by two experienced neuroanatomists. All images were resliced at isotropic 0.85 mm3 resolution using a 3‐D, 15‐voxel‐wide sinc interpolation kernel.
RF inhomogeneity correction
All images were corrected RF for inhomogeneity artifact. RF inhomogeneity artifact manifests itself as a low‐frequency variation of MRI intensity, which impedes intensity‐based image analysis unless corrected. We used a correction algorithm developed by Styner et al. [2000] to correct images in this study. This algorithm takes into account an a priori, parametric model of tissue class statistics and calculates a polynomial fit for the inhomogeneity field. This algorithm was chosen over other popular RF‐inhomogeneity correction methods such as N3 [Sled et al., 1998] and FAST [Zhang et al., 2001] because during internal evaluation it provided superior correction for images acquired at our center.
Brain tissue partial‐volume segmentation
A fuzzy‐classifier‐based, anatomical segmentation method [Herndon et al., 1998; Mangin et al., 1996] was used to segment MRI images into WM, GM, and CSF. A fuzzy‐classifier approach provides a solution to partial voxel averaging which arises when there is more than one tissue type (e.g., WM and GM present within a single voxel). In such a case, the effective T 1 relaxation time and voxel intensity will be a superposition of signals from each of the tissues present within a voxel. Herndon's algorithm uses a fuzzy‐classifier built specifically for the Elscint 2‐T MRI scanner to estimate each voxel's fractional tissue composition based on the voxel's T 1 relaxation time. As a result, this algorithm produces a 3‐D map of partial volume coefficients for each tissue type (i.e., CSF, GM, and WM). Partial volume coefficients vary in value from 0, indicating absence of a tissue class within a voxel, to 1.0, indicating that a tissue class completely fills the voxel.
Brainvisa (BV) sulcal extraction and labeling
All images were imported into the BV database and processed through BV sulcal extraction and identification pipelines (Fig. 1). The first step identifies cerebral hemispheres and cerebellum using a technique based on 3‐D erosion and template‐based 3‐D seed growth [Mangin et al., 1996, 2004] (Fig. 1). The medial surface of the cortical folds is then obtained using a homotopic erosion technique [Mangin et al., 1995]. A “crevasse detector” is used to reconstruct sulcal structures as the medial surfaces from the two opposing gyral banks that span from the most internal point of sulcal fold to the convex hull of the cortex [Mangin et al., 1995, 2004] (Fig. 1B).
Figure 1.
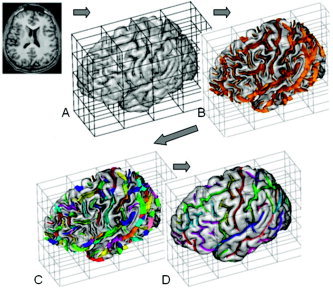
BrainVisa sulcal extraction and identification pipelines. Sulcal extraction pipeline identifies cerebral hemispheres and cerebellum (A). Next, homotopic erosion and a crevasse detector were used to reconstruct sulcal surface as the medial surface of the two opposing gyral banks (B). Sulcal identification pipeline uses a congregation of 500 artificial neural network‐based pattern classifiers to reconstruct (C) and identify (D) sulcal landmarks in accordance with a learning performed on 26 expertly segmented datasets.
The sulcal identification pipeline incorporates a congregation of 500 artificial neural network‐based pattern classifiers. Each classifier is tuned to identify a particular feature of the sulcal patterns (Fig. 1C,D). These neural networks work collaboratively to perform identification of 56 sulcal structures for each hemisphere. The neural networks were trained on a database of 26 expertly classified images, resulting in a classification accuracy ranging from 95% for primary and secondary furrows to about 70% for the highly variable tertiary sulcal structures [Riviere et al., 2002].
Manual verification of automated labeling
Two experienced neuroanatomists reviewed results of automated labeling. In an infrequent event (∼5%) that a sulcus was assigned an incorrect label, it was manually relabeled. The main task of manual processing was removal of anastomotic sulci (AS) associated with the sulci used in this project. AS are small, accessory sulci, usually less than 5 mm in length, originating, usually at a right angle, from the stem of the main sulcus and considered random folds [Ono et al., 1990]. AS were excluded from this analysis since a width measurement performed at the intersections between the main sulcus and an AS, especially along the direction of the AS, would show an exaggerated value.
Selection of Sulcal Structures
Fourteen primary and secondary furrows were selected for this analysis (See Figure 2, Table II). Selected structures had a very high intersubject incidence rate (∼99%) and were present in all subjects. Neither tertiary structures, such as middle temporal and intermediate frontal sulci, nor AS were used in this analysis because tertiary structures are often absent (incidence rate of ∼30–70%) and AS are random folds [Ono et al., 1990]. The only primary furrow omitted from this analysis was the calcarine sulcus. This is a deeply furrowed structure whose consistent extraction was obstructed by the high geometrical complexity of its deep lateral aspect.
Figure 2.
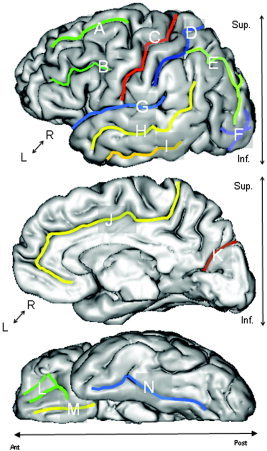
Measurements were performed for the following sulcal structures: Lateral View (top): superior frontal (A), inferior frontal (B), central (C), postcentral (D), intraparietal (E), lateral and transverse occipital and lunar sulcus (F), sylvian fissure (G), superior temporal (H), and inferior temporal (I). Medial View (middle): anterior cingulate and posterior cingulate sulci were combined (J) and parieto‐occipital fissure. Inferior View (bottom): orbital‐frontal (L), olfactory (M), collateral and rhinal sulci were combined (N).
Table II.
Sulcal structures used in this analysis and their lobar association
| Lobe | Structure |
|---|---|
| Frontal | Superior frontal sulcus |
| Inferior frontal sulcus | |
| Orbital sulcus | |
| Parietal | Postcentral sulcus |
| Intraparietal fissure | |
| Temporal | Superior temporal sulcus |
| Inferior temporal sulcus | |
| Limbic | Cingulate sulcus |
| Occipital Lobe | Lateral occipital, transverse occipital and lunate sulci |
| Inter‐lobar | Central sulcus |
| Sylvian fissure | |
| Parietaloccipital fissure | |
| Collateral + rhinal sulci |
Special attention was given to the cingulate, collateral, and rhinal sulci. Cingulate sulcus is interrupted in about half of the population (55%) and is often divided into anterior and posterior cingulate sulci [Ono et al., 1990]. To establish intersubject consistency, the measurements for anterior and posterior portions of cingulate sulcus were combined. A similar approach was taken for rhinal and collateral sulci; since rhinal sulcus continues as collateral sulcus in about 30% of the population [Ono et al., 1990], their measurements were combined.
Sulcal Width and Depth Measurements
Average sulcal width
We defined the average sulcal width for an individual sulcal structure as the average width of the intrasulcal CSF (ISCSF) along the normal projections to the medial sulcal mesh (Fig. 3B). Medial sulcal meshes for each sulcus were created by the BV sulcal extraction pipeline and labeled by automated/manual labeling. Geometrically, a medial sulcal mesh transverses the ISCSF in the middle of the sulcal “width” dimension, parallel to the sulcal borders and spans the entire sulcal “depth” dimension (Fig. 3B). To calculate sulcal width for individual sulci (Fig. 3A), we first identified the ISCSF for this structure as follows: The medial sulcal mesh for each sulcus was used to seed a 3‐D region growing algorithm to mask CSF volume associated with this sulcal structure. In order to prevent region‐growing from “spilling over” into intersecting sulci, points that were further than 10 mm away from the sulcal skeleton were rejected. The convex hull of cortical GM ribbon was then used to isolate ISCSF from sub‐arachnoid CSF. ISCSF partial volume values were then analyzed along each normal trajectory. The Euclidean distance between two voxels, on either side of the sulcal surface, consisting of less than 10% CSF was taken as a sulcal width (Fig. 3C). Sulcal width measurements were averaged along the entire sulcal surface area, resulting in 2,500–5,000 measurements per individual structure. Width measurements from points located within 4 mm distances from an intersection between an AS and/or other sulci were excluded from averaging.
Figure 3.
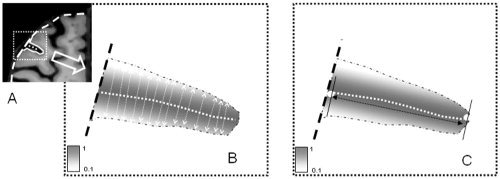
A: Intersulcal CSF was bounded by the opposing GM banks of gyri and by the convex hull of the cortex. B: Average sulcal width is calculated in the normal direction to sulcal skeleton (dotted line). C: Average sulcal depth is calculated as the Euclidean distance between superficial and deep ends of the sulcal surface.
Average sulcal depth
The average sulcal depth was calculated as the average Euclidean distance between the points along the deepest edge of the sulcal skeleton surface and the nearest points on the outer edge of the sulcal ribbon, as in Figure 3C.
Age‐related trends in sulcal morphology
Multivariate analysis of covariance (MANCOVA) and linear regression analysis (LRA) were used to examine age‐related changes in sulcal depth and width as a function of gender, hemisphere, cortex type, and sulcal region. MANCOVA tests were used to examine whether the effects of the dependent variables (sulcal width and depth) varied with the factors being analyzed. MANCOVA yields a statistical test of multivariate effects, Wilk's Lambda (&Λ;), along with its corresponding F value, as well as a measure of multivariate effect size, partial η2. LRA uses a least squares fit to calculate the slope, intercept, correlations, and standard errors for regressions of a criterion variable such as sulcal width and depth on a predictor variable (age).
The multivariate analysis involved two steps. In first step, an omnibus MANCOVA was used to examine age‐related trends in sulcal width and depth as a function of gender, hemisphere, and sulcal region, with age being treated as a continuous covariate. In the second step, MANCOVA was used to examine age‐related trends for the width and depth measures in sulci associated with unimodal and multimodal cortexes. In the later MANCOVA, sulcal width and (separately) sulcal depth measurements were pooled and averaged across sulcal regions for unimodal (central and occipital sulci) and multimodal (superior frontal, cingulate, and intraparietal sulci) cortexes. This test treated sulcal region as a factor with two levels, one for unimodal cortex and one for multimodal cortex.
Finally, LRA was used to probe significant multivariate effects obtained in the MANCOVAs (if any). This was used to minimize type 1 error rates, which are inflated when a series of fragmented, univariate tests are performed post hoc [for a similar argument, see Stevens, 1992, p. 152].
RESULTS
Analysis Examining 14 Sulcal Regions
The omnibus MANCOVA examined age‐related trends in sulcal width and depth as a function of gender, hemisphere, and sulcal region. The analysis treated sulcal region as a within‐subjects factor with 14 levels (one for each of the 14 sulci), hemisphere as a within‐subjects factor with two levels, gender as a between‐subjects factor with two levels, and age as a continuous covariate. The MANCOVA yielded significant main effects of age [Wilk's Λ; = 0.18, F(2,84) = 195.15, P < 0.0001, partial η2 = 0.82], and sulcal region [Wilk's Λ; = 0.03, F(26,60) = 90.97, P < 0.0001, partial η2 = 0.98]. These main effects were qualified by a significant interaction of age and region [Wilk's Λ; = 0.21, F(26,60) = 8.63, P < 0.0001, partial η2 = 0.79], and by a significant interaction of age, region, and gender [Wilk's &Λ; = 0.55, F(26,60) = 1.88, P = 0.02, partial η2 = 0.45]. No additional significant effects were obtained.
Age Trends for Individual Sulcal Regions
The significant multivariate interaction of age and region was probed by regressing sulcal width and (separately) sulcal depth on age for each of the 14 sulcal regions (Fig. 4). Table III reports the slope (B coefficient), intercept (I), and correlations (r) of these regressions. Age‐related trends for sulcal width indicated a regionally heterogeneous, gradual increase of sulcal width with age. The largest slope was observed for the superior frontal sulcus, which showed an increase of 0.94 mm/decade. The lowest linear increase (0.45 mm/decade) was observed for the occipital lobe sulci. The largest correlation (r = 0.83) with age was observed for the collateral sulcus; the lowest correlation (r = 0.67) was observed for the inferior temporal sulcus (Table III). There was a highly significant (P < 10−10) correlation between sulcal width and a subject's age for each sulci. Age‐related trends for sulcal depth indicated a gradual decrease in sulcal depth with age for all 14 sulcal regions. The slopes varied from −0.61 mm/decade for intraparietal sulcus to −0.08 mm/decade for orbito‐frontal sulcus. Average depth vs. age correlation coefficients were significant (P < 0.05) for all structures except the inferior frontal and orbito‐frontal sulci, although to a lesser degree than sulcal width measurements.
Figure 4.
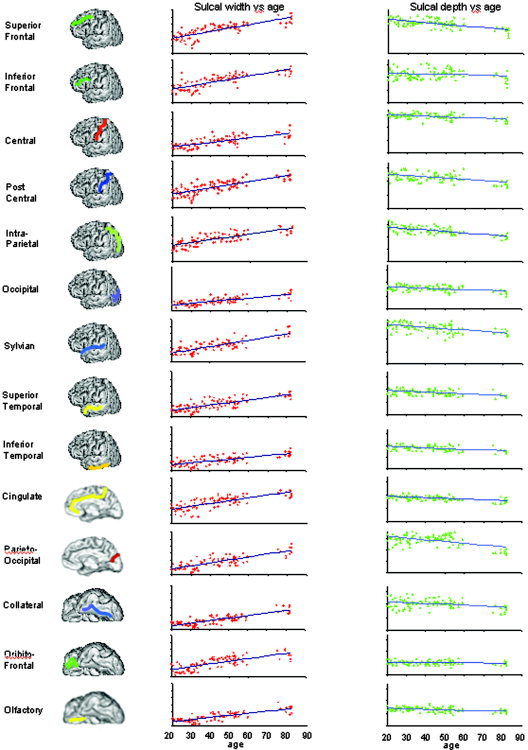
Scatterplots and trendlines for sulcal width (red) and sulcal depth (green) measurements plotted vs. subject's age. The vertical scale is 0.0–12.0 mm for sulcal width vs. age plots and 0.0–17.0 mm for sulcal depth vs. age plots.
Table III.
Slope, intercept, and correlation linear regression coefficients for average sulcal width and depth aging trends
| Name | Average sulcal width | Average sulcal depth | ||||
|---|---|---|---|---|---|---|
| B (mm/decade) | I (mm) | r | B (mm/decade) | I (mm) | r | |
| Superior frontal | 0.94 | 2.3 | 0.79 | −0.59 | 13.5 | −0.60 |
| Inferior frontal | 0.76 | 1.7 | 0.77 | −0.20 | 12.2 | −0.18 |
| Central | 0.62 | 1.1 | 0.71 | −0.33 | 15.7 | −0.50 |
| Post central | 0.79 | 1.9 | 0.76 | −0.44 | 13.4 | −0.48 |
| Intraparietal | 0.61 | 2.5 | 0.72 | −0.61 | 15.3 | −0.63 |
| Occipital | 0.45 | 0.7 | 0.73 | −0.20 | 9.0 | −0.45 |
| Sylvian | 0.84 | 0.8 | 0.78 | −0.58 | 20.0 | −0.41 |
| Sup temporal | 0.68 | 0.4 | 0.76 | −0.58 | 17.3 | −0.49 |
| Inferior temporal | 0.50 | 0.5 | 0.67 | −0.30 | 10.1 | −0.47 |
| Cingulate | 0.77 | 2.1 | 0.72 | −0.25 | 9.9 | −0.50 |
| Parietooccipital | 0.80 | 0.3 | 0.79 | −0.70 | 17.1 | −0.45 |
| Collateral | 0.68 | 0.2 | 0.83 | −0.36 | 12.0 | −0.34 |
| Orbitofrontal | 0.81 | 0.5 | 0.74 | −0.1 | 5.7 | −0.16 |
| Olfactory | 0.59 | 0.0 | 0.78 | −0.2 | 7.5 | −0.36 |
Gender‐Related Differences in Aging Trends
The significant three‐way interaction of age, gender, and region revealed by the omnibus MANCOVA was probed by regressing sulcal width and depth on age for males and females, separately for all 14 sulci. Table IV and Figure 5 report the results of these regressions for the three (of 14) sulcal regions in which males and female differed significantly. Significant gender differences in sulcal width and depth were observed for the collateral sulcus, cingulate sulcus, and superior temporal sulcus. In these regions, males had significantly larger slopes for both average sulcal width (t = 3.52, P < 0.01) and average sulcal depth (t = 2.45, P < 0.05) than did females (Table IV). There was no significant intergender difference detected in the average intercept or correlation coefficients (Table IV).
Table IV.
Slope, intercept, and correlation linear regression coefficients for individual sulcal structures that showed statistically significant intergender differences
| Name | Males | Females | ||||
|---|---|---|---|---|---|---|
| B (mm/decade) | I (mm) | r | B (mm/decade) | I (mm) | r | |
| Average sulcal width | ||||||
| Collateral | 0.82 ± 0.06 | −0.1 ± 0.30 | 0.87 | 0.54 ± 0.07 | 0.3 ± 0.31 | 0.80 |
| Cingulate | 0.88 ± 0.10 | 1.6 ± 0.51 | 0.75 | 0.66 ± 0.10 | 2.7 ± 0.52 | 0.70 |
| Superior temporal | 0.83 ± 0.08 | −0.1 ± 0.43 | 0.80 | 0.58 ± 0.09 | 0.6 ± 0.41 | 0.64 |
| Average sulcal depth | ||||||
| Collateral | −0.4 ± 0.14 | 12.1 ± 0.71 | −0.33 | −0.2 ± 0.16 | 11.4 ± 0.72 | −0.24 |
| Cingulate | −0.35 ± 0.10 | 10.1 ± 0.30 | −0.65 | −0.19 ± 0.07 | 9.78 ± 0.30 | −0.45 |
| Superior temporal | −0.63 ± 0.46 | 17.3 ± 0.82 | −0.47 | −0.60 ± 0.15 | 17.9 ± 0.71 | −0.52 |
Figure 5.
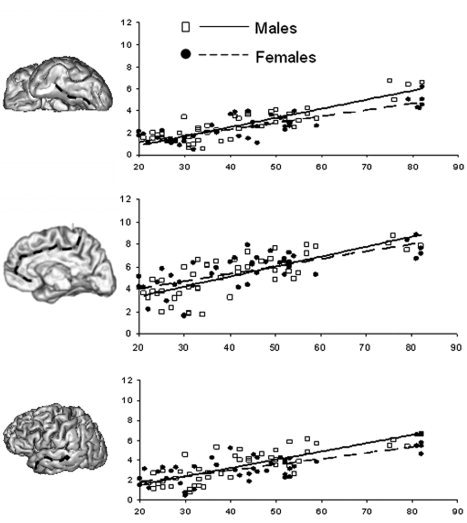
Gender‐dependence of the age‐related sulcal width trends for collateral (top), cingulate (middle), and superior temporal (bottom) sulci.
Age‐Related Trends in Unimodal vs. Multimodal Cortexes
The MANCOVA of unimodal and multimodal cortexes treated cortex type as a within‐subjects factor with two levels and treated age as a continuous covariate. Since no a priori predictions regarding the effects of gender and hemisphere were made, the MANCOVA excluded these factors to simplify the analysis and to reduce type 1 error rates. The results revealed a significant main effect of age [Wilk's &Λ; = 0.21, F(2,87) = 167.21, P < 0.0001, partial η2 = 0.79], which replicated the age effect of the omnibus MANCOVA. The analysis also yielded a significant main effect of cortex type [Wilk's Λ; = 0.61, F(2,87) = 27.46, P < 0.0001, partial η2 = 0.39], which was qualified by significant interaction of cortex type and age [Wilk's Λ; = 0.67, F(2,87) = 21.60, P < 0.0001, partial η2 = 0.33].
The significant interaction of cortex type and age was probed by regressing sulcal width and (separately) sulcal depth on age for unimodal and multimodal cortexes. Table V reports the results of these regressions. As indicated by the slope of the regressions, sulcal width increased with age for both types of cortex, and this increase was significantly greater for multimodal than for unimodal cortex (t = 3.72, P < 0.02). Although sulcal depth decreased with age for both types of cortex, with the rate of decline being ∼50% higher for multimodal than for unimodal cortex, the difference between the two types of cortex on the depth measure was not significant (t = 1.91, P > 0.05) (Table V). No statistically significant difference for intercept values was detected for either sulcal width or sulcal depth trends.
Table V.
Slope, intercept, and correlation linear regression coefficients for pooled unimodal (central and occipital sulci) and multimodal (superior frontal, intraparietal and cingulate sulci) cortexes
| Name | Width | Depth | ||||
|---|---|---|---|---|---|---|
| B (mm/decade) | I (mm) | r | B (mm/decade) | I (mm) | r | |
| Unimodal | 0.54 ± 0.05 | 0.88 ± 0.40 | 0.72 | −0.30 ± 0.10 | 12.5 ± 1.02 | −0.48 |
| Multimodal | 0.77 ± 0.07 | 0.76 ± 0.42 | 0.76 | −0.47 ± 0.07 | 12.9 ± 1.13 | −0.59 |
DISCUSSION
Result Analysis
We quantified age‐related trends of sulcal morphology in 14 primary and secondary cortical furrows in a cross‐sectional study of 90 healthy adults ages 20–82 years. Highly significant (P < 0.05) increase in sulcal width and decrease in sulcal depth with age were observed. The overall rate of increase in sulcal width with age was 0.71 mm/decade, which was about twice the rate of age‐related decrease in sulcal depth, 0.38 mm/decade. While widening of cortical sulci with age is a well‐known phenomenon, the age‐related reduction in sulcal depth has not been previously reported.
Our regional trends corroborate the hypothesis of significant, regionally heterogeneous pattern of morphological changes in cortex with aging. The observed regional sulcal trends are consistent with reports from regional histological, anatomical, and metabolic studies [Bartzokis et al., 2003; Good et al., 2001; Jernigan et al., 2001; Magnotta et al., 1999; Meltzer et al., 2003; Raz et al., 1997; Symonds et al., 1999; Xu et al., 2000; Yanase et al., 2005]. Sulci in cerebral lobes with predominantly multimodal function such as the frontal, parietal lobes and cingulate gyrus showed more rapid change with age than sulci located in cerebral lobes with predominantly unimodal sensory functions such as occipital and, to a lesser degree, temporal. The regionality of age‐related trends went beyond lobar organization. Aging trends for individual sulci indicated that sulci located within the same lobe could have statistically different rates of age‐related change. This was the case for the frontal lobe where the “widening” trend of the superior frontal sulcus was significantly more pronounced (P < 0.01) than in the inferior frontal sulcus. Superior frontal sulcus also showed the highest age‐related “widening” slope. The finding of accelerated GM volume decline in superior frontal area has been the most consistently reported observation in the anatomical and metabolic studies of aging [Good et al., 2001; Magnotta et al., 1999; Meltzer et al., 2003; Raz et al., 1997; Sowell et al., 2002; Xu et al., 2000; Yanase et al., 2005]. Other sulci, commonly used as anatomical concomitants for multimodal functional areas, such as intraparietal, postcentral, and cingulate, all showed highly significant age‐related changes in both sulcal width and depth. The smallest age‐related changes were observed in the occipital lobe sulci followed by the inferior frontal and olfactory and all of these cortices have been consistently reported as relatively “spared” by aging in the neuroimaging literature [Good et al., 2001; Magnotta et al., 1999; Meltzer et al., 2003; Raz et al., 1997; Sowell et al., 2002; Xu et al., 2000; Yanase et al., 2005].
Consistent with prior neuroimaging research, significant intergender differences in sulcal morphology trends were found [Good et al., 2001; Raz et al., 1997; Xu et al., 2000]. In particular, significant intergender differences were observed for the superior temporal, collateral, and cingulate sulci (Table IV), where males showed a larger age‐related increase in sulcal width than females. Intergender aging differences for the superior temporal lobe were previously reported [Raz et al., 1997; Xu et al., 2000]. The findings of intergender differences for the collateral and cingulate sulci are new. The intergender difference in the intraparietal sulcus “widening” slope came close to reaching statistical significance (two‐tail P < 0.08), which is similar to a previous report [Xu et al., 2000].
The within‐subject increase in the sulcal width for all sulci was highly inversely correlated with the decrease in the sulcal depth (r = −0.676, P < 0.0001). This suggests shrinkage of the cortical surface area and an overall decrease in brain volume. Global scaling coefficients, obtained after normalization to the Talairach frame, corroborate this (Fig. 6). The Talairach atlas is based on the brain of a 67‐year‐old female. Subjects in the 20–60 age range had average scaling factors of less than one (0.95 ± 0.02), indicating that their brains were larger than Talairach's model. Subjects ages 75–80 had an average scaling factor larger than one (1.07 ± 0.03), indicating that their brains were smaller than Talairach's model. Our finding that sulcal width as well as sulcal depth changes during aging support the notion that cortical convolutions are malleable in normal adulthood as well as during development and in response to pathological factors such as tumors. These results are consistent with the hypothesis that mechanical tension along axons and dendrites plays a role in shape changes during adulthood [Van Essen, 1997].
Figure 6.
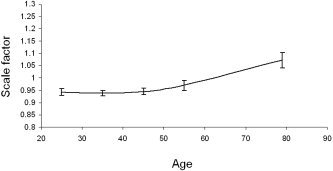
Average global spatial normalization scaling coefficients for each decade following transformation into the Talairach frame.
The finding of age‐related shallowing of cortical sulci and the global two‐to‐one relationship between sulcal width and depth aging trends may offer an explanation for the stability of the cortical gyrification index (GI) with age. The GI is a ratio of total to superficially exposed cortical surface areas. While changes in sulcal and gyral curvatures correlate strongly with age [Magnotta et al., 1999], the GI measurements were reported to be fairly independent of the subject's age [Zilles et al., 1988]. The relationship between sulcal width and depth, observed here, may account for the age‐related stability of GI, as the observed age‐related decrease in sulcal depth is offset by widening of the sulci, which keeps the ratio between total and exposed surface areas less variable with age.
Subjects and Methods
Method
Analysis of sulcal morphology provided a unique and precise way to track cortical changes associated with aging. This analysis is based on the contrast between GM and CSF, which unlike contrast between GM and WM, remains stable with age and offers an age‐independent basis for measurements. Although sulcal morphology trends do not provide direct insight into the cellular/molecular nature of aging, the mechanisms behind them are thought to be intimately tied to regional reduction in GM and WM gyral volumes. Magnotta et al. [1999] examined the age‐related changes in sulcal/gyral curvature and found them to be highly correlated with age‐related changes in thickness of the cortical GM mantle. The uniform, extra‐sulcal (gyral) and intra‐sulcal (internal) age‐related reduction in the thickness of the cortical mantle reported by Magnotta et al. [1999] and others [Good et al., 2001; Raz et al., 1997; Sowell et al., 2002; Xu et al., 2000] alone can neither predict the age‐related sulcal shallowing nor explain the two‐to‐one relationship between sulcal width/depth aging trends observed here. It has been shown that age‐related decline in gyral GM volumes has a concomitant reduction in the gyral WM volumes [Bartzokis et al., 2003; Jernigan et al., 2001; Symonds et al., 1999]. This might be causing an age‐related “debulking” of gyral volumes and is responsible for the reduction in sulcal depth. We are planning to perform an investigation that thoroughly incorporates sulcal, cortical mantle thickness, and regional WM measures needed to substantiate this hypothesis.
We used linear trend analysis to estimate age‐related trends of sulcal. Data presented by Sowell et al. [2002] and others [Good et al., 2001; Jernigan et al., 2001; Raz et al., 1997; Xu et al., 2000] indicated that age‐related trends of GM decline are significantly nonlinear. However, we think that linear regression analysis is appropriate here. It appears that nonlinearity in age‐related GM trends is most prominent before the age of 30 [Sowell et al., 2002] and thought to be caused by the maturation processes. The GM volumes appear to decline linearly after age 30 [Raz et al., 1997; Sowell et al., 2002]. Furthermore, it is not clear whether the nonlinearity of age‐related GM‐decline translates into nonlinearity of sulcal trend, as Sowell et al. [2002] indicated that regional CSF volume increased linearly with age.
A limitation of our subject population is the gap in the age range of the sample, which did not include participants age 61 and 74 years old. This age gap could have exerted significant statistical leverage in the regressions of the sulcal measures on age, which, in turn, could have inflated the magnitude of age effects. We examined this possibility by omitting the oldest participants, (age 75–82 years old) prior to regressing the sulcal measures on age. The results of these analyses were identical to the results obtained when the oldest participants were included. In particular, sulcal width still increased significantly with age (B = 0.80 ± 0.07 mm/decade, intercept = 0.69, t = 11.38, P < 0.0001), whereas sulcal depth still decreased significantly with age (B = −0.21mm/decade ± 0.05, intercept = 12.10, t = −4.21, P < 0.0001).
We do not yet know whether our explication of “widening” and “shallowing” of cortical sulci in the normal population has salient implications for brain function. We plan to correlate the changes in sulcal morphology with the subject's performance on neuropsychological testing as well as with the volume of white matter hyperintensities, which start to appear in the fifth and sixth decades of life and increase linearly with age [Wen and Sachdev, 2004]. Our methodology is also ideally suited for performing longitudinal studies from sequential MRI and can be used to assess whole‐brain and regional atrophy rates in mild cognitive impairment and probable dementia of Alzheimer's type.
Acknowledgements
We thank Dr. George Altomare for proofreading and stylistic comments.
REFERENCES
- Amunts K, Zilles K, Armstrong E, Schleicher A, Kretschmann HJ (2001): Advances in cytoarchitectonic mapping of the human cerebral cortex. Neuroimaging Clin N Am 11: 151–169. [PubMed] [Google Scholar]
- Ashburner J, Friston K (2000): Voxel‐based morphometry—the methods. Neuroimage 11: 805–821. [DOI] [PubMed] [Google Scholar]
- Bartzokis G, Cummings JL, Sultzer D, Henderson VW, Nuechterlein KH, Mintz J (2003): White matter structural integrity in healthy aging adults and patients with Alzheimer disease: a magnetic resonance imaging study. Arch Neurol 60: 393–398. [DOI] [PubMed] [Google Scholar]
- Breger RK, Yetkin FZ, Fischer ME, Papke RA, Haughton VM, Rimm AA (1991): T1 and T2 in the cerebrum: correlation with age, gender, and demographic factors. Radiology 181: 545–547. [DOI] [PubMed] [Google Scholar]
- Chang L, Ernst T, Poland RE, Jenden DJ (1996): In vivo proton magnetic resonance spectroscopy of the normal aging human brain. Life Sci 58: 2049–2056. [DOI] [PubMed] [Google Scholar]
- Cho S, Jones D, Reddick WE, Ogg RJ, Steen RG (1997): Establishing norms for age‐related changes in proton T1 of human brain tissue in vivo. Magn Reson Imaging 15: 1133–1143. [DOI] [PubMed] [Google Scholar]
- Duan H, Wearne SL, Rocher AB, Macedo A, Morrison JH, Hof PR (2003): Age‐related dendritic and spine changes in corticocortically projecting neurons in macaque monkeys. Cereb Cortex 13: 950–961. [DOI] [PubMed] [Google Scholar]
- Flood D, Coleman P (1988): Neuron numbers and size in aging brain: comparison of human, monkey and rodent data. Neurobiol Aging 9: 453–463. [DOI] [PubMed] [Google Scholar]
- Freedman M, Knoefel J, Maeser M, Levine H (1994): Computerized axial tomography in aging In: Albert ML, ed. Clinical neurology of aging. New York: Oxford University Press; p 139–148. [Google Scholar]
- Good CD, Johnsrude IS, Ashburner J, Henson RN, Friston KJ, Frackowiak RS (2001): A voxel‐based morphometric study of ageing in 465 normal adult human brains. Neuroimage 14: 21–36. [DOI] [PubMed] [Google Scholar]
- Haacke E (1999): Magnetic resonance imaging: physical principles and sequence design. New York: John Wiley & Sons. [Google Scholar]
- Herndon RC, Lancaster JL, Toga AW, Fox PT (1996): Quantification of white matter and gray matter volumes from T1 parametric images using fuzzy classifiers. J Magn Reson Imaging 6: 425–435. [DOI] [PubMed] [Google Scholar]
- Herndon RC, Lancaster JL, Giedd J, Fox PT (1998): Quantification of white matter and gray matter volumes from 3‐D magnetic resonance volume studies using fuzzy classifiers. J Magn Reson Imaging 8: 1097–1105. [DOI] [PubMed] [Google Scholar]
- Jernigan TL, Archibald SL, Fennema‐Notestine C, Gamst AC, Stout JC, Bonner J, Hesselink JR (2001): Effects of age on tissues and regions of the cerebrum and cerebellum. Neurobiol Aging 22: 581–594. [DOI] [PubMed] [Google Scholar]
- Lancaster JL, Fox PT, Downs H, Nickerson DS, Hander TA, El Mallah M et al. (1999): Global spatial normalization of human brain using convex hulls. J Nucl Med 40: 942–955. [PubMed] [Google Scholar]
- Magnotta VA, Andreasen NC, Schultz SK, Harris G, Cizadlo T, Heckel D et al. (1999): Quantitative in vivo measurement of gyrification in the human brain: changes associated with aging. Cereb Cortex 9: 151–160. [DOI] [PubMed] [Google Scholar]
- Mangin JF, Frouin V, Bloch I, Régis J, López‐Krahe J (1995): From 3D Magnetic Resonance Images to Structural Representations of the Cortex Topography Using Topology Preserving Deformations. J Math Imaging Vis 5: 297–318. [Google Scholar]
- Mangin JF, Frouin V, Régis J, Bloch I, Belin P, Samson Y (1996): Towards better management of cortical anatomy in multi‐modal multi‐individual brain studies. Phys Med 12: 103–107. [Google Scholar]
- Mangin JF, Rivière D, Coulon O, Poupon C, Cachia A, Cointepas Y et al. (2004): Coordinate‐based versus structural approaches to brain image analysis. Artif Intell Med 30: 77–97. [DOI] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J (1995): A probabilistic atlas of the human brain: theory and rationale for its development. The International Consortium for Brain Mapping (ICBM) . Neuroimage 2: 89–101. [DOI] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans A, Fox PT, Lancaster JL, Zilles K et al. (2001): A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM). Philos Trans R Soc Lond B Biol Sci 356: 1293–1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzer CC, Becker JT, Price JC, Moses E (2003): Positron emission tomography imaging of the aging brain. Neuroimaging Clin N Am 13: 759–767. [DOI] [PubMed] [Google Scholar]
- Morrison JH, Hof PR (1997): Life and death of neurons in the aging brain. Science 278: 412–419. [DOI] [PubMed] [Google Scholar]
- Ono M, Kubik S, Abernathey C (1990): Atlas of the cerebral sulci. New York: Thieme Medical. [Google Scholar]
- Pfefferbaum A, Sullivan EV, Jernigan TL, Zipursky RB, Rosenbloom MJ, Yesavage JA et al. (1990): A quantitative analysis of CT and cognitive measures in normal aging and Alzheimer's disease. Psychiatry Res 35: 115–136. [DOI] [PubMed] [Google Scholar]
- Raz N, Gunning FM, Head D, Dupuis JH, McQuain J, Briggs SD et al. (1997): Selective aging of the human cerebral cortex observed in vivo: differential vulnerability of the prefrontal gray matter. Cereb Cortex 7: 268–282. [DOI] [PubMed] [Google Scholar]
- Rivière D, Mangin JF, Papadopoulos‐Orfanos D, Martinez JM, Frouin V, Régis J (2002): Automatic recognition of cortical sulci of the Human Brain using a congregation of neural networks. Med Image Anal 6: 77–92. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC (1998): A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging 17: 87–97. [DOI] [PubMed] [Google Scholar]
- Smith SM (2002): Fast robust automated brain extraction. Hum Brain Mapp 17: 143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sowell ER, Thompson PM, Rex D, Kornsand D, Tessner KD, Jernigan TL et al. (2002): Mapping sulcal pattern asymmetry and local cortical surface gray matter distribution in vivo: maturation in perisylvian cortices. Cereb Cortex 12: 17–26. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, Toga AW (2003): Mapping cortical change across the human life span. Nat Neurosci 6: 309–315. [DOI] [PubMed] [Google Scholar]
- Steen RG, Gronemeyer SA, Taylor JS (1995): Age‐related changes in proton T1 values of normal human brain. J Magn Reson Imaging 1995: 1. [DOI] [PubMed] [Google Scholar]
- Steiner I, Gomori JM, Melamed (1985): Progressive brain atrophy during normal aging in man: a quantitative computerized tomography study. Isr J Med Sci 21: 279–282. [PubMed] [Google Scholar]
- Stevens J (1992): Applied multivariate statistics for the social sciences, 2nd ed. Hillsdale, NJ: Erlbaum. [Google Scholar]
- Styner M, Brechbühler C, Székely G, Gerig G (2000): Parametric estimate of intensity inhomogeneities applied to MRI. IEEE Trans Med Imaging 19: 153–165. [DOI] [PubMed] [Google Scholar]
- Symonds LL, Archibald SL, Grant I, Zisook S, Jernigan TL (1999): Does an increase in sulcal or ventricular fluid predict where brain tissue is lost? J Neuroimaging 9: 201–209. [DOI] [PubMed] [Google Scholar]
- Van Essen DC (1997): A tension‐based theory of morphogenesis and compact wiring in the central nervous system. Nature 385: 313–318. [DOI] [PubMed] [Google Scholar]
- Wen W, Sachdev P (2004): The topography of white matter hyperintensities on brain MRI in healthy 60‐ to 64‐year‐old individuals. NeuroImage 22: 144–154. [DOI] [PubMed] [Google Scholar]
- Wright IC, McGuire PK, Poline JB, Travere JM, Murray RM, Frith CD et al. (1995): A voxel‐based method for the statistical analysis of gray and white matter density applied to schizophrenia. Neuroimage 2: 244–252. [DOI] [PubMed] [Google Scholar]
- Xu J, Kobayashi S, Yamaguchi S, Iijima K, Okada K, Yamashita K (2000): Gender effects on age‐related changes in brain structure. AJNR Am J Neuroradiol 21: 112–118. [PMC free article] [PubMed] [Google Scholar]
- Yanase D, Matsunari I, Yajima K, Chen W, Fujikawa A, Nishimura S, Matsuda H, Yamada M (2005): Brain FDG PET study of normal aging in Japanese: effect of atrophy correction. Eur J Nucl Med Mol Imaging 32: 794–805. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S (2001): Segmentation of brain MR images through a hidden Markov random field model and the expectation maximization algorithm. IEEE Trans Medical Imaging 20: 45–57. [DOI] [PubMed] [Google Scholar]
- Zilles K, Armstrong E, Schleicher A, Kretschmann HJ (1988): The human pattern of gyrification in the cerebral cortex. Anat Embryol (Berl) 179: 173–179. [DOI] [PubMed] [Google Scholar]
- Zilles K, Palomero‐Gallagher N, Grefkes C, Scheperjans F, Boy C, Amunts K et al. (2002): Architectonics of the human cerebral cortex and transmitter receptor fingerprints: reconciling functional neuroanatomy and neurochemistry. Eur Neuropsychopharmacol 12: 587–599. [DOI] [PubMed] [Google Scholar]


