A new approach to neuroimaging with magnetoencephalography

Abstract

We discuss the application of beamforming techniques to the field of magnetoencephalography (MEG). We argue that beamformers have given us an insight into the dynamics of oscillatory changes across the cortex not explored previously with traditional analysis techniques that rely on averaged evoked responses. We review several experiments that have used beamformers, with special emphasis on those in which the results have been compared to those observed in functional magnetic resonance imaging (fMRI) and on those studying induced phenomena. We suggest that the success of the beamformer technique, despite the assumption that there are no linear interactions between the mesoscopic local field potentials across distinct cortical areas, may tell us something of the balance between functional integration and segregation in the human brain. What is more, MEG beamformer analysis facilitates the study of these complex interactions within cortical networks that are involved in both sensory‐motor and cognitive processes. Hum. Brain Mapp 25:199–211, 2005. © 2005 Wiley‐Liss, Inc.

INTRODUCTION

In recent years, functional magnetic resonance imaging (fMRI) has become the preeminent technique for functional neuroimaging of sensory and cognitive function [Berns,1999; Stern and Silbersweig,2001]. Despite the advantage of its much higher temporal resolution, magnetoencephalography (MEG) has not yet been widely adopted as a cognitive neuroimaging technique.

One possible reason why MEG has had relatively limited application in this context is that most MEG analysis has relied previously on averaging of brain responses evoked by a given stimulus. To obtain a detectable average signal, the temporal pattern of brain activation must be time‐ and phase‐ locked to a stimulus onset. Consequently, MEG has been most suited to the recording of evoked responses in the primary sensory and motor domains, where time‐ and phase‐locked stimulus driven activations predominate.

In the last few years, a computational method using a linear combination of sensor outputs, namely a beamforming approach developed originally for radar applications [see van Veen and Buckley,1988], has been applied successfully to the analysis of electroencephalographic (EEG) and MEG data [e.g., Cheyne et al.,2003; Dziewas et al.,2003; Fawcett et al.,2004; Furlong et al.,2004; Gaetz and Cheyne,2003; Hall et al.,2004,2005; Hashimoto et al.,2001a,b; Herdman et al.,2003; Hirata et al.,2002; Huang et al.,2004; Ihara et al.,2003; Ishii et al.,1999,2002,2003; Iwaki et al.,1999; Kamada et al.,1998; Ploner et al.,2002; Robinson et al.,2002; Robinson and Vrba,1999; Sekihara et al.,2001,2002; Taniguchi et al.,2000; Ukai et al.,2002; van Drongelen et al.,1996; van Veen et al.,1997; Xiang et al.,2001,2003]. This spatial filtering technique does not rely on the brain responses being phase‐locked across trials and therefore experimental paradigms familiar from fMRI and positron emission tomography (PET) studies can now be used with MEG [Singh et al.,2002,2003]. The aim of this article is to describe the basic principles of the beamforming technique and its application to study induced and evoked phenomena in MEG data, using experimental studies as illustrative examples.

We first describe the beamformer technique and illustrate how volumetric beamformer images can be used for group neuroimaging. This is followed by a comparison of MEG beamformers to source reconstruction algorithms that are typically used to analyse average evoked responses. We then discuss the limitations of averaging with respect to the study of cognitive processes and induced phenomena, and suggest that beamformer methods can be exploited to circumvent these problems. Subsequently, a literature review of beamformer applications in studies on evoked and induced phenomena is provided to give an overview, rather than a detailed description, of the breadth of experiments that can be analysed using the beamformer methodology. Finally, we discuss how the success of beamformer algorithms may provide a clue as to the nature of electrical neuronal interactions.

BEAMFORMER ANALYSIS OF MEG DATA

Beamforming techniques were developed for radar applications [see van Veen and Buckley,1988] to modify the sensitivity profile of fixed array radars, such that signals coming from a location of interest were received whereas signals coming from other locations were attenuated. This focusing, or “beam forming,” is achieved by selectively weighting the contribution that each sensor makes to the overall beamformer output. Increasing the sensitivity to signals coming from a location of interest, for example a region in the brain, can obviously be exploited for reconstruction of the neuronal sources generating EEG and MEG data. However, the beamformer approach has been introduced only recently to this field [Robinson and Vrba,1999; Sekihara et al.,2001; van Drongelen et al.,1996; van Veen et al.,1997]. Source reconstruction is achieved by first defining a source space formed by a volumetric grid of target locations. For each target location, a set of beamformer weights is then determined, forming an optimum spatial filter for that location (see Appendix). Computation of these beamformer weights involves the data covariance matrix [see Barnes and Hillebrand,2003; Robinson and Vrba,1999; van Drongelen et al.,1996; van Veen et al.,1997], hence beamformer analysis can localise activity that is time‐locked but not necessarily phase‐locked to stimulus presentation. The output of the beamformer is subsequently obtained by applying the spatial filter to the recorded MEG data, simply by multiplying the signal in each MEG sensor with its associated beamformer weight and summing the weighted sensor signals. Computing the beamformer output for each location independently allows for the reconstruction of multiple (uncorrelated) sources without making prior assumptions about the total number of active sources [Robinson and Vrba,1999]. Various parameters can be computed based on the beamformer output for a target location, for example, the Neural Activity Index (see Appendix). Such an index of neuronal activity can be computed sequentially for a set of voxels in the brain, forming a volumetric spatial image of brain activity. In simulations, these volumetric images typically show a peak centred around the electrical source location with a width that depends on the signal‐to‐noise ratio (SNR) of the data [Barnes and Hillebrand,2003; Gross et al.,2001; van Drongelen et al.,1996; van Veen et al.,1997] and on the specific beamformer implementation that was used to form the image. A description of beamformer design strategies is given in van Veen and Buckley [1988], and Huang et al. [2004] discuss the theoretical and practical commonalities, differences, and relative performance of different beamformer implementations. It has been shown in simulations that the spatial resolution of the volumetric beamformer images is inhomogeneous across the brain [Barnes and Hillebrand,2003; Gross et al.,2001,2003; van Veen et al.,1997; Vrba and Robinson,2001a], with the highest spatial resolution being at the locations of active sources. Using a retinotopic mapping MEG experiment, Barnes et al. [2004] have shown recently that the spatial resolution in the visual cortex varies between 2 and 15–20 mm, and that 80% of the voxels had a full‐width half‐maximum (FWHM) of less than 10 mm.

When a boxcar experimental design is used, one can statistically compare the active and passive experimental states for each target voxel in the beamformer images, forming so‐called statistical parametric maps, or SPMs, to highlight brain regions that were activated to a different extent in the active and passive states. Barnes and Hillebrand [2003] have shown recently that corrected significance levels can be assigned to the SPMs that are obtained with the beamformer analysis, based on spatial smoothness [see also Gross et al.,2003]. Additionally, Singh et al. [2003] described how nonparametric methods [Nichols and Holmes,2001] can be utilised to assign voxel and cluster significance to group averaged beamformer SPMs. Such statistical methods are essential if quantitative comparisons are to be made between the SPMs for different cohorts of subjects, experimental conditions, or modalities. In particular, one attribute of cognitive processes is the large intersubject variability [McGonigle et al.,2000; Miller et al.,2002; although see Xiong et al.,2000] and a statistical analysis on the group data is therefore necessary to reveal the most prominent responses across the group. This approach was first used in PET studies and subsequently applied to fMRI [Friston et al.,1990,1991; Lueck et al.,1989]. The same statistical analysis methods can now also be applied to MEG/EEG data [Park et al.,2002; Singh et al.,2002,2003].

COMPARING MEG BEAMFORMERS TO OTHER SOURCE RECONSTRUCTION ALGORITHMS

Successful localisation of neuronal activity from measured MEG data relies on solving the inverse problem, which has an infinite number of possible solutions. It is therefore necessary to seek an assumption set that is both realistic and renders the problem soluble [see Baillet et al.,2001 for an excellent review]. The most common initial assumption is that a small area of active cortex can be modelled as an equivalent current dipole. Generally, this assumption is reasonable given that the active area is small relative to the distance from which it is observed [Snyder,1991].

Dipole‐fitting algorithms minimise the difference between measured and estimated fields and make the assumption that only a small number of sources are concurrently active over a short period. The shorter the time used in the analysis, the more plausible the assumption, and typically one attempts to explain subsequent short (∼10–100 ms) blocks of time with models that each consist of a few dipoles [Mosher et al.,1992; Scherg and Berg,1991; Scherg and von Cramon,1985,1986; see also Michel et al.,2001]. Typically this assumption holds well for primary sensory experiments [e.g., Jousmaki and Forss,1998; Snyder,1991; Torquati et al.,2002] in which averaging is used to increase SNR and extract only those cortical areas that respond in a causal and phase‐locked manner to the stimulus. The results obtained with dipole fitting become less stable as the number of active sources increases and are highly dependent on the correct estimation of model order [Supek and Aine,1993].

For minimum norm algorithms, the assumption is that the source configuration with the least energy that also minimises the difference between measured and estimated fields accounts for the measured data [Hämäläinen and Ilmoniemi,1984; Singh et al.,1984]. One problem with this constraint is that such a source configuration must always exist at the most superficial layer of the source space, and hence some arbitrary depth bias must be factored into the calculations. In related imaging approaches the location bias can be based on fMRI data [Dale et al.,2000], Bayesian inference [Baillet and Garnero,1997] or empirical estimation through simulated data [Ioannides et al.,1995].

The main assumption behind beamformer analysis is that each cortical source has a time course that is not linearly correlated with any other source. The assumption is implicit in the minimum power constraint, in combination with the constraint that there is unity passband for each source element of interest (see Appendix). When sources are perfectly linearly correlated the beamformer will recover very little or no power. The reason for this is that as the sources are correlated, the forward solutions (lead field vectors) for the different correlated sources will add as vectors. The vector sum will be different from each constituent vector and in fact may not even correspond to the lead field for any single source within the brain. Power minimisation subject to the unity passband from the selected voxel will then reject this sum vector because it does not match the lead field vector expected at that voxel. Recently, a new beamformer utilising a higher‐order covariance matrix has been proposed that has shown promise in localising strongly correlated activity in simulations and an MEG median‐nerve experiment [Huang et al.,2004].

It should also be emphasised that although all the above algorithms have a different evolution, and different accepted best practice, mathematically they are very similar. Mosher et al. [2003] have shown the beamformer approach to be a special case of the minimum norm where the a priori information of uncorrelated sources is used to constrain the solution. The work shows that the difference between all linear inverses lies in the prior assumptions on the shape of the current covariance matrix (Fig. 1). For beamformers, it is assumed to be diagonal (sources uncorrelated, see Fig. 2), and for weighted minimum norm estimates it is weighted such that current contribution from certain parts (e.g., deep) of the source volume have more influence. Similarly, the unfocused beamformer, where the beamformer weights are based on white sensor noise, has been shown to reproduce the error surface travelled over when using a single dipole fit approach [Hillebrand and Barnes,2003].

Figure 1.

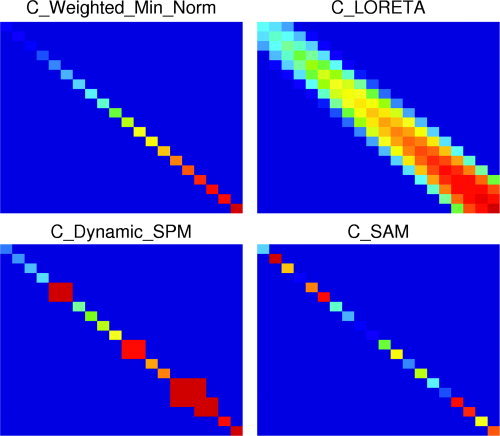
Schematics of source covariance matrices for different source reconstruction algorithms. Each element represents the covariance between a source and another source, with the distance to the sensors for each source increasing from top to bottom and from left to right. All panels have the same arbitrary scaling, with the blue‐yellow‐red colour scale representing increasing source covariance. Top left: The minimum norm approach assumes that no sources within the brain are linearly correlated, hence the diagonal source covariance matrix. Additionally, the increased weighting for deeper sources can be used to correct for the depth bias of minimum norm approaches. Although no correlation between sources is specified a priori, the minimum norm approach does not exclude correlated sources from the solutions. Top right: LORETA [Pasqual‐Marqui et al.,1994] assumes that active areas have a certain spatial extent that is represented by the “broad” diagonal of the source covariance matrix. Bottom left: Dynamic SPM [Dale et al.,2000] is based on the weighted minimum norm approach. Additionally, the source covariance for elements at fMRI hotspots (three hotspots in this illustration) can be increased to bring the MEG results in agreement with fMRI results. Bottom right: SAM [Robinson and Vrba,1999] assumes that no sources within the brain are linearly correlated, hence the diagonal source covariance matrix. The value of the diagonal elements is determined by the data covariance matrix [Mosher et al.,2003].

Figure 2.

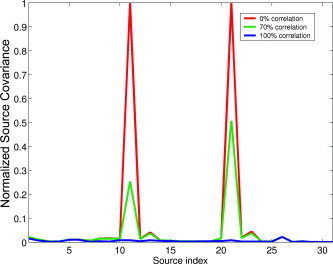
Diagonal elements of the SAM source covariance matrix for a set of target locations along a line. MEG data was simulated for two sources with different amounts of correlation between the respective time courses. This figure does not show actual source reconstructions, but simply the elements of the source covariance matrix that SAM assumes. It is clear that the assumption of uncorrelated sources, in combination with the fact that the source covariance matrix is determined by the data covariance [Mosher et al.,2003], modifies the source covariance matrix in such a way that perfectly correlated sources cannot be detected with SAM. However, it is also clear from this figure that partially correlated sources are not excluded from detection. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

To summarise, the main differences in the algorithms have been in their application: minimum norm estimates and dipole fits have been used mainly to explain the stimulus‐locked average [with a few notable exceptions, e.g., David et al.,2002; Ioannides,2001]. Conversely, beamformers have been most successful in identifying induced changes in cortical oscillatory power that do not result in a strong average signal (but see the Evoked responses section). In the next section, we discuss some potential pitfalls in the averaging process.

LIMITATIONS INTRODUCED BY TIME‐DOMAIN AVERAGING

An advantage of MEG is that the magnetic fields recorded outside the head are related directly to the electrical neuronal activity. The typical time scale of the dynamics of neuronal populations, and therefore the time resolution of the acquired MEG data, is on the order of milliseconds (only limited by the sampling rate). MEG has been used with great success in studies of the relationship between the latency and amplitude of evoked responses and stimulus parameters in visual, auditory, and somatosensory paradigms [e.g., Jousmaki and Forss,1998; Okada et al.,1982; Roberts et al.,2000; Torquati et al.,2002]. However, the magnetic fields produced by the neuronal currents are much weaker than are the magnetic fields produced by external noise sources and for successful source reconstruction this has traditionally meant increasing the SNR of MEG data by means of averaging [Schimmel,1967]. This requires the recording of many (∼100) individual responses to an internal or external stimulus and will identify only that part of the signal that exhibits only a small variability to the repeated presentations. That is, the neuronal responses need to be both time‐ and phase‐locked to the stimulus to be measured reliably in the averaged evoked response. MEG experiments involving cognitive paradigms are complicated by this requirement of phase‐locking with traditional analysis methods [see for example Hari et al.,2000]. Averaging individual responses with a latency jitter of only 2 ms can reduce the peak amplitude of an average response by as much as 26% (see Fig. 3). This jitter is much smaller than the inherent jitter in the exact timing of cognitive processes [see Michalewski et al.,1986]. Techniques based on the haemodynamic response, like PET and fMRI, rely on changes in blood flow and therefore have an inherently lower time resolution (on the order of seconds) than MEG has. Consequently, these techniques are less sensitive to variability in the latency of individual responses (see Fig. 3, tolerating jitter of the order of seconds) and have been used in cognitive paradigms with great success [Cabeza and Nyberg,2000; Nyberg,2001].

Figure 3.

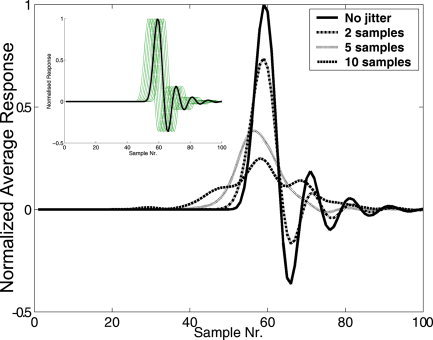
Responses obtained from averaging 100 simulated, noise‐free epochs. The latency of each epoch was jittered by an amount taken from a Gaussian distribution (σ = 2, 5, or 10 samples) with zero mean. The inset shows the original epoch and the jittered epochs for the σ = 2 case. The effect of jitter depends on the width of the peak, and was chosen here to be representative for a typical, early latency, evoked response peak. Note the rapid decrease in the evoked response peak when the latency jitter increases. Acceptable levels of jittering are one or two samples, causing a reduction of 6–26% of the peak amplitude. This means that for MEG a jitter of 1–2 ms is acceptable and for BOLD fMRI the acceptable jitter is on the order of 1–2 s, assuming that the BOLD response is sampled at about 1 Hz. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

That said, MEG and EEG studies have successfully localised cognitive components of the evoked response, such as the P300 and N400, using traditional source reconstruction methods based on averaged responses, such as equivalent current dipole analysis and techniques based on distributed source models [e.g., Anderer et al.,2003; Halgren et al.,2002; Pylkkänen and Marantz,2003; Tarkka et al.,1996].

When studying the evoked response, the ongoing activity is often ignored or not quantified, whereas it has been demonstrated that ongoing activity plays an important role in cortical function [Arieli et al.,1996; Karakas et al.,2000; Kenet et al.,2003; Makeig et al.,2002; Ringach,2003]. It has been demonstrated that induced changes in the power of cortical rhythms that are time‐locked but not necessarily phase‐locked to a stimulus, so‐called “event‐related synchronisation and desynchronisation” (ERS/ERD) [Pfurtscheller and Lopes da Silva,1999], covary in a variety of different sensory‐motor and cognitive tasks. For example, the amplitude of μ‐rhythm (9–11 Hz) in the somatosensory cortex reduces when a subject clenches the fist and the alpha rhythm (8–13 Hz) in the visual cortex increases in power when the eyes are closed [e.g., Chapman et al.,1984; Niedermeyer,1993]. Moreover, these rhythms, their complexity and dynamics, have been invoked as the mechanism underlying consciousness [Engel et al.,2001; Llinás et al.,1998; Singer,1998; Tononi and Edelman,1998]. Additionally, it has been shown that cognitive tasks induce ERD and ERS [Basar et al.,2001] and it has been demonstrated that evoked and induced responses are related differentially to specific components of cognitive processing [e.g., Eulitz et al.,2000; Foucher et al.,2003]. These studies, and the growing literature on ERD and ERS, highlight the importance of these induced phenomena in the understanding of brain function.

To localise induced phenomena and study cognitive function with MEG we therefore need an analysis tool that does not rely on average evoked responses and that can reconstruct multiple active neuronal sources: beamforming techniques fulfil this requirement.

BEAMFORMER APPLICATIONS

Evoked Responses

One of the problems implicit in estimating the neuronal origins of the evoked response using beamformers is that of correlated sources. This is a problem for two reasons. Firstly, the duration of the evoked response is typically very short (∼100 ms) leading to low degrees of freedom in the measurement and possible spurious correlations. Secondly, all the source activity picked up through averaging will be time‐locked to the stimulus event and is therefore likely to have a common driving force, making it more likely that any two sources will have inherently similar time series. Despite this, beamformer analysis has been utilised successfully in many paradigms studying phase‐locked responses.

Transient and steady‐state auditory evoked responses have been localised with a beamforming technique known as synthetic aperture magnetometry (SAM) [Robinson and Vrba,1999], and the results showed good agreement, bilaterally, in the temporal and spatial domain with the results obtained from dipole fit analysis and signal space projection, respectively [Herdman et al.,2003]. The beamformer was able to reconstruct the bilateral sources successfully, despite the similarity of the time courses of activation, using the sensors above each hemisphere separately. In contrast to dipole fitting [Vrba et al.,1999], using only a subset of channels does not introduce systematic spatial errors in the source reconstruction. Only the SNR of the reconstructed time courses is affected because the beamformer passes only that part of the recorded signal that corresponds to the forward solution for a source at a target location. Conversely, with dipole fitting, the difference between the measured data (from all selected channels) and the forward solution for the model is minimised so that any signal not accounted for by the forward solution contributes, erroneously, to the source reconstruction.

The beamformer implementation developed by Sekihara et al. [2001] has been used to analyse the initial peak of the somatosensory evoked field (SEF) after median nerve [Hashimoto et al.,2001a] and posterior tibial nerve [Hashimoto et al.,2001b] stimulation. They reported two spatially distinct sources underlying the single peaked tibial nerve response: one in the anterior part of the foot area of the primary somatosensory cortex (SI) and one in the posterior part of SI. Median nerve stimulation revealed two spatially distinct sources in areas 3b and 1 of SI. The source in area 3b moved toward the mediolateral direction during its active phase, whereas the source in area 1 was stationary. Frequency‐specific responses of the somatosensory cortex to median nerve stimulation have also been investigated by means of SAM analysis of single trial responses and the locations of the reconstructed sources have been compared to the dipole location fitted to the averaged evoked response (N20m) [Gaetz and Cheyne,2003; Hirata et al.,2002; Ihara et al.,2003; Xiang et al.,2003]. Both techniques localised a source to SI, with the source localised with SAM displaying a short burst of activity in the 60–100 Hz band and a longer increase in power in the 10–40 Hz band [Gaetz and Cheyne,2003]. In a similar study, Ihara et al. [2003] reported an increase in source power in the 60 Hz band in SI as well as an initial reduction in the 40 Hz band, followed by an increase in source power in the same area. Moreover, power increases in the 70–90 Hz band were found for sources in SI and secondary somatosensory cortex (SII). Xiang et al. [2003] also demonstrated reproducible source reconstructions for increases in activity in the 30–60 Hz and 60–120 Hz band in SI, but decreases in activity in these frequency bands were not well localised. Conversely, Hirata et al. [2002] did find reductions in source power (8–13, 13–25, and 25–50 Hz) in areas around the central sulcus. They further found reliable localisation of increases in power in SI (50–200 Hz). SAM has further been used to localise ERD/ERS in motor tasks, such as finger extension and hand grasping [Taniguchi et al.,2000] and the use of chopsticks [Ishii et al.,2002]. Perhaps the success of the application of beamformers to analysis of data from the somatosensory cortex is due to the rather high frequencies intrinsic to these areas (>20 Hz), which make the prospect of spurious correlations less likely. This might explain why Ihara et al. [2003] were able to localise high gamma band (70–90 Hz) activity in both contralateral SI and contralateral SII in the same time window. Additionally, two active sources may be reconstructed successfully when the time courses of activation are not correlated perfectly [Hashimoto et al.,2001a,b].

Other beamformer applications include a mental rotation task [Iwaki et al.,1999], resolution of visual cortical areas with moving random dot stimuli [Toyama et al.,1999], and in silent reading and silent naming tasks [Kamada et al.,1998; Kober et al.,2001].

Induced Responses

Several experiments have now been reported that demonstrate the localisation of induced activity that is inherently poorly time‐locked to the stimulus presentation.

Recent studies [Singh et al.,2002,2003] demonstrate that the SPMs obtained with a beamformer analysis can be spatially normalised and subsequently averaged across subjects to form an SPM for the group as a whole. Two cognitive paradigms were used in this study: a language task involving covert letter fluency and a biological motion direction discrimination task. The same experimental boxcar design was used in both the MEG and blood oxygenation level‐dependent (BOLD) fMRI recordings. Both experiments revealed striking similarities between the location of the BOLD response, and the location of frequency‐specific decreases in cortical power obtained with the MEG beamformer (Fig. 4). These results not only give weight to the assumptions behind the beamformer technology, but also show that both increases and decreases in electrical oscillatory power can give rise to a positive BOLD response. Similarly, Hall et al. [2005] recently used SAM to investigate the cortical response to contrast in primary visual cortex. They reported a striking similarity between the contrast response function in humans (ERS in the gamma band) and the local field potential as measured in primates [Logothetis et al.,2001].

Figure 4.

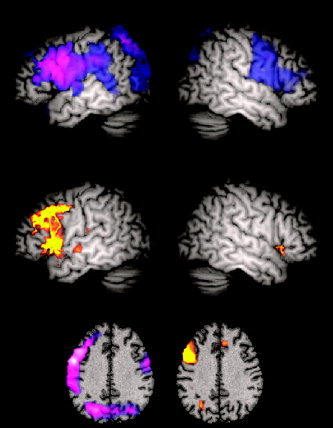
Results of group‐averaged MEG (top) and fMRI (middle) experiments for a covert letter fluency task, superimposed on a template brain and thresholded at P < 0.05 (corrected) [for details, see Singh et al.,2002]. The top panel displays the group SAM analysis of the MEG data, showing the peak power increase or decrease at each voxel in the brain, irrespective of which frequency band the power change occurred in. The blue‐purple‐white colour scale depicts decreases in signal power in the active phase, compared to the passive baseline. The middle panel shows group fMRI data. The red‐orange‐yellow colour scale depicts increasing BOLD amplitude. The bottom panel shows the peak group SAM (left) and fMRI (right) data superimposed on a slice through the template brain from the Montreal Neurological Institute (MNI) at a z coordinate of +35. Note the close spatial correspondence between the group MEG and fMRI results, despite the fact that two different imaging modalities were used and two different cohorts of subjects participated in the experiments.

Xiang et al. [2001] studied silent processing of words using SAM. Cortical power changes related to implicit word processing were localised to the occipital cortex (15–30 Hz ERD), parietal/occipital cortex (30–60 Hz and 60–125 Hz ERS) and Broca's/Wernicke's areas (60–125 Hz ERD). Similar activations were found for displays of non‐words, although the activation of Broca's and Wernicke's area was much weaker.

It has also been demonstrated that beamformers can be used to localise theta rhythms to the medial prefrontal cortex when subjects carry out a task with high attentional demands, such as mental calculation [Ishii et al.,1999] and, frequency‐specific responses of a cortical network activated by a Stroop task can be localised successfully [Ukai et al.,2002]. Additionally, sleep spindles (10–15 Hz) could be localised to the frontal and parietal cortices [Ishii et al.,2003] and responses to painful stimulation have been studied successfully with beamformer analysis [Ploner et al.,2002]. Cheyne et al. [2003] reported differential effects on cortical rhythms for tactile sensation during a finger‐brushing task, as compared to the observation of finger brushing, or object movement itself.

The work by Fawcett et al. [2004] investigated both evoked and induced phenomena using a reversing checkerboard stimulus of varying temporal frequency. The magnitude of the phase‐locked (stimulus‐driven) response in primary visual cortex was found to vary parametrically with frequency and no event‐related responses were found in these regions. However, ERD was found in extrastriate areas (V5/MT), which also varied parametrically with the temporal frequency of the stimulus.

In a single case study on a subject experiencing migraine‐induced visual aura, Hall et al. [2004] showed ERD in the alpha band in both extrastriate and temporal cortex that persisted for the duration of the reported visual illusions. Also noted were changes in the gamma band in the left temporal lobe that returned to baseline some 8–10 min after the reported end of the visual aura.

A final example of an experiment that is very difficult to carry out as an evoked response paradigm is the study of the cortical network involved in swallowing [Dziewas et al.,2003; Furlong et al.,2004]. The study by Furlong et al. [2004] not only localised the cortical regions involved but, more importantly, also determined the sequence of cortical activation from the receipt of a water bolus into the mouth to the swallow and post‐swallow phases, as well as the response to a simple tongue movement (Fig. 5). Volitional swallowing and tongue movement both induced similar responses in the superior sensorimotor cortex. However, significantly different activation was observed, most notably in the caudolateral sensorimotor cortex during water infusion, demonstrating that sensory input from the tongue activates caudolateral sensorimotor cortex, which strongly modulates superior sensory‐motor cortical areas involved in the volitional phase of swallowing. From a methodological viewpoint, this work is exciting as it was possible to localise electrical activity due to the tongue muscles. The resultant group statistical image [see Furlong et al.,2004] of an activation site just below the SPM glass brain [SPM99; Friston et al.,1995] gives confidence in not only the beamformer methodology and statistical methods used, but also shows that, given sufficient signal strength, MEG can accurately localise very distant sources.

Figure 5.

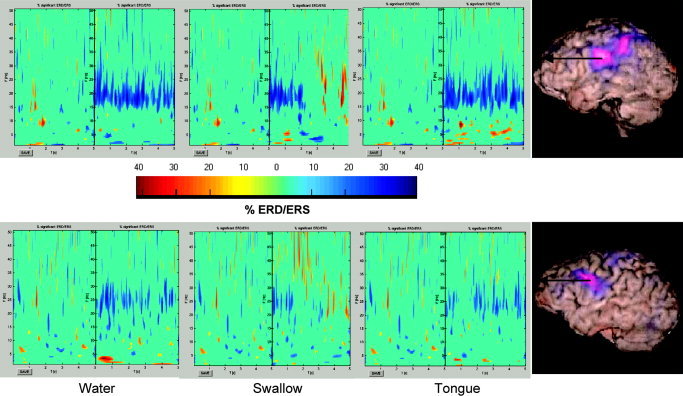
Time–frequency wavelet plots (three panels on the left) computed for an active area (left caudolateral precentral gyrus, marked in the right panels) identified with the beamformer in two representative subjects. MRI‐SAM images (right panels) were computed for the water versus rest phase (25–40 Hz band) in a swallowing experiment [see Furlong et al.,2004 for details], with the blue‐purple‐white colour scale depicting decreases in signal power in the water phase compared to that in the rest phase. The central dividing line in the time–frequency plots indicates the end of the 5 s of the passive period and 0 s for the commencement of the 5 s of the active phase. Colours represent significant ERD/ERS, with blues/purples indicating a decrease in power (ERD) and reds/yellows an increase in power (ERS). ERD/ERS that was not significant (P > 0.05) was set to zero [Graimann et al.,2002]. This demonstrates that it is possible to localise non‐phase‐locked responses and get timing (and spectral) information. Note also that the time–frequency resolution can be optimised using wavelet analysis [see Fawcett et al.,2004].

USING THE HIGH TEMPORAL RESOLUTION

So far we have shown how beamformer analysis can be used to study evoked and induced responses in individuals and across cohorts of subjects. An attractive feature of MEG is its high temporal resolution. At first it seems that beamformer analysis does little to exploit this, as it is based typically on comparison of relatively long (∼1 s) time windows. It should not be overlooked that window length is traded directly against accurate spectral estimates. Similarly, because at each target location the output of the beamformer is formed as a weighted sum of the sensor signals (see Appendix), an estimate of neuronal activity at millisecond resolution is directly available. This should enable the study of the dynamics of neuronal populations and complex interactions between regions. The fact that beamformer analysis has been applied successfully to MEG data may be a clue to the nature of such interactions. The beamformer analysis would fail if corticocortical interactions on a macroscopic scale were perfectly linear and coherent (see Appendix). Either such interactions must be nonlinear, short‐lived, or transient over the analysis time window. Recent work [Hadjipapas et al.,2005] has shown that as long as a linear correlation exists over less than 30% of a typical analysis time window the beamformer output will be minimally degraded. Theories of the brain as a metastable dynamical system suggest that changes in state, for example corresponding to changes in cognition or perception, are brought about through nonlinear coupling between areas [Kelso,1995]. An interesting analogy is with neural nets comprised of nonlinearly connected elements. These nonlinear connections bestow a complexity on the system that gives it memory and adaptability [Maass et al.,2002].

Concluding Remarks

The application of beamformer analysis to EEG and MEG data has already proven successful in many experimental paradigms. We consider the main advance in beamformer imaging to be that it has lead indirectly to renewed interest in electrical phenomena of induced oscillatory change. These changes covary with BOLD fMRI signal change. This is interesting for two reasons: firstly, it gives weight to the assumptions behind beamformer analysis; secondly, it suggests that a number of electrical phenomena (not just the evoked response) covary with haemodynamic changes in the cortex. If beamformers are successful in a large range of experimental designs, what does this tell us about how the brain works? Any long‐range linear interactions across the cortex would violate the assumption of uncorrelated sources behind the beamformer technique. That is, the success of the beamformer assumption lends weight to theoretical arguments [Bressler and Kelso,2001; Friston2000; Sporns et al.,2000] that communication between brain areas must be nonlinear, as a linear brain would lack complexity.

Paradoxically, to use MEG to find out what is going on in the brain, it seems that we must first speculate about how the brain operates. The studies reported above demonstrate that the assumption that remote corticocortical interactions are uncorrelated results in plausible physiologic solutions, and perhaps indicates that nonlinearity, or transient linearity, is the rule in such interactions.

The Basics of Beamforming

The output of a beamformer at a location of interest can be defined as the weighted sum of the output of all (N) signal channels [van Veen et al.,1997], or mathematically:

(1)

where V is the beamformer output (source strength in nAm), W is the 1 × N weight vector (for a given direction of the source at the target location), and B the N × T matrix of the magnetic field at the sensor locations at all (T) latencies. Note that the beamformer output at a target location has the same temporal resolution as the recorded MEG signals, and is therefore often referred to as a virtual electrode.

The weights determine the spatial filtering characteristics of the beamformer and are designed to increase the sensitivity to signals from a location of interest while reducing the contribution of signals from (noise) sources at different locations (Fig. A1). The beamformer weights for a source at a location of interest are determined completely by the data covariance matrix and the forward solution (lead field) for the target source [see Robinson and Vrba,1999; van Drongelen et al.,1996; van Veen et al.,1997]. It is therefore important that an unbiased estimate of the data covariance matrix is computed by using enough data samples. In practice, trials with a length of several seconds are usually recorded, as the induced responses of interest can take several seconds to return to baseline [e.g., Furlong et al.,2004; Neuper and Pfurtscheller,2001]. The effects of non‐stationarities in the MEG signals on the estimate of the data covariance matrix, and therefore the beamformer images, have yet to be studied. In addition, the forward solution for an equivalent current dipole is typically used for the weight computation. If the recorded MEG signal originates from an extended source, then the actual forward solution will deviate from the dipolar forward solution and the beamformer will suppress the activity from the extended source [Vrba,2002]. This effect is worse for data with high SNR, when the resolution of the beamformer is high enough to discriminate between the actual and modelled forward solutions [Hillebrand and Barnes,2003; Vrba,2002]. We envisage the incorporation of more sophisticated forward models [e.g., Jerbi et al.,2002] in the beamformer formulation so that extended activity can be localised.

Figure A1.

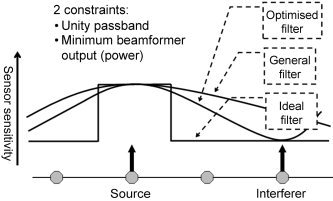
Illustration of the design of a spatial filter for a source at a target location. The ideal transfer function in general can not be achieved because there are only a limited number of sensors (typically ∼150). However, an optimum transfer function can be obtained by applying a unity passband constraint in combination with a minimum output power constraint [van Veen et al.,1997]. The second constraint would without the first constraint result in a spatial filter that does not let any signal through, not even from the target location. The first constraint states that signal from the target location should be let through completely, so the only way to minimise the output power is to reduce the contribution from other sources to the spatial filter output, resulting in a narrowing of the passband of the spatial filter. The contribution to the beamformer output from sources away from the target location is small for the optimum spatial filter, whereas it can be large for a nonoptimum beamformer. Signal from the target location will be cancelled if it is correlated with signal from another location [van Veen et al.,1997; Vrba,2002], as is explained in the text. The main assumption underlying beamformer analysis is therefore that there are no correlated sources within the brain, an assumption that is not necessarily fulfilled when distinct areas are driven simultaneously by an external stimulus or another cortical area. However, it has been shown [van Veen et al.,1997] that the beamformer performance is relatively robust to correlated activity and induced activity is unlikely to be strongly correlated across the brain. Moreover, the effect of correlated activity at distant locations can be reduced by selecting only those sensors covering the target location.

The power of the beamformer output can be computed for each voxel in a predefined source space independently and sequentially. This results in a volumetric image (SPM) of source power with relatively low spatial resolution. A better parameter to map is the Neural Activity Index [van Veen et al.,1997] or the pseudo‐Z statistic [Robinson and Vrba,1999], defined as the projected source power divided by the projected noise power. Moreover, the spatial resolution of the SPM can be increased further by making a statistical comparison between the beamformer output for an active state and the beamformer output for a passive state, in a specified frequency band [Robinson and Vrba,1999; Vrba and Robinson,2001b]. In our experience narrow frequency bands are often desirable for the statistical comparisons, but the computation of the data covariance matrix should be carried out with broadband data. The reason for this is that covariance estimates based on low degrees of freedom tend to overestimate covariance between channels, leading to spurious correlations that will cause the beamformer to suppress the activity of uncorrelated sources erroneously. Barnes and Hillebrand [2003] have shown that the beamformer design and statistical test stages can be decoupled, such that the beamformer weights are computed using broadband data, and the statistical comparisons are carried out with narrowband data.

Figure A2 demonstrates the ability to localise both stimulus driven (phase‐locked) power changes as well as induced (non‐phase‐locked) changes in power for an experiment where the right index finger was stimulated electrically using two ring electrodes placed one either side of the proximal interphalangeal joint. An analysis based on the average response to the 3 Hz stimulation would only be able to localise the phase‐locked 3 Hz response and not the induced responses at 12 and 20–25 Hz.

Figure A2.

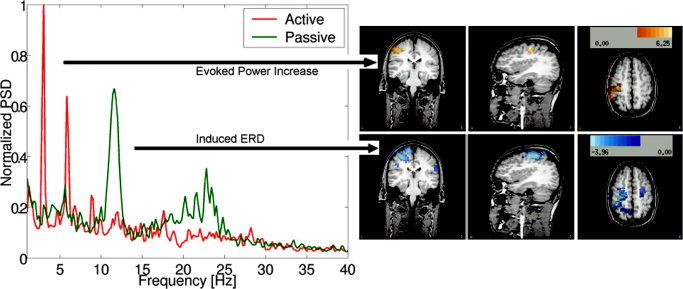
Left: Power‐spectrum of the beamformer output for the peak activity in the somatosensory cortex to 3 Hz stimulation of the right index finger, showing a stimulus driven increase in power in the active period compared to that in the passive period (ERS) at 3 Hz and harmonics of 3 Hz. There is also an induced reduction in power around 12 Hz (μ‐rhythm) at the same location. The beamformer images (right) computed for the 2.95–3.05 Hz band and the 11.8–12.2 Hz band both show peaks in the somatosensory cortex.