ALE meta‐analysis: Controlling the false discovery rate and performing statistical contrasts

Abstract

Activation likelihood estimation (ALE) has greatly advanced voxel‐based meta‐analysis research in the field of functional neuroimaging. We present two improvements to the ALE method. First, we evaluate the feasibility of two techniques for correcting for multiple comparisons: the single threshold test and a procedure that controls the false discovery rate (FDR). To test these techniques, foci from four different topics within the literature were analyzed: overt speech in stuttering subjects, the color‐word Stroop task, picture‐naming tasks, and painful stimulation. In addition, the performance of each thresholding method was tested on randomly generated foci. We found that the FDR method more effectively controls the rate of false positives in meta‐analyses of small or large numbers of foci. Second, we propose a technique for making statistical comparisons of ALE meta‐analyses and investigate its efficacy on different groups of foci divided by task or response type and random groups of similarly obtained foci. We then give an example of how comparisons of this sort may lead to advanced designs in future meta‐analytic research. Hum Brain Mapp 25:155–164, 2005. © 2005 Wiley‐Liss, Inc.

INTRODUCTION

In the field of functional neuroimaging, the art of summarizing previous results has progressed from simple textual summaries to tabular or graphical reviews to sophisticated function‐location meta‐analysis. Function‐location meta‐analysis has evolved into a quantitative method for synthesizing independent bodies of work and is critical in understanding the status of neuroimaging research in a particular cognitive domain [Fox et al.,1998]. Activation likelihood estimation (ALE) is a quantitative meta‐analysis method that was developed concurrently but independently by Turkeltaub et al. [2002] and Chein et al. [2002].

Turkeltaub et al. [2002] presented a meta‐analysis of single‐word reading and verified their results with a functional magnetic resonance imaging (fMRI) study of 32 subjects performing aloud word reading. Similar activation patterns were determined for both the ALE meta‐analysis and the fMRI experiment. Chein et al. [2002] presented a meta‐analysis of working memory studies and determined the presence of functional dissociation in Broca's area with regard to performance or lexical status. The analysis of Chein et al. [2002] was termed aggregated Gaussian‐estimated sources (AGES) and follows the same general procedure detailed by Turkeltaub et al. [2002]. The simultaneous development by two groups of the same voxel‐based meta‐analytic tool is strongly indicative of the timeliness and utility of this form of meta‐analysis. For simplicity, we henceforth refer to this method as an ALE meta‐analysis.

Activation Likelihood Estimation

In ALE, 3‐D coordinates in stereotactic space are pooled from a number of like studies. These coordinates are generally published relative to Talairach [Talairach and Tournoux,1988] or Montreal Neurological Institute (MNI) space [Collins et al.,1994] and must be spatially renormalized to a single template. This transformation is carried out using the Brett transform [Brett,1999]. Once all coordinates refer to locations in a single stereotactic space, the ALE analysis begins.

ALE statistic

Each reported coordinate (focus) is modeled by a 3‐D Gaussian distribution, defined by a user‐specified full‐width half‐maximum (FWHM). Let X _i denote the event that the ith focus is located in a given voxel. The probability of X _i occurring at voxel x, y, z is

(1)

where d _i is the Euclidean distance from the center of the voxel to the ith focus, σ is the standard deviation of the Gaussian distribution, and Pr(X _i) satisfies 0 ≤ Pr(X _i) ≤ 1. To obtain the probability estimate for the entire voxel volume instead of just its central point, the Gaussian probability density is multiplied by ΔV = 8 mm³ (corresponding to voxel dimensions of 2 mm × 2 mm × 2 mm). If X denotes the event that any foci are located within a given voxel, then it can be shown that Pr(X) is defined as the union of all Pr(X _i), where Pr(X _i) is shown in equation (1). This value is defined as the ALE statistic (see equation [9] in the Appendix).

Permutation tests

The ALE statistic is computed at every voxel in the brain. To make a valid assessment of the significance of the results, a procedure for testing the statistic images was developed. Because no assumptions can be made as to the distribution of the ALE statistic, a nonparametric permutation test [Good,1994] was utilized to test the null hypothesis that the foci are spread uniformly throughout the brain. In this test, x random foci are generated, where x equals the number of foci in the ALE meta‐analysis, and the corresponding ALE values for these random foci are computed. This process of randomization and computation of relabeled statistics is repeated 1,000–5,000 times. The set of ALE values calculated from the random foci form the null distribution of the test statistic. In Turkeltaub et al. [2002], 1,000 permutations were used to determine which tests were statistically significant and threshold the resultant ALE map. A whole‐brain histogram was computed in which the null hypothesis of uniformly distributed foci was rejected for voxels with an ALE value greater than the critical threshold, defined as the 100(1 − α)th percentile of the permutation distribution, where α refers to the desired level of significance.

Modifications to the ALE Approach

When ALE was introduced to the brain imaging community, Turkeltaub et al. [2002] provided discussion of its limitations and areas in need of further development. Several factors that have not been addressed to date are the effects of including articles with different numbers of subjects, varying intensities of activation across different clusters of activation (e.g., t statistics or Z values), or modeling foci using a non‐Gaussian distribution. In addition, it is unknown to what extent the results may be affected by the inclusion of articles that report a different number of activation foci. Any group of studies selected for inclusion in a meta‐analysis will report a different number of foci (n) across experiments. As all foci are weighted equally in the ALE method, this gives stronger influence to those studies that report a larger number of foci. Because obtaining a large number of reported foci is often due in part to a lenient threshold, a greater weighting toward statistically less rigorous studies may occur.

Although the above issues are undoubtedly important, we chose here to attend to the matters of thresholding the ALE maps and performing a statistical comparison of two ALE meta‐analyses. Our first objective thus was to improve upon the permutation test suggested by Turkeltaub et al. [2002] to derive more accurately null distributions for the ALE statistic and implement a correction for the multiple comparisons problem. The second objective was to establish a reliable method for testing for the differences between two ALE meta‐analyses, a goal that is dependent on the conclusions reached in the first objective.

Correction for Multiple Comparisons

According to Turkeltaub et al. [2002], the values from the ALE images were tested against null distributions derived from “all values obtained from all randomizations.” Pooling all values neglects the effects of testing all voxels simultaneously, and does not exert any control over the family‐wise Type I error. Turkeltaub et al. [2002] compensated for using uncorrected P values by applying a conservative threshold of P < 0.0001. Under permutation test theory, there are several options for controlling the rate of false rejections that accompany standard voxel‐by‐voxel testing. We discuss two of these methods, the single threshold test and a procedure that controls the false discovery rate.

Single threshold test

One approach to correcting for multiple comparisons within the framework of permutation testing is to perform a single threshold test and generate the null distribution of the maximal statistic [Holmes et al.,1996; Laird et al.,2002; Nichols and Holmes,2002]. The 95th percentile of the null distribution of the maximal statistic can be used as a threshold on the ALE statistic map; use of this threshold allows one to reject the null at individual voxels while knowing that the chance of family wise error (FWE; one or more false positives) is controlled at 5%. Consideration of the maximal statistic effectively solves the multiple comparison problem because rejection of the omnibus hypothesis is determined by the maximum value of the test statistic over the entire image. That is, extending a voxel‐level permutation test to an image‐level permutation test simply requires considering a statistic that summarizes the voxel statistics, in this case their maximum. For each permutation, instead of recording all voxel statistic values, only the maximal statistic across the brain is recorded. Corrected P values for each voxel are obtained by evaluating the percentage of the permutation distribution for the maximal statistic that is greater than or equal to the voxel statistic.

Controlling the false discovery rate

A second method for correcting for multiple comparisons is to determine an appropriate threshold while controlling the false discovery rate (FDR), defined as the expected proportion of falsely rejected voxels among those rejected [Benjamini and Hochberg,1995; Genovese et al.,2002]. The FDR correction guarantees that in the set of voxels deemed significant for a test of α = 0.05, there are on average no more than 5% voxels that are false positives. In this method, the rate q is specified such that the mean FDR is no larger than q. Typically, q is set to traditional significance levels that range from 0.05 to 0.01. The uncorrected P values from all voxels are ranked from smallest to largest and the image‐wise threshold is declared as the largest P for which:

(2)

where i indexes the ranked P values, V is the total number of voxels, and c(V) is a constant. Two choices exist for this constant: c(V) = 1 for test statistics that have positive regression dependency on the test statistics corresponding to the true null hypothesis, such as in multivariate normal data where the covariance matrix has all positive elements, and c(V)=Σ_i=1 ^V1/i for all other forms of dependency [Benjamini and Hochberg,1995; Genovese et al.,2002].

It was stated previously that permutation tests generally require 1,000–5,000 permutations. In an ALE meta‐analysis corrected for multiple comparisons using the FDR method, the choice of this parameter depends on the desired precision of the voxelwise (uncorrected) P values. For example, if 1,000 permutations are used to generate a null distribution at a particular voxel, and no relabeled statistic was found as large or larger than the observed statistic, then it can be concluded that the voxel in question is characterized by P < 0.001. If the same is observed for 5,000 permutations, then P < 0.0002 for that voxel. The number of permutations in this type of ALE meta‐analysis thus depends on the desired trade‐off between precision and computational time.

We propose that implementing an FDR‐controlling procedure for the permutation test method described above will provide an effective technique for thresholding the ALE meta‐analysis maps by simultaneously minimizing Type I error and maximizing sensitivity. It is our contention that although the single threshold test greatly reduces the rate of false positives inherent in standard voxel‐based hypothesis testing, ultimately this method is too conservative in its estimation of the false‐positive rate. Although the single threshold test's control of the FWE is very specific, it has limited power. The FDR method uses a more lenient measure of false positives, hence has more power. The FDR method is distinguished by the fact that it controls the proportion of false rejections relative to the number of rejected tests, rather than the number of total tests, and thus offers improved thresholding.

Statistical Comparison of ALE Maps

The second goal of this study is to establish a reliable method for testing the differences between two ALE meta‐analyses. A typical meta‐analysis in functional neuroimaging assesses the activation results from a group of similar studies. These studies may investigate neural responses by way of a similar paradigm or within a common behavioral domain. Even in a homogeneous group of studies there exist differences in subject groups, presentation stimuli, or the manner in which tasks are carried out. Further insight therefore may be gained by carrying out a number of sub‐meta‐analyses that contrast the relative properties of different groups of foci.

Several meta‐analyses presented in this issue involve contrasting meta‐analyses in this way. For example, in the stuttering meta‐analysis, the overt speech patterns of controls vs. stutterers were compared [Brown et al.,2005]. The Stroop meta‐analysis separated the studies by verbal and manual response to examine the effects of response type [Laird et al.,2005]. In the picture‐naming meta‐analysis, separate analyses were carried out to test the effect of different baseline conditions [Price et al.,2005]. Lastly, the meta‐analysis of pain studies determined the response‐related differences brought on by stimulating the right versus left side of the body [Farrell et al.,2005].

Each of these groups of foci can be analyzed to produce individual ALE maps. Drawing conclusions based on the results of these meta‐analyses necessitates the ability to compare ALE maps. Although some insight may be gained from visual comparison between maps or overlaying the results on a single image, certain circumstances may call for a formal comparison of the difference between two ALE maps. We propose that assessing the observed difference under the null hypothesis that both sets of coordinates are distributed uniformly will provide a technique for evaluating the differences between ALE meta‐analyses.

MATERIALS AND METHODS

Correction for Multiple Comparisons

We carried out ALE meta‐analyses using a FWHM of 10 mm (corresponding to a σ = 4.2466) on four groups of functional neuroimaging articles for a wide range of topics that included varying numbers of foci: (1) overt speech in stuttering subjects, n =154; (2) the color–word Stroop task, n = 205; (3) picture‐naming tasks, n = 288; and (4) painful stimulation, n = 424. All four ALE maps were thresholded in three ways as described below.

First, the threshold was applied as described in Turkeltaub et al. [2002], using no correction for multiple comparisons. All values from all randomizations were used to generate the null distribution of the ALE statistic. For 5,000 permutations, the null distribution was composed of 5,000 × V values, for V number of voxels.

Second, we carried out the permutation test for each map and recorded the maximum ALE value for each permutation. Once this null distribution for the maximal statistic was generated, we utilized it to determine the appropriate threshold for the ALE maps. According to this test, the null distribution was composed of 5,000 maximal ALE values for 5,000 permutations.

Third, we computed the threshold according to an FDR‐controlled procedure. Whereas the two previous techniques determined an appropriate threshold that was applied to the ALE statistic, the FDR method thresholds the P values at each voxel. To control the FDR in an ALE meta‐analysis, the uncorrected P values thus were computed. To determine the P value at each voxel, voxelwise permutation distributions were computed and P values were extracted by determining the percentile of the observed ALE statistic. To alleviate computational load, uncorrected P values were calculated by tabulating the number of relabeled statistics that were as large or larger than the ALE statistic computed from the real data, divided by the number of permutations. Once the uncorrected P values were obtained, we determined the appropriate threshold according to the FDR method [Genovese et al.,2002]. We chose to use the more conservative, distribution‐free version of FDR in which c(V) = Σ${}_{\mathit{\text{V}}}^{\mathit{\text{i}}\text{=1}}$1/i so that no unwarranted assumptions were made concerning the distribution of P values from the ALE statistic.

For each of these three methods of determining the image‐wise threshold, 5,000 permutations were used to derive the null permutation distributions. The number of random foci used in the permutation tests was equal to the number of foci used to generate the ALE map. Each map was thresholded at P < 0.05 and overlaid onto an anatomical template generated by spatially normalizing the International Consortium for Brain Mapping (ICBM) template to Talairach space [Kochunov et al.,2002]. An additional map was created for each group and thresholded at an uncorrected P < 0.0001 to make a fair comparison of the results presented by Turkeltaub et al. [2002] to the methods that correct for multiple comparisons.

To test further the relative performance of the thresholding techniques, we obtained random sets of foci from the BrainMap database (online at http://brainmap.org/). Using a random experiment number generator in the workspace of BrainMap Search&View, four groups were created: 168 foci, 233 foci, 274 foci, and 347 foci. ALE meta‐analyses were carried out on these randomly grouped foci and the ALE maps were thresholded at P < 0.05 according to the three different methods.

Statistical Comparison of ALE Maps

To determine the difference between two ALE images, consider two groups of foci: group X with n _x number of foci and group Y with n _y number of foci. As discussed previously, calculation of Pr(X) for all voxels gives an ALE map for the coordinates from group X. Likewise, Pr(Y) can be computed in a meta‐analysis of the coordinates from group Y. Subtracting the ALE values calculated from group Y from the those calculated from group X, Pr(X) − Pr(Y), gives a measure of the difference in convergence in the two maps. To test the null hypothesis that the observed difference is zero for two sets of random foci, we carry out a permutation test in which the null distribution for Pr(X) − Pr(Y) is generated using many sets of n _x random foci and sets of n _y random foci.

We divided each of the four meta‐analyses into groups. Subtraction meta‐analyses using a FWHM of 10 mm were carried out for: (1) overt speech in stutterers (n = 154) and controls (n = 73); (2) verbal (n = 153) and manual (n = 52) responses in the Stroop task; (3) silent (n = 149) and speaking (n = 139) baselines in picture‐naming tasks; and (4) right (n = 175) and left (n = 249) painful stimulation. Maps of the differences between each group of foci were created. Separate ALE meta‐analyses were carried out for these groups of studies as well and overlaid onto single image. All images are thresholded at P < 0.05, corrected using the FDR method.

To test the efficacy of this technique, we additionally examined the group of coordinates collected from studies that elicited painful stimulation on the left side of the body (n = 249). These coordinates were divided randomly into two groups (n = 124) and (n = 125) and difference maps were generated for each group. It was hypothesized that the percent of suprathreshold voxels in the resultant difference images would be very small because the difference in ALE maps between such similar groups of foci was expected to be negligible.

Software and Computing Resources

The algorithm for ALE analysis was obtained from Georgetown's Center for the Study of Learning (online at http://csl.georgetown.edu/software/). All ALE meta‐analyses carried out in this study utilized a Java software application that was developed at the Research Imaging Center in San Antonio. In this application, an extension for controlling the FDR rate was added (according to the script available online at http://www.sph.umich.edu/~nichols/FDR/), the statistical comparison for two meta‐analyses was implemented, and a graphical user interface was created. All computations were carried out on a cluster of Macintosh computers using Apple Computer's Xgrid Technology Preview 2 (online at http://www.apple.com/acg/xgrid/). The cluster was comprised of seven Dual 1.8‐GHz Power Mac G5s and three 1.6 GHz Power Mac G5s. Using this Apple cluster markedly decreased the time required to carry out the permutation tests. For example, the ALE meta‐analysis of the Stroop task (n = 205) was carried out in 23 min on the grid (which translates to 3 hr, 56 min on one dual‐processor 1.8‐GHz Power Mac G5). The comparison meta‐analysis of verbal and manual Stroop (153 foci and 52 foci, respectively) was completed in 25 min using the grid, as compared to 4 hr, 14 min on one dual‐processor 1.8‐GHz Power Mac G5.

RESULTS

Correction for Multiple Comparisons

We compared three thresholding techniques on ALE meta‐analysis maps using: (1) uncorrected P values [Turkeltaub et al.,2002]; (2) P values corrected using the single threshold test that requires generation of the null distribution of the maximal statistic [Nichols and Holmes,2002]; and (3) P values corrected using the FDR method [Genovese et al.,2002]. As expected, a much larger number of voxels were deemed significant when using uncorrected P values as compared to corrected P values (Table I). Figure 1 shows the comparison between each thresholding technique for each of the four meta‐analyses carried out: (1) overt speech in stutterers; (2) the Stroop task; (3) picture naming; and (4) painful stimulation. These meta‐analyses were chosen for their varying extent of activation and the total number of included foci. It can be seen that although the use of uncorrected P values results in an acceptable image in Figure 1a (stuttering), this method is not an appropriate choice when involving a large number of foci such as seen in Figure 1d (pain). Conversely, although the maximal statistic method seems an acceptable if somewhat conservative approach in Figure 1d, it is obviously too strict for a smaller number of foci as seen in Figure 1a. Similar results were also obtained for testing the difference between thresholding techniques in groups of random foci (Table II). For the ALE maps that were created with the same threshold (P < 0.0001) used in Turkeltaub et al. [2002], the percent of suprathreshold voxels were 0.136% (stuttering), 0.282% (Stroop), 1.393% (picture naming), and 2.521% (pain).

Table I.

Percent of voxels above threshold P < 0.05

Task (n)	Uncorrected (%)	Single threshold test (%)	FDR (%)
Stuttering (154)	5.956	0.005	1.399
Stroop (205)	7.052	0.051	1.647
Picture naming (288)	8.829	0.401	3.540
Pain (424)	10.462	1.179	4.185

Four meta‐analyses were carried out on a variety of different tasks. Each ALE map was thresholded using uncorrected P values, P values computed using the single threshold test, and false discovery rate (FDR)‐corrected P values. For all meta‐analyses, the single threshold test found the smallest number of voxels to be significant. As expected, using uncorrected P values found the largest number of voxels to be significant.

Figure 1.

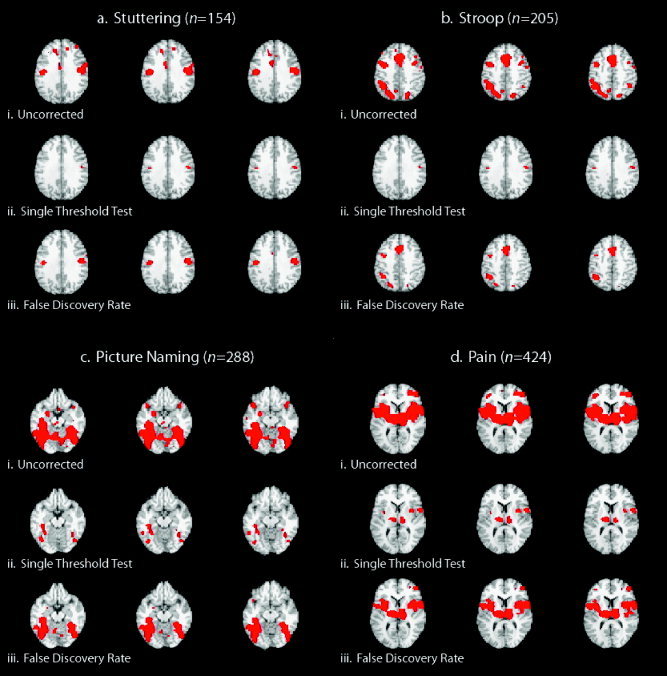
Comparison of different thresholding techniques. Meta‐analyses of overt speech in stuttering subjects (a), the Stroop task (b), picture naming (c), and painful stimulation were carried out (d) and the resultant ALE maps were thresholded in three different ways at P < 0.05: (i) using uncorrected P values; (ii) using P values that were corrected using the single threshold test that generates the null distribution for the maximal ALE statistic; and (iii) FDR‐corrected P values. Three contiguous slices are presented for each meta‐analysis result: z = 28–32 mm for stuttering; z = 40–44 mm for Stroop; z = −16 to −12 mm for picture naming; and z = 6–10 mm for painful stimulation (n, number of foci)

Table II.

Percent of voxels above threshold P < 0.05 in meta‐analyses of random foci

Group (n)	Uncorrected (%)	Single threshold test (%)	FDR (%)
1 (168)	6.360	0.025	1.175
2 (233)	6.477	0.004	1.273
3 (274)	6.311	0.007	1.050
4 (347)	7.364	0.353	1.848

Four meta‐analyses were carried out on random sets of foci generated in the BrainMap database environment. Each ALE map was created according to the three methods of thresholding. Again, all meta‐analyses found that correcting P values using the false discovery rate (FDR) method most effective fsin minimizing Type I error while maximizing sensitivity.

Statistical Comparison of ALE Maps

We carried out individual ALE meta‐analyses for each of the eight subgroups of foci and overlaid each pair of maps onto a composite image. Figure 2i presents overt speech (a) in stutterers (yellow) and controls (blue), the Stroop task (b) with verbal (yellow) and manual (blue) responses, picture‐naming tasks (c) with silent (yellow) and speaking (blue) baselines, and painful stimulation (d) to the right (yellow) and left (blue). In this Figure the color green indicates the regions of overlap between the separate meta‐analyses. Figure 2ii presents the results of the comparison meta‐analyses for these same subgroups. The yellow and blue regions still refer to the groups of foci specified above, but now indicate regions in which there exists a statistical difference between subgroups. Regions of overlap (areas in which ALE values were significant for both meta‐analyses) are no longer seen. This was expected, as the difference between the ALE values in these regions was not determined to be significant.

Figure 2.

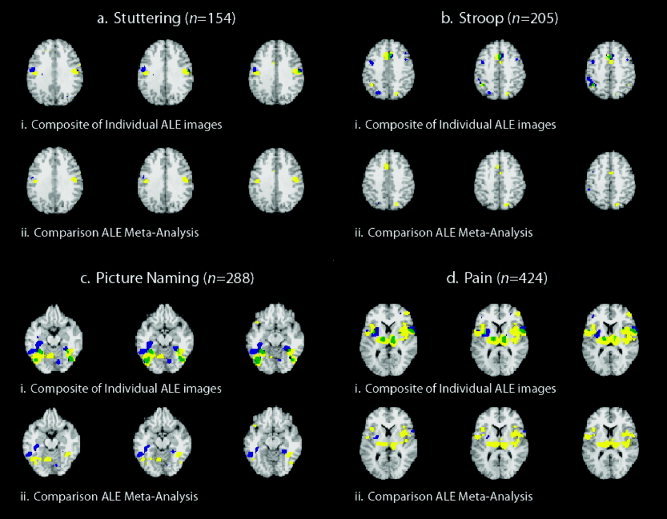
Statistical comparisons of ALE maps. ALE meta‐analyses (P < 0.05) for different groups of foci were carried out and are presented here as overlays of separate meta‐analyses (i) or as comparison meta‐analyses computed as a single ALE image (ii). Meta‐analyses carried out were for overt speech (a) in stuttering subjects (yellow) and controls (blue), the Stroop task (b) with a verbal (yellow) and manual (blue) responses, picture‐naming tasks (c) with a silent (yellow) or speaking (blue) baselines, and painful stimulation to the right (d) (yellow) and left (blue). Green indicates overlap between the individual meta‐analyses (blue + yellow). Three contiguous slices are presented for each meta‐analysis result: z = 28–32 mm for stuttering; z = 40–44 mm for Stroop; z = −16 to −12 mm for picture naming; and z = 6–10 mm for painful stimulation. (n, number of foci).

In comparing groups of similar coordinates obtained from studies of painful stimulation on the left side of the body, the average percentage of suprathreshold voxels was 0.996%, with a standard deviation of 0.173%. In contrast, the difference image between right (n = 175) and left (n = 249) painful stimulation resulted in 2.072% of voxels above threshold. In the comparison of silent (n = 149) and speaking (n = 139) baselines in picture‐naming tasks, the percentage of voxels above threshold was 1.596%, which is perhaps a more relevant comparison to the two groups of left pain coordinates in terms of the number of included foci.

DISCUSSION

Correction for Multiple Comparisons

We have presented three methods of assessing statistical significance in an ALE meta‐analysis of functional neuroimaging data. Figure 1 gives evidence to the large effect that the number of foci has on the ALE meta‐analysis results. A relatively large number of total foci will result in relatively large clusters of significant activation likelihood. The single threshold test proved to exert very strong control over Type I error and considerably reduced the number of significant voxels in both random groups of foci and groups obtained from similar studies in the literature. As the number of foci included in a meta‐analysis increases, it becomes more difficult to control Type I error. As the number of foci decreases, it is apparent that the single threshold test is not capable of controlling Type II error. Although maximal statistic correction reduces the high rate of false positives that occur when testing voxelwise hypotheses, this method exerts strong control over Type I error in that the chance of rejecting one or more voxels in which the null hypothesis is true is less than or equal to α. Due to the adaptive nature of the method, thresholding ALE maps using FDR‐corrected P values represents an excellent compromise between using uncorrected P values and applying a threshold that is too conservative using the single threshold test.

Although applying a conservative threshold to uncorrected P values was effective for Turkeltaub et al. [2002] whose meta‐analysis used only 172 foci, this is not an appropriate solution for ALE thresholding, especially for large meta‐analyses (n > 250). It is clear that thresholding the ALE maps at P < 0.0001 (uncorrected) produced results that most closely matched the FDR‐corrected results. When establishing the relative performance of these three different methods of thresholding, comparisons should be made for images in which the same threshold has been applied (P < 0.05). Even though the ALE maps thresholded at P < 0.0001 (uncorrected) and P < 0.05 (corrected using the FDR method) may seem similar, we argue in support of the latter method as it is statistically more valid.

Turkeltaub et al. [2002] provided a thorough discussion of the ALE method. When comparing their meta‐analysis results to results from an fMRI study, a trend was noticed toward high ALE values in more centrally located voxels in the brain. This bias was attributed to the fact that voxels located deeper in the brain are more likely to have higher ALE values than are voxels on the edge of the brain, because voxels deep within the brain have a larger number of existing neighbors in which activation foci may be located. Employing voxelwise null distributions in the FDR method corrects for this central drift tendency because individual distributions of the ALE statistic are estimated with respect to each voxel, rather than relying on a single whole‐brain distribution.

It is clear that ALE results are dependent on the number of foci in the analysis, and the FDR method is the best choice for thresholding ALE maps for both large and small number of foci. Although the dependency on n causes some difficulty when assessing and making inferences on the results of a meta‐analysis of 75 foci and another of 375 foci, it is not necessarily an artifact that invalidates the ALE method itself. Rather, it exemplifies the difference between testing for statistical significance and examining the effect size. The number of foci is not a direct factor in the ALE meta‐analysis but rather an indirect result of the heterogeneous state of the current design standards in functional neuroimaging. That is, the number of foci produced in any single contrast is a direct result of many factors, such as the number of subjects studied, selected statistical threshold, statistical power of the imaging paradigm, or the smoothness of the data. These factors are interrelated and affect the outcome of any individual activation study. Pooling multiple studies and searching for function‐location correspondences will always be limited by these differences, but just in the same way that individual studies are also limited. Each factor that contributes to the diverse nature of the meta‐data in a complicated and coupled fashion is a result of the meta‐data itself and represents a side effect of the larger problem of noncompliance to rigid standards in data reporting. We do not suggest a mechanism for normalizing ALE meta‐analyses by the number of foci, despite the fact that this would facilitate comparison among meta‐analyses. Instead, we suggest that the dependence on this parameter should be preserved as a valuable indicator of the robustness of the meta‐analysis results.

A question that should be addressed is the minimum number of foci required for an ALE meta‐analysis. One factor that influences this issue is the nature of the pooled studies. Studies that probe sensory tasks such as simple auditory or visual stimulation typically only observe activation in a few primary sensory regions. More complex cognitive tasks tend to activate a larger network of cortical regions that often extend across multiple lobes; thus, a meta‐analysis of sensory studies will typically require a fewer minimum number of foci than a meta‐analysis of a cognitive task would, because fewer nodes are involved in these systems. For example, a meta‐analysis that included 82 foci from studies that investigated activation due to monaural auditory stimulation revealed robust agreement in the primary auditory cortex [Petacchi et al.,2005]. In contrast, the results of the meta‐analysis on the Stroop task with a manual response displayed weaker concordance results as it included only 52 foci spread throughout the brain.

At the essence of this question is the issue of how many foci located within a few millimeters are necessary for convergence of an ALE cluster. Unfortunately, this answer is linked directly to the number of total foci being pooled because the FDR method is adaptive to the signal strength of each individual data set. For small numbers of foci, as few as three to four nearby coordinates may contribute to a significant ALE cluster. Meta‐analyses of larger numbers of foci will require greater pooling of clusters of proximate foci to constitute significant ALE peaks. We thus cannot resolve the issue of a minimum number of foci to any finite degree. Instead, we point out that the type of task and degree of consistency across results all contribute to the answer and must be inspected on a case‐by‐case basis.

Statistical Comparison of ALE Maps

We have described a statistical method above for testing the difference between two ALE meta‐analyses. Ideally, this technique will encourage the development of advanced meta‐analysis design. The potential use of this technique of comparing meta‐analyses can be illustrated using the meta‐analysis of picture naming presented by Price et al. [2005].

Friston et al. [1996] and Price et al. [1997] have shown that cognitive subtraction is not always effective in isolating the cognitive process of interest in cases where the application of the pure insertion principle may be unwarranted due to nonadditive factors. In such cases, factorial analysis is useful in determining both the main effects and interactions of interest.

The picture‐naming meta‐analysis first pooled all coordinates obtained by contrasting an activation condition (naming) to a baseline condition, regardless of response type. A secondary analysis was carried out in which picture‐naming foci were split into four groups:

• Group A: overt naming, silent baseline.

• Group B: covert naming, silent baseline.

• Group C: overt naming, speaking baseline.

• Group D: covert naming, speaking baseline.

Price et al. [2005] focused on the main effect of all studies that pooled data from all four groups and the main effect of baseline by comparing Groups A + B with Groups C + D. However, using this design, it would also have been possible to extract the main effect of overt vs. covert responses (A+C) – (B+D) and the interaction between the effect of baseline and the effect of overt vs. covert (A−B) – (C−D). This would conform to a classical analysis of a factorial design [Friston et al.,1996]. It is our hope that future meta‐analyses will incorporate advanced designs of this type and thus promote the growth of new methods in the field of meta‐analysis.

Caution should be exercised when carrying out formal comparisons of ALE meta‐analyses when the groups are disparate in total number of foci. In these cases, it is impossible to say with any certainty whether the difference maps reflect activation difference across groups of studies or simply show the effect of one group having a greater number of coordinates. To circumvent this, a subset of random experiments should be extracted from the larger set and used as foci for generating the difference map. In the meta‐analysis of the n‐back task [Owen et al.,2005], the n‐back coordinates were divided into two groups based on the presentation of verbal or nonverbal stimuli. Significantly more studies used verbal stimuli (21 contrasts with 226 foci) and nonverbal stimuli (9 contrasts with 76 foci), thus a random subset of verbal coordinates were selected to be compared against the nonverbal group. Instead of choosing 76 random foci, we randomly chose 9 contrasts to preserve the overall structure of the data. The comparison between verbal and nonverbal stimuli in the n‐back task therefore included 76 nonverbal coordinates and 106 randomly chosen verbal coordinates, which reduced the disparity in number of foci. Optimally, many iterations of choosing random subsamples should carried out to characterize fully the difference between the two maps.

CONCLUSIONS

The ALE method was extended to include a correction for the multiple comparisons problem that controls the FDR. In addition, we presented a quantitative technique for assessing the difference between two meta‐analysis images to facilitate advanced ALE meta‐analyses. We chose to address these two issues rather than undertaking some of the other concerns raised by Turkeltaub et al. [2002] because we felt the need for these specific developments was most pressing. Future work will test the feasibility of incorporating a weighting factor for the number of subjects in each study and the intensity of activation for all clusters into the ALE algorithm.

Computation of the ALE statistic

Each reported coordinate (focus) is modeled by a three‐dimensional Gaussian distribution, defined by a user‐specified FWHM. Let X _i denote the event that the ith focus is located in a given voxel. The probability of X _i occurring at voxel x, y, z is

(a.1)

where d _i is the Euclidean distance from the center of the voxel to the ith focus, σ is the standard deviation of the Gaussian distribution, and Pr(X _i) satisfies 0 ≤ Pr(X _i) ≤ 1. In order to obtain the probability estimate for the entire voxel volume, instead of just its central point, the Gaussian probability density is multiplied by ΔV = 8 mm³ (corresponding to voxel dimensions of 2 mm × 2 mm × 2 mm)

Let X denote the event that any foci are located within a given voxel. For mutually exclusive events, this probability is equal to

(a.2)

for n foci. However, since it is possible to have two clusters of activation from different experiments that have centers of mass located in the same voxel, the events X _i are not mutually exclusive. Thus, it is reasonable to assume that these events are independent. The probability Pr(X) is defined as the probability of the union if all X _i

(a.3)

(a.4)

De Morgan's law states that for two events, A and B, the complement of their union is equal to the intersection of their individual complements. That is,

(a.5)

Thus,

(a.6)

For independent events X _i

(a.7)

Thus, the probability that any foci are located within a given voxel is defined as

(a.8)

(a.9)

where Pr(X _i) is defined above in equation [a.1].