Formal characterization and extension of the linearized diffusion tensor model

Abstract

We analyzed the properties of the logarithm of the Rician distribution leading to a full characterization of the probability law of the errors in the linearized diffusion tensor model. An almost complete lack of bias, a simple relation between the variance and the signal‐to‐noise ratio in the original complex data, and a close approximation to normality facilitated estimation of the tensor components by an iterative weighted least squares algorithm. The theory of the linear model has also been used to derive the distribution of mean diffusivity, to develop an informative statistical test for relative lack of fit of the ellipsoidal (or spherical) model compared to an unrestricted linear model in which no specific shape is assumed for the diffusion process, and to estimate the signal‐to‐noise ratios in the original data. The false discovery rate (FDR) has been used to control thresholds for statistical significance in the context of multiple comparisons at voxel level. The methods are illustrated by application to three diffusion tensor imaging (DTI) datasets of clinical interest: a healthy volunteer, a patient with acute brain injury, and a patient with hydrocephalus. Interestingly, some salient features, such as a region normally comprising the basal ganglia and internal capsule, and areas of edema in patients with brain injury and hydrocephalus, had patterns of error largely independent from their mean diffusivities. These observations were made in brain regions with sufficiently large signal‐to‐noise ratios (>2) to justify the assumptions of the log Rician probability model. The combination of diffusivity and its error may provide added value in diagnostic DTI of acute pathologic expansion of the extracellular fluid compartment in brain parenchymal tissue. Hum. Brain Mapping 24:144–155, 2005. © 2004 Wiley‐Liss, Inc.

INTRODUCTION

Although the functions relating the magnetic resonance signal with a diffusion tensor in diffusion tensor imaging (DTI) have a nonlinear nature, they are linearized frequently to benefit from the technical simplicity of the transformed model [Anderson, 2001; Basser et al., 1994; Papadakis et al., 1999]. One direct advantage of a linear model is that under some mild assumptions, least squares estimates have optimal properties such as lack of bias and low variance [Rawlings et al., 1998]. Additionally, if the assumptions of normality and independence of the errors are met, they can be used to derive the distributional properties of the least squares estimates of the parameters. Normality of the residuals has been assumed frequently in the linearized diffusion tensor model to explore some of the statistical features of the estimated tensor [Anderson, 2001; Papadakis et al., 1999].

It is well known that due to the nonlinear transformations involved in the construction of the intensity images from the original complex data, the noise will be described properly by a Rician probability law [Rice, 1944; Sijbers et al., 1998]. Fortunately, unless the signal‐to‐noise ratio (SNR) is very low, the Rician distribution can be approximated closely by a normal distribution [Pajevic and Basser, 2003; Sijbers et al., 1998]. However, when logarithms are applied to the intensity values to obtain the linear equations, their probability law changes (it is not Rician anymore) and the normal approximation may not be tenable. Moreover, it is not even clear that the expectation of such a “log Rician” probability law will equal the real intensity, i.e., that the errors in the observed intensities will be centered at zero, which may lead to systematic biases in the least squares estimates of the tensor values.

On the other hand, despite extensive work in the development of new descriptors to summarize the properties of diffusion, proper statistical methods to assess the uncertainty of basic quantities such as the mean diffusivity remain missing. Indeed, assessment of the accuracy of any estimated quantities will be crucial to draw reliable conclusions from them.

Two different causes may lead to high levels of error in estimates of the components of the tensor. Either the acquired data is quite noisy, with high levels of error without any structure (in which case no other model will better describe the data), or it may be that although noise levels are rather low, the ellipsoidal (or spherical) model does not describe the structure of the data adequately. Lack of fit tests should be carried out to discriminate between the two situations described above. In fact, several authors have proposed lack of fit tests for DTI models. Basser et al. [1994] thus devised a test to assess the lack of fit of the spherical model by comparing it with the more flexible ellipsoidal model, i.e., a test to check for anisotropy. Alexander et al. [2002] proposed a similar test to discriminate among models of increasing complexity derived from truncation of the spherical harmonic expansion.

Finally, a multiple comparisons problem will arise if the results of many tests are analyzed simultaneously. Although classic solutions have been available for many years (such as the Bonferroni correction), they lead to overconservative corrections when the number of tests is particularly large (which is the case for tests applied at the voxel level). Recently, a new approach based on controlling the expected proportion of false positives has overcome this problem. Indeed, the false discovery rate method (FDR) [Benjamini and Hochberg, 1995; Benjamini and Yekuteli, 2001] already has been applied successfully in other modalities of magnetic resonance imaging (MRI) [Genovese et al., 2002].

In this study, we develop further several aspects of the statistical framework of DTI: (1) we analyze statistical properties of the logarithm of the Rician distribution; (2) we combine this new probability law with the deterministic equations of DTI and define weighted least squares (WLS) estimators of the parameters; (3) we also find the statistical distribution of the errors of mean diffusivity; and (4) we define and implement a test for relative lack of fit of the ellipsoidal (or spherical) model using an algorithm to control the FDR over multiple dependent tests at voxel level. Finally, these methods are applied to three datasets of clinical interest: a healthy volunteer, a patient with acute brain injury, and a patient with hydrocephalus.

SUBJECTS AND METHODS

Diffusion Tensor Imaging

Subjects

Informed consent was obtained before scanning from a healthy volunteer and from the patient with hydrocephalus. For the patient with head injury, assent to these studies was obtained from the next of kin. This study was approved by the Local Research Ethics Committee of Addenbrooke's Hospital NHS Trust, Cambridge, UK.

The healthy volunteer was a 37‐year‐old man with no history of neurologic problems. The patient with acute head injury was a 36‐year‐old man who had suffered a severe traumatic brain injury after falling down a flight of stairs. Computed tomography images demonstrated bifrontal cerebral contusions, which were more severe on the right. MR imaging, including DTI, was carried out on posttrauma Day 5. The T2‐weighted image demonstrated low signal in the right frontal lobe consistent with blood products surrounded by an area of increased signal. There was also effacement of the frontal horn of the right lateral ventricle and the white matter of the left frontal lobe demonstrated increased signal, presumably due to edema. The patient with hydrocephalus was a 77‐year‐old man with a history of cognitive decline, decreased mobility, and incontinence. A computerized infusion study demonstrated a resistance to outflow R_CSF = 25.89 mm Hg ml⁻¹ min⁻¹ and a pressure to volume index (PVI) of 21.07 ml, indicative of hydrocephalus.

Data acquisition

DTI data were acquired using a 3‐T whole body magnet (Oxford Magnet Technology, Oxford, UK) connected to a Bruker console (Bruker Medspec 30/100 spectrometer; Bruker Medizintechnik, Etlingen, Germany). A single‐shot spin‐echo (SE) echoplanar imaging (EPI) technique was used, with Stejskal‐Tanner diffusion sensitizing pulses [Stejskal and Tanner, 1965]. Imaging parameters were: TR = 5,070 ms; TE = 107 ms; α = 90 degrees; δ = 21 ms; and Δ = 66 ms. Eight interleaved, 5‐mm thick, supratentorial slices were acquired with a phase template in a near axial plane, using a 128 × 128 matrix and field of view (FOV) of 25 × 25 cm. For each slice, images were collected from 12 non‐collinear gradient directions (Papadakis et al. 1999) with the following spherical angles (in degrees): (53, 19), (20, 274), (61, 76), (59, 124), (48, 238), (42, 157), (68, 307), (73, 184), (72, 335), (18, 42), (88, 218), and (82, 268). For each gradient direction, an unweighted b ₀ image and five diffusion‐weighted images were collected at equally spaced b‐values in the range b _min = 318 s/mm² to b _max = 1,541 s/mm².

Ideal DTI Model Without Noise

Under the ideal situation of no noise, the link between a given signal intensity (ϕ_i) and the tensor (D) has been modeled through an exponential function [Basser et al., 1994; Papadakis et al., 1999]

(1)

in which b _i is the b‐value used (a parameter directly linked to the magnitude of the gradients [see Stejskal and Tanner, 1965]), ϕ₀ is the intensity to be found when the b‐value is zero, and g _i is the unit length vector pointing to the direction of acquisition

(2)

The model of equation (1) can be linearized by applying logarithms

(3)

and by further developing the quadratic form, it can be given as a simple linear equation

(4)

where

(5)

is a known vector and β = (β₁ … β₇)′ is a column vector containing the unknown value of logϕ₀ (denoted as β₁) and the six unknown parameters of the tensor, coded as

(6)

Finally, all n equations describing the intensities for a given voxel can be presented as a single linear system

(7)

where Φ is the column vector containing the n intensities and X is the matrix with ith row equal to the respective x _i vector (i: 1, …, n).

Log Rician Model for DTI Noise

In the ideal situation of zero noise, the values from β would be obtained by solving the deterministic linear system of equation (7). However, the observed intensities are naturally contaminated by noise and these equations do not hold anymore.

Under the supposition of no motion or other artifacts, the main source of noise in MR images is thermal noise [Haacke et al., 1999]. Although the structure of such noise in the originally acquired complex data is assumed to be Gaussian, the nonlinear transformation involved in the construction of the image of intensities leads to a Rician probability law for the observed intensity z _i [Rice, 1944]:

(8)

where I ₀ is the modified zero‐order Bessel function, σ${}_{\text{2}}^{\mathit{\text{i}}}$ is the variance of the noise in the original complex data, and ϕ_i is the actual unknown intensity (the norm of the complex vector with real and imaginary parts Re [ϕ_i] and Im[ϕ_i]). However, when the logarithm is applied to linearize this equation, i.e., y _i = log(z _i), the probability law changes again. Applying the general rule for transformed laws

(9)

leads to

(10)

Its expectation can be obtained analytically by E(y_i) = ∫${}_{\text{∞}}^{\text{0}}$ log(z_i)f_Z(z_i)dz_i, giving

(11)

where the integral is an incomplete gamma function with ϕ${}_{\text{2}}^{\text{i}}$/2σ${}_{\text{2}}^{\text{i}}$ as the lower boundary. Now, if we define the error as the difference between the actual logϕ_i and the observed log‐intensity (y _i), i.e.,

(12)

its probability law can be obtained using the same principles of equation (9), leading to

(13)

Interestingly, this law has the convenient property of depending solely on ρ_i = ϕ_i/σ_i, which is a measure of SNR in the originally acquired data, and equation (13) can be rewritten as

(14)

Figure 1 shows the shape of equation (14) for different values of the SNR. As the SNR increases, the function becomes more symmetrical and gets closer to a Gaussian law. As a consequence of the unique dependence of equation (14) on ρ_i, its expectation and variance will also only depend on ρ_i. The expectation can be derived directly from equation (11):

(15)

Figure 1.

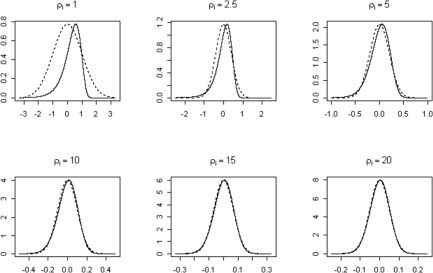
Plots of the log Rician probability distribution of the errors of the linearized tensor model (solid line) assuming different values of the SNR, ρ_i. As SNR increases, the error distribution conforms closer to a normal distribution (broken line) with mean zero and standard deviation equal to the inverse of the SNR, i.e., N(0, ρ${}_{\text{−1}}^{\mathit{\text{i}}}$).

As shown in Figure 2a, it drops almost to zero for moderate values of ρ_i:

(16)

Figure 2.

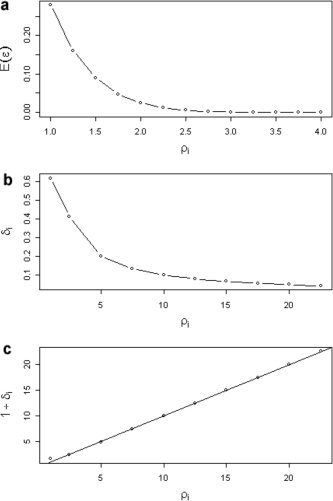
Properties of the log Rician error distribution as a function of SNR. A: Plot showing the sharp drop (to zero) of the expectation of the error derived from the log Rician distribution as the SNR ρ_i increases. B: The standard deviation of the errors δ _i also declines monotonically as a function of increasing SNR,ρ_i. C: There is a simple relation of identity between SNR ρ_i and standard deviation of the errors δ _i, provided SNR is at least moderately high.

This is equivalent to the fact that E(y_i) ≈ log(ϕ_i) for moderate values of SNR, i.e., the observed log‐intensities will be centered around the unknown real values. Finally, the variance of the law of equation (14) (which is obviously the same as the variance of equation [10]) cannot be given analytically and should be obtained by numerical integration. Figure 2b shows the values of the standard deviation of ϵ_i (δ _i) as a function of ρ_i. Interestingly, as is shown graphically in Figure 2c, an extremely simple equality holds true for moderate and high values of ρ_i:

(17)

Weighted Least Squares Algorithm for Model Parameter Estimation

Once both the deterministic model and the probabilistic model for the noise have been developed, they can be combined in a single model to estimate parameters of the tensor. First, all n intensities (see equation [12]) observed in a voxel are summarized in a single equation

(18)

with Y being the vector of n observed log‐intensities and ϵ being the vector of n independent error terms distributed under the log Rician probability law of equation (14). Equation (18) may now be combined with the deterministic model of equation (7) to give

(19)

As seen in the previous section (equations [(16), (17)]), for moderate values of ρ_i it can be assumed realistically that

(20)

and

(21)

If the variance of noise in the original complex data is now considered constant (σ${}_{\text{2}}^{\text{i}}$ = σ²) for all n intensity measurements of a given voxel, which seems a reasonable assumption because the main error source is usually the bandwidth used in the receptor system [Haacke et al., 1999], equation (21) may be given as

(22)

where I is the identity matrix.

The model characterized by equations (19), (20), and (22) clearly resembles the type of model for which the weighted least squares estimators (WLS) are optimal (in terms of minimum variance and bias of the estimates) [Rawlings et al., 1998]. Here, (IΦ)⁻² is not known and should be estimated beforehand. Because the ordinary least squares (OLS) estimates remain unbiased under inequality of variances, they can be used to give a preliminary estimate of Φ:

(23)

and this vector can be used in equation (22) to approximate the weighing matrix

(24)

required for the WLS estimates of β and σ² [Rawlings et al., 1998]

(25)

(26)

Not only the tensor components and logϕ₀ are estimated, but also the variance of the noise in the original data, σ². At some extra computational cost there is also the possibility of improving initial estimates of the weighting matrix by obtaining iterated estimates of expected intensities. Specifically, the estimate of expected intensities found at the end of the second step can be substituted iteratively in equation (24) to refine incrementally the estimated weighting matrix.

Assessment of Uncertainty of Mean Diffusivity Estimates

The standard theory on WLS can be used to give formulas for the expectation and variance of

(27)

and

(28)

Additionally, for moderate values of ρ_i, the probability law for the errors clearly approaches a normal distribution (see Fig. 1). This fact will lead also to the approximate normality of .. Thanks to the invariance property of the trace of a matrix, the mean diffusivity [Basser and Pierpaoli, 1996] can be estimated directly from the trace of the fitted tensor

(29)

Because M̂ is a linear combination of some elements in , the normality of will also lead to the normality of M̂. Specifically, taking equations (27) and (28) into account, it can be shown easily that

(30)

where

(31)

In equation (28) σ² is unknown and the estimate given by equation (26) should be used instead, leading to

(32)

Next, the ratio

(33)

will approximately follow a t distribution with n − (7 + 1) degrees of freedom (df), and this may be used to give a confidence interval for the mean diffusivity

(34)

Other simple but quite useful statistics may be obtained from those shown above. The coefficient of variation of the mean diffusivity CV = (M̂)/M̂ is a measure of error standardized by the mean, and the range of the confidence interval 2t_(n−p,α/2) 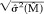is an alternative scalar measure of dispersion.

Because all statistics described in this section are quantified for each voxel of the dataset, the total set of values can be displayed informatively as images. High levels of error in these statistic images may suggest local inadequacy of the diffusion model. With this in mind, a new test for lack of fit of the commonly used ellipsoidal diffusion model is proposed below.

Statistical Test for Goodness of Fit of Ellipsoidal (and Spherical) Models of the Tensor

The theory of linear models can be used to choose between two linear models [Christensen, 1996]. Provided that one model is a submodel of the other, in the sense that

(35)

where C(X _i) is the subspace spanned by the columns of X _i, a statistical test can be used to decide whether the reduced submodel is as good as the extended full model. Such a test requires the previous fitting of the full model (full) and the reduced submodel (sub) to calculate the sum of squares of the error (SS _E)

(36)

for both models. It also requires the degrees of freedom of the error df _E given by n − Dim(C[X _i]). Under the null hypothesis that the reduced model is as good as the full model, the ratio

(37)

will then follow an F probability distribution with [df _E(sub) − df _E(full)] and df _E(full) degrees of freedom [Christensen, 1996].

We wish to test the relative goodness of fit of an ellipsoidal (reduced) model of diffusion compared to an unrestricted (full) model that imposes no prior constraints on direction of diffusion in a voxel. To do this, we must first prove that the subspace spanned by the columns of the design matrix of the restricted model is contained in the subspace of the design matrix of the full model, i.e., equation (35) holds true. If we start with the linearized model for a single direction k, where the intensities will depend only on the b values applied (given as a vector B) and the unknown diffusivity γ_k in the given direction, we have

(38)

where Y _k is the vector of logarithms of intensities obtained for the kth direction, 1^j is a column vector of ones of order j (j being the number of b values), and ζ_k is the unknown vector of errors (with the same properties as ϵ in equation [18]). If we make the obvious assumption of a unique ϕ₀ and the same B for all m directions sampled, we can combine the model of equation (38) for all m directions in a single linear model

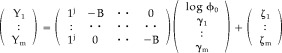(39)

that may be given in a simpler form as

(40)

We then need to prove that

(41)

where X is the design matrix of equation (19). We first divide the rows of X into m submatrices linked to the m directions

(42)

For any direction k, we have

(43)

where

(44)

and the components of r are, in turn, defined by the components of the unit length vector giving the direction (see equation [2]). In consequence, the extensive form for the ellipsoidal model is

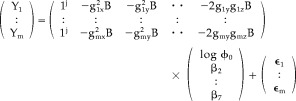(45)

from which it may be shown that each column of X is a linear combination of columns of Z. Indeed, besides the trivial case of the column of ones present in both matrices, any other column of X is a linear combination of the rest of the columns of Z:

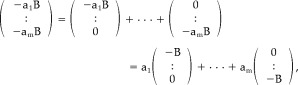(46)

the a _k being any of the scalars in the vector of equation (44).

By showing that all columns of X are linear combinations of columns of Z, equation (41) is proved and we have shown that an ellipsoidal model is properly comparable to the unrestricted linear model using the F ratio, equation (37), for inference. Because the spherical model exists in a subspace of the ellipsoidal model, an analogous argument can be made to use equation (37) to test its relative goodness of fit, i.e., to test the spherical model against the unrestricted linear model. By the same token, it must be understood that the test is limited to comparison of nested linear models; it cannot be used, for example, to compare goodness of fit of linear and nonlinear models. Finally, it should be noted that the weighting matrix W of equation (36) has to be the same for both the full model and the restricted model. In fact, W will be estimated previously from the full model as defined by equations (23) and (24).

Correction for Multiple Comparisons by the FDR

If this test is applied to a large number of spatially correlated voxels, a probabilistic threshold for statistical significance that accounts for multiple, nonindependent comparisons will be strictly necessary. We can define an acceptable voxel‐wise significance threshold in terms of the overall FDR for dependent tests [Benjamini and Yekuteli, 2001]. First, the individual P values for each of the n voxels tested are sorted in ascending order

(47)

An upper limit (q) for the acceptable proportion of false positive tests is then arbitrarily set, e.g., q = 0.01. Next, the number of null hypotheses to be rejected is given by a simple rule

(48)

Finally, all tests (voxels) with a p‐value equal or smaller than p(k) are considered significant (this is equivalent to rejecting the first k tests as ordered in equation [47]).

WLS Estimation of SNRs

All statistical methods developed in the previous subsections rely on the approximate equalities given by equations (16) and (17). The accuracy of these equalities, in turn, depends on the SNRs in the original data, ρ_i. Specifically, as ρ_i decreases, the accuracy of the results will also diminish (see Figs. 1 and 2). Consequently, although the results obtained from the proposed methods may remain quite informative under low signal‐to‐noise conditions, the exact numerical values will be less reliable and more biased.

Usefully, WLS estimators can be extended to estimate ρ_i for any voxel in all the input intensity images through

(49)

where _i is the WLS estimate of its respective vector in the unrestricted linear model of equation (40) and _i is the square root of the estimate of the variance of the same model (both quantities are estimated when testing for lack of fit of the ellipsoidal or spherical models).

Because accuracy of these signal‐to‐noise estimators relies also on the assumptions of equations (16) and (17), low values estimated by equation (49) would be less accurate. Finally, the lowest SNRs are expected in images created with the highest b‐value. Estimating ρ_i in these images first will be the most efficient way to check the general reliability of the results.

RESULTS

Healthy Volunteer Dataset

Statistic images obtained by applying the proposed methods to analysis of one slice of the image of the healthy volunteer are shown in Figure 3. Some patterns observed in the image representing the range of the 95% confidence intervals for the mean diffusivity (Fig. 3b) are correlated positively with the features observed in the image of estimated mean diffusivities (Fig. 3a). An obvious example of this is provided by the “ghost,” highlighted by the green region in the lower part of the images, which has both high mean diffusivity and high error.

Figure 3.

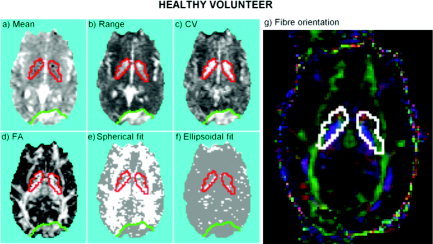
Healthy volunteer: statistic images estimated in a single slice of DTI data. A: Mean diffusivity. B: Range of the confidence interval of mean diffusivity. C: Coefficient of variation (CV). D: Fractional anisotropy (FA). E: Test for goodness of fit of spherical (isotropic diffusion) tensor model: voxels where the null hypothesis has been rejected are colored white, FDR is controlled at 1%. F: Test for goodness of fit of ellipsoidal model: voxels where the null hypothesis has been rejected are colored white, FDR is controlled at 1%. G: Fiber orientation map, highlighting juxtaposition of differently orientated tracts in the bilateral subcortical regions of interest (delimited by red lines) that are characterized by low mean/high error diffusivity.

However, this correlation between mean diffusivities and their errors is not always evident (or at least does not have the same strength), as is shown by the inhomogeneities in the image of the coefficient of variation (CV; Fig. 3c). To put it another way, there are some patterns observed in the image of the range of confidence intervals that are not noticeable in the image of the mean diffusivities. In particular, two symmetric regions (highlighted in red) have estimated diffusivities similar to these in the surrounding areas (Fig. 3a) but clearly higher errors than them (Fig. 3b,c).

Although the shape and location of these two symmetric regions is clearly related to the basal ganglia, the image of estimated fractional anisotropies (FA; Fig. 3d) also suggests a high density of myelinated fibers. Despite this, as shown by the test for isotropy or goodness of fit of a spherical diffusion model thresholded to control the FDR at 1% (Fig. 3e), these regions also contain a considerable number of voxels that conform to the spherical model. Such agreement with the spherical model is not caused simply by a low anisotropy (which would have to be visible in the FA image). Instead, it is probably a result of a higher level of noise that has led to locally lower statistical power and thus to an inability to reject the null hypothesis of isotropy, i.e., that the spherical model is as good as the full model.

Although the test for a significant difference in goodness of fit between ellipsoidal and unrestricted models was not refuted often (Fig. 3f; FDR = 1%), implying that the ellipsoidal model was generally adequate to explain diffusion processes in these data, there were a number of highly anisotropic voxels in these subcortical regions where the ellipsoidal model provided a relatively poor fit. One interpretation is that there may be contiguous fiber tracts of different orientations in these regions. This is consistent with the fiber orientation map (see Fig. 3g, where fiber orientation was estimated by the first eigenvector of the estimated ellipsoids [Pajevic and Pierpaoli, 1999]), indicating that anteroposterior tracts (green voxels) are juxtaposed with a superoinferior tract (probably the internal capsule; blue voxels) in the medial edges of these regions.

In general, it is important to emphasize that failure to refute either the spherical or ellipsoidal models in these data does not prove that the reduced model in question is the correct model for local diffusion but merely that, given the levels of noise in the data, there is no significant improvement to be gained by a less restricted model.

Acute Brain Injury Patient

Areas of edema caused by a massive head injury are shown, encircled by a blue line, in Figure 4. As observed in the healthy volunteer image, although there are some similarities between the image of estimated mean diffusivities (Fig. 4a) and the image of the range of their confidence intervals (Fig. 4b), these images are also locally different.

Figure 4.

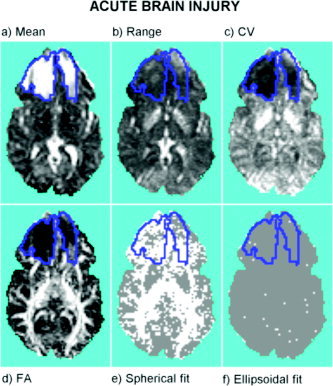
Acute brain injury: statistic images estimated in a single slice of DTI data. a: Mean diffusivity. b: Range of the confidence interval of mean diffusivity. c: Coefficient of variation (CV). d: Fractional anisotropy (FA). e: Test for goodness of fit of spherical (isotropic diffusion) tensor model: voxels where the null hypothesis has been rejected are colored white, FDR is controlled at 1%. f: Test for goodness of fit of ellipsoidal model: voxels where the null hypothesis has been rejected are colored white, FDR is controlled at 1%. The two frontal regions delimited by blue boundaries show extensive post‐traumatic edema characterized by high mean/low error diffusivity.

For example, in contrast with regions of basal and ventricular cerebrospinal fluid (CSF), which have large diffusivities and large errors, the edematous frontal areas have large diffusivity but small errors, which leads to especially low values for the coefficient of variation in the edematous regions (see Fig. 4c).

The image of FA (Fig. 4d) shows the loss of structure and the increase in isotropy in the edematous regions, which agrees with the presence of some voxels where the spherical model is not significantly worse than the unrestricted linear model (Fig. 4e). The lower noise relative to the magnitude of the diffusivities (the lower coefficient of variation) observed within the edema may have led to higher statistical power and to a relatively lower proportion of nonrejected voxels. If the relative error had been the same as in the rest of the brain, even more voxels would have been described adequately by a spherical model.

As in the case of the healthy volunteer image, the test for lack of fit of the ellipsoidal model was not significant in most of the voxels (Fig. 4f) suggesting that, considering the level of noise in the images, the ellipsoidal model is adequately adaptive to the diffusion process in most voxels.

Finally, it is interesting to note that the bilateral subcortical pattern of high error/low mean diffusivity observed in the healthy volunteer image (red regions in Fig. 3) is also evident in this image. Indeed, the salience of this region in both the coefficient of variation map (Fig. 4c) and the spherical model test map (Fig. 4d) is even greater than in corresponding images derived from the healthy volunteer image.

Hydrocephalus Patient

The results for this patient have some similarities to the results for the patient with acute brain injury. The expanded ventricles containing free CSF, which have the highest mean diffusivities (Fig. 5a), also showed the highest levels of error in the image of the range of confidence intervals (Fig. 5b). This in turn has led to intermediate values for the coefficients of variation (Fig. 5c). However, in areas where CSF has pathologically infiltrated the brain parenchyma (regions highlighted in magenta), mean diffusivity was high but the error in estimation was low. This combination of high diffusivity and low error (high coefficient of variation) in periventricular areas of the hydrocephalic brain is similar to that seen in edematous regions of the acutely injured brain and suggests that the combination of mean diffusivity and its error may provide added value in diagnosis of pathologic expansion of the extracellular fluid compartment in parenchymal brain tissue.

Figure 5.

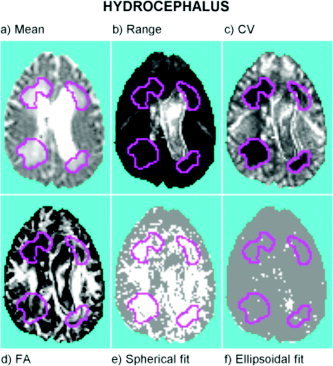
Hydrocephalus: statistic images estimated in a single slice of DTI data. a: Mean diffusivity. b: Range of the confidence interval of mean diffusivity. c: Coefficient of variation (CV). d: Fractional anisotropy (FA). e: Test for goodness of fit of spherical (isotropic diffusion) tensor model: voxels where the null hypothesis has been rejected are colored white, FDR is controlled at 1%. f: Test for goodness of fit of ellipsoidal model: voxels where the null hypothesis has been rejected are colored white, FDR is controlled at 1%. The four periventricular regions delimited by magenta boundaries show edema characterized by high mean/low error diffusivity.

Although some loss of structure may be expected in these periventricular regions (see the low FA values in the upper left region of Fig. 5d), the test for isotropy has been refuted at almost all voxels (Fig. 5e). This again may be explained by a higher relative accuracy in such areas, i.e., the coefficient of variation is locally low (see Fig. 5c). Once again, the test for lack of fit of the ellipsoidal model has only been significant in a few voxels, pointing to the fact that the ellipsoidal model is adequate considering the levels of accuracy present in the data. Finally, although not shown here, the region of low diffusivity/high error related to the basal ganglia and the internal capsule was also found in this dataset.

Analysis of the Assumptions of the Model

SNRs in the original datasets were estimated using equation (49). Specifically, the averaged maps for all images acquired with the lowest b‐value (318 s/mm²) and the highest b‐value (1,541 s/mm²) are shown in Figure 6 for the three slices illustrated previously in Figures 3, 4, 5. As expected, all voxels acquired using the lowest b‐value had rather high mean SNRs (most greater than 5), which were clearly adequate to justify the assumptions of the model. However, a considerable number of voxels acquired with the highest b‐value had rather low mean SNRs. Many voxels located in the CSF or affected by strong “ghost” artifacts had mean values of the SNR less than 1, clearly violating the assumptions of the proposed model. Such low mean values were rarely found in voxels representing parenchymal brain tissue, where the mean SNR was usually greater than 2 (a reasonable threshold for satisfying the assumptions of the model). In particular, the SNR (at highest b‐values) was 2 or greater for the basal ganglia/internal capsule region identified initially in the healthy volunteer image, as well as for the pathologic regions of the images acquired from the acute brain injury and hydrocephalus patients, implying that these observations are not prejudiced substantively by departure from the key model assumption of adequate SNR.

Figure 6.

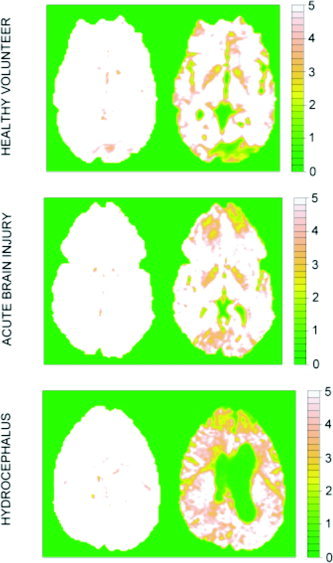
Signal‐to‐noise maps for healthy volunteer, acute brain injury, and hydrocephalus DTI datasets. Left column: SNR is generally high (>5) in images acquired with the lowest b‐value (318 s/mm²). Right column: SNR is too low to justify assumptions of log Rician model only in areas of the image acquired at highest b‐value (1,541 s/mm²), which represent free CSF or are dominated by ghosting artifacts.

DISCUSSION

The properties of the logarithm of the Rician distribution for the errors of the linearized DTI model have been analyzed. Interestingly, we have shown that this new probability law depends solely on the SNR in the complex data as acquired originally. In addition, for moderate values of the SNR (approximately greater than 2), the log Rician probability law has several convenient properties: (1) it has null expectation; (2) its variance equals the reciprocal of the squared SNR; and (3) it can be closely approximated by a normal probability law (parameterized by this mean and variance). This simple structure for the errors has led to simple estimators for the parameters of the tensor and for the variance of the noise in the original data; specifically, a two‐step weighted least squares estimator has been proposed. By assessing the properties of the errors in the estimates of the tensor through linear model theory, we have also been able to define a probability law for the estimate of the mean diffusivity and to derive confidence intervals for the true values of the mean diffusivity.

Additionally, by proving that (restricted) spherical and ellipsoidal models are submodels of an unrestricted linear model, we have developed a test for their relative lack of fit. Specifically, both restricted submodels (the sphere and the ellipsoid) are comparable to the full model in which no geometrical shape is presupposed for the global diffusion process but the diffusion in each direction is explained by an univariate linearized model. Finally, FDR methodology was proposed to handle the problem of multiple comparisons that arises by testing each voxel in an image volume. The benefit of estimating properties of the model and conducting related significance tests at each voxel is evident from the resulting statistic images (Figs. 3, 4, 5), which are much more informative than are the plots created from a few regions of interest.

The visual analysis of the statistic images derived from the three different datasets has revealed several interesting observations. Although the errors of the mean diffusivity estimates may sometimes be correlated positively with the magnitudes of the mean diffusivities, this association is not inevitable. An area of high error/low mean diffusivity, perhaps due to locally juxtaposed fiber tracts of different orientations, was observed repeatedly in a subcortical region comprising basal ganglia and internal capsule. The converse pattern, of low error/high mean diffusivity, was observed in edematous brain regions associated with both acute brain injury and hydrocephalus. We conclude that consideration of errors as well as mean diffusivities may provide added value in DTI diagnosis of acute pathologic expansion of the extracellular fluid compartment in parenchymal brain tissue.

On a more methodologic note, the potential independence of means and errors raises some concerns about results based solely on inspection of mean diffusivity in a few regions of interest. The appropriate consideration of errors in addition to means arguably becomes even more critical in interpretation of several datasets acquired from different individuals, or on different scanners, or at different time points.

Two main results can be derived from the images of statistical tests: although an important proportion of the brain (mainly white matter) has significant levels of anisotropy, i.e., the spheroidal model provides a significantly less good fit than does the full model, the ellipsoidal model generally seems good enough for most brain tissue. In interpreting these results, it is important to remember that the outcomes of tests of lack of fit are dependent largely on the levels of noise and amount of data available. The p‐values resulting from the spherical model test therefore cannot be used to quantify in absolute terms the degree of anisotropy; for this purpose, an index such as fractional anisotropy should be applied instead. On the other hand, although (theoretically) we are checking whether a given voxel conforms to the spherical model, we know that perfect isotropy will never be present in the brain parenchyma (all biological structures are anisotropic in some degree). A nonsignificant result will therefore not mean that the voxel is perfectly isotropic but that the patterns of anisotropy observed (and quantified by the FA index) are dominated mainly by the noise in the data. In consequence, any conclusions drawn from the FA index will be highly unreliable in voxels where the spherical model is not refuted, e.g., tractography involving nonsignificant voxels will probably lead to erroneous results. Under these circumstances, we will prefer the spherical (isotropic) model not because it is true but because, considering the level of noise in the data and the statistical power available, we cannot fit a more complex model with confidence. Exactly the same rationale can be applied to interpretation of the test for lack of fit of the ellipsoidal model. Although a perfectly ellipsoidal diffusivity may not be expected anywhere in the brain, it may remain the best option for modeling voxels where it is not refuted, simply because of limited precision and availability of data. Fitting a more complex model may simply risk fitting spurious trends created by noise.