Abstract
A method for the modeling of human movement‐related cortical activity from combined electroencephalography (EEG) and magnetoencephalography (MEG) data is proposed. This method includes a subject's multi‐compartment head model (scalp, skull, dura mater, cortex) constructed from magnetic resonance images, multi‐dipole source model, and a regularized linear inverse source estimate based on boundary element mathematics. Linear inverse source estimates of cortical activity were regularized by taking into account the covariance of background EG and MEG sensor noise. EEG (121 sensors) and MEG (43 sensors) data were recorded in separate sessions whereas normal subjects executed voluntary right one‐digit movements. Linear inverse source solution of EEG, MEG, and EEG‐MEG data were quantitatively evaluated by using three performance indexes. The first two indexes (Dipole Localization Error [DLE] and Spatial Dispersion [SDis]) were used to compute the localization power for the source solutions obtained. Such indexes were based on the information provided by the column of the resolution matrix (i.e., impulse response). Ideal DLE values tend to zero (the source current was correctly retrieved by the procedure). In contrast, high DLE values suggest severe mislocalization in the source reconstruction. A high value of SDis at a source space point mean that such a source will be retrieved by a large area with the linear inverse source estimation. The remaining performance index assessed the quality of the source solution based on the information provided by the rows of the resolution matrix R, i.e., resolution kernels. The i‐th resolution kernels of the matrix R describe how the estimation of the i‐th source is distorted by the concomitant activity of all other sources. A statistically significant lower dipole localization error was observed and lower spatial dispersion in source solutions produced by combined EEG‐MEG data than from EEG and MEG data considered separately (P < 0.05). These effects were not due to an increased number of sensors in the combined EEG‐MEG solutions. They result from the independence of source information conveyed by the multimodal measurements. From a physiological point of view, the linear inverse source solution of EEG‐MEG data suggested a contralaterally preponderant bilateral activation of primary sensorimotor cortex from the preparation to the execution of the movement. This activation was associated with that of the supplementary motor area. The activation of bilateral primary sensorimotor cortical areas was greater during the processing of afferent information related to the ongoing movement than in the preparation for the motor act. In conclusion, the linear inverse source estimate of combined MEG and EEG data improves the estimate of movement‐related cortical activity. Hum. Brain Mapping 14:197–209, 2001. © 2001 Wiley‐Liss, Inc.
Keywords: linear inverse source estimate, EEG/MEG integration, movement‐related potentials
INTRODUCTION
Electroencephalography (EEG) and magnetoencephalography (MEG) are useful techniques for the study of brain dynamics and functional cortical connectivity due to their high temporal resolution (msec) [Nunez, 1995, 1981]. EEG reflects the activity of cortical generators oriented both tangentially and radially with respect to the scalp surface. The different electrical conductivity of brain, skull, and scalp, however, blurs markedly the EEG potential distributions and makes the localization of the underlying cortical generators problematic. The distortion of the recorded scalp potential distribution is further increased by the ears and eyeholes, which represent shunt paths for intra‐cranial currents [Nunez, 1981, 1995]. These problems are known as “volume conduction effects” in the recording of EEG activity. In the last few years, however, a new technology called high resolution EEG, has markedly enhanced the spatial resolution of the conventional EEG (2–3 cm vs. 6–9 cm) [Gevins et al., 1995]. This technology consists of both high spatial sampling of the surface EEG potential (64–128 channels), the use of realistic models for the head and cortical surfaces, and the use of spatial enhancement techniques such as Laplacian transformation or neural current density estimation [Babiloni et al., 1996; Gevins et al., 1999; Hjorth, 1975; Le and Gevins, 1993; Nunez et al., 1991, 1994].
Magnetoencephalography (MEG) localizes and characterizes the electrical activity of the central nervous system by measuring the associated magnetic fields generated by the synchronous neural assemblies in the brain. MEG measurements of brain activity are insensitive to the volume conductor effects that afflicts the EEG recordings. With respect to EEG, MEG is sensitive mainly to the tangential component of the current flow in the pyramidal cells in the cerebral cortex. Taken together, EEG and MEG offer complementary information about the brain neural processes because they pick‐up different aspects of the quasi‐static electromagnetic field produced by neural generators [Nunez, 1995].
Mathematical models for the head as volume conductor and for the neural sources are employed by linear and non linear minimization procedures to localize putative sources of EEG and MEG data. Several studies have indicated the adequacy of the equivalent current dipole as a model for the cortical sources [Nunez, 1981, 1995], whereas the importance of realistic head volume conductor models for the localization of cortical activity has been stressed more recently [Gevins et al., 1991, 1999; Nunez, 1995]. Results of previous intracranial EEG studies have led support to the idea that high resolution EEG techniques (including head/source models and proper regularized inverse procedures) might model with an acceptable approximation the strengths and extension of cortical sources of surface EEG data, at least in certain conditions [Le and Gevins, 1993; Gevins et al., 1994]. When the EEG and MEG activity is mainly generated by circumscribed cortical sources (i.e., short‐latency evoked potentials/magnetic fields), the location and strength of these sources can be reliably estimated by the dipolar localization technique [Salmelin et al., 1995; Scherg et al., 1984]. With this technique, the use of combined EEG and MEG data increases the stability and accuracy of the source solutions estimated on the basis of EEG and MEG data considered separately [Fuchs et al., 1998; Stok et al., 1987]. In contrast, when EEG and MEG activity is generated by extended cortical sources (i.e., event‐related potentials/magnetic fields), the underlying cortical sources can be described by using a distributed source model with spherical or realistic head models [Dale and Sereno, 1993; Grave de Peralta et al., 1997; Pascual‐Marqui, 1995]. With this approach, thousands of equivalent current dipoles covering the cortical surface modeled were used, and their strength was estimated by using linear and non linear inverse procedures [Dale and Sereno, 1993; Uutela et al., 1999]. In the context of the linear inverse source estimate approach, the advantage of combining EEG and MEG data has not yet been definitively demonstrated. A simulation study has shown an improved spatial accuracy of the linear inverse source solutions, when EEG and MEG data are fused together [Phillips et al., 1997]. Furthermore, a recent simulation study has pointed to a non linear weighting between EEG and MEG modalities by using a scaling method dependent on the source location [Baillet et al., 1999]. Demonstration of the usefulness of EEG and MEG integration on empirical data, however, is still lacking.
In the present study, a method for the modeling of human movement‐related cortical activity from combined high‐resolution EEG and MEG data is proposed. This method includes realistic subject's multi‐compartment head model, multi‐dipole source model, and a regularized linear inverse source estimate based on boundary element mathematics. Linear inverse source estimates of cortical activity were regularized by taking into account the covariance of background EEG and MEG sensor noise. The EEG (121 sensors) and MEG (43 sensors) data were recorded in separate sessions whereas normal subjects executed voluntary right one‐digit movements (i.e., an unaimed self‐paced extension of the right index). Linear inverse source solutions of EEG, MEG, and EEG‐MEG data were quantitatively evaluated by using appropriate figures of merit which describe as the cortical activity can be precisely retrieved, for the whole modeled cortical space as well as for each cortical regions of interest. It is noteworthy that the effect of EEG‐MEG sensors on the linear inverse source solutions was evaluated by comparing the current density solution using a different number of spatial samples (single or combined EEG and MEG modalities).
We studied the performance of the linear inverse estimation of combined EEG‐MEG data on scalp movement‐related potentials, because the cortical generators of these potentials have been extensively studied with previous subdural EEG recordings [Ikeda et al., 1992, 1995; Neshige et al., 1988] and with source estimation procedures applied on surface EEG and MEG data [Babiloni et al., 1999a; Kristeva et al., 1991; Salmelin et al., 1995; Urbano et al., 1998]. This provided a solid anchor point for validation purposes. The results of subdural EEG recordings have shown a circumscribed involvement of the human primary sensorimotor (M1‐S1) and supplementary motor (SMA) cortices in the generation of the readiness potentials preceding self‐paced voluntary finger movements [Ikeda et al., 1992, 1995; Neshige et al., 1988; Rektor et al., 1994]. These findings lend support to previous dipole source localization modeling from corresponding surface EEG and MEG data [Erdler et al., 2000; Kristeva et al., 1991; Toro et al., 1993]. In this regard, it is important to stress that a recent MEG source estimation study has allowed the modeling of SMA involvement during the movement preparation in normal subjects [Baillet et al., 2001]. Indeed, this study updated previous ideas that magnetic fields generated by bilateral SMAs cancel each other during the movement preparation [Kristeva et al., 1991; Lang et al., 1991].
METHODS
Realistic Head and Source Models
Sixty‐four t1‐weighted sagittal magnetic resonance (mr) images were acquired (30 msec repetition time, 5 msec echo time, and 3 mm slice thickness without gap) from the subject's head. These images were processed with contouring and triangulation algorithms for the construction of a model reproducing the scalp, skull, and dura mater surfaces with about 1,000 triangles for each surface. The source model was built with the following procedure: 1) the points belonging to the mr images of the cortex were selected with a semiautomatic procedure (threshold algorithm); 2) these points were sub‐sampled from 12,000–14,000 to 2,400–4,100, so that the general features of the neocortical envelope were well preserved especially in correspondence of pre‐ and post‐central gyri and frontal mesial area; 3) the sub‐sampled points of the cortex were triangulated with 5,000–7,000 triangles); and 4) an orthogonal unitary equivalent current dipole was placed in the center of each triangle forming the cortex compartment. The average distance between points of the cortical tessellated surfaces was equal to 3.6 mm in the first subject, whereas 3.1 mm was obtained for the second subject. Figure 1 shows the multi‐compartment head model of Subject 1.
Figure 1.
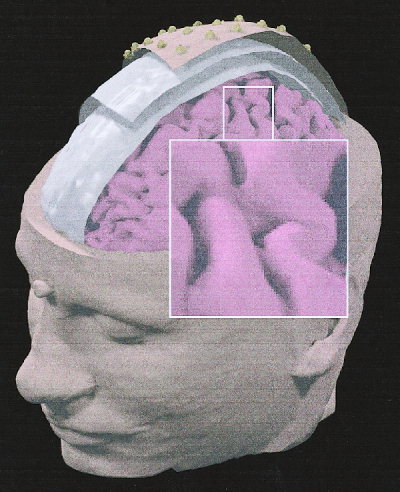
Realistic magnetic resonance (MR)‐constructed head model of Subject 1. The structures modeling the scalp, skull, dura mater and cerebral cortex are presented. On the visible modeled scalp surface, electrode density can be appreciated (spatial sampling: 128 electrodes). The inset shows the modeled central sulcus and the left primary sensorimotor area contralateral to the side of the movement (right middle finger extension).
Cortical regions of interest (ROIs) were represented by the supplementary motor area (SMA), as well as the right and left primary sensory‐motor areas (S1‐M1). The boundaries of these ROIs were traced on the basis of the following anatomical landmarks: 1) the pre‐central and central (omega zone) sulci, delimitating the precentral gyrus for the M1‐ROIs; 2) the central (omega zone) and postcentral sulci, delimitating the postcentral gyrus for the S1‐ROIs; and 3) the sulcus anterior to the vertical anterior commissure line, the medial precentral sulcus, and the cingulate sulcus, delimitating the medial frontal gyrus for the SMA‐ROI. The M1‐ and S1‐ROIs were located anteriorly and posteriorly to the central sulcus, respectively. The M1‐ROI did not extend anteriorly up to the precentral sulcus, but might include a minor part of the ventral premotor area lying in the lateral precentral gyrus (border region between Brodmann areas 4 and 6). Finally, the SMA‐ROI did not comprise the cingulate motor areas located in the upper bank of the cingulate sulcus.
Combined Electric and Magnetic Forward Solution
The forward solution specifying the potential scalp field due to an arbitrary dipole source configuration can be computed on the basis of the linear system
| (1) |
where 1) E is the electric lead field matrix obtained by the boundary element technique for the realistic MR‐constructed head model [Hämäläinen and Sarvas, 1989; Lynn and Timlake, 1968]; 2) B is the magnetic lead field matrix obtained for the same head model [Hämäläinen and Sarvas, 1989]; 3) x is the array of the unknown cortical dipole strengths; 4) v is the array of the recorded potential values; and 5) m is the array of magnetic values. The lead field matrix E and the array v must be referenced consistently. To scale EEG and MEG, the rows of the lead field matrix E and B were first normalized by the rows norm [Baillet et al., 1999; Phillips et al., 1997]. This scaling was applied equally on the electrical and magnetic measurements arrays, v and m. After row normalization the linear system can be restated as
| (2) |
where A is the matrix composed by the normalized electric and magnetic lead fields and b is the normalized measurement array of EEG and MEG data (v and m, respectively).
Regularization
Because the number of dipoles was much higher than the spatial measurements, the linear system of equation (2) has infinite solutions. Furthermore, the linear system was ill‐conditioned as a result of the substantial equivalence of several columns of the electromagnetic lead field matrix A. Regularization of the linear inverse problem consisted in the reduction of the oscillatory modes generated by vectors associated with the smallest singular values of the lead field matrix A. This was performed introducing additional and a priori information on the sources to be estimated. The general formulation of the linear inverse problem based on this assumption is
| (3) |
where W d is equal to the inverse of the covariance matrix of the normalized EEG and MEG sensors noise and W x is the matrix that regulates how each EEG or MEG sensor is influenced by dipoles located at different depths into the source model (column norm normalization). More specifically, “column‐norm normalization” refers to the weighting of source amplitudes by the norm of the associated column in the gain matrix A [Pascual‐Marqui, 1995]. An “ad hoc” choice for the regularization parameter of the linear system of equation (3) was obtained by the L‐curve approach [Hansen, 1992]. This curve, which plots the Wd‐weighted residual norm vs. the Wx‐weighted solution norm at different λ values, was used to choose the correct amount of regularization in the solution of the linear inverse problem. Computation of the L‐curves and optimal λ correction values was performed with the original Hansen's routines [Hansen, 1994].
Evaluation and Comparison of Linear Inverse Solutions
Equation (3) provides a unique solution vector ξ by computing a particular pseudo‐inverse matrix G
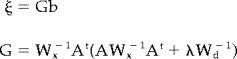 |
(4) |
under the hypothesis that the metrics of the source and data space are invertible. To draw an useful relationship between the unknown cortical source strengths (x) and the estimated ones (ξ), the resolution matrix R is defined as the pseudo‐inverse G multiplied by lead‐field matrix A [Menke, 1989]. Thus, we have
| (5) |
where the resolution matrix R is a N × N matrix in which N is the number of dipoles in the model. This matrix provides the mathematical framework to evaluate quantitatively linear inverse source solutions from EEG and MEG considered separately or combined EEG‐MEG data. Previous studies have suggested that the resolution matrix R analysis is the most appropriate tool to compare and evaluate distributed linear inverse source solutions [Grave de Peralta et al., 1996; Menke, 1989; Pascual‐Marqui, 1995]. In total, we used three indexes based on the resolution matrix R. The first two indexes served to compute the localization power of the linear inverse source solutions (Dipole Localization Error [DLE] and Spatial Dispersion [SDis]). These indexes are based on the information provided by the column of the resolution matrix (i.e., impulse response).
The DLE [Pascual‐Marqui, 1995] relative to the j‐th dipole was computed according to the equation
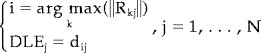 |
(6) |
where N is the total number of dipoles, i is the location in which the maximum of the i‐th column of the resolution matrix R is detected, and d ij is the distance between the j‐th source point (generating the field to model) and the i‐th point (where the maximum of the modeled source current is detected). The DLE represents the errors due to the estimated position of the maximum activity in the modulus of the mapped source currents, when a single dipole is used as a source of the potential [Pascual‐Marqui, 1995]. Ideal DLE values tend to zero (source current correctly retrieved by the procedure). In contrast, high DLE values suggest a severe mislocalization in the source reconstruction.
The second index, SDis measures the blurring of the estimated solution [Pascual‐Marqui, 1995]. The SDis of the j‐th source is expressed by
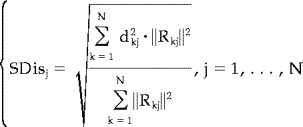 |
(7) |
where symbols have the same meaning as described above. High values of SDis at a source space point would mean that the activity produced by that source is retrieved by a large area of activation in the source space. SDis should ideally tend toward zero, meaning that the estimation procedure marks as active sources very close to the true one. High values of SDis demonstrate the unreliability of the solution, as sources far away from the true one are considered responsible for the observed measures.
The third performance index assesses the quality of the source solution based on the rows of the resolution matrix R, i.e., resolution kernels [Grave de Peralta and Gonzalez Andino, 1998; Grave de Peralta et al., 1997]. The i‐th resolution kernel of the matrix R describes how the estimation of the i‐th source is distorted by the concomitant activity of all other sources. For each component of the source vector the Resolution Index (RI) is defined as:
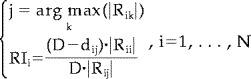 |
(8) |
where 1) D is the maximum distance between the cortical points; 2) |R ii| is the absolute value of the i‐th diagonal element of the resolution matrix R; 2) |R ij| is the absolute value of the maximum of the considered resolution kernel; and 4) d ij is the distance between the cortical point associated with this row and the point j in which the maximum value of the i‐th row is found. A high value of RI indicates that the activity at that source space point is correctly retrieved. RI values tending to zero would express either that the main peak is far away from the target source point or that the amplitude of the source point resolution kernel is small [Grave de Peralta et al., 1997; Grave de Peralta and Gonzalez Andino, 1998].
The DLE, SDis, and RI indexes were applied to the resolution matrices obtained from the linear inverse source solutions, which were computed by using only the EEG or MEG data or the combined EEG and MEG data of both subjects. For each resolution matrix, the mean and standard deviation of the three indexes were computed on the dipoles belonging to each ROI (modeled M1 and S1 of both hemispheres and modeled SMA) as well as belonging to the whole cortical source space. Statistical analysis was performed with the Student's t‐test. Bonferroni correction for multiple t‐testing minimized alpha inflation due to multiple t‐test comparisons [Zar, 1984].
Influence of Sensor Number on the Linear Inverse Solutions
A principal source of variance for the present results was due to the different number of sensors used in the EEG, MEG, and the combined EEG‐MEG case. Accuracy of the linear inverse source solutions could be affected by the total amount of spatial sample (EEG+MEG) rather than to the combination of EEG and MEG data per se. Thus, we compared source estimate obtained by the integration of the whole EEG data set (121 electrodes) vs. combined MEG (43 sensors) and sub‐sampled EEG (61 electrodes) data. Performance indexes assessing the quality of the current strengths of the estimated source were then applied.
Subjects and Task
Two healthy, right‐handed [Oldfield, 1971] male volunteers participated in the present study. The experiments were undertaken with the understanding and written consent of each participant. General procedures were approved by the local institutional ethics committee. For these experiments, a sound‐damped and electromagnetically‐shielded room was used. Motor task consisted of brisk, internally triggered unilateral right middle finger extensions followed by a passive return to the original resting position (inter‐movement interval: 2–12 sec). A brief training was performed to make the motor performance stable and reproducible during the EEG and MEG recordings. Furthermore, the surface EMG activity of bilateral axial and proximal muscles of the two participants was also recorded, to monitor co‐activation of these muscles in concomitance with the finger movement. No notable co‐activation of axial and proximal muscles was observed.
EEG Recording
EEG activity was recorded (0.1–100 Hz bandpass) with 128 electrodes (linked earlobe electrical reference). Electrode positions and reference landmarks were digitized for subsequent integration between the EEG, MEG, and MR data. Electrooculogram (EOG; 0.1–100 Hz bandpass) and electromyogram (EMG; 1–100 Hz bandpass) from m. extensor digitorum of both sides were also recorded. EOG served to control blinking/eye movements and EMG to control operating muscle response and involuntary mirror movements. All data were acquired (400 Hz sampling rate) from 3 sec before to 1 sec after the onset (zerotime) of the EMG response from the operating muscle. About 200 single trials were collected for each subject.
MEG Recordings
During the MEG recordings, subject's head was stabilized by a vacuum cast. Subjects were asked to avoid blinking, eye movements, and respiration immediately before and during the movement. MEG activity was recorded (0.16–250 Hz bandpass) in separate blocks from the left and the right hemisphere by a dewar (diameter: 16 cm) including an array of 25 sensors. This array comprised 9 magnetometers with a 80 mm2 integrated pick‐up coil (plus 3 reference channels to be used for noise cancellation) and 16 axial gradiometers (250 mm2 area, 8 cm baseline). The noise spectral density of each sensor channel was 5–7 fT per square root Hz at 1 Hz. A very short time interval (i.e., few minutes) between alternating right and left hemisphere recordings made the off‐line joining of the two MEG sequential data set reliable. In two separate recordings the sensor array was centered on the C3 or C4 site of the 10‐20 International system, which roughly overlie the hand representation of the left and right M1‐S1, respectively. EOG (0.16–250 Hz bandpass) and EMG (1–250 Hz bandpass) activity was also recorded as during the EEG recordings. Data recordings were performed in blocks lasting about 10 min (10 min inter‐block interval). All data were gathered in a continuous mode (1,000 Hz sampling rate). The positions of the sensor array with respect to the subject's anatomical landmarks (nasion, inion, and preauricular points) were detected after 1 or 2 recording blocks, to register subtle head movements across the experimental session. Such detection was obtained by positioning three coils on the subject head. The positions of these fiducial landmarks were also digitized off‐line for the subsequent integration between EEG, MEG, and MR data.
Data Analysis
The precise onset of the EMG response (zero time) was determined manually in the EEG and MEG data by two expert experimenters. The EEG and MEG segments (single trials) free from eye or mirror movements were averaged with respect to the zerotime, digitally bandpassed (0.1–30 Hz), and sub‐sampled to 200 Hz to have coincident EEG and MEG samples. Subsequent data analysis regarded main peaks (p) of EEG‐MEG activity related to the preparation (Readiness Field, RF; Readiness Potential, RP) and execution (first Movement‐Evoked Field, MEF1; first Movement‐Related Response, MRR1) of the movement. It should be noted that the term Movement‐Evoked Potential (MEP) was not used here, because that usually serves to identify EMG responses to transcranial magnetic stimulation. At least 150 single trials of artifact free EEG and MEG measurements were used for each subject, to derive averaged movement related responses. Due to artifacts, the EEG and MEG data from seven electric and magnetic sensors were removed in both subjects. Covariance matrices of noise for the EEG and MEG modalities were estimated by computing the average of inter‐sensor covariance across all the artifact‐free single trials of the sample covariance matrices. These sample covariance matrices were estimated at the rest period occurring from 3 to 2 sec premovement. Finally, the EEG and MEG artifact free single trials were averaged separately and served as inputs for the linear inverse source estimate.
RESULTS
Similar recorded EEG/MEG data and linear inverse source solutions were obtained in both subjects. This was valuable for the topography of the main EEG/MEG peaks and for the time course of the current density waveforms estimated at the regions of interest. Therefore, we always refer to the results of one of them (Subject 1) in the present section. Figure 2 plots the mean MEG (lower diagram) and EEG (upper diagram) wave forms, recorded in Subject 1 from two selected magnetic (M1 and M2); this is not to be confused with acronyms of cortical areas) and electric (E1 and E2) sensors in the hemisphere contralateral to the finger movement. With the MEG wave forms, the RF was represented by a slow magnetic shift, starting at about −0.5 sec before the movement onset (zero time) and peaking close to zerotime (RFp). The RF showed contralateral lateral‐frontal positivity (outward field flow)/medial‐parietal negativity (inward field flow) and ipsilateral lateral‐frontal negativity/medial‐parietal positivity. The MEF1 was represented by transient magnetic shifts peaking at about +105 msec (MEF1p). With respect to the RF‐MF, the MEF1 presented high amplitude and reversed polarity over the contralateral hemisphere as well as low amplitude and non‐reversed polarity over the ipsilateral hemisphere. The EEG wave forms were characterized by a bilateral parietal slow negative shift (RP) starting earlier than RF. The RP was followed by a bilateral frontoparietal transient shift (MRR1) after zerotime. The RP and MRR1 peak at about −90 msec and +90 msec, respectively. Due to the strong head volume conduction effects, the contralateral preponderance of the RP and MRR1 was modest in amplitude.
Figure 2.
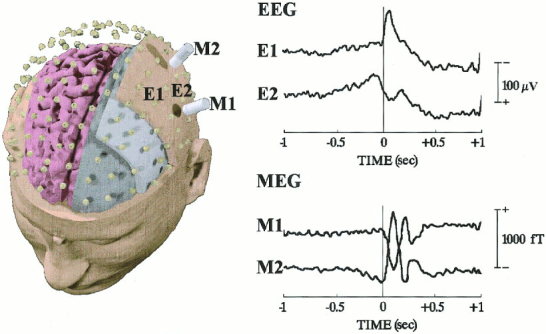
Disposition of the electric (up) and magnetic (bottom) sensors for the recording of EEG and MEG data related to unilateral unaimed right‐middle finger voluntary movements (separate recording sessions). Averaged MEG and EEG time‐series (wave forms) recorded from two selected magnetic (M1 and M2) and electric (E1 and E2) sensors are shown on the right of the figure. These sensors overlay the primary sensorimotor cortex contralateral to the movement.
Figure 3 reports the mean values of DLE, SDis and RI indexes computed from the linear inverse source estimates of EEG, MEG and combined EEG‐MEG data, for each ROI and for the whole source space (All). In particular, the index values were computed by surface data relative to 43 magnetic sensors, 61 electric sensors, 104 sensors (61 electric and 43 magnetic ones), 121 electric sensors and 164 (121 electric and 43 magnetic) sensors. For each ROI and for the whole source space, the lowest DLE and SDis values were observed with 164 sensors (121 electric and 43 magnetic ones) and 104 sensors (61 electric and 43 magnetic ones). Importantly, the DLE and SDis values computed from these 104 sensors were statistically (P < 0.05) lower than those obtained with 121 electric sensors. Accordingly, the RI values were greater (P < 0.05) with 164 sensors (121 electric and 43 magnetic ones) and 104 sensors (61 electric and 43 magnetic ones) than with 121 and 61 electric sensors. This was true for each ROI and all source space.
Figure 3.
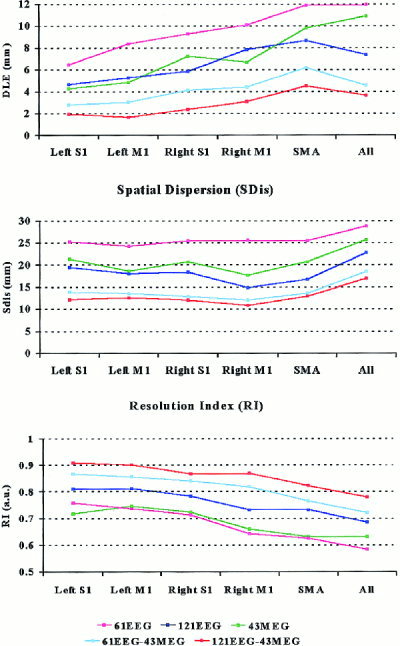
Mean values of DLE (upper diagram), SDis (central diagram) and RI (lower diagram) indexes computed from the linear inverse source estimates of EEG, MEG and combined EEG‐MEG data, for each ROI (left and right M1 and S1) as well as for the whole cortical source space (All). In particular, the index values were computed by surface data relative to 43 magnetic sensors, 61 electric sensors, 104 sensors (61 electric and 43 magnetic ones), 121 electric sensors and 164 sensors (121 electric and 43 magnetic ones). Acronyms: S1, primary somatosensory area; M1, primary motor area; SMA, supplementary motor area.
Figure 4 shows amplitude color 3‐D maps of linear inverse source estimates from recorded EEG, MEG, and EEG‐MEG data. The linear inverse source estimate of MRR1 peak (EEG data) was characterized by a bilateral large frontal negativity and a slight centro‐parietal positivity across the central sulcus of the contralateral side. The linear inverse source estimate of MEF1 peak (MEG data) modeled a more restricted and contralaterally preponderant negativity over M1‐S1s. The linear inverse source estimate of combined MRR1‐MEF1 peaks modeled also multiple restricted negative foci located mainly in the SMA and contralateral M1‐S1. Meanwhile, this estimate modeled moderate positivity values (blue colors) across the whole sensorimotor cortex, in relation to those obtained in the EEG and MEG estimates considered separately. It is worth noting that the most frontal positivity found in the only EEG solution could be explained as a large recruitment of frontal equivalent dipoles, to explain the scalp potentials that are expected to be generated mainly by the central sensorimotor cortex [Urbano et al., 1998]. Indeed, this would indicate a considerable DLE and SDis. Consistently, the frontal positivity was completely absent in the combined EEG‐MEG solutions, which were proved to present low DLE and SDis values (see Fig. 3)
Figure 4.
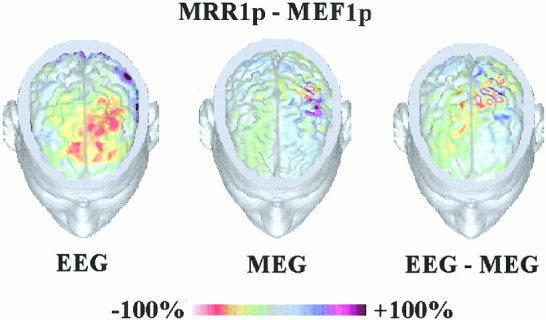
Cortical current source density estimates of EEG, MEG, and combined EEG‐MEG data. The estimates of the cortical current strengths are represented on the realistic MR‐constructed subject's head model. Percent color scale is normalized with reference to the maximum amplitude calculated for each map. Maximum negativity (−100%) is coded in red and maximum positivity (+100%) is coded in violet.
Figure 5 plots the estimated time courses of each ROI during the preparation and execution of movement. These estimates were based on the potentials/fields recorded from EEG (121 sensors), MEG (43 sensors) and combined EEG‐MEG data. The RP or RF started simultaneously in all ROIs. The RP (EEG solution) was earlier in latency than the RF (MEG solution). Furthermore, the RP was relatively stronger in amplitude than the RF in all ROIs, especially the SMA‐ROI. Consistently, the contralateral MEF1 was much larger in amplitude than that of the RF (MEG solutions). The ipsilateral MRR1 amplitude (EEG solution) was larger than that of the ipsilateral MEF1 (MEG solution). Finally, the linear inverse source estimates of combined EEG‐MEG data included the main features obtained from EEG and MEG data considered separately. In particular, a strong MRR1‐MEF1 was observed on the modeled contralateral M1 and S1 and a marked RP‐RF was reconstructed on the modeled SMA. It is worth noting that there was no discrimination in time between the activity of modeled S1 and M1. This would be due to the limited spatial resolution of the data: in fact, the MRR1‐MEF1 peaks of the modeled contralateral M1 and S1 had the same latencies even if the most direct and quick anatomical connections between the peripheral somatosensory receptors and cortex (i.e., medial lemniscal system) impinge S1.
Figure 5.
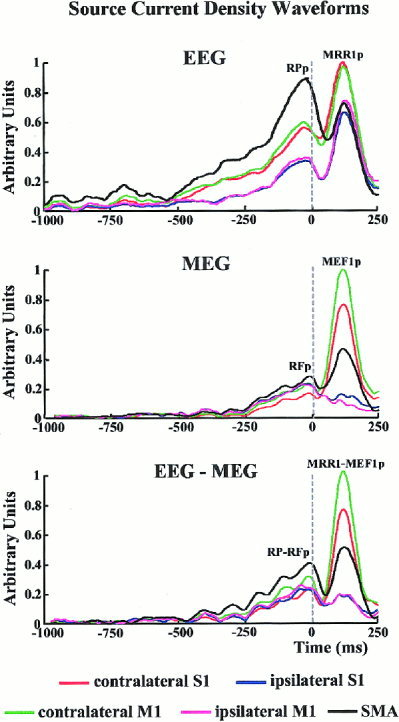
Time series of cortical current density estimates modeling activity of each ROI during the movement preparation and execution. These estimates reflect the potentials/fields recorded from EEG (121 electric sensors; upper diagram), MEG (43 magnetic sensors; central diagram) and EEG‐MEG (121 electric and 43 magnetic sensors, lower diagram) data. Time is relative to the onset (zerotime) of the electromyographic (EMG) responses recorded from the operating muscle. Each colored waveform refers to the time varying current activity in a particular region of interest.
DISCUSSION
This study presents performances of a method for the modeling of human event‐related cortical activity from combined EEG‐MEG data. This method uses realistic MR‐constructed subject's head models and linear inverse source estimate. Performances of the source estimation method were evaluated by resolution matrix indexes from simulated high resolution EEG‐MEG data. It is notable that resolution matrix indexes were based on both impulse responses (DLE and SDis) and resolution kernels (RI), which are reliable yardsticks for the evaluation of the mathematical quality of linear inverse source solutions [Grave de Peralta et al., 1997; Menke, 1989; Pascual‐Marqui, 1995]. Simulation results suggest that the linear inverse source estimates are mathematically more accurate from EEG‐MEG data than from EEG and MEG data considered separately. This is true for all ROIs considered separately as well as for the whole modeled cortical source space.
It may be argued that lambda term can be chosen in accordance with an optimal value of the indexes used (such as the DLE or SDis). This would be a true optimal choice for the hyperparameter and could be more natural rather than plotting these indices a posteriori on the base of the lambda values. A computational problem would arise, however, because many resolution matrices R (whose dimensions are N × N, with N = 5,000 or 7,000 in our case) have to be computed to obtain an accurate description of the evolution of the hyperparameter lambda.
An important source of variance in the linear inverse source analysis of combined EEG‐MEG data might be caused by the non‐simultaneous recording of these data sets, when attentional, learning and emotional variables are unpaired across the recording blocks. Regarding the present experiments, it must be stressed that movement‐related potentials/fields are very stable across experimental sessions performed in different days. Furthermore, the participating subjects were firstly trained to stabilize a simple motor performance in which learning, attentive and emotional concomitants seem to be negligible. Finally, the possibility of combining MEG and EEG data recorded in different experimental sessions can disclose many occasions of scientific and clinical cooperation. In contrast, the use of simultaneous multimodal EEG‐MEG recordings is nowadays possible only in a very few laboratories.
In our experiments, the improved quality of the linear inverse source solutions depended not only on the amount of spatial samples (EEG or MEG sensors) used as an input, but also on the combination of EEG‐MEG data per se. In fact, the resolution matrix indexes improved not only using 121 rather than 61 EEG sensors, but also using 104 multi‐modal sensors (61 electric and 43 magnetic ones) rather than 121 electric sensors. A reasonable explanation is that the EEG and MEG data would provide independent spatial source information, whereas the spatial information conveyed by sensors of a single modality would be highly correlated. These results extend previous evidence based on dipole source localization [Stok et al., 1987] and on the solution of the inverse problem from experimental [Fuchs et al., 1998] and simulated data [Baillet et al., 1999]. It is noteworthy that, compared to previous evidence, the present results were obtained by MR‐based realistic head and cortical models with simulated EEG and MEG data and an application to empirical highly sampled EEG and MEG data was furnished.
Recently, it has been argued that resolution matrix indexes founded on resolution kernels could be at least in part affected by a bias, if the modeled source space fits the entire brain volume [Pascual‐Marqui, 1999]. If this is the case, sources nearest to the sensors would be favored in the linear inverse solutions. We used no tomographic source space (i.e., source space filling the entire volume of the brain compartment). Instead, we used a source space closely distributed on the surface of the modeled realistic cortical envelope. Thus, the problem was strongly reduced, and would consider only the minority of dipoles belonging to the crowns of the modeled cortical surface. They would be favored with respect to those buried into the cortical sulci. On the whole, the reliability of our results is supported by the fact that the values of resolution matrix indexes based on the impulse responses (i.e., not affected by such a bias) are fully in agreement with those based on the resolution kernels.
An extensive analysis of cortical responses to voluntary movements was beyond the scope of the present study. Therefore, only two subjects were used for the data collection, given that MR‐based realistic head modeling is a very time‐consuming procedures. The converging results, however, obtained in the two subjects seem to be of interest from a physiological point of view. There are at least four points of interest. First, with combined EEG‐MEG data, a maximum cortical activation was modeled in the contralateral primary sensorimotor areas (M1‐S1) and in the mesial frontal area (including SMA) during both the movement preparation and execution. It is worth noting that, the onset of preparatory cortical source activity was earlier when computed from EEG than MEG data, suggesting that the sources of the crown and surface aspect of the cortical central areas are especially involved in the motor planning. Remarkably, these zones would process somatosensory proprioceptive and motor information. Second, the similar onset latency of the modeled activation agrees with a parallel preparatory involvement of M1‐S1 and SMA in the motor planning. This does not support the idea that SMA triggers M1 before the movement initiation [Kornhuber and Deecke, 1985] and is in line with previous subdural recordings in epilepsy patients [Ikeda et al., 1995; Neshige et al., 1988]. Third, the magnitude of the M1‐S1 and SMA activation is larger during the execution than the preparation of the movement, which could plausibly be due to the concomitant cortical processing of the motor command and peripheral reafferent input provoked by the ongoing motor performance. An augmented flux of central and peripheral sensorimotor information would account for this result. The involvement of the SMA in the somatosensory information processing is consistent with a detailed somatotopic somatosensory and motor representation within this area [Allison et al., 1996]. Furthermore, it was demonstrated that SMA responds to passive movements and median nerve stimulation [Hallet, 1994]. It can be speculated that the cortical imaging techniques with low temporal resolution (i.e., functional MR imaging) would return mainly the cortical response to the reafferent information processing concomitant with the ongoing movement. This provides an insightful example of the importance of combing the spatial resolution of functional MR imaging with the excellent time resolution of high resolution EEG‐MEG techniques. Fourth, a modest but perceivable activity was modeled in the ipsilateral M1 and S1, during the movement execution. This supports the idea of a distributed bilateral organization of the cortical motor system even for the execution of simple unilateral distal movements [Wiesendanger et al., 1996]. The involvement of both ipsilateral M1 and S1 during the movement is controversial [Babiloni et al., 1999b; Cheyne et al., 1997; Salmelin et al., 1995]. It would be mainly induced by the movement‐evoked somatosensory information supplied by double crossed and uncrossed pathways. A putative double crossed pathway would include dorsal‐column lemniscal system and transcallosal M1‐S1 connections. A putative uncrossed pathway may comprise spinoreticular, spinomesencephalic and spinocerebellar connection systems. The ipsilateral M1‐S1 activation accompanying the movement execution would subserve transcallosal inhibition of the small uncrossed pyramidal pathway originating from the contralateral M1‐S1 or would be used for a postural stabilization of the proximal muscles.
In conclusion, the present results suggest that the linear inverse source estimates of the combined EEG‐MEG data improve with respect to those of EEG or MEG data considered separately. The methodological approach includes MR‐based realistic head and cortical source modeling, high spatial sampling of empirical EEG and MEG data, and regularized linear inverse estimate mathematics (weighted minimum norm source estimate). The application of this technology supports the hypothesis that in humans the preparation and execution of one of the simple unilateral volitional digit acts is subserved by a distributed cortical system including SMA and contralaterally preponderant M1 and S1.
Acknowledgements
The authors wish to thank Prof. Fabrizio Eusebi for his continuous support and Dr. Davide Moretti for his contribution to the data analysis.
REFERENCES
- Allison T, McCarthy G, Luby M, Puce A, Spencer DD (1996): Localization of functional regions of human mesial cortex by somatosensory evoked potential recording and by cortical stimulation. Electroencephalogr Clin Neurophysiol 100: 126–140. [DOI] [PubMed] [Google Scholar]
- Babiloni F, Babiloni C, Carducci F, Fattorini L, Onorati P, Urbano A (1996): Spline Laplacian estimate of EEG potentials over a realistic magnetic resonance‐constructed scalp surface model. Electroencephalogr Clin Neurophysiol 98: 363–373. [DOI] [PubMed] [Google Scholar]
- Babiloni C, Carducci F, Pizzella V, Indovina I, Romani GL, Rossini PM, Babiloni F (1999a): Bilateral neuromagnetic activation of human primary sensorimotor cortex in preparation and execution of unilateral voluntary finger movements. Brain Res 827: 234–236. [DOI] [PubMed] [Google Scholar]
- Babiloni C, Carducci F, Cincotti F, Rossini PM, Neuper C, Pfurtscheller G, Babiloni F (1999b): Human movement‐related potentials vs desynchronization of EEG alpha rhythm: a high‐resolution EEG study. Neuroimage 10: 658–665. [DOI] [PubMed] [Google Scholar]
- Baillet S, Garnero L, Marin G, Hugonin JP (1999): Combined MEG and EEG source imaging by minimization of mutual information. IEEE Trans Biomed Eng 46: 522–534. [DOI] [PubMed] [Google Scholar]
- Baillet S, Leahy R, Singh M, Shattuck D, Mosher JC (2001): Supplementary motor area activation preceding voluntary finger movements as evidenced by magnetoencephalography and fMRI. Int J Bioelectromagnetism 3(1): http://www.ee.tut.fi/rgi/ijbem. [Google Scholar]
- Cheyne D, Endo H, Takeda T, Weinberg H (1997): Sensory feedback contributes to early movement‐evoked fields during voluntary finger movements in humans. Brain Res 771: 196–202. [DOI] [PubMed] [Google Scholar]
- Dale A, Sereno M (1993): Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: a linear approach. J Cogn Neurosci 5: 162–176. [DOI] [PubMed] [Google Scholar]
- Erdler M, Beisteiner R, Mayer D, Kaindl T, Edward V, Windischberger C, Lindinger G, Deecke L (2000): Supplementary motor area activation preceding voluntary movement is detectable with a whole‐scalp magnetoencephalography system. Neuroimage 11: 697–707. [DOI] [PubMed] [Google Scholar]
- Fuchs M, Wagner M, Wischmann HA, Kohler T, Theissen A, Drenckhahn R, Buchner H (1998): Improving source reconstruction by combining bioelectrical and biomagnetic data. Electroencephalogr Clin Neurophysiol 107: 69–80. [DOI] [PubMed] [Google Scholar]
- Gevins A, Cutillo B, Desmond J, Ward M, Bressler S, Barbero N, Laxer K (1994): Subdural grid recordings of distributed neocortical networks involved with somatosensory discrimination. Electroencephalogr Clin Neurophysiol 92: 282–290. [DOI] [PubMed] [Google Scholar]
- Gevins A, Leong H, Smith M, Le J, Du R (1995): Mapping cognitive brain function with modern high‐resolution electroencephalography. Trends Neurosci 18: 429–436. [DOI] [PubMed] [Google Scholar]
- Gevins A, Le J, Leong H, McEvoy LK, Smith ME (1999): Deblurring. J Clin Neurophysiol 16: 204–213. [DOI] [PubMed] [Google Scholar]
- Grave de Peralta R, Gonzalez Andino S, Lutkenhoner B (1996): Figures of merit to compare linear distributed inverse solutions. Brain Topogr 9: 117–124. [Google Scholar]
- Grave de Peralta R, Gonzalez Andino S (1998): Distributed source models: standard solutions and new developments In: Uhl C, editor. Analysis of neurophysiological brain functioning. New York: Springer Verlag, p 176–201. [Google Scholar]
- Grave de Peralta R, Hauk O, Gonzalez Andino S, Vogt H, Michel CM (1997): Linear inverse solution with optimal resolution kernels applied to the electromagnetic tomography. Hum Brain Mapp 5: 454–467. [DOI] [PubMed] [Google Scholar]
- Hallett M (1994): Movement‐related cortical potentials. Electromyogr Clin Neurophysiol 34: 5–13. [PubMed] [Google Scholar]
- Hämäläinen M, Sarvas J (1989): Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans Biomed Eng 36: 165–171. [DOI] [PubMed] [Google Scholar]
- Hansen PC (1992): Analysis of discrete ill‐posed problems by means of the L‐curve. SIAM Review 34: 561–580. [Google Scholar]
- Hansen PC (1994): Regularization tools, a Matlab package for analysis and solution of discrete ill‐posed problems. Numerical Algorithms 6: 1–35. [Google Scholar]
- Hjorth B (1975): An online transformation of EEG scalp potentials into orthogonal source derivations. Electroencephalogr Clin Neurophysiol 39: 526–530. [DOI] [PubMed] [Google Scholar]
- Ikeda A, Luders HO, Shibasaki H, Collura TF, Burgess R, Morris HH III, Hamano T (1995): Movement‐related potentials associated with bilateral simultaneous and unilateral movements recorded from human supplementary motor area. Electroencephalogr Clin Neurophysiol 95: 323–334. [DOI] [PubMed] [Google Scholar]
- Ikeda A, Luders HO, Burgess R, Shibasaki H (1992): Movement‐related potentials recorded from supplementary motor area and primary motor area. Brain 115: 1017–1043. [DOI] [PubMed] [Google Scholar]
- Kornhuber HH, Deecke L (1985): The starting function of the SMA. Behav Brain Sci 8: 591–592. [Google Scholar]
- Kristeva R, Cheyne D, Deecke L (1991): Neuromagnetic fields accompanying unilateral and bilateral voluntary movements: topography and analysis of cortical sources. Electroencephalogr Clin Neurophysiol 81: 284–298. [DOI] [PubMed] [Google Scholar]
- Lang W, Cheyne D, Kristeva R, Beisteiner R, Lindinger G, Deecke L (1991): Three‐dimensional localization of SMA activity preceding voluntary movement. Exp Brain Res 87: 688–695. [DOI] [PubMed] [Google Scholar]
- Le J, Gevins A (1993): A method to reduce blur distortion from EEGs using a realistic head model. IEEE Trans Biomed Eng 40: 517–528. [DOI] [PubMed] [Google Scholar]
- Lynn M, Timlake W (1968): On the numerical solution of the singular integral equations of potential theory. Numer Math 11: 77–98. [Google Scholar]
- Menke W (1989): Geophysical data analysis: discrete inverse theory. San Diego: Academic Press. [Google Scholar]
- Neshige R, Luders H, Shibasaki H (1988): Recording of movement‐related potentials from scalp and cortex in man. Brain 111: 719–736. [PubMed] [Google Scholar]
- Nunez PL (1981): Electric fields of the brain. New York: Oxford University Press. [Google Scholar]
- Nunez PL, Pilgreen K, Westdorp A, Law S, Nelson A (1991): A visual study of surface potentials and Laplacians due to distributed neocortical sources: computer simulations and evoked potentials. Brain Topogr 4: 151–168. [DOI] [PubMed] [Google Scholar]
- Nunez PL, Silberstein RB, Cadiush PJ, Wijesinghe J, Westdorp AF, Srinivasan R. (1994): A theoretical and experimental study of high resolution EEG based on surface Laplacians and cortical imaging. Electroencephalogr Clin Neurophysiol 90: 40–57. [DOI] [PubMed] [Google Scholar]
- Nunez PL (1995): Neocortical dynamics and human EEG rhythms. New York: Oxford University Press, p 722. [Google Scholar]
- Oldfield P (1971): The Edinburgh inventory. Neuropsychology 3: 124–132. [Google Scholar]
- Pascual‐Marqui RD (1995): Reply to comments by Hämäläinen, Ilmoniemi and Nunez. ISBET Newsletter 6: 16–28. [Google Scholar]
- Pascual‐Marqui RD (1999): Review of methods for solving the EEG inverse problem. Int J Bioelectromagnetism 1: http://www.ee.tut.fi/rgi/ijbem/volume1/number1/html/ar10.html. [Google Scholar]
- Phillips JW, Leahy R, Mosher JC (1997): Imaging neural activity using MEG and EEG. IEEE Eng Med Biol Mag 16: 34–41. [DOI] [PubMed] [Google Scholar]
- Rektor I, Feve A, Buser P, Bathien N, Lamarche M (1994): Intracerebral recording of movement‐related readiness potentials: an exploration in epileptic patients. Electroencephalogr Clin Neurophysiol 90: 273–283. [DOI] [PubMed] [Google Scholar]
- Salmelin R, Forss N, Knuutila J, Hari R (1995): Bilateral activation of the human somatomotor cortex by distal hand movements. Electroencephalogr Clin Neurophysiol 95: 444–452. [DOI] [PubMed] [Google Scholar]
- Scherg M, von Cramon D, Elton M (1984): Brain‐stem auditory‐evoked potentials in post‐comatose patients after severe closed head trauma. J Neurol 231: 1–5. [DOI] [PubMed] [Google Scholar]
- Stok CJ, Meijs JW, Peters MJ (1987): Inverse solutions based on MEG and EEG applied to volume conductor analysis. Phys Med Biol 32: 99–104. [DOI] [PubMed] [Google Scholar]
- Toro C, Matsumoto J, Deuschl G, Roth J, Hallett M. (1993): Source analysis of scalp‐recorded movement‐related electrical potentials. Electroencephalogr Clin Neurophysiol 86: 167–175. [DOI] [PubMed] [Google Scholar]
- Urbano A, Babiloni C, Onorati P, Carducci F, Ambrosini A, Fattorini L, Babiloni F (1998): Responses of human primary sensorimotor and supplementary motor areas to internally triggered unilateral and simultaneous bilateral one‐digit movements. A high‐resolution EEG study. Eur J Neurosci 10: 765–770. [DOI] [PubMed] [Google Scholar]
- Uutela K, Hamalainen M, Somersalo E. (1999): Visualization of magnetoencephalographic data using minimum current estimates. Neuroimage 10: 173–180. [DOI] [PubMed] [Google Scholar]
- Wiesendanger M, Rouiller E, Kazelnnikov O, Perrig S (1996): Is the SMA a bilaterally organized system? Adv Neurol 70: 71–83. [PubMed] [Google Scholar]
- Zar H (1984): Biostatistical analysis. New York: Prentice‐Hall. [Google Scholar]


