Abstract
This work presents a new algorithm (nonuniform intensity correction; NIC) for correction of intensity inhomogeneities in T1‐weighted magnetic resonance (MR) images. The bias field and a bias‐free image are obtained through an iterative process that uses brain tissue segmentation. The algorithm was validated by means of realistic phantom images and a set of 24 real images. The first evaluation phase was based on a public domain phantom dataset, used previously to assess bias field correction algorithms. NIC performed similar to previously described methods in removing the bias field from phantom images, without introduction of degradation in the absence of intensity inhomogeneity. The real image dataset was used to compare the performance of this new algorithm to that of other widely used methods (N3, SPM'99, and SPM2). This dataset included both low and high bias field images from two different MR scanners of low (0.5 T) and medium (1.5 T) static fields. Using standard quality criteria for determining the goodness of the different methods, NIC achieved the best results, correcting the images of the real MR dataset, enabling its systematic use in images from both low and medium static field MR scanners. A limitation of our method is that it might fail if the bias field is so high that the initial histogram does not show bimodal distribution for white and gray matter. Hum. Brain Mapping 22:133–144, 2004. © 2004 Wiley‐Liss, Inc.
Keywords: nonuniform intensity correction, NIC, magnetic resonance imaging, bias field, intensity inhomogeneities, segmentation algorithms
INTRODUCTION
Segmentation of magnetic resonance (MR) images is a fundamental procedure for the quantitative study of different brain pathologies such as multiple sclerosis [Miller et al., 2002], Alzheimer's disease [Good et al., 2002], or schizophrenia [Lawrie and Abukmeil, 1998; Weinberger and McClure, 2002]. Automatic segmentation of MR scans is very useful for these applications, although it may be hindered by several acquisition‐related artifacts.
One such artifact is the lack of homogeneity of the radiofrequency (RF) or B1 field, also known as “illumination artifact” or “bias field,” which consists of a smooth multiplicative variation of intensity levels across the MR image. In a standard 1.5 T MR scanner, the magnitude of this intensity variation may even exceed 30% of the signal value [Guillemaud and Brady, 1997]. Although this artifact may be unnoticeable to the eye, it can clearly degrade the volumetric quantification of cerebral tissues, particularly when using automatic segmentation algorithms based on intensity levels. For this reason, bias field correction algorithms are used mainly to reduce classification error rates (CER) when segmenting images into different tissue types.
This artifact may have several causes, such as lack of uniform sensitivity of the RF emitting and receiving coils, static field (B0) inhomogeneities, gradient‐induced eddy currents, magnetic susceptibility of tissue, interslice cross‐talk, RF standing wave effects, and attenuation of the RF signal inside the object [Simmons et al., 1994; Sled and Pike, 1998]. Magnitude of the bias field is stronger in high static field machines because of the higher RF frequencies used. A corrective calibration, as is usually carried out with magnetic field inhomogeneity [Cusack et al., 2003], is not feasible because the attenuation depends on every individual sample and precludes any static correction. Some methods developed for the measurement of the RF inhomogeneity in vivo are not practical for the clinical routine, as they require specific equipment and are time consuming [Sled and Pike, 1998]. Correction of the bias field therefore is addressed usually by post‐acquisition mathematical algorithms.
The different correction strategies proposed can be classified roughly into two types, depending on whether they use segmentation or not. Many examples can be found of different algorithms for correcting intensity inhomogeneities that do not use any segmentation. Homomorphic filtering methods [Brinkmann et al., 1998; Johnston et al., 1996] assumed no overlapping between the low‐frequency bias field and the high‐frequency image information. Dawant et al. [1993] proposed a method to correct image intensities based on a previous selection (either manual or automatic) of reference points in white matter. The method in DeCarli et al. [1996] was based on differences between local and global medians. Vokurka et al. [1999] combined two methods to correct intra‐ and interslice intensity nonuniformity, whose effect on surface coil images was studied further [Vokurka et al., 2001]. Cohen et al. [2000] applied a gaussian filtering scheme, minimizing filtering artifacts by assigning the mean signal intensity to the background voxels. The methods by Mangin [2000] and Likar et al. [2001] fitted the bias field with parametric basis functions whose coefficients were determined through entropy minimization. Another approach has been to take the intensity inhomogeneity artifact into account during the MR reconstruction process [Schomberg, 1999].
All these methods do not make use of any tissue segmentation; however, the bias field correction can be improved noticeably by taking advantage of a tissue classification. Following this strategy, different methods have been developed that simultaneously carry out the tissue segmentation and the field correction. An iterative method based on the expectation‐maximization (EM) algorithm was proposed by Wells et al. [1996] and improved by Guillemaud and Brady [1997]. All these methods involve the following steps: (1) classification of the image voxels into a set of predefined tissue classes; (2) calculation of a bias‐free image by assigning voxels in each class its mean tissue intensity; (3) calculation of a residual image as the subtraction of the bias‐free image from the original image; (4) estimation of the bias field by smoothing the residual image; and (5) correction of the original image using this estimated bias field. The whole process is iterated until no improvement is observed in a certain quality parameter.
The method in Ashburner and Friston [1997] introduced prior spatial information into the classification step by making use of a probabilistic template. This method, detailed further by Ashburner and Friston [2000], was included in the SPM99 software package, and a newer version of the algorithm (SPM2) has been released recently [Ashburner, 2002]. Van Leemput et al. [1999a, b] modified the algorithm by adding a Markov model to steer the tissue classification. Several other methods have adopted similar strategies: The N3 algorithm [nonparametric nonuniform intensity normalization; Sled et al., 1998] used an iterative algorithm to estimate both the multiplicative bias field (represented by a combination of smooth B‐splines) and the distribution of the true tissue intensities in the MR volume. Shattuck et al. [2001] followed an analogous scheme, also fitting B‐splines to local estimates of the bias field. Pham and Prince [1999] and Ahmed et al. [2002] estimated the bias field using an adaptive fuzzy C‐means classification together with a multiscale pyramidal algorithm. Zhang et al. [2001] made use of a hidden Markov model to simultaneously carry out the segmentation and the correction. Marroquin et al. [2002] modeled separately the intensity inhomogeneity of each tissue class using parametric models.
The lack of an optimal solution is thus highlighted by many bias field correction strategies in the literature. Unfortunately, evaluation and testing of all these algorithms have not received the same attention. Velthuizen et al. [1998] carried out a review of MRI intensity nonuniformity correction methods and an evaluation of their impact on measurements of brain tumor volumes. They reported that tumor segmentation was not improved by these methods, and the result was attributed to the fact that tumors are usually very localized. Another comprehensive article by Arnold et al. [2001] showed a quantitative comparison of the six most representative algorithms used currently to correct inhomogeneity artifacts. Their main conclusion was that none of the methods performed ideally in all cases, particularly considering that some methods were not robust with images showing little or no bias field effect. Locally adaptive methods provided more accurate corrections than did non‐adaptive techniques, suggesting that the former are more efficient when dealing with some features of brain anatomical variability, like the asymmetry between left and right hemispheres. Chard et al. [2002] investigated the reproducibility of the SPM99 segmentation method for the assessment of brain volume measurements and concluded that the bias field correction markedly improved the repeatability of tissue segmentation.
Despite its unquestionable interest, the use of real image datasets to measure the efficiency and robustness of the inhomogeneity correction raises the problem of establishing appropriate goodness criteria. The use of phantom images simplifies evaluation of correction algorithms, because a bias field of known magnitude can be added easily. When measuring the efficiency of correction algorithms with real image datasets, the actual bias field in the images is not known.
Our work presents a new, locally adaptive algorithm for correction of the bias field artifact in T1‐weighted MR scans based on minimization of the CER between different cerebral tissues. The algorithm has been validated with an available realistic phantom, used previously in the study by Arnold et al. [2001]. Our results were compared to those reported in that work. In addition, the usefulness of our algorithm for segmentation has been evaluated on real images obtained by scanning a set of subjects in two MR machines of low (0.5 T) and medium (1.5 T) field. The algorithm was compared to three of the most widely used correction methods (N3 [Sled et al., 1998], SPM99 [Ashburner and Friston, 2000], and SPM2 [Ashburner, 2002]), using commonly accepted criteria.
MATERIAL AND METHODS
The rationale of our algorithm (NIC; nonuniform intensity correction) is to make use of the estimated error rate of a tissue segmentation as a goodness parameter for correction of the bias field. The algorithm estimates a CER by modeling tissue intensities with a mixture of basis functions and measuring their overlap.
Description of the NIC Algorithm
The NIC algorithm iterates two major stages, “tissue classification” and “bias field estimation.” The tissue classification stage provides information to create a bias‐free image, used in the second stage to obtain both an estimation of the inhomogeneity field in the original image and a CER. Because the bias field is assumed to be smooth and multiplicative, it can be estimated as the quotient between smoothed versions of the original and bias‐free images. The algorithm iterates until no improvement of the CER is achieved in three successive steps. Figure 1 shows a flowchart of the whole process.
Figure 1.
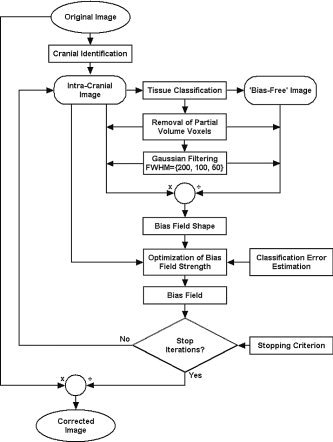
Flowchart of the NIC algorithm.
Tissue Classification
For the algorithm to operate properly, no more than three tissues types must appear: gray matter, white matter, and cerebrospinal fluid (CSF). This makes it necessary to exclude all the extracranial voxels using a segmentation method. In our case, this segmentation, available previously, had been obtained by thresholding the original image and manually editing the extracranial mask obtained. This task is not critical, however, and could be accomplished using any of the many different automatic methods available [Atkins and Mackiewich, 1998; Brummer et al., 1993; Shattuck et al., 2001; Stokking et al., 2000]. The histogram of the masked image is modeled with five basis functions: three gaussians corresponding to pure cerebral tissues (white and gray matter and CSF) and two additional probability densities for partial volume voxels, assumed to contain only two pure tissues (gray–white matter and CSF–gray matter). Different statistical models for partial volume voxels are thoroughly described in Santago and Gage [1995]. Following the notation of Ruan et al. [2000], the partial volume density functions are defined by
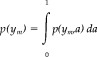 |
(1) |
where
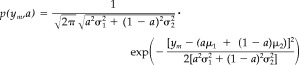 |
(2) |
being p(y m, a) the probability of a voxel with proportions of pure tissues a and (1 − a) to present an intensity level y m. Mean and standard deviation of the intensity levels of the pure tissues are represented by (μ1, μ2) and (σ1, σ2) respectively (Fig. 2a). This model assumes that all a values occur with the same probability, because partial volume voxels may consist of any fraction of pure tissue classes. Parameters of the basis functions are estimated iteratively with an EM (expectation‐maximization) algorithm [Dempster et al., 1977]. At each EM iteration, a Bayesian approach is used to calculate the classification thresholds that yield the minimum error rate. This error rate is estimated as the overlap between pure tissue distributions (Fig. 2b). The EM algorithm stops when the segmentation thresholds do not change in 10 consecutive iterations. The result of this stage is an estimation of the parameters of basis functions that model the image histogram.
Figure 2.
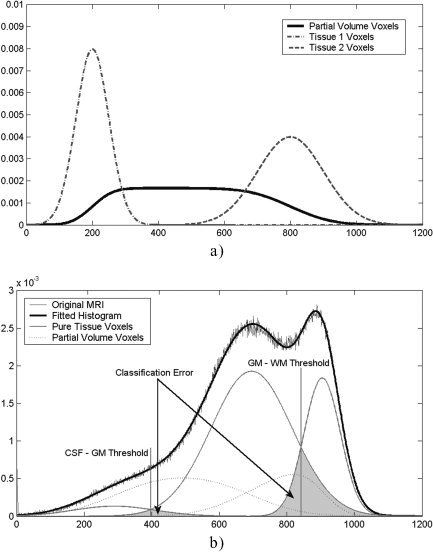
a: Example of a theoretical density distribution for the partial volume voxels according to the model implemented in the NIC algorithm. Probability density functions of two tissue types and of their partial volume voxels are shown (Tissue 1 mean = 200 ± 50; Tissue 2 mean = 800 ± 100). b: Example of real MR histogram fitted by five basis functions. Pure tissue and partial volume voxel basis functions are highlighted. The segmentation error can be estimated as the overlap between the basis functions.
Bias Field Estimation
In this stage, the parameters of the basis functions provided by the tissue classification are used to create a bias‐free image. Those intracranial voxels with an intensity level within the 95% confidence intervals (95% CI) of any of the two partial volume basis functions are classified as partial volume. The remaining intracranial voxels are considered pure tissue and classified into gray matter, white matter, and CSF using the minimum error‐rate classification thresholds obtained in the tissue classification stage. The value of these pure tissue voxels is changed to the mean intensity of their corresponding tissue class (Fig. 3b), thus producing a bias‐free image. Following the strategy proposed by Cohen et al. [2000] to reduce filtering artifacts, the values of all extracranial and partial volume voxels are set to the mean intracranial intensity both in the bias‐free image and in the original one. Both images are then filtered with the same gaussian kernel. When the CER is no longer improved using a particular kernel size, its full width at half maximum (FWHM) is reduced to a half. With our images, the kernel size varied from 200 mm in the first iteration to 50 mm in the last one.
Figure 3.
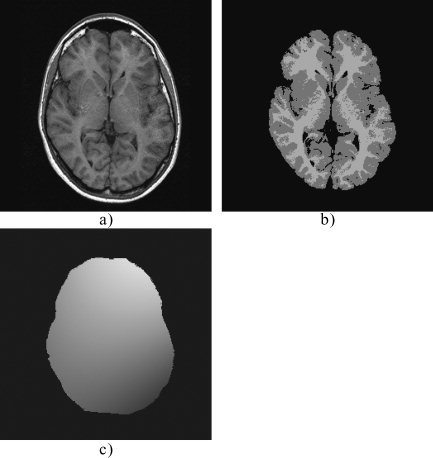
Processing steps of the NIC bias correction algorithm. a: Original image. b: Segmented image (extracerebral and partial volume voxels have been excluded). c: Estimated bias field obtained as the quotient between smoothed versions of the original (a) and segmented images (b).
At this point, the bias field is estimated as the quotient between the smoothed versions of the original and bias‐free images (Fig. 3c). This procedure, however, does not provide a good estimation of the magnitude of the bias field, but the estimation can be optimized further to minimize the classification error. To this end, the original image is corrected with bias fields of different magnitudes, from 0–40% in steps of 1%, selecting the value that yields the lowest classification error.
A bias‐corrected MR image is calculated as the quotient between the original image and the estimated bias field. This corrected MR image is then entered as the original image in the tissue classification step, iterating the whole procedure until no improvement in the classification error is obtained in three consecutive steps. The parameter minimized by the NIC algorithm is actually the CER, despite the use of a maximum‐likelihood EM algorithm in the tissue classification stage.
Validation
With the aim of thoroughly testing the performance of the NIC algorithm, both phantom and real image datasets were used. The main advantage of using realistic phantom images is that it enables assessment of the accuracy of the algorithm. The procedure works by adding a known multiplicative bias field and measuring the difference between the applied and extracted bias fields. These phantom images, on the other hand, may not be representative of real clinical cases. To assess the performance of the algorithm with real cases, we followed a different strategy. Because in this case the actual bias field was unknown, the evaluation was carried out by comparing parameters that estimate the residual amount of variability of every tissue in the image after correcting the bias field.
Phantom Dataset
To facilitate comparison of our results to previous ones, we evaluated the NIC algorithm following the methodology proposed by Arnold et al. [2001], who studied six inhomogeneity correction methods 1: N3 [Sled et al., 1998]; HUM [Brinkmann et al., 1998]; EQ [Cohen et al., 2000]; BFC [Shattuck et al., 2001]; SPM [Ashburner and Friston, 2000]; and CMA.2 A paraboloidal and a sinusoidal bias field of maximum magnitude ±8% bias fields were added to a realistic MR brain phantom [Collins et al., 1998] with 3% gaussian noise. These phantom images are freely available in the Internet.3 The quality of the correction was assessed by a scatterplot of applied versus extracted bias fields and its correlation coefficient (r). Ideally, the applied and extracted bias should have exactly the same shape and magnitude, with the scatterplot showing a perfectly straight slope of b = 1 with a correlation coefficient of r = 1. The algorithm was also applied to the original phantom image without bias field to verify that no degradation was introduced in this case.
Real Image Dataset
Our real image dataset consisted of 24 brain MR images of four healthy volunteers. Images were acquired in two clinical scanners (Gyroscan; Philips, The Netherlands) using a head coil, with 12 images at 0.5 T and 12 at 1.5 T. Each subject was scanned three times in every MR system. MR images were acquired using a T1‐weighted 3D gradient echo sequence (flip angle = 30 degrees, repetition time = 15.4 msec, echo time = 4.6 msec), with a matrix size of 256 × 256 × 110, and voxel size of 0.98 × 0.98 × 1.10 mm. The MRI acquisition protocol was intended to produce bias fields of different strength and shape. Images at the higher B0 field (1.5 T, 64 MHz) were expected to present a stronger bias field than were those obtained at a lower field (0.5 T, 22 MHz), because the intensity inhomogeneity depended on RF signal attenuation inside the object under study [Sled and Pike, 1998]. To modify the shape of the bias field, the scanner bed was moved ±1.5 cm in the second and third repetitions, presuming that a change in the relative positions of the emitting and receiving coils should produce a different map of sensitivity, thus varying the shape of the bias field [Deichmann et al., 2002].
We used four parameters to assess the quality of intensity inhomogeneity correction: the coefficients of variation of gray and white matter; the coefficient of joint variation of gray and white matter; and the CER (the parameter minimized by our algorithm). The coefficient of variation of the white matter (CVWM) and gray matter (CVGM) have been employed widely as goodness parameters [Chard et al., 2002; Dawant et al., 1993; Likar et al., 2001; Sled et al., 1998]. Coefficients of variation constitute a scale‐independent measurement of the voxel intensity variability for any particular tissue type. Their interpretation may be difficult, however, when one tissue shows improvement and other shows degradation. Another parameter, the coefficient of joint variation of white and gray matter (CJVWG), was proposed to overcome this problem [Likar et al., 2001]. It is defined by
| (3) |
and represents the sum of the standard deviations of the voxel intensities in WM and GM, normalized by the difference of their means. The coefficient of joint variation remains an approximate measurement of the classification error, as it does not take into account the relative amounts of the two tissues. Figure 4 shows an example of how two artificial tissue types with the same coefficient of joint variation may present a different classification error. For this reason, we estimated the quality of the classification by the CER. The calculation of all these quality parameters requires the identification of WM, GM, and CSF in the images. To this end, we used the classification method presented above.
Figure 4.
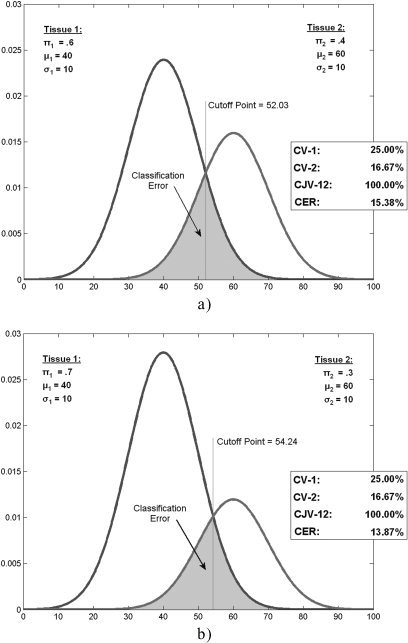
Examples of probability density functions with the same mean, variance (thus presenting the same coefficient of variation CV), and coefficient of joint variation (CJV). CER, however, is higher when the relative amounts of the two tissues (π1 and π2) are closer.
The four quality parameters were calculated in the original image dataset and after bias field correction by the NIC algorithm and by three other methods: N3 [Sled et al., 1998], SPM99 [Ashburner and Friston, 2000] and SPM2 [Ashburner, 2002]. These algorithms were chosen based on their public availability4 and wide use by the neuroscience community. The SPM99 software includes two bias correction techniques, one intended for high magnitude bias fields (SPM99‐S) and the other for moderate bias fields (SPM99‐L). Tunable parameters in all algorithms were left at their default values.
As a preceding validation step, to make sure that the four goodness parameters used were appropriate markers of intensity inhomogeneity, these parameters were calculated on phantom images with three bias fields of known magnitude (0, 20, and 40%). The phantom images used for this purpose were three BrainWeb Normal Brain Database5 T1‐weighted images with 3% gaussian noise.
RESULTS
Results of the validation of the standard quality criteria (CVGM, CVWM, and CJVWG) showed that higher values of these parameters corresponded to higher tissue dispersion caused by stronger bias fields (Table I).
Table I.
Quality criteria measured on the Brain Web phantom with 0, 20, and 40% bias field magnitude
| Brain Web | CVWM (%) | CVGM (%) | CJVWG (%) | CER (%) |
|---|---|---|---|---|
| 0% bias field | 4.84 | 7.03 | 43.02 | 0.65 |
| 20% bias field | 5.89 | 8.97 | 48.91 | 1.32 |
| 40% bias field | 7.56 | 12.26 | 59.84 | 3.22 |
All quality parameters represent the amount of bias field in the images. CVWM, coefficient of variation of white matter; CVGM, coefficient of variation of the gray matter; CJVWG, coefficient of joint variation of white and gray matter; CER, classification error rate.
The CER also increased with the amount of known bias field in the phantom images (Table I). Furthermore, the same pattern of correspondence between increased coefficients of variation and CER was also observed when using the set of real images (Table II). These results support the validity of using the CER criterion as a measurement of the amount of bias field in the images.
Table II.
Mean and range of the four quality criteria
| Method | CVWM (%) | CVGM (%) | CJVWG (%) | CER (%) |
|---|---|---|---|---|
| 0.5 T (n = 12) | ||||
| Uncorrected | 5.39 (4.81, 5.96) | 15.12 (13.27, 17.36) | 108.75 (100.50, 138.71) | 10.29 (9.40, 13.81) |
| SPM99‐L | 9.14 (5.03, 34.77) | 14.59 (10.60, 20.40) | 129.15 (116.17, 177.92) | 11.14 (10.49, 16.15) |
| SPM99‐S | 10.13 (4.71, 33.82) | 13.54 (10.17, 17.48) | 132.03 (110.65, 170.94) | 10.83 (9.63, 17.37) |
| SPM2 | 5.29 (4.63, 6.24) | 19.19 (10.73, 25.72) | 122.17 (102.62, 156.21) | 10.53 (9.38, 15.34) |
| N3 | 5.15 (4.55, 5.42) | 14.29 (12.90, 16.71) | 113.65 (105.27, 135.79) | 10.51 (9.73, 14.36) |
| NIC | 5.02 (4.39, 5.29) | 14.48 (12.73, 16.56) | 105.81 (99.84, 126.69) | 9.79 (8.86, 13.44) |
| 1.5 T (n = 12) | ||||
| Uncorrected | 6.52 (5.79, 7.59) | 16.75 (12.74, 20.74) | 83.92 (76.37, 97.10) | 9.08 (8.74, 12.79) |
| SPM99‐L | 6.26 (4.70, 7.41) | 17.34 (14.44, 21.49) | 105.97 (86.30, 135.33) | 12.90 (10.08, 18.87) |
| SPM99‐S | 5.53 (4.57, 6.22) | 16.31 (13.80, 19.89) | 93.40 (78.19, 107.37) | 10.61 (8.99, 14.64) |
| SPM2 | 7.50 (5.39, 8.67) | 15.97 (12.00, 20.52) | 88.69 (76.80, 99.76) | 9.77 (8.69, 12.37) |
| N3 | 5.88 (5.36, 6.45) | 16.47 (14.75, 19.82) | 83.95 (77.03, 91.37) | 8.84 (8.15, 11.39) |
| NIC | 5.84 (5.30, 6.57) | 15.70 (12.32, 19.88) | 80.77 (74.95, 88.85) | 8.04 (7.18, 10.96) |
Coefficient of variation of white matter (CVWM), coefficient of variation of the gray matter (CVGM), coefficient of joint variation of white and gray matter (CJVWG), and classification error rate (CER) in the uncorrected original and corrected real images when using the SPM99, SPM2, N3, and NIC methods. Lower values denote lower bias field in the images.
Validation of NIC Using Phantom Images
Scatterplots of the applied versus extracted bias field (Fig. 5a,b) showed a slightly higher coefficient of correlation (r = 0.98) for the paraboloidal bias than for the sinusoidal one (r = 0.96). In the case of no bias field, the NIC algorithm proved to be robust: correlation between the original and corrected intensity values showed perfect agreement (r = 1.000) (Fig. 5c).
Figure 5.
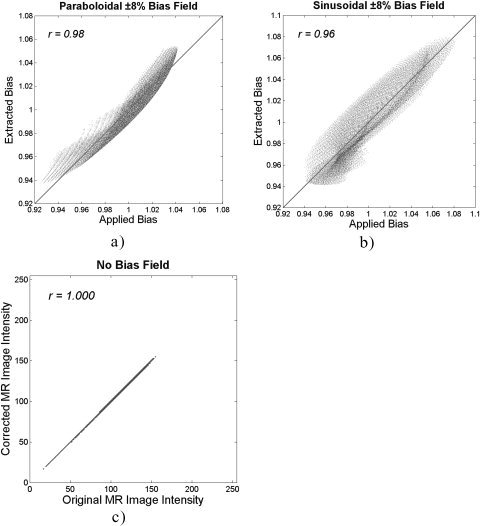
Scatterplots and correlation coefficients between the applied versus extracted bias on phantom images containing ±8% paraboloidal bias field (a), ±8% sinusoidal bias field (b), and no bias field (c).
Comparison to Other Methods Using Real Images
Maximum values of estimated bias field in the 0.5 T and 1.5 T images were 13.03 ± 3.03% and 17.92 ± 4.61%, respectively. The CER obtained after segmentation of these raw images without any bias correction showed a mean value of 10.29 ± 1.68% and 9.08 ± 1.33%, respectively, for the 0.5 T and 1.5 T image sets. Segmentation error was lower for the 1.5 T images, probably because of their better signal‐to‐noise ratio as compared to the 0.5 T images.
To assess improvement in segmentation due to reduction of bias field artifact, the four quality parameters were calculated in the original image and after correction with the N3, SPM'99, SPM2, and NIC algorithms.
The NIC algorithm achieved the highest reduction in the CJVWG and in the CER (Table II). This lower segmentation error reflects a more efficient reduction of the bias field artifact by the NIC algorithm. Although the reduction of the segmentation error achieved by the NIC algorithm (Table II) might seem too small to be relevant, it represents an improvement of 4.86% and 11.45% for the 0.5 and 1.5 T images, respectively, with respect to the original segmentation errors of the uncorrected images.
Figure 6 shows an example of MR scan corrected by the NIC algorithm. Figure 7 shows the evolution of the bias field estimation through several iterations, and the evolution of the corresponding segmentation can be seen in Figure 8.
Figure 6.
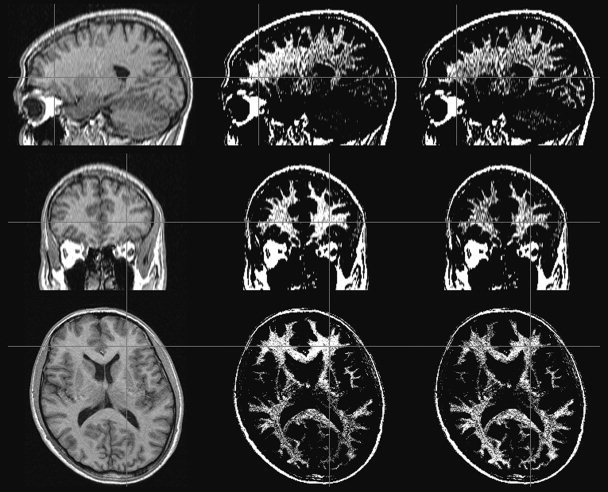
NIC algorithm applied to a real MR image. Left: Original image, where the intensity inhomogeneity is almost unnoticeable. Middle: Original image adjusting the window‐level around the mean intensity of the white matter. Note the smooth intensity variations caused by the bias field. Right: Corrected image with the same window level.
Figure 7.

Top: Evolution of the bias field along several iterations. Bottom: change in the estimated bias field per iteration. FWHM value corresponds to the smoothing gaussian kernel (see text).
Figure 8.
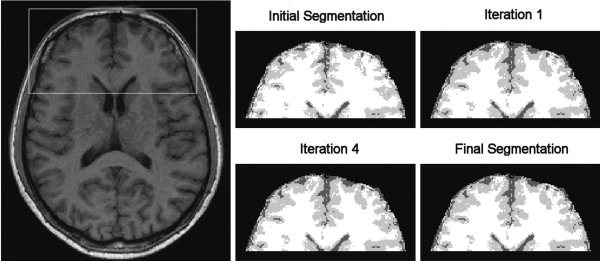
Evolution of the segmentation of the frontal lobe: initial image, first and fourth iterations and final result of the NIC algorithm.
DISCUSSION
Performance of NIC on Phantom Images
The validation with phantom images used the same methodology and datasets used in the reference work of Arnold et al. [2001], thus enabling a direct comparison with our results for the NIC algorithm. Arnold et al. [2001] showed that both N3 and BFC achieved the best performance when correcting the paraboloidal bias field (correlation coefficient between applied versus extracted fields, r = 0.98). N3 yielded the best results in the removal of the sinusoidal field (r = 0.96), and the HUM method introduced lower degradation when correcting phantom images without bias field (r = 0.999).
Comparing the applied versus extracted bias fields (Fig. 5), the NIC algorithm obtained the same correlation coefficient (r = 0.98) as N3 and BFC did for the ±8% parabolic bias field. The NIC algorithm also achieved the same quality as that of the N3 method in the correction of the ±8% sinusoidal bias field (r = 0.96). When correcting phantom images without bias field, the NIC method showed better results (r = 1.000) than did HUM (r = 0.999) and N3 (r = 0.997). Although it is debatable whether such small differences in the performance of the different methods on phantom images are relevant in practice, the performance of NIC has proven to be as good as that of the best available methods.
Summarizing the phantom‐based evaluation in a variety of bias field conditions, it can be stated that the NIC algorithm showed better performance in correcting the bias field than did the methods evaluated in Arnold et al. [2001] and was the only one that did not introduce degradation when no bias field was present.
Performance of NIC on Real Images
Regardless of the promising results obtained using phantom images, the potential usefulness of the NIC algorithm should be evaluated in the scope of practical applications of tissue segmentation of real sets of images. Our experimental setup allowed us to test the algorithm in high and low bias field conditions. The comparison of the performance in reducing the segmentation error achieved by the five methods tested (SPM99‐S, SPM99‐L, SPM2, N3, and NIC) suggested that the NIC algorithm was the more efficient method, as it consistently showed better values for all four quality criteria (Table II). The SPM99‐S and N3 methods, compared to the NIC algorithm, achieved a higher reduction of the CVGM in the 0.5 T images. The SPM99‐S method also yielded a better result for the CVWM for 0.5 T images. CJVWG and CER values, however, showed worse results for those methods, reaching an overall performance below that of the NIC algorithm.
Regarding the robustness of the different algorithms in low bias field conditions (at 0.5 T), NIC was the only method that did not degrade the original scans, still reducing the segmentation error with respect to the initial images (Table II). A possible reason for the worse results on 0.5 T images may be the lower contrast of these images. Our method, however, performed better than the others did without any particular tuning for this type of images. This result enables a systematic use of NIC in images with either intense or mild bias field artifact.
Regarding the consequences of the bias field correction on the quality of the segmentation, Chard et al. [2002] found significant improvement of the reproducibility of volume measurements of brain tissues after correcting intensity inhomogeneities with the SPM99 algorithm. An improvement in reproducibility of such measurements thus is expected also when using our method, given its superior performance with respect to SPM99.
The smoothing carried out on the bias field estimate had a significant impact on the results of the correction method. Conventional filtering techniques are unsatisfactory for this application due to boundary effects that significantly degrade overall performance [Sled et al., 1998]. Most standard methods model the bias field with low spatial frequency functions, such as a discrete cosine set [Ashburner and Friston, 2000; Ashburner, 2002], low order polynomials [Likar et al., 2001; Van Leemput et al., 1999a] or 3‐D splines [Sled et al., 1998]. The NIC algorithm uses a gaussian kernel to smooth the “residual” image. The degree of smoothing is a tunable parameter in all these methods; the highest bias field spatial frequency in both SPM99 and SPM2 algorithms corresponds, by default, to 1/8 of the image dimensions. For a standard field of view of 256 × 256 mm, the maximum frequency component corresponds to about 32 mm, as compared to the NIC algorithm, which uses a minimum FWHM of 50 mm.
The overall degree of smoothing in the N3 algorithm is the result of the combination of several parameters, such as the distance between the B‐spline basis functions and their smoothness, among others. It thus is difficult to determine the actual degree of smoothing. With NIC, however, the smoothness is directly expressed in spatial units.
A possible caveat in our evaluation procedure is that the CER, used as the goodness criteria minimized by the NIC algorithm, has also been one of the quality parameters used for assessing bias field correction. CER values thus might be prone to show better results in images corrected by the NIC algorithm. Nevertheless, we have shown also that the NIC algorithm achieves similarly good results when using the other quality criteria in both phantom and real image data sets (Tables I and II).
The NIC method requires the MR segmentation step to be able to identify white and gray matter, which may fail if the histogram has an unexpected shape, e.g., when correcting images from very high field scanners. In this case, as Mangin [2000] has shown for 3 T scanners, the image histogram may not show a bimodal distribution for white and gray matter. Although our work has applied the NIC algorithm only to T1‐weighted MR scans, its segmentation scheme allows a straightforward extension to multispectral images.
In summary, the new method (NIC) for correction of intensity inhomogeneities in MR images performed similar to previously described methods in removing the bias field from phantom images while not introducing degradation when no intensity inhomogeneity was present. The performance of the proposed algorithm in the correction of real MR images has also been compared to that of other three widely used methods (N3, SPM99, and SPM2). NIC achieved the best results for low (0.5 T) and high (1.5 T) bias field images, enabling its systematic use in images from both low and medium static field MR scanners. The NIC algorithm presented in this study seems a valuable alternative to methods currently available for bias field correction.
Footnotes
N3, nonparametric, nonuniform intensity normalization; HUM, homomorphic unsharp masking; EQ, equalize; BFC, bias field corrector; SPM, statistical parametric mapping.
Developed and provided by the Center for Morphometric Analysis at the Massachusetts General Hospital.
Available online at http://pet.med.va.gov:8080/distrib/nu_compare.html
N3: Available online at http://www.bic.mni.mcgill.ca/software/N3; SPM'99: http://www.fil.ion.ucl.ac.uk/spm; SPM2: http://www.fil.ion.ucl.ac.uk/spm/spm2b.html
Available online at http://www.bic.mni.mcgill.ca/brainweb/selection_normal.html
REFERENCES
- Ahmed MN, Yamany SM, Mohamed N, Farag AA, Moriarty T (2002): modified fuzzy C‐means algorithm for bias field estimation and segmentation of MRI data. IEEE Trans Med Imaging 21: 193–199. [DOI] [PubMed] [Google Scholar]
- Arnold JB, Liow JS, Schaper KA, Stern JJ, Sled JG, Shattuck DW, Worth AJ, Cohen MS, Leahy RM, Mazziotta JC, Rottenberg DA (2001): Qualitative and quantitative evaluation of six algorithms for correcting intensity nonuniformity effects. Neuroimage 13: 931–943. [DOI] [PubMed] [Google Scholar]
- Ashburner J (2002): Another MRI bias correction approach. In: 8th International Conference on Functional Mapping of the Human Brain, 25–28 September, Sendai, Japan.
- Ashburner J, Friston K (1997): Multimodal image coregistration and partitioning: a unified framework. Neuroimage 6: 209–217. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ (2000): Voxel‐based morphometry: the methods. Neuroimage 11: 805–821. [DOI] [PubMed] [Google Scholar]
- Atkins MS, Mackiewich BT (1998): Fully automatic segmentation of the brain in MRI. IEEE Trans Med Imaging 17: 98–107. [DOI] [PubMed] [Google Scholar]
- Brinkmann BH, Manduca A, Robb RA (1998): Optimized homomorphic unsharp masking for MR grayscale inhomogeneity correction. IEEE Trans Med Imaging 17: 161–171. [DOI] [PubMed] [Google Scholar]
- Brummer ME, Mersereau RM, Eisner RL, Lewine RR (1993): Automatic detection of brain contours in MRI datasets. IEEE Trans Med Imaging 12: 153–166. [DOI] [PubMed] [Google Scholar]
- Chard DT, Parker GJ, Griffin CMB, Thompson AJ, Miller DH (2002): The reproducibility and sensitivity of brain tissue volume measurements derived from an SPM‐based segmentation methodology. J Magn Reson Imaging 15: 259–267. [DOI] [PubMed] [Google Scholar]
- Cohen MS, DuBois RM, Zeineh MM (2000): Rapid and effective correction of RF inhomogeneity for high field magnetic resonance imaging. Hum Brain Mapp 10: 204–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, Evans AC (1998): Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging 17: 463–468. [DOI] [PubMed] [Google Scholar]
- Cusack R, Brett M, Osswald K (2003): An evaluation of the use of magnetic field maps to undistort echo‐planar images. Neuroimage 18: 127–142. [DOI] [PubMed] [Google Scholar]
- Dawant BM, Zijdenbos AP, Margolin RA (1993): Correction of intensity variations in MR images for computer‐aided tissue classification. IEEE Trans Med Imaging 12: 770–781. [DOI] [PubMed] [Google Scholar]
- DeCarli C, Murphy DGM, Teichberg D, Campbell G, Sobering GS (1996): Local histogram correction of MRI spatially dependent image pixel intensity nonuniformity. J Magn Reson Imaging 6: 519–528. [DOI] [PubMed] [Google Scholar]
- Deichmann R, Good CD, Turner R (2002): RF inhomogeneity compensation in structural brain imaging. Magn Reson Med 47: 398–402. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB (1977): Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc 39: 1–38. [Google Scholar]
- Good CD, Scahill RI, Fox NC, Ashburner J, Friston KJ, Chan D, Crum WR, Rossor MN, Frackowiak RS (2002): Automatic differentiation of anatomical patterns in the human brain: validation with studies of degenerative dementias. Neuroimage 17: 29–46. [DOI] [PubMed] [Google Scholar]
- Guillemaud R, Brady M (1997): Estimating the bias field of MR images. IEEE Trans Med Imaging 16: 238–251. [DOI] [PubMed] [Google Scholar]
- Johnston B, Atkins MS, Mackiewich B, Anderson M (1996): Segmentation of multiple sclerosis lesions in intensity corrected multispectral MRI. IEEE Trans Med Imaging 15: 154–169. [DOI] [PubMed] [Google Scholar]
- Lawrie SM, Abukmeil SS (1998): Brain abnormality in schizophrenia. A systematic and quantitative review of volumetric magnetic resonance imaging studies. Br J Psychiatry 172: 110–120. [DOI] [PubMed] [Google Scholar]
- Likar B, Viergever MA, Pernus F (2001): Retrospective correction of MR intensity inhomogeneity by information minimization. IEEE Trans Med Imaging 20: 1398–1410. [DOI] [PubMed] [Google Scholar]
- Mangin JF (2000): Entropy minimization for automatic correction of intensity nonuniformity In: IEEE workshop in mathematical methods in biomedical image analysis. Hilton Head Island. SC: IEEE Press; p 162–169. [Google Scholar]
- Marroquin JL, Vemuri BC, Botello S, Calderón F, Fernández‐Bouzas A (2002): An accurate and efficient bayesian method for automatic segmentation of brain MRI. IEEE Trans Med Imaging 21: 934–945. [DOI] [PubMed] [Google Scholar]
- Miller DH, Barkhof F, Frank JA, Parker GJ, Thompson AJ (2002): Measurement of atrophy in multiple sclerosis: pathological basis, methodological aspects and clinical relevance. Brain 125: 1676–1695. [DOI] [PubMed] [Google Scholar]
- Pham DL, Prince JL (1999): Adaptive fuzzy segmentation of magnetic resonance images. IEEE Trans Med Imaging 18: 737–752. [DOI] [PubMed] [Google Scholar]
- Ruan S, Jaggi C, Xue J, Fadili J, Bloyet D (2000): Brain tissue classification of magnetic resonance images using partial volume modeling. IEEE Trans Med Imaging 19: 1179–1187. [DOI] [PubMed] [Google Scholar]
- Santago P, Gage HD (1995): Statistical models of partial volume effect. IEEE Trans Image Process 4: 1531–1540. [DOI] [PubMed] [Google Scholar]
- Schomberg H (1999): Off‐resonance correction of MR images. IEEE Trans Med Imaging 18: 481–495. [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Sandor‐Leahy SR, Schaper KA, Rottenberg DA, Leahy RM (2001): Magnetic resonance image tissue classification using a partial volume model. Neuroimage 13: 856–876. [DOI] [PubMed] [Google Scholar]
- Simmons A, Tofts PS, Barker GJ, Arridge SR (1994): Sources of intensity nonuniformity in spin echo images at 1.5 T. Magn Reson Med 32: 121–128. [DOI] [PubMed] [Google Scholar]
- Sled JG, Pike GB (1998): Standing‐wave and RF penetration artifacts caused by elliptic geometry: an electrodynamic analysis of MRI. IEEE Trans Med Imaging 17: 653–662. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC (1998): A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging 17: 87–97. [DOI] [PubMed] [Google Scholar]
- Stokking R, Vincken KL, Viergever MA (2000): Automatic morphology‐based brain segmentation (MBRASE) from MRI‐T1 data. Neuroimage 12: 726–738. [DOI] [PubMed] [Google Scholar]
- Van Leemput K, Maes F, Vandermeulen D, Suetens P (1999a): Automated model‐based bias field correction of MR images of the brain. IEEE Trans Med Imaging 18: 885–896. [DOI] [PubMed] [Google Scholar]
- Van Leemput K, Maes F, Vandermeulen D, Suetens P (1999b): Automated model‐based tissue classification of MR images of the brain. IEEE Trans Med Imaging 18: 897–908. [DOI] [PubMed] [Google Scholar]
- Velthuizen RP, Cantor AB, Lin H, Fletcher LM, Clarke LP (1998): Review and evaluation of MRI nonuniformity correction for brain tumor response measurements. Med Phys 25: 1655–1666. [DOI] [PubMed] [Google Scholar]
- Vokurka EA, Thacker NA, Jackson A (1999): A fast model independent method for automatic correction of intensity nonuniformity in MRI data. J Magn Reson Imaging 10: 550–562. [DOI] [PubMed] [Google Scholar]
- Vokurka EA, Watson NA, Watson Y, Thacker NA, Jackson A (2001): Improved high resolution MR imaging for surface coils using automated intensity non‐uniformity correction: feasibility study in the orbit. J Magn Reson Imaging 14: 540–546. [DOI] [PubMed] [Google Scholar]
- Weinberger DR, McClure RK (2002): Neurotoxicity, neuroplasticity, and magnetic resonance imaging morphometry: what is happening in the schizophrenic brain? Arch Gen Psychiatry 59: 553–558. [DOI] [PubMed] [Google Scholar]
- Wells WM, Grimson WEL, Kikinis R, Jolesz FA (1996): Adaptive segmentation of MRI data. IEEE Trans Med Imaging 15: 429–442. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S (2001): Segmentation of brain MR images through a hidden Markov random field model and the expectation‐maximization algorithm. IEEE Trans Med Imaging 20: 45–57. [DOI] [PubMed] [Google Scholar]


