Monte Carlo simulation studies of EEG and MEG localization accuracy

Abstract

Both electroencephalography (EEG) and magnetoencephalography (MEG) are currently used to localize brain activity. The accuracy of source localization depends on numerous factors, including the specific inverse approach and source model, fundamental differences in EEG and MEG data, and the accuracy of the volume conductor model of the head (i.e., the forward model). Using Monte Carlo simulations, this study removes the effect of forward model errors and theoretically compares the use of EEG alone, MEG alone, and combined EEG/MEG data sets for source localization. Here, we use a linear estimation inverse approach with a distributed source model and a realistic forward head model. We evaluated its accuracy using the crosstalk and point spread metrics. The crosstalk metric for a specified location on the cortex describes the amount of activity incorrectly localized onto that location from other locations. The point spread metric provides the complementary measure: for that same location, the point spread describes the mis‐localization of activity from that specified location to other locations in the brain. We also propose and examine the utility of a “noise sensitivity normalized” inverse operator. Given our particular forward and inverse models, our results show that 1) surprisingly, EEG localization is more accurate than MEG localization for the same number of sensors averaged over many source locations and orientations; 2) as expected, combining EEG with MEG produces the best accuracy for the same total number of sensors; 3) the noise sensitivity normalized inverse operator improves the spatial resolution relative to the standard linear estimation operator; and 4) use of an a priori fMRI constraint universally reduces both crosstalk and point spread. Hum. Brain Mapping 16:47–62, 2002. © 2002 Wiley‐Liss, Inc.

INTRODUCTION

The electromagnetic inverse problem for the human brain is to determine the neural source distribution that gives rise to external electromagnetic potentials and fields, measured by electroencephalography (EEG) and magnetoencephalography (MEG), respectively. There is great interest in the assessment of the relative accuracy of EEG and MEG for source localization. The accuracy of a solution to the inverse problem using EEG and MEG data depends on numerous factors, however, including the particular inverse approach and source model, fundamental differences in EEG and MEG data, and the accuracy of the volume conductor model of the head (i.e., the forward model).

There has been some debate over the relative accuracy of EEG or MEG based source localization. Experimental EEG studies using phantoms [Henderson et al., 1975] and implanted electrodes in epilepsy patients [Smith et al., 1983, 1985] have been reported. Those studies found a localization accuracy of 10 mm for the phantoms to 20 mm in the patients. In comparison, MEG studies reported localization accuracy of 3 mm in spherical phantoms [Barth et al., 1986; Hansen et al., 1988; Janday and Swithenby, 1987; Yamamoto et al., 1988] and 4–8 mm for skull phantoms [Barth et al., 1986; Janday and Swithenby, 1987; Weinberger et al., 1986; Yamamoto et al., 1988]. Based on these results, it has been commonly assumed that MEG localization accuracy is far superior to that of EEG.

There were theoretical reasons, however, to believe that the MEG and EEG accuracy should be comparable. In an attempt to directly address this controversy, both MEG and EEG measurements were made while generating current dipoles from implanted electrodes in an epilepsy patient [Cohen et al., 1990]. A sinusoidal stimulus waveform was used to remove the spike artifacts that likely contributed to the poor EEG localization performance of the previous EEG measurements [Smith et al., 1983, 1985]. The average MEG and EEG localization errors for dipoles with sufficiently good signal to noise were found to be 8 mm and 10 mm, respectively [Cohen et al., 1990]. These results suggested that MEG and EEG provide comparable accuracy.

Unfortunately, further experimental data have not necessarily clarified this issue of relative accuracy. Phantom studies have reported localization accuracy for EEG of 7–8 mm [Leahy et al., 1998] and for MEG of 2–4 mm [Gharib et al., 1995; Leahy et al., 1998; Menninghaus et al., 1994]. The localization superiority of MEG over EEG is less obvious in data from measurements made in patients. Using data generated from artificial current dipoles implanted in epilepsy patients the localization accuracy of EEG was 10–17 mm [Cuffin et al., 1991; Cuffin, 1996; Krings et al., 1999] with the best EEG accuracy in one patient of 1–4 mm [Cuffin, 1996]. This is compared to a localization accuracy of 17 mm for MEG measurements of artificial dipoles generated from implanted subdural strips [Balish et al., 1991]. Other studies have estimated accuracy by comparing lesion data (e.g., tumor, epileptogenic focus) in epileptic patients with the non‐invasive location estimates from EEG [Diekmann et al., 1998; Herrendorf et al., 2000; Ko et al., 1998; Krings et al., 1998; Nakasato et al., 1994] or MEG [Diekmann et al., 1998; Ko et al., 1998; Mikuni et al., 1997; Nakasato et al., 1994; Sutherling et al., 1987, 1988a,b; Stefan et al., 1994; Tiihonen et al., 1990]. Similar to the results of the artificial current dipoles, the EEG and MEG accuracy were comparable (ranging from 10–20 mm).

Generally, in experimental studies it is difficult to separate the effect of errors in the head model from localization errors due to inherent differences between EEG and MEG. Specifically, there are fundamental differences between the forward solution accuracy required by EEG and MEG, with MEG requiring a simpler model [Hamalainen and Sarvas, 1989; Meijs et al., 1987, 1989]. Therefore, one would expect better accuracy for experimental MEG data using the more accurate MEG head model. Through the use of modeling studies, it is possible to examine the relative accuracy of EEG and MEG by using the same forward solution to generate both the synthetic external EEG/MEG measurements and the resulting inverse solution. In other words, modeling studies can examine EEG and MEG localization accuracy unbiased by possible inaccuracies in the forward model that may differentially affect localization of experimental EEG or MEG measurements. Even the modeling studies, however, have been equivocal. Some modeling work found MEG to be more accurate than EEG [Murro et al., 1995; Stok, 1987], whereas others found EEG and MEG accuracy to be comparable [Malmivuo et al., 1997], or EEG accuracy better than MEG [Mosher et al., 1993; Pascual‐Marqui and Biscay‐Lirio, 1993].

Clearly, the data from phantoms, patients, and theoretical studies give conflicting evidence for the relative accuracy of EEG and MEG. There are numerous confounding factors in the interpretation of all of these data. For example, experimental measurements in phantoms and living human heads may reflect the higher accuracy of the MEG forward solution, measurement errors, or differences in signal to noise. Also, many of the modeling studies used spherical head models with differences between EEG and MEG sensor sampling.

Here, we specifically examined inherent differences in EEG and MEG data by using a single realistic head model for the both the forward and inverse computations. In other words, we have removed the effect of forward model errors from our analysis. For these model studies, we used 1) a linear estimation technique; 2) a distributed source model; 3) a realistic forward head model; and 4) similar EEG and MEG sensor placement. In addition, we present a noise sensitivity normalized inverse operator that is based on the linear estimation approach. Monte Carlo modeling studies (sampling over numerous source locations, size and orientations) were used to determine the theoretical limits (i.e., assuming no errors in the head model) of EEG and MEG localization using our particular source model and inverse procedure. Localization estimates were computed using MEG or EEG data, both separately and combined. The effect of sensor sampling density (i.e., number of sensors) was also examined. In addition, as it is becoming more common to utilize other spatial information, such as functional magnetic resonance imaging (fMRI), we also modeled the effect of fMRI spatial constraints on the relative accuracy of EEG and MEG source localization [Liu et al., 1998].

Previous ECD localization accuracy studies typically report error in millimeters between known and modeled dipole locations. Unfortunately, it is difficult to characterize localization accuracy in terms of a distance error for the linear estimation approach using a distributed source model because of the extended nature of the localization estimates. It is more appropriate to define localization accuracy and resolution in terms of metrics that include the spatial aspect of the extended source distributions. Therefore, we quantified localization accuracy using a crosstalk metric [Liu et al., 1998] and a point spread metric that are specified by the resolution matrix [Grave de Peralta Menendez et al., 1996, 1997; Grave de Peralta‐Menendez and Gonzalez‐Andino, 1998; Lutkenhoner and Grave de Peralta Menendez, 1997; Menke, 1989]. These two metrics provide complementary accuracy information. They specify from where and to where activity is incorrectly localized. The crosstalk metric for a specified location on the cortex describes the amount of activity incorrectly localized onto that location from other locations. The point spread metric provides the complementary measure: for that same location, the point spread describes the mis‐localization of activity from that specified location to other locations in the brain. Lower crosstalk and point spread values indicate higher localization accuracy.

The crosstalk and point spread metrics are also useful beyond the context of these modeling studies. When analyzing experimental data, one can calculate crosstalk and point spread maps that are only based upon the inverse operator and forward solution, and are independent of the actual experimental data. For a given estimated distribution of cortical activity, these maps can aid in determining the confidence of the spatiotemporal estimates. For example, if one were to estimate the activity at a location that had a focal crosstalk and point spread map, one would be more confident that this estimate was, in fact, correct.

METHODS

Forward solution

The realistic boundary element method (BEM) was adapted for calculating both the EEG and MEG forward solutions [de Munck, 1992; Oostendorp and van Oosterom, 1989]. Both forward solution computations require the locations of all possible sources, the sensor locations, and the sensor orientations (for MEG only). For this analysis, we restricted all sources to be within the cortex of the brain. Therefore, by construction, we did not analyze non‐cortical structures, such as the cerebellum and basal ganglia. Each possible cortical source was represented by a current dipole oriented normal to the cortical surface, i.e., both the location and orientation were constrained by the cortical surface.

The computation of the MEG forward solution has been shown to only require the inner skull boundary to achieve an accurate solution [Hamalainen and Sarvas, 1989; Meijs et al., 1987, 1989]. The EEG forward solution computation requires the specification of boundaries between brain and skull, skull and scalp, scalp and air, and the relative conductivities of each of those regions. We assumed conductivity ratios of 1:0. 0125:1 for brain:skull:scalp [Cuffin, 1990].

The conductivity boundaries required for computation of the EEG and MEG forward solutions were automatically reconstructed from a high‐resolution T1‐weighted 3D MRI using our previously described technique [Dale et al., 1999; Dale and Sereno, 1993; Fischl et al., 1999]. The realistic surfaces used in our calculations are shown in Figure 1. Each of the conductivity boundaries was represented by 642 vertices. The cortical surface was initially tessellated with about 150,000 vertices per hemisphere. For the inverse computation, the cortical surface was decimated to approximately 3,000 dipoles per hemisphere, which is roughly equivalent to 1 dipole every 10 mm along the cortical surface.

Figure 1.

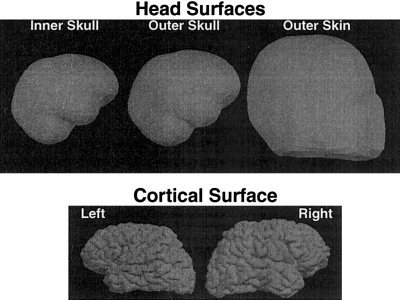
EEG/MEG forward solution surfaces. The top figures show the three head surfaces used in the calculation of the forward solutions. The bottom figures are the left and right cortical surfaces used to determine the locations and orientations of the sources. The MEG forward solution was computed using only the inner skull surface, whereas the EEG forward solution requires all three boundaries.

The computation of the forward solution also requires specification of the EEG electrode or MEG sensor locations. We began with a realistic sensor description of 122 MEG sensors [Knuutila et al., 1993], which is the same configuration that was used in our previous modeling study [Liu et al., 1998]. The 122 MEG sensors are placed at 61 discrete locations, with two orthogonal planar gradiometers at each location. The 61 locations were subsampled to 30 locations. Both the 61 and 30 locations were distributed over the entire head. For the two sets of locations, we created three types of MEG sensor configurations: magnetometer, radial gradiometer, and two orthogonal planar gradiometers. To minimize effects from sampling differences, the EEG sensor locations were determined by projecting the 61 and 30 MEG locations onto the outer skin. We also modeled the effects of using various combinations of MEG and EEG sensor configurations. The MEG sensor locations are shown in Figure 2, overlaid on an axial maximum intensity projection of the T1‐weighted MRI. The EEG sensor locations are shown similarly in Figure 3.

Figure 2.

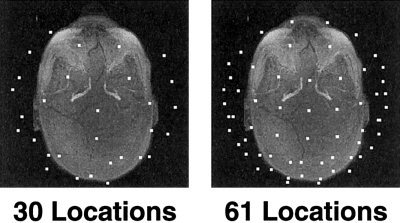
MEG sensor locations. Two different sets of locations.

Figure 3.

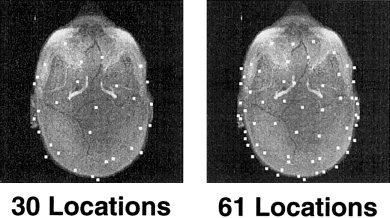
EEG sensor locations. Two different sets of locations.

For the combined EEG/MEG sensor configurations, the gain matrix (A) contains both the EEG and MEG forward solutions that were calculated separately. The dimensions of the combined gain matrix are [(number of EEG sensors plus number of MEG sensors) × (number of dipoles)].

Inverse operator

The linear inverse operator used here can be derived in various ways. In the appendix, we detail four different derivations: 1) minimization of expected error [Dale and Sereno, 1993]; 2) Bayesian formulation [Gelb, 1974; Phillips et al., 1997a,b]; 3) Tichonov regularization [Tichonov and Arsenin, 1977]; and 4) generalized Wiener filtering [Deutsch, 1965; Smith, 1992; Sekihara and Scholz, 1995, 1996]. Assuming appropriate initial conditions, all derivations result in the following (or equivalent) expression for the linear inverse operator:

(1)

Crosstalk metric

To quantify one aspect of the accuracy of the linear estimation technique, we used a crosstalk metric [Liu et al., 1998], which is similar to the averaging kernel of the Backus‐Gilbert method [Backus and Gilbert, 1970]. The crosstalk metric describes the sensitivity of the estimate at a specified location to activity at other locations. A location with lower crosstalk is less biased by activity at other locations, and provides a more accurate estimate for activity at that location. A more formal description of the crosstalk metric follows.

The estimated source strength (ŝ _i) at each location i can be written as a weighted sum of the actual source strengths at all locations, plus a noise contribution. This is due to the linearity of both the forward solution and this inverse operator. More formally,

(2)

(3)

(4)

(5)

where W _i is the ith row of W, and ã _j is the jth column of à (i.e., the “true” lead field including orientation information at location j). Depending on the particular type of mis‐specification being examined through model studies, A (the forward model used in the calculation of W) and à (the forward model with no errors) may or may not be equivalent. Note, that when determining the crosstalk metric for experimental data, A and à will always be the same. The first term in equation (5) is the sum of the activity (s _j) at every location j, weighted by the scalar w _i ã _j. The second term reflects the noise contribution to the estimated activity at location i.

An explicit expression for the relative sensitivity of the estimate for a given location (i) to activity coming from other locations (j) is desired. A crosstalk metric (ξ) is defined as follows:

(6)

where WÃ is the resolution matrix [Grave de Peralta Menendez et al., 1996, 1997; Grave de Peralta‐Menendez and Gonzalez‐Andino, 1998; Lutkenhoner and Grave de Peralta Menendez, 1997; Menke, 1989].

By comparing equations (5) and (6), one can see that the crosstalk metric ξ_ij describes the sensitivity (or weighting) of the estimate at location i to activity at location j relative to activity at location i. A crosstalk value of 0% means that the estimated activity at location i is completely insensitive to activity at location j. A crosstalk value of 100% means that the estimated activity at location i is equally sensitive to activity at locations i and j. For any particular location, the crosstalk from all other locations can be calculated. For some particular location i, this computation corresponds to the ith row of the resolution matrix (WA). We refer to this spatial representation of the crosstalk metric as the “crosstalk map” for the specified location.

Both the crosstalk metric and the crosstalk map are specified for a given source. To simplify the representation of the crosstalk at all locations, we define an average crosstalk map (ACM). For each location on the cortical surface we compute the average of the crosstalks between the specified location (i) location and all other locations (j) on the surface:

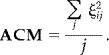(7)

Point spread metric

Closely related to the crosstalk metric is the point spread metric. The point spread for a location i describes the sensitivity of the estimates at other locations j to activity at location i. A location with lower point spread has a smaller spatial extent. The point spread metric (ρ) is defined as:

(8)

where WÃ is the resolution matrix. The point spread map, more commonly known as the point spread function (PSF), for a given location i corresponds to the ith column of the crosstalk matrix (WA). Similar to the average crosstalk map, we define the average PSF maps (APSF). For each location we average the point spread between the specified location (i) location and all other locations (j) on the surface:

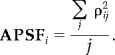(9)

One can see that crosstalk and point spread are closely related. The crosstalk map and the point spread map correspond to the rows and columns, respectively, of the resolution matrix WA. In the linear estimation framework examined up to this point, we can show that the resolution matrix is symmetric, and therefore the crosstalk map and the PSF for a given location are equivalent. The resolution matrix is given by:

(10)

The transpose of the resolution matrix is:

(11)

(12)

The term inside the parentheses is also symmetric (since the noise covariance matrix, C, is symmetric):

(13)

The source covariance matrix (R) is also symmetric, so we can rewrite equation (12):

(14)

Because the term, A ^T(ARA ^T + C)⁻¹ A, and R are both symmetric, we have:

(15)

thus, demonstrating that the resolution matrix is symmetric.

The relationship between the crosstalk metric and the point spread metric can be more easily seen graphically (Fig. 4). The location of interest (i.e., location i) is marked in green. The arrows indicate the “direction” of mis‐specification, or where activity is mis‐localized. The crosstalk metric describes the activity from other locations that is mis‐localized onto the location of interest (arrows point towards location i). Conversely, the point spread metric describes activity that is mis‐localized from location i (arrows point away from location i).

Figure 4.

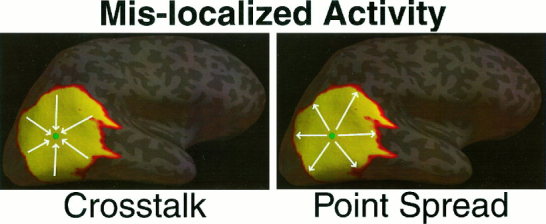
Mis‐localized activity specified by the Crosstalk and the Point Spread metrics. The arrows indicate the “direction” of mis‐specification.

Given that the crosstalk map and the point spread function are equivalent for the linear estimation operator, our discussion applies equally to both. Various suggested improvements to the linear estimation technique, however, will result in a non‐symmetric resolution matrix. For example, the Backus‐Gilbert method [Backus and Gilbert, 1970; Grave de Peralta Menendez et al., 1996; Grave de Peralta Menendez and Gonzalez Andino, 1999] that explicitly minimizes the crosstalk, will result in some sort of tradeoff with the point spread function. Our noise normalized linear inverse, presented below, also yields a non‐symmetric resolution matrix.

Noise sensitivity normalization

Similar to the statistical analysis of functional MRI, we are primarily interested in locations whose activity (i.e., “signal”) is significantly larger than the noise. Therefore, we propose to normalize each row of the inverse operator based on the noise sensitivity of the inverse operator at that location. Locations that have low noise sensitivity are given a larger weighting than those locations with high noise sensitivity. We can estimate the noise sensitivity by projecting the noise covariance estimate into the inverse operator. The new inverse operator will be pre‐multiplied by a diagonal noise sensitivity matrix (D), square in the number of dipoles, where each diagonal element is:

(16)

The noise sensitivity normalized inverse is now:

(17)

The resulting activity estimates will now resemble an F‐statistic, instead of an activation power [Dale et al., 2000]. Our new activity estimates, ŝ ${}_{\text{ns\_norm}}^{\text{i}}$, at each location i, which we refer to as “noise sensitivity normalized estimates”, are:

(18)

For these model studies, we have assumed Gaussian, white noise, so the noise covariance matrix (C) is a multiple of the identity matrix. In this particular case, this noise sensitivity normalization corresponds to normalizing the rows of the inverse operator by the norm of the row:

(19)

We note that because we are scaling each row of W by a single value, the rows of the resolution matrix are simply scaled by that same value. Therefore our crosstalk metric remains unchanged with this noise sensitivity normalization. The PSF, however, will be affected since the scaling of each column of W is not uniform.

Monte Carlo simulations

As pointed out by numerous authors [e.g., Fuchs et al., 1998; Hari et al., 1988; Liu et al., 1998; Murro et al., 1995; Supek and Aine, 1993], localization accuracy is highly dependent on the location of the source. Therefore, to better approximate realistic data which can occur anywhere in the brain, our simulations use a large random sampling of source locations to provide an average estimate of localization accuracy.

Either 5, 10, or 20 sources were randomly located on the cortical surface, each with varying volumetric extent (1 cm or 2 cm diameter). The random selection ensures no systemic location bias in these model studies. The numbers and extents of sources were chosen to represent experimentally realistic regions of brain activity that might be seen with a given cognitive task. The diagonal elements of R (the a priori source covariance estimates R _ii = σ${}_{\text{2}}^{\mathit{\text{i}}}$) were set to 1 or 0.01. These values correspond to fMRI weightings of 0% (equivalent to minimum norm) and 90%, respectively. Previous modeling studies suggest that an fMRI weighting of 90% represents a reasonable compromise between separation of activity from correctly localized sources (by fMRI) and minimization of error due to missing fMRI sources [Liu et al., 1998].

We made no a priori assumptions about source correlation. Therefore, the off‐diagonal elements of R were set to zero, i.e., R _ij = 0 for i ≠ j. It should be noted that this does not force the sources to be uncorrelated or orthogonal in time. Noise was assumed to be additive, Gaussian, uniform, and spatially uncorrelated. More precisely, 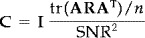, where I is the identity matrix, tr is the trace of a square matrix, SNR is the assumed rms signal‐to‐noise ratio, and n is the number of sensors. Here, a conservative SNR of 10 was assumed.

In these model studies, the number of MEG sensors was assumed to be either 30, 60 (30 locations with two orthogonal planar gradiometers), 61 or 122 (61 locations with two orthogonal planar gradiometers), with the smaller numbers of sensors subsampled from the complete 122 channel description to still give full head coverage at a sparser sampling. For the EEG sensors, 30 or 61 sensors were distributed over the entire head. To minimize any sampling differences between MEG and EEG, the locations of the EEG sensors were based on the corresponding MEG sensor configuration projected down onto the outer skin surface. In addition, all combinations of MEG and EEG sensors were studied. For each of the sensor configurations, the crosstalk was averaged over the different number and extent of sources.

For comparison of the noise sensitivity normalized inverse, the average crosstalk map and the average PSF were computed at each source location. No fMRI weighting was used, thus removing the need for Monte Carlo simulations.

One additional set of modeling studies was performed here. In computing the EEG forward solution, conductivity ratios, not exact conductivities, of the different head regions were used. If the actual conductivities differ from the assumed conductivities, even though the conductivity ratios are correctly estimated, then the computed source activities using EEG will not be in the same units as the computed source activities using MEG. This effectively introduces a scaling factor between the EEG and MEG forward solutions [Fuchs et al., 1998]. We modeled the effect of mis‐estimating the scaling factor between EEG and MEG forward solutions (corresponding to the mis‐estimate of the actual conductivities) from 0.2–5. The scaling factor was incorporated into the combined EEG/MEG forward solution by multiplying those rows corresponding to EEG sensors by the factor. This scaled gain matrix was used in the computation of the inverse operator. The correct gain matrix (i.e., a scaling factor of 1) was used for the crosstalk metric computation. More explicitly, if we represent the scaled forward solution by A _s and the true forward solution by Ã, the crosstalk matrix is given by:

(20)

For this portion of the model studies, we assumed 30 EEG electrodes and 30 MEG radial gradiometers, and an fMRI weighting of 90%.

RESULTS

Figures 5 and 8 show the average crosstalk vs. sensor configuration. No fMRI weighting (equivalent to minimum norm) was used in Figure 5. An fMRI weighting of 90% was used in Figure 8. As a reminder, the crosstalk metric specifies the amount of variance from another location that is incorrectly mapped to the location of interest.

Figure 5.

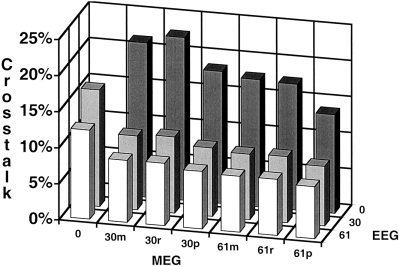
Average crosstalk vs. sensor number; no fMRI weighting. The sensor configuration consisted of 30 magnetometers (30m), 30 radial gradiometers (30r), 60 orthogonal planar gradiometers (30p), 61 magnetometers (61m), 61 radial gradiometers (61r), 122 orthogonal planar gradiometers (61p), 30 EEG sensors, 61 EEG sensors, and all possible combinations of MEG and EEG sensors. The crosstalk values were averaged over a range of source number (5, 10, or 20 sources) and extent (1 cm or 2 cm in diameter).

Figure 8.

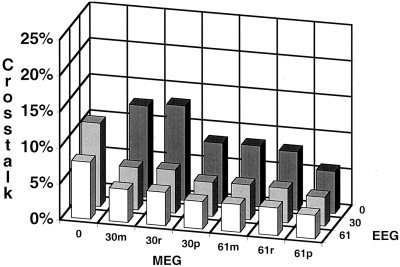
Average crosstalk vs. sensor number; 90% fMRI weighting. The sensor configuration consisted of 30 magnetometers (30m), 30 radial gradiometers (30r), 60 orthogonal planar gradiometers (30p), 61 magnetometers (61m), 61 radial gradiometers (61r), 122 orthogonal planar gradiometers (61p), 30 EEG sensors, 61 EEG sensors, and all possible combinations of MEG and EEG sensors. The crosstalk values were averaged over a range of source number (5, 10, or 20 sources) and extent (1 cm or 2 cm in diameter).

Increasing the number of sensors for both MEG and EEG decreases the average crosstalk (i.e., improves average localization accuracy). There is little difference between equal numbers of magnetometers, radial gradiometers or planar gradiometers. The average crosstalk for the EEG configurations is smaller than that for the same number of MEG sensors. Perhaps most importantly, there is a large decrease in crosstalk with the combined sensor configurations.

The average crosstalk map and average PSF map for three different sensor configurations (60 MEG planar gradiometers, 61 EEG sensors and the combined 61 EEG/ 60 MEG sensors) are shown on the inflated cortical surface in Figure 6. No fMRI weighting was used. As expected, the crosstalk and PSF maps are equivalent. For the same number of sensors, EEG (7.7% ± 6.1%) has lower average crosstalk than MEG (17.3% ± 37.0%). This difference is largely due to the very large crosstalk for MEG measurements of the deep or radial sources. The combined EEG/MEG sensor configuration provides the lowest average crosstalk. There is large spatial variability in the crosstalk map, especially for the MEG sensors, demonstrating that the crosstalk map and point spread are highly dependent of the cortical location of the source. For both MEG and EEG, the crosstalk is larger in the depths of the sulci than on the gyri, with the largest crosstalk in the insula, inferior frontal and superior temporal cortex. The MEG average crosstalk maps also demonstrate the orientation dependence of MEG. For MEG, source locations on the crowns of gyri that are largely radial in orientation have very high average crosstalk (e.g., see white arrow).

Figure 6.

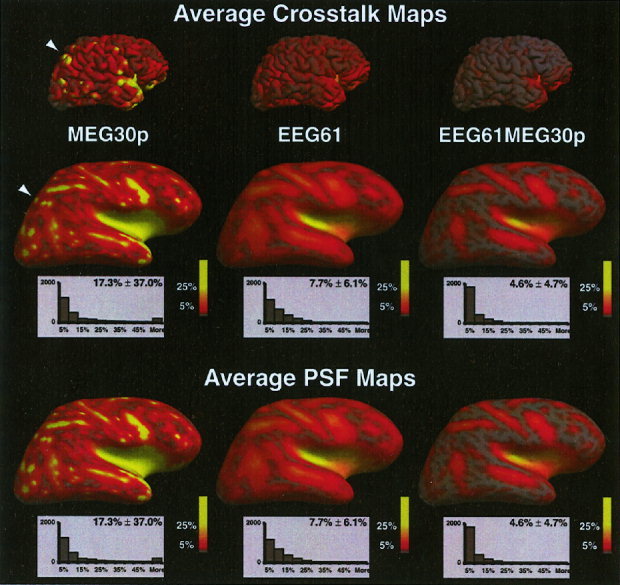
Average crosstalk map and average point spread function map at each location for three different sensor configurations. The average crosstalk or point spread for each location is encoded in color. Full red equals 5% and full yellow equals 25% crosstalk or point spread. Below each map is the histogram of the number of dipoles with average crosstalk/point spread values within a 5% bin. No fMRI weighting was used.

The average crosstalk and average PSF maps for three different sensor configurations (60 MEG planar gradiometers, 61 EEG sensors and the combined 61 EEG/ 60 MEG sensors) using the noise sensitivity normalized inverse operator are shown in Figure 7. No fMRI weighting was used. The crosstalk maps are unchanged from Figure 6. The PSF maps are greatly different, however, especially for 60 MEG planar gradiometers alone. There is greater spatial uniformity and no PSFs are greater than 20% with the noise sensitivity normalized inverse. The average PSF over all locations is lower for the normalized inverse, with the largest gain occurring for MEG sensors alone (70% lower).

Figure 7.

Average crosstalk and average PSF maps for the noise sensitivity normalized inverse operator. The average crosstalk or point spread for each location is encoded in color. Full red equals 5% and full yellow equals 25% crosstalk or point spread. Below each map is the histogram of the number of dipoles with average crosstalk/point spread values within a 5% bin. No fMRI weighting was used.

The general trend of the results using fMRI weighting (Fig. 8) is similar to that without fMRI weighting (Figure 5). The addition of fMRI information results in lower crosstalk for all sensor configurations. However, it should be noted that this improvement is for those sources that are correctly specified by fMRI. In cases where fMRI has mis‐specified the source, crosstalk increases relative to the fMRI unweighted solution shown in Figure 5 [Liu et al., 1998]. Increasing the number of sensors, regardless of the type, improves localization accuracy. The localization accuracy for the same number of sensors is only slightly better with EEG. The average crosstalk for the combined EEG and MEG sensors is lower than either EEG or MEG alone, with 61 EEG and 122 MEG (61p) sensors providing the lowest crosstalk of the different sensor configurations studied.

The observed improvement in localization accuracy obtained by combining EEG and MEG data assumes that one knows the proper scaling factor between the two forward solutions. If this scaling factor is unknown, additional errors can arise. Figure 9 demonstrates the effect of mis‐specifying the EEG/MEG scaling factor.

Figure 9.

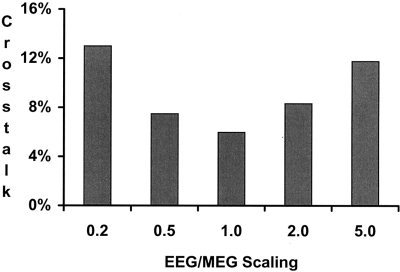
Average crosstalk vs. EEG/MEG forward solution scaling. A sensor configuration of 30 EEG sensors and 30 MEG radial gradiometers was used. An fMRI weighting of 90% was used. The scaling factor between the EEG and MEG forward solutions was varied from 0.2–5. A scaling factor of 1 assumes no error in the scaling between EEG and MEG forward solutions. The crosstalk values were averaged over a range of source number (5, 10, or 20 sources) and extent (1 cm or 2 cm in diameter).

An increasing discrepancy between the EEG and MEG forward solution (modeled by a deviation of the EEG/MEG scaling factor from unity) results in increasingly larger average crosstalk.

DISCUSSION

Assuming equal SNR, changes in the sensor configuration produce similar results independent of the use of fMRI weighting. Not surprisingly, increasing sensor number, regardless of the type of MEG sensor, results in improved localization accuracy. Comparing MEG to EEG for the same number of sensors, we see that, on average, EEG is superior to MEG. In fact, when using no fMRI weighting, 30 EEG sensors (16.1%) are comparable to 61 MEG magnetometers (17.6%) or radial gradiometers (17.4%). The superiority of EEG over MEG results from the greater depth and orientation sensitivity of MEG. For EEG sensors alone, there are no average crosstalk values greater than 40%. In comparison, for 60 MEG planar gradiometers, 12% of the sources have average crosstalk values greater than 40%. These sources fall into two categories: deep cortical sources and sources that are largely radial in orientation. Although the fMRI weighting constraint reduces crosstalk for properly detected sources in all cases, the relative difference between EEG and MEG are less pronounced with fMRI weighting. When including the fMRI constraint, the crosstalk is largely defined by the spatial priors provided by the fMRI. Subsequently, the inverse operator is less sensitive to depth and orientation.

The lowest crosstalk is achieved by combining EEG and MEG sensors. Using 61 EEG sensors and 122 MEG planar gradiometers together results in one‐third of the average crosstalk of 30 MEG sensors alone. The largest reductions in crosstalk (a decrease of >50% in crosstalk) are seen when going from 0 to 30 EEG sensors in addition to any number of MEG sensors. The next largest decreases in crosstalk occur with the addition of 30 MEG sensors (magnetometers or radial gradiometers) to any number of EEG sensors. Once both EEG and MEG sensors are included, there are only small decreases in crosstalk. This last result suggests an important experimental consideration. Increasing MEG sensors does not increase the setup time for the experiment, whereas the placement of numerous EEG sensors can be extremely time consuming. Significant gains in localization accuracy can be achieved simply by placing a small number of EEG channels to be recorded simultaneously with a large number of MEG channels. Clearly a combined EEG/MEG approach is superior to using either technique independently, regardless of whether fMRI information is included.

Our results compared the average crosstalk to the average PSF over all locations. Using the standard linear estimation inverse operator, the crosstalk map and the PSF are equivalent (i.e., the resolution matrix is symmetric). This equivalence will not necessarily be true when using other inverse operators. In fact, the crosstalk map and PSF reflect two different aspects of localization accuracy. The crosstalk metric for a specified location on the cortex describes the amount of activity incorrectly localized onto that location from other locations, whereas the point spread metric provides the complementary measure: for that same location, the point spread describes the mis‐localization of activity from that specified location to other locations in the brain. If the crosstalk map for a location showed only a single point at that same location, i.e., a delta function, the estimate at that location would completely reflect activity at that location. Conversely, if the PSF for a given location was a single point at that same location, a point source would be spatially localized as a point source.

Typically, neither the crosstalk map nor the PSF would be a map with only a single point. Importantly, the spatial extent of these two maps can be used to determine the confidence of the estimates. If there are other active areas that overlap with the crosstalk map for a given location, the activity at that location is affected by those other areas. In that situation, the estimate for that location will not only reflect activity from that location, but will represent a weighted sum of all the activity within the region defined by the crosstalk map. If, on the other hand, there are no other active areas within a crosstalk map, one can be confident that the estimated activity reflects the true activity. The PSF is easier to interpret than the crosstalk map. The PSF for a location defines the spatial extent of activity that would be localized for a point source at that location. Any activity in the region defined by the PSF cannot be separated from activity at the given location.

Although the noise sensitivity normalized inverse has no effect on the crosstalk map, there is significant improvement in the point spread function, especially for deep and radial sources for MEG sensors alone. Therefore, we would expect to have more focal sources with similar temporal accuracy as the unnormalized inverse operator. Note, that there is a disadvantage to using the noise sensitivity normalized inverse operator. Because each location has a different normalization factor, direct amplitude comparisons between the timecourses of different locations cannot be made. One can, however, still make amplitude comparisons for a given location across different task paradigms.

Many empirical experiments are now collecting EEG and MEG data simultaneously. Both types of data are acquired in the hope of producing more accurate source localization estimates. To maximally use this combined information, the scaling factor between the two different types of data must be known. Because the EEG forward solution can be calculated using conductivity ratios instead of actual conductivities, there can be a discrepancy between EEG and MEG with respect to the units of the estimated source strengths. Thus, when combining the two techniques, error is introduced if the EEG/MEG forward solution scaling factor is mis‐estimated. We find that even if the conductivity ratios are known, the actual scaling factor between EEG and MEG needs to be known within a factor of 2. If the scaling factor is mis‐estimated by a factor of 0.2 (or 5), the average crosstalk is over twice as large as when the scaling factor is correctly determined.

Certain caveats apply to these results. First, to specifically evaluate the inverse procedure, we assumed that there were no errors in the EEG and MEG forward solutions. Currently, the MEG forward solution is more accurate than the EEG forward solution, owing to the fact that the MEG forward solution requires only the inner skull surface and does not depend on the conductivities of the various tissue types in the brain [Hamalainen and Sarvas, 1989; Meijs et al., 1987, 1989]. If errors in the head model are included, which is likely to be the case with the currently available head models, the EEG accuracy will worsen relative to the MEG accuracy. It is likely, however, that future work will greatly increase the accuracy of the EEG head model, making this first caveat less relevant. Second, we also assumed equal signal‐to‐noise ratios for all sensor configurations. In cases where the SNR differs (such as magnetometers versus radial gradiometers), localization using the configuration with the best SNR will result in greater accuracy than is shown here. Finally, for the randomly placed sources, we did not restrict the source orientations (i.e., radial and tangential sources were equally probably in the Monte Carlo simulations). As discussed above, since MEG poorly localizes radial versus tangential sources, some of the predicted superiority of EEG is due to this orientation dependence of MEG.

Recently, other simulations examining the combination of EEG and MEG measurements were presented [Fuchs et al., 1998]. Fuchs et al. [1998] used a single equivalent current dipole (ECD) inverse approach to localize test dipoles in a spherical three‐shell head model. Because these authors used a different forward model, inverse method and source model, our results are not directly comparable. Similar results, however, were obtained with respect to two findings: 1) increasing sensor number decreases localization errors and 2) a combination of EEG and MEG is better than either modality alone.

Overall, these results demonstrate that both EEG and MEG are useful technologies for the localization of brain activity. The lowest crosstalk was achieved by combining EEG and MEG data, providing motivation for further development of both methodologies. A large reduction in the PSF (i.e., increase in spatial accuracy) was provided by using the noise sensitivity normalized inverse operator. More accurate head models will improve localization accuracy, but will not eliminate the need for the acquisition of simultaneous EEG and MEG information.

INVERSE OPERATOR DERIVATIONS

The linear inverse operator that we use here can be derived in various ways. We detail four different derivations: 1) minimization of expected error [Dale and Sereno, 1993], 2) Bayesian formulation [Gelb, 1974; Phillips et al., 1997a,b], 3) Tichonov regularization [Tichonov and Arsenin, 1977], and 4) generalized Wiener filtering [Deutsch, 1965; Smith, 1992; Sekihara and Scholz, 1995, 1996]. All derivations arrive at equivalent inverse operators, given certain initial conditions.

The minimization of expected error begins with a set of measurements

(21)

where x is the measurement vector, A is the gain matrix, s is the strength of each dipole component, and n is the noise vector. One would like to calculate a linear inverse operator W that minimizes the expected difference between the estimated and the correct source solution. The expected error can be defined as:

(22)

Here we assume that both n and s are normally distributed with zero mean. Using their corresponding covariance matrices C and R, the expected error can be rewritten as:

(23)

(24)

(25)

where M=WA−I

(26)

(27)

where tr(A) is the trace of A and is defined as the sum of the diagonal entries. Re‐expanding the expression gives:

(28)

This expression can be explicitly minimized by taking the derivative with respect to W, setting it to zero and solving for W.

(29)

Solving for W:

(30)

(31)

This yields the expression for the linear inverse operator:

(32)

The Bayesian linear inverse derivation begins with the expression for conditional probability:

(33)

which one would like to maximize. Beginning with a measurement vector x:

(34)

where A is the gain matrix, s is the strength of each dipole component, and n is the noise vector. Assuming both nand s are normally distributed with zero mean and covariance matrices C and R, respectively, one can rewrite P(x|s) and P(s):

(35)

(36)

This gives a simplified Bayesian expression:

(37)

(38)

(39)

(40)

Taking the derivative with respect to s and setting it to zero:

(41)

Solving for s gives:

(42)

which yields the expression for the Bayesian linear operator

(43)

The above Bayesian linear operator is very similar to that derived using Tichonov regularization. Again, one begins with a measurement vector x:

(44)

A smoothing functional F is defined as:

(45)

where λ and M are added for regularization. To calculate the operator, the smoothing functional is explicitly minimized (taking its derivative and setting it to zero). Solving for s:

(46)

(47)

(48)

(49)

This is equivalent to the Bayesian linear operator when C = C ⁻¹ = I and λM ^T M = R ⁻¹. Wiener filtering (also known as the Kalman‐Bucy method) filtering uses an optimal linear filter to minimize the expected error between the actual source (i.e., input) and the estimated source (i.e., noisy output):

(50)

The operator must satisfy the Wiener‐Hopf equation:

(51)

where Ψ_sx = 〈sx ^T〉 and Ψ_x = 〈xx ^T〉. Expanding the covariance terms gives:

(52)

(53)

Because the signal and noise are independent, the signal‐noise covariance terms (e.g., 〈sn ^T〉) equal zero, leaving:

(54)

Again, because the signal and noise are independent, we can separate the terms on the right side:

(55)

(56)

Thus, the inverse operator is:

(57)

These particular inverse derivations are very general and allow us to express many different kinds of inverse methods. For example, arbitrary basis functions can be used in the inverse approach by constructing R such that

(58)

where U is an orthonormal set of basis vectors. Replacing R in equation (57) yields:

(59)

(60)

(61)

The new inverse operator using the arbitrary basis functions is simply the original forward solution projected onto the new basis functions. As another example, the low resolution electromagnetic tomography (LORETA) inverse method [Lantz et al., 1997; Pascual‐Marqui et al., 1994], which imposes a smoothness constraint on the inverse solution, can also be expressed in this framework. LORETA specifies R ⁻¹, instead of R:

(62)

where, V is a diagonal matrix with each diagonal element equal to the norm of the corresponding lead field vector and B is the discrete Laplacian operator.

Finally, it is possible to show that these various linear operators are equivalent (assuming that both (ARA ^T + C) and (A ^T C ⁻¹ A + R ⁻¹) are invertible).

(63)

(64)

(65)

(66)

Although these two expressions are equivalent, it is computationally more efficient to use the first expression (based on the minimization of expected error) since it only requires the inversion of a matrix that is square in the number of sensors, compared to square in the number of dipoles. Typically, the number of sensors is on the order of 200, whereas the number of dipoles can easily be in the thousands.