Imaging the electrical activity of the brain: ELECTRA

Abstract

The construction of a tomography of neuronal sources is limited by a lack of information. A possible way around this problem is to change the biophysical model that underlies the statement of the inverse problem, i.e., searching for magnitudes that can be better determined from the available data. In this report, we describe a mathematical characterization of the type of currents that are actually able to produce the scalp‐recorded EEG. Considering this characterization, we reformulate the bioelectric inverse problem. This approach, called ELECTRA, yields some advantages over the classical formulation in terms of the current density vector: (1) the number of unknowns can be reduced, which is equivalent to increasing the number of independent measurements, (2) the constraints used to reformulate the problem are undeniable since they do not imply any hypothesis about brain function but are instead based on the character of the measurements, and (3) existing experimental evidence suggests that the proposed source model characterizes the type of currents that arise in excitable tissues. We conclude that if the latter fact proves to be true for brain tissues, then no additional information is added to the inverse problem by using a more general source model than the one proposed here. Images obtained using this method for synthetic data, as well as early and middle components of human visual evoked responses to checkerboard stimuli, are presented to illustrate the characteristics of the reconstructed maps and their interpretation. Hum. Brain Mapping 9:1–12, 2000. © 2000 Wiley‐Liss, Inc.

INTRODUCTION

The construction of a 3D tomography of the brain electromagnetic activity leads to an inverse problem with a nonunique solution. In its standard formulation, the main goal of the inverse problem is to determine the primary current distribution within the brain on the basis of a discrete set of electric and/or magnetic data recorded from the surface [Sarvas, 1987]. Since different current distributions lead to the same data on the scalp surface [Hämäläinen et al., 1993], additional constraints have to be incorporated to insure a unique solution. Although many different constraints have been proposed and evaluated to solve this problem [see George et al., 1996 Grave de Peralta Menendez and Gonzalez Andino, 1999 for review], there is no evidence so far that the reconstructions obtained are reliable enough to be interpreted as a tomography of the neuronal sources.

For linear inverse solutions, theoretical and computer simulation studies [Grave de Peralta Menendez and Gonzalez Andino, 1999; Grave de Peralta Menendez and Gonzalez Andino, 1998] suggest that the reconstructions obtained are generally blurred, corrupted by spurious sources, and that they might miss some of the deeper active sources, especially in the presence of simultaneous cortical activity. Most of these problems are due to the incorrect estimation of the source amplitudes, an effect that has also been reported for nonlinear solutions [Ioannides, 1994]. Many of these limitations can be predicted from the analysis of the continuous inverse problem, which does not have a unique solution even in the case of infinite measurements. The discrete and generally small number of measurements available in practice is a serious additional shortcoming when comparing this inverse problem with some of those that appear associated to alternative techniques of brain imaging (e.g., PET, fMRI).

Simply put, a unique construction of a 3D tomography of the neuronal generators is impossible due to a lack of information. Electric or magnetic data (or even a combination of them) are insufficient to reconstruct arbitrary current distributions within the brain. Possible alternatives to alleviate this situation are: (1) increase the information content of the measurements, (2) introduce additional plausible constraints about the nature of the generators of the activity, or (3) reformulate the inverse problem in terms of neurophysiologically meaningful quantities, which can be better determined from the available data.

In this report, we prove that by using a mathematical characterization of the type of currents that are able to produce the scalp‐recorded EEG, it is possible to reformulate the inverse problem in more restrictive terms. This approach, called ELECTRA (electrical analysis), can be applied only to electrical recordings. ELECTRA is based on the fact that independent of the volume conductor model used to describe the head, solenoidal currents do not contribute to the EEG, and thus electric measurements are entirely determined by irrotational currents. Furthermore, available experimental evidence in excitable tissues shows that irrotational currents are several orders of magnitude higher than solenoidal currents [Plonsey, 1982]. Therefore, we propose to constraint the source model used in the inverse problem statement to the irrotational currents. Starting from basic Maxwell equations, we prove that by constraining the currents to be irrotational, three equivalent alternative formulations of the problem can be stated, based on the estimation of: (1) potential distribution, (2) current source density, or (3) an irrotational current density vector. It is shown that this approach bears several advantages over the classical formulation in terms of the current density.

In a theoretical section, we briefly describe the biophysical basis of the bioelectric inverse problem, and a decomposition is used to prove that only irrotational currents are capable of producing electric measurements. Afterward, the three equivalent formulations are introduced. Synthetic data are used to evaluate the possibilities of ELECTRA to recover both the instantaneous potential maps and the potential waveshapes for the case of simultaneously active sources. The results of applying ELECTRA to the analysis of earlier and middle components of visual evoked responses to checkerboard stimuli are presented. The plausible neurophysiological interpretation of the reconstructed maps is then discussed. The last section considers general aspects of this approach and some future trends.

BASIC THEORY

The frequency content of electrophysiological signals as well as the conductivity parameters of physiological media, let us assume that all fields of biological origin are quasi static [Plonsey, 1982]. This allows us to establish the relationship between the primary current J_p and the measured voltages V throughout the Poisson equation, i.e., 1

(1)

where σ stands for the conductivity of the media. The solution of this differential equation always can be expressed in terms of the Green function ψ [Roach, 1970] (also called scalar lead field in electrocardiography) [Pilkington, 1989] as: 2

(2)

where 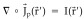is a volume source density function usually referred as the current source density (CSD) [Mitzdorf and Singer, 1977]. The Green function contains information about the geometrical and electrical properties of the media and the boundary conditions. Since the primary current distribution is bounded to the brain, equation (2) can be rewritten using Green identities as [Pilkington, 1989]: 3

(3)

4

(4)

is the vector lead field or lead field [Pilkington, 1989]. Equation (3) is the basis for the present formulation of the inverse problem in terms of distributed source models [Hämäläinen and Ilmoniemi, 1984]. This formulation allows a similar analysis of the EEG and MEG in terms of common sources 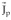, but it does not explicitly take into account, as in (2), that measured potentials receive no contribution from solenoidal currents. To further illustrate this last point, let us recall that any vector field can be decomposed into an irrotational part 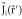, a solenoidal part 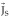, and a current that is the gradient of a harmonic function 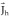. Thus the primary current density can be decomposed into: 5

(5)

6

(6)

The symbol zero (0) stands for the corresponding neutro for the addition of functions. Substitution of (5) into (2) leads to:

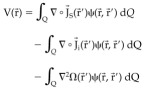Due to (6) only the second integral contributes to the measured potentials. Thus the scalp‐recorded EEG receives contribution only from the divergence of the irrotational component of the primary current distribution. In other words, it means that the EEG generators fulfill: 7

(7)

where φ is proportional to the potential distribution within the brain. Now, combining (3), (4), and (7), we can express the basic biophysical relationship between the plausible generators and the measurements as: 8

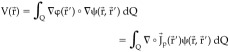(8)

Equation (8) can be equivalently solved for three different physical magnitudes all consistent with the assumed source model (irrotational currents): (1) the estimation of an irrotational current density vector 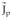= ∇φ with the vector lead field ∇ψ, (2) the estimation of a scalar field, the current source density (CSD), ∇ °  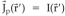with the scalar lead field ψ, (3) the estimation of a scalar field, the potential distribution φ in Q with a transformed scalar lead field .

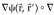To consider in more detail the third alternative, let us define the linear operator ℛ as: 9

(9)

Then, (8) can be written as: 10

(10)

Although the formulations given in (8)–(10) are more restrictive than that in (2), the solution is still nonunique. Thus additional constraints have to be incorporated. In our particular case we use as regularization a term based on a heuristically designed homogenizer operator described in Grave de Peralta Menendez and Gonzalez Andino [1999], which establishes the dependency between the function values at a point and its neighbors. In contrast to differential or interpolator operators that apply the same rule for all the points of the solution space, this solution method controls the type of relationship that should exist for each particular region. This flexible approach allows the construction of solutions that are more or less sensitive in some predetermined regions. Note, however, that any numerical method can be applied to the solution of (8)–(10). ELECTRA denotes the use of a restricted source model in the inverse problem formulation and not a particular numerical method for solving underdetermined systems.

EVALUATION OF ELECTRA: GENERAL AND PARTICULAR COMMENTS

The evaluation of the basic merits and limitations of distributed solutions is far from a trivial problem. Because distributed solutions are designed to deal with simultaneously active generators, their properties cannot be evaluated on the basis of simulations assuming single sources. Each linear inverse is optimal for a given type of sources, namely, those that can be expressed as a linear combination of the columns of the inverse matrix, and these are the sources that can be perfectly retrieved. Moreover, even if the inverse map obtained for a single generator appears correct in terms of the position of the maximum, the typical underestimation of the source strength renders the retrieval of simultaneously active sources difficult, especially if they have different eccentricities. As a general rule, conclusions about the possibilities of a linear inverse based on the recovery of single sources mask the basic limitations of the solution for the case of multiple sources.

To simplify the evaluation of a distributed solution, the task can be separated into two parts: (1) the appraisal of the neurophysiological validity of the selected source model and/or the constraints incorporated to the solution, and (2) the evaluation of the capabilities of the numerical method used to solve the underdetermined linear system to retrieve sources of the selected type all over the solution space. Aspect (1) can be evaluated only on the basis of experimental data or incontrovertible large‐scale physical evidences. Aspect (2) requires either simulations that consider simultaneously active sources or more general evaluation methods based on the properties of the model resolution matrix [Grave de Peralta et al., 1996, 1997a].

So far, all distributed linear inverse solutions considered an identical source model, that of a current density vector at each solution point. It means that up to now, distributed solutions basically differ on the a priori information they incorporated to solve aspect (2), i.e., minimum norm, weighted minimum norm, resolution optimization, etc. Theoretically to evaluate the differences between these solutions, it was sufficient to compare them on the basis of their model resolution matrix. This is no longer the case with ELECTRA, which proposes a more restricted source model than the one considered so far in the sense of excluding the existence of irrotational currents. Although further experiments are required to evaluate if such sources describe all source configurations that can arise in the human brain, there is no doubt that potential gradients exist and describe most of our reliable experimental knowledge about the generators in animals and humans. Current dipoles are, strictly speaking, a physical source model. Such a model might well represent some experimental situations while failing in others [Alarcon et al., 1994].

Not even a comparison of ELECTRA with the other classical distributed solutions in terms of the resolution kernels is straightforward. The dimensions of the resolution matrix for the classical solutions triplicates that of ELECTRA's resolution matrix. We also have to be aware that ELECTRA, as a linear inverse solution to an underdetermined problem, cannot get rid of the basic limitations of these methods. This is why instead of comparing this solution with the ones previously proposed, we prefer to evaluate with simulations if ELECTRA is capable of adequately retrieving both, the position of simultaneously active sources and the potential waveshapes in depth. The latter aspect, often ignored in the discussion of distributed solutions, have for us two appealing elements: (1) the high temporal resolution of bioelectromagnetic recording techniques is inherited by a linear inverse and is not attainable by any other brain mapping method of higher spatial resolution, (2) even if the instantaneous recuperation of simultaneously active sources could not be possible due to the well‐described limitations of linear solutions, a separation of simultaneously active brain areas might still be possible in terms of their waveshapes. Thus the evaluation of the possibilities of ELECTRA to provide an adequate combined reconstruction of the spatio temporal features of the generators is the point to which we address the simulations that follow.

RETRIEVAL OF POTENTIAL WAVESHAPES WITH ELECTRA: SYNTHETIC DATA

We carried out a set of simulations in which two time courses that differ in terms of their frequency content and time of maximal amplitude were assumed to represent the intracranial potential of two randomly selected points of the solution space. The time courses (see insets in Figs 1, 2, 3) insure that both sources are simultaneously active during a large part of the time analysis window. A four‐layer spherical model was selected to construct the lead field matrix using radius and conductivities as described in Stok [1986]. The solution space consisted of 1,152 nodes covering the upper half of the innermost sphere. Measurement points were assumed to be distributed in the upper part of the external sphere in a configuration typically used in our lab for the study of the visual system [Pegna et al., 1997].

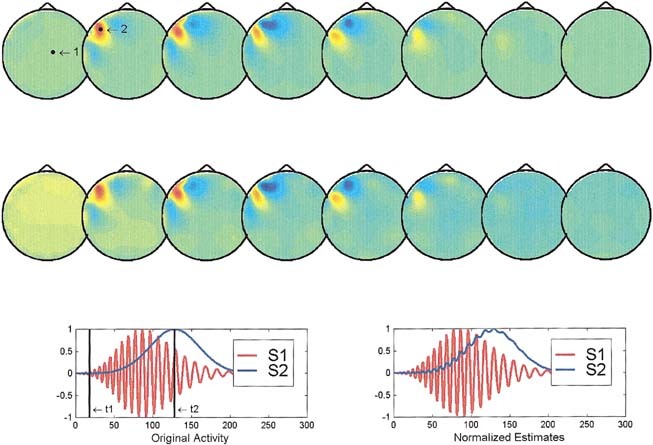
Figure 1.

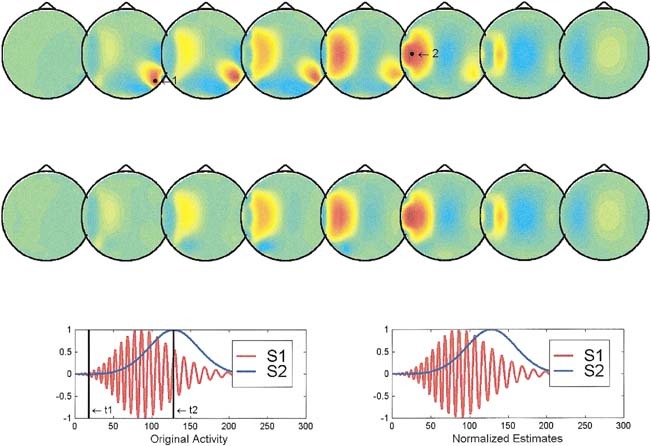
Reconstruction of the instantaneous maps and waveshapes provided by ELECTRA for two cortical sources. In this figure (and Figs 2, 3), the solution space is divided into eight axial slices with z values ranging from zero to 7. The insets at the third line show the theoretical (left) and estimated (right) waveshapes used in this simulation for the sources 1 (red) and 2 (blue). The actual source positions are marked in the top reconstructed map by black dots. The black vertical lines in the insets mark the time instants t1 and t2, at which the potential distribution is reconstructed. Top reconstruction corresponds to t1 and second reconstruction (middle line) to t2. The waveshapes estimated by ELECTRA are given for the actual positions of both sources. Original and estimated waveshapes are scaled by their maximum value to have unitary amplitude.

Figure 2.

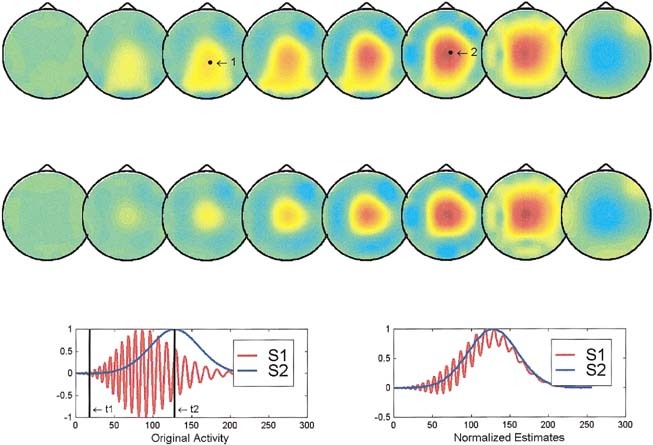
Simulated and reconstructed instantaneous maps and waveshapes provided by ELECTRA for two deep sources. Same organization as Figure 1.

Figure 3.

Reconstruction of the instantaneous maps and waveshapes provided by ELECTRA for one superficial and one deep source. Same organization as Figure 1.

Two aspects were evaluated over the set of simulations: (1) the capability of the method to determine correctly the position of each of the two sources at the times of maximum activation, and (2) the differences between the estimated waveshapes and the original ones. Note that the sources used in the simulations do not attempt to describe typically used source models (e.g. dipoles or monopoles) but instead waveshapes as the ones we can record in depth with intracranial electrodes and which is precisely the goal of this implementation of ELECTRA.

Figures 1, 2, 3 illustrate interesting typical situations found in the simulations corresponding to: (1) two simultaneously active cortical sources, (2) two simultaneously active deep sources, and (3) a cortical and a deep source. The waveshapes are scaled by their maximum value to have unitary amplitude in order to compensate by the underestimation of the source strength known to affect the reconstruction.

In the case of two cortical sources (Fig. 1), both the instantaneous reconstruction and the estimated waveshapes are satisfactory except for an amplitude factor. The instantaneous reconstructed maps at times t1 (upper reconstruction) and t2 (lower reconstruction) show approximately the same position as the actual sources (black dots in the upper reconstructed maps). The estimated (right inset) and theoretical waveshapes (left inset at the bottom) are indistinguishable one from the other. From our simulation results, we can conclude that in similar situations the inverse can provide reliable information about the spatial and temporal properties of the sources at least for nonnoisy data. As shown in Figure 2, the situation is somewhat worse if both sources are deep. The instantaneous reconstructed potential map shows no clear distinction between both sources, but a similar quite blurred central maximum from which nearly no inferences can be extracted unless some a priori information is available. The temporal courses, although slightly more entangled than in the previous case, suggest a clearer separation of the two sources than that evident from the instantaneous maps. This situation illustrates cases where a combined spatio‐temporal analysis of the inverse might be beneficial to circumvent the limitations of the methods. The last situation shown in Figure 3, that of a superficial and a deep source, clearly shows that the instantaneous reconstruction is unable to detect the deeper source and exhibits maxima, at both time frames, only for the most superficial location. In spite of that, the recovery of the waveshape is not worse than in the previous case, which suggests that a spatio temporal or spatio frequency based analysis might still allow us to differentiate both areas.

ANALYZING VISUAL EVOKED RESPONSES WITH ELECTRA

In the experimental protocol, 41 channel‐evoked potentials (EP) were recorded in 25 healthy subjects. Checkerboard reversal stimuli (500 ms) were presented to the left, the center, or the right visual field. The mean average response over subjects was computed and the two first maxima of the global field power [Lehmann, 1987] were selected for each condition. The volume conductor model, i.e., lead field and solution space, is identical to the one considered in the simulations. The lowest slice of the solution space is approximately on the level of the plane formed by electrodes T3, T4, and Fpz.

Figure 4 shows reconstructed 3‐D potential maps for the right and central visual field stimulation for the early peak and a middle latency peak. Left visual field stimulation is omitted because it is (except for a mirrored reflection) identical to the right stimulation. Consistent with the basic anatomical, electrophysiological, and clinical evidence [for reviews see, e.g., Regan, 1989; Lehmann et al., 1980], the lateralized stimuli (right and left) led to activation of the occipital areas contralateral to the stimulated field, whereas full‐field stimulation induced symmetrical activation of the occipital areas of both hemispheres. This was found for the early as well as the middle latency response. However, in contrast to equivalent dipole reconstruction [Seki et al., 1996], or to estimations of the norm of the current density [Grave de Peralta et al., 1997b], the ELECTRA solution of the 3D potential distribution leads to several new findings: (1) several different areas seem to be activated simultaneously with either positive or negative potential; one might speculate that these multiple active areas within striate and extrastriate areas correspond to the repeatedly described parallel processing within the complex functional network of the visual cortex [e.g. Van Essen et al., 1992]; (2) areas clearly outside of the striate cortex are activated already at 70 msec poststimulus, and recent findings of the speed of simple as well as complex stimulus recognition support this result [ffytche et al., 1995; Seeck et al., 1997]; and (3) the full‐field VEP response is not the algebraic sum of the two half‐field responses as proposed in earlier VEP waveform studies [Blumhardt and Halliday, 1979]. This might suggest that complex interhemispheric activation and inhibition might be present not only in later [Regard et al., 1994], but also in early steps of information processing. Even though these new findings might be supported by several recent studies on neural networks and parallel processing, the interpretation of the display of potential distributions with positive and negative values still deserves further studies.

Figure 4.

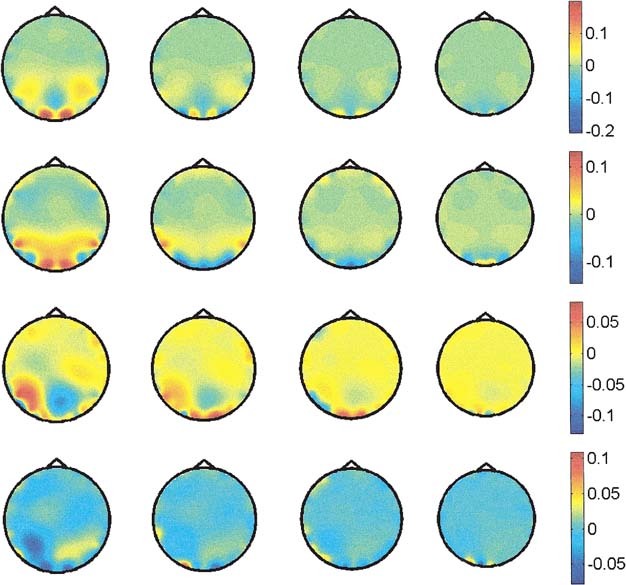
Potential distribution in depth obtained using ELECTRA for central (CVF) and right (RVF) visual field stimulation. First row shows the early response for CVF at 72 msec after stimuli onset, and second row at 92 msec. Third and fourth rows show the early response (75 msec) and middle latency response (109 msec) for RVF. Only the four lowest slices are shown because no significant activity is observed in the upper ones.

Figure 5 shows the estimated intracranial waveshapes for the case of central visual field stimulation at some selected knots. At the top of the figure, the waveshapes at some frontal knots are shown, which clearly contrast in terms of their amplitude with the occipital knots shown at the bottom. Insets to the left show the approximate location of these knots, which presumably belong to primary visual areas. Note that we selected frontal and occipital knots of similar eccentricity in order to avoid differences due to incorrect estimation of the source strength. The first evident fact in this figure is that occipital knots clearly exhibit waveshapes that resemble typical event‐related potential recordings, whereas frontal knots show no clear response. A second remarkable fact is the existence of waveshapes that differ in their morphology at adjacent brain knots, suggesting that the spatial resolution attainable by the inverse at these eccentric nodes is at the order of the discretization grid. A last but not least important fact is the clear polarity inversion observed between the two last adjacent knots at the middle line.

Figure 5.

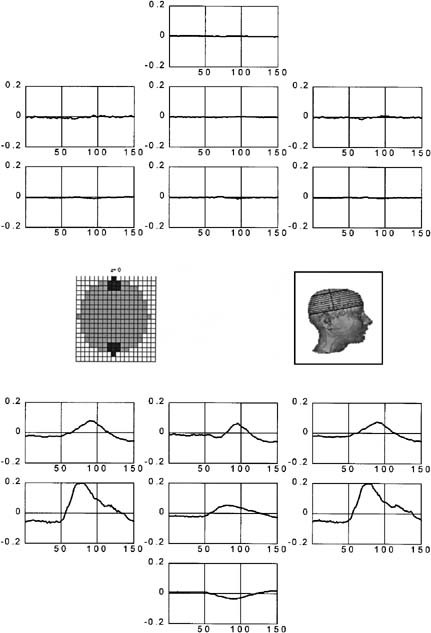
Waveshapes in depth estimated by ELECTRA for central visual field stimulation. The estimates are shown at the knots represented at the left inset, which corresponds to the lowest slice in the reconstruction space. Posterior knots depicted at the bottom presumably belong to primary visual areas, whereas frontal knots are shown for comparison purposes.

INTERPRETING RECONSTRUCTED MAPS

Intracranial recordings of the electric potentials have been used for a long time either for clinical or research purposes [Niedermeyer, 1992, refs therein; Seeck et al., 1995]. Nonetheless, due to the impossibility of covering the whole brain with intracranial electrodes, a whole 3D instantaneous reconstruction of the potential distribution inside the human brain such as the one aimed by ELECTRA has never been available. This might lead to some confusion, especially when one tries to interpret the somehow complex distributions of positivities and negativities that appear in the instantaneous maps obtained for the evoked responses. Most of the confusion probably arises from the impossibility to associate uniquely each positivity to a respective negativity without observing the waveshapes at each knot. Also in the analysis of distributed inverse solution, we are accustomed to looking at maps of the current density displayed in terms of the modulus of the currents. The maxima of these maps are generally interpreted as the generators of the measured activity. However, in physical terms a generator of the activity is defined as a place where there is a source or a sink of current, and this does not necessarily coincide with the maxima of the modulus of the estimated current density vector. A more adequate map of the electrical generators of the activity is given by the current source density (CSD) that might be directly reconstructed from equation (2) or (8). Due to numerical reasons, we do not encourage the estimation of the CSD from the estimated potentials. Sites of high spatial 3D variation of the potential in the reconstructed maps are candidates for being generators. Nonetheless, visual estimation of the sites of maximal 3D variation is not easy, and one has to take into account polarity as well as intensity of the maps.

To interpret the reconstruction provided by ELECTRA, we recommend inspecting both the instantaneous reconstructed maps and the estimated waveshapes. In strict resemblance with intracranial recordings, source strength as well as polarity inversions between electrode points should be taken into account in any analysis. As suggested by the synthetic data, a combined spatio temporal analysis of the results seems to be the better option to arrive at reasonable conclusions about the processes under study. We believe that since polarity information is of relevance for the interpretation of depth recordings, reconstruction algorithms that give this information seem to be of advantage. This might allow the differentiation of cortical activity induced by synaptic connections at deep vs. superficial layers, since those differ in terms of polarity [Martin, 1991]. However, for that, it is necessary for the spatial resolution of the reconstruction to allow a clear differentiation of the polarity associated with the innermost and outermost layers of the cortical surface. Even though a thorough analysis of the resolution is required, the preliminary results described here for experimental human data suggest that at least for the outermost cortical layers, it is possible to detect polarity inversions between adjacent knots. In any case, using these types of studies capably requires additional work, especially with regards to matching functional information with anatomical data through the use of realistically shaped brain models.

DISCUSSION

In the first section we showed that electric measurements convey no information about the solenoidal part of the currents. On this basis we reformulate the inverse problem in terms of scalar or vector quantities, and one of these equivalent alternatives, the estimation of the potential in depth, was applied to the analysis of experimental data. It must be emphasized that a different physical magnitude is obtained with each of the proposed alternatives, i.e. (1) an irrotational current density vector, (2) the current source density, or (3) the potential distribution. Although from equations (8)–(10), follow that these three magnitudes are not mathematically independent, different neurophysiological information can be extracted from each of these maps, an aspect we are currently studying. Note also that direct experimental validation of ELECTRA is possible using simultaneous depth and surface recordings since the estimated potential patterns are directly linked to the intracranial recordings.

A remarkable property when applying this approach to the analysis of experimental data is the higher level of spatial detail in the reconstruction when compared with the analysis of the same data using the more classical formulation in terms of the modulus of the current density vector. In this approach, a differentiation of sources at different eccentricities seems possible. The explanation for this enhanced spatial resolution lies in the fact that any attempt to localize the solenoidal (invisible) currents relies exclusively on the use of a priori information. However, this information is already insufficient to determine completely the irrotational (measurable) part. The restrictive source model of ELECTRA excludes from the feasible solution set all currents that are not irrotational and thus leads to a better determined inverse problem. In addition, a reduction of the number of unknowns in the discrete inverse problem (from a vector to a scalar field) is possible, which implies faster computations as well as a less underdetermined algebraic linear system. As an additional advantage, the statement of the problem in terms of a scalar magnitude facilitates the inclusion of additional a priori information from other complementary brain images.

In contrast to the downward continuation methods used, e.g., in Gevins et al. [1995] and Babiloni et al. [1997], the potential reconstruction provided by ELECTRA is fully 3D and is not confined to the outermost surface of the cortex. The downward continuation method possesses, in contrast, a unique solution that is not the case for ELECTRA.

From the discussion presented here, one might conclude that electroencephalography is of limited use since it provides information exclusively about the irrotational part of the current distribution even if both irrotational and solenoidal currents might, in principle, arise in excitable tissues. If so, the only way to retrieve information about the solenoidal part would be the inclusion of some specific a priori information about this nonmeasurable part, or the use of magnetic measurements. However, it has been shown by comparison of the relative field strength from both primary and secondary microscopic sources in axonal and cardiac tissue that only the latter are significant [Plonsey, 1982]. Now, since the microscopic secondary and primary sources together constitute the primary macroscopic currents, the validity of Plonsey's result for brain tissue implies that both macroscopic primary and secondary sources are ohmic. As ohmic currents, they can be expressed as the gradient of the electrical potential, i.e., they are irrotational currents. This reasoning leads to the conclusion that if microscopic secondary sources are the significant ones also for tissues in the brain, then the approach used in ELECTRA is not only concordant with the character of the measurements, but is also a completely adequate neurophysiological characterization of the currents arising within the human brain. Furthermore, as suggested in Plonsey [1982], measurements of the external bioelectric field completely determine the external biomagnetic field. If correct, then no substantial information about brain activity generators is added by using magnetic measurements, or a more complex source model than the one proposed in ELECTRA. Nevertheless, further experimental research in this direction is needed.

CONCLUSIONS

We have used a decomposition of the currents to restrict the bioelectric inverse problem to the search of measurable sources (irrotational currents). It was shown that using irrotational currents as the source model allows the estimation of scalar fields instead of vector fields, which is equivalent to increasing the amount of independent measurements. A plausible interpretation of the obtained reconstruction was given using as illustration the results obtained with ELECTRA in both synthetic data and visual‐evoked responses. As particular advantages of the described method (ELECTRA) over the more classical solution in terms of the estimation of the current density vector, we showed that: (1) the amount of computational effort can be reduced, (2) the problem can be stated in terms of a magnitude that is experimentally measurable and thus the solutions can be evaluated theoretically and experimentally, (3) the reconstructed maps show more spatial details, differentiating active regions at different depths, and (4) the constraints used to reformulate the problem are of undeniable value since they do not imply any hypothesis about brain functioning, but are instead based on the character of the measurements and available experimental evidence [Plonsey, 1982].